竞赛物理中的数学方法
物理竞赛所有公式(完整资料).doc

此文档下载后即可编辑第一章 质点运动学和牛顿运动定律1.1平均速度 v =t△△r1.2 瞬时速度 v=lim 0△t →△t△r =dt dr1. 3速度v=dt ds==→→lim lim 0△t 0△t △t △r 1.6 平均加速度a =△t△v1.7瞬时加速度(加速度)a=lim△t →△t △v =dtdv1.8瞬时加速度a=dt dv =22dtrd1.11匀速直线运动质点坐标x=x 0+vt1.12变速运动速度 v=v 0+at 1.13变速运动质点坐标x=x 0+v 0t+21at 21.14速度随坐标变化公式:v 2-v 02=2a(x-x 0)1.15自由落体运动 1.16竖直上抛运动⎪⎩⎪⎨⎧===gyv at y gt v 22122 ⎪⎪⎩⎪⎪⎨⎧-=-=-=gy v v gt t v y gt v v 221202200 1.17 抛体运动速度分量⎩⎨⎧-==gt a v v av v yx sin cos 001.18抛体运动距离分量⎪⎩⎪⎨⎧-•=•=20021sin cos gt t a v y t a v x1.19射程 X=g av 2sin 201.20射高Y=gav 22sin 201.21飞行时间y=xtga —ggx 21.22轨迹方程y=xtga —av gx 2202cos 21.23向心加速度 a=Rv 21.24圆周运动加速度等于切向加速度与法向加速度矢量和a=a t +a n1.25 加速度数值 a=22n t a a +1.26 法向加速度和匀速圆周运动的向心加速度相同a n =Rv 21.27切向加速度只改变速度的大小a t =dtdv1.28 ωΦR dt d R dt ds v ===1.29角速度 dtφωd =1.30角加速度 22dt dt d d φωα== 1.31角加速度a 与线加速度a n 、a t 间的关系a n =222)(ωωR RR R v ==a t =αωR dtd R dt dv ==牛顿第一定律:任何物体都保持静止或匀速直线运动状态,除非它受到作用力而被迫改变这种状态。
高中物理奥赛常用数学公式

中学物理奥赛常用数学公式一、等差、等比数列1.定义:{}1n n n a a d a +-=⇔是等差数列{}1,(0,0)n n n n a q a q a a +=≠≠⇔是等比数列,, (,)2a b a b a b +±等差中项等比中项同号2.公式(1)通项1(1)()n m a a n d a n m d =+-=+- 11n n m n m a a q a q --==(2)前n 项和 11(1)(1)()222n n n a a n n n n s n na d na d +--==+=+- 1(1)2n s d a n n =+-也是等差数列 111(1)1111n n n a a q a q q qq s na q ⎧--=≠⎪--=⎨⎪=⎩二.数列求和 (1)2222(1)(21)123...6n n n n ++++++=(2) 223332(1)12(12)4n n n n ++++=+++= 三、三角公式1、和差角公式 ()()()sin sin cos cos sin cos cos cos sin sin tan tan tan()1tan tan tan tan tan()(1tan tan )sin cos a b αβαβαβαβαβαβαβαβαβαβαβαβαααϕ±=±±=±±=±=±+=+ 2、倍角公式 万能公式22tan sin 22sin cos 1tan ααααα==+ 2222221tan cos 2cos sin 2cos 112sin 1tan ααααααα-=-=-=-=+23332tan tan 21tan sin 33sin 4sin cos 4cos 3cos ααααααααα=-=-=- 3、半角公式,升降幂公式22221cos 1cos 1cos 1cos sin sin cos tan 222221cos sin 1cos 1cos 21cos 2sin cos 221cos 2cos 1cos 2sin 22ααααααααααααααααααα-+--=±=±=±==++-+==+=-=4、积化和差,和差化积公式sin sin 2sin cos sin sin 2sin cos 2222cos cos 2cos cos cos cos 2sin cos 222211sin cos [sin()sin()]cos cos [cos()cos()]221sin sin [cos()cos()]2αβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβ+--++=-=+-+-+=-=-=++-=++-=-+--(2)正弦定理 2sin sin sin abcR A B C ===(R 是ABC ∆外接圆半径)(3)余弦定理 2222cos c a b ab C =+- 222cos 2a b c C ab +-=(4)11sin ()()()224ABC a abcS ah ab C pr p p a p b p c R ∆=====---其中2a b cp ++=为半周长四、重要不等式1.222(,0)1122a b a bab a b a b++≥≥≥>+2.22233(,,0)11133a b c a b cabc a b c a b c++++≥≥≥>++3.222(,)22a b a b ab ab a b R ++⎛⎫≤≤∈ ⎪⎝⎭3(,,0)3a b c abc a b c ++⎛⎫≤> ⎪⎝⎭五、球1、222R r d =+2、球面距离l R θ=⋅ 2222222cos 22cos R R AB R AB r r r θβ+-==+-(β是径度差) 3、24S R π=球内接长方体 222224l R a b c ==++ 侧棱两两垂直的三棱锥补形⇒长方体⇒球内接长方体4、体积 343V R π= 3S V R R S V '''==球球球球多面体内切球半径 : 3V r S =全 六、二项式定理(1)011()n n n n n n n n a b C a C a b C b -+=+++(2)22(1)11n nx nx nx c x +≈+≈++ 七、导数1.()()()00000x x f x x f x y f x lim lim x x∆→∆→+∆-∆'==∆∆ ()()00f x x f x x x ⇔==在处可导,注意:在处不可导二、运算法则:()()()()()()()21234x u U V U V UV U V UV U U V UV y y u x V V ''''''±=±=+'''-⎛⎫'''== ⎪⎝⎭ 三、导数公式(1)0C '= (2)()1n n x nx -'=(3)()x x e e '= (4)()x x a a ln a '=(5)1(ln x )x '= (6)11(log )log ln a a x e x x a'== (7)(sin )cos x x '= (8)(cos )sin x x '=-8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足不L,则AH=2OL中考不须要,竞赛中很明显的结论9、三角形的外心,垂心,重心在同一条直线上。
物理竞赛极值问题解法例谈

物理竞赛极值问题解法例谈极值问题,是物理竞赛中较为常见的一类问题。
解答这类问题,除了用到相关的物理知识,一般都要借助一定的数学知识才能完成。
现将初中物理竞赛中,常见的几类极值问题的解答方法,举例介绍如下。
一.利用“三角形两边之和大于第三边”求解例1.某中学举办了一次别开生面的“物理体育比赛”。
比赛中有个项目:运动员从如图1(a)所示的A点起跑,到MN槽线上抱起一个实心球,然后跑到B点。
比赛时,谁用的时间最少谁胜。
试问运动员比赛时,应沿着什么路线跑最好?图1(a)图1(b)析与解:假设某运动员在槽线上抱起一个实心球所用的时间、运动员跑步的速度是一定的,那么,他跑过的路程如果最短,则他所用的时间最少。
因此,本题实际上是一道路程极值问题。
如图1(b)所示,作B关于槽线MN的对称点B′,图中、、等,都是可能的路线。
显然,、路线,分别与、、等长,而由“三角形两边之和大于第三边”的结论可知,图中的(直线段)最短,即路线最短。
故,运动员比赛时,应沿着路线跑最好。
二.利用“正弦函数sinθ的最大值为1”求解例2.如图2(a)所示,某人站在离平直公路垂直距离为60m的A处,发现公路上有一汽车,从B处以v0=10m/s的速度沿公路匀速行驶,B与人相距100m。
问此人最少要以多大的速度,沿什么方向奔跑才能与汽车相遇?析与解:设人以速度v,沿与AB成θ角的方向奔跑,如图2(b)所示,并在C处与汽车相遇,所用的时间为t。
则有BC=v0t,AC=vt。
作BE⊥AC,由三角形AOC与三角形BEC相似得:又:,故:BE=AB sinθ,所以:整理得:代入数值计算得:上式中,要使v最小,应使sinθ最大,即sinθ=1,θ=90°时,v最小为v min=6m/s。
故,此人最少要以6m/s的速度,沿与AB成90°的方向向公路奔跑,才能与汽车相遇。
三.利用“”求解例3.如图3所示,一根均匀杠杆,每米长重λ=30N,现以杆的A端为支点,在杆的B端施一竖直向上的力F,在距杆的A端a=0.2m处挂一个重G=300N的重物,要使杠杆在水平位置平衡,求:杠杆为多长时,加在B端的力F有最小值?最小力F是多大?图3析与解:如不考虑杆重,则杠杆越长,力F就越小。
物理比赛中的数学知识
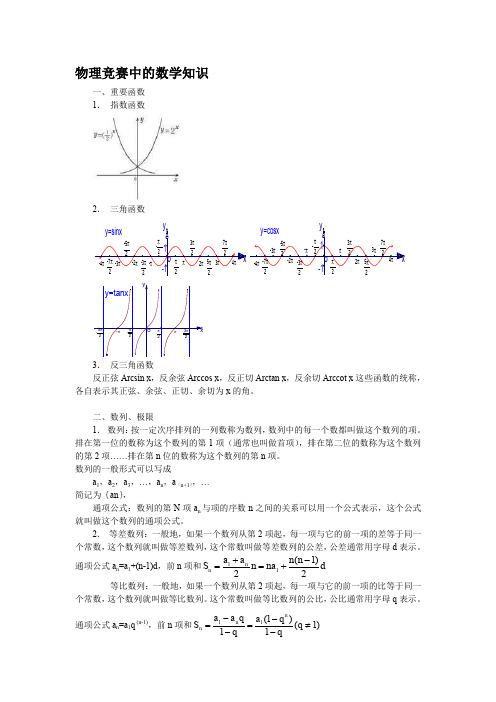
物理竞赛中的数学知识一、重要函数 1. 指数函数2. 三角函数3. 反三角函数反正弦Arcsin x ,反余弦Arccos x ,反正切Arctan x ,反余切Arccot x 这些函数的统称,各自表示其正弦、余弦、正切、余切为x 的角。
二、数列、极限 1. 数列:按一定次序排列的一列数称为数列,数列中的每一个数都叫做这个数列的项。
排在第一位的数称为这个数列的第1项(通常也叫做首项),排在第二位的数称为这个数列的第2项……排在第n 位的数称为这个数列的第n 项。
数列的一般形式可以写成 a 1,a 2,a 3,…,a n ,a (n+1),… 简记为{an },通项公式:数列的第N 项a n 与项的序数n 之间的关系可以用一个公式表示,这个公式就叫做这个数列的通项公式。
2. 等差数列:一般地,如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母d 表示。
通项公式a n =a 1+(n-1)d ,前n 项和11(1)22n n a a n n S n na d +-==+ 等比数列:一般地,如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列。
这个常数叫做等比数列的公比,公比通常用字母q 表示。
通项公式a n =a 1q(n-1),前n 项和11(1)(1)11n n n a a q a q S q q q--==≠--所有项和1(1)1n a S q q=<-3. 求和符号4. 数列的极限:设数列{}n a ,当项数n 无限增大时,若通项n a 无限接近某个常数A ,则称数列{}n a 收敛于A ,或称A 为数列{}n a 的极限,记作A a n n =∞→lim否则称数列{}n a 发散或n n a ∞→lim 不存在.三、函数的极限:在自变量x 的某变化过程中,对应的函数值f (x )无限接近于常数A ,则称常数A 是函数f (x )当自变量x 在该变化过程中的极限。
初中物理竞赛解题方法大全

初中物理竞赛解题方法大全初中物理竞赛是一个对学生物理知识、物理思维和实验操作能力进行综合考察的竞赛项目。
要在竞赛中获得好成绩,除了掌握扎实的物理知识外,还需要具备一些解题方法和技巧。
以下是一些常见的初中物理竞赛解题方法,供参考。
1.熟练掌握基本概念和公式:考生需要牢记物理学科的基本概念和公式,并且能够熟练运用。
在解题过程中,可以通过列式分析、代入计算等方式,将问题转化为已知条件与求解量之间的关系,然后运用相应的公式进行计算。
2.善于利用图表和图像:物理学中常会给出图表和图像,考生应善于利用这些信息。
例如,可以通过直线斜率、图像形状等信息来确定数量关系、规律以及物理实际意义。
3.运用比例关系:物理学中经常涉及到比例关系。
考生可以通过构建适当的比例关系来解题。
例如,可以通过利用物理量之间的比例关系,建立方程来求解问题。
4.运用向量法:对于涉及方向和大小的物理问题,可以运用向量法进行解题。
利用平衡法则、合力法则等,将问题转化为向量运算,并求解。
5.利用能量守恒和动量守恒:能量守恒和动量守恒是物理学中的重要原理。
考生可以根据题目给出的条件,运用这些守恒原理来解题。
例如,可以通过利用动能、势能、机械能以及动量的守恒关系,找到问题的解法。
6.利用几何光学原理:几何光学是物理学中的一个重要分支,考生需要掌握相关的几何光学原理。
例如,可以通过利用光的反射、折射、透镜成像等原理,解决相关的光学问题。
7.运用电路分析法:电路分析是物理学中的一个重要内容。
对于电路相关的问题,考生可以通过利用欧姆定律、基尔霍夫定律等,进行电路分析和计算。
8.运用实验法:物理学是实验科学,实验是物理学中重要的研究方法。
考生可以通过模拟实验、构建实验思维模型等方法,来解决与实验相关的问题。
10.高效备考和练习:参加物理竞赛需要大量的备考和练习。
考生需要选择合适的参考书和题库,进行针对性的备考和练习,熟悉常见的解题方法和技巧。
同时,要不断总结经验,巩固学习成果。
物理竞赛公式大全

2.18 L mvr sin 同上
2.21 M Fd Fr sin F 对参考点的力矩
1.43 胡克定律 F= — kx (k 是比例常数,称为弹簧的劲度 系数 )
1.44 最大静摩擦力 f 最大=μ 0N ( μ 0 静摩擦系数)
2.22 M r F 力矩
2.24 M
dL
作用在质点上的合外力矩等于质点角动
v2
an=
R
(Rω) 2 R
Rω2
a
dv
t=
dω R
Rα
dt dt
牛顿第一定律: 任何物体都保持静止或匀速直线运动 状态,除非它受到作用力而被迫改变这种状态。
牛顿第二定律: 物体受到外力作用时, 所获得的加速 度 a 的大小与外力 F 的大小成正比, 与物体的质量 m成反 比;加速度的方向与外力的方向相同。 1.37 F=ma
牛顿第三定律:若物体 A 以力 F1 作用与物体 B,则同 时物体 B 必以力 F2 作用与物体 A;这两个力的大小相等、 方向相反,而且沿同一直线。
万有引力定律:自然界任何两质点间存在着相互吸 引力, 其大小与两质点质量的乘积成正比, 与两质点间的 距离的二次方成反比;引力的方向沿两质点的连线
1.39
2.33 Mdt dL 冲量距
(m1v10+m2 v20) 左面为系统所受的外力的总动量,第一项为系统的
t
L
2.34 Mdt
dL L L0 I I 0
t0
L0
末动量,二为初动量
2.35 L I 常量
n
2.13 质点系的动量定理:
Fi △t
i1
n
mi vi
i1
n
mi vi 0
物理竞赛解题思路
物理竞赛解题思路物理竞赛是一项考验学生物理知识和解答能力的竞技活动。
为了在物理竞赛中取得好成绩,除了扎实的物理知识储备外,解题思路的灵活运用也是至关重要的。
本文将介绍一些物理竞赛中常用的解题思路,帮助大家在比赛中取得优异成绩。
一、理解题意在开始解题之前,首先要仔细理解题目的要求。
阅读题目时要注意关键词、数据和已知条件。
可以将题目中的关键信息标记出来,有助于后续解题过程中的思路清晰和避免遗漏。
二、分析物理原理理解题目要求后,接下来需要分析题目中涉及的物理原理。
对于给定的物理现象或问题,需要根据所学的物理知识进行合理的分析和推理。
将问题归类到已知的物理原理或概念上,并应用相应的公式、定律或原理进行推导和计算。
三、运用数学工具物理与数学有着紧密的联系,数学工具在解题过程中发挥着重要的作用。
对于一些需要精确计算的问题,需要灵活运用代数、几何和微积分等数学工具进行计算和推导。
同时,注意合理选取坐标系、使用矢量和向量等数学工具,有助于简化问题和提高解题的效率。
四、熟练掌握实验方法物理竞赛中常常会涉及实验和观察类题目,对于这类题目,掌握实验方法是解题的关键。
熟悉各种物理实验的操作步骤和基本原理,善于观察和分析实验现象,并能灵活运用所学的物理知识进行解答。
五、掌握解题技巧在物理竞赛中,掌握一些解题技巧是提高解题能力的有效途径。
例如,对于难题可以先解决一些简单的部分,逐步扩展解决范围;在解决复杂问题时,可以通过化繁为简、分步推导等方法简化问题;对于多个物理概念同时出现的问题,要善于找到彼此之间的关联点等等。
掌握这些解题技巧可以提高解题的效率和准确度。
六、刻苦训练与模拟考试除了上述的解题思路,刻苦训练和模拟考试也是提高物理竞赛成绩的重要途径。
通过大量的练习和模拟考试,能够加深对物理知识的理解和运用,培养解题的敏捷性和灵活性。
通过理解题意、分析物理原理、运用数学工具、熟练掌握实验方法、掌握解题技巧以及刻苦训练与模拟考试等方法,我们可以提高在物理竞赛中解题的能力和水平。
拓展第一讲 物理竞赛中的数学基础
第一讲物理竞赛中的数学基础一、勾股定理勾股定理又叫毕氏定理:在一个直角三角形中,斜边边长的平方等于两条直角边边长平方之和。
据考证,人类对这条定理的认识,少说也超过4000 年!又据记载,现时世上一共有超过300 个对这定理的证明!勾股定理,主要应用是直角三角形中已知两边求第三边。
1、应用勾股定理求最短距离。
我们已经学过平面内两点之间线段最短的道理,也就是说两点之间的所有连线,最短路线是两点之间的线段。
但在立体图形中不同的侧面上两点之间,曲面上的两点之间的最短距离如何解决,我们分两个小问题来讲。
(1)圆柱形物体上的两点的最短路线。
圆柱体是立体图形,两点之间的连线绝大部分是曲线,应该不是最短的,但有人只凭直觉、感觉,认为如图所示的A→B→C的路线最短,是错误的。
解决问题的方法是将圆柱的侧面展开转化为平面图形来解决。
如图,将右上圆柱的侧面沿母线AB展开后是矩形ABB′A′,不难看出,从A到C的最短路线应是矩形ABCD的对角线AC,这时AC是一个直角三角形的斜边,可用勾股定理解决,其中矩形ABB′A′长、宽分别是圆柱的高与底面周长。
(2)长方体(或正方体)面上两点间的距离。
长方体(或正方体)是立体图形,它的每个面都是平面,如果计算同一个面上两点之间的距离,则比较简单。
如果计算不在同一个面上的两点之间的距离,就变成了两个平面之间的问题,必须将它们转化到同一个平面内。
就需把长方体(或正方体)的侧面设法展开成为一个平面,且使计算距离的两个点所在的平面放在一起,这样可利用勾股定理解决问题。
如图,一个正方块,求A点到E点的最短距离,可把AA′D′D与A′B′C′D′展成一个平面,A 与E之间的最短距离就是RtΔADE的斜边AE的长,可根据题目中给出的数据,用勾股定理加以解决。
2、应用勾股定理可测量建筑物高度、河宽等,主要是在测量设计时构造直角三角形,其中两边可测,利用勾股定理求出无法直接测的距离,如测A、B间距离,可在与AB成90°的方向选一点C(可测出AC),同时,CB可直接测得,可用勾股定理算出AB,AB2=BC2-AC2。
高中物理竞赛的数学基础
普通物理的数学基础选自赵凯华老师新概念力学一、微积分初步物理学研究的是物质的运动规律,因此我们经常遇到的物理量大多数是变量,而我们要研究的正是一些变量彼此间的联系。
这样,微积分这个数学工具就成为必要的了。
我们考虑到,读者在学习基础物理课时若能较早地掌握一些微积分的初步知识,对于物理学的一些基本概念和规律的深入理解是很有好处的。
所以我们在这里先简单地介绍一下微积分中最基本的概念和简单的计算方法,在讲述方法上不求严格和完整,而是较多地借助于直观并密切地结合物理课的需要。
至于更系统和更深入地掌握微积分的知识和方法,读者将通过高等数学课程的学习去完成。
§1.函数及其图形本节中的不少内容读者在初等数学及中学物理课中已学过了,现在我们只是把它们联系起来复习一下。
1.1函数自变量和因变量绝对常量和任意常量在数学中函数的功能是这样定义的:有两个互相联系的变量x和y,如果每当变量x取定了某个数值后,按照一定的规律就可以确定y的对应值,我们就称y是x的函数,并记作y=f(x),(A.1)其中x叫做自变量,y叫做因变量,f是一个函数记号,它表示y和x数值的对应关系。
有时把y=f(x)也记作y=y(x)。
如果在同一个问题中遇到几个不同形式的函数,我们也可以用其它字母作为函数记号,如 (x)、ψ(x)等等。
①常见的函数可以用公式来表达,例如e x等等。
在函数的表达式中,除变量外,还往往包含一些不变的量,如上面切问题中出现时数值都是确定不变的,这类常量叫做绝对常量;另一类如a、b、c等,它们的数值需要在具体问题中具体给定,这类常量叫做任意常量。
在数学中经常用拉丁字母中最前面几个(如a、b、c)代表任意常量,最后面几个(x、y、z)代表变量。
当y=f(x)的具体形式给定后,我们就可以确定与自变量的任一特定值x0相对应的函数值f(x0)。
例如:(1)若y=f(x)=3+2x,则当x=-2时y=f(-2)=3+2×(-2)=-1.一般地说,当x=x0时,y=f(x0)=3+2x0.1.2函数的图形在解析几何学和物理学中经常用平面上的曲线来表示两个变量之间的函数关系,这种方法对于我们直观地了解一个函数的特征是很有帮助的。
高中奥林匹克物理竞赛解题方法之十三降维法
例1:如图13—1所示,倾角θ=30°的粗糙斜面上放一物体,物体重为G ,静止在斜面上。
现用与斜面底边平行的力F=G/2推该物体,物体恰好在斜面内做匀速直线运动,则物体与斜面间的动摩擦因数μ等于多少?物体匀速运动的方向如何?解析:物体在重力、推力、斜面给的支持力和摩擦力四个力的作用下做匀速直线运动,所以受力平衡。
但这四个力不在同一平面内,不容易看出它们之间的关系。
我们把这些力分解在两个平面内,就可以将空间问题变为平面问题,使问题得到解决。
将重力沿斜面、垂直于斜面分解。
我们从上面、侧面观察,图13—1—甲、图13—1—乙所示。
如图13—1—甲所示,推力F 与重力沿斜面的分力G 1的合力F ′为:G G F F 22212=+='F ′的方向沿斜面向下与推力成α角,则︒=∴==451tan 1ααFG这就是物体做匀速运动的方向物体受到的滑动摩擦力与F ′平衡,即2/2G F f ='=所以摩擦因数:3630cos 2/2=︒==G G F f N μ例2:如图13—2所示,一个直径为D 的圆柱体,其侧面刻有螺距为h 的光滑的螺旋形凹槽,槽内有一小球,为使小球能自由下落,必须要以多大的加速度来拉缠在圆柱体侧面的绳子?解析:将圆柱体的侧面等距螺旋形凹槽展开成为平面上的斜槽,如图13—2—甲所示,当圆柱体转一周,相当于沿斜槽下降一个螺距h ,当圆柱转n 周时,外侧面上一共移动的水平距离为22122at n D =π① 圆弧槽内小球下降的高度为221gt nh=② 解①、②两式,可得,为使螺旋形槽内小球能自由下落,圆柱体侧面绳子拉动的加速度应为hDgaπ=例3:如图13—3所示,表面光滑的实心圆球B 的半径R=20cm ,质量M=20kg ,悬线长L=30cm 。
正方形物块A 的厚度△h=10cm ,质量m=2kg ,物体A 与墙之间的动摩擦因数μ=0.2,取g=10m/s 2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
. 参考文献
程稼夫, 中学物理竞赛・力学篇, Sep. 15, 2015 张大同, 高中物理竞赛教程
name
Dec. 2 2018
竞赛物理中的数学方法
9/9
n ∑ i=1
i=
n (n + 1) 2
(1)
其中 i 可以理解成是一个变量,只能整数的从 1 变到 n. 常用的一些结论如下: n ∑ n (n + 1) (2n + 1) , i2 = 6 i=1
name Dec. 2 2018
n ∑
n (n + 1) i = 2 i=1
3
[
]2 (2)
3/9
竞赛物理中的数学方法
(4)
(5)
name
Dec. 2 2018源自竞赛物理中的数学方法6/9
提纲 微元法 导数 三角函数 积分 参考文献
. 辅助角公式
( ) √ a b 2 2 a sin α + b cos α = a + b √ sin α + √ cos α a2 + b2 a2 + b2 √ = a2 + b2 sin (α + φ) b a b 其中 φ 满足 sin φ = √ , cos φ = √ ,也就是 tan φ = a a2 + b2 a2 + b2
提纲 微元法 导数 三角函数 积分 参考文献
.
竞赛物理中的数学方法
. ——物理竞赛绪论 李宁
lining200901@ /
山东省青岛第五十八中学 物理教研组
December 2, 2018
name
Dec. 2 2018
竞赛物理中的数学方法
a
(7)
(8)
积分实际上是求函数与坐标轴围成面积的问题,常常应用于变速运动求位移,变力做功, 以及微元法解决问题时. 计算:已知函数 f (x) = x2 ,求在区间 [0, 2] 上函数图像与 x 轴围成的面积.
name Dec. 2 2018 竞赛物理中的数学方法 8/9
提纲 微元法 导数 三角函数 积分 参考文献
导数 y ′ = cos x y ′ = − sin x y ′ = u′ (x)v (x) + u(x)v ′ (x)
y ′ = ex
name
Dec. 2 2018
竞赛物理中的数学方法
4/9
提纲 微元法 导数 三角函数 积分 参考文献
. 三角函数
对于常见的正弦函数 (f (x) = sin x)、余弦函数 (f (x) = cos x)、正切函数 (f (x) = tan x)、余切函数 (f (x) = cot x) 初中已经学过,不再赘述.先介绍两个定理 在如下图所示的三角形中,边角有如下关系:
提纲 微元法 导数 三角函数 积分 参考文献
. 导数
Table: 常用导数表
原函数 y = ax y = xn y = ln x
导数 y′ = a y ′ = nxn−1 y=
1 x
原函数 y = ax2 y= y=e
1 x x
导数 y ′ = 2ax
1 y′ = − x 2
原函数 y = sin x y = cos x y = u(x) · v (x)
1/9
提纲 微元法 导数 三角函数 积分 参考文献
. 提纲
提纲 微元法 导数 三角函数 积分 参考文献
name
Dec. 2 2018
竞赛物理中的数学方法
2/9
提纲 微元法 导数 三角函数 积分 参考文献
. 微元法
微元法:为了分析清楚物理量之间的关系,尤其是定量的关系,往往采用微元法.也 就是分析,经历了一段极小的时间 ∆t ,改变了一个小长度 ∆x ,或者一个小角度 ∆θ 之 后,有什么变化.利用几何的知识,就可以解决问题了. 微元法的好处是把曲线变成直线,非线性变成线性,非理想模型变成理想模型,把线 性的变量变成常量.这个也是微积分的一个基本思想. ∑ 1. 累加求和:我们用符号 来表示累加求和,用法如下:
正弦定理: b c a = = sin A sin B sin C
name Dec. 2 2018 竞赛物理中的数学方法
(3)
5/9
提纲 微元法 导数 三角函数 积分 参考文献
. 余弦定理:
c2 = a2 + b2 − 2ab cos C 再介绍几个和差关系: sin (α + β ) = sin α cos β + cos α sin β cos (α + β ) = cos α cos β − sin α sin β sin 2α = 2 sin α cos α cos 2α = cos2 α − sin2 β
(6)
name
Dec. 2 2018
竞赛物理中的数学方法
7/9
提纲 微元法 导数 三角函数 积分 参考文献
. 基本不等式
1. 基本不等式 若 a, b ∈ R,则 a2 + b2 ≥ 2ab ,均值不等式的一般形式表述为 √ a + b ≥ 2 ab 2. 积分知识 积分是微分的逆运算,牛顿 -莱布尼兹公式如下: ∫ b f (x) dx = F (x) b a = F (b) − F (a)
