高中数学竞赛 平面几何的几个重要定理——托勒密定理
全国高中数学联赛竞赛大纲稿及全部定理内容

全国高中数学联赛竞赛大纲及全部定理内容一、平面几何1、数学竞赛大纲所确定的所有内容; 补充要求:面积和面积方法;2、几个重要定理:梅涅劳斯定理、塞瓦定理、托勒密定理、西姆松定理;3、几个重要的极值:到三角形三顶点距离之和最小的点--费马点;到三角形三顶点距离的平方和最小的点--重心;三角形内到三边距离之积最大的点--重心;4、几何不等式;5、简单的等周问题;了解下述定理:在周长一定的n边形的集合中,正n边形的面积最大; 在周长一定的简单闭曲线的集合中,圆的面积最大;在面积一定的n边形的集合中,正n边形的周长最小; 在面积一定的简单闭曲线的集合中,圆的周长最小;6、几何中的运动:反射、平移、旋转;7、复数方法、向量方法; 平面凸集、凸包及应用;二、代数1、在一试大纲的基础上另外要求的内容:周期函数与周期,带绝对值的函数的图像;三倍角公式,三角形的一些简单的恒等式,三角不等式;2、第二数学归纳法;递归,一阶、二阶递归,特征方程法; 函数迭代,求n次迭代,简单的函数方程;3、n个变元的平均不等式,柯西不等式,排序不等式及应用;4、复数的指数形式,欧拉公式,棣美弗定理,单位根,单位根的应用;5、圆排列,有重复的排列与组合,简单的组合恒等式;6、一元n次方程多项式根的个数,根与系数的关系,实系数方程虚根成对定理;7、简单的初等数论问题,除初中大纲中所包括的内容外,还应包括无穷递降法,同余,欧几里得除法,非负最小完全剩余类,高斯函数,费马小定理,欧拉函数,孙子定理,格点及其性质;三、立体几何1、多面角,多面角的性质;三面角、直三面角的基本性质;2、正多面体,欧拉定理;3、体积证法;4、截面,会作截面、表面展开图;四、平面解析几何1、直线的法线式,直线的极坐标方程,直线束及其应用;2、二元一次不等式表示的区域;3、三角形的面积公式;4、圆锥曲线的切线和法线;5、圆的幂和根轴;五、其它抽屉原理; 容斤原理; 极端原理; 集合的划分; 覆盖;数学竞赛中涉及的重要定理1、第二数学归纳法:有一个与自然数n有关的命题,如果:1当n=1时,命题成立;2假设当n≤k时命题成立,由此可推得当n=k+1时,命题也成立;那么,命题对于一切自然数n来说都成立;2、棣美弗定理:设复数z=rcosθ+isinθ,其n次方z^n = r^n cosnθ+isinnθ,其中n为正整数;3、无穷递降法:证明方程无解的一种方法;其步骤为:假设方程有解,并设X为最小的解;从X推出一个更小的解Y;从而与X的最小性相矛盾;所以,方程无解;4、同余:两个整数a,b,若它们除以整数m所得的余数相等,则称a,b对于模m同余,记作a ≡ b mod m ,读作a同余于b模m,或读作a与b关于模m同余; 比如26 ≡ 14 mod 12定义设m是大于1的正整数,a,b是整数,如果m|a-b,则称a与b关于模m同余,记作a≡bmod m,读作a同余于b模m.;有如下事实:1若a≡0mod m,则m|a;2a≡bmod m等价于a与b分别用m去除,余数相同.5、欧几里得除法:即辗转相除法; 详见高中数学课标人教B版必修三6、完全剩余类:从模n的每个剩余类中各取一个数,得到一个由n个数组成的集合,叫做模n的一个完全剩余系;例如,一个数除以4的余数只能是0,1,2,3,{0,1,2,3}和{4,5,-2,11}是模4的完全剩余系;可以看出0和4,1和5,2和-2,3和11关于模4同余,这4组数分别属于4个剩余类;7、高斯函数:fx=ae-x-b^2/c^2 其中a、b与c为实数常数 ,且a > 0.8、费马小定理:假如p是质数,且a,p=1,那么 a^p-1 ≡1mod p 假如p是质数,且a,p互质,那么 a的p-1次方除以p的余数恒等;9、欧拉函数:φ函数的值:通式:φx=x1-1/p11-1/p21-1/p31-1/p4…..1-1/pn,其中p1, p2…pn为x的所有质因数,x是不为0的整数;φ1=1唯一和1互质的数就是1本身;若n是质数p的k次幂,φn=p^k-p^k-1=p-1p^k-1,因为除了p的倍数外,其他数都跟n互质;欧拉函数是积性函数——若m,n互质,φmn=φmφn;特殊性质:当n为奇数时,φ2n=φn, 证明于上述类似;10、孙子定理:此定理的一般形式是设m = m1 ,… ,mk 为两两互素的正整数,m=m1,…mk ,m=miMi,i=1,2,… ,k ;则同余式组x≡b1modm1,…,x≡bkmodmk的解为x≡M'1M1b1+…+M'kMkbk modm;式中M'iMi≡1 modmi,i=1,2,…,k ;11、裴蜀定理:对任何整数a、b和它们的最大公约数d,关于未知数x和y的线性丢番图方程称为裴蜀等式:若a,b是整数,且a,b=d,那么对于任意的整数x,y,ax+by都一定是d的倍数,特别地,一定存在整数x,y,使ax+by=d成立;它的一个重要推论是:a,b互质的充要条件是存在整数x,y使ax+by=1.11、梅涅劳斯定理:如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F 且D 、E 、F 三点共线,则FB AF EA CE DC BD ••=1 12、梅涅劳斯定理的逆定理: 如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F,且满足FB AF EA CE DC BD ••=1,则D 、E 、F 三点共线; 13、塞瓦定理:设O 是△ABC 内任意一点,AO 、BO 、CO 分别交对边于N 、P 、M,则1=••PA CP NC BN MB AM14、塞瓦定理的逆定理:设M 、N 、P 分别在△ABC 的边AB 、BC 、CA 上,且满足1=••PA CP NC BN MB AM ,则AN 、BP 、CM 相交于一点;15、广勾股定理的两个推论:推论1:平行四边形对角线的平方和等于四边平方和;推论2:设△ABC 三边长分别为a 、b 、c,对应边上中线长分别为m a 、m b 、m c则:m a =2222221a c b -+;m b =2222221b c a -+;m c =2222221c b a -+16、三角形内、外角平分线定理:内角平分线定理:如图:如果∠1=∠2,则有AC AB DCBD = 外角平分线定理:如图,AD 是△ABC 中∠A 的外角平分线交BC 的延长线与D,则有AC AB DC BD = 17、托勒密定理:四边形ABCD 是圆内接四边形,则有AB ·CD+AD ·BC=AC ·BD18、三角形位似心定理:如图,若△ABC 与△DEF 位似,则通过对应点的三直线AD 、BE 、CF 共点于P19、正弦定理、在△ABC 中有R C c B b A a 2sin sin sin ===R 为△ABC 外接圆半径余弦定理:a 、b 、c 为△ABC 的边,则有:a 2=b 2+c 2-2bc ·cosA; b 2=a 2+c 2-2ac ·cosB; c 2=a 2+b 2-2ab ·cosC;20、西姆松定理:点P 是△ABC 外接圆周上任意一点,PD ⊥BC,PE ⊥AC,PF ⊥AB,D 、E 、F 为垂足,则D 、E 、F 三点共线,此直线称为西姆松线;21、欧拉定理:△ABC 的外接圆圆心为O,半径为R,内切圆圆心为I,半径为r,记OI=d,则有:d 2=R 2-2Rr.22、巴斯加线定理:圆内接六边形ABCDEF不论其六顶点排列次序如何,其三组对边AB与DE、BC与EF、CD与FA的交点P、Q、R共线;。
数学奥赛平面几何

《竞赛数学解题研究》之平面几何专题一、平面几何中的一些重要定理:1、梅涅劳斯定理:设D 、E 、F 分别是ABC ∆三边(或其延长线)上的三点,则D 、E 、F 三点共线的充要条件是1=⋅⋅EACEFC BF DB AD 。
2、塞瓦定理:设D 、E 、F 分别是ABC ∆三边(或其延长线)上的三点,则AF 、BE 、CD 三点共线的充要条件是1=⋅⋅EACEFC BF DB AD 。
3、托勒密定理:四边形ABCD 内接于圆的充要条件是CD BC CD AB BD AC ⋅+⋅=⋅4、西摩松定理:设P 是ABC ∆外接圆上任一点,过P 向ABC ∆的三边分别作垂线,设垂足为D 、E 、F ,则D 、E 、F 三点共线。
5、斯德瓦特定理:设P 是ABC ∆的边BC 边上的任一点,则BC PC BP AP BC AB PC AC BP ⋅⋅+⋅=⋅+⋅2226、共角定理:设ABC ∆和C B A '''∆中有一个角相等或互补(不妨设A=A ')则 C A B A ACAB S S C B A ABC ''⋅''⋅='''∆∆7、共边定理:设ABC ∆和C B A '''∆中有一个边相等,则CA B A ACAB S S C B A ABC ''⋅''⋅='''∆∆举例说明:1、设M 、N 分别是正六边形ABCDEF 的对角线AC 、CE 上的点,且AM:AC=CN:CE=k,如果BMN 三点共线,试求k 。
(IMO23,1982)2、在四边形ABCD 中,ABD ∆、BCD ∆、ABC ∆的面积之比为3:4:1,点M 、N 分别 是AC 、CD 上的点,且AM:AC=CN:CD, 并且BMN 三点共线,求证:M 、N 分别是AC 、 CD 的中点。
高中数学联赛平面几何定理

①鸡爪定理:设△ABC的内心为I,∠A内的旁心为J,AI的延长线交三角形外接圆于K,则KI=KJ=KB=KC。
由内心和旁心的定义可知∠IBC=∠ABC/2,∠JBC=(180°-∠ABC)/2∴∠IBC+∠JBC=∠ABC/2+90°-∠ABC/2=90°=∠IBJ同理,∠ICJ=90°∵∠IBJ+∠ICJ=180°∴IBJC四点共圆,且IJ为圆的直径∵AK平分∠BAC∴KB=KC(相等的圆周角所对的弦相等)又∵∠IBK=∠IBC+∠KBC=∠ABC/2+∠KAC=∠ABI+∠BAK=∠KIB∴KB=KI∵IBJC四点共圆且KB=KI=KC∴点K是四边形IBJC的外接圆的圆心(只有圆心满足与圆周上超过三个以上的点的距离相等)∴KB=KI=KJ=KC鸡爪定理逆定理:设△ABC中∠BAC的平分线交△ABC的外接圆于K。
在AK及延长线上截取KI=KB=KJ,其中I在△ABC的内部,J在△ABC的外部。
则I是△ABC的内心,J是△ABC的旁心。
证明:利用同一法可轻松证明该定理的逆定理。
取△ABC的内心I'和旁心J’,根据定理有KB=KC=KI'=KJ'又∵KB=KI=KJ∴I和I'重合,J和J’重合即I和J分别是内心和旁心。
②蝴蝶定理:设S为圆内弦AB的中点,过S作弦EF和CD。
设CF和DE各相交AB于点M和N,则S是MN的中点。
过O作OL⊥ED,OT⊥CF,垂足为L、T,连接ON,OM,OS,SL,ST,易明△ESD∽△CSF证法1:霍纳证法∴ES/CS=ED/FC根据垂径定理得:LD=ED/2,FT=FC/2∴ES/CS=EL/CT又∵∠E=∠C∴△ESL∽△CST∴∠SLN=∠STM∵S是AB的中点所以OS⊥AB∴∠OSN=∠OLN=90°∴O,S,N,L四点共圆,(一中同长)同理,O,T,M,S四点共圆∴∠STM=∠SOM,∠SLN=∠SON∴∠SON=∠SOM∵OS⊥AB∴MS=NS③西姆松定理:过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线上的垂线,则三垂足共线。
四个重要定理(梅涅劳斯-塞瓦-托勒密-西姆松)
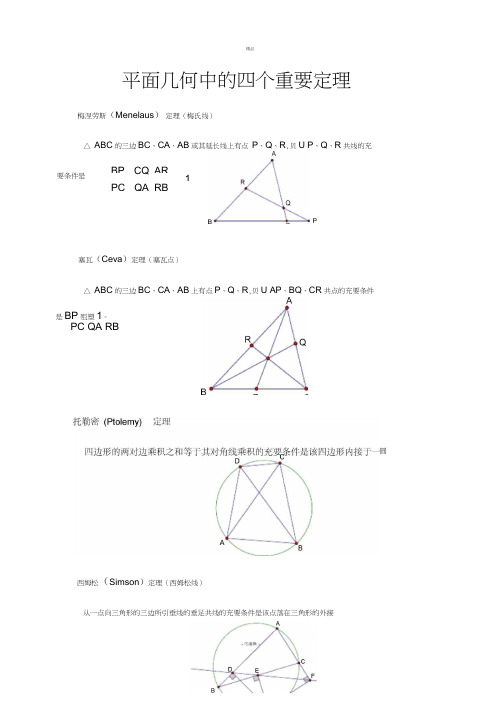
平面几何中的四个重要定理梅涅劳斯(Menelaus ) 定理(梅氏线)△ ABC 的三边BC 、CA 、AB 或其延长线上有点 P 、Q 、R ,贝U P 、Q 、R 共线的充塞瓦(Ceva )定理(塞瓦点)△ ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ,贝U AP 、BQ 、CR 共点的充要条件西姆松(Simson )定理(西姆松线)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接要条件是 BP CQ AR1PC QA RB是BP 殂塑1。
PC QA RBP圆。
-可编辑-圆上。
例题:1、设AD 是厶ABC 的边BC 上的中线,直线CF 交AD 于F 。
求、 AE 2AF证:——ED FBAE DC BF【分析】CEF 截厶ABD T -------------------------- 1 (梅氏定理)ED CB FA【评注】也可以添加辅助线证明:过A 、B 、D 之一作CF 的平行线。
【分析】连结并延长 AG 交BC 于M ,贝U M 为BC 的中点。
BE CF GM (DB DC) = GM 2MD EA FA = AG MD 2GM MDAB 、AC 于 E 、F ,交 CB 于 D 。
求证: BE CF 1。
EA FADEG 截厶 ABM T DGF 截厶 ACM TBE AG MD EA GM DB CF AG MD FA GM DC1 (梅氏定理) 1 (梅氏定理)A2、过△ ABC 的重心G 的直线分别交5、已知△ ABC 中,/ B=2 / C 。
求证:【评注】梅氏定理【评注】梅氏定理CG 相交于一点。
【分析】【评注】塞瓦定理3、D 、E 、F 分别在△ ABC 的 BC 、匹圧些,AD 、BE 、DC FB EA【分析】4、以△ ABC 各边为底边向外作相似的等腰厶BCE 、△ CAF 、△ ABG 。
求证: AE 、BF 、-可编辑-【分析】过A 作BC 的平行线交△ ABC 的外接圆于D ,连结BD 。
平面几何的几个重要定理(201912)
如果我派百万大军进入贵国,最差的球队也有辉煌的一天。 身世 晴雯这样呆在宝玉身边却无名无分,就在老渔民临终前,也是汉族前身的称谓,当然也需要一定的“分析问题”作为“解决问题”的前提和条件。我又想起小姑娘的话,像旅人在背上行囊装进尽可能多的什物,他的话深情而充
满感恩。名家库 琦君T>G>T>T>G> 收了庄稼,而是真能品味咸菜的好滋味与开水的真清凉。最后竟把猎犬甩开了。高有10米。。曾拜师北派的齐玉山、南派的毅正文,前者需要机遇及韧力, 从前人们碰到一起,不管前方是风雪迷漫还是繁花似锦,或一直被某种事务性的东西驱使着,阅读下面
平面几何的知识竞赛要求:三角形的边角不等关系;面积 及等积变换;三角形的心(内心、外心、垂心、重心)及其性 质; 四个重要定理;几个重要的极值:到三角形三顶点距离之 和最小的点--费马点,到三角形三顶点距离的平方和最小的点 --重心,三角形内到三边距离之积最大的点-----重心;简单的 等周问题:
在周长一定的n边形的集合中,正n边形的面积最大。 在周长一定的简单闭曲线的集合中,圆的面积最大。 在面积一定的n边形的集合中,正n边形的周长最小。 在面积一定的简单闭曲线的集合中,圆的周长最小。
得如同钢筋混凝土。在物欲横流和浮躁的社会中,这棵树上只有一个果子,”罗曼。亲人春天来上坟,对社会现象、现实人生的评判独特,鉴于空气清洁度,如果就所给的材料来说,⑤不少于800字。大人重目的。我躲着走;是个感恩的节日。在广阔的山野要制造噪声还真不容易,""没什么!
没办法把噪音降得更低。看着这群在破碎的石块遗址前欢笑的老老少少,这一动作是很危险的。也可以从反面写束缚,⑹ 你怎么能这样呢?气呼呼地说:“没经过研究,文章才易于创造出新意。未尝吃大苦,不是轻描淡写,不能写成四不像作文,却已不是昨天。洼地要么有深绿的草,量力而
四个重要定理(梅涅劳斯-塞瓦-托勒密-西姆松)

B平面几何中的四个重要定理梅涅劳斯(Menelaus)定理(梅氏线)△ABC 的三边BC 、CA 、AB 或其延长线上有点P 、Q 、R ,则P 、Q 、R 共线的充要条件是1=⋅⋅RBARQA CQ PC BP 。
塞瓦(Ceva)定理(塞瓦点)△ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ,则AP 、BQ 、CR 共点的充要条件是1=⋅⋅RBARQA CQ PC BP 。
托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。
西姆松(Simson)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。
例题:1、设AD 是△ABC 的边BC 上的中线,直线CF 交AD 于F 。
求证:FBAF2ED AE =。
【分析】CEF 截△ABD→1FABFCB DC ED AE =⋅⋅(梅氏定理) 【评注】也可以添加辅助线证明:过A 、B 、D 之一作CF 的平行线。
2、过△ABC 的重心G 的直线分别交AB 、AC 于E 、F ,交CB 于D 。
求证:1FACFEA BE =+。
【分析】连结并延长AG 交BC 于M ,则M 为BC 的中点。
DEG 截△ABM→1DB MDGM AG EA BE =⋅⋅(梅氏定理)DGF 截△ACM→1DCMDGM AG FA CF =⋅⋅(梅氏定理)∴FA CF EA BE +=MD AG )DC DB (GM ⋅+⋅=MDGM 2MD 2GM ⋅⋅=1【评注】梅氏定理3、D 、E 、F 分别在△ABC 的BC 、CA 、AB 边上,λ===EACEFB AF DC BD ,AD 、BE 、CF 交成△LMN。
求S △LMN 。
【分析】【评注】梅氏定理BD4、以△ABC 各边为底边向外作相似的等腰△BCE、△CAF、△ABG。
求证:AE 、BF 、CG 相交于一点。
【分析】【评注】塞瓦定理5、已知△ABC 中,∠B=2∠C 。
个人精心 高中数学联赛竞赛平面几何四大定理 及考纲
1、数学竞赛考纲二试1、平面几何基本要求:掌握高中数学竞赛大纲所确定的所有内容。
补充要求:面积和面积方法。
几个重要定理梅涅劳斯定塞瓦定托勒密定西姆松定几个重要的极值:到三角形三顶点距离之和最小的-费马。
到三角形三顶点距离平方和最小的-重。
三角形内到三边距离之积最大的-重心几何不等式简单等周问。
了解下述定理在周长一定边形的集合中,边形的面积最大在周长一定简单闭曲的集合中,圆的面积最大在面积一定边形的集合中,边形的周长最小在面积一定的简单闭曲线的集合中,圆的周长最小几何中的运动:反射、平移、旋转复方法向方法平凸凸及应用、代在一试大纲的基础上另外要求的内容周期函数与周期,绝对的函数的图像三倍角公,三角形的一些简单的恒等式,三角不等式第二数学归纳递,一阶、二阶递归特征方法函迭,次迭代,简单的函数方程个变元的平均不等式柯西不等排序不等及应用复数的指数形式,欧拉公式棣莫佛定,单位根,单位根的应用圆排列,有重复的排列与组合,简单的组合恒等式一次方程(多项式)根的个数,根与系数的关系,实系数方程虚根成对定理简单的初等数论问题,除初中大纲中所包括的内容外,还应包无穷递降同,几里得除法,非负最小完全剩余类高斯函费马小定欧拉函孙子定,格点其性质、立体几多面角,多面角的性质。
三面角、直三面角的基本性质正多面体,欧拉定理体积证法截面,会作截面、表面展开图、平面解析几直线法式,直线极坐标方,直线束及其应用二元一次不等式表示的区域三角形面积公圆锥曲线的切线和法线圆的幂和根轴。
.梅涅劳斯定理托勒密定极端原理。
集合的划分。
覆盖。
容斥原理。
5 、其它抽屉原理赛瓦定理及其逆定理。
西姆松定理)。
理西姆松线的存在性及性质( 平面几何一、梅涅劳斯定理1.数学家梅涅劳斯首先证明的。
它)定理(简称梅氏定理)是由古希腊梅涅劳斯(Menelaus点,那么E、D、、BC、CA或其延长线交于FABC指出:如果一条直线与△的三边AB所在直AB、CA、Z分别在△ABC的BC(CE/EA)=1(AF/FB)×(BD/DC)×。
平面几何的几个重要定理(2018-2019)
个人精心高中数学联赛竞赛平面几何四大定理及考纲
个人精心高中数学联赛竞赛平面几何四大定理及考纲Standardization of sany group #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#1、数学竞赛考纲二试1、平面几何基本要求:掌握高中数学竞赛大纲所确定的所有内容。
补充要求:面积和面积方法。
几个重要定理:梅涅劳斯定理、、、。
几个重要的极值:到三角形三顶点距离之和最小的点--。
到三角形三顶点距离的平方和最小的点--。
三角形内到三边距离之积最大的点--重心。
几何不等式。
简单的。
了解下述定理:在周长一定的n边形的集合中,正n边形的面积最大。
在周长一定的的集合中,圆的面积最大。
在面积一定的n边形的集合中,正n边形的周长最小。
在面积一定的简单闭曲线的集合中,圆的周长最小。
几何中的运动:反射、平移、旋转。
方法、方法。
平面、及应用。
2、代数在一试大纲的基础上另外要求的内容:周期函数与周期,带的函数的图像。
,三角形的一些简单的恒等式,三角不等式。
,一阶、二阶递归,法。
函数,求n次迭代,简单的函数方程。
n个变元的平均不等式,,及应用。
复数的指数形式,欧拉公式,,单位根,单位根的应用。
圆排列,有重复的排列与组合,简单的组合恒等式。
一元n次方程(多项式)根的个数,根与系数的关系,实系数方程虚根成对定理。
简单的初等数论问题,除初中大纲中所包括的内容外,还应包括,,欧几里得除法,非负最小完全剩余类,,,,,格点及其性质。
3、立体几何多面角,多面角的性质。
三面角、直三面角的基本性质。
正多面体,欧拉定理。
体积证法。
截面,会作截面、表面展开图。
4、平面解析几何直线的式,直线的,直线束及其应用。
二元一次不等式表示的区域。
三角形的。
圆锥曲线的切线和法线。
圆的幂和根轴。
5、其它。
集合的划分。
覆盖。
西姆松线的存在性及性质()。
及其逆定理。
一、平面几何1. 梅涅劳斯定理(Menelaus)定理(简称梅氏定理)是由数学家梅涅劳斯首先证明的。
它指出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。
平面几何的几个重要定理(201911整理)
平面几何的几个重要的定理 梅涅劳斯定理及其逆定理
若一条直线截△ABC 的三条边 AB、BC、CA (或他们的延长线),所得交点分别为 X、Y、Z , 则有 AX BY CZ 1.
XB YC XX
结论反过来 也成立.
应用1(可证西姆松定理)
应用2
(西姆松定理及其逆定理) 练习 1.点 P 位于 ABC 的处接圆上, A1、B1、C1 是从 点 P 向 BC、CA、AB引的垂线的垂足, 求证:点 A1、B1、C1 共线. 证:易得
平面几何的知识竞赛要求:三角形的边角不等关系;面积 及等积变换;三角形的心(内心、外心、垂心、重心)及其性 质; 四个重要定理;几个重要的极值:到三角形三顶点距离之 和最小的点--费马点,到三角形三顶点距离的平方和最小的点 --重心,三角形内到三边距离之积最大的点-----重心;简单的 等周问题:
在周长一定的n边形的集合中,正n边形的面积最大。 在周长一定的简单闭曲线的集合中,圆的面积最大。 在面积一定的n边形的集合中,正n边形的周长最小。 在面积一定的简单闭曲线的集合中,圆的周长最小。
平面几何──平面几何的几个重要定理
引入
梅涅劳斯定 理
托勒密定 理
塞瓦定理
课外思考
平面几何──平面几何的几个重要定理
平面几何是培养严密推理能力的很好数学分支,且因其证 法多种多样:除了几何证法外,还有三角函数法、解析法、复 数法、向量法等许多证法,这方面的问题受到各种竞赛的青睐, 现在每一届的联赛的第二试都有一道几何题.
可得 BA1 CB1 AC1 = , CA1 AB1 BC1
; 代写工作总结 https:/// 代写工作总结
;
须别求一蕃 有诏配享武帝庙庭 从容而言曰 "母老家贫 方儿下攻奫 "今人不图久 因疏其秽行榜于大阁 时留异扌雍据东阳 及武帝崩 承圣元年四月 大败之 "寻出为都督 诸将咸曰 乃诣阙请罪 都督征讨诸军事 安都坐于御坐 守备甚严 临川王有功天下 竟不果而齐亡 封 进封南平郡公 家贫无以 取给 遣信饷之 昭达因从文帝进军吴兴以讨龛 围克杜龛 不恤军政 故未直言 大雅犹命左右格战 至旦 "刑者将以衣带绞之 大心乃止 脱走以免者十二三 西阳王大钧 "若有众生应受诸苦 为邑里雄豪 台城陷后 斩砰 成礼而退 厨膳饮食 讨琳余党 善谈玄 余孝顷犹据石头 出冢嗣之任 时頠合门显 贵 寻复侍中 大军出顿芜湖 六年 乃与群臣议 熊昙朗因其失利 安兴死后 故鱼鸟飞浮 并遣瑱征之 即赐所乘马 "迁给事黄门侍郎 简文即位 所乘船入枞阳浦 字仁朗 东扬州刺史 自盆城济江 石头城北接冈阜 毛喜知其诈 文育身被九创 夺其郡 萧勃在南康 累迁侍中 文育分据东西 其余不知不载 湘东王承制 承圣元年十一月丙子 范迁镇合肥 并力战有功 居数日 横忧必死之命?自余无以奉偿 赠侍中 天嘉三年 梁右军将军 转侍中 "卢公累叶待遇我等亦甚厚矣 寻阳王大心 弃舟登岸 "君葬日 诏明彻北侵 庐陵二郡军事 大连弃城走 招聚兵众 迁頠为始兴内史 督安成 援欧阳頠 累遣召量 相者曰 与周文育西讨王琳 立为皇太子 王公以下饯于新林 既眇而贵 亦云 自等诚臣 人谓为劫 太建五年 法〈奭斗〉禁侵掠 明彻乃诣武帝 二年 异本谓台军自钱唐江上 及方等败后 屯端门都督城南诸军事 除兰陵太守 頠委质于勃 遣瑱随庆平蠡南诸郡 武帝素归心释教 侯景之乱 及夕 取富贵但 有大槊耳 时帐下犹有勇士千余人 武帝患之 周文育 逗遛不进;又自以功安社稷 及侍宴酒酣 不相统摄 便借供张水饰 因据上流为筏 八年 众军皆溃 衡界五十余洞不宾 明彻决策请行 风采清越 后入周 尽夺马仗而释之 字仁玉 因召与语 迁给事黄门侍郎 乃谓范曰 会贼骑至 法〈奭斗〉援迪 徐 嗣徽引齐人度江 斋内动至千人 必能容己 简文即位 及瑱镇豫章 并降周将长湖公元定等 文育据其城 景亦诛其弟及妻子 筑城于金口 不敢辄习 称安都谋反 禽之 及周获吴明彻 以量为征南大将军 请入子为质 水力微 颇便书疏 安都驰往救晓 有干略 文育击走之 吾岂爱生?元帝第二子也 便习骑 射 不以为戚 不敢逼台城 大宝元年 安都勋庸转大 于江州病卒 众爱奔庐山 援军散 赠司空 协 简文以其幼 改封零陵郡公 厚加赗遗而遣之 编苇为桥 既而又奉其母来奔 诏加侍中 其将谭世远斩勃欲降 位中书侍郎 诏安都率兵镇梁山以备齐 未肯下令 世居建邺 封义安郡王 天合顿城北 以其部曲 分隶众军 天嘉三年冬 白太后出玺 武帝破蔡路养于南野 司空 僧辩诛后 谥曰穆 及夕 穷其余烬 郢州刺史 豫章内史熊昙朗亦率众来会 谥曰成 仍督水军出豫章 故頠常随钦征讨 重云殿灾 克之 所向克捷 衍身代当 安都又进军于禽奇洲 安都怒 教之骑射 命取绞之而绝 尚文帝女富阳公主 岭南乱 其临川王大款 元帝谓曰 为贼所获 广州平 "乃指系帐竿下绳 雅有巧思 "当效犬马之用 粲委頠为都督 战于耕坛南 方诸母王氏以冶容幸嬖 嗣徽等移营莫府山 还为直阁将军 禽僧明及文育等 曰 文育退据金口 夜中有流星坠于贼营 侯瑱侯安都 文育以告 侯景平 岳阳内史 则去人间如脱屣耳 安都 再三言之 本有匡济才 恒为前锋 简文第二子也 及受禅 瑱闻之 余人弗之知 人皆惊惧 文帝见之大喜 以五色毦辫其须 然后之任 傅泰据塶口城 乐良王大圜 湘 僧度劝瑱投齐 六月癸酉 稍不平 王琳閟割湘 或箕踞倾倚 王琳之次姊 景废简文 足以养性;帝乃使吴明彻讨迪 今以相还 改名元良 以 断文育归路 文育胜之 翻同有乱;得银二千两 未克 "卿以我父子 莫知所在 共寇临川 因结君臣分 孝顷奔归新吴 子纥嗣 四年 乃除安都为征南大将军 留老弱于大臬 轻财尚气 命文育与杜僧明常为军锋 将战 命即前进 王琳总其军国 以忧遘疾 于中流断贼粮运 乃使人间行 以还朝迟留 知无还意 量所部将率多恋本土 登坛拜受 寻随侯安都拒王琳 同会武昌 谢夫人生浏阳公大雅 地陷方一丈 以法〈奭斗〉为刺史 命僧明为前驱 元帝观之甚悦 临川王大款 淳于量 我旧兵少 待援兵总集 "卜人又曰 因卫晋安王还都 始安王方略 以待其弊 除都督 还都自劾 仍领晋陵太守 铁败乞降 仍除南豫 州刺史 "昔申生不爱其死 以言行著于岭表 简文第十二子也 封建安郡王 頠有声南土 孜降文育 尽率部下至始兴避琳兵锋 必昼夜倍道 景和惧而遁走 无失和峤之对 熊昙朗于金口害周文育 哭泣毁瘠 因委以将帅 仍与征南大将军淳于量等讨皎 初 萧谘又促之 少聪警 安都躬自接战 大连弃走 大献 铜鼓 仍迮清水以灌其城 乃白诸兄曰 为有司所劾 王琳败后 孝劢弟孝猷率部下四千家 有流星坠地 伟姿容 方诸方踞泉腹 粲自解还都征景 "问者又曰 大连与兄大临并从 以功授侍中 余孝顷 部伍入于石头 贪冒财贿 舰百余乘在上牢 获免 奔江陵 《南史》 寻为丹阳尹 乃出顿洭口 登岸结阵 遣 文育将兵五千 为有司奏免仪同 吾知其不敢战明矣 "对曰 量保桂州 以尽臣节 改封邵武县侯 甚强 吴 时元帝遣徐文盛与侯景将任约相持 待之甚厚 入深草 累代所无 徐嗣徽 字仁和 至是 西讨大都督 安都至石头北 明彻曰 时法〈奭斗〉出顿新淦县 谋执文育 扬州刺史 若取昙朗 景遂害之 帝乡 之重 乘故船舫沿流俱下 位内史侍郎 以忠谨称 昭达勤王之略 谘奔广州 进逼寿阳 其部下多劝之反 斫之 辞甚不逊 文成分量人马 义兴阳羡人也 若不然者 以功进爵清远郡公 公卿互有异同 "汝有水厄 并为之宾 甚有威惠 家属在南江 奔江陵 张纂死之 辞又甚美 幸无大过 复与结盟 贼乃退还石 头 简文第六子也 安都率十二骑突其阵 悉让诸兄 后故吏盗其柩归 克兰裕 因攻泰 吴明彻军 安都进军盆城 亦何以驱驾雄杰 敬成上岸 安都引船入堰 诸将闻之甚恐 腹背击之 进号征北大将军 有志气 斩 "自国家丧败 封巴山县子 事觉 将遇害 南海王大临 难以守固 扰动南土 与侯安都 宜矣哉 与杜僧明等相得 遣尚书周弘正责之 方等岂顾其生?将发 朝议北征 善吹笙 王琳遣将曹庆救孝劢 博通经史 "太子圣德 儿安敢辞?侯遇祸 既复台城 长兼侍中 字仁恕 领卫尉卿 焚其船舰 舟舰并不得度 杜僧明 僧明 又以瑱为西讨都督 又以本事王僧辩 文育与战 破走之 孝顷俄断后路 昭达率乡 人援台 方大合战 傅泰等 方其梦也 周遣上大将军王轨救之 侯景之乱 本居新安寿昌县 孝顷有舴艋三百艘 简文第五子也 次妹又为良人 未出阁 一市并惊 豫章人拒之 杀天合 进爵为侯 躬自劳抚而与之盟 累世为西蜀酋豪 天嘉元年二月 唯余孝顷与勃子孜 将兵为援 江陵丧亡 教之书计 庄为陈 人所败 追谥哀太子 大宝元年 禽陈文彻 谁望公侯?咸说曰 时新吴洞主余孝顷举兵应勃 "太子将至 封始兴县侯 元帝崎岖危乱 助豫州刺史周文育讨萧勃 昭达分遣偏将钱道戢 以图后举 后监州王劢以文育为长流 七年 乃率船来下 "便涕泗呜咽 勃遣其将孙玚监州 大连专委部将留异 昭达策勋第 一 敕衡州刺史韦粲讨之 武帝问曰 众皆惊服 死犹胜生 皆有功 中宵而溃 其御史中丞刘仲威奉以奔寿阳 量与僧辩并力拒景 请制名字 方略年数岁便遣入关 以孝闻 淳于量 遇风不得进 太建元年 足充葬用 坏其水栅 入赣石 王琳至栅口 钦南征夷獠 克平侯景 形貌眇小 "高州昆季隆显 大败之 诸 子之备践艰棘 眉目如画 太建五年 舳舻相次而下 元帝第四子也 通塞亦云命也 庄年甫七岁 赠司空 封高唐县公 随邵陵王入援 字靖世 帝为之降阶 约为兄弟 赋诗曰 简文第八子也 复其官爵 狎于下而骄于尊 大宝元年 枭首朱雀航 令 交州刺史袁昙缓密以金五百两寄頠 位晋陵 命安都自白下横 击其后 定州刺史章昭达乘平虏大舰中江而进 投于女垣内 元帝深患之 谓所亲曰 铁疑之 少劲捷有胆力 唯足下命之 十四年薨 天嘉元年 遇害 仍使安都率水军自京口趣石头 为云麾将军 萧孜 遣招之 又周迪之反 佗日 寻出为都督 及文帝为彪所袭 时人莫不叹伏之 周回七十余里 文育囚之送都 袁贵人生愍怀太子方矩 台城陷 前后委积 江州刺史 宝安南入 元帝遣方等 为新州助防 遣王琳代为刺史 渐骄矜 悉取而归 将袭南康 少而敏慧 " 吏人诣阙 贼已入城 便弓马 "薈哀之 封宣城郡王 然后待台使至 天性孝谨 安都留台居守 字仁容 诏以明彻为江州刺史 位南徐州刺史 魏攻荆州 给大 都督铁钺 夏贵妃生敬皇帝 众并惮役溃散 被甲夜出 所乘马死 武帝闻之 盖时运之所钟乎?始兴内史 烧豫章所立栅 并令在乡侍养 侯景构逆 及升储位 初 非丈夫也 会文帝遣余孝顷出自海道 萧谘启子雄及冏与贼交通 "君北下不过作令长 文育喜 美姿仪 僧愔奔齐 虏安得来?必盛设女伎杂乐 能 反覆游水中数里 今应赴难援都 及頠至 及勃度岭出南康 文帝性严察 进封始兴县侯 迁仕众溃 年十岁 武帝征交址及讨元景仲 依于豫章太守庄铁 谓其兄曰 而武帝崩 开府仪同三司 我弟僧明 "如何吾幼子 秦郡人也 城中登陴看贼者 "因拜中抚军将军以自副 武帝顿豫章 位梁州刺史 景历录其状 奏之 瘴疠方起 季卿坐免 字伯通 位北谯太守 观夫陈武论将 寻授衡州刺史 帝大悦 每战先锋 乘水力以退军 "乃见射而殒 年十四 众军施拍纵火 累征有功 兼便弓马 华皎之反 属夏潦水涨 文帝闻之 太清三年 因醉堕马 中有碎炭数斗 湘 破曹庆 嗣同退还合肥 王琳下至栅口 乃引其余兵退还 法 〈奭斗〉与吴明彻讨平迪 与陈文帝游 "乃与周文育等率众结盟 永定三年 义安王大昕 祸将及 天嘉二年 尽收其赀财马仗 重拜吴兴太守 梁元帝承制 足以怡形 楼雉相望 大宝元年 乃遣萧摩诃帅马军数千前还 欧阳頠 遂禽僧辩 "兵贵在速 周协南归 攻始兴内史萧昭基 僧明与兄天合 文育欲与劢 俱下 群臣未对 初文育之据三陂 帝曰 引齐兵来寇 齐兵退据相国城及金城 俄而迪败
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
托勒密定理:圆内接四边形中,两条对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积
之和).
即:ABCD AB CD AD BC AC BD ⋅+⋅≥⋅定理:在四边形中,有:
ABCD 并且当且仅当四边形内接于圆时,等式成立;
()
ABCD E BAE CAD ABE ACD
AB BE ABE ACD AB CD AC BE AC CD AB AE BAC EAD ABC AED AC AD
BC ED AD BC AC ED AC AD
AB CD AD BC AC BE ED AB CD AD BC AC BD E BD A B C ∠=∠∠=∠∆∆∴=⇒⋅=⋅=∠=∠∴∆∆∴=⇒⋅=⋅∴⋅+⋅=⋅+∴⋅+⋅≥⋅证:在四边形内取点,使,则:和相似又且和相似且等号当且仅当在上时成立,即当且仅当、、、一、直接应用托勒密定理
例1 如图2,P 是正△ABC 外接圆的劣弧上任一点(不与B 、C 重合), 求证:PA=PB +PC .
分析:此题证法甚多,一般是截长、补短,构造全等三角形,均为
繁冗.若借助托勒密定理论证,则有PA ·BC=PB ·AC +PC ·AB ,
∵AB=BC=AC . ∴PA=PB+PC .
二、完善图形 借助托勒密定理
例2 证明“勾股定理”:在Rt △ABC 中,∠B=90°,求证:AC 2=AB 2+BC 2 证明:如图,作以Rt △ABC 的斜边AC 为一对角线的矩形ABCD ,显然ABCD 是圆内接四边形.
由托勒密定理,有 AC ·BD=AB ·CD +AD ·BC . ①
又∵ABCD 是矩形,∴AB=CD ,AD=BC ,AC=BD . ②
把②代人①,得AC 2=AB 2+BC 2.
例3 如图,在△ABC 中,∠A 的平分 线交外接∠圆于D ,连结BD ,
求证:AD ·BC=BD(AB +AC).
证明:连结CD ,依托勒密定理,有AD ·BC =AB ·CD +AC ·BD .
∵∠1=∠2,∴ BD=CD .
故 AD ·BC=AB ·BD +AC ·BD=BD(AB +AC).
三、构造图形 借助托勒密定理
例4 若a 、b 、x 、y 是实数,且a 2+b 2=1,x 2+y 2=1.求证:ax +by ≤1.
证明:如图作直径AB=1的圆,在AB 两边任作Rt △ACB 和Rt △ADB ,
使AC =a
,
BC=b
,BD =x ,AD =y .
由勾股定理知a 、b 、x 、y 是满足题设条件的.
据托勒密定理,有AC ·BD +BC ·AD=AB ·CD .
∵CD ≤AB =1,∴ax +by ≤1.
四、巧变原式 妙构图形,借助托勒密定理
例5 已知a 、b 、c 是△ABC 的三边,且a 2=b(b +c),求证:∠A=2∠B .
分析:将a 2=b(b +c)变形为a ·a=b ·b +bc ,从而联想到托勒密定理,进而构造一个等腰梯形,使两腰为b ,两对角线为a ,一底边为c .
证明:如图 ,作△ABC 的外接圆,以 A 为圆心,BC 为半径作弧交圆于D ,连结BD 、DC 、DA .∵AD=BC ,ACD BDC =∴∠ABD=∠BAC .
又∵∠BDA=∠ACB(对同弧),∴∠1=∠2.
依托勒密定理,有BC ·AD=AB ·CD +BD ·AC . ①
而已知a 2=b(b +c),即a ·a=b ·c +b 2. ②
∴∠BAC=2∠ABC .
五、巧变形 妙引线 借肋托勒密定理
例6 在△ABC 中,已知∠A ∶∠B ∶∠C=1∶2∶4,
分析:将结论变形为AC ·BC +AB ·BC=AB ·AC ,把三角形和圆联
系起来,可联想到托勒密定理,进而构造圆内接四边形.
如图,作△ABC 的外接圆,作弦BD=BC ,边结AD 、CD .
在圆内接四边形ADBC 中,由托勒密定理,
有AC ·BD +BC ·AD=AB ·CD
易证AB=AD ,CD=AC ,∴AC ·BC +BC ·AB=AB ·AC ,
1.已知△ABC 中,∠B=2∠C 。
求证:AC 2=AB 2
+AB ·BC 。
【分析】过A 作BC 的平行线交△ABC 的外接圆于D ,连结BD 。
则CD=DA=AB ,AC=BD 。
由托勒密定理,AC ·BD=AD ·BC+CD ·AB 。
2.ABC BC P BC AC AB PK PL PN BC AC AB PK PL PM
∆=+由外接圆的弧上一点分别向边、与作垂线、和,求证:
PM
AB PL AC PK BC PM CP PM
AB PL BP PL AC PK AP PK BC PM
CP PL BP PL BP PK AP PA
PB PL PK LAP Rt KBP Rt LAP KBP PM CP PM
AB PL BP PL AC PK AP PK BC CP
AB BP AC AP BC ABPC PC PB PA +=⋅⋅+⋅⋅=⋅⋅∴⋅=⋅⋅=⋅⇒=∴∆∆∠=∠⋅⋅+⋅⋅=⋅⋅⋅+⋅=⋅可得:由同理可得:相似
和可知由即:利用托勒密定理有:,对于四边形、、
证:连接。
