2016-2017学年第一学期三年级数学期中质量检测卷[精品]
南京郑和外国语学校2016-2017学年度第一学期初一年级数学期中测试卷

南京郑和外国语学校2016-2017学年度第一学期初一年级数学期中测试卷一、选择题1.5-的相反数是() A.15- B.15C.5-D.5 2.代数式232xy -的系数与次数分别是()A.8-,4B.6-,3C.2-,7D.2-,43.下列等式中是一元一次方程的是() A.113x+= B.3132x x -= C.34x y -= D.2210x x --= 4.有这样一组数:8-,2.7,132-,π2,0.66666……,0,2,0.080080008……(相邻两个8之间依次增加一个0),其中是无理数的有()A.0个B.1个C.2个D.3个5.下列去括号正确的是()A.(25)25x x -+=-+B.1(42)222x x --=-+ C.12(23)33m n m n -=+ D.222233m x m x ⎛⎫--=-+ ⎪⎝⎭6.下列各组数中,数值相等的是()A.43和34B.24-和2(4)- C .32-和3(2)- D .2(23)-⨯和2223-⨯7.若3m =,2n =,且0n m<,则m n +的值是() A.1± B.1 C.1或5 D.1-8.如图,M 、N 、P 、R 分别是数轴上四个整数所对应的点,其中有一点是原点,并且1MN NP PR ===,数a 对应的点在M 与N 之间,数b 对应的点在P 与R 之间,若3a b +=,则原点是()A.N 或PB.M 或RC.M 或ND.P 或R二、填空题9.若某次数学考试标准考试成绩定为85分,规定高于标准记为正,两位学生的成绩记作:9+分和3-,则第一位学生的实际得分为_____________分.10.一个数的平方是2564,那么这个数是__________. 11.我国18岁以下未成人约有304000000人,该数据用科学记数法可表示为__________.12.为鼓励居民节约用电,某地对居民用户用电收费标准如下规定:每户每月用电如果不超过100度,那么每按a 元收费;如果超过100度,那么超过部分每度电按b 元收费.某户居民在一个月内用电160度,则他这个月应缴纳电费______________元.13.若414n x y +与25m x y -的和仍为单项式,则m n -=___________.14.若2x =是关于x 的方程2310x m --=的解,则m 的值为_____________.15.若23x y -=-,则52x y -+的值是_____________.16.如图所示是计算机程序计算,若开始输入1x =-,则最后输出的结果是____________.17.已知5a =,3b =,且a b b a -=-,那么a b +=______________. x b aR P NM18.德国数学家洛萨提出了一个猜想:如果n 为奇数,我们计算31n +;如果n 为偶数,我们除以2,不断重复这样的运算,经过有限步骤后一定可以得到1.例如,5n =时,经过上述运算,依次得到一列数是:5,16,8,4,2,1(注:5n =作为数列中第一个数)若小明同学对某个整数n ,按照上述运算,得到一列数,已知第八个数为1,则整数n 的所有可能取值中,最小的值为____________.三、解答题19.将 2.5--,3.5,0,100(1)-,(2)--各数在数轴上表示出来.20.计算题(1)44(14)(66)6+-+-+ (2)12345935⎛⎫-+⨯ ⎪⎝⎭(3)94(81)(16)49-÷⨯÷- (4)201621(1)133(3)2⎛⎫---÷⨯-- ⎪⎝⎭21.解方程:(1)2(2)3(21)x x +=+ (2)3157146y y ---=. 22.先化简,再求值:22113124323x x y x y ⎛⎫⎛⎫--+-+ ⎪ ⎪⎝⎭⎝⎭,其中32x =,2y =- 23.对于有理数a 、b ,定义运算:1a b a b ab ⊗=⨯-+.(1)计算(3)4-⊗的值;(2)填空:5(2)⊗-___________(2)5-⊗.(填“>”或“=”或“<”);(3)试用学习有理数的经验和方法来探究这种新运算“⊗”是否具有交换律?请写出你的探究过程. 24.某公司在甲、乙两座仓库分别有农用车10辆和8辆,现需要调往A 县12辆,调往B 县6辆,已知从甲仓库调运一辆农用车到A 县和B 县的运费分别为40元和80元,从乙仓库调运一辆农用车到A 县和B 县的运费为30元和50元,设从甲仓库调往A 县农用车x 辆.(1)甲仓库调往B 县农用车____________辆,乙仓库调往A 县农用车____________辆.(用含x 的代数式表示)(2)用含x 的代数式表示公司从甲、乙两座仓库调运农用车到A 、B 两县一共所需要的总运费. (3)在(2)的基础上,求当从甲仓库调往A 县农用车4辆时,总运费是多少?25.阅读材料:我们知道:如果点A 、B 在数轴上分别表示有理数a 、b ,那么A 、B 两点之间的距离表示为AB ,在数轴上A 、B 两点之间的距离AB a b =-.根据上述材料,利用数轴解答下列问题:(1)如果点A 在数轴上表示2-,将点A 先向左平移2个单位长度,再向右移动7个单位长度,那么终点B 在数轴上表示的数是____________;(2)数轴上表示x 和1的两个点之间的距离是__________;(3)若327x x -++=,则x 的值是____________;(4)在(1)的条件下,设点P 在数轴上表示的数为x ,当2PA PB -=时,则x 的值是___________.26.阅读材料,解答下列问题:如图,图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,四三层有5个圆圈,……,第六层有11个圆圈.(1)如果要你继续画下去,那么第八层有__________个不同的小圆圈,第n 层有_________个小圆圈b a 0BA(2)数图中的圆圈个数可以有多种不同的方法.比如:前两层的圆圈个数可以有多种不同的方法.由此得,3132+=.同样,由前三层的圆圈个数和得:21353++=.由前四层的圆圈个数和得:213574+++=.由前五层的圆圈个数和得:2135795++++=.……根据上述过程,请你猜想:13519++++=……___________;从1开始的n 个连续奇数之和是_________.(3)运用以上规律计算:101103105199++++……的和.(4)实际应用:事实上计算时,我们发现,从第一个数开始,后面的每个数与它的前面一个数的差都是一个相等的常数,具有这种规律的一列数,除了直接相加外,我们还可以用下列公式来求和S ,1()2n n a a S +=(其中n 表示数的个数,1a 表示第一个数,n a 表示最后一个数),所以50(199)135********⨯++++++==……. 用上面的知识解答下面问题:某公司对外招商承包一分公司,符合条件的两企业A 、B 分别拟定上缴利润方案如下:A :每年结算一次上缴利润,第一年上缴1.5万元,以后每年比前一年增加1万元;B :每半年结算一次上缴利润,第一个半年上缴0.3万元,以后每半年比前年增加0.3万元; ①如果承包期限为n 年,试用n 的代数式分别表示出A 、B 两企业上缴利润的总金额.②当承包期限20n =时,通过计算说明哪个企业上缴利润的总金额比较多?多多少元?。
西吉县2016至2017学年度第二学期七年级数学(下)中期质量检测试卷

七年级数学(下)期中试卷 第1页,共8页七年级数学(下)期中试卷 第2页,共8页…………密…………封…………线…………内…………不…………要…………答…………题…………○………班级: 姓名: 学号:西吉县2016至2017学年度第二学期期中质量检测试卷七年级数学(下)试题命题:西吉三中 张尚注意事项: 1.考试内容:第五章 相交线与平行线 第六章 实数 第七章 平面直角坐标系 2.本试卷共8页,全卷总分120分,答题时间120分钟 3.答题前将密封线内的项目填写清楚3.使用答题卡的考生,将所有答案全部答在答题卡相应的位置上.一、选择题:(每小题3分,共24分)1.如图所示,∠1和∠2是对顶角的是( )2.16的平方根是( )A.4B.±4C.8D.±83.在实数-3.14, 2, 0, π,16, 0.1010010001……中无理数的个数有 ( ) A.1个 B.2个 C.3个 D.4个 4.立方根等于它本身的有( )A.-1,0,1B.0,1C.0,-1D.15.线段CD 是由线段AB 平移得到的,点A(1,2)的对应点C(3,4),则点B(4,7)的对应点D 的坐标为( )A .(-1,0) B. (6,9) C .(0,-1) D .(9,6)6.下列图形中,由AB ∥CD ,能得到∠1=∠2的是( )A. B. C. D. 7.如果点P (5,y )在第四象限,则y 的取值范围( )A.y<0B.y>0C.y 大于或等于0D.y 小于或等于0 . 8.如图,AB//EF, BC//DE, ∠B=70°,则∠E 的度数为( )。
A 、90°, B 、110° C 、130°, D 、160°,二、填空题:(每小题3分,共24分) 9的平方根是 ;10.已知81.16=4.1,则1681.0=____________. 11.如图,直线AB 、CD 相交于点O ,OE ⊥AB ,O 为垂足, 如果∠EOD = 38°,则∠AOC = .12.如图,直线a 和b 相交于点O ,若∠1=50°, 则∠2= 度,∠3= 度.13.如图,已知∠1=∠2,∠B=40°,则∠3= 度.总分 一 二 三 四 复核人12 1 2121 2ABCDABC DABCD A BCD11题图ABE FCD12题图13题图…………○…………密…………封…………线…………内…………不…………要…………答…………题…………14.在数轴上离原点的距离为的点表示的数是 ;15.把命题“同角的补角相等”改写成“如果......,那么......”的形式: 。
16-17一登分表
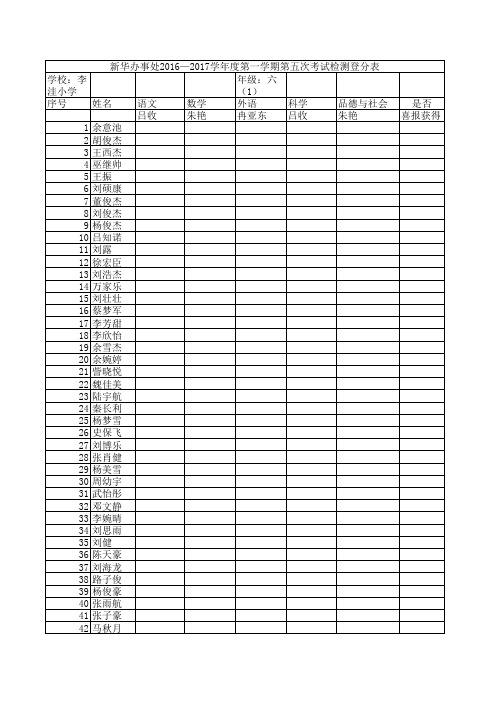
学校:李 洼小学
年级:六(2)
序号 姓名 语文
数学
外语
科学
品德与社会
吕收
贾全平 冉亚东 贾全平 贾全平
1 余志文
2 张家乐
3 董梦雪
4 吕胜南
5 王宇航
6 肖文强
7 于振威
8 刘浩然
9 刘羽杰
10 朱祥宇
11 蔡佳乐
12 余满江
13 许为
14 朱志杰
15 刘鹏程
16 刘忠義
17 邹义杰
18 胡可
19 胡晓倩
新华办事处2016—2017学年度第一学期第五次考试检测登分表
学校:李 洼小学
年级:四 年级(2) 班
序号 姓名 语文
数学
英语
思品
科学
曹慧
何颖华 于红
何颖华 谷春颍
1 宗立慧
2 宗佳琦
3 刘浩宇
4 李依灵
5 吕超凡
6 吕俊豪
7 陈智贤
8 胡瑞
9 张宇翔
10 李宇豪
11 吕如意
12 余俊豪
13 余佳豪
新华办事处2016—2017学年度第一学期第五次考试检测登分表
学校:李 洼小学
年级:五年级(1)班
序号 姓名 语文
数学
英语
科学
品德与社会
刘超
邓宁玉 高超
史金杰 邓宁玉
1 张豪杰
2 刘智俊
3 刘俊
4 邓煜
5 余东瑞
6 吕羿
7 余春祥
8 李亮
9 陈炜
10 刘于豪
11 杨雨晴
12 路晨晨
13 王雨彤
14 高佳瑞
15 史雪晴
16 蔡晓萍
2016-----2017学年度九集中学第一阶段测试数学试卷(1)

2016----2017学年度九集中学八上第一阶段测试数学试卷一.选择题(12小题,每小题3分,共36分。
)1.下列式子:①;②;③﹣;④;⑤,是二次根式的有()A.①③B.①③⑤C.①②③D.①②③⑤2.若式子有意义,则x的取值范围为()A.x≥2 B.x≠3 C.x≥2或x≠3 D.x≥2且x≠33.下列各式中,与是同类二次根式的是()A .B .C .D .4.下列计算中正确的是()A .+=B .﹣=C.2+=2D .+=45.如图所示:数轴上点A所表示的数为a,则a的值是()A .+1B .﹣+1C .﹣1D .6.若一直角三角形两边长分别为12和5,则第三边长为()A.13 B.13或C.13或15 D.157.如图,已知两正方形的面积分别是25和169,则字母B所代表的正方形的面积是()A.12 B.13 C.144 D.1948.A、B、C、D为同一平面内四个点,从下面这四个条件中任意选两个,能使四边形ABCD是平行四边形选法有()①AB∥CD ②AB=CD ③BC∥AD ④BC=AD.A.5种B.4种C.3种D.2种9.如图,△ABC中,已知AB=8,∠C=90°,∠A=30°,DE是中位线,则DE的长为()A.4 B.3 C .D.210.如图,平行四边形ABCD的顶点坐标分别为A(1,4)、B(1,1)、C(5,2),则点D的坐标为()A.(5,5)B.(5,6)C.(6,6)D.(5,4)11.如图,四边形ABCD的对角线互相平分,要使它成为矩形,那么需要添加的条件是()A.AB=CD B.AD=BC C.AB=BC D.AC=BD12.如图,在矩形ABCD中,AB=3,AD=4,P是AD上一动点,PF⊥BD于F,PE⊥AC于E,则PE+PF的值为()A .B .C .D.5二.填空题(共5小题,每小题3分,共15分。
)13.已知最简二次根式与能合并成一个二次根式,则(a+b)2012的值为14.如图,将一根25cm长的细木棒放入长、宽、高分别为8cm、6cm 和cm的长方体无盖盒子中,则细木棒露在盒外面的最短长度是cm.15.如图,某宾馆在重新装修后,准备在大厅的主楼梯上铺上红色地毯,已知这种地毯每平方米售价20元,主楼梯宽2米.则购地毯至少需要元.16如图,矩形ABCD的周长为12cm,E为BC的中点,AE⊥ED于点E,则AB=.17.如图,在△ABC中,AB=AC=7,BC=6,AF⊥BC于F,BE⊥AC于E,D是AB的中点,则△DEF的周长是.三.解答题(共9小题,共66分)18.(8分)计算:(1) (2)2﹣2﹣4×+|﹣|+(3.14﹣π)0 19.(5分)先化简,再求值:(+)÷,其中a=+1.20.(5分)某工厂的大门如图所示,其中四边形ABCD是长方形,上部是以AB为直径的半圆,其中AD=2.3米,AB=2米,现有一辆装满货物的卡车,高2.5米,宽1.6米,问这辆车能否通过厂门?说明理由.21.(8分)如图,在▱ABCD中,F是AD的中点,延长BC到点E,使CE=BC,连接DE,CF.(1)求证:四边形CEDF是平行四边形;(2)若AB=4,AD=6,∠B=60°,求DE的长.22.(6分)如图,△ABC中,点D,E分别是边BC,AC的中点,连接DE,AD,点F在BA的延长线上,且AF=AB,连接EF,判断四边形ADEF的形状,并加以证明.23.(6分)如图所示,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.请判断△PMN的形状,并说明理由.24.(8分)如图,△ABC中,AD是高,CE是中线,点G是CE的中点,DG⊥CE,点G为垂足.(1)求证:DC=BE;(2)若∠AEC=66°,求∠BCE的度数.25.(10分)如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)线段BD与CD有什么数量关系,并说明理由;(2)当△ABC满足什么条件时(指△ABC的三条边、三个角满足什么),四边形AFBD是矩形?并说明理由.26.(10分)如图,O是矩形ABCD的对角线的交点,E、F、G、H分别是OA、OB、OC、OD上的点,且AE=BF=CG=DH.(1)求证:四边形EFGH是矩形;(2)若E、F、G、H分别是OA、OB、OC、OD的中点,且DG⊥AC,OF=2cm,求矩形ABCD的面积.2016-----2017学年度九集中学第一阶段测试数学试卷一.选择题(共13小题)1.(2016春•鄂城区期中)下列式子:①;②;③﹣;④;⑤,是二次根式的有()A.①③B.①③⑤C.①②③D.①②③⑤【解答】解:是二次根式的有①③⑤;②中被开方数小于0无意义,④是三次根式.故选B.2.(2016•乐亭县一模)若式子有意义,则x的取值范围为()A.x≥2 B.x≠3 C.x≥2或x≠3 D.x≥2且x≠3【解答】解:根据二次根式有意义,分式有意义得:x﹣2≥0且x﹣3≠0,解得:x≥2且x≠3.故选D.3.(2016•黄冈模拟)下列各式中,与是同类二次根式的是()A .B .C .D .【解答】解:A 、=3与被开方数不同,不是同类二次根式;B 、=3与被开方数相同,是同类二次根式;C 、=3与被开方数不同,不是同类二次根式;D 、=2与被开方数不同,不是同类二次根式.故选B.4.(2016春•平南县期末)下列计算中正确的是()A .+= B .﹣= C.2+=2D .+=4【解答】解:A 、和不是同类二次根式,不能合并,故本选项错误;B 、和不是同类二次根式,不能合并,故本选项错误;C、2和不是同类二次根式,不能合并,故本选项错误;D 、+=2+2=4,计算正确,故本选项正确.故选D.5.如图所示:数轴上点A所表示的数为a,则a的值是()A .+1B .﹣+1C .﹣1D .【解答】解:图中的直角三角形的两直角边为1和2,∴斜边长为:=,∴﹣1到A 的距离是,那么点A 所表示的数为:﹣1.故选C.6.若一直角三角形两边长分别为12和5,则第三边长为()A.13 B.13或C.13或15 D.15【解答】解:当12是斜边时,第三边是=;当12是直角边时,第三边是=13.故选B.7.(2016春•平南县期末)如图,已知两正方形的面积分别是25和169,则字母B所代表的正方形的面积是()A.12 B.13 C.144 D.194【解答】解:字母B所代表的正方形的面积=169﹣25=144.故选C.8.【解答】解:①和③根据两组对边分别平行的四边形是平行四边形,能推出四边形ABCD为平行四边形;①和②,③和④根据一组对边平行且相等的四边形是平行四边形,能推出四边形ABCD为平行四边形;②和④根据两组对边分别相等的四边形是平行四边形,能推出四边形ABCD为平行四边形;所以能推出四边形ABCD为平行四边形的有四组,故选B.9.如图,△ABC中,已知AB=8,∠C=90°,∠A=30°,DE是中位线,则DE的长为()A.4 B.3 C .D.2【解答】解:∵∠C=90°,∠A=30°,∴BC=AB=4,又∵DE是中位线,∴DE=BC=2.故选D.10.(2016•武汉校级模拟)如图,▱ABCD的顶点坐标分别为A(1,4)、B(1,1)、C(5,2),则点D的坐标为()A.(5,5) B.(5,6) C.(6,6) D.(5,4)【解答】解:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∵A(1,4)、B(1,1)、C(5,2),∴AB=3,∴点D的坐标为(5,5).故选A.11.如图,四边形ABCD的对角线互相平分,要使它成为矩形,那么需要添加的条件是()A.AB=CD B.AD=BC C.AB=BC D.AC=BD【解答】解:可添加AC=BD,∵四边形ABCD的对角线互相平分,∴四边形ABCD是平行四边形,∵AC=BD,根据矩形判定定理对角线相等的平行四边形是矩形,∴四边形ABCD是矩形,故选:D.12.(2016春•莘县期中)如图,在矩形ABCD中,AB=3,AD=4,P是AD上一动点,PF⊥BD于F,PE⊥AC于E,则PE+PF的值为()A .B .C .D.5【解答】解:连接OP,∵四边形ABCD是矩形,∴∠BAD=90°,AC=BD,OA=OC,OB=OD,∴OA=OD=BD,S△AOD=S△AOB,∵AB=3,AD=4,∴S矩形ABCD=3×4=12,BD==5,∴S△AOD=S矩形ABCD=3,OA=OC=,∵S△AOD=S△AOP+S△DOP =OA•PE +OD•PF=××PE +××PF=(PE+PF)=3,∴PE+PF=.故选B.二.填空题(共4小题)13.已知最简二次根式与能合并成一个二次根式,则(a+b)2012的值为1.【解答】解:根据题意得:4a+3b=2a﹣b,b+3=2则a=2,b=﹣1所以a+b=1则(a+b)2012的值为1.故答案是:1.14.【解答】解:由题意知:盒子底面对角长为=10cm,盒子的对角线长:=20cm,细木棒长25cm,故细木棒露在盒外面的最短长度是:25﹣20=5cm.故答案为:515.如图,某宾馆在重新装修后,准备在大厅的主楼梯上铺上红色地毯,已知这种地毯每平方米售价20元,主楼梯宽2米.则购地毯至少需要280元.【解答】解:利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,∵所有竖直台阶的长为5,水平台阶的长为=4,∴地毯的长度为3+4=7米,地毯的面积为7×2=14平方米,∴购买这种地毯至少需要20×14=280元.故答案为:280.16.解:设AB的长度为xcm,则AE=x,AD=2x,依题意列方程得x+2x=6,x=2,所以AB=2cm.故答案为:2.17.(2016秋•苏州期末)如图,在△ABC中,AB=AC=7,BC=6,AF⊥BC于F,BE⊥AC于E,D是AB的中点,则△DEF的周长是10.【解答】解:∵AF⊥BC,BE⊥AC,D是AB的中点,∴DE=DF=AB=×7=3.5,∵AB=AC,AF⊥BC,∴点F是BC的中点,∵BE⊥AC,∴EF=BC=×6=3,∴△DEF的周长=DE+DF+EF=3.5+3.5+3=10.故答案为:10.三.解答题(共9小题)18.(2016•德州校级自主招生)计算:.【解答】解:原式=﹣+2=4﹣+2=4+.计算:2﹣2﹣4×+|﹣|+(3.14﹣π)0.【解答】解:原式=﹣4×+2+1=19.【解答】解:原式=(+)÷,=•,=•,=.当a=+1时,原式==.20.(2014秋•昌图县期末)某工厂的大门如图所示,其中四边形ABCD是长方形,上部是以AB为直径的半圆,其中AD=2.3米,AB=2米,现有一辆装满货物的卡车,高2.5米,宽1.6米,问这辆车能否通过厂门?说明理由.【解答】解:能通过,理由如下:设点O为半圆的圆心,则O为AB的中点,OG为半圆的半径,如图,∵直径AB=2(已知),∴半径OG=1,OF=1.6÷2=0.8,∴在Rt△OFG中,FG2=OG2﹣OF2=12﹣0.82=0.36;∴FG=0.6∴EG=0.6+2.3=2.9>2.5.∴能通过.21.(2013•北京)如图,在▱ABCD中,F是AD的中点,延长BC到点E,使CE=BC,连接DE,CF.(1)求证:四边形CEDF是平行四边形;(2)若AB=4,AD=6,∠B=60°,求DE的长.【解答】证明:(1)在▱ABCD中,AD∥BC,且AD=BC.∵F是AD的中点,∴DF=.又∵CE=BC,∴DF=CE,且DF∥CE,∴四边形CEDF是平行四边形;(2)解:如图,过点D作DH⊥BE于点H.在▱ABCD中,∵∠B=60°,∴∠DCE=60°.∵AB=4,∴CD=AB=4,∴CH=CD=2,DH=2.在▱CEDF中,CE=DF=AD=3,则EH=1.∴在Rt△DHE中,根据勾股定理知DE==.22.如图,△ABC中,点D,E分别是边BC,AC的中点,连接DE,AD,点F在BA的延长线上,且AF=AB,连接EF,判断四边形ADEF的形状,并加以证明.【解答】答:四边形ADEF是平行四边形.证明:∵点D,E分别是边BC,AC的中点,∴DE∥BF,DE=AB,∵AF=AB,∴DE=AF,∴四边形ADEF是平行四边形.23.如图所示,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.请判断△PMN的形状,并说明理由.【解答】解:△PMN是等腰三角形.理由如下:∵点P是BD的中点,点M是CD的中点,∴PM=BC,同理:PN=AD,∵AD=BC,∴PM=PN,∴△PMN是等腰三角形.24.(2016秋•泰兴市校级期中)如图,△ABC中,AD是高,CE是中线,点G是CE的中点,DG⊥CE,点G为垂足.(1)求证:DC=BE;(2)若∠AEC=66°,求∠BCE的度数.【解答】解:(1)如图,∵G是CE的中点,DG⊥CE,∴DG是CE的垂直平分线,∴DE=DC,∵AD是高,CE是中线,∴DE是Rt△ADB的斜边AB上的中线,∴DE=BE=AB,∴DC=BE;(2)∵DE=DC,∴∠DEC=∠BCE,∴∠EDB=∠DEC+∠BCE=2∠BCE,∵DE=BE,∴∠B=∠EDB,∴∠B=2∠BCE,∴∠AEC=3∠BCE=66°,则∠BCE=22°.25.【解答】解:(1)BD=CD.理由如下:依题意得AF∥BC,∴∠AFE=∠DCE,∵E是AD的中点,∴AE=DE,在△AEF和△DEC中,,∴△AEF≌△DEC(AAS),∴AF=CD,∵AF=BD,∴BD=CD;(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.理由如下:∵AF∥BD,AF=BD,∴四边形AFBD是平行四边形,∵AB=AC,BD=CD(三线合一),∴∠ADB=90°,∴▱AFBD是矩形.26.如图,O是矩形ABCD的对角线的交点,E、F、G、H分别是OA、OB、OC、OD 上的点,且AE=BF=CG=DH.(1)求证:四边形EFGH是矩形;(2)若E、F、G、H分别是OA、OB、OC、OD的中点,且DG⊥AC,OF=2cm,求矩形ABCD的面积.【解答】(1)证明:∵四边形ABCD是矩形,∴OA=0B=OC=OD,∵AE=BF=CG=DH,∴AO﹣AE=OB﹣BF=CO﹣CG=DO﹣DH,即:OE=OF=OG=OH,∴四边形EFGH是矩形;(2)解:∵G是OC的中点,∴GO=GC,∵DG⊥AC,∴∠DGO=∠DGC=90°,又∵DG=DG,∴△DGC≌△DGO,∴CD=OD,∵F是BO中点,OF=2cm,∴BO=4cm,∵四边形ABCD是矩形,∴DO=BO=4cm,∴DC=4cm,DB=8cm,∴CB==4,∴矩形ABCD的面积=4×4=16cm2.。
宜春三中2016-2017学年七年级上期中数学试卷含答案解析

2016-2017学年江西省宜春三中七年级(上)期中数学试卷一、选择题:1.﹣3的倒数是()A.﹣3 B.3 C.﹣ D.2.下列运算有错误的是()A.8﹣(﹣2)=10 B.﹣5÷(﹣)=10 C.(﹣5)+(+3)=﹣8 D.﹣1×(﹣)=3.预计下届世博会将吸引约69 000 000人次参观.将69 000 000用科学记数法表示正确的是()A.0.69×108B.6.9×106C.6.9×107D.69×1064.在数轴上有两个点A、B,点A表示﹣3,点B与点A相距5.5个单位长度,则点B表示的数为()A.﹣2.5或8.5 B.2.5或﹣8.5 C.﹣2.5 D.﹣8.55.下列式子:x2+2, +4,,,﹣5x,0中,整式的个数是()A.6 B.5 C.4 D.36.长方形窗户上的装饰物如图所示,它是由半径均为b的两个四分之一圆组成,则能射进阳光部分的面积是()A.2a2﹣πb2 B.2a2﹣b2C.2ab﹣πb2D.2ab﹣b27.已知多项式x2+3x=3,可求得另一个多项式3x2+9x﹣4的值为()A.3 B.4 C.5 D.6二、填空题:(本大题共8小题,每小题3分,共24分)8.如果把收入30元记作+30元,那么支出20元可记作.9.用四舍五入法将1.893 5取近似数并精确到0.001,得到的值是.10.多项式x3y+2xy2﹣y5﹣12x3是次多项式,它的最高次项是.11.若有理数a,b满足|a+3|+(b﹣2)2=0,则a b= .12.若单项式﹣3a m b3与4a2b n是同类项,则m+n= .13.若a与b互为相反数,c与d互为倒数,则(a+b)3﹣3(cd)2015= .14.规定一种新运算 a△b=a×b﹣a+b+1.如,3△4=3×4﹣3+4+1=12﹣3+4+1=14,则﹣2△5= .15.用火柴棒按如图所示的方式摆图形,按照这样的规律继续摆下去,第n个图形需要根火柴棒(用含n的代数式表示).三、计算题16.计算:﹣3.7﹣(﹣)﹣1.3.17.计算:(﹣﹣+)÷(﹣)18.计算:[(﹣1)100+(1﹣)×]÷(﹣32+2)19.﹣24﹣×[5﹣(﹣3)2].四、解答题20.化简求值:(3a2b﹣2ab2)﹣(ab2﹣2a2b+7),其中a=﹣1,b=2.21.在数轴上表示下列各数:1.5,0,﹣3,﹣(﹣),﹣|﹣4|,并用“<”号把它们连接起来.(2)根据(1)中的数轴,找出大于﹣|﹣4|的最小整数和小于﹣(﹣)的最大整数,并求出它们的和.22.如图,将边长为2的小正方形和边长为x的大正方形放在一起.(1)用x表示阴影部分的面积;(2)计算当x=5时,阴影部分的面积.五、23.某市有甲、乙两种出租车,他们的服务质量相同.甲的计价方式为:当行驶路程不超过3千米时收费10元,每超过1千米则另外收费1.2元(不足1千米按1千米收费);乙的计价方式为:当行驶路程不超过3千米时收费8元,每超过1千米则另外收费1.8元(不足1千米按1千米收费).某人到该市出差,需要乘坐的路程为x千米.(1)当x=5时,请分别求出乘坐甲、乙两种出租车的费用;(2)用代数式表示此人分别乘坐甲、乙出租车各所需要的费用;(3)假设此人乘坐的路程为13千米多一点,请问他乘坐哪种车较合算?24.已知a,b,c在数轴上的位置如图所示,所对应的点分别为A,B,C.(1)填空:A、B之间的距离为,B、C之间的距离为,A、C之间的距离为;(2)化简:|a+b|﹣|c﹣b|+|b﹣a|;(3)a、b、c在数轴上的位置如图所示,且c2=4,﹣b的倒数是它本身,a的绝对值的相反数是﹣2,求﹣a+2b﹣c﹣2(a﹣4c﹣b)的值.2016-2017学年江西省宜春三中七年级(上)期中数学试卷参考答案与试题解析一、选择题:1.﹣3的倒数是()A.﹣3 B.3 C.﹣ D.【考点】倒数.【分析】根据倒数的定义可得﹣3的倒数是﹣.【解答】解:﹣3的倒数是﹣.故选:C.【点评】主要考查倒数的概念及性质.倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.2.下列运算有错误的是()A.8﹣(﹣2)=10 B.﹣5÷(﹣)=10 C.(﹣5)+(+3)=﹣8 D.﹣1×(﹣)=【考点】有理数的混合运算.【专题】计算题.【分析】原式各项计算得到结果,即可做出判断.【解答】解:A、原式=8+2=10,正确;B、原式=﹣5×(﹣2)=10,正确;C、原式=﹣5+3=﹣2,错误;D、原式=,正确.故选C【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.3.预计下届世博会将吸引约69 000 000人次参观.将69 000 000用科学记数法表示正确的是()A.0.69×108B.6.9×106C.6.9×107D.69×106【考点】科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将69 000 000用科学记数法表示为:6.9×107.故选:C.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.4.在数轴上有两个点A、B,点A表示﹣3,点B与点A相距5.5个单位长度,则点B表示的数为()A.﹣2.5或8.5 B.2.5或﹣8.5 C.﹣2.5 D.﹣8.5【考点】数轴.【分析】设B点表示的数为b,再根据数轴上两点间的距离公式求出b的值即可.【解答】解:设B点表示的数为b,∵点A表示﹣3,点B与点A相距5.5个单位长度,∴|b+3|=5.5,解得b=2.5或﹣8.5.故选B.【点评】本题考查的是数轴,熟知数轴上两点间的距离公式是解答此题的关键.5.下列式子:x2+2, +4,,,﹣5x,0中,整式的个数是()A.6 B.5 C.4 D.3【考点】整式.【专题】应用题.【分析】根据整式的定义分析判断各个式子,从而得到正确选项.【解答】解:式子x2+2,,﹣5x,0,符合整式的定义,都是整式;+4,这两个式子的分母中都含有字母,不是整式.故整式共有4个.故选:C.【点评】本题主要考查了整式的定义:单项式和多项式统称为整式.注意整式是有理式的一部分,在有理式中可以包含加,减,乘,除四种运算,但在整式中除式不能含有字母.单项式是数字或字母的积,其中单独的一个数或字母也是单项式;多项式是几个单项式的和,多项式含有加减运算.6.长方形窗户上的装饰物如图所示,它是由半径均为b的两个四分之一圆组成,则能射进阳光部分的面积是()A.2a2﹣πb2 B.2a2﹣b2C.2ab﹣πb2D.2ab﹣b2【考点】列代数式.【分析】根据题意列出代数式解答即可.【解答】解:能射进阳光部分的面积是2ab﹣b2,故选D【点评】此题考查了列代数式,弄清题意是解本题的关键.7.已知多项式x2+3x=3,可求得另一个多项式3x2+9x﹣4的值为()A.3 B.4 C.5 D.6【考点】代数式求值.【分析】先把3x2+9x﹣4变形为3(x2+3x)﹣4,然后把x2+3x=3整体代入计算即可.【解答】解:∵x2+3x=3,∴3x2+9x﹣4=3(x2+3x)﹣4=3×3﹣4=9﹣4=5.故选:C.【点评】本题考查了代数式求值:先把所求的代数式根据已知条件进行变形,然后利用整体思想进行计算.二、填空题:(本大题共8小题,每小题3分,共24分)8.如果把收入30元记作+30元,那么支出20元可记作﹣20元.【考点】正数和负数.【分析】答题时首先知道正负数的含义,在用正负数表示向指定方向变化的量时,通常把向指定方向变化的量规定为正数,而把向指定方向的相反方向变化的量规定为负数.【解答】解:由收入为正数,则支出为负数,故收入30元记作+30元,那么支出20元可记作﹣20元.【点评】本题主要考查正数和负数的知识点,理解正数与负数的相反意义,比较简单.9.用四舍五入法将1.893 5取近似数并精确到0.001,得到的值是 1.894 .【考点】近似数和有效数字.【分析】精确到哪一位,即对下一位的数字进行四舍五入.【解答】解:用四舍五入法将1.893 5取近似数并精确到0.001,得到的值是1.894.故答案为:1.894.【点评】本题主要考查了近似数与精确度,近似数最后一位在哪一位,就精确到哪一位.10.多项式x3y+2xy2﹣y5﹣12x3是 5 次多项式,它的最高次项是﹣y5.【考点】多项式.【分析】根据多项式次数的定义求解.多项式的次数是多项式中最高次项的次数,据此即可求解.【解答】解:多项式x3y+2xy2﹣y5﹣12x3是5次多项式,它的最高次项是﹣y5.故答案为:5,﹣y5.【点评】此题考查的是多项式的定义,多项式中每个单项式叫做多项式的项,这些单项式中的最高次数,就是这个多项式的次数.11.若有理数a,b满足|a+3|+(b﹣2)2=0,则a b= 9 .【考点】非负数的性质:偶次方;非负数的性质:绝对值.【分析】根据非负数的性质列出方程求出a、b的值,代入所求代数式计算即可.【解答】解:由题意得,a+3=0,b﹣2=0,解得,a=﹣3,b=2,则a b=9.故答案为:9.【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.12.若单项式﹣3a m b3与4a2b n是同类项,则m+n= 5 .【考点】同类项.【分析】根据同类项的定义解答.【解答】解:∵单项式﹣3a m b3与4a2b n是同类项,∴m=2,n=3,m+n=2+3=5.故答案为5.【点评】本题考查了同类项的定义,要注意同类项定义中的两个“相同”:(1)所含字母相同;(2)相同字母的指数相同,是易混点,因此成了中考的常考点.13.若a与b互为相反数,c与d互为倒数,则(a+b)3﹣3(cd)2015= ﹣3 .【考点】代数式求值.【分析】根据a与b互为相反数,c与d互为倒数,可以得到:a+b=0,cd=1.代入求值即可求解.【解答】解:∵a与b互为相反数,c与d互为倒数,∴a+b=0,cd=1.∴(a+b)3﹣3(cd)2015=0﹣3×1=﹣3.故答案是:﹣3.【点评】本题考查了相反数,倒数的定义,正确理解定义是关键.14.规定一种新运算 a△b=a×b﹣a+b+1.如,3△4=3×4﹣3+4+1=12﹣3+4+1=14,则﹣2△5= ﹣2 .【考点】有理数的混合运算.【专题】计算题;实数.【分析】原式利用题中的新定义计算即可得到结果.【解答】解:根据题中的新定义得:﹣2△5=﹣10+2+5+1=﹣2,故答案为:﹣2【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.15.用火柴棒按如图所示的方式摆图形,按照这样的规律继续摆下去,第n个图形需要5n+1 根火柴棒(用含n的代数式表示).【考点】规律型:图形的变化类.【分析】仔细观察发现每增加一个正六边形其火柴根数增加5根,将此规律用代数式表示出来即可.【解答】解:由图可知:图形标号(1)的火柴棒根数为6;图形标号(2)的火柴棒根数为11;图形标号(3)的火柴棒根数为16;…由该搭建方式可得出规律:图形标号每增加1,火柴棒的个数增加5,所以可以得出规律:搭第n个图形需要火柴根数为:6+5(n﹣1)=5n+1,故答案为:5n+1.【点评】本题是一道关于图形变化规律型的,关键在于通过题中图形的变化情况,通过归纳与总结找出普遍规律求解即可.三、计算题16.计算:﹣3.7﹣(﹣)﹣1.3.【考点】有理数的减法.【分析】根据有理数的减法运算法则和加法运算法则进行计算即可得解.【解答】解:﹣3.7﹣(﹣)﹣1.3,=+﹣3.7﹣1.3,=1﹣5,=﹣4.【点评】本题考查了有理数的减法和加法运算,熟记运算法则是解题的关键.17.计算:(﹣﹣+)÷(﹣)【考点】有理数的除法.【分析】将除法变为乘法,再根据乘法分配律计算即可求解.【解答】解:原式=(﹣﹣+)×(﹣36)=﹣×(﹣36)﹣×(﹣36)+×(﹣36)=27+20﹣21=26.【点评】此题考查有理数的混合运算,掌握运算顺序,正确判定运算符号计算即可.18.计算:[(﹣1)100+(1﹣)×]÷(﹣32+2)【考点】有理数的混合运算.【专题】计算题;实数.【分析】原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.【解答】解:原式=(1+)÷(﹣7)=×(﹣)=﹣.【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.19.﹣24﹣×[5﹣(﹣3)2].【考点】有理数的混合运算.【分析】首先计算括号内的式子,计算乘方,然后计算乘法,最后进行加减即可.【解答】解:原式=﹣16﹣×(5﹣9)=﹣16﹣×(﹣4)=﹣16+2=﹣14【点评】本题考查的是有理数的运算能力.注意:要正确掌握运算顺序,即乘方运算(和以后学习的开方运算)叫做三级运算;乘法和除法叫做二级运算;加法和减法叫做一级运算.在混合运算中要特别注意运算顺序:先三级,后二级,再一级;有括号的先算括号里面的;同级运算按从左到右的顺序.四、解答题20.化简求值:(3a2b﹣2ab2)﹣(ab2﹣2a2b+7),其中a=﹣1,b=2.【考点】整式的加减—化简求值.【专题】计算题;整式.【分析】原式去括号合并得到最简结果,把a与b的值代入计算即可求出值.【解答】解:原式=3a2b﹣2ab2﹣ab2+2a2b﹣7=5a2b﹣3ab2﹣7,当a=﹣1,b=2时,原式=10+12﹣7=15.【点评】此题考查了整式的加减﹣化简求值,熟练掌握运算法则是解本题的关键.21.(1)在数轴上表示下列各数:1.5,0,﹣3,﹣(﹣),﹣|﹣4|,并用“<”号把它们连接起来.(2)根据(1)中的数轴,找出大于﹣|﹣4|的最小整数和小于﹣(﹣)的最大整数,并求出它们的和.【考点】有理数大小比较;数轴;绝对值.【分析】(1)先在数轴上表示各个数,再比较即可;(2)先找出最小整数和最大整数,再求出和即可.【解答】解:(1)﹣|﹣4|<﹣3<0<1.5<﹣(﹣);(2)大于﹣|﹣4|的最小整数是﹣4,小于﹣(﹣)的最大整数是5,和为﹣4+5=1.【点评】本题考查了数轴,绝对值,有理数的大小比较的应用,能在数轴上正确表示出各个数是解此题的关键.22.如图,将边长为2的小正方形和边长为x的大正方形放在一起.(1)用x表示阴影部分的面积;(2)计算当x=5时,阴影部分的面积.【考点】列代数式.【分析】阴影部分面积利用三角形面积公式进行计算,代入已知数值即可求得面积具体数值.【解答】解:(1)阴影部分的面积为×2(2+x)+x2;(2)x=5时,×2(2+x)+x2=2+5+12.5=19.5【点评】此题考查列代数式问题,关键是利用三角形面积公式计算三角形的面积解答即可.五、23.某市有甲、乙两种出租车,他们的服务质量相同.甲的计价方式为:当行驶路程不超过3千米时收费10元,每超过1千米则另外收费1.2元(不足1千米按1千米收费);乙的计价方式为:当行驶路程不超过3千米时收费8元,每超过1千米则另外收费1.8元(不足1千米按1千米收费).某人到该市出差,需要乘坐的路程为x千米.(1)当x=5时,请分别求出乘坐甲、乙两种出租车的费用;(2)用代数式表示此人分别乘坐甲、乙出租车各所需要的费用;(3)假设此人乘坐的路程为13千米多一点,请问他乘坐哪种车较合算?【考点】代数式求值;列代数式.【分析】(1)根据甲乙两种出租车的计价方式分别列式计算即可得解;(2)都分x≤3和x>3两种情况列式表示即可;(3)将x=14分别代入代数式计算即可得解.【解答】解:(1)当x=5时,甲的费用=10+(5﹣3)×1.2=10+2.4=12.4(元),乙的费用=8+(5﹣3)×1.8=8+3.6=11.6(元),答:乘坐甲、乙两种出租车的费用分别为12.4元,11.6元;(2)甲的费用,乙的费用;(3)∵此人乘坐的路程为13千米多一点,∴x=14,甲的费用10+1.2(14﹣3)=10+13.2=23.2(元),乙的费用8+1.8(14﹣3)=8+19.8=27.8(元),∵23.2<27.8,∴他乘坐甲出租车更合算.【点评】本题考查了代数式求值,读懂题目信息,理解两种出租车的计价方式并准确列出算式是解题的关键.24.已知a,b,c在数轴上的位置如图所示,所对应的点分别为A,B,C.(1)填空:A、B之间的距离为a﹣b ,B、C之间的距离为b﹣c ,A、C之间的距离为a﹣c ;(2)化简:|a+b|﹣|c﹣b|+|b﹣a|;(3)a、b、c在数轴上的位置如图所示,且c2=4,﹣b的倒数是它本身,a的绝对值的相反数是﹣2,求﹣a+2b﹣c﹣2(a﹣4c﹣b)的值.【考点】整式的加减;数轴;相反数;绝对值;倒数.【分析】(1).根据两点间距离公式可得;(2)结合数轴根据绝对值性质去绝对值符号,再合并即可得;(3)根据a、b、c在数轴上的位置,结合题目条件得出c=﹣2,b=﹣1,a=2,再将其代入化简后的代数式即可【解答】解:(1)由数轴可知,A、B之间的距离为a﹣b,B、C之间的距离为b﹣c,A、C之间的距离为a﹣c,故答案为:a﹣b,b﹣c,a﹣c;(2)由数轴可知,c<b<0<a,∴原式=a+b+c﹣b﹣(b﹣a)=a+b+c﹣b﹣b+a=2a﹣b+c;(3)由题意得c=﹣2,b=﹣1,a=2,原式=﹣a+2b﹣c﹣2a+8c+2b=﹣3a+4b+7c,当c=﹣2,b=﹣1,a=2时,原式=﹣3×2+4×(﹣1)+7×(﹣2)=﹣6﹣4﹣14=﹣24.【点评】本题主要考查数轴、绝对值性质、整式的化简求值,根据数轴和题目条件判断出a、b、c 的大小关系和数值是解题的关键.。
2016一年级数学期中试卷

2016—2017学年一年级数学上册期中试卷(请认真书写,卷面5分)一、我会填。
(每空1分,6、8题每空2分)1.看图写数。
2.按顺序填数。
(共3分)3.和8相邻的两个数是()和()。
4. 7比4多(),()比9少3。
5. 比一比。
比多()。
比少()6.右边有()个涂上色。
7. 我们上下楼梯要靠()行。
8. 用()个相同的小正方体可以拼成一个大正方体。
二、认识图形我最棒!1. 连一连。
(6分)2. 下面的图形是由几个拼成的?填在( )里。
(6分)( )( ) ( )3. 数一数,填一填。
(8分)三、 画一画。
1.仔细观察下图,在正确答案的下面打“√”。
(共4分)在 的(上 下)面。
在 的 (上 下)面。
在 的 (左 右)面。
在的 (左 右)面。
2.根据算式画图。
(共6分)3+4=() 6-3=()四、我会看图列式。
(共24分)1. 2.3. 4.8只?个5. 6只还剩几个?一共有几只?7. 看图写出两道加法算式和两道减法算式。
(12分)五、口算。
(将口算题卡的答案写在下面的答题卡上,共8分。
)口算答题卡2016—2017一年级上册期中口算试题把答案写在答题卡上。
(满分8分,每小题0.2分,时间5分钟。
)1.直接写得数。
○19-6=○7 6+2= ○135-4=○19 0+9=○256+4=○2 8-1= ○8 8-3= ○14 8-2= ○20 4+4= ○26 10-5=○3 4+2= ○9 1+8= ○15 9-2= ○21 5-3= ○27 3-3=○4 6+1= ○10 9+1= ○16 8-7= ○22 6-3= ○28 0+10=○5 2+4= ○11 1+6= ○17 1+9= ○23 10-3= ○29 7-3=○6 7-4= ○12 4+0= ○18 9-4= ○24 7-6= ○30 4+5=2.在○里填上“+”、“-”、“>”、“<”或“=”。
○18-8○8 ○4 8○2=10 ○7 10○2=8 ○107-2○ 4 ○25○5=0 ○5 3+4○8 ○8 7-0○7○33○5=8 ○69○0=9 ○9 9-5○3。
安徽省合肥2016-2017学年七年级下期中数学试卷及答案解析
2016-2017学年安徽省合肥七年级(下)期中数学试卷一、选择题(每小题3分,共30分)1.等于()A.﹣3 B.3 C.D.﹣2.下列运算正确的是()A.3a+2b=5ab B.a3•a2=a5C.a8•a2=a4D.(2a2)3=﹣6a63.已知空气的单位体积质量为1.24×10﹣3克/厘米3,1.24×10﹣3用小数表示为()A.0.000124 B.0.0124 C.﹣0.00124 D.0.001244.计算的平方根为()A.±4 B.±2 C.4 D.±5.若2x=3,4y=5,则2x﹣2y的值为()A.B.﹣2 C.D.6.加上下列单项式后,仍不能使4x2+1成为一个整式的完全平方式的是()A.4x4B.4x C.﹣4x D.2x7.长方形的面积为4a2﹣6ab+2a,若它的一边长为2a,则它的周长为()A.4a﹣3b B.8a﹣6b C.4a﹣3b+1 D.8a﹣6b+28.若使代数式的值在﹣1和2之间,m可以取的整数有()A.1个B.2个C.3个D.4个9.已知关于x的不等式组整数解有4个,则b的取值范围是()A.7≤b<8 B.7≤b≤8 C.8≤b<9 D.8≤b≤910.7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足()A.a= b B.a=3b C.a= b D.a=4b二、填空题(每小题4分,共20分)11.因式分解:4mn﹣mn3= .12.若与|x+2y﹣5|互为相反数,则(x﹣y)2017= .13.某数的平方根是2a+3和a﹣15,则这个数为.14.已知不等式组的解集为﹣1<x<2,则(m+n)2012= .15.在数轴上,点A(表示整数a)在原点的左侧,点B(表示整数b)在原点的右侧.若|a﹣b|=2016,且AO=2BO,则a+b的值为.三、解答题(第16、17、18题各6分,第19、20题各10分,第21题12分,共50分)16.计算:17.解不等式组,并将解集在数轴上表示出来.18.先化简,再求值,(3x+2)(3x﹣2)﹣5x(x﹣1)﹣(2x﹣1)2,其中x=﹣.19.已知:a+b=2,ab=1.求:(1)a﹣b(2)a2﹣b2+4b.20.若2(x+4)﹣5<3(x+1)+4的最小整数解是方程的解,求代数式m2﹣2m+11的平方根的值.21.某学校组织340名师生进行长途考察活动,带有行李170件,计划租用甲、乙两种型号的汽车10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.(1)请你帮助学校设计所有可行的租车方案;(2)如果甲车的租金为每辆2000元,乙车的租金为每辆1800元,问哪种可行方案使租车费用最省?2016-2017学年安徽省合肥七年级(下)期中数学试卷参考答案与试题解析一、选择题(每小题3分,共30分)1.等于()A.﹣3 B.3 C.D.﹣【考点】24:立方根.【分析】运用开立方的方法计算.【解答】解: =﹣3,故选A.2.下列运算正确的是()A.3a+2b=5ab B.a3•a2=a5C.a8•a2=a4D.(2a2)3=﹣6a6【考点】48:同底数幂的除法;35:合并同类项;46:同底数幂的乘法;47:幂的乘方与积的乘方.【分析】根据同底数幂的除法,底数不变指数相减;合并同类项,系数相加字母和字母的指数不变;同底数幂的乘法,底数不变指数相加;幂的乘方,底数不变指数相乘,对各选项计算后利用排除法求解.【解答】解:A、不是同类项,不能合并,选项错误;B、正确;C、a8•a2=a10,选项错误;D、(2a2)3=8a6,选项错误.故选B.3.已知空气的单位体积质量为1.24×10﹣3克/厘米3,1.24×10﹣3用小数表示为()A.0.000124 B.0.0124 C.﹣0.00124 D.0.00124【考点】1K:科学记数法—原数.【分析】科学记数法的标准形式为a×10n(1≤|a|<10,n为整数).本题把数据“1.24×10﹣3中1.24的小数点向左移动3位就可以得到.【解答】解:把数据“1.24×10﹣3中1.24的小数点向左移动3位就可以得到为0.001 24.故选D.4.计算的平方根为()A.±4 B.±2 C.4 D.±【考点】21:平方根;22:算术平方根.【分析】首先根据算术平方根的定义求出的值,然后根据平方根的定义即可求出结果.【解答】解:∵=4,又∵(±2)2=4,∴4的平方根是±2,即的平方根±2.故选B.5.若2x=3,4y=5,则2x﹣2y的值为()A.B.﹣2 C.D.【考点】48:同底数幂的除法.【分析】利用同底数幂除法的逆运算法则计算即可.【解答】解:∵2x=3,4y=5,∴2x﹣2y=2x÷22y,=2x÷4y,=3÷5,=0.6.故选:A.6.加上下列单项式后,仍不能使4x2+1成为一个整式的完全平方式的是()A.4x4B.4x C.﹣4x D.2x【考点】4E:完全平方式.【分析】根据完全平方公式的结构对各选项进行验证即可得解. 【解答】解:A 、4x 4+4x 2+1=(2x 2+1)2,故本选项错误; B 、4x+4x 2+1=(2x+1)2,故本选项错误; C 、﹣4x+4x 2+1=(2x ﹣1)2,故本选项错误;D 、2x+4x 2+1不能构成完全平方公式结构,故本选项正确. 故选D .7.长方形的面积为4a 2﹣6ab+2a ,若它的一边长为2a ,则它的周长为( ) A .4a ﹣3b B .8a ﹣6b C .4a ﹣3b+1 D .8a ﹣6b+2【考点】4H :整式的除法.【分析】首先利用面积除以一边长即可求得令一边长,则周长即可求解. 【解答】解:另一边长是:(4a 2﹣6ab+2a )÷2a=2a ﹣3b+1, 则周长是:2[(2a ﹣3b+1)+2a]=8a ﹣6b+2. 故选D .8.若使代数式的值在﹣1和2之间,m 可以取的整数有( )A .1个B .2个C .3个D .4个【考点】CC :一元一次不等式组的整数解.【分析】由题意可得不等式组,解不等式组,得到不等式组的解集,然后求其整数解.【解答】解:由题意可得,由①得m >﹣,由②得m <,所以不等式组的解集为﹣<x <, 则m 可以取的整数有0,1共2个. 故选:B .9.已知关于x的不等式组整数解有4个,则b的取值范围是()A.7≤b<8 B.7≤b≤8 C.8≤b<9 D.8≤b≤9【考点】CC:一元一次不等式组的整数解.【分析】首先确定不等式组的解集,先利用含b的式子表示,根据整数解的个数就可以确定有哪些整数解,根据解的情况可以得到关于b的不等式,从而求出b 的范围.【解答】解:由不等式x﹣b≤0,得:x≤b,由不等式x﹣2≥3,得:x≥5,∵不等式组有4个整数解,∴其整数解为5、6、7、8,则8≤b<9,故选:C.10.7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足()A.a= b B.a=3b C.a= b D.a=4b【考点】4I:整式的混合运算.【分析】表示出左上角与右下角部分的面积,求出之差,根据差与BC无关即可求出a与b的关系式.【解答】解:左上角阴影部分的长为AE,宽为AF=3b,右下角阴影部分的长为PC,宽为a,∵AD=BC,即AE+ED=AE+a,BC=BP+PC=4b+PC,∴AE+a=4b+PC,即AE﹣PC=4b﹣a,∴阴影部分面积之差S=AE•AF﹣PC•CG=3bAE﹣aPC=3b(PC+4b﹣a)﹣aPC=(3b ﹣a)PC+12b2﹣3ab,则3b﹣a=0,即a=3b.解法二:既然BC是变化的,当点P与点C重合开始,然后BC向右伸展,设向右伸展长度为X,左上阴影增加的是3bX,右下阴影增加的是aX,因为S不变,∴增加的面积相等,∴3bX=aX,∴a=3b.故选:B.二、填空题(每小题4分,共20分)11.因式分解:4mn﹣mn3= mn(2+n)(2﹣n).【考点】55:提公因式法与公式法的综合运用.【分析】原式提取公因式,再利用平方差公式分解即可.【解答】解:原式=mn(4﹣n2)=mn(2+n)(2﹣n),故答案为:mn(2+n)(2﹣n)12.若与|x+2y﹣5|互为相反数,则(x﹣y)2017= ﹣1 .【考点】98:解二元一次方程组;16:非负数的性质:绝对值;23:非负数的性质:算术平方根.【分析】利用相反数性质及非负数性质列出方程组,求出方程组的解得到x与y的值,代入原式计算即可得到结果.【解答】解:∵与|x+2y﹣5|互为相反数,∴+|x+2y﹣5|=0,∴,①×2+②得:5x=5,解得:x=1,把x=1代入②得:y=2,则原式=﹣1,故答案为:﹣113.某数的平方根是2a+3和a﹣15,则这个数为121 .【考点】21:平方根;86:解一元一次方程.【分析】根据正数有两个平方根,这两个平方根互为相反数,据此即可得到关于a的方程即可求得a的值,进而求得这个数的值.【解答】解:根据题意得:2a+3+(a﹣15)=0,解得a=4,则这个数是(2a+3)2=121.故答案为:121.14.已知不等式组的解集为﹣1<x<2,则(m+n)2012= 1 .【考点】CB:解一元一次不等式组;98:解二元一次方程组;C6:解一元一次不等式.【分析】求出不等式组的解集,根据已知不等式组的解集得出m+n﹣2=﹣1,m=2,求出m、n的值,再代入求出即可.【解答】解:,解不等式①得:x>m+n﹣2,解不等式②得:x<m,∴不等式组的解集为:m+n﹣2<x<m,∵不等式组的解集为﹣1<x<2,∴m+n﹣2=﹣1,m=2,解得:m=2,n=﹣1,∴(m+n)2012=(2﹣1)2012=1.故答案为:1.15.在数轴上,点A(表示整数a)在原点的左侧,点B(表示整数b)在原点的右侧.若|a﹣b|=2016,且AO=2BO,则a+b的值为﹣672 .【考点】33:代数式求值;13:数轴.【分析】依据绝对自的定义可知b﹣a=2016,﹣a=2b,从而可求得a、b的值,故此可求得a+b的值.【解答】解:∵点A(表示整数a)在原点的左侧,点B(表示整数b)在原点的右侧,∴a<0,b>0.又∵|a﹣b|=2016,∴b﹣a=2016.∵AO=2BO,∴﹣a=2b.∴3b=2016.解得:b=672.∴a=﹣1344.∴a+b=﹣1344+672=﹣672.故答案为:﹣672.三、解答题(第16、17、18题各6分,第19、20题各10分,第21题12分,共50分)16.计算:【考点】73:二次根式的性质与化简;15:绝对值;6E:零指数幂;6F:负整数指数幂.【分析】理解绝对值的意义:负数的绝对值是它的相反数;表示的算术平方根即;一个数的负指数次幂等于这个数的正指数次幂的倒数;任何不等于0的数的0次幂都等于1.【解答】解:原式=2﹣+﹣1=1.17.解不等式组,并将解集在数轴上表示出来.【考点】CB :解一元一次不等式组;C4:在数轴上表示不等式的解集.【分析】分别解出两不等式的解集再求其公共解.【解答】解:解不等式①得x <﹣解不等式②得x ≥﹣1∴不等式组的解集为﹣1≤x <﹣.其解集在数轴上表示为:如图所示.18.先化简,再求值,(3x+2)(3x ﹣2)﹣5x (x ﹣1)﹣(2x ﹣1)2,其中x=﹣.【考点】4J :整式的混合运算—化简求值.【分析】首先根据整式相乘的法则和平方差公式、完全平方公式去掉括号,然后合并同类项,最后代入数据计算即可求解.【解答】解:原式=9x 2﹣4﹣(5x 2﹣5x )﹣(4x 2﹣4x+1)=9x 2﹣4﹣5x 2+5x ﹣4x 2+4x ﹣1=9x ﹣5,当时,原式==﹣3﹣5=﹣8.19.已知:a+b=2,ab=1.求:(1)a﹣b(2)a2﹣b2+4b.【考点】4C:完全平方公式.【分析】根据完全平方公式进行变形,再整体代入求出即可.【解答】解:(1)∵a+b=2,ab=1,∴(a﹣b)2=(a+b)2﹣4ab=4﹣4=0,则a﹣b=0,(2)∵a+b=2,ab=1,a﹣b=0∴a2﹣b2+4b=420.若2(x+4)﹣5<3(x+1)+4的最小整数解是方程的解,求代数式m2﹣2m+11的平方根的值.【考点】C7:一元一次不等式的整数解;21:平方根;85:一元一次方程的解.【分析】首先计算出不等式的解集,从而确定出最小整数解,进而得到x的值,再把x的值代入方程算出m的值,然后再次把m的值代入代数式m2﹣2m+11计算出结果,再算出平方根即可.【解答】解:解不等式得:x>﹣4则x的最小整数解为﹣3,当x=﹣3时,×(﹣3)+3m=5,解得:m=2,把m=2代入m2﹣2m+11得:22﹣2×2+11=11,11平方根为±.故代数式m2﹣2m+11的平方根的值为±.21.某学校组织340名师生进行长途考察活动,带有行李170件,计划租用甲、乙两种型号的汽车10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.(1)请你帮助学校设计所有可行的租车方案;(2)如果甲车的租金为每辆2000元,乙车的租金为每辆1800元,问哪种可行方案使租车费用最省?【考点】CE:一元一次不等式组的应用.【分析】(1)设租用甲车x辆,则乙车(10﹣x)辆.不等关系:①两种车共坐人数不小于340人;②两种车共载行李不小于170件.(2)因为车的总数是一定的,所以费用少的车越多越省.【解答】解:(1)设租用甲车x辆,则乙车(10﹣x)辆.根据题意,得,解,得4≤x≤7.5.又x是整数,∴x=4或5或6或7.共有四种方案:①甲4辆,乙6辆;②甲5辆,乙5辆;③甲6辆,乙4辆;④甲7辆,乙3辆.(2)①甲4辆,乙6辆;总费用为4×2000+6×1800=18800元;②甲5辆,乙5辆;总费用5×2000+5×1800=19000元;③甲6辆,乙4辆;总费用为6×2000+4×1800=19200元;④甲7辆,乙3辆.总费用为7×2000+3×1800=19400元;因为乙车的租金少,所以乙车越多,总费用越少.故选方案①.2017年5月24日。
安徽省蚌埠市三校(六中、新城实验、慕远)2016-2017学年八年级第一学期期中联考数学试卷
安徽省蚌埠市三校(六中、新城实验、慕远)2016-2017学年八年级数学上学期期中联考试题一.选择题(本大题共10小题,每小题3分,共30分)1. 在平面直角坐标系中,点(-1,2)在 ( ).(A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限2. 下列语句中,不是命题的是 ( ).(A )直角都等于90°(B )对顶角相等 (C )互补的两个角不相等 (D )作线段AB3. 一个三角形的三个外角之比为3:4:5,则这个三角形内角之比是 ( ).(A )5:4:3 (B )4:3:2 (C )3:2:1 (D )5:3:14.在如图所示的象棋盘上,若“帅”和“相”所在的坐标分别是(1,-2)和(3,-2)上,则“炮”的坐标是 ( ).(A )(-1,1) (B )(-1,2) (C )(-2,1) (D )(-2,2)5.已知一次函数y kx b x =+-的图象与x 轴的正半轴相交,且函数值y 随自变量x 的增大而增大,则,k b 的取值情况为 ( ).(A )1,0k b >< (B )1,0k b >> (C )0,0k b >> (D )0,0k b ><6.在下列条件中,①∠A +∠B =∠C ;②∠A :∠B :∠C =1:2:3;③∠A =12∠B =13∠C ;④∠A =∠B =2∠C ;⑤∠A =2∠B =3∠C ,能确定△ABC 为直角三角形的条件有( ).(A )2个 (B )3个 (C )4个 (D )5个7.直线11:l y k x b =+与直线22:l y k x c =+在同一平面直角坐标系中的图象如图所示,则关于x 的不等式12k x b k x c +<+的解集为 ( ).(A )1x > (B )1x < (C )2x >- (D )2x <-8. 如图,在长方形ABCD 中,AB =2,BC =1,运点P 从点B 出发,沿路线B →C →D 作匀速运动,那么△ABP 的面积y 与点P 运动的路程x 之间的函数图象大致是 ( ).第4题图第7题图第8题图9. 如图,∠MAN =100°,点B ,C 是射线AM ,AN 上的动点,∠ACB 的平分线和∠MBC 的平分线所在直线相交于点D ,则∠BDC 的大小为 ( ).(A )40° (B )50° (C )80° (D )随点B ,C 的移动而变化10.如图,△ABC 的顶点坐标分别为A (1,0),B (4,0),C (1,4),将△ABC 沿x 轴向右平移,当点C 落在直线26y x =-上时,线段BC 扫过的面积为 ( ).(C) (D )16(A )4 (B )811.填空题(本大题共8小题,每小题3分,共24分)(1) 点M (3,-1)到x 轴距离是 ,到y 轴距离是 .(2) 把一副常用的三角板如图所示拼在一起,那么图中∠ABF = .(3)已知直线y kx b =+经过点(-2,2),并且与直线21y x =+平行,那么b = .(4)已知点A (11,x y ),B (22,x y )是一次函数25y x =-+图象上的两点,当12x x >时,1y 2y .(填“>”、“=”或“<”)(5).如图,已知一次函数3y kx =+和y x b =-+的图象交于点P (2,4),则关于x 的方程3kx x b +=-+的解是 .(6).如图,已知在△ABC 中,∠ABC 与∠ACB 的平分线交于点P ,当∠A =70°时,则∠BPC 的度数第15题图 第16题图第17题图第9题图第10题图第12题。
2016-2017学年上期厦门一中高一数学期中考试卷(含答案)
福建省厦门第一中学2016-2017学年度半期考高一(上)数学试卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题所给出的四个备选项中,只有一项是符合题目要求的.1. 已知集合{}{}a x x B x x A <=≤=|,1|2,若B A ⊆,则实数a 的取值范围是( )A .()1,∞-B .(]1,-∞-C .()∞+,1D .[)∞+,1 2. 函数()x x x f 2)1ln(-+=的一个零点所在的区间是( ) A .()10,B .()21,C .()32,D .()43,3. 已知函数)(x f y =定义域是[]4,1-,则()1-=x f y 的定义域是( )A .[]50,B .[]4,1-C .[]2,3-D .[]3.2-4. 函数()()4log 221-=x x f 的单调递增区间为( )A .()∞+,0B .()0,∞-C .()∞+,2D .()2,-∞-5. 函数()()()()221log 3232≥<⎩⎨⎧-=-x x x x f x ,若()1=a f ,则a 的值是( ) A .2B . 1C . 1或2D .1或-26. 已知集合{}k x N x A 2log 1|<<∈=,集合A 中恰有8个子集,则( ) A .816>>kB .816≥≥kC .1632>≥kD .1632≥≥k7. 已知定义在R 上的函数(),12-=xx f 记()()()0,5log ,3log 25.0f c f b f a ===,则c b a ,,的大小关系为( ) A .c b a <<B .b c a <<C .b a c <<D .a b c <<8. 已知函数()()()()0,0,log 312<<<<-⎪⎭⎫⎝⎛=c f b f a f c b a x x f x,实数d 是函数()x f 的一个零点,则其中一定不可能成立的是( ) A .a d < B .b d > C .c d < D .c d >9. 已知()()2,42-=-=x x g x x f ,则下列结论正确的是( )A .()()()x g x f x h +=是偶函数B .()()()x g x f x h =是奇函数C .()()()xx g x f x h -=2是偶函数 D .()()()x g x f x h -=2是奇函数 10. 已知函数,24221434+++=⎪⎭⎫ ⎝⎛+x x x x f 则=⎪⎭⎫⎝⎛++⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛201710162017220171f f f ( ) A .2017B .2016C .4034D .403211. 函数()x f 是定义在R 上的奇函数,当0>x 时,()()⎪⎩⎪⎨⎧>-≤<=1121102x x f x x f x,,,则方程()x x f 1=在[]5,3-上的所有实根之和为( ) A .0B .2C .4D .612. 对于定义域为D 的函数()y f x =和常数c ,若对任意正实数ξ,D x ∈∃,使得()ξ<-<c x f 0恒成立,则称函数()x f y =为“敛c 函数”.现给出如下函数:① ()();Z x x x f ∈=② ()()Z x x f x∈+⎪⎭⎫⎝⎛=121;③()x x f 2log =;④()xx x f 1-=.其中为“敛1函数”的个数为( ) A .1 B .2C .3D .4A .二、填空题:本大题4小题,每小题5分,共20分.把答案填在答题卡相应位置. 13. 已知2211xx x x f +=⎪⎭⎫ ⎝⎛-,则()=3f . 14. 已知,2log 1log 132=+aa 则=a . 15. 已知函数()31010x x f x x ⎧+≥=⎨<⎩,则满足不等式()()x f x f 212>-的x 的取值范围是 .16. 已知函数()()⎩⎨⎧≥+-<-=0460lg 2x x x x x x f ,若关于x 的方程()()012=+-x bf x f有8个不同的根,则实数b 的取值范围是 .三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17. (本小题满分10分) 已知定义在R 上的偶函数()x f ,当0≥x 时,()x x x f 22+-=(1)求函数()x f 在R 上的解析式;(2)若函数()x f 在区间[]m ,1-上不单调,求实数m 的取值范围.18. (本小题满分12分)已知{}{}12|,12|2+==-+-==x y x B x x y y A(1)求B A ,()B A C R ;;(2)若{},,2|C B C m x m x C =<<-= 求m 的取值范围.19. (本小题满分12分)已知()x f 对任意的实数n m ,都有:()()(),1-+=+n f m f n m f 且当0>x 时,有()1>x f .(1)求()0f ;(2)求证:()x f 在R 上为增函数;(3)若(),76=f 且关于x 的不等式()()322<-+-x x f ax f 对任意的[)+∞-∈,1x 恒成立,求实数a 的取值范围.20. (本小题满分12分)设函数()())10(1≠>--=-a a a k a x f xx且是定义域为R 的奇函数.(1)求k 的值; (2)若()231=f ,试讨论函数()()x f m a a x g xx ⋅-+=-222在[)∞+,1上零点的个数情况.21. (本小题满分12分)某企业投入81万元经销某产品,经销时间共60个月,市场调研表明,该企业在经销这个产品期间第x 个月的利润函数()()⎪⎩⎪⎨⎧∈∈≤≤≤≤=**)(60211012011N x N x x x x x f (单位:万元).为了获得更多地利润,企业将每月获得的利润再投入到次月的经营中,记第x 个月的利润率为(),个月的资金总和第个月的利润第x x x g =例如()()()()218133f f f g ++=. (1)求()10g ;(2)求第x 个月的当月利润率;(3)求该企业经销此产品期间,哪一个月的当月利润率最大,并求出该月的当月利润率.22. (本小题满分12分)设()()()10log ≠>=a a x g x f a 且. (1)若()()13log 21-=x x f ,且满足()1>x f ,求x 的取值范围;(2)若(),2x ax x g -=是否存在a 使得()x f 在区间⎥⎦⎤⎢⎣⎡321,上是增函数?如果存在,说明a 可以取哪些值;如果不存在,请说明理由;(3)定义在[]q p ,上的一个函数()x m ,用分法q x x x x x p T n i i =<<<<<<=- 110:将区间[]q p ,任意划分成n 个小区间,如果存在一个常数0>M ,使得不等式()()()()()()()()M x m x m x m x m x m x m x m x m n n i i ≤-++-++-+---111201 恒成立,则称函数()x m 为在[]q p ,上的有界变差函数.试确定一个a 的值,使函数()()x ax x f a -=2log 为在⎥⎦⎤⎢⎣⎡321,上的有界变差函数,并求M 的最小值.答案1—5:CBADA 6—10:CCDDD 11—12:CC13: 11 15: ()12,1-- 16: ⎥⎦⎤⎝⎛417,2。
王民小学2016至2017学年度第一学期五年级数学中期考试题(卷)
王民小学2016至2017学年度第一学期五年级数学中期考试题(卷)一、填空.(每空1分,共22分)1. 3.05×2.7的积是()位小数;2.3÷1.25的商的最高位在()位上2.通常横排叫作().竖排叫作().用()表示位置。
3.小明在教室的座位用数对表示为(3,7)那么他正前面的一位同学的座位可用()表示。
4. 3.2525…是()循环小数,循环节是(),用简便记法写作()。
5. 22÷1.2=()÷12;3.27÷1.4=()÷156.一堆煤,一辆车7.12次运完,实际需要运()次;20元可买6.9瓶饮料,实际能买()瓶。
7.近似值5.9是有一个精确的两位小数四舍五入得到的,则这个数最大是(),最小是()。
8.求3.8的百分之九是多少,列式为()。
9.计算1.68×3.7时,先把1.68扩大到原数的()倍,再把3.7扩大到原数的()倍,这时积就扩大到它的()倍,要使积不变,就要将得到的积缩小到它的(),得()。
10.一根绳子长m米,用去5米,还剩()米。
二、判断。
(共7分)1.在小数除法中,如果被除数是三位小数,那么商也一定是三位小数()2.盒子里放着99个红球和1个白球,任意摸出一个球,一定是红球()3.点A(3,5)向左平移2格,平移后的位置一定是(3,6)()4.循环小数一定是无限小数,无限小数也一定是循环小数()5.一个自然数乘小数,积一定比这个自然数小()6.一个三位小数精确到十分位是5.7,那么这个数最大是5.749()。
7. 12除可以用12÷表示()三、选择。
(每小题2分,共10分)1.与13.57÷2.3的结果相等的算式是( ) A. 135.7÷23 B. 1.357÷23 C.13.57÷0.232.如果甲×1.1=乙÷1.1(甲,乙均不为0)那么甲( )乙。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一学期三年级数学期中质量检测卷
一、我会填(每空1分,共21分)
1、学过的时间单位有( )( )( ),计量很短的时间时,常用比分小的单位( )
om
2、5吨 =( )千克 6分米 =( )厘米 180分=( )时
5分=( )秒 1时40分=( )分 80毫米=( )厘米
1075千克=( )吨( )千克
3、在( )里填上合适的单位。
① 爸爸每天工作8( )。 ② 李静跑50米的时间是12( )。
③ 做一次深呼吸要4( )。 ④马拉松长跑比赛全程约42( )。
⑤黑板长40( )。
4、体育老师对第一小组同学进行50米跑测试,成绩如下:小红9秒,小明8秒,小丽11
秒,小军10秒。( )跑得最快,( )跑得最慢。
5、星期天小强8:45出发从家去图书馆,路上用了20分钟,小强到达图书馆的时间是( ),
他在图书馆呆了40分钟后,原路返回,到家时的时间是( )。
二、判一判:对的打“√”,错的打“×”。(10分)
1、在百米赛跑中,东东用了140分。 ( )
2、火车下午1:05从南京出发,当天下午3:50到达上海,火车共走了2小时45分。
( )绿色圃小学教育
3、一个篮球重250千克。 ( )
4、因为400>4,所以400米>4千米。 ( )
5、40毫米与4分米同样长。 ( )
三、把正确答案的序号填在( )里。(10分)
1、1吨棉花比1吨石头( )。
A、轻 B、重 C、一样重
2、小明的身高是156( )。
omA、厘米 B、分米 C、米
3、小丽1分钟写4个大字,写20个大字需多长时间?列式为( )。
A 、1×4 B、4×1 C、20÷4
4、1米和10厘米比较( )。
A、1米长 B、10厘米长 C、一样长
5、一场电影大约要播放( )。
A、90秒 B、90分 C、9小时
四、勤奋的你算一算:(28分)
1、 直接写出得数。(12分)
76+45= 43-18= 64+29= 801-346=
135+62= 256+144= 70+34= 90-24=
500-150= 405-126= 789+328= 486-165=
2、用竖式计算并验算。(16分)
392-178= 534+228=
486+217= 700-218=
五、灵巧的你做一做:按要求画线段。(6分)
①画一条长55毫米的线段。
②画一条比5厘米短3毫米的线段。
六、智慧的你试一试:(25分)
1、图书馆买5本一样的书,每本厚8毫米,一共厚多少毫米,合多少厘米?(6分)
2、养鸡场有公鸡168只,公鸡比母鸡少382只,母鸡有多少只?(6分)
3、火车9:40开车,李华从家到火车站要35分钟,李华需几时几分从家出发才能赶上火车?
(6分)
4、瑶瑶和婷婷比赛跳绳。婷婷三次共跳了490下,瑶瑶前两次都跳了158下,她第三次要
跳多少下才能和婷婷一样多?(7分)
