小学五年级奥数第36讲 火车行程问题(含答案分析)
奥数行程问题讲解及训练(讲义)- 数学五年级下册

小学高部奥数行程问题讲解及训练一、弄清思路行程问题是小学奥数题的重要组成部分,那么如何学好行程问题?下面由多年从教经验的老师来回答这个问题:因为行程的复杂,所以很多同学一开始就会有畏难心理。
因此,学习行程一定要循序渐进,不要贪多,力争学一个知识点就要能吃透它。
我们要知道,学习奥数有四种境界:第一种:课堂理解。
就是说能够听懂老师讲解的题目;第二种:能够解题。
就是说同学听懂了还能做出作业。
第三种:能够讲题。
就是不仅自己会做,还要能够讲给家长或同学听。
第四种:能够编题。
就是自己领悟这个知识了,自己能够根据例题出题目,并且解出来。
这也是解决向数题的最高境界了。
其实大部分同学学习奥数都只停留在第一种境界,有的甚至还达不到,能够达到第三种境界的同学考取重点中学实验班基本上没有什么问题了。
而要想在行程上一点问题没有,则要求同学达到第四种境界。
即系统学习,还要能深刻理解,刻苦钻研。
而这四种境界则是学习行程的四个阶段或者说好的方法。
二、基本公式1、一般行程问题公式平均速度×时间=路程;路程÷时间=平均速度;路程÷平均速度=时间。
2、列车过桥问题公式(桥长+列车长)÷速度=过桥时间;(桥长+列车长)÷过桥时间=速度;速度×过桥时间=桥、车长度之和。
3、同向行程问题公式追及(拉开)路程÷(速度差)=追及(拉开)时间;追及(拉开)路程÷追及(拉开)时间=速度差;(速度差)×追及(拉开)时间=追及(拉开)路程。
4、反向行程问题公式反向行程问题可以分为“相遇问题”(二人从两地出发,相向而行)和“相离问题”(两人背向而行)两种。
这两种题,都可用下面的公式解答:(速度和)×相遇(离)时间=相遇(离)路程;相遇(离)路程÷(速度和)=相遇(离)时间;相遇(离)路程÷相遇(离)时间=速度和。
5、行船问题公式(1)一般公式:静水速度(船速)+水流速度(水速)=顺水速度;船速-水速=逆水速度;(顺水速度+逆水速度)÷2=船速;(顺水速度-逆水速度)÷2=水速。
【数学思维】 五年级奥数行程问题

【数学思维】行程问题之概论行程问题破题密钥:核心公式:路程=速度X时间常用方法:列方程、解方程解题关键:除了一部分应用固定公式的题型,行程问题都要求大家按照方程的方法来解答,而不是构造一些看些巧妙的绚丽方法。
这是因为行程问题变化比较多,过程可能会比较复杂,但唯一不变的是两个维度的关系:(1)每一段行程单元都有S=vt;(2)不同行程单元之间,S之间、v之间、t之间都有关系。
只要把握住这两个维度的关系,方程(组)是很容易列出来的。
行程问题模块主要有基础行程问题、相对速度问题和典型行程模型三大块。
基础行程问题:双人运动型、变速运动型、提前出发型、迟到早到型、火车运动型、比例计算型、间歇运动型、图示解析型等。
相对速度问题:相遇追及型、环形运动型、流水行船型、扶梯上下型、队伍行进型、往返相遇型等。
典型行程模型:不变速沿途数车、不间歇多次相遇、无动力顺水漂流等模型。
相遇问题【例1】两列对开的火车途中相遇,甲车上的乘客从看到乙车到乙车从旁边开过去,共用6秒钟.已知甲车每小时行45千米,乙车每小时行36千米,乙车全长多少米?【练习1】列车通过250米长的隧道用25秒,通过210米长的隧道用23秒,又知列车的前方有一辆与它行驶方向相同的货车,货车车身长320米,速度为每秒17米,列车与货车从相遇到离开需多少秒?【例2】甲、乙两地间的路程是600千米,上午8点客车以平均每小时60千米的速度从甲地开往乙地.货车以平均每小时50千米的速度从乙地开往甲地.要使两车在全程的中点相遇,货车必须在上午几点出发?【练习1】甲乙两地相距450千米,快慢两列火车同时从两地相向开出,3小时后两车在距中点12千米处相遇,快车每小时比慢车每小时快多少千米?【练习2】甲乙两站相距360千米.客车和货车同时从甲站出发驶向乙站,客车每小时行60千米,货车每小时行40千米,客车到达乙站后停留0.5小时,又以原速返回甲站,两车对面相遇的地点离乙站多少千米?【练习3】两地相距540千米.甲、乙两车往返行驶于两地之间,都是到达一地之后立即返回,乙车比甲车快.设两辆车同时从地出发后第一次和第二次相遇都在途中地.那么,到两车第三次相遇为止,乙车共走了多少千米?【例3】两地间的距离是950米.甲、乙两人同时由地出发往返锻炼.甲步行每分走40米,乙跑步每分行150米,40分后停止运动.甲、乙二人第几次迎面相遇时距地最近,距离是多少米?【练习1】甲、乙两个运动员分别从相距100米的直跑道两端同时相对出发,甲以每秒6.25米,乙以每秒3.75米的速度来回匀速跑步,他们共同跑了8分32秒,在这段时间内两人多次相遇(两人同时到达同一地点叫做相遇).他们最后一次相遇的地点离乙的起点有多少米?甲追上乙几次?甲与乙迎面相遇几次?【例4】一条单线铁路线上有五个车站,它们之间的路程如下图所示(单位:千米).两列火车从相向对开,车先开了3分钟,每小时行60千米,车每小时行50千米,两车在车站上才能停车,互相让道、错车.两车应该安排在哪一个车站会车(相遇),才能使停车等候的时间最短,先到的火车至少要停车多长时间?。
五年级知识点:行程问题例题专练,附解析

五年级知识点:行程问题例题专练,附解析行程问题中包括:火车过桥、流水行船、沿途数车、猎狗追兔、环形行程、多人行程,等等。
每一类问题都有自己的特点,解决方法也有所不同,但是,行程问题无论怎么变化,都离不开“三个量,三个关系”:这三个量是:路程(s)、速度(v)、时间(t),三个关系:1. 简单行程:路程= 速度×时间2. 相遇问题:路程和= 速度和×时间3. 追击问题:路程差= 速度差×时间牢牢把握住这三个量以及它们之间的三种关系,就会发现解决行程问题还是有很多方法可循的。
如“多人行程问题”,实际最常见的是“三人行程”有这样一道应用题:“一辆汽车从A地开往B地,每小时行48千米,行了5小时到达B地。
A、B两地相距多少千米?”我相信,同学们都能很快地列式解答,即48×5=24O(千米),从而求得A、B两地相距24O千米。
但遇到较复杂的行程问题,往往会觉得无从下手。
其实,只要是行程问题,不管怎么复杂,都可以根据“路程=速度×时间”这一基本数量关系来解答。
下面我们一起来解答几道题目。
例:两辆汽车同时从A、B两地相向开出,甲车每小时行48千米,乙车每小时行50千米,5小时相遇。
求A、B两地间的距离。
分析:求两地间的路程,就是两车原来相隔路程,也就是求两车在5小时里所走路程的和。
根据“路程=速度×时间”,可以先算出每小时两车一共行多少千米,再与相遇时间相乘,就可求得两地相距多少千米。
(48+50)×5=490(千米)答:A、B两地间相距是490千米。
现在我们就以这道题为基础来进行改编练习。
1.把原题的“5小时相遇”这一条件改为“5小时后还相距15千米”,问题不变。
我们可以按原题进行分析,所不同的是:这里两车没有相遇,还相距15千米。
这样,两地间的路程就不仅仅是两车5小时里所走的路程和了,还必须加上没有走的15千米。
可这样列式解答。
(48+50)×5+15=490+15=505(千米)答:A、B两地间相距505千米。
小学五年级奥数行程问题专项突破(附答案)

小学五年级奥数题型专项突破(二)行程问题专题1 常见路程计算一、专题解析行程应用题是专门讲物体运动的速度、时间、路程三者关系的应用题。
行程问题的主要数量关系是:路程=速度×时间。
知道三个量中的两个量,就能求出第三个量。
二、精讲精练【例题1】甲、乙两车同时从东、西两地相向开出,甲车每小时行56千米,乙车每小时行48千米。
两车在距中点32千米处相遇,东、西两地相距多少千米?【思路导航】从图中可以看出,两车相遇时,甲车比乙车多行了32×2=64(千米)。
两车同时出发,为什么甲车会比乙车多行64千米呢?因为甲车每小时比乙车多行56-48=8(千米)。
64里包含8个8,所以此时两车各行了8小时,东、西两地的路程只要用(56+48)×8就能得出。
32×2÷(56-48)=8(小时)(56+48)×8=832(千米)答:东、西两地相距832千米。
练习11、小玲每分钟行100米,小平每分钟行80米,两人同时从学校和少年宫出发,相向而行,并在离中点120米处相遇。
学校到少年宫有多少米?2、一辆汽车和一辆摩托车同时从甲、乙两地相对开出,汽车每小时行40千米,摩托车每小时行65千米,当摩托车行到两地中点处时,与汽车还相距75千米。
甲、乙两地相距多少千米?3、甲、乙二人同时从东村到西村,甲每分钟行120米,乙每分钟行100米,结果甲比乙早5分钟到达西村。
东村到西村的路程是多少米?【例题2】快车和慢车同时从甲、乙两地相向开出,乙车每小时行40千米,经过3小时,快车已驶过中点25千米,这时快车与慢车还相距7千米。
慢车每小时行多少千米?【思路导航】快车3小时行驶40×3=120(千米),这时快车已驶过中点25千米,说明甲、乙两地间路程的一半是120-25=95(千米)。
此时,慢车行了95-25-7=63(千米),因此慢车每小时行63÷3=21(千米)。
【小高数学知识点】火车行程问题
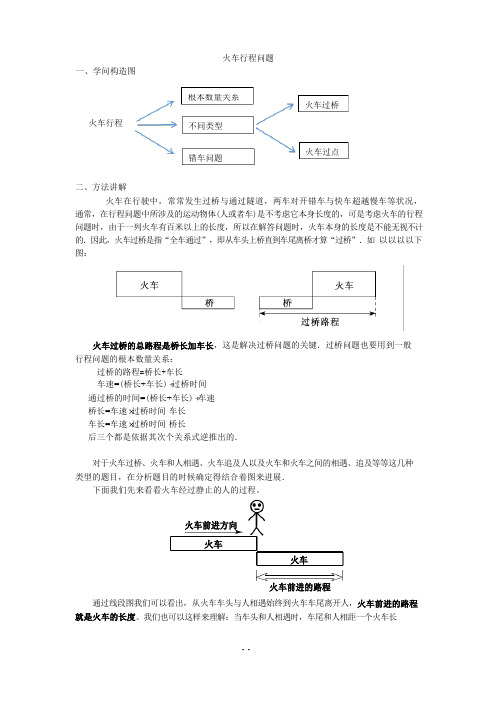
火车过桥 火车过点火车前进方向火车火车行程问题一、学问构造图火车行程二、方法讲解火车在行驶中,常常发生过桥与通过隧道,两车对开错车与快车超越慢车等状况, 通常,在行程问题中所涉及的运动物体(人或者车)是不考虑它本身长度的,可是考虑火车的行程问题时,由于一列火车有百米以上的长度,所以在解答问题时,火车本身的长度是不能无视不计的.因此,火车过桥是指“全车通过”,即从车头上桥直到车尾离桥才算“过桥”.如 以以以以下图:火车过桥的总路程是桥长加车长,这是解决过桥问题的关键.过桥问题也要用到一般行程问题的根本数量关系:过桥的路程=桥长+车长车速=(桥长+车长)÷过桥时间通过桥的时间=(桥长+车长)÷车速桥长=车速×过桥时间-车长车长=车速×过桥时间-桥长后三个都是依据其次个关系式逆推出的.对于火车过桥、火车和人相遇、火车追及人以及火车和火车之间的相遇、追及等等这几种类型的题目,在分析题目的时候确定得结合着图来进展.下面我们先来看看火车经过静止的人的过程。
火车前进的路程通过线段图我们可以看出,从火车车头与人相遇始终到火车车尾离开人,火车前进的路程就是火车的长度。
我们也可以这样来理解:当车头和人相遇时,车尾和人相距一个火车长火车根本数量关系不同类型错车问题度,所以整个过程就是车尾和人的相遇问题。
以上是人不动状况下的火车行程问题,下面我们来介绍一下行人和火车的相遇和追及问题,如以以以以下图所示:火车前进方向车尾离开行人车头遇到行人 火车行人的路程火车前进的路程火车的长度我们可以将火车看成一个点:开头的时候行人和车尾的距离为一个车长,完毕的时候行人和车尾相遇了。
也就是说,从火车与行人的相遇到错开,这个过程可以看成是行人与车尾相遇了。
也就是说,从火车与行人的相遇到错开,这个过程可以看成是行人与车尾的相遇问题,火车和行人经过的路程和等于火车的长度。
类似的,对于火车追行人的过程,从追上到离开,火车和行人的路程差等于火车的长 度。
【小学精品奥数】火车问题.学生版

1、会熟练解决基本的火车过桥问题.2、掌握人和火车、火车与火车的相遇追及问题与火车过桥的区别与联系.3、掌握火车与多人多次相遇与追及问题火车过桥常见题型及解题方法 (一)、行程问题基本公式:路程=速度⨯时间总路程=平均速度⨯总时间;(二)、相遇、追及问题:速度和⨯相遇时间=相遇路程速度差⨯追及时间=追及路程;(三)、火车过桥问题1、火车过桥(隧道):一个有长度、有速度,一个有长度、但没速度,解法:火车车长+桥(隧道)长度(总路程) =火车速度×通过的时间;2、火车+树(电线杆):一个有长度、有速度,一个没长度、没速度,解法:火车车长(总路程)=火车速度×通过时间;2、火车+人:一个有长度、有速度,一个没长度、但有速度,(1)、火车+迎面行走的人:相当于相遇问题,解法:火车车长(总路程) =(火车速度+人的速度)×迎面错过的时间;(2)火车+同向行走的人:相当于追及问题,解法:火车车长(总路程) =(火车速度—人的速度) ×追及的时间;(3)火车+坐在火车上的人:火车与人的相遇和追及问题解法:火车车长(总路程) =(火车速度±人的速度) ×迎面错过的时间(追及的时间);4、火车+火车:一个有长度、有速度,一个也有长度、有速度,(1)错车问题:相当于相遇问题,解法:快车车长+慢车车长(总路程) = (快车速度+慢车速度) ×错车时间;(2)超车问题:相当于追及问题,解法:快车车长+慢车车长(总路程) = (快车速度—慢车速度) ×错车时间;老师提醒学生注意:对于火车过桥、火车和人相遇、火车追及人以及火车和火车之间的相遇、追及知识精讲教学目标火车问题等等这几种类型的题目,在分析题目的时候一定得结合着图来进行。
模块一、火车过桥(隧道、树)问题【例1】一列火车长200米,以60米每秒的速度前进,它通过一座220米长的大桥用时多少?【巩固】一列火车长360米,每秒钟行驶16米,全车通过一条隧道需要90秒钟,求这条隧道长多少米?【巩固】一列火车经过南京长江大桥,大桥长6700米,这列火车长100米,火车每分钟行400米,这列客车经过长江大桥需要多少分钟?火车行驶路程火车火车桥【巩固】长150米的火车以18米/秒的速度穿越一条300米的隧道.那么火车穿越隧道(进入隧道直至完全离开)要多长时间?【巩固】一列长240米的火车以每秒30米的速度过一座桥,从车头上桥到车尾离桥用了1分钟,求这座桥长多少米?【巩固】一列火车长160米,全车通过一座桥需要30秒钟,这列火车每秒行20米,求这座桥的长度.【例2】四、五、六3个年级各有100名学生去春游,都分成2列(竖排)并列行进.四、五、六年级的学生相邻两行之间的距离分别是1米、2米、3米,年级之间相距5米.他们每分钟都行走90米,整个队伍通过某座桥用4分钟,那么这座桥长米.【巩固】一个车队以6米/秒的速度缓缓通过一座长250 米的大桥,共用152秒.已知每辆车长6米,两车间隔10米.问:这个车队共有多少辆车?【巩固】一个车队以4米/秒的速度缓缓通过一座长200米的大桥,共用115秒。
五年级奥赛起跑线 行程问题(三)
行程问题(三)例1 一列火车长150米,每秒行20米,全车通过一座长450米的大桥,需要多少时间?例2 一列火车通过一个长530米的隧道要40秒,以同样的速度通过一座长380米的大桥要用30秒。
求这列火车的速度及车长。
例3 某人沿着铁路旁的便道步行,一列客车从身后开来,在此人身旁通过的时间是7秒。
已知客车长105米,每小时行72千米。
问:步行的人每秒行多少米?(行人前胸至后背的宽度忽略不计。
)例4 有甲、乙两列火车,甲车长130米,每秒行23米,乙车长250米,每秒行15米。
现在两车相向而行,从两车相遇到离开需要多少时间?1、一列火车长360米,每秒行15米,全车通过一个小山洞需40秒。
这个山洞长多少米?2、一列火车通过2040米的大桥需要60秒,以同样的速度通过1720米的隧道需用52秒。
求这列列车的速度和车长。
3、一支1800米长的队伍以每分钟90米的速度行进,队伍前端的联络员用9分钟的时间跑到队伍末尾传达命令。
联络员每分钟跑多少米?4、小张以每秒3米的速度沿着铁路跑步,迎面开来一列长147米的火车,它的行驶速度是每秒18米。
火车经过小张身边要多少秒?5、一列快车和一列慢车相向而行,快车的车身长270米,慢车的车身长360米,坐在快车上的人看见慢车从身边驶过的时间是12秒,那么,坐在慢车上的人看见快车从身边驶过的时间是多少?6、在一个600米长的环形跑道上,兄妹两人同时从同一起点都按顺时针方向跑步,两人每隔12分钟相遇一次。
若两人速度不变,还是在原出发点同时出发,哥哥改为按逆时针方向跑,则两人每隔4分钟相遇一次。
两人跑一圈各要几分钟?(哥哥的速度比妹妹快)7、甲列车长500米,乙列车长400米,已知甲、乙两列车的速度分别为每秒20米和每秒25米,两列车相向而行,从车头相遇到车尾相离需要多少秒?8、在300米长的环形跑道上,甲、乙两人同时同向并排起跑,甲平均每秒跑5米,乙平均每秒跑4.4米。
两人起跑后的第一次相遇在起跑线前面多少米处?9、一个人站在铁道旁,听见远处传来的火车汽笛声后,再过57秒火车经过他面前。
人教版五年级奥数练习:火车行程问题 (2)
人教版五年级奥数练习:火车行程问题
例2 一列火车长180米,每秒钟行25米。
全车通过一条120米的山洞,需要多长时间?
分析由于火车长180米,我们以车头为准,当车进入山洞行120米,虽然车头出山洞,但180米的车身仍在山洞里。
因此,火车必须再行180米,才能全部通过山洞。
即火车共要行180+120=300米,需要300÷25=12秒。
练习二
1,一列火车长360米,每秒行18米。
全车通过一座长90米的大桥,需要多长时间?
2,一座大桥长2100米。
一列火车以每分钟800米的速度通过这座大桥,从车头上桥到车尾离开共用3.1分钟。
这列火车长多少米?
3,一列火车通过200米的大桥需要80秒,同样的速度通过144米长的隧道需要72秒。
求火车的速度和车长。
第1 页共1 页。
五年级奥数专题 火车问题初步(学生版)
学科培优数学“火车问题初步”学生姓名授课日期教师姓名授课时长知识定位在行程问题这个大家族中,除了我们常常研究的相遇与追击外,还有三大类我们必须了解的问题:火车过桥、流水行程和时钟问题.它们虽然也涉及速度、时间、路程这三个基本关系,但在应用中要兼顾考虑一些其它因素,譬如:火车车长、水流速度等等.其中火车过桥、流水行程是我们在以前的学习中已经有所接触的内容,在下面的学习中我们先回忆巩固原有基本概念,而后相应的拓展提高!知识梳理一、解火车过桥问题常用方法⑴火车过桥时间是指从车头上桥起到车尾离桥所用的时间,因此火车的路程是桥长与车身长度之和.⑵火车与人错身时,忽略人本身的长度,两者路程和为火车本身长度;火车与火车错身时,两者路程和则为两车身长度之和.⑶火车与火车上的人错身时,只要认为人具备所在火车的速度,而忽略本身的长度,那么他所看到的错车的相应路程仍只是对面火车的长度.对于火车过桥、火车和人相遇、火车追及人、以及火车和火车之间的相遇、追及等等这几种类型的题目,在分析题目的时候一定得结合着图来进行.【重点难点解析】1.火车过桥要谨记车身长度2.火车与多人多次相遇与追及【竞赛考点挖掘】1. 火车与多人多次相遇与追及例题精讲【试题来源】【题目】慢车的车身长是142米,车速是每秒17米,快车车身长是173米,车速是每秒22,慢车在前面行驶,快车从后面追上到完全超过慢车需要多少时间?【试题来源】【题目】一列客车长190米,一列货车长240米,两车分别以每秒20米和23米的速度相向行进,在双轨铁路上,两车从车头相遇到车尾相离共需要多少时间.【试题来源】【题目】一列长72米的列车,追上长108米的货车到完全超过用了10秒,如果货车速度为原来的1.4倍,那么列车追上到超过货车就需要15秒。
货车的速度是每秒多少米?【试题来源】【题目】长180米的客车速度是每秒15米,它追上并超过长100米的货车用了28秒,如果两列火车相向而行,从相遇到完全离开需要多少时间?【试题来源】【题目】快车长106米,慢车长74米,两车同向而行,快车追上慢车后,又经过1分钟才超过慢车;如果相向而行,车头相接后经过12秒两车完全离开。
小学行程问题专项火车过桥问题讲义解析版
火车过桥问题练习题总结:一列火车过桥(山洞、隧道),求过桥时间:过桥时间=(桥长+车长)÷车速一列火车过两座长度不同的桥(山洞、隧道):(长桥-短桥)÷(过长桥时间-过短桥时间)=火车速度一列火车完全在桥上(山洞、隧道)的时间:在桥上时间=(桥长-车长)÷车速例题整理:1.一列火车长245米,它以每秒25米的速度通过一座长405米的铁桥,火车过这座桥要多少秒?两找一求:已知路程和速度,求时间关系式:时间=路程÷速度路程=桥长+车长解析:(245+405)÷25=26(秒)答:火车过这座桥要26秒。
2.一座大桥长2400米,一列火车以每分钟864米的速度,通过这座桥,从车头上桥到车尾离开桥用了3分钟,这列火车有多长?两找一求:已知速度和时间,求路程关系式:路程=速度x时间路程=桥长+车长解析:864x3-2400=192(米)答:火车长192米。
3.小贝站在铁路旁边用两个秒表侧一列火车速度。
他发现这列火车通过一座660米的大桥需要40秒,以同样的速度从他身边开过需要10秒,请你根据小贝提供的数据算出火车的车身长是多少米。
两找一求:已知路程差和时间,求路程关系式:路程=速度x时间速度=路程差÷时间差火车速度:660÷(40-10)=22(米/秒)火车长度:22x10=220(米)答:这列火车的长度是220米。
4.一列火车穿过一个长1150米的隧道需要52秒,以同样的速度通过一座长650米的铁桥需要32秒,这列火车的速度和车长各是多少?两找一求:已知路程和时间,求速度关系式:速度=路程÷时间速度=路程差÷时间差列式:火车速度:(1150-650)÷(52-32)=500÷20=25(米/秒)车长:25x32-650=150(米) 或者25x52-1150=150(米)答:火车的速度是25米每秒,车长150米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第36讲火车行程问题一、专题简析:有关火车过桥、火车过隧道、两列火车车头相遇到车尾相离等问题,也是一种行程问题。
在考虑速度、时间和路程三种数量关系时,必须考虑到火车本身的长度。
如果有些问题不容易一下子看出运动过程中的数量关系,可以利用作图或演示的方法来帮助解题。
解答火车行程问题可记住以下几点:1、火车过桥(或隧道)所用的时间=[桥(隧道长)+火车车长]÷火车的速度;2、两列火车相向而行,从相遇到相离所用的时间=两火车车身长度和÷两车速度和;3、两车同向而行,快车从追上到超过慢车所用的时间=两车车身长度和÷两车速度差。
二、精讲精练例1甲火车长210米,每秒行18米;乙火车长140米,每秒行13米。
乙火车在前,两火车在双轨车道上行驶。
甲火车从后面追上到完全超过乙火车要用多少秒?练习一1、一列快车长150米,每秒行22米;一列慢车长100米,每秒行14米。
快车从后面追上慢车到超过慢车,共需几秒钟?2、小明以每秒2米的速度沿铁路旁的人行道跑步,身后开来一列长188米的火车,火车每秒行18米。
问:火车追上小明到完全超过小明共用了多少秒钟?例2 一列火车长180米,每秒钟行25米。
全车通过一条120米的山洞,需要多长时间?练习二1、一列火车长360米,每秒行18米。
全车通过一座长90米的大桥,需要多长时间?2、一座大桥长2100米。
一列火车以每分钟800米的速度通过这座大桥,从车头上桥到车尾离开共用3.1分钟。
这列火车长多少米?例3 有两列火车,一车长130米,每秒行23米;另一列火车长250米,每秒行15米。
现在两车相向而行,从相遇到离开需要几秒钟?练习三1、有两列火车,一列长260米,每秒行18米;另一列长220米,每秒行30米。
现两列车相向而行,从相遇到相离需要几秒钟?2、一列火车长500米,要穿过一个长150米的山洞,如果火车每秒钟行26米,那么,从车头进洞到车长全部离开山洞一共要用几秒钟?例4 一列火车通过2400米的大桥需要3分钟,用同样的速度从路边的一根电线杆旁边通过,只用了1分钟。
求这列火车的速度。
练习四1、一列火车从小明身旁通过用了15秒,用同样的速度通过一座长100米的桥用了20秒。
这列火车的速度是多少?2、一列火车长900米,从路旁的一棵大树旁通过用了1.5分钟,以同样的速度通过一座大桥用了3.5分钟。
求这座大桥的长度。
例5甲列车每秒行20米,乙列车每秒行14米,若两列车齐头并进,则甲车行40秒超过乙车;若两列车齐尾并进,则甲车行30秒超过乙车。
甲列车和乙列车各长多少米?练习五1、一列快车长200米,每秒行22米;一列慢车长160米,每秒行17米。
两列车齐头并进,快车超过慢车要多少秒?若齐尾并进,快车超过慢车要多少秒?2、快车每秒行18米,慢车每秒行10米。
两列火车同时同方向齐头并进,行10秒钟后快车超过慢车;如果两列火车齐尾并进,则7秒钟后快车超过慢车。
求两列火车的车长。
三、课后作业1、A火车长180米,每秒行18米;B火车每秒行15米。
两火车同方向行驶,A 火车从追上B火车到超过它共用了100秒钟,求B火车长多少米?2、一列火车通过200米的大桥需要80秒,同样的速度通过144米长的隧道需要72秒。
求火车的速度和车长。
3、一列火车长210米,以每秒40米的速度过一座桥,从上桥到离开桥共用20秒。
桥长多少米?4、五年级384个同学排成两路纵队去郊游,每两个同学相隔0.5米,队伍以每分钟55米的速度通过一座长207米的大桥,一共需要多少时间?5、王叔叔沿铁路边散步,他每分钟走50米,迎面驶来一列长280米的列车,他与列车车头相遇到车尾相离共用了半分钟,求这列火车的速度。
第36周火车行程问题专题简析:有关火车过桥、火车过隧道、两列火车车头相遇到车尾相离等问题,也是一种行程问题。
在考虑速度、时间和路程三种数量关系时,必须考虑到火车本身的长度。
如果有些问题不容易一下子看出运动过程中的数量关系,可以利用作图或演示的方法来帮助解题。
解答火车行程问题可记住以下几点:1,火车过桥(或隧道)所用的时间=[桥(隧道长)+火车车长]÷火车的速度;2,两列火车相向而行,从相遇到相离所用的时间=两火车车身长度和÷两车速度和;3,两车同向而行,快车从追上到超过慢车所用的时间=两车车身长度和÷两车速度差。
例1 甲火车长210米,每秒行18米;乙火车长140米,每秒行13米。
乙火车在前,两火车在双轨车道上行驶。
甲火车从后面追上到完全超过乙火车要用多少秒?分析甲火车从追上到超过乙火车,比乙火车多行了甲、乙两火车车身长度的和,而两车速度的差是18-13=5米,因此,甲火车从追上到超过乙火车所用的时间是:(210+140)÷(18-13)=70秒。
练习一1,一列快车长150米,每秒行22米;一列慢车长100米,每秒行14米。
快车从后面追上慢车到超过慢车,共需几秒钟?答案解:,(秒);答:快车从追上慢车到完全超过慢车需要31.25秒.解析根据题意可知,“快车从追上慢车到完全超过慢车”就是快车车尾上的点追及慢车车头的点,因此追及的路程应该为两个车长的和,速度应该是两列火车的速度差,再根据时间=路程速度,就可以求出快车穿过慢车的时间.这是一个典型的列车追及问题,根据快车从追上慢车完全超过慢车所行的路程是两个车长的和,快车穿过慢车时,所行驶的速度是两列火车的速度差,就可以求出快车穿过慢车的时间.2,小明以每秒2米的速度沿铁路旁的人行道跑步,身后开来一列长188米的火车,火车每秒行18米。
问:火车追上小明到完全超过小明共用了多少秒钟?答案解:(秒)答:火车追上小明到完全超过小明共用了11.75秒.解析火车追上小明到完全超过小明,追及路程就是火车的车身长度188米,二者的速度差是米,根据追及时间=追及路程速度差即可解答.3,A火车长180米,每秒行18米;B火车每秒行15米。
两火车同方向行驶,A火车从追上B火车到超过它共用了100秒钟,求B火车长多少米?答案解:100×(18-15)=300(米)300-180=120(米)答:B火车长120米.故答案为:120米.注意灵活掌握行程问题.此题考查了学生解决实际问题的方法的掌握,根据题目要求和给出的数据解答,A火车超过B火车要走过A车长+B车长,先求出总长,然后再进行计算,学生一定要细心.解析根据题目要求和给出的数据解答,A火车超过B火车要走过A车长+B车长,先求出总长,然后再进行计算,学生一定要细心.例2 一列火车长180米,每秒钟行25米。
全车通过一条120米的山洞,需要多长时间?分析由于火车长180米,我们以车头为准,当车进入山洞行120米,虽然车头出山洞,但180米的车身仍在山洞里。
因此,火车必须再行180米,才能全部通过山洞。
即火车共要行180+120=300米,需要300÷25=12秒。
练习二1,一列火车长360米,每秒行18米。
全车通过一座长90米的大桥,需要多长时间?答案解:,(秒),答:需要25秒.解析这列火车通过90米长的桥,一共需要行驶路程应该是:桥的长度加火车的车长,先求出桥的长度和火车的车长总和,再根据时间=路程速度即可解答.解答本题的关键是明确一共需要行驶路程应该是:桥的长度加火车的车长.2,一座大桥长2100米。
一列火车以每分钟800米的速度通过这座大桥,从车头上桥到车尾离开共用3.1分钟。
这列火车长多少米?答案车长为X,列车一共行进了车头上桥到车尾离开,1个车长和大桥的长度3,一列火车通过200米的大桥需要80秒,同样的速度通过144米长的隧道需要72秒。
求火车的速度和车长。
答案解:火车的速度为:(米/秒)车长为:(米)答:火车的速度为米/秒;火车长为304米.解析火车完全穿过大桥所行的路程=大桥的长度+车身长度,而车身的长度是一定的,根据路程差时间差=速度可知,火的车的速度为:米/秒;由此可得车长为(米).例3 有两列火车,一车长130米,每秒行23米;另一列火车长250米,每秒行15米。
现在两车相向而行,从相遇到离开需要几秒钟?分析从两车车头相遇到两车车尾相离,一共要行130+250=380米,两车每秒共行23+15=38米,所以,从相遇到相离一共要经过10秒钟。
练习三1,有两列火车,一列长260米,每秒行18米;另一列长216米,每秒行30米。
现两列车相向而行,从相遇到相离需要几秒钟?答案解:(360+216)÷(18+30)=12(秒)相向而行,速度求和.解析两列火车走过两个火车车长2,一列火车长500米,要穿过一个长150米的山洞,如果火车每秒钟行26米,那么,从车头进洞到车长全部离开山洞一共要用几秒钟?答案秒3,一列火车长210米,以每秒40米的速度过一座桥,从上桥到离开桥共用20秒。
桥长多少米?答案设桥长为x所以桥长590米例4 一列火车通过2400米的大桥需要3分钟,用同样的速度从路边的一根电线杆旁边通过,只用了1分钟。
求这列火车的速度。
分析火车通过大桥时,所行的路程是桥长加火车的长,而通过电线杆时,行的路程就是火车的长度。
因此,3分钟比1分钟多的2分钟内,就行了2400米,火车的速度是每分钟行2400÷2=1200米。
练习四1,一列火车从小明身旁通过用了15秒,用同样的速度通过一座长100米的桥用了20秒。
这列火车的速度是多少?答案解:100÷(20-15)=20(米/秒)解析从小明身旁通过走过的是火车车长,则火车过桥用了(20-15)秒火车过桥走过的是火车车身长和桥长.2,一列火车长900米,从路旁的一棵大树旁通过用了1.5分钟,以同样的速度通过一座大桥用了3.5分钟。
求这座大桥的长度。
答案解:(米)答:这座大桥的长度是1200米.解析根据路程时间=速度,用火车长除以1.5分钟,求出火车的速度;通过大桥时,行驶的路程是大桥和火车的长度和,再根据路程=速度时间,求出火车和桥长度的和,进而求出大桥的长.3,五年级384个同学排成两路纵队去郊游,每两个同学相隔0.5米,队伍以每分钟61米的速度通过一座长207米的大桥,一共需要多少时间?答案解:394÷2-1=196(个)207+0.5×196=305(米)305÷61=5(分)答:一共需要5分钟.这个问题属于植树问题,197人之间有196个间隔,还要注意计算通过桥长时加上队伍全长,再根据路程、速度、时间之间的关系即可解决,计算要细心.解析394人排成两路纵队,每路纵队394÷2=197人,间隔数是197-1=196个,队伍长=196个间隔全长=间隔长×间隔数=0.5×196=98米,从排头两人上桥到排尾两人离开桥,应行路程=桥长+队伍全长=207+98=305米,时间=路程÷速度即可求出.例5 甲列车每秒行20米,乙列车每秒行14米,若两列车齐头并进,则甲车行40秒超过乙车;若两列车齐尾并进,则甲车行30秒超过乙车。
