材料力学第二章习题【含答案】
材料力学习题册_参考答案(1-9章)

第一章 绪 论一、选择题1.根据均匀性假设,可认为构件的( C )在各处相同。
A.应力B. 应变C.材料的弹性系数D. 位移2.构件的强度是指( C ),刚度是指( A ),稳定性是指( B )。
A.在外力作用下构件抵抗变形的能力B.在外力作用下构件保持原有平衡 状态的能力C.在外力作用下构件抵抗强度破坏的能力3.单元体变形后的形状如下图虚线所示,则 A 点剪应变依次为图(a) ( A ),图(b)( C ),图(c) ( B )。
A. 0B. 2rC. rD.1.5 r4.下列结论中( C )是正确的。
A.内力是应力的代数和; B.应力是内力的平均值; C.应力是内力的集度; D.内力必大于应力; 5. 两根截面面积相等但截面形状和材料不同的拉杆受同样大小的轴向拉力,它们的应 力是否相等( B )。
A.不相等; B.相等; C.不能确定; 6.为把变形固体抽象为力学模型,材料力学课程对变形固体作出一些假设,其中均匀性假设是指( C )。
A. 认为组成固体的物质不留空隙地充满了固体的体积; B. 认为沿任何方向固体的力学性能都是相同的; C. 认为在固体内到处都有相同的力学性能; D. 认为固体内到处的应力都是相同的。
二、填空题1.材料力学对变形固体的基本假设是 连续性假设 , 均匀性假设 , 各向同性假设 。
2.材料力学的任务是满足 强度 , 刚度 , 稳定性 的要求下,为设计经济安全的构-1-件提供必要的理论基础和计算方法。
3.外力按其作用的方式可以分为 表面力 和 体积力 ,按载荷随时间的变化情况可以分为 静载荷 和 动载荷 。
4.度量一点处变形程度的两个基本量是 (正)应变ε 和 切应变γ。
三、判断题1.因为构件是变形固体,在研究构件平衡时,应按变形后的尺寸进行计算。
( × )2.外力就是构件所承受的载荷。
(×)3.用截面法求内力时,可以保留截开后构件的任一部分进行平衡计算。
(优)优选材料力学第二章课后习题参考答案pptppt文档
变形几何方程
变形几何方程
d
பைடு நூலகம்
2F
32.6mm
切应力
拉伸强度与剪切强度
其它: 1.书写要规范, 2.答案不能用分数、根号, 3.中间步骤过多或过少; 4.作业本不要一分为二,图要在同一侧。
谢谢观看
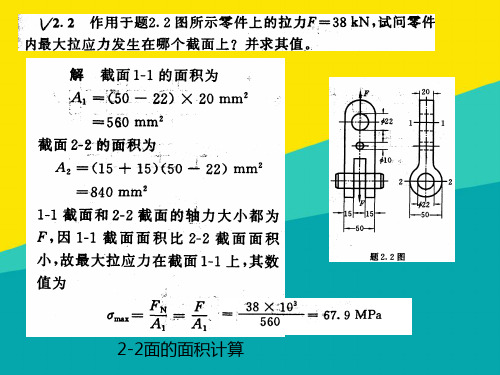
2-2面的面积计算
①最大切应力;②单位;③公式又推导一遍。
圆整b=120mm,h=165mm
①思路; ②表达; ③计算结果保留数字。
①单位;②轴力图。
(3)理由阐述不准确
考虑自重时没考虑
用卡氏定理
①受力图; ②力的方向与变形假设 不一致; ③步骤思路表现不清。
②力的方向与变形假设不一致; 圆整b=120mm,h=165mm 答答圆圆②圆 答圆答答圆圆答 答答答②②圆圆圆圆答答答圆②案案整整力整案整案案整整案案案案力力整整整整案案案整力不 不 bb的 b不 b不 不 bb不不 不 不 的 的 bbbb不 不 不 b的===========能能方能能能能 能能能方方能能能方1111111111122222222222用用向用用用用 用用用向向用用用向00000000000mmmmmmmmmmm分分与分分分分 分分分与与分分分与mmmmmmmmmmm数数变数数数数 数数数变变数数数变,,,,,,,,,,,hhhhhhhhhhh、、形、、、、 、、、形形、、、形===========11111111111根根假根根根根 根根根假假根根根假66666666666号号设号号号号 号号号设设号号号设55555555555mmmmmmmmmmm,,不,,,,,,,不不,,,不mmmmmmmmmmm一一一一致致致致;;;; ②力的方向与变形假设不一致; 圆整b=120mm,h=165mm
第二章材料的力学行为课后习题答案
第二章 材料的力学行为1.说明下列力学性能指标的名称、单位及其含义:σb 、σs 、σ0.2、σ-1、δ、αk答:σb 抗拉强度:单位为MPa ,指材料在拉伸断裂前所能够承受的最大拉应力。
σs 屈服强度:单位MPa ,指材料开始产生宏观塑性变形时的应力。
σ0.2国标GB228-87规定发生0.2%残余伸长的应力作为屈服点。
δ:可测力学性能指标中的塑性指标αk 冲击韧性,指用一定尺寸和形状的金属试样,在规定类型的冲击试验上受冲击负荷折断时,试样刻槽处单位横截面上所消耗的冲击功2.试绘出低碳钢的σ-ε曲线,指出在曲线上哪些出现颈缩现象;如果拉断后试棒上没有颈缩,是否表示它未发生塑性变形?答:低碳钢的σ-ε曲线如下图,试样将在曲线B 点处出现颈缩现象。
如果拉断后试棒上没有颈缩,并不表示它未发生塑性变形,只是塑性变形量很小。
3.在什么条件下,应用布氏硬度试验比洛氏硬度试验好?在测试低硬度零件的时候,布氏硬度比洛氏硬度要更准确些,当然零件厚度及相关尺寸必须满足布氏硬度测试的条件。
洛式硬度压痕很小,测量值有局部性,须测数点求平均值,适用成品和薄片,归于无损检测一类。
布式硬度压痕较大,测量值准,不适用成品和薄片,一般不归于无损检测一类。
4. K σ与1c K 的概念有什么不同?答:K σ是工程材料中的材料的屈服点。
只要裂纹很尖锐,顶端附近各点应力K σ的大小取决与一比例系数1K 。
由于1K 反映了裂纹尖端附近各点的强弱,故称为应力强度因子。
当1K 增大到某一临界值时,就会使裂纹尖端附近各点的应力大到足以是裂纹失稳扩展,从而引起脆断。
这个应力强度因子的临界值,称为材料的断裂韧性,用1c K 表示。
5.在什么情况下应考虑材料的高低温性能?它们的主要性能指标是什么?答:对于不是在常温下工作的材料,不能的简单地用应力-应变关系来评定力学性能,而需要加入温度与时间两个因素,需要考虑材料的高低温性能。
金属材料的高温性能用蠕变强度和持久强度来表示。
材料力学第二章习题选及其解答

2-1. 试求图示各杆1-1、2-2、3-3截面的轴力, 并作轴力图。
解: (a)(1)求约束反力kNR R X 500203040 0==-++-=∑(2)求截面1-1的轴力kNN NR X 500011==+-=∑(3)求截面2-2的轴力kNN NR X 10040 022==++-=∑(4)求截面3-3的轴力(a) (b)kNN NR X 2003040 033-==+++-=∑(5)画轴力图(b)(1)求截面1-1的轴力01=N(2)求截面2-2的轴力 PN4022==(3)求截面3-3的轴力PN P P NX 304 033==-+=∑(4)画轴力图2-2. 作用图示零件上的拉力P=38kN ,试问零件内最大拉应力发生于哪个横截面上?并求其值。
解:(1)1-1截面MPa A P 86.6720)2250(3103811=⨯-⨯==σ(2)2-2截面MPa A P 33.63152021038322=⨯⨯⨯==σ(3)3-3截面MPa A P 24.45215)2250(1038333=⨯⨯-⨯==σ(4)最大拉应力MPa 86.671max ==σσ2-3. 在图示结构中,若钢拉杆BC 的横截面直径为10mm ,试求拉杆内的应力。
设由BC 联接的两部分均为刚体。
3 3解:(1)以刚体CAE 为研究对象∑=⨯-⨯+⨯=035.15.4 0'P N N mC E A (2)以刚体BDE 为研究对象075.05.1 0=⨯-⨯=∑B E DN N m(3)联立求解kNN N N N N C EE C B 6 '=∴==(4)拉杆内的应力MPa A N B 4.7610410623=⨯⨯⨯==πσ 2-4. 图示结构中,1、2两杆的横截面直径分别为10mm 和20mm ,试求两杆内的应力。
设两根横梁皆为刚体。
解:(1)以整体为研究对象,易见A 处的水平约束反力为零; (2)以AB 为研究对象由平衡方程知0===A B B R Y X(3)以杆BD由平衡方程求得KNN N NY KNN N mC20010 01001101 021211==--===⨯-⨯=∑∑(4)杆内的应力为1MPa A N MPa A N 7.63204102012710410102322223111=⨯⨯⨯===⨯⨯⨯==πσπσ2-7. 某拉伸试验机的示意图如图所示。
材料力学第五版第二章习题答案

F F
m m
m m
F
(b)
FN
x m m
FN F
F
(c)
FN
(a)
F
m
m
F
(b)
F
FN
m
FN
x m m
m
FN F
F
(c)
若用平行于杆轴线的坐标表示横截面的位置,用 垂直于杆轴线的坐标表示横截面上轴力的数值, 所绘出的图线可以表明轴力与截面位置的关系, 称为轴力图。
F F F
讨论: ( 1) 0
90 (2) 45 45
0
max 0 (横截面) 0 (纵截面) max 0 / 2 min 0 / 2
0 0
(横截面) (纵截面)
90
观察现象:
等直杆相邻两条横向线在杆受拉(压)后仍 为直线,仍相互平行,且仍垂直于杆的轴线。 F
a a' b' b c c' d' d
F
平面假设
原为平面的横截面在杆变形后仍为平面, 对于拉(压)杆且仍相互平行,仍垂直于轴线。
推论:
1、等直拉(压)杆受力时没有发生剪切变形, 因而横截面上没有切应力。 2、拉(压)杆受力后任意两个横截面之间纵向线 段的伸长(缩短)变形是均匀的。 亦即横截面上各点处的正应力 都相等。
FN,max FN2 50kN
补充 例题1
l
F
F
q=F/l
F 2l l 3 F
解: 1、求支反力
1 FR 1 F F F 2 F'=2ql F 3 F 2 q
FR
材料力学第五版课后习题答案详解

Microsoft Corporation材料力学课后答案[键入文档副标题]lenovo[选取日期]第二章轴向拉伸和压缩2-12-22-32-42-52-62-72-82-9下页2-1试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a)解:;;(b)解:;;(c)解:;。
(d)解:。
返回2-2 试求图示等直杆横截面1-1,2-2和3-3上的轴力,并作轴力图。
若横截面面积,试求各横截面上的应力。
解:返回2-3试求图示阶梯状直杆横截面1-1,2-2和3-3上的轴力,并作轴力图。
若横截面面积,,,并求各横截面上的应力。
解:返回2-4 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个75mm×8mm的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EG横截面上的应力。
解:=1)求内力取I-I分离体得(拉)取节点E为分离体,故(拉)2)求应力75×8等边角钢的面积A=11.5 cm2(拉)(拉)2-5(2-6)图示拉杆承受轴向拉力,杆的横截面面积。
如以表示斜截面与横截面的夹角,试求当,30,45,60,90时各斜截面上的正应力和切应力,并用图表示其方向。
解:2-6(2-8) 一木桩柱受力如图所示。
柱的横截面为边长200mm的正方形,材料可认为符合胡克定律,其弹性模量E=10 GPa。
如不计柱的自重,试求:(1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的纵向线应变;(4)柱的总变形。
解:(压)(压)。
材料力学内部习题集及答案
第二章 轴向拉伸和压缩2-1一圆截面直杆,其直径d =20mm,长L =40m ,材料的弹性模量E =200GPa ,容重γ=80kN/m 3,杆的上端固定,下端作用有拉力F =4KN ,试求此杆的:⑴最大正应力; ⑵最大线应变; ⑶最大切应力;⑷下端处横截面的位移∆。
解:首先作直杆的轴力图⑴最大的轴向拉力为232N,max 80100.024*********.8N 44d F V F L F ππγγ=+=+=⨯⨯⨯⨯+= 故最大正应力为:N,maxN,maxN,maxmax 222445004.8=15.94MPa 3.140.024F F F Addσππ⨯====⨯⑵最大线应变为:64maxmax915.94100.7971020010E σε-⨯===⨯⨯ ⑶当α(α为杆内斜截面与横截面的夹角)为45︒时,maxmax 7.97MPa 2ασττ===⑷取A 点为x 轴起点,2N (25.124000)N 4d F Vx F x F x πγγ=+=+=+故下端处横截面的位移为:240N 0025.1240001d d (12.564000)2.87mm LL F x x x x x EA EA EA+∆===⋅+=⎰⎰2-2试求垂直悬挂且仅受自重作用的等截面直杆的总伸长△L 。
已知杆横截面面积为A ,长度为L ,材料的容重为γ。
解:距离A 为x 处的轴力为 所以总伸长2N 00()L d d 2LL F x Ax L x x EA EA Eγγ∆===⎰⎰ 2-3图示结构,已知两杆的横截面面积均为A =200mm 2,材料的弹性模量E =200GPa 。
在结点A 处受荷载F 作用,今通过试验测得两杆的纵向线应变分别为ε1=4×10-4,ε2=2×10-4,试确定荷载P 及其方位角θ的大小。
解:由胡克定律得 相应杆上的轴力为取A 节点为研究对象,由力的平衡方程得解上述方程组得2-4图示杆受轴向荷载F 1、F 2作用,且F 1=F 2=F ,已知杆的横截面面积为A ,材料的应力-应变关系为ε=c σn,其中c 、n 为由试验测定的常数。
材料力学第2章
FN2 3F /4 3 100 103 σ 137.9 106 Pa 137.9MPa [ ] 6 A2 (b 2d ) 4 8 (100 2 16) 10
由计算结果可知,该连接处安全。
例题2-2 某接头部位的销钉承担荷载如图2-11所示。已知连接处的受力和几何
(2)校 挤压面上的挤压力 Fbs 4 挤压应力:
Fbs F /4 100 103 bs * 195.3 106 Pa 195.3MPa [σ bs ] 6 d A bs 4 8 16 10
(3)校核钢板的抗拉强度。 沿第一排孔的中心线将钢板截开, 取右部分受力如图(d),则
2.2
连接部位的失效形式
(a) 螺栓连接
(b)连接件被剪断
(c) 连接部位挤压破坏 图2-4
(d)被连接件强度破坏
2.3
连接件的实用计算
2.3.1 连接件剪切的实用计算——单剪
F F
(b)
F
(a) 图2-5
FS
(c)
(d)
FS ——剪切面上的剪力 As ——剪切面面积
F
x
0
FS F
FS As
尺寸分别为:F=100 kN,D=45 mm,d1=32 mm,d2=34 mm,δ=12 mm。试计 算销钉的切应力 和挤压应力 bs 。
图2-11 例题2-2图
【解】(1)销钉的剪切面积
As πd1 3.14 32mm 12mm 1206mm2
(2)销钉的挤压面积
Abs
FN1 F
FN1 F 100 103 6 148.8 10 Pa 148.8MPa 6 A1 (b d ) 8 (100 16) 10
材料力学第2章作业答案
2-1画出各杆的轴力图
2-11图示桁架,由圆截面杆1与杆2组成,并在节点A承受载荷F=80kN作用。
杆1、杆2的直径分别为d1=30mm和d2=20mm,两杆的材料相同,屈服极限σs=320MPa,安全因数n s=2.0。
试校核桁架的强度。
解:由A点的平衡方程
可求得1、2两杆的轴力分别为
由此可见,桁架满足强度条件。
2-14图示桁架,承受载荷F作用。
试计算该载荷的许用值[F]。
设各杆的横截面面积均为A,许用应力均为[σ]。
解:由C点的平衡条件
由B点的平衡条件
1杆轴力为最大,由其强度条件
2-17图示圆截面杆件,承受轴向拉力F作用。
设拉杆的直径为d,端部墩头的直径为D,高度为h,试从强度方面考虑,建立三者间的合理比值。
已知许用应力[σ]=120MPa,许用切应力[τ]=90MPa,许用挤压应力[σbs]=240MPa。
解:由正应力强度条件
由切应力强度条件
由挤压强度条件
式(1):式(3)得
式(1):式(2)得
故D:h:d=1.225:0.333:1
2-18图示摇臂,承受载荷F1与F2作用。
试确定轴销B的直径d。
已知载荷F1=50kN,F2=35.4kN,许用切应力[τ]=100MPa,许用挤压应力[σbs]=240MPa。
解:摇臂ABC受F1、F2及B点支座反力F B三力作用,根据三力平衡汇交定理知F B的方向如图(b)所示。
由平衡条件
由切应力强度条件
由挤压强度条件
故轴销B的直径。
材料力学答案第二章
第二章拉伸、压缩与剪切第二章答案2.1求图示各杆指定截面的轴力,并作轴力图。
(a)4 40kN 350kN 225kN 1 20kNzP*1解:F R=5kNF R F N4 4 40kN 3 r - 1 1 FN3F N4=F R=5 kN FN3=F R+40=45 kNF N22 25kN 20kN•IT 121 20kNF NI]—^1F N2=-25+20=-5 kN FN i=20kN 45kN5kN20kN6kN10kN1 10kN2 6kN6kN1 — 1截面:F N 1=10 kN2—2截面:F N 2=10-10=010kN10kNF N 23—3截面:F N 33—I_|_6kN3F N 3=6 kN10kN1F N 1I © I2.2图示一面积为100mm 200mm的矩形截面杆,受拉力 F = 20kN的作用,试求:(1)m-m 上的应力;(2)最大正应力max 和最大剪应力 max 的大小及其作用1MPa2.3图示一正方形截面的阶梯形混凝土柱。
设重力加速度2.04 103kg/m 3,F = 100kN ,许用应力和b 。
解: pF 20 10330°0.1 0.21MPacos 230.75 MPa4严旦 0.433M Pa2 2max0.5 MPa-的斜截面 6面的方位角。
maxg = 9.8m/s 2,混凝土的密度为2MPa 。
试根据强度条件选择截面宽度a解:2.04 1039.8 22. 4N i4a2, 1 F NJ10 4 N/m 2 P4a2―3P100F N2在图示杆系中,BC试求夹角的值。
4a2103[],AC和100 103106 4 2 1040.228m4b2104 4 0.228 104 4 b2304.16V2 106 4 2 1040.398m 398mmBC两杆的材料相同,且抗拉和抗压许用应力相等,同为杆保持水平,长度为I ,AC杆的长度可随角的大小而变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精品文档
AHA12GAGGAGAGGAFFFFAFAF
浙江科技学院
2015-2016学年第一学期考试试卷 A 卷
考试科目 材料力学 考试方式 闭 完成时限 2 小时
拟题人 陈梦涛 审核人 批准人 2015 年 9 月17 日
建工 学院 2014 年级 土木工程 专业
一、单项选择题(每小题3分,计30分)
1. 对于塑性材料来说,胡克定律(Hooke's law)使用的
范围是 。
A.p; B. p; C. s; D.
s
2.实心圆截面杆直径为D,受拉伸时的绝对变形为
mml1
。仅当直径变为2D时,绝对变形
l
为 。
A.1mm B.1/2 mm C.1/4 mm D.2mm
3. 下列有关受压柱截面核心的说法中,正确的
是 。
A.当压力P作用在截面核心内时,柱中只有拉应力。
B.当压力P作用在截面核心内时,柱中只有压应力。
C.当压力P作用在截面核心外时,柱中只有压应力。
精品文档
AHA12GAGGAGAGGAFFFFAFAF
D.当压力P作用在截面核心外时,柱中只有拉应力。
4. 构件的强度、刚度和稳定
性 。
A.只与材料的力学性质有关; B.只与构件的形状
尺寸关;
C.与二者都有关;
D.与二者都无关。
5. 如右图所示,设虚线表示为单元体变形后的形状,
则该单元体的剪应变
为 。
A. α; B.π/2-α; C.π/2-2
α; D.2α
6. 图示一杆件的拉压刚度为EA,
在图示外力作用下其应变能U的下
列表达式是 。
7.
应力-应变曲线的纵、横坐标分别为σ=FN /A,ε
题5
题6
精品文档
AHA12GAGGAGAGGAFFFFAFAF
=△L / L,其中 。
A.A 和L 均为初始值;
B.A 和L 均为瞬时值;
C.A 为初始值,L 为瞬时值;
D.A 为瞬时值,L 均为初始值。
8. 设一阶梯形杆的轴力沿杆轴是变化的,则发生破坏
的截面上 。
A.外力一定最大,且面积一定最小; B.轴力一
定最大,且面积一定最小;
精品文档
AHA12GAGGAGAGGAFFFFAFAF
C.轴力不一定最大,但面积一定最小; D.轴力与
面积之比一定最大。
9. 图示拉杆的外表面上画有一斜线,当
拉杆受力变形时,斜线将发
生 。
A.
平动 ; B.转动 C.平动加转动; D.
不动
10.
图10所示钢杆,放置在两刚性平面之间,杆
内无初始应力。当温度均匀升高m℃后,杆上任一
点A处的应力ζ与纵向应变ε之值的可能发生的
情形是 。
A、ζ≠0,ε=0 ; B、ζ=0,ε=0; C、ζ≠0,
ε≠0 ;D、ζ=0,ε≠0
二、画出各构件的内力图(第1,2小题各3分,第3小
题4分,共10分)
(1) (2)
题9
题
精品文档
AHA12GAGGAGAGGAFFFFAFAF
(3)
三,是非题(每小题3分,共12分)
( )1.低碳钢一类的塑性材料,各种复杂应力状态
下都会发生屈服,所以一般采用形状改变能
密度理论;
( )2.衡量脆性材料拉伸强度的唯一指标是材料的
拉伸强度b;
( )3.对于拉伸曲线上没有屈服平台的合金塑性材
料,工程上规定σ0.2作为名义屈服极限,此
时相对应的应变量为ε=0.2%
( )4.若梁某截面的上表面正应力为-120MPa,则
该截面的下表面正应力为+120Mpa;
四.计算题(共48分)
1.(13分)现有如图所示一实心圆钢杆
AB和AC在A点以铰链相互连接,在A点处
精品文档
AHA12GAGGAGAGGAFFFFAFAF
有一铅垂向下的力F=35kN。已知杆AB和AC的直径分别
为12mm和15mm,圆钢杆的弹性模量E=210GPa。求:①
AB、AC杆的应力及线应变 ②A点在铅垂方向的位移;
精品文档
AHA12GAGGAGAGGAFFFFAFAF
2.(10分)简易起重设备的计算简
图如图所示,若已知斜杆AB是用两
根63mm*40mm*4mm的不等边角钢组
成,该角钢的许用应力[σ]=170MPa。
试问在提起重量为P=24kN的物体
时,该起重机能否顺利完成工作?
(题1
精品文档
AHA12GAGGAGAGGAFFFFAFAF
3. (7分)图示结构中BD为刚性梁,
杆1,2用同一种材料制成,横截面
面积相等,50PkN,求1,2杆的轴
力。
精品文档
AHA12GAGGAGAGGAFFFFAFAF
4.(8分)已知混凝土的密度为2.25×
103kg/m3,许用压应力[σ]=2MPa。试按强度条
件确定所示混凝土柱所需的横截面积A1和A2。
若混凝土的弹性模量E=20GPa,试求柱顶A的
位移。
5.(12分)结构受力如图a所示。BD杆
精品文档
AHA12GAGGAGAGGAFFFFAFAF
可视为刚体,AB和CD两杆的横截面面积分别为
150mm2,400mm2,其材料的应力-应变曲线分别表示于图b
中。求(1)当F到达何值时,BD杆件开始明显倾斜(以
AB杆获BC杆中的应力到达屈服极限时作为杆件产生明
显变形的标志);(2)若设计要求安全系数N=2,试求结
构能承受的许用荷载[F]
如有侵权请联系告知删除,感谢你们的配合!
!22759 58E7 壧37855 93DF 鏟 29818 747A 瑺J28394 6EEA 滪?[ 31520 7B20 笠26246 6686 暆|K
