2015届中考数学一轮复习训练:第26课时《圆的基本性质》 (浙教版) (2)
浙教版 初中数学培优讲义 九年级 第三章 《圆的基本性质》全章复习与巩固—知识讲解(提高) 学生版
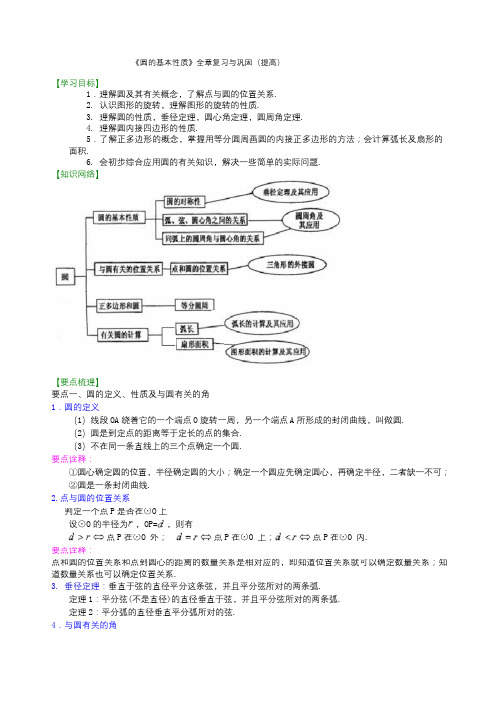
《圆的基本性质》全章复习与巩固(提高)【学习目标】1.理解圆及其有关概念,了解点与圆的位置关系.2.认识图形的旋转,理解图形的旋转的性质.3.理解圆的性质,垂径定理,圆心角定理,圆周角定理.4.理解圆内接四边形的性质.5.了解正多边形的概念,掌握用等分圆周画圆的内接正多边形的方法;会计算弧长及扇形的面积.6.会初步综合应用圆的有关知识,解决一些简单的实际问题.【知识网络】【要点梳理】要点一、圆的定义、性质及与圆有关的角1.圆的定义(1)线段OA绕着它的一个端点O旋转一周,另一个端点A所形成的封闭曲线,叫做圆.(2)圆是到定点的距离等于定长的点的集合.(3)不在同一条直线上的三个点确定一个圆.要点诠释:①圆心确定圆的位置,半径确定圆的大小;确定一个圆应先确定圆心,再确定半径,二者缺一不可;②圆是一条封闭曲线.2.点与圆的位置关系判定一个点P是否在⊙O上设⊙O的半径为,OP=,则有点P在⊙O外;点P在⊙O上;点P在⊙O内.要点诠释:点和圆的位置关系和点到圆心的距离的数量关系是相对应的,即知道位置关系就可以确定数量关系;知道数量关系也可以确定位置关系.3.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.定理1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.定理2:平分弧的直径垂直平分弧所对的弦.4.与圆有关的角圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.在同圆或者等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一对量相等,那么它们所对应的其余各对量都相等.圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的一半.90°的圆周角所对的弦为直径;半圆或直径所对的圆周角为直角.在同圆或者等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.5.圆内接四边形圆内接四边形的对角互补.要点二、图形的旋转在平面内,一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动叫做旋转.这个定点叫做旋转中心,转过的角叫做旋转角.图形经过旋转所得的图形和原图形全等.对应点到旋转中心的距离相等.任何一对对应点与旋转中心连线所成的角度等于旋转的角度.要点三、正多边形各边相等,各内角也相等的多边形是正多边形.要点诠释:判断一个多边形是否是正多边形,必须满足两个条件:(1)各边相等;(2)各角相等;缺一不可.如菱形的各边都相等,矩形的各角都相等,但它们都不是正多边形(正方形是正多边形).正多边形的外接圆和圆的内接正多边形正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.要点四、弧长及扇形的面积圆心角为、半径为R的弧长..圆心角为,半径为R,弧长为的扇形的面积要点诠释:(1)对于扇形面积公式,关键要理解圆心角是1°的扇形面积是圆面积的,即;(2)在扇形面积公式中,涉及三个量:扇形面积S、扇形半径R、扇形的圆心角,知道其中的两个量就可以求出第三个量.(3)扇形面积公式,可根据题目条件灵活选择使用,它与三角形面积公式有点类似,可类比记忆;(4)扇形两个面积公式之间的联系:.【典型例题】类型一、圆的基础知识1. 如图,已知⊙O是以数轴的原点O 为圆心,半径为1 的圆,∠AOB=45°,点在数轴上运动,若P过点P 且与OA 平行(或重合)的直线与⊙O有公共点, 设OP=x,则的取值范围是().xA.-1≤x≤1B.2≤x≤2C.0≤x≤2D.x>2举一反三:【变式】如图,已知⊙O是以数轴的原点为圆心,半径为1 的圆,∠AOB=45°,点P 在数轴上运动,若过点P 且与OB 平行的直线于⊙O有公共点,设P(x,0),则x 的取值范围是().B.0<x≤1C.- 2≤x<0 或0<x≤2D.x>1类型二、弧、弦、圆心角、圆周角的关系及垂径定理2.如图所示,已知在⊙O中,AB 是⊙O的直径,弦CG⊥AB于D,F 是⊙O上的点,且C F C B,BF 交CG 于点E,求证:CE=BE.举一反三:【变式】如图所示,在⊙O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC 的长为()A.19 B.16 C.18 D.20类型三、图形的旋转3.如图,△ABC 中,AB=4 ,BC=6 ,∠B=60°,将△ABC沿射线BC 的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C 重合,则平移的距离和旋转角的度数分别为()类型四、圆中有关的计算4.如图,A B为⊙O直径,C为⊙O上一点,点D是的中点,D E⊥A C于E,D F⊥A B于F.(1)判断DE与⊙O的位置关系,并证明你的结论;(2)若OF=4,求A C的长度.举一反三:【变式】如图,⊙O是△A B C的外接圆,A B是⊙O的直径,FO⊥A B,垂足为点O,连接AF并延长交⊙O于点D,连接O D交B C于点E,∠B=30°,F O=2.(1)求A C的长度;(2)求图中阴影部分的面积.(计算结果保留根号)类型五、圆与其他知识的综合运用5..6.如图,直径AB为6 的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是().A. 3B. 6C. 5D. 4举一反三:【变式】某中学举办校园文化艺术节,小颖设计了同学们喜欢的图案“我的宝贝”,图案的一部分是以斜边长为 12cm 的等腰直角三角形的各边为直径作的半圆,如图所示,则图中阴影部分的面积为( ).A. B.72 C.36 D.72《圆的基本性质》全章复习与巩固—巩固练习(提高)【巩固练习】一、选择题1.对于下列命题:①任意一个三角形一定有一个外接圆,并且只有一个外接圆;②任意一个圆一定有一个内接三角形,并且只有一个内接三角形;③任意三角形一定有一个内切圆,并且只有一个内切圆;④任意一个圆一定有一个外切三角形,并且只有一个外切三角形.其中,正确的有( ).A.1 个B.2 个C.3 个D.4 个2.圆锥的底面半径为4cm,高为5cm,则它的表面积为()A.12πcm2 B.26πcm2C.πcm D.(4 +16)πcm223.设计一个商标图案,如图所示,在矩形ABCD 中,AB=2BC,且AB=8cm,以A 为圆心、AD 的长为半径作半圆,则商标图案(阴影部分)的面积等于( ).A.(4π+8)cm2B.(4π+16)cm2C.(3π+8)cm2D.(3π+16)cm24.如图,已知P 是⊙O外一点,Q 是⊙O上的动点,线段PQ 的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,则线段OM 的最小值是()A.0 B.1 C.2 D.35. “圆材埋壁”是我国古代著名的数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表示为:如图所示,CD 为⊙O的直径,弦AB⊥CD于E,CE=1 寸,AB=10 寸,则直径CD 的长为( )A.12.5 寸B.13 寸C.25 寸D.26 寸6.如图,在Rt△ABC中,∠BAC=90°.如果将该三角形绕点A 按顺时针方向旋转到△AB C 的位置,点B1 1 1 恰好落在边BC 的中点处.那么旋转的角度等于()A.55°B.60°C.65°D.80 °7.一条弦的两个端点把圆周分成4:5 两部分,则该弦所对的圆周角为( ).A.80°B.100°C.80°或100°D.160°或200°8.如图,圆O 的直径AB 垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD 的长为()A.22B.4 C.42D.8二、填空题9.如下左图,是的内接三角形,,点P 在上移动(点P 不与点A、C 重合),则的变化范围是__ ________.10.如图,⊙0中,弦AB 与弦CD 交于E,连接AC,OE,BD,若AE=BE,AC∥0E,则∠CDB=.11.如图,半圆O 的直径AB=10cm,弦AC=6cm,AD 平分∠BAC,则AD 的长为______cm.12.如图,在正方形ABCD 中,E、F 分别是边BC、CD 上的点,∠EAF=45°,△ECF的周长为4,则正方形ABCD 的边长为_______.13.如图,以△ABC的边BC 为直径的⊙O分别交AB、AC 于点D、E,连结OD、OE,若∠A=65°,则∠DOE=_______.2a14.已知正方形ABCD 外接圆的直径为,截去四个角成一正八边形,则这个正八边形EFGHIJLK 的边长为____ ____,面积为_____ ___.15.如图,AB 为⊙O的直径,AB=AC,BC 交⊙O于点D,AC 交⊙O于点E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧是劣弧的 2 倍;⑤AE=BC,其中正确的序号是.16.如图,AB、CD 是半径为5 的⊙O的两条弦,AB=8,CD=6,MN 是直径,AB⊥MN于点E,CD⊥MN于点F,P 为EF 上的任意一点,则PA+PC 的最小值为_______.三、解答题17.(二模)如图,已知四边形AB C D内接于圆,对角线A C与B D相交于点E,F在A C上,A B=A D,∠BFC=∠B A D=2∠DFC.(1)若∠DFC=40°,求∠CBF的度数;(2)求证:C D⊥DF.18.已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求:(1)圆心O到AQ的距离;(2)线段EF的长.19.如图,相交两圆的公共弦长为120cm,它分别是一圆内接正六边形的边和另一圆内接正方形的边.求两圆相交弧间阴影部分的面积.(1)求证:∠A=∠AEB;(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.17.(二模)如图,已知四边形AB C D内接于圆,对角线A C与B D相交于点E,F在A C上,A B=A D,∠BFC=∠B A D=2∠DFC.(1)若∠DFC=40°,求∠CBF的度数;(2)求证:C D⊥DF.18.已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求:(1)圆心O到AQ的距离;(2)线段EF的长.19.如图,相交两圆的公共弦长为120cm,它分别是一圆内接正六边形的边和另一圆内接正方形的边.求两圆相交弧间阴影部分的面积.(1)求证:∠A=∠AEB;(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.17.(二模)如图,已知四边形AB C D内接于圆,对角线A C与B D相交于点E,F在A C上,A B=A D,∠BFC=∠B A D=2∠DFC.(1)若∠DFC=40°,求∠CBF的度数;(2)求证:C D⊥DF.18.已知:如图,∠PAQ=30°,在边AP上顺次截取AB=3cm,BC=10cm,以BC为直径作⊙O交射线AQ于E、F两点,求:(1)圆心O到AQ的距离;(2)线段EF的长.19.如图,相交两圆的公共弦长为120cm,它分别是一圆内接正六边形的边和另一圆内接正方形的边.求两圆相交弧间阴影部分的面积.(1)求证:∠A=∠AEB;(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.。
2015中考试题研究数学(浙江)精品复习课件:第24讲+圆的基本性质

②阴影部分面积是12(k1+k2); ③当∠AOC=90°时,|k1|=|k2|; ④若 OABC 是菱形,则两双曲线既关于 x 轴对称,也关于 y 轴 对称. 其中正确的是__①④__.(把所有正确的结论的序号都填上)
解析:
作 AE⊥y 轴于点 E,CF⊥y 轴于点 F,如图,∵四边形 OABC 是平行四边形, ∴S△AOB=S△COB,∴AE=CF,∴OM=ON,∵S△AOM=12|k1|=12OM·AM,S△CON= 12|k2|=12ON·CN,∴ACMN =||kk12||,所以①正确;∵S△AOM=12|k1|,S△CON=12|k2|,∴S 阴 影部分=S△AOM+S△CON=12(|k1|+|k2|),而 k1>0,k2<0,∴S 阴影部分=},所以②错误; 当∠AOC=90°,∴四边形 OABC 是矩形,∴不能确定 OA 与 OC 相等,而 OM =ON,∴不能判断△AOM≌△OCN,∴不能判断 AM=CN,∴不能确定|k1|=|k2|, 所以③错误;若 OABC 是菱形,则 OA=OC,而 OM=ON,∴Rt△AOM≌Rt△ CON,∴AM=CN,∴|k1|=|k2|,∴k1=-k2,∴两双曲线既关于 x 轴对称,也关 于 y 轴对称,所以④正确.故答案为①④
C . 60°
D.50°
2.(2014·杭州)已知直线a∥b,若∠1=40°50′,则∠2 =__∠B__.
3.(2014·温州)如图,直线AB,CD被BC所截,若AB∥CD, ∠1=45°,∠2=35°,则∠3=__70__度.
4.(2012·嘉兴)已知△ABC中,∠B是∠A的2倍,∠C比∠A大 20°,则∠A等于( A )
2.圆的有关性质 (1)圆的对称性: ①圆是__轴对称__图形,其对称轴是__过圆心的任意 一条直线__. ②圆是__中心对称__图形,对称中心是__圆心__. ③旋转不变性,即圆绕着它的圆心旋转任意一个角度, 都能与原来的图形重合.
2015年河北中考数学总复习课件(第26课时_圆的有关概念与性质)

第26课时┃ 圆的有关概念与性质
课 前 热 身
1.若⊙O 的半径为 5 cm,点 A 到圆心 O 的距离为 4 cm,则 点 A 与⊙O 的位置关系是 ( C ) A.点 A 在⊙O 外 B.点 A 在⊙O 上 C.点 A 在⊙O 内 D.不能确定 ︵ 2. [2014· 温州] 如图 26-1, 已知点 A, B, C 在⊙O 上, ACB 为优弧, 下列选项中与∠AOB 相等的是 ( A )
考点聚焦
冀考探究
第26课时┃ 圆的有关概念与性质
考点2 圆心角、弧、弦之间的关系 弦 相 在同圆或等圆中,相等的圆心角所对的______ 等,所对的______ 弧 也相等 在同圆或等圆中,两个圆心角、所对应的两条弦 和所对应的两条弧这三组量中,只要有一组量相 等,其他两组量就分别相等
性质 推论
冀考解读
第26课时 圆的有关概念与性质
第26课时┃ 圆的有关概念与性质
冀 考 解 读
考点梳理 常考题型 年份 2015 热度预测 确定圆的条件 选择、填空 ☆☆ 点和圆的位置 选择、填空 ☆☆ 关系 圆心角、弧、弦 选择、填空、 ☆☆☆ 之间的关系 解答 圆周角定理及其 选择、填空、 2012 ☆☆☆☆ 推论 解答 2013 2012 垂径定理及其 选择、填空、 ☆☆☆☆ 2013 推论 解答 2014
课前热身
考点聚焦
冀考探究
第26课时┃ 圆的有关概念与性质
考点3 圆周角
Hale Waihona Puke 圆周角 定义 圆周角 定理 推论 1 推论 2
顶点在圆上,两边都与圆相交的角叫做圆周角 圆上一条弧所对的圆周角等于它所对的圆心角 的________ 一半 直角 ; 直径所对的圆周角是______ 90°的圆周角所对 直径 的弦是______ 同弧所对的圆周角______ 相等
中考数学第一部分考点研究复习第六章圆第26课时圆的基本性质练习含解析

2019-2020年中考数学第一部分考点研究复习第六章圆第26课时圆的基本性质练习含解析基础过关1. (xx 济宁)如图,在⊙O 中,AB ︵=AC ︵,∠AOB =40°,则∠ADC 的度数是( ) A. 40° B. 30° C. 20° D. 15°第1题图 第2题图2. (xx 张家界)如图,AB 是⊙O 的直径,BC 是⊙O 的弦,若∠OBC =60°,则∠BAC 的度数是( )A. 75°B. 60°C. 45°D. 30°3. (xx 自贡)如图,在⊙O 中,弦AB 与CD 交于点M ,∠A =45°,∠AMD =75°,则∠B 的度数是( )A. 15°B. 25°C. 30°D. 75°第3题图 第4题图4. (xx 陕西)如图,⊙O 的半径为4,△ABC 是⊙O 的内接三角形,连接OB 、OC ,若∠BAC 与∠BOC 互补,则弦BC 的长为( )A. 3 3B. 4 3C. 5 3D. 6 35. (xx 毕节)如图,点A 、B 、C 在⊙O 上,∠A =36°,∠C =28°,则∠B =( )A. 100°B. 72°C. 64°D. 36°第5题图 第6题图6. (xx 聊城)如图,四边形ABCD 内接于⊙O ,F 是CD ︵上一点,且DF ︵=BC ︵,连接CF 并延长交AD 的延长线于点E ,连接AC ,若∠ABC =105°,∠BAC =25°,则∠E 的度数为( )A. 45°B. 50°C. 55°D. 60°7. (xx 南宁)如图,点A ,B ,C ,P 在⊙O 上,CD ⊥OA ,CE ⊥OB ,垂足分别为D ,E ,∠DCE =40°,则∠P 的度数为( )A. 140°B. 70° C .60° D. 40°第7题图 第8题图8. (xx 泰安)如图,点A 、B 、C 是圆O 上的三点,且四边形ABCO 是平行四边形,OF ⊥OC 交圆O 于点F ,则∠BAF 等于( )A. 12.5°B. 15°C. 20°D. 22.5°9. (xx 达州)如图,半径为3的⊙A 经过原点O 和点C (0,2),B 是y 轴左侧⊙A 优弧上一点,则tan ∠OBC 为( )A. 13B. 2 2C. 24D. 223第9题图 第10题图10. (xx 杭州)如图,已知AC 是⊙O 的直径,点B 在圆周上(不与A ,C 重合),点D 在AC 的延长线上,连接BD 交⊙O 于点E ,若∠AOB =3∠ADB ,则( ) A. DE =EB B. 2DE =EBC. 3DE =DOD. DE =OB11. (xx 黄冈)如图,⊙O 是△ABC 的外接圆,∠AOB =70°,AB =AC ,则∠ABC =________.第11题图 第12题图12. (xx 娄底)如图,四边形ABCD 为⊙O 的内接四边形,已知∠C =∠D ,则AB 与CD 的位置关系是________.13. (xx 贵阳)如图,已知⊙O 的半径为6 cm ,弦AB 的长为8 cm ,P 是AB 延长线上一点,BP =2 cm ,则tan ∠OPA 的值是________.第13题图 第14题图14. (xx 长春)如图,在⊙O 中,AB 是弦,C 是AB ︵上一点,若∠OAB =25°,∠OCA =40°,则∠BOC 的大小为________度.15. (xx 永州)如图,在⊙O 中,A ,B 是圆上的两点,已知∠AOB =40°,直径CD ∥AB ,连接AC ,则∠BAC =________度.第15题图 第16题图16. (xx 南京二模)如图,MN 是⊙O 的直径,矩形ABCD 的顶点A 、D 在MN 上,顶点B 、C 在⊙O 上,若⊙O 的半径为5,AB =4,则AD 的长为________.17. (xx 宁夏)已知△ABC ,以AB 为直径的⊙O 分别交AC 于D ,BC 于E ,连接ED .若ED =EC . (1)求证:AB =AC ;(2)若AB =4,BC =23,求CD 的长.第17题图 满分冲关1. (xx 泸州)以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( ) A.38 B. 34 C. 24 D. 282. (xx 安徽)如图,Rt △ABC 中,AB ⊥BC ,AB =6,BC =4,P 是△ABC 内部的一个动点,且满足∠PAB =∠PBC .则线段CP 长的最小值为( )A. 32B. 2C. 81313D. 121313第2题图 第3题图3. (xx 海南)如图,AB 是⊙O 的直径,AC 、BC 是⊙O 的弦,直径DE ⊥AC 于点P .若点D 在优弧ABC ︵上,AB =8,BC =3,则DP =________.4. (xx 威海)如图,正方形ABCD 内接于⊙O ,其边长为4,则⊙O 的内接正三角形EFG 的边长为____________.第4题图 第5题图5. (xx 雅安)如图,在△ABC 中,AB =AC =10,以AB 为直径的⊙O 与BC 交于点D ,与AC 交于点E ,连OD 交BE 于点M ,且MD =2,则BE 长为________.6. (xx 株洲)已知AB 是半径为1的圆O 直径,C 是圆上一点,D 是BC 延长线上一点,过D 点的直线交AC 于E 点,交AB 于F 点,且△AEF 为等边三角形.(1)求证:△DFB 是等腰三角形; (2)若DA =7AF ,求证CF ⊥AB .第6题图答案基础过关1. C 【解析】如解图,连接CO ,∵AB ︵=AC ︵,∴∠AOC =∠AOB =40°,∴∠ADC =12∠AOC =12×40°=20°.第1题解图2. D 【解析】∵AB 是⊙O 的直径,∴∠ACB =90°,∵∠ABC =60°,∴∠BAC =90°-∠ABC =90°-60°=30°.3. C 【解析】∵∠C =∠AMD -∠A =30°,又∵∠C 与∠B 为同弧所对的圆周角,∴∠B =∠C =30°.4. B 【解析】如解图,延长CO 交⊙O 于点A ′,连接A ′B .设∠BAC =α,则∠BOC =2∠BAC =2α,∵∠BAC +∠BOC =180°,∴α+2α=180°,∴α=60°.又∵∠BAC 和∠BA ′C 都为BC ︵所对的圆周角,∴∠BAC =∠BA ′C =60°.∵CA ′为直径,故∠A ′BC =90°,则在Rt △A ′BC 中,由勾股定理得:BC =A ′C ·sin∠BA ′C =2×4×32=4 3.第4题解图5. C 【解析】如解图,设OB 与AC 的交点为E ,∵∠A =36°,∴∠O =72°,∴∠AEB =∠OEC =180°-72°-28°=80°,∴∠B =180°-80°-36°=64°.第5题解图6. B 【解析】∵四边形ABCD 是⊙O 的内接四边形,∠ABC =105°,∴∠ADC =75°,∵,∴∠DCF =∠BAC =25°,∴∠E =∠ADC -∠DCF =50°.7. B 【解析】由题知,∠DCE =40°,在四边形CDOE 中,∠CDO =∠CEO =90°, ∴∠DOE =360°-90°-90°-40°=140°,根据圆周角定理,得∠P =12∠AOB =12×140°=70°.8. B 【解析】如解图,∵四边形ABCO 是平行四边形,OA =OC ,∴四边形ABCO 是菱形,连接OB ,则△OBC 和△OAB 是等边三角形,∴∠COB =∠AOB =60°,∴∠AOC =120°,∵OF ⊥OC ,∴∠AOF =30°,∴∠BOF =∠AOB -∠AOF =30°,根据圆周角定理得:∠BAF =12∠BOF=15°.第8题解图 第9题解图9. C 【解析】如解图,设⊙A 与x 轴的另一个交点为D ,连接CD ,则∠OBC =∠ODC ,∴tan ∠OBC =tan ∠ODC =OC OD =2CD 2-OC 2=262-22=24. 10. D 【解析】如解图,连接OE ,则∠OBE =∠OEB ,∵∠AOB =∠OBE +∠ADB , ∠AOB =3∠ADB ,∴∠OBE = 2∠ADB ,∴∠OEB =2∠ADB ,∵∠OEB =∠D +∠DOE ,∴∠D =∠DOE ,∴DE =OB ,D 选项正确;若EB =OE =OB ,即△OBE 是等边三角形时,DE =EB 才成立,∴A 选项错误;若∠BOE =90°,即△OBE 是等腰直角三角形时,BE =2OE ,则2DE =EB 才成立,所以B 选项错误;若OD =3OE =3OB ,则3DE =DO 才成立,∴C 选项错误,故选D.第10题解图11. 35° 【解析】先根据“同弧所对圆周角是圆心角的一半”得∠BCA =12∠AOB ,又∵AB=AC ,∴∠ABC =∠BCA =12∠AOB =35°.12. 平行 【解析】∵四边形ABCD 是⊙O 的内接四边形,∴∠A +∠C =180°.∵∠D =∠C ,∴∠A +∠D =180°.∴AB ∥CD . 13.53【解析】如解图,连接OB ,过点O 作OM ⊥AB 于点M , ∵OA =OB =6 cm ,OM ⊥AB , ∴在等腰△OAB 中,BM =AB 2=12×8=4 cm.∴在Rt △BOM 中,OM=62-42=2 5 cm.PM =BM +BP =6 cm ,∴在Rt △OPM 中,tan ∠OPA =OM PM =256=53.第13题解图14. 30 【解析】∵OA =OB =OC ,∴∠B =∠OAB =25°,∠OAC =∠OCA =40°,∴∠AOB =180°-2×25°=130°,∠AOC =180°-2×40°=100°,∴∠BOC =∠AOB -∠AOC =130°-100°=30°.15. 35 【解析】∵OA =OB ,∴∠OAB =∠B ,∵∠AOB =40°,∴∠B =70°,∵CO ∥AB ,∴∠B =∠COB =70°,∴∠BAC =12∠BOC =35°.16. 6 【解析】如解图,连接OB ,∵四边形ABCD 是矩形,∴AB =CD =4,∠BAO =∠CDO =90°,∵OB =5,∴AO =52-42=3,同理可得:DO =3,∴AD =3+3=6.第16题解图17. (1)证明:∵ED =EC , ∴∠EDC =∠C ,∵四边形ABED 是⊙O 的内接四边形, ∴∠B +∠EDA =180°, 又∵∠EDA +∠EDC =180°, ∴∠EDC =∠B , ∴∠B =∠C , ∴AB =AC ;(2)解:如解图,连接AE ,第17题解图 ∵AB 为直径, ∴AE ⊥BC , 由(1)知AB =AC , ∴BE =CE =12BC =3,∵∠B =∠C ,∠C =∠CDE , ∴∠B =∠CDE , ∴△CED ∽△CAB , ∴CE CA =CD CB,即CE ·CB =CD ·CA , 又∵AC =AB =4,∴3·23=4CD , ∴CD =32.满分冲关1. D 【解析】半径为1的圆内接正三角形的边心距为12,内接正方形的边心距为22,内接正六边形的边心距为32,由12、22和32为边组成三角形时,由(12)2+(22)2=(32)2可得该三角形是直角三角形,所以该三角形的面积为12×22×12=28.2. B 【解析】如解图,∵∠PAB =∠PBC ,∠ABC =90°,∴∠BAP +∠PBA =90°,∴∠APB =90°,∴点P 始终在以AB 的中点O 为圆心,OA =OB =OP =12AB =3为半径的圆上,由解图知,只有当点P 在OC 与⊙O 的交点处时, PC 的长最小,即为P ′C .在Rt △OBC 中,OC =OB 2+BC 2=32+42=5,∴P ′C =OC -OP ′=5-3=2,∴线段CP 长的最小值为2.第2题解图3. 5.5 【解析】∵AB 和DE 都是⊙O 的直径,∴OA =OB =OD =4,∠C =90°,又∵DE ⊥AC ,∴OP ∥BC ,∴△AOP ∽△ABC ,∴OP BC =AO AB ,即OP 3=48,∴OP =1.5.∴DP =OP +OD =5.5.4. 2 6 【解析】如解图,连接AC 、OF ,正方形ABCD 的边长为4,AC =42+42=42,即直径是42,∴半径OF =2 2.过点O 作OM ⊥EF ,∵△FGE 是等边三角形,∴FG =FE ,又∵OF 过圆心,∴OF 平分∠GFE ,∴∠OFM =12∠GFE =12×60°=30°, ∴OM =12OF =12×22=2(在直角三角形中,30°角所对的直角边等于斜边的一半),∴MF =OF 2-OM 2=(22)2-(2)2=6,∴EF =2MF =26,∴正三角形EFG 的边长是2 6.第4题解图 第5题解图5. 8 【解析】连接AD ,如解图,∵AB 是⊙O 的直径,∴AD ⊥BC ,∵AB =AC ,∴BD =CD ,∴OD 是△ABC 的中位线,∴DO =12AC ,点M 是BE 的中点.∴MD 是△BCE 的中位线,∴CE =2MD=4,∵AC =10,∴AE =6,∵AB 是⊙O 的直径,∴∠AEB =90°,在Rt △ABE 中,由勾股定理得BE =AB 2-AE 2=102-62=8. 6. (1)证明:∵AB 为直径, ∴∠ACB =90°, ∵△AEF 是等边三角形, ∴∠EAF =∠EFA =60°, ∴∠ABC =30°,∵∠AEF =∠CED =60°,AC ⊥DB , ∴∠FDB =30°, ∴∠FBD =∠FDB , ∴FB =FD ,∴△DFB 是等腰三角形; (2)解:设AF =a , 则AD =7a ,连接OC ,如解图,则△AOC 是等边三角形,第6题解图由题意得,BF =2-a =DF , ∴DE =2-a -a =2-2a ,CE =1-a , 在Rt △ADC 中,DC ==, 在△DCE 中,tan30°=CE DC ==33, 解得,a =-2(舍去)或a =12,在△AOC 中,OA =1, ∴AF =12=12OA ,则根据等边三角形的性质可得CF⊥OA,即CF⊥AB. .27323 6ABB 檻20457 4FE9 俩20095 4E7F 乿026346 66EA 曪31257 7A19 稙39210 992A 餪I37786 939A 鎚22858 594A 奊I20903 51A7 冧。
附解析2015中考试题研究数学浙江精品复习 考点跟踪突破26圆的弧长和图形面积的计算

附解析2015中考试题研究数学浙江精品复习考点跟踪突破26圆的弧长和图形面积的计算考点跟踪突破26 圆的弧长和图形面积的计算一、选择题(每小题6分,共30分)1.(2014·襄阳)用一个圆心角为120°,半径为3的扇形作一个圆锥的侧面,则这个圆锥的底面半径为( B ) A .12 B .1 C .32D .2 2.(2013·河北)如图,AB 是⊙O 的直径,弦CD ⊥AB ,∠C =30°,CD =23,则S 阴影=( D )A .πB .2πC .23 3D .23π 3.(2014·金华)一张圆心角为45°的扇形纸板和一张圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( A )A .5∶4B .5∶2C .5∶2D .5∶ 24.(2014·东营)如图,已知扇形的圆心角为60°,半径为3,则图中弓形的面积为( C )A.4π-334B.π-34C.2π-334D.π-3325.(2013·山西)如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形EBF的半径为2,圆心角为60°,则图中阴影部分的面积是( B )A.23π-32B.23π- 3C.π-32D.π- 3二、填空题(每小题6分,共30分)6.(2014·泰州)圆锥的底面半径为6 cm,母线长为10 cm,则圆锥的侧面积为__60π__cm2.7.(2013·重庆)如图,一个圆心角为90°的扇形,半径OA=2,那么图中阴影部分的面积为__π-2__.(结果保留π).,第7题图),第8题图)8.(2013·泸州)如图,从半径为9 cm的圆形纸片上剪去13圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为__35__ cm.9.(2013·昆明)如图,从直径为4 cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O,A,B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是__22__cm.10.(2013·烟台)如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以点B为圆心,BA长为半径画AC︵,连接AF,CF,则图中阴影部分面积为__4π__.三、解答题(共40分)11.(10分)(2013·新疆)如图,已知⊙O的半径为4,CD是⊙O的直径,AC为⊙O的弦,B 为CD延长线上的一点,∠ABC=30°,且AB =AC.(1)求证:AB为⊙O的切线;(2)求弦AC的长;(3)求图中阴影部分的面积.解:(1)证明:如图,连接OA.∵AB=AC,∠ABC=30°,∴∠ABC=∠ACB=30°.∴∠AOB=2∠ACB=60°,∴在△ABO中,∠OAB =180°-∠ABO-∠AOB=90°,即AB⊥OA,又∵OA是⊙O的半径,∴AB为⊙O 的切线(2)解:如图,连接AD.∵CD是⊙O的直径,∴∠DAC=90°.∵由(1)知,∠ACB=30°,∴AD=12CD=4,则根据勾股定理知AC=CD2-AD2=43,即弦AC的长是4 3(3)由(2)知,在△ADC中,∠DAC=90°,AD=4,AC=43,则S△ADC=12AD·AC=12×4×43=8 3.∵点O是△ADC斜边上的中点,∴S△AOC =12S△ADC=4 3.根据图示知,S阴影=S扇形AOD +S△AOC=60π×42360+43=83π+43,即图中阴影部分的面积是83π+4 312.(10分)(2014·滨州)如图,点D 在⊙O 的直径AB 的延长线上,点C 在⊙O 上,AC =CD ,∠ACD =120°.(1)求证:CD 是⊙O 的切线;(2)若⊙O 的半径为2,求图中阴影部分的面积.解:(1)证明:连接OC.∵AC =CD ,∠ACD=120°,∴∠A =∠D =30°.∵OA =OC ,∴∠2=∠A =30°.∴∠OCD =90°.∴CD 是⊙O 的切线(2)解:∵∠A =30°,∴∠1=2∠A =60°.∴S 扇形BOC =60π×22360=2π3.在Rt △OCD 中,∵CD OC =tan 60°,∴CD =2 3.∴S Rt △OCD =12OC·CD =12×2×23=2 3.∴图中阴影部分的面积为23-2π313.(10分)(2014·襄阳)如图,在正方形ABCD 中,AD =2,E 是AB 的中点,将△BEC 绕点B 逆时针旋转90°后,点E 落在CB 的延长线上点F 处,点C 落在点A 处.再将线段AF 绕点F 顺时针旋转90°得线段FG ,连接EF ,CG.(1)求证:EF ∥CG ;(2)求点C ,点A 在旋转过程中形成的AC︵,AG︵与线段CG 所围成的阴影部分的面积.解:(1)证明:在正方形ABCD 中,AB =BC=AD =2,∠ABC =90°,∵△BEC 绕点B 逆时针旋转90°得到△ABF ,∴△ABF ≌△CBE ,∴∠FAB =∠ECB ,∠ABF =∠CBE =90°,AF =EC ,∴∠AFB +∠FAB =90°,∵线段AF 绕点F 顺时针旋转90°得线段FG ,∴∠AFB +∠CFG =∠AFG =90°,∴∠CFG =∠FAB =∠ECB ,∴EC ∥FG ,∵AF =EC ,AF =FG ,∴EC =FG ,∴四边形EFGC 是平行四边形,∴EF ∥CG(2)解:∵AD =2,E 是AB 的中点,∴FE=BE =12AB =12×2=1,∴AF =AB 2+BF 2=22+12=5,由平行四边形的性质,△FEC ≌△CGF ,∴S △FEC =S △CGF ,∴S 阴影=S 扇形BAC +S△ABF +S △FGC -S 扇形FAG =90·π·22360+12×2×1+12×(1+2)×1-90·π·(5)2360=52-π414.(10分)(2013·龙岩)如图①,在矩形纸片ABCD 中,AB =3+1,AD = 3.(1)如图②,将矩形纸片向上方翻折,使点D恰好落在AB 边上的D′处,压平折痕交CD 于点E ,则折痕AE 的长为__6__;(2)如图③,再将四边形BCED′沿D′E 向左翻折,压平后得四边形B′C′ED′,B ′C′交AE于点F ,则四边形B ′FED′的面积为__3-12__; (3)如图④,将图②中的△AED′绕点E 顺时针旋转α角,得到△A′ED″,使得EA′恰好经过顶点B ,求弧D′D″的长.(结果保留π)解:(2)由(1)知,C ′E =1=C′F ,∴S 四边形B′FED′=S矩形B′D′EC′-S△EC′F=3-12(3)∵∠C=90°,BC=3,EC=1,∴tan∠BEC=BCCE=3,∴∠BEC=60°,由翻折可知:∠DEA=45°,∴∠AEA′=75°=∠D′ED″,∴D′D″︵=75×π×3180=53 12π。
(浙江专版)中考数学复习方案 第六单元 圆 课时训练(26)圆的基本性质试题-人教版初中九年级全册数

课时训练(二十六)圆的基本性质|夯实基础|1.[2019·凉山州]下列命题:①直线外一点到这条直线的垂线段,叫做点到直线的距离;②两点之间线段最短;③相等的圆心角所对的弧相等;④平分弦的直径垂直于弦.其中,真命题的个数为()A.1B.2C.3D.42.[2019·某某]如图K26-1,点A,B,C均在☉O上,当∠OBC=40°时,∠A的度数是()图K26-1A.50°B.55°C.60°D.65°3.在Rt△ABC中,∠ACB=90°,AC=3,BC=4,CP,CM分别是AB上的高和中线,如果圆A是以点A为圆心,半径长为2的圆,那么下列判断正确的是()A.点P,M均在圆A内B.点P,M均在圆A外C.点P在圆A内,点M在圆A外D.点P在圆A外,点M在圆A内⏜的中点,若∠ABC=30°,则弦AB的长为() 4.[2018·威海]如图K26-2,☉O的半径为5,AB为弦,点C为AA图K26-2B.5A.12C.5√3D.5√325.[2019·某某]如图K26-3,四边形ABCD是菱形,☉O经过点A,C,D,与BC相交于点E,连结AC,AE.若∠D=80°,则∠EAC的度数为()图K26-3A.20°B.25°C.30°D.35°6.[2019·威海]如图K26-4,☉P与x轴交于点A(—5,0),B(1,0),与y轴的正半轴交于点C,若∠ACB=60°,则点C的纵坐标为()图K26-4A.√13+√3B.2√2+√3C.4√2D.2√2+27.[2018·某某]如图K26-5,AB是☉O的直径,点C是半径OA的中点,过点C作DE⊥AB,交☉O于D,E两点,过点D作直径DF,连结AF,则∠DFA=.图K26-58.[2019·某某]如图K26-6,AC是圆内接四边形ABCD的一条对角线,点D关于AC的对称点E在边BC上,连结AE,若∠ABC=64°,则∠BAE的度数为.图K26-69.[2018·某某]等腰三角形ABC中,顶角A为40°,点P在以A为圆心,BC长为半径的圆上,且BP=BA,则∠PBC 的度数为.10.如图K26-7,在△ABC中,AB=AC,以AC为直径的☉O交AB于点D,交BC于点E.(1)求证:BE=CE;(2)若BD=2,BE=3,求AC的长.图K26-711.[2019·某某]筒车是我国古代发明的一种水利灌溉工具.如图K26-8,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理.如图②,筒车盛水桶的运行轨道是以轴心O为圆心的圆.已知圆心在水面上方,且圆被水面截得的弦AB的长为6米,∠OAB=41.3°.若点C为运行轨道的最高点(C,O的连线垂直于AB).求点C到弦AB所在直线的距离.(参考数据:sin41.3°≈0.66,cos41.3°≈0.75,tan41.3°≈0.88)图K26-812.[2019·某某]在屏幕上有如下内容:如图K26-9,△ABC内接于圆O,直径AB的长为2,过点C的切线交AB的延长线于点D.X老师要求添加条件后,编制一道题目,并解答.(1)在屏幕内容中添加条件∠D=30°,求AD的长,请你解答.(2)以下是小明,小聪的对话:小明:我加的条件是BD=1,就可以求出AD的长.小聪:你这样太简单了,我加的是∠A=30°,连结OC,就可以证明△ACB与△DCO全等.参考此对话,在屏幕内容中添加条件,编制一道题目(可以添线、添字母),并解答.图K26-9|拓展提升|x2-4与x轴交于A,B两点,P是以点C(0,3)为圆心,2为半径的圆上的13.[2019·某某]如图K26-10,抛物线y=14动点,Q是线段PA的中点,连结OQ.则线段OQ的最大值是()图K26-10A .3B .√412C .72D .4 14.[2019·某某]如图K26-11①,☉O 经过等边三角形ABC 的顶点A ,C (圆心O 在△ABC 内),分别与AB ,CB 的延长线交于点D ,E ,连结DE ,BF ⊥EC 交AE 于点F. (1)求证:BD=BE ;(2)当AF ∶EF=3∶2,AC=6时,求AE 的长; (3)设AAAA =x ,tan∠DAE=y. ①求y 关于x 的函数表达式;②如图②,连结OF ,OB ,若△AEC 的面积是△OFB 面积的10倍,求y 的值.图K26-11【参考答案】1.A2.A3.C4.D[解析]如图,连结OA ,OC ,OC 交AB 于点M.根据垂径定理可知OC 垂直平分AB ,因为∠ABC=30°,故∠AOC=60°,在Rt △AOM 中,sin60°=AA AA =AA 5=√32,故AM=5√32,即AB=5√3.故选D .5.C[解析]∵四边形ABCD 是菱形,∠D=80°,∴∠ACB=12∠DCB=12(180°-∠D )=50°. ∵四边形AECD 是圆内接四边形, ∴∠AEB=∠D=80°, ∴∠EAC=∠AEB-∠ACE=30°.6.B[解析]连结PA ,PB ,PC ,过点P 分别作PF ⊥AB ,PE ⊥OC ,垂足为F ,E.由题意可知:四边形PFOE 为矩形, ∴PE=OF ,PF=OE.∵∠ACB=60°,∴∠APB=120°. ∵PA=PB ,∴∠PAB=∠PBA=30°. ∵PF ⊥AB ,∴AF=BF=3,∴PE=OF=2. ∵tan30°=AA AA ,cos30°=AAAA, ∴PF=√3,AP=2√3, ∴OE=√3,PC=2√3.在Rt △PEC 中,CE=√AA 2-AA 2=2√2, ∴OC=CE+EO=2√2+√3.7.30°[解析]∵AB ⊥DE ,且C 为OA 中点,∴OC=AC=12DO ,∴∠DOC=60°.∴∠DFA=30°.8.52°[解析]∵圆内接四边形ABCD , ∴∠B+∠D=180°, ∵∠B=64°,∴∠D=116°, 又∵点D 关于AC 的对称点是点E , ∴∠D=∠AEC=116°, 又∵∠AEC=∠B+∠BAE , ∴∠BAE=52°.9.30°或110°[解析]分两种情况:(1)如图,BP=BA=AC ,AP=BC ,∴四边形APBC 为平行四边形,∴∠BAC=∠ABP=40°,∠ABC=∠ACB=70°,∴∠PBC=∠ABP+∠ABC=40°+70°=110°.(2)如图,∵AP=BC ,BP=AC ,AB=AB , ∴△BAP ≌△ABC ,∠PBA=∠BAC=40°, ∴∠PBC=∠ABC-∠ABP=70°-40°=30°.10.解:(1)证明:如图①,连结AE. ∵AC 为☉O 的直径, ∴∠AEC=90°,∴AE ⊥BC. 又∵AB=AC ,∴BE=CE.(2)如图②,连结DE.∵四边形ACED 为☉O 的内接四边形, ∴∠BED=∠BAC.又∵∠B=∠B ,∴△BED ∽△BAC , ∴AA AA =AAAA . ∵BE=CE=3,∴BC=6.又∵BD=2,∴3AA =26,∴BA=9,∴AC=9.11.解:连结CO 并延长,交AB 于点D ,∴CD ⊥AB ,且D 为AB 中点,所求运行轨道的最高点C 到弦AB 所在直线的距离即为线段CD 的长.在Rt △AOD 中,∵AD=12AB=3,∠OAD=41.3°,∴OD=AD ·tan41.3°≈3×0.88=2.64,OA=AAcos41.3°≈30.75=4, ∴CD=CO+OD=AO+OD=4+2.64=6.64(米).答:运行轨道的最高点C 到弦AB 所在直线的距离约为6.64米.12.解:(1)连结OC ,如图.∵CD 与☉O 相切, ∴∠OCD=90°, 又∵∠D=30°, ∴OD=2OC=2, ∴AD=OA+OD=3.(2)一类:通过几何、代数方法的综合运用,解得所编制题目的答案. 如:加条件CP 是直径,连结PD ,设BD=x ,PD=y ,求y 关于x 的关系式.解答略. 二类:通过三角形全等,三角形相似,解得所编制题目的答案. 如:加条件∠ABC=60°,连结OC ,求证:△ACB ≌△DCO.解答略. 如:加条件∠ABC=60°,求BC 的长.解答略. 13.C[解析] 连结BP ,如图, 当y=0时,14x 2-4=0, 解得x 1=4,x 2=-4, 则A (-4,0),B (4,0), ∵Q 是线段PA 的中点, ∴OQ 为△ABP 的中位线, ∴OQ=12BP ,当BP 最大时,OQ 最大,而BP 过圆心C 时,PB 最大,如图,点P 运动到P'位置时,BP 最大,∵BC=√32+42=5, ∴BP'=5+2=7,∴线段OQ 的最大值是72.14.[解析] (1)利用等边三角形的性质和圆周角定理,得到∠BED=∠BDE ,由等角对等边,得到结论;(2)作AG ⊥EC 于点G ,由三线合一求出AG ,BG 长,利用平行线分线段成比例,求得EB ,进而通过勾股定理得到AE 的长;(3)①作EH ⊥AD 于点H ,构造直角三角形,利用比例关系,写出EH ,AH 的代数式,进而求得y 关于x 的表达式;②作OM ⊥EC 于点M ,构造相似,得到比例式,表示出两个三角形的面积,根据10倍关系,得到方程,即可解得y 的值.解:(1)证明:∵△ABC 为等边三角形,∴∠BAC=∠C=60°,∵∠DEB=∠BAC=60°,∠D=∠C=60°,∴∠DEB=∠D ,∴BD=BE. (2)如图,过点A 作AG ⊥EC 于点G ,∵△ABC 为等边三角形,AC=6, ∴BG=12BC=12AC=3.在Rt △ABG 中,AG=√3BG=3√3. ∵BF ⊥EC ,∴BF ∥AG ,∴AA AA =AAAA. ∵AF ∶EF=3∶2, ∴BE=23BG=2, ∴EG=BE+BG=2+3=5,∴在Rt △AEG 中,AE=√AA 2+AA 2=2√13. (3)①如图,过点E 作EH ⊥AD 于点H ,∵∠EBD=∠ABC=60°,∴在Rt △BEH 中,AA AA =sin60°=√32, ∴EH=√32BE ,BH=12BE.∵AA AA =AAAA=x , ∴BG=xBE , ∴AB=BC=2BG=2xBE ,∴AH=AB+BH=2xBE+12BE=2x+12BE. Rt △AHE中,tan ∠EAD=AA AA =√32AA (2A +12)AA =√34A +1,∴y=√34A +1.②如图,过点O 作OM ⊥EC 于点M ,设BE=a ,∵AA AA =AAAA=x , ∴CG=BG=xBE=ax , ∴EC=CG+BG+BE=a+2ax , ∴EM=12EC=12a+ax ,∴BM=EM-BE=ax-12a , ∵BF ∥AG , ∴△EBF ∽△EGA , ∴AA AA =AAAA =AA +AA =11+A . ∵AG=√3BG=√3ax ,word11 / 11 ∴BF=11+A AG=√3AA1+A ,△OFB 的面积=AA ·AA 2=12×√3AA A +1ax-12a ,△AEC 的面积=AA ·AA 2=12×√3ax (a+2ax ),∵△AEC 的面积是△OFB 的面积的10倍, ∴10×12×√3AAA +1ax-12a =12×√3ax (a+2ax ), ∴2x 2-7x+6=0,解得x 1=2,x 2=32,∴y=√39或√37.。
第26讲 圆的基本性质 2025年中考一轮数学专题复习课件(湖南)(共22张PPT)
线段 OA 叫作半径
(1)圆是轴对称图形,任意一条直径所在的直线都是它
的对称轴;
对称
(2)圆是中心对称图形, 圆心
是它的对称中心;
性 (3)圆具有旋转不变性,即圆绕圆心旋转任意角度都与
自身重合
考点清单
考点 ❷
垂径定理及其推论【省卷T26,长沙T9】
垂径定理 【2022课标要求变化:选学内容变为必学内容】
弦 AC 的长为4 3 ,则∠ COB = 60
☉ O 的半径 r = 4
∠ BD A= 90°
°,
.
∠ B A C= 30°
由 垂 径 定 理 得 CD = 2 3
∠ COB = 60°
r=
sin60°
=4
考点清单
考点 ❶
圆的定义及对称性
圆是所有到定点的距离等于定长的点的集合,
其中定点称为 圆心 ,定长称为半径,
若四边形 OABC 是菱形,则∠ D = 60
°.
∠ ABC =∠ AOC
∠ ABC +∠ D =180°
∠ AOC =2∠ D
3∠ D =180°
∠ D =60°
例4题 图
对点演练
5. (2024·广元)如下图,已知四边形 ABCD 是☉ O 的内接四边
形,点 E 为 AD 延长线上一点,∠ AOC =128°,则∠ CDE =
03
重难精讲
变式探究
第六单元 第26讲
重点精讲·变式探究
例1 (2023·永州改编)如下图,☉ O 是一个盛有水的容器的横
截面,☉ O 的半径为 10 cm,水面的宽 CD =12 cm,往容器中
浙教版九年级上册数学第3章 圆的基本性质含答案(查漏补缺)
浙教版九年级上册数学第3章圆的基本性质含答案一、单选题(共15题,共计45分)1、如图,在半圆的直径上作4个正三角形,如这半圆周长为C1,这4个正三角形的周长和为C2,则C1和C2的大小关系是()A.C1>C2B.C1<C2C.C1=C2D.不能确定2、如图,⊙O1与⊙O2相交于A,B两点,经过点A的直线CD分别与⊙O1、⊙O2交于C、D,经过点B的直线EF分别与⊙O1、⊙O2交于E、F,且EF∥O1O2.下列结论:①CE∥DF;②∠D=∠F;③EF=2O1O2.必定成立的有()A.0个B.1个C.2个D.3个3、如图,AB为圆O的直径,点C为圆上一点,若∠OCA=25°,则∠BOC=()A.30°B.40°C.50°D.60°4、如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连接OB,OC.若∠BAC 与∠BOC互补,则弦BC的长为()A.4B.3C.2D.5、如图,在直角坐标系中,点A(0,3)、点B(4,3)、点C(0,-1),则△ABC 外接圆的半径为( )A.2B.3C.4D.6、在⊙O中, 所对的圆心角为60°,半径为5cm,则的长为( )A. B. C. D.7、已知∠ADB,作图.步骤1:以点D为圆心,适当长为半径画弧,分别交DA、DB于点M、N;再分别以点M、N为圆心,大于MN长为半径画弧交于点E,画射线DE.步骤2:在DB上任取一点O,以点O为圆心,OD长为半径画半圆,分别交DA、DB、DE于点P、Q、C;步骤3:连结PQ、OC.则下列判断:① ;②OC∥DA;③DP=PQ;④OC 垂直平分PQ,其中正确的结论有()A.①③④B.①②④C.②③④D.①②③④8、下列四个图中,∠x是圆周角的是()A. B. C. D.9、如图,在△ABC中,∠B=90°,AB=4,BC=3,将△ABC绕点A逆时针旋转,使点B落在线段AC上的点D处,点C落在点E处,则C、E两点间的距离为()A. B.2 C.3 D.210、如图,AB是⊙O的直径,CD是弦,AB⊥CD,垂足为点E,连接OD、CB、AC,∠DOB=60°,EB=2,那么CD的长为()A. B.2 C.3 D.411、如图,I是△ABC的内心,AI的延长线与△ABC的外接圆相交于点D,与BC 交于点E,连接BI、CI、BD、DC.下列说法中正确的有()①∠CAD绕点A顺时针旋转一定的角度一定能与∠DAB重合;②I到△ABC三个顶点的距离相等;③∠BIC=90°+ ∠BAC;④线段DI是线段DE与DA的比例中项;⑤点D是△BIC的外心.A.1个B.2个C.3个D.4个12、如图,AB是⊙O的直径,点E是AB上一点,过点E作CD⊥AB,交⊙O于点C,D,以下结论正确的是()A.若⊙ O的半径是2,点E是OB的中点,则CD=B.若CD=,则⊙ O的半径是1 C.若∠ CAB=30°,则四边形OCBD是菱形 D.若四边形OCBD是平行四边形,则∠ CAB=60°13、在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数()A.35°B.40°C.45°D.65°14、下列说法正确的个数是()①直径是圆的对称轴;②半径相等的两个半圆是等弧;③长度相等的两条弧是等弧;④和圆有一个公共点的直线是圆的切线.A.1B.2C.3D.415、一个扇形的弧长是20πcm,面积是240πcm2,则这个扇形的圆心角等于()A.160°B.150°C.120°D.60°二、填空题(共10题,共计30分)16、赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的直径=________米.17、如图,在⊙O中,C是弦AB上一点,AC=2,CB=4.连接OC,过点C作DC⊥OC,与⊙O交于点D,DC的长为________.18、若圆内接正六边形的半径等于4,则它的面积等于________ .19、已知扇形的圆心角为120°,弧长为6π,则扇形的面积是________.20、如图,在菱形ABCD中,AB=BD,点E、F分别是线段AB、AD上的动点(不与端点重合),且AE=DF,BF与DE相交于点G.给出如下几个结论:①△AED≌△DFB;②∠BGE大小会发生变化;③CG平分∠BGD;④若AF=2DF,则BG=6GF;.其中正确的结论有________(填序号).21、为庆祝祖国华诞,某单位排练的节目需用到如图所示的扇形布扇,布扇完全打开后,外侧两竹条,夹角为,,贴布部分,则贴布部分的面积约为________ .22、如图,在半径为的中,劣弧的长为,则________度.23、如图,四边形ABCD内接于⊙O,E为直径CD延长线上一点,且AB∥CD,若∠C=70°,则∠ADE的大小为________.24、如图,A,B是上的两个点,,若点C也在上(点C不与点A,B重合),则的度数为________.25、圆是________ 图形,其对称轴是任意一条________ 的直线.三、解答题(共5题,共计25分)26、圆锥的底面半径为3cm,侧面展开图是圆心角为120º的扇形,求圆锥的全面积。
浙教版数学九年级上册第三章圆的基本性质(含答案)
浙教版数学九年级上册第三章圆的基本性质一、选择题1.下列说法正确的是( )A.三个点可以确定一个圆B.半圆(或直径)所对的圆周角是直角C.相等的圆心角所对的弧相等D.长度相等的弧是等弧2.已知一个扇形的面积是24π,弧长是2π,则这个扇形的半径为( )A.24B.22C.12D.63.如图,点A、B、C在⊙O上,∠C=40∘,则∠AOB的度数是( )A.50∘B.60∘C.70∘D.80∘4.如图,AB是⊙O的直径,弦CD⊥AB于点E,若BE=5,AE=1,则弦CD的长是()A.5B.5C.25D.65.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )A.28°B.30°C.36°D.56°6.如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则BC的长为( )A .103πB .109πC .59πD .518π7.如图, AB 是半圆O 的直径,点C ,D 在半圆O 上.若 ∠ABC =50° ,则 ∠BDC 的度数为( )A .90°B .100°C .130°D .140°8. 如图,正六边形ABCDEF 内接于⊙O ,若⊙O 的周长等于6π,则正六边形的边长为( )A .3B .6C .3D .239.如图,正五边形ABCDE 内接于⊙O ,阅读以下作图过程:①作直径AF ;②以点F 为圆心,FO 为半径作圆弧,与⊙O 交于点M ,N ;③连接AM ,MN ,AN .结论Ⅰ:△AMN 是等边三角形;结论Ⅱ:从点A 开始,以DN 长为半径,在⊙O 上依次截取点,再依次连接这些分点,得到正十八边形.对于结论Ⅰ和结论Ⅱ,下列判断正确的是( )A .Ⅰ和Ⅱ都对B .Ⅰ和Ⅱ都不对C.Ⅰ不对Ⅱ对D.Ⅰ对Ⅱ不对10.如图,抛物线y=x2﹣8x+15与x轴交于A、B两点,对称轴与x轴交于点C,点D(0,﹣2),点E (0,﹣6),点P是平面内一动点,且满足∠DPE=90°,M是线段PB的中点,连接CM.则线段CM的最大值是( )A.3B.412C.72D.5二、填空题11.如图,在⊙O中,弦AB,CD相交于点P.若∠A=40°,∠APD=75°,则∠B= °.12.如图,AB、AC是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N.如果MN=2.5,那么BC= .13.如图,四边形ABCD内接于⊙O ,若四边形ABCD的外角∠DCE=65°,则∠BAD的度数是 .14.如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=70°,则∠EAC的度数为 .15.我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的割圆术:“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率π的近似值为3.1416.如图,⊙O的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计⊙O,若用圆内接正十二边形作近似估计,可得π的估计值为 .的面积,可得π的估计值为33216.如图,点M(2,0)、N(0,4),以点M为圆心5为半径作⊙M交y轴于A、B两点,点C为⊙M上一动点,连接CN,取CN中点D,连接AD、BD,则A D2+B D2的最大值为 .三、解答题17.如图,四边形ABCD为⊙O的内接四边形,AC是⊙O的直径,AD=BD,∠CAB=32°.求∠ACD的度数.18.如图,OC为⊙O的半径,弦AB⊥OC于点D,OC=10,CD=4,求AB的长.19.如图,正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求解答下列问题:(1)△A1B1C1与△ABC关于坐标原点O成中心对称,则B1的坐标为__________;(2)BC与B1C1的位置和数量关系为___________;(3)将△ABC绕某点逆时针旋转90°后,其对应点分别为A2(−1,−2),B2(1,−3),C2(0,−5),则旋转中心的坐标为___________.20.如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,(1)求∠ACB的度数;(2)求BC的长;(3)求AD,BD的长.21.如图,AB是⊙O的直径,C是⏜BD的中点,CE⊥AB于点E,BD交CE于点F.(1)求证:CF=BF.(2)若CD=6,AC=8,求⊙O的半径及CE的长.22.如图所示,AB为☉O的直径,AC是☉O的一条弦,D为BC的中点,作DE⊥AC于点E,交AB的延长线于点F,连接DA.(1)若AB=90 cm,则圆心O到EF的距离是多少?说明你的理由.(2)若DA=DF=63,求阴影部分的面积(结果保留π).23.如图,AB是⊙O的直径,弦CD⊥AB与点E,已知AB=10,AE=8,点P为AB上任意一点,(点P不与A、B重合),连结CP并延长与⊙O交于点Q,连QD,PD,AD.(1)求CD的长.(2)若CP=PQ,直接写出AP的长.(3)①若点P在A,E之间(点P不与点E重合),求证:∠ADP=∠ADQ.②若点P在B,E之间(点P不与点E重合),求∠ADP与∠ADQ满足的关系.答案解析部分1.【答案】B2.【答案】A3.【答案】D4.【答案】C5.【答案】A6.【答案】B7.【答案】D8.【答案】C9.【答案】D10.【答案】C11.【答案】3512.【答案】513.【答案】65°14.【答案】15°15.【答案】316.【答案】49217.【答案】61°18.【答案】1619.【答案】(1)(2,2);(2)平行且相等;(3)(0,−1).20.【答案】(1)∠ACB=90°(2)BC=8cm(3)BD=AD=52cm21.【答案】(1)证明:∵AB是⊙O的直径,∴∠ACB=90°,∴∠A=90°-∠ABC.∵CE⊥AB,∴∠ECB=90°-∠ABC,又∵C 是BD 的中点,∴CD =BC ,∴∠DBC=∠A ,∴∠ECB=∠DBC ,∴CF= BF ;(2)解:∵BC =CD ,∴BC=CD=6.在Rt △ABC 中,AB= BC 2+AC 2=62+82=10,∴⊙O 的半径为5;∵S △ABC = 12AB×CE= 12BC×AC ,∴CE= BC ×AC AB =6×810=245.22.【答案】(1)解:如图所示,连接OD ,∵D 为BC 的中点,∴∠CAD=∠BAD.∵OA=OD ,∴∠BAD=∠ADO.∴∠CAD=∠ADO.∴OD ∥AE.∵DE ⊥AC ,∴OD ⊥EF.∴OD 的长是圆心O 到EF 的距离.∵AB=90 cm ,∴OD=12AB=45 cm.(2)解:如图所示,过点O 作OG ⊥AD 交AD 于点G.∵DA=DF ,∴∠F=∠BAD.由(1),得∠CAD=∠BAD ,∵∠F+∠BAD+∠CAD=90°,∴∠F=∠BAD=∠CAD=30°.∴∠BOD=2∠BAD=60°,OF=2OD.∵在Rt△ODF中,OF2-OD2=DF2,∴(2OD)2-OD2=(63)2,解得OD=6.在Rt△OAG中,OA=OD=6,∠OAG=30°,AG=OA2−O G2=33,AD=23,S△AOD=1×63×3=93.2+93=6π+93.∴S阴影=S扇形OBD+S△AOD=60π×6236023.【答案】(1)解:连接OD,∵直径AB=10,AE=8,∴BE=2.∴OE=5-2=3.又∵AB⊥CD,在Rt△PED中,P D2=P E2+E D2∴ED=52−32=4∴CD=2ED=8(2)解:若CP=PQ,则点P与点O重合,或点P与点E重合.所以AP=5或8(3)解:①连接AC,由图可知∠ACQ=∠ADQ,因为AB是⊙O的直径,AB⊥CD,所以CE=DE,即AB是CD的垂直平分线,所以AC=AD,PC=PD,因为AP=AP,所以∠ACP=∠ADP,所以∠ADP=∠ADQ.②∠ADP+∠ADQ=180°.理由如下:连接AC,因为AB是直径,AB⊥CD,所以AC=AD,CE=DE,所以△ACP≌△ADP(SSS),所以∠ACP=∠ADP,因为∠ACP=12ADQ,∠ADQ=12ACQ,所以∠ACP+∠ADQ=12(ADQ+ACQ)=180°.。
中考数学复习方案 第六单元 圆 第26课时 圆的有关性质课件
的圆心为D,若点A,E,B在同一(tóngyī)直线上, ∠CAB=54°,设∠ABC=θ,那么θ=
24°
高
频
考
向
探
究
图26-6
第十六页,共四十八页。
.
基
础
知
识
巩
固
题组二 易错题
【失分点】
同(等)圆中,同(等)弧或弦所对的圆周角大于“圆外角”;不能灵活运用圆周角定理及其推论,且
忽略分类(fēn lèi)讨论.
∠OCB=60°,∠COB=45°,则 OC 的长是
高
频
考
向
探
究
图26-12
第二十九页,共四十八页。
.
基
础
知
识
巩
固
高
频
考
向
探
究
[答案] 3+1
[解析]连接 AB,设△ OCB 的外接圆圆心为 M,则 AB 为☉M 的直径.
Rt△ ABO 中,∠BAO=∠OCB=60°,∴OB= 3OA= 3 × 2= 6.
高
频
考
向
探
究
6.如图 26-7,已知 AC 是☉O 的直径,点 B 在圆周上(不与 A,C 重合),点 D 在 AC 的延
长线上,连接 BD 交☉O 于点 E,若∠AOB=3∠ADB,则(
A.DE=EB
B. 2DE=EB
C. 3DE=DO
D.DE=OB
)
图26-7
第十七页,共四十八页。
基
础
知
识
巩
固
过点 B 作 BD⊥OC 于点 D.
2
Rt△ OBD 中,∠COB=45°,则 OD=BD= OB= 3.
