惠州市2016届高三第一次调研考试(文科数学)含解析
惠州市届高三第一次调研考试.文数

惠州市2017届高三第一次调研考试数学(文科)注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、准考证号、座位号、学校、班级等考生信息填写在答题卡上。
2. 回答第Ⅰ卷时,选出每个小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号,写在本试卷上无效。
3. 回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4. 考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
(1) 已知},log |{},16,8,4,2,1{2A x x y y B A ∈===,则=B A ()(A) }2,1{(B)}8,4,2{(C)}4,2,1{(D)}8,4,2,1{(2) 若复数z 满足)1()21(i z i -=+,则=||z ()(A)52 (B)53 (C)510 (D)10(3) 若21)tan(,31tan =+=βαα,则=βtan () (A) 71 (B) 61 (C) 75(D)65 (4) 函数R x px x x y ∈+=,||()(A) 是偶函数(B) 是奇函数 (C) 不具有奇偶性(D) 奇偶性与p 有关(5) 若向量)2,1(+=x 和向量)1,1(-=平行,则=+||()(A)10(B)210 (C)2(D)22 (6) 等比数列}{n a 的各项为正数,且187465=+a a a a 则=+++1032313log log log a a a ()(A)12(B)10(C)8(D) 5log 23+(7) 命题“任意0],2,1[2≤-∈a x x ”为真命题的一个充分不必要条件是()(A)4≥a(B)4≤a(C)5≥a(D)5≤a(8) 已知⎪⎩⎪⎨⎧≥-+≤--≥-020630y x y x y x ,则yx z +=22的最小值是()(A) 1(B) 16(C) 8(D) 4(9) 执行如图所示的程序框图,则输出S 的值为()(A)2 (B)3- (C) 21-(D) 31(10) 某几何体的三视图如右图,其正视图中的曲线部分为半圆,则该几何体的表面积为()(A) 2)19(cm π+(B) 2)422(cm π+(C) 2)42610(cm π++ (D) 2)42613(cm π++ (11) 已知三棱锥ABC S -的底面是以AB 为斜边的等腰直角三角形,2,2====SC SB SA AB ,则三棱锥的外接球的球心到平面ABC 的距离是() (A) 33 (B) 1(C)3(D)233 (12) 双曲线M :)0,0(12222>>=-b a by a x 的实轴的两个端点为B A 、,点P 为双曲线M 上除B A 、外的一个动点,若动点Q 满足PB QB PA QA ⊥⊥,,则动点Q 的轨迹为() (A) 圆(B) 椭圆(C) 双曲线(D) 抛物线第Ⅱ卷本卷包括必考题和选考题两部分。
惠州市2016高三第二次调研考试数学(文科)答案,最新
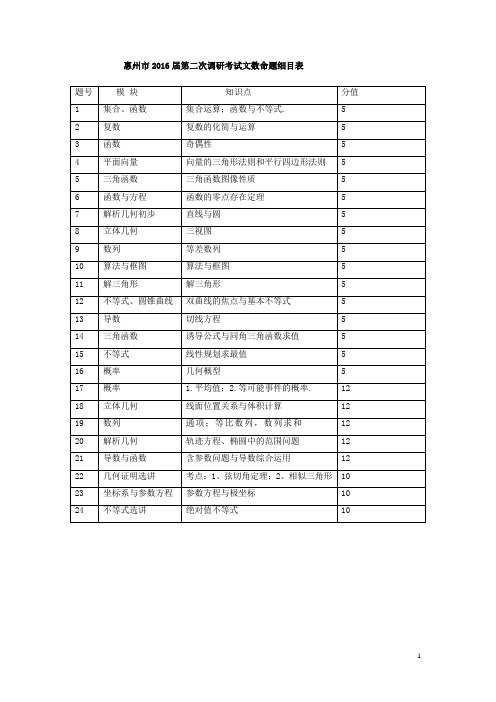
惠州市2016届第二次调研考试文数命题细目表题号模块知识点分值1 集合、函数集合运算;函数与不等式. 52 复数复数的化简与运算 53 函数奇偶性 54 平面向量向量的三角形法则和平行四边形法则 55 三角函数三角函数图像性质 56 函数与方程函数的零点存在定理 57 解析几何初步直线与圆 58 立体几何三视图 59 数列等差数列 510 算法与框图算法与框图 511 解三角形解三角形 512 不等式、圆锥曲线双曲线的焦点与基本不等式 513 导数切线方程 514 三角函数诱导公式与同角三角函数求值 515 不等式线性规划求最值 516 概率几何概型 517 概率 1.平均值;2.等可能事件的概率. 1218 立体几何线面位置关系与体积计算1219 数列通项;等比数列,数列求和1220 解析几何轨迹方程、椭圆中的范围问题1221 导数与函数含参数问题与导数综合运用1222 几何证明选讲考点:1、弦切角定理;2、相似三角形1023 坐标系与参数方程参数方程与极坐标1024 不等式选讲绝对值不等式10惠州市2016届高三第二次调研考试文科数学参考解答:一、选择题(每小题5分,满分60分) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案CAADDCCBDBAB1、【解析】{}{}2=0xA y y y y ==>,{}31B x x x =><-或,所以{}3A B x x => ,故选C.2、【解析】111122i ii i i -++=+=+,选A. 3、【解析】(2)(2)16,(2)26f f f +-=-=-,选A. 4、【解析】在△OAC 中,M 为AC 中点,根据平行四边形法则,有2OC OM += OA ,同理有2OB OM +=OD ,故4OA OC OB OC OM +++=,选D.5、【解析】选D.6、【解析】因为f(2)>0,f(3)<0,f(4)>0,f(5)<0,所以在区间[2,3],[3,4],[4,5]内有零点, 选C.7、【解析】圆心(1,2),圆心到直线的距离1+4-5+5=15d =,半径5r =,所以最后弦长为222(5)14-=.故选C.8、【解析】根据几何体的三视图确定几何体的形状,并画出几何体的直观图,标示已知线段的长度,最后求各个面的面积确定最大值.将三视图还原成几何体的直观图,如图所示.由三视图可知,四面体的四个面都是直角三角形,面积分别为6,8,10,62,所以面积最大的是10, 选B.9、【解析】1111(2)n n n n n n n n a a a a n a a a a -+-+⋅⋅=≥--两边取倒数可得:111111n n n na a a a -+-=-,所以1n a ⎧⎫⎨⎬⎩⎭是等差数列,首项1112a =,公差d =11122-=,所以()10010011111001502250a a =+-=⇒=,故选D. 10、【解析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算并输出i 值.解:根据题意,本程序框图中循环体为“直到型”循环结构第1次循环:S=0+1=1,i=2,a=1×2+1=3; 第2次循环:S=1+3=4,i=3,a=3×3+4=13; 第3次循环:S=4+13=17,i=4,a=13×4+17=69; 第4次循环:S=17+69=86,i=5,a=69×5+86=431; 第5次循环:S=86+431=517,i=6,a=431×6+517≥500; 跳出循环,输出i=6.故选B . 11、【解析】120AC =,60sin 75AB =,sin 30sin 45AB BC=, 所以sin 45602120(31)sin30sin(3045)AB BC ⨯===-+ .选A12、【解析】由题意,A B 两点为2(4,0)b ±-,因此2224(4)ABCS b b b b ∆=-=-22(4)22b b +-≤=,当且仅当224b b =-,即2b =时等号成立.故最大值为2,选B . 13、答案:1-=x y【解析】(1)求切点:把1x =带入原函数,解得y=0,所以切点为(1,0) (2)求斜率:1'(),'(1)1,f x f x==根据点斜式写出方程: 1y x =- 14、答案:45-【解析】tan 2α= ,22220152sin cos 2tan 4cos(2)sin 22sin cos 1tan 5παααααααα--=-==-=-++ 15、答案:13[,]42【解析】根据题意作出不等式组所表示的可行域如图阴影部分所示,即ABC ∆的边界及其内部,因为12y x ++表示可行域内一点(),x y 和点()2,1P --连线的斜率,由图可知12PB PC y k k x +≤≤+,根据原不等式组解得()()2,0,0,2B C , 所以0112111322202422y y x x ++++≤≤⇒≤≤++++.16、答案:324ππ+【解析】如图,集合A 表示的点集是圆O 内部(含边界),集合B 表示的点集是直线AB 下方的弓形区域,2416S ππ=⨯=圆, 31164412842S ππ=⨯+⨯⨯=+弓,因此所求概率为12832164P ππππ++==.17、(本小题满分12分) (I )6条道路的平均得分为5.7)1098765(61=+++++…………3分 ∴该市的总体交通状况等级为合格. …………5分(II )设A 表示事件“样本平均数与总体平均数之差的绝对值不超过5.0”. …………7分 从6条道路中抽取2条的得分组成的所有基本事件为:)6,5(,)7,5(,)8,5(,)9,5(,)10,5(,)7,6(,)8,6(,)9,6(,)10,6(,)8,7(,)9,7(,)10,7(,)9,8(,)10,8(,)10,9(,共15个基本事件 …………9分事件A 包括)9,5(,)10,5(,)8,6(,)9,6(,)10,6(,)8,7(,)9,7(共7个基本事件,………10分 ∴157)(=A P . ……………………………………11分 答:该样本平均数与总体平均数之差的绝对值不超过5.0的概率为157.…………12分 18. (本小题满分12分)解:(I )过C 作AB CM ⊥,垂足为M ,因为,DC AD ⊥所以四边形ADCM 为矩形.…………2分所以2==MB AM ,又因为4,2==AB AD 所以22=AC ,2=CM ,22=BC所以222AB BC AC =+,所以BC AC ⊥;…………4分因为AF ⊥平面ABCD ,,//BE AF 所以BE ⊥平面ABCD ,所以AC BE ⊥,……6分 又因为⊂BE 平面BCE ,⊂BC 平面BCE ,B BC BE =⋂所以⊥AC 平面BCE .…………………………………………………………8分 (II )因为AF ⊥平面ABCD ,所以CM AF ⊥,又因为AB CM ⊥,⊂AF 平面ABEF ,⊂AB 平面ABEF ,A AB AF =⋂xy ABO所以⊥CM 平面ABEF .……10分E BCF C BEFV V --=3824261213131=⨯⨯⨯=⨯⨯⨯⨯=⨯==∆--CM EF BE CM S V V BEF BEF C BCF E ……………………12分 19、(本小题满分12分)(I )解析:当111,12n a a =+=时,解得11a =………1分2n n S n a +=,① 当2,n ≥时11(1)2n n S n a --+-=②①-②得1122n n n a a a -+=-即121n n a a -=+………………………………………3分 即112(1)(2)n n a a n -+=+≥又112a +=所以{}1n a +是以2为首项,2为公比的等比数列……………………………4分 即12n n a +=故21n n a =-(*n N ∈)…………………………………5分 (II )(21)2n n n b n n n =-=⨯-…………6分设23122232......2n n K n =⨯+⨯+⨯++⨯………………………①23121222......2n n K n +=⨯+⨯++⨯………………………………②……7分①-②得231222......22n n n K n +-=++++-⨯1(1)22n n K n +=-⨯+………………………………………………………………9分即1(1)22n n K n +=-⨯+,∴1(1)(1)222n n n n T n ++=-⨯+-,……………………………10分 21(1)22201582n n n n T n n +++=-⨯+>⇒≥,……………………11分∴满足条件的最小正整数8n =…………………………………………12分.20、解:(I )由题意得,当点P 是椭圆的上、下顶点时,12PF F ∆的面积取最大值……1分 此时 12121,432PF F S F F OP bc bc ∆==∴= ……2分 1,23,42e b a === ……3分 所以椭圆方程为2211612x y +=……4分 (II )由(I )得,则1F 的坐标为2,0-()…… 5分因为0AC BD =,所以AC BD ⊥①当直线AC 与BD 中有一条直线斜率不存在时,易得6814AC BD +=+=……6分②当直线AC 斜率0k k ≠存在且时,其方程为(2)y k x =+,设112,2(,)()A x y C x y ,则点A 、C 的坐标是方程组22(2)11612y k x x y =+⎧⎪⎨+=⎪⎩的解,2222(34)1616480k x k x k +++-=…………7分22121222161648,3434k k x x x x k k --+==++ ……………………8分2212224(1)134k AC k x x k +=+-=+此时直线BD 的方程为1(2)y x k=-+…………………………………………………9分 同理由221(2)11612y x kx y ⎧=-+⎪⎪⎨⎪+=⎪⎩可得2224(1)43k BD k +=+ 2222222224(1)24(1)168(1)4334(43)(34)k k k AC BD k k k k ++++=+=++++ ……………………10分令21t k =+,则 2168(1)112AC BD t t t +=>-+…………………………11分2111,04t t t -><≤ ,216896[,14)1712AC BD t t+=∈-+综上,AC BD + 的取值范围是96[,14]7…………………………12分21.解:(I )()()()()ab x a x b f x x a b x x--'=-++=………2分 ()0f e '= ,a e ≠ b e ∴=………3分(II )由(I )得21()()ln 2f x x a e x ae x =-++,()()()x a x e f x x --'=①当1a e≤时,由()>0f x '得x e >;由()0f x '<得1x e e <<…………………4分此时()f x 在1(,)e e上单调递减,在()e +∞,上单调递增.2211()()ln 022f e e a e e ae e e =-++=-< ,242221112()()2(2)(2)(2)()0222f e e a e e ae e e e a e e e e=-++=--≥-->……5分 (或当x →+∞时,()0f x >亦可)∴要使得()f x 在1[,)e+∞上有且只有两个零点,则只需2111()ln 2a e f ae e e e e+=-+222(12)2(1)02e e e ae --+=≥,即22122(1+)e a e e -≤…6分 ②当1a e e<<时,由()>0f x '得1x a e <<或x e >;由()0f x '<得a x e <<.此时()f x 在(,)a e 上单调递减,在1(,)a e和()e +∞,上单调递增. ……………………7分此时222111()ln ln 0222f a a ae ae a a ae ae e a =--+<--+=-<,∴此时()f x 在[)e +∞,至多只有一个零点,不合题意………8分 ③当a e >时,由()0f x '>得1x e e<<或>x a ,由()0f x '<得e x a <<,………9分 ()f x 在1(,)e e 和()a +∞,上单调递增,在(,)e a 上单调递减,且21()02f e e =-<,…10分∴()f x 在1[,)e+∞至多只有一个零点,不合题意………………………11分综上所述,a 的取值范围为2212(]2(1+)e e e --∞,………12分 22.(本小题满分10分)解:(I )连结OE .∵点D 是BC 的中点,点O 是AB 的中点, ∴AC OD 21//=,∴A BOD ∠=∠,AEO EOD ∠=∠. ∵OE OA =,∴AEO A ∠=∠,∴EOD BOD ∠=∠.在EOD ∆和BOD ∆中, ∵OE OB =,EOD BOD ∴∆≅∆,∴90OED OBD ∠=∠=,即OE ED ⊥.∵E 是圆O 上一点,∴DE 是圆O 的切线. ……5分(II )延长DO 交圆O 于点F .∵EOD ∆≌BOD ∆,∴DB DE =. ∵点D 是BC 的中点,∴DB BC 2=.∵,DE DB 是圆O 的切线,∴DE DB =.∴222DE DB DE BC DE =⋅=⋅.ABCD EMO∵OF AB OD AC 2,2==,∴DF DM OF OD DM AB AC DM AB DM AC DM ⋅=+⋅=+⋅=⋅+⋅2)22()(. ∵DE 是圆O 的切线,DF 是圆O 的割线,∴DF DM DE ⋅=2,∴AB DM AC DM BC DE ⋅+⋅=⋅……10分23.解析:(I )将直线:l 12232x t y t ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数)消去参数t ,化为普通方程3230x y --=,……………………2分将cos sin x y ρθρθ=⎧⎨=⎩代入3230x y --=得3cos sin 230ρθρθ--=.…………4分(II )方法一:C 的普通方程为2240x y x +-=.………………6分 由22323040x y x y x ⎧--=⎪⎨+-=⎪⎩解得:13x y =⎧⎪⎨=-⎪⎩或33x y =⎧⎪⎨=⎪⎩………………8分 所以l 与C 交点的极坐标分别为:5(2,)3π ,(23,)6π.………………10分 方法二:由3cos sin 2304cos ρθρθρθ⎧--=⎪⎨=⎪⎩,……………6分得:sin(2)03πθ-=,又因为0,02ρθπ≥≤<………………8分所以253ρπθ=⎧⎪⎨=⎪⎩或236ρπθ⎧=⎪⎨=⎪⎩所以l 与C 交点的极坐标分别为:5(2,)3π ,(23,)6π.………………10分 24.解析:(I )当1a =时,|21||21|2x x x -++≤+1242x x x ⎧≤-⎪⇒⎨⎪-≤+⎩无解,111022222+x x x ⎧-<<⎪⇒≤<⎨⎪≤⎩,11222342x x x x ⎧≥⎪⇒≤≤⎨⎪≤+⎩……3分 综上,不等式的解集为2{0}3x x ≤≤.………………5分(II )|2||21|2x a x x -++≥+,转化为|2||21|20x a x x -++--≥ 令()|2||21|2h x x a x x =-++--,因为a>0,所以153,21()1,2231,2x a x a h x x a x a x a x ⎧-+-≤-⎪⎪⎪=-+--<<⎨⎪⎪--≥⎪⎩,………8分在a>0下易得min ()12ah x =-,令10,2a -≥a 得 2.a ≥a ………………10分。
深圳市2016届高三年级第一次调研考试(文数)

深圳市2016届高三年级第一次调研考试(文数)绝密★启用前深圳市2016届高三年级第一次调研考试数学(文科)本试卷共8页,24小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹的签字笔在答题卡指定位置填写自己的学校、姓名和考生号,并将条形码正向准确粘贴在答题卡的贴条形码区,请保持条形码整洁、不污损.2.选择题每小题选出答案后,用2B铅笔把答案涂在答题卷相应的位置上.3.非选择题必须用0.5毫米黑色字迹的签字笔作答,答案必须写在答题卡各题目指定区域内;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.作答选做题时,请先用2B铅笔填涂选做题的题号对应的信息点,再做答.(4)研究人员随机调查统计了某地1000名“上班族” 每天在工作之余使用手机上网的时间,并将其绘制为如图所示的频率分布直方图.若同一组数据用该区间的中点值作代表,则可估计该地“上班族”每天在工作之余使用手机上网的平均时间是(A )1.78小时(B )2.24小时(C )3.56小时(D )4.32小时(5)已知函数2()cos sin f x x x=-,下列说法错误..的是 (A )f (x)的最小正周期为π (B )2x π=是f (x)的一条对称轴(C )f (x) 在(4π-,4π)上单调递增 (D )| f (x)|的值域是[0,1](6)直线y=k(x+1)(k ∈R )与不等式组2202200x y x y x +-≤⎧⎪--≤⎨⎪≥⎩,表示的平面区域有公共点,则k 的取值范围是(A )[-2,2] (B )(-∞, -2] [2,+ ∞)(C)[-12,12] (D)(-∞,-12][12, +∞)(7)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则在该几何体中,最长的棱的长度是(A)42(B)25(C)6 (D)43(8)函数f(x)=xcosx在[-π,π]的大致图象为(A)(B)(C)(D)(9)已知22ππα-<<,且sin cos 2αα+=,则a 的值为(A )-12π (B )12π (C )-512π(D )512π(10)已知A ,B ,C 是球面上三点,且AB=6,BC=8,AC=10,球心O 到平面ABC 的距离等于该球半径的12,则此球的表面积为(A )1003π (B )2003π (C )4003π (D )4009π(11)过抛物线y 2=2px(p>0)的焦点F ,且倾斜角为4π的直线与抛物线交于A,B 两 点,若弦AB 的垂直平分线经过点(0,2),则p 等于(A )25 (B )23(C )45 (D )43(12)已知a >0,若函数2324ln ,0,()34,0,a x x x f x x a x x ⎧⋅->⎪=⎨--≤⎪⎩且g(x)=f(x)+2a 至少..有三个 零点,则a 的取值范围是(A )(12,1] (B )(1,2] (C )(1, +∞) (D )[1, +∞)第Ⅱ卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须作答。
广东省惠州市届高三数学上学期第一次调研试卷文(含解析)(1)【含答案】

广东省惠州市2015届高三上学期第一次调研数学试卷(文科)一、选择题(本大题共10小题,每小题5分,满分50分.每小题给出的四个选项中,只有一项是符合题目要求.)1.(5分)复数Z=(其中i为虚数单位)的虚部是()A.﹣B.i C.D.﹣i2.(5分)已知集合A={x|y=lg(x+3)},B={x|x≥2},则A∩B=()A.(﹣3,2] B.(﹣3,+∞)C.[2,+∞)D.[﹣3,+∞)3.(5分)下列函数在定义域内为奇函数的是()A.y=x+B.y=xsinx C.y=|x|﹣1 D.y=cosx4.(5分)命题“若x2<1,则﹣1<x<1”的逆否命题是()A.若x2≥1,则x≥1或x≤﹣1 B.若﹣1<x<1,则x2<1C.若x>1或x<﹣1,则x2>1 D.若x≥1或x≤﹣1,则x2≥15.(5分)若向量=(1,2),=(4,5),则=()A.(5,7)B.(﹣3,﹣3)C.(3,3)D.(﹣5,﹣7)6.(5分)若函数f(x)=x3+x2﹣2x﹣2的一个正数零点附近的函数值用二分法计算,其参考数据如下:f (1)=﹣2 f (1.5)=0.625 f (1.25)=﹣0.984f (1.375)=﹣0.260 f (1.4375)=0.162 f (1.40625)=﹣0.054那么方程x3+x2﹣2x﹣2=0的一个近似根(精确到0.1)为()A.1.2 B.1.3 C.1.4 D.1.57.(5分)执行如图所示的程序框图,若输入n的值为7,则输出的s的值为()A.22 B.16 C.15 D.118.(5分)函数f(x)=sin(ωx+φ)(x∈R,ω>0,|φ|<)的部分图象如图所示,则ω,φ的值分别是()A.2,﹣B.2,﹣C.4,﹣D.4,9.(5分)若双曲线的离心率为,则其渐近线的斜率为()A.±2B.C.D.10.(5分)已知函数.若f(﹣a)+f(a)≤2f(1),则a的取值范围是()A.[﹣1,0)B.[0,1] C.[﹣1,1] D.[﹣2,2]二、填空题:(本大题共3小题,考生作答4小题,每小题5分,满分15分.)(一)必做题(11~13题)11.(5分)计算:log318﹣log32=.12.(5分)满足约束条件的目标函数z=x+y的最大值为.13.(5分)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于 cm3.三.(二)选做题:第14、15题为选做题,考生只选做其中一题,两题全答的,只计前一题的得分.(坐标系与参数方程选做题)14.(5分)(坐标系与参数方程选做题)已知在平面直角坐标系xoy中,圆C的参数方程为,(θ为参数),以ox为极轴建立极坐标系,直线l的极坐标方程为=0,则圆C截直线l所得的弦长为.(几何证明选讲选做题)三、解答题:(本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤.)16.(12分)设函数f(x)=cosx+sinx+1(1)求函数f(x)的值域和函数的单调递增区间;(2)当f(a)=,且<α<时,求sin(2α+)的值.17.(12分)为了了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:喜爱打篮球不喜爱打篮球合计男生20 5 25女生10 15 25合计30 20 50(Ⅰ)用分层抽样的方法在喜欢打篮球的学生中抽6人,其中男生抽多少人?(Ⅱ)在上述抽取的6人中选2人,求恰有一名女生的概率.18.(14分)如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,.(1)求证:平面BCF∥面AED;(2)若BF=BD=a,求四棱锥A﹣BDEF的体积.19.(14分)已知等差数列{a n}的首项a1=1,公差d>0,且a2,a5,a14分别是等比数列{b n}的b2,b3,b4.(Ⅰ)求数列{a n}与{b n}的通项公式;(Ⅱ)设数列{c n}对任意自然数n均有=a n+1成立,求c1+c2+…+c2014的值.20.(14分)已知椭圆C1的离心率为e=,过C1的左焦点F1的直线l:x﹣y+2=0被圆C2:(x﹣3)2+(y﹣3)2=r2(r>0)截得的弦长为2.(1)求椭圆C1的方程;(2)设C1的右焦点为F2,在圆C2上是否存在点P,满足|PF1|=|PF2|,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.21.(14分)已知函数.(Ⅰ)当a=﹣1时,求曲线y=f(x)在点(2,f(2))处的切线方程;(Ⅱ)当时,讨论f(x)的单调性.广东省惠州市2015届高三上学期第一次调研数学试卷(文科)参考答案与试题解析一、选择题(本大题共10小题,每小题5分,满分50分.每小题给出的四个选项中,只有一项是符合题目要求.)1.(5分)复数Z=(其中i为虚数单位)的虚部是()A.﹣B.i C.D.﹣i考点:复数代数形式的乘除运算.专题:计算题;数系的扩充和复数.分析:先化简复数,由虚部的定义可得答案.解答:解:复数Z===,则虚部为,故选:C.点评:本题考查复数的基本概念,属基础题.2.(5分)已知集合A={x|y=lg(x+3)},B={x|x≥2},则A∩B=()A.(﹣3,2] B.(﹣3,+∞)C.[2,+∞)D.[﹣3,+∞)考点:交集及其运算.专题:集合.分析:求出A中x的范围确定出A,找出A与B的交集即可.解答:解:由A中y=lg(x+3),得到x+3>0,即x>﹣3,∴A=(﹣3,+∞),∵B=[2,+∞),∴A∩B=[2,+∞).故选:C.点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.3.(5分)下列函数在定义域内为奇函数的是()A.y=x+B.y=xsinx C.y=|x|﹣1 D.y=cosx考点:函数奇偶性的判断.专题:函数的性质及应用.分析:根据函数奇偶性的性质和定义进行判断即可.解答:解:A.函数f(x)的定义域为{x|x≠0},则f(﹣x)=﹣x﹣=﹣(x+)=﹣f(x),则函数是奇函数.B.f(﹣x)=﹣xsin(﹣x)=xsinx=f(x)为偶函数,C.f(﹣x)=|﹣x|﹣1=|x|﹣1=f(x)为偶函数,D.f(﹣x)=cos(﹣x)=cosx=f(x),为偶函数.故选:A点评:本题主要考查函数奇偶性的判断,要求熟练掌握常见函数的奇偶性,比较基础.4.(5分)命题“若x2<1,则﹣1<x<1”的逆否命题是()A.若x2≥1,则x≥1或x≤﹣1 B.若﹣1<x<1,则x2<1C.若x>1或x<﹣1,则x2>1 D.若x≥1或x≤﹣1,则x2≥1考点:四种命题.分析:根据逆否命题的定义,直接写出答案即可,要注意“且”形式的命题的否定.解答:解:原命题的条件是““若x2<1”,结论为“﹣1<x<1”,则其逆否命题是:若x≥1或x≤﹣1,则x2≥1.故选D.点评:解题时,要注意原命题的结论“﹣1<x<1”,是复合命题“且”的形式,否定时,要用“或”形式的符合命题.5.(5分)若向量=(1,2),=(4,5),则=()A.(5,7)B.(﹣3,﹣3)C.(3,3)D.(﹣5,﹣7)考点:向量的减法及其几何意义;平面向量的坐标运算.专题:平面向量及应用.分析:直接利用向量的减法运算法则求解即可.解答:解:∵向量=(1,2),=(4,5),∴==(1,2)﹣(4,5)=(﹣3,﹣3);故选:B.点评:本题考查向量的减法运算以及减法的几何意义,基本知识的考查.6.(5分)若函数f(x)=x3+x2﹣2x﹣2的一个正数零点附近的函数值用二分法计算,其参考数据如下:f (1)=﹣2 f (1.5)=0.625 f (1.25)=﹣0.984f (1.375)=﹣0.260 f (1.4375)=0.162 f (1.40625)=﹣0.054那么方程x3+x2﹣2x﹣2=0的一个近似根(精确到0.1)为()A.1.2 B.1.3 C.1.4 D.1.5考点:二分法求方程的近似解.专题:应用题.分析:由图中参考数据可得f(1.43750>0,f(1.40625)<0,又因为题中要求精确到0.1可得答案.解答:解:由图中参考数据可得f(1.43750)>0,f(1.40625)<0,又因为题中要求精确到0.1,所以近似根为 1.4故选 C.点评:本题本题主要考查用二分法求区间根的问题,属于基础题型.在利用二分法求区间根的问题上,如果题中有根的精确度的限制,在解题时就一定要计算到满足要求才能结束.7.(5分)执行如图所示的程序框图,若输入n的值为7,则输出的s的值为()A.22 B.16 C.15 D.11考点:程序框图.专题:算法和程序框图.分析:根据程序运行条件,分别进行判断,即可得到结论.解答:解:第一次运行,i=1,满足条件i<7,s=1+0=1.i=2,第二次运行,i=2,满足条件i<7,s=1+1=2.i=3,第三次运行,i=3,满足条件i<7, s=2+2=4.i=4,第四次运行,i=4,满足条件i<7,s=4+3=7.i=5,第五次运行,i=5,满足条件i<7,s=7+4=11.i=6,第六次运行,i=6,满足条件i<7,s=11+5=16.i=7,此时i=7,不满足条件i<7,程序终止,输出s=16,故选:B.点评:本题主要考查程序框图的识别和判断,根据运行条件分别进行验证即可得到结论.8.(5分)函数f(x)=sin(ωx+φ)(x∈R,ω>0,|φ|<)的部分图象如图所示,则ω,φ的值分别是()A.2,﹣B.2,﹣C.4,﹣D.4,考点:由y=Asin(ωx+φ)的部分图象确定其解析式.专题:三角函数的图像与性质.分析:由函数的图象可得,代入周期公式求得ω的值,再由五点作图的第二点列式求得φ的值.解答:解:由图知,∴T=π,即=π,解得:ω=2.由五点作图的第二点可知,2×+φ=,即φ=﹣,满足|φ|<,∴ω,φ的值分别是2,﹣.故选:A.点评:本题考查由y=Asin(ωx+φ)的部分图象求解函数解析式,解答的关键是由五点作图的某一点列式求解φ的值,是基础题.9.(5分)若双曲线的离心率为,则其渐近线的斜率为()A.±2B.C.D.考点:双曲线的简单性质.专题:圆锥曲线的定义、性质与方程.分析:由双曲线的离心率为,可得,解得即可.解答:解:∵双曲线的离心率为,∴,解得.∴其渐近线的斜率为.故选:B.点评:本题考查了双曲线的标准方程及其性质,属于基础题.10.(5分)已知函数.若f(﹣a)+f(a)≤2f(1),则a的取值范围是()A.[﹣1,0)B.[0,1] C.[﹣1,1] D.[﹣2,2]考点:分段函数的应用.专题:函数的性质及应用.分析:根据a的取值范围,把不等式f(﹣a)+f(a)≤2f(1)转化为不等式组求解,最后取并集得答案.解答:解:由,则不等式f(﹣a)+f(a)≤2f(1)等价于:或即①或②解①得:0≤a≤1;解②得:﹣1≤a<0.∴a的取值范围是[﹣1,1].故选:C.点评:本题考查分段函数求值及不等式的解法,训练了分类讨论的数学思想方法,属中档题.二、填空题:(本大题共3小题,考生作答4小题,每小题5分,满分15分.)(一)必做题(11~13题)11.(5分)计算:log318﹣log32=2.考点:对数的运算性质.专题:函数的性质及应用.分析:根据对数的运算法则求得要求式子的值.解答:解:log318﹣log32==log39=2,故答案为:2.点评:本题主要考查对数的运算性质的应用,属于基础题.12.(5分)满足约束条件的目标函数z=x+y的最大值为.考点:简单线性规划.专题:不等式的解法及应用.分析:先根据约束条件画出平面区域,然后平移直线y=﹣x,当过点A时,直线在y轴上的截距最大,从而求出所求.解答:解:满足约束条件的平面区域如下图所示:平移直线y=﹣x,由图易得,由得A(,).平移直线z=x+y可得,当x=,y=时,目标函数z=x+y的最大值为.故答案为:.点评:本题考查的知识点是简单的线性规划,画出满足约束条件的可行域是关键,属于基础题.13.(5分)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于24 cm3.考点:由三视图求面积、体积.专题:立体几何.分析:先根据三视图判断几何体的形状,再利用体积公式计算即可.解答:解:几何体为三棱柱去掉一个三棱锥后的几何体,底面是直角三角形,直角边分别为3,4,侧面的高为5,被截取的棱锥的高为3.如图:V=V棱柱﹣V棱锥==24(cm3)故答案为:24.点评:本题考查几何体的三视图及几何体的体积计算.V椎体=Sh,V柱体=Sh.考查空间想象能力.三.(二)选做题:第14、15题为选做题,考生只选做其中一题,两题全答的,只计前一题的得分.(坐标系与参数方程选做题)14.(5分)(坐标系与参数方程选做题)已知在平面直角坐标系xoy中,圆C的参数方程为,(θ为参数),以ox为极轴建立极坐标系,直线l的极坐标方程为=0,则圆C截直线l所得的弦长为4.考点:简单曲线的极坐标方程;圆的参数方程.专题:直线与圆.分析:首先把给出的圆的参数方程和直线的极坐标方程化为普通方程,然后运用数形结合即可解得答案.解答:解:由,得,两式平方相加得:①,由,得:,即②,如图圆心C到直线的距离为,所以直线L被圆C所截得的弦长为|AB|=.故答案为.点评:本题考查了简单曲线的极坐标方程和圆的参数方程,考查了数形结合的解题思想,考查了灵活处理和解决问题的能力,是中档题.(几何证明选讲选做题)三、解答题:(本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤.)16.(12分)设函数f(x)=cosx+sinx+1(1)求函数f(x)的值域和函数的单调递增区间;(2)当f(a)=,且<α<时,求sin(2α+)的值.考点:三角函数中的恒等变换应用;正弦函数的图象.专题:三角函数的求值;三角函数的图像与性质.分析:(1)根据三角函数的关系式,即可求求函数f(x)的值域和函数的单调递增区间.(2)根据三角函数的诱导公式即可得到结论.解答:解:(1)依题意f(x)=cosx+sinx+1=sin(x+)+1,∵﹣1≤sin(x+)≤1,则∵0≤sin(x+)+1≤2,函数f(x)的值域是[0,2],令﹣+2kπ≤x+≤2kπ+,k∈Z,解得﹣+2kπ≤x≤+2kπ,k∈Z,所以函数f(x)的单调增区间为[﹣+2kπ,+2kπ],k∈Z.(2)由f(a)=sin(α+)+1=,得sin(α+)=,∵<α<,∴<α+<π时,得cos(α+)=,∴sin(2α+)=sin2(α+)=2sin(α+)cos(α+)=﹣2××=.点评:本题主要考查三角函数的图象和性质以及三角函数求值,考查学生的运算能力,利用三角函数的诱导公式进行化简即可得到结论.17.(12分)为了了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:喜爱打篮球不喜爱打篮球合计男生20 5 25女生10 15 25合计30 20 50(Ⅰ)用分层抽样的方法在喜欢打篮球的学生中抽6人,其中男生抽多少人?(Ⅱ)在上述抽取的6人中选2人,求恰有一名女生的概率.考点:古典概型及其概率计算公式;分层抽样方法.专题:综合题;概率与统计.分析:(Ⅰ)根据分层抽样的方法,在喜欢打蓝球的学生中抽6人,先计算了抽取比例,再根据比例即可求出男生应该抽取人数.(Ⅱ)在上述抽取的6名学生中,女生的有2人,男生4人.女生2人记A,B;男生4人为c,d,e,f,列出其一切可能的结果组成的基本事件个数,通过列举得到满足条件事件数,求出概率.解答:解:(Ⅰ)在喜欢打蓝球的学生中抽6人,则抽取比例为,∴男生应该抽取20×=4人.(Ⅱ)在上述抽取的6名学生中,女生有2人,男生4人.女生2人记A,B;男生4人为c,d,e,f,则从6名学生任取2名的所有情况为:(A,B)、(A,c)、(A,d)、(A,e)、(A,f)、(B,c)、(B,d)、(B,e)、(B,f)、(c,d)、(c,e)、(c,f)、(d,e)、(d,f)、(e,f)共15种情况,其中恰有1名女生情况有:(A,c)、(A,d)、(A,e)、(A,f)、(B,c)、(B,d)、(B,e)、(B,f),共8种情况,故上述抽取的6人中选2人,恰有一名女生的概率概率为P=.点评:本题是一个统计综合题,包含抽样与概率,本题通过创设情境激发学生学习数学的情感,帮助培养其严谨治学的态度.18.(14分)如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,.(1)求证:平面BCF∥面AED;(2)若BF=BD=a,求四棱锥A﹣BDEF的体积.考点:棱柱、棱锥、棱台的体积;平面与平面平行的性质.专题:综合题;空间位置关系与距离.分析:(1)证明FB∥平面AED,BC∥平面AED,利用面面平行的判定定理可得结论;(2)连接AC,AC∩BD=O,证明AO⊥面BDEF,即可求出四棱锥A﹣BDEF的体积.解答:(1)证明:∵ABCD是菱形,∴BC∥AD,∵BC⊄面ADE,AD⊂面ADE,∴BC∥面ADE…(3分)∵BDEF是矩形,∴BF∥DE,∵BF⊄面ADE,DE⊂面ADE,∴BF∥面ADE,∵BC⊂面BCF,BF⊂面BCF,BC∩BF=B,∴面BCF∥面ADE…(6分)(2)解:连接AC,AC∩BD=O∵ABCD是菱形,∴AC⊥BD∵ED⊥面ABCD,AC⊂面ABCD,∴ED⊥AC,∵ED,BD⊂面BDEF,ED∩BD=D,∴AO⊥面BDEF,…(10分)∴AO为四棱锥A﹣BDEF的高由ABCD是菱形,,则△ABD为等边三角形,由BF=BD=a,则,∵,∴…(14分)点评:本题考查线面平行、面面平行,考查四棱锥的体积,考查学生分析解决问题的能力,正确运用线面平行、面面平行是关键.19.(14分)已知等差数列{a n}的首项a1=1,公差d>0,且a2,a5,a14分别是等比数列{b n}的b2,b3,b4.(Ⅰ)求数列{a n}与{b n}的通项公式;(Ⅱ)设数列{c n}对任意自然数n均有=a n+1成立,求c1+c2+…+c2014的值.考点:数列的求和.专题:综合题;等差数列与等比数列.分析:(Ⅰ)依题意,a2,a5,a14成等比数列⇒(1+4d)2=(1+d)(1+13d),可求得d,继而可求得数列{a n}的通项公式;由b2=a2=3,b3=a5=9,可求得q与其首项,从而可得数列{b n}的通项公式;(Ⅱ)由(Ⅰ)知a n=2n﹣1,b n=3n﹣1,由++…+=a n+1,可求得c1=b1a2=3,=a n+1﹣a n=2(n≥2),于是可求得数列{c n}的通项公式,继而可求得c1+c2+…+c2014的值.解答:解:(Ⅰ)∵a2=1+d,a5=1+4d,a14=1+13d,∵a2,a5,a14成等比数列,∴(1+4d)2=(1+d)(1+13d),解得d=2,∴a n=1+(n﹣1)×2=2n﹣1;又b2=a2=3,b3=a5=9,∴q=3,b1=1,∴b n=3n﹣1.(Ⅱ)∵++…+=a n+1,∴=a2,即c1=b1a2=3,又++…+=a n(n≥2),∴=a n+1﹣a n=2(n≥2),∴c n=2b n=2•3n﹣1(n≥2),∴c n=.∴c1+c2+…+c2014=3+2•3+2•32+…+2•32013=3+2(3+•32+ (32013)=3+2•=32014.点评:本题考查数列的求和,着重考查等差数列与等比数列的通项公式,考查逻辑思维与综合分析、运算能力,属于难题.20.(14分)已知椭圆C1的离心率为e=,过C1的左焦点F1的直线l:x﹣y+2=0被圆C2:(x﹣3)2+(y﹣3)2=r2(r>0)截得的弦长为2.(1)求椭圆C1的方程;(2)设C1的右焦点为F2,在圆C2上是否存在点P,满足|PF1|=|PF2|,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.考点:直线与圆锥曲线的综合问题;椭圆的标准方程.专题:综合题;探究型;存在型.分析:对第(1)问,由a2=b2+c2,及F1的坐标满足直线l的方程,联立此三个方程,即得a2,b2,从而得椭圆方程;对第(2)问,根据弦长,利用垂径定理与勾股定理得方程,可求得圆的半径r,从而确定圆的方程,再由条件|PF1|=|PF2|,将点P满足的关系式列出,通过此关系式与已知圆C2的方程联系,再探求点P的存在性.解答:解:在直线l的方程x﹣y+2=0中,令y=0,得x=﹣2,即得F1(﹣2,0),∴c=2,又∵离心率,∴a2=6,b2=a2﹣c2=2,∴椭圆C1的方程为.(2)∵圆心C2(3,3)到直线l:x﹣y+2=0的距离为d=,又直线l被圆C2截得的弦长为,∴由垂径定理得,故圆C2的方程为.设圆C2上存在点P(x,y),满足,即|PF1|=3|PF2|.∵F1(﹣2,0),F2(2,0),则,整理得,此方程表示圆心在点,半径是的圆,∴|CC2|=,故有,即两圆相交,有两个公共点.∴圆C2上存在两个不同点P,满足|PF1|=.点评:1.求椭圆的方程,关键是确定a2,b2,常用到关系式及a2=b2+c2,再找一个关系式,一般可解出a,b.2.本题采用交集思想巧妙地处理了点P的存在性.本解法是用圆特有的方式判断两圆的公共点个数,若联立两曲线的方程,消去 x或y,用判别式来判断也可以,其适用范围更广,但计算量相对大一些.21.(14分)已知函数.(Ⅰ)当a=﹣1时,求曲线y=f(x)在点(2,f(2))处的切线方程;(Ⅱ)当时,讨论f(x)的单调性.考点:利用导数研究曲线上某点切线方程;利用导数研究函数的单调性.专题:导数的综合应用.分析:(Ⅰ)欲求出切线方程,只须求出其斜率即可,故先利用导数求出在x=2处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.(Ⅱ)利用导数来讨论函数的单调性即可,具体的步骤是:(1)确定 f(x)的定义域;(2)求导数fˊ(x);(3)在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0;(4)确定函数的单调区间.若在函数式中含字母系数,往往要分类讨论.解答:解:(Ⅰ)当a=﹣1时,f(x)=lnx+x+﹣1,x∈(0,+∞),所以f′(x)=+1﹣,因此,f′(2)=1,即曲线y=f(x)在点(2,f(2))处的切线斜率为1,又f(2)=ln2+2,y=f(x)在点(2,f(2))处的切线方程为y﹣(ln2+2)=x﹣2,所以曲线,即x﹣y+ln2=0;(Ⅱ)因为,所以=,x∈(0,+∞),令g(x)=ax2﹣x+1﹣a,x∈(0,+∞),(1)当a=0时,g(x)=﹣x+1,x∈(0,+∞),所以,当x∈(0,1)时,g(x)>0,此时f′(x)<0,函数f(x)单调递减;(2)当a≠0时,由g(x)=0,即ax2﹣x+1﹣a=0,解得x1=1,x2=﹣1.①当a=时,x1=x2,g(x)≥0恒成立,此时f′(x)≤0,函数f(x)在(0,+∞)上单调递减;②当0<a<时,x∈(0,1)时,g(x)>0,此时f′(x)<0,函数f(x)单调递减,x∈(1,﹣1)时,g(x)<0,此时f′(x)>0,函数f(x)单调递增,x∈(﹣1,+∞)时,g(x)>0,此时f′(x)<0,函数f(x)单调递减;③当a<0时,由于﹣1<0,x∈(0,1)时,g(x)>0,此时f′(x)<0函数f(x)单调递减;x∈(1,+∞)时,g(x)<0此时函数f′(x)>0函数f(x)单调递增.综上所述:当a≤0时,函数f(x)在(0,1)上单调递减;函数f(x)在(1,+∞)上单调递增当a=时,函数f(x)在(0,+∞)上单调递减当0<a<时,函数f(x)在(0,1)上单调递减;函数f(x)在(1,﹣1)上单调递增;函数f(x)在(﹣1,+∞)上单调递减.点评:本小题主要考查导数的概念、利用导数研究函数的单调性、导数的几何意义和利用导数研究函数性质的能力,考查分类讨论思想、数形结合思想和等价变换思想.。
惠州市届高三第一次调研考试文数

惠州市2017届高三第一次调研考试数学(文科)注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、准考证号、座位号、学校、班级等考生信息填写在答题卡上。
2. 回答第Ⅰ卷时,选出每个小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号,写在本试卷上无效。
3. 回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4. 考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
(1) 已知},log |{},16,8,4,2,1{2A x x y y B A ∈===,则=B A ()(A) }2,1{(B) }8,4,2{(C) }4,2,1{(D) }8,4,2,1{(2) 若复数z 满足)1()21(i z i -=+,则=||z ()(A) 52(B) 53(C)510(D) 10(3) 若21)tan(,31tan =+=βαα,则=βtan ()(A) 71 (B) 61 (C) 75(D) 65(4) 函数R x px x x y ∈+=,||()(A) 是偶函数(B) 是奇函数(C) 不具有奇偶性(D) 奇偶性与p 有关(5) 若向量)2,1(+=x 和向量)1,1(-=平行,则=+||()(A) 10(B)210(C) 2 (D)22(6) 等比数列}{n a 的各项为正数,且187465=+a a a a 则=+++1032313log log log a a a ()(A) 12(B) 10(C) 8(D) 5log 23+(7) 命题“任意0],2,1[2≤-∈a x x ”为真命题的一个充分不必要条件是()(A) 4≥a (B) 4≤a (C) 5≥a (D) 5≤a(8) 已知⎪⎩⎪⎨⎧≥-+≤--≥-020630y x y x y x ,则y x z +=22的最小值是()(A) 1 (B) 16 (C) 8 (D) 4 (9) 执行如图所示的程序框图,则输出S 的值为()(A) 2 (B) 3-(C) 21- (D) 31(10) 某几何体的三视图如右图,其正视图中的曲线部分为半圆,则该几何体的表面积为()(A) 2)19(cm π+(B) 2)422(cm π+ (C) 2)42610(cm π++ (D) 2)42613(cm π++(11) 已知三棱锥ABC S -的底面是以AB 为斜边的等腰直角三角形,2,2====SC SB SA AB ,则三棱锥的外接球的球心到平面ABC 的距离是() (A)33(B) 1(C) 3(D) 233(12) 双曲线M :)0,0(12222>>=-b a by a x 的实轴的两个端点为B A 、,点P 为双曲线M 上除B A 、外的一个动点,若动点Q 满足PB QB PA QA ⊥⊥,,则动点Q 的轨迹为() (A) 圆(B) 椭圆(C) 双曲线(D) 抛物线第Ⅱ卷本卷包括必考题和选考题两部分。
广东省惠州市2016届高三数学4月模拟考试试题文(20210531074217)

所以ABAE ,,,3 分ADAC即 AB AC ADAE,,, 4 分又 ABBC ,所以 AC BC AD AE,,, 5 分(Ⅱ)因为 FC 是圆 O 的切线,所以 FC 2FA FB , ,,,6 分又 AF 2,CF 2 2,所以 BF4, AB 2 ,,,, 7 分因为 ACF FBC , CFBAFC ,所以 AFC CFB,,, 8 分所以AFAC,得 AC2,cos ACD2,sin ACD14 sin AEB ,, 9 分FCBC44所以 AEsin AB4 14 ,,,10 分AEB723. (本小题满分 10 分)(Ⅰ)消去参数得直线 l 的普通方程为 3x y3 0 ,,,, 2 分 由23sin 得圆 C 的直角坐标方程 x 2y 2 2 3 y0 .,,,5 分(Ⅱ)由直线 l 的参数方程可知直线过点P ,,,6 分把直线 l 的参数方程代入圆 C 的直角坐标方程x 2 y 2 23 y 0 ,得 (11 t )2 (3 t 3) 23 , ,,,,7 分22化简得 t 2 4t 10 ,12 0 ,故设t 1 ,t 2是上述方程的两个实数根, 所以 t 1 t 2 4,t 1t21 ,,,8 分A, B 两点对应的参数分别为 t 1, t 2 ,,,,,,, 9 分 所以 | PA|| PB| | t 1 | | t 2 | t 1 t 24 .,,,,,,10 分24. (本小题满分10 分)(Ⅰ) 当 a 2时,f (x)x 2x 1,原不等式等价于2x22 x1x1221,或,或,,,,,,3 分x 2 x1123x+2x3x+2x322解得 x11 或 x1或44不等式的解集为 { x | x11 或 x 1}4 4,,,,,,4 分,,,,,,,,5 分(Ⅱ) f (m) f (1) m a m11a11,,,,, 6 分m a m m am a 1a1112 m18 分mmm a,,,,a m2(| m | 1 ) 4 ,当且仅当m1时等号成立。
广东省惠州市2016届高三上学期第二次调研考试数学(文)试题 含解析
惠州市2016届高三第二次调研考试文科数学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项 是符合题目要求的.1。
若集合{}2xA y y ==,2{|230,}B x xx x =-->∈R ,那么A B =( )(A)(]0,3 (B )[]1,3- (C )()3,+∞ (D)()()0,13,-+∞ 【答案】C 【解析】试题分析:{}{}2=0xA y y y y ==>,{}31B x x x =><-或,∴{}3AB x x =>,故选C 。
考点:集合的交集运算。
2.在复平面内,复数11i i++所对应的点位于( )(A )第一象限 (B )第二象限 (C )第三象限(D )第四象限【答案】A 【解析】试题分析:111122i i i i i -++=+=+,选A. 考点:复数的运算. 3.已知53()sin 8f x axbx x =++-且10)2(=-f ,那么=)2(f ( )(A)26- (B)26 (C )10- (D )10 【答案】A【解析】试题分析:53(2)22sin 28f a b =⨯+⨯+-,53(2)22sin 28f a b -=-⨯-⨯--,∴(2)(2)16f f +-=-,∵10)2(=-f ,∴(2)26f =-,选A. 考点:函数的奇偶性。
4。
设M 是平行四边形ABCD的对角线的交点,O 为任意一点,则=+++OD OC OB OA ()(A )OM(B )OM 2 (C )OM 3 (D )OM 4【答案】D 【解析】试题分析:在△OAC 中,M 为AC 中点,根据平行四边形法则,有2OC OM+=OA ,同理有2OB OM +=OD ,故4OA OC OB OC OM +++=,选D 。
考点:向量的运算.5.函数()()sin f x A x ωϕ=+(其中0,2A πϕ><)的图像如图所示,为了得到()sin2g x x =的图像,则只需将()f x 的图像( )(A )向左平移3π个长度单位 (B )向右平移3π个长度单位(C)向左平移6π个长度单位 (D )向右平移6π个长度单位6。
2016年深圳市高三年级第一次调研考试数学(文科)试题
一、 选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是
符合题目要求的.
(1)已知集合 A 1,0,1 , B y y x2 x, x A ,则 A B =
(A) 0
(B)2
(C) 0,1
(D) 1, 0
(2)若平面向量 a (m,1) , b (2,1) ,且 (a 2b) // b ,则 m =
深圳市 2016 年高三年级第一次调研考试数学(文科)试题 第 8 页 共 8 页
(Ⅰ)根据上表数据,完成下列茎叶图,并分别求出 A,B 两类户型住宅每平方米销
售价格的中位数;
A 户型
B 户型
2. 3. 4.
(Ⅱ)该公司决定对上述 24 套住房通过抽签方式销售,购房者根据自己的需求只能 在其中一种户型中通过抽签方式随机获取房.号.,每位购房者只有一次抽签机会.
小明是第一位抽签的员工,经测算其购买能力最多为 320 万元,抽签后所抽得住房价 格在其购买能力范围内则确定购买,否则,将放弃此次购房资格.为了使其购房成功的概 率更大,他应该选择哪一种户型抽签?
.(参考数据:
sin15 0.2588, sin 7.5 0.1305 )
深圳市 2016 年高三年级第一次调研考试数学(文科)试题 第 4 页 共 8 页
开始 n6
S 1 n sin 360
2
n
n 2n
否 S 3.10
是 输出in
k 结束
(16)在平面直角坐标系 xOy 中,已知△ABC 的顶点 B(5,0) 和 C(5,0) ,顶点 A 在双曲
(A)1
(B) 2
(C) 3
(D) 4
(3)设 i
广东省惠州市2016届高三数学4月模拟考试试题文
20. (本小题满分12 分)解:(Ⅰ)设点M 的坐标为(x, y) , k A1My(x2)①,,, 1 分x 2kA2 My(x2)②,,,2分x 2① ②得y23整理得x2y21,,,3分4,43x24∴轨迹 C 的方程为x2y2 1 ( x 2 ),,,4分43(Ⅱ)点 A(1,t ) ( t0)在轨迹M上∴1t 21,解得 t3,即点 A 的坐标为(1,3) ,, 5 分4322设 k AE k ,则直线AE的方程为:y k( x1)3x2y 21,并整理得2,代入43(3 4k2 )x2(12k 8k2 )x4k 212k30,,, 6 分设 E(x E , y E ) , F (x F ,y F ) ,3) 在轨迹C上,∴x E4k212k37 分∵点 A(1,34k 2③ ,,,2y E kx E 3k④,,,8 分2又 k AE kAF0 得 k AF k ,将③、④式中的k 代换成k ,可得x F4k 212 k 3, y F kx F3k,,,9 分34k 22∴直线 EF 的斜率K EF y F y E k (x F x E ) 2k,,,10 分x F x E x F x E∵ x xF 8k 26, x x24k,,,11 分E4k 23FE4k 23k 8k262k k(8k 26)2k(4k23)1∴k EF 4k23,,,12 分24k24k24k 2321.(本小题满分 12 分)(Ⅰ)函数 f ( x) 的定义域为(0,) .,,, 1 分f(x)112ax2x1,,, 2 分2axx.xa0,方程2ax2x 10 的判别式18a .9专业资料整理专业资料整理①当 a1 0 ,∴ f (x)0 ,故函数 f ( x) 在 (0,) 上递减 ,,,3 分时,8②当 0 a1 0 ,由 f (x)0 1 1 8a1 1 8a4 分时,可得 x 14a, x 24a . ,,,8x(0, x 1 )x 1( x 1, x 2 )x 2( x 2 ,)f ( x)f ( x)↘ 极小值↗极大值 ↘函数 f (x) 的减区 间为 (0, x 1 ), ( x 2 , ) ;增区间为 ( x 1 , x 2 ) .,,,5分所以,当 a 1f ( x) 在 (0,) 上递减;时,8当 0 a1 时, f ( x) 在 (11 8a ,1 18a) 上递增,在 (0,11 8a ) ,8 4a 4a4a(11 8a , ) 上递减 . ,,,6 分4a(Ⅱ)由(Ⅰ)知当 0a1 时,函数 f (x) 有两个极值点 x 1 , x2 ,且 x 1 x 21, x 1 x 21 ,,82a2a7 分f ( x 1 ) f ( x 2 ) x 1 ax 12 ln x 1 x 2 ax 22 ln x 2( x 1 x 2 ) a( x 12 x 22 ) ln( x 1x 2 ) ( x 1 x 2 ) a[( x 1 x 2 )2 2 x 1x 2 ] ln( x 1 x 2 ) ,,,8 分1 ln 11,,, 9 分4a 2a设1t4, 则 1 ln 1 1tln t1h(t ),,,10 分2a4a 2a 2¢ 1 1t - 2> 0,h (t) = -t=2t2所以 h(t) 在 (4, +? ) 上递增, h(t ) > h(4) = 3 - 2ln2 ,,,11 分所以 f (x 1)f ( x 2 ) 3 2 ln 2,,, 12 分请考生在第 22、23、24 题中任选一题做答。
广东省深圳市2016届高三第一次调研考试理科数学试题Word版含答案
2016年深圳市高三年级第一次调研考试数学(理科) 2016.2.25一.选择题:本大题共12小题,每题5分,总分值60分,在每题给出的四个选项中,只有一项为哪一项符合题目要求的1.已知集合{})3)(1(|+-==x x y x A ,{}1log |2≤=x x B ,那么=B A ( )A .{}13|≤≤-x xB .{}10|≤<x xC .{}23|≤≤-x xD .{}2|≤x x 2.设i 为虚数单位,复数z 知足i i z 43+=⋅,那么z 在复平面内对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限3.已知平面向量a 、b 2=a 1=b ,a 与b 的夹角为︒120,且()()b a b a -⊥+2λ,那么实数λ的值为( )A .7-B .3-C .2D .34.若y x ,知足约束条件⎪⎩⎪⎨⎧≥≤--≤-+0033022x y x y x ,那么y x z -=的最小值为( )A .3-B .1C .2-D .2 5.公差为1的等差数列{}n a 中,631,,a a a 成等比数列,那么{}n a 的前10项和为( )A .65B .80C .85D .1706.假设函数)2)(2sin(2)(πϕϕ<+=x x f 的图像过点)1,6(π,那么该函数图像的一条对称轴方程是( )A .12π=x B .125π=x C .6π=x D .3π=x7.62)1)(2(x x x -+的展开式中常数项为( ) A .40- B .25- C .25 D .558.如图,网格纸上小正方形的边长为,粗线画出的是某几何体的三视图, 那么在该几何体中,最长的棱的长度是( )A .24B .52C .6D .34 9.4名同窗参加3项不同的课外活动,假设每名同窗可自由选择参加其中 的一项,那么每项活动至少有一名同窗参加的概率为( )A .94B .274C .649D .64310.点S 、A 、B 、C 在半径为2的同一球面上,点S 到平面ABC 的距离为21,3===CA BC AB ,那么点S 与ABC ∆中心的距离为( )A .3B .2C .1D .2111.过点)2,0(b 的直线l 与双曲线)0,(1:2222>=-b a b y a x C 的一条斜率为正值的渐进线平行,假设双曲线C 的右支上的点到直线l 的距离恒大于b ,那么双曲线C 的离心率为取值范围是( )A .(]2,1B .()+∞,2C .()2,1D .()2,112.函数x ax x x f +-=2ln )(有两个零点,那么实数a 的取值范围是( ) A .()1,0 B .()1,∞- C .⎪⎭⎫ ⎝⎛+∞-21,e e D .⎪⎭⎫⎝⎛+21,0e e二.填空题:本大题4小题,每题5分,总分值20分13.已知)(x f ,)(x g 别离是概念域为R 的奇函数和偶函数,且xx g x f 3)()(=+,那么)1(f 的值为______14.公元263年左右,我国数学家刘徽发觉当圆内接正多边形的边数无 限增加时,多边形面积可无穷逼近圆的面积,并创建了“割圆术”,利 用“割圆术”刘徽取得了圆周率精准到小数点后两位的近似值14.3,这 确实是闻名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程 序框图,那么输出的值为_______(参考数据:2588.015sin =︒,1305.05.7sin =︒)15.过抛物线)0(22>=p px y 的核心F ,且倾斜角为4π的直线与抛物线交于B A ,两点,假设弦AB 的垂直平分线通过点)2,0(,那么p 等于_______16.数列{}n a 知足)2(,2,211212≥⎪⎩⎪⎨⎧≥<=---n n a a n a n a n n n n ,假设{}n a 为等比数列,那么1a 的取值范围是_______三.解答题:本大题共8小题,总分值70分,解答须写出文字说明、证明进程或演算步骤 17.(本小题总分值12分)如图,在ABC ∆中,︒=∠60C ,D 是BC 上一点,31=AB ,20=BD ,21=AD(1)求B ∠cos 的值;(2)求BAC ∠sin 的值和边BC 的长18.(本小题总分值12分)依照某水文观测点的历史统计数据,取得某河流水位X(单位:米)的频率散布直方图如下:将河流水位在以上6段的频率作为相应段的概率,并假设每一年河流水位互不阻碍 (1)求以后三年,最多有1年河流水位)31,27[∈X 的概率(结果用分数表示);(2)该河流对沿河A 企业阻碍如下:当)27,23[∈X 时,可不能造成阻碍;当)31,27[∈X 时,损失10000元;当)35,31[∈X 时,损失60000元,为减少损失,现有种应付方案: 方案一:防御35米的最高水位,需要工程费用3800元; 方案二:防御不超过31米的水位,需要工程费用2000元; 方案三:不采取方法;试比较哪一种方案较好,并请说理由19.(本小题总分值12分)如图,四棱锥ABCD P -中,底面ABCD 是边长为2的菱形,︒=∠60ABC ,PB PA ⊥,2=PC(1)求证:平面⊥PAB 平面ABCD ;(2)假设PB PA =,求二面角D PC A --的余弦值20.(本小题总分值12分)已知椭圆)0(1:2222>>=+b a b y a x E 的离心率为22,直线03=++y x 与椭圆E 仅有一个公共点(1)求椭圆E 的方程;(2)直线l 被圆3:22=+y x O 截得的弦长为3,且与椭圆E 交于B A ,两点,求ABO ∆面积的最大值21.(本小题总分值12分)已知函数xexxf)1()(+=和函数2)1)(()(--=xaexg x(e为自然对数的底数)(1)求函数)(xf的单调区间;(2)判定函数)(xg的极值点的个数,并说明理由;(3)假设函数)(xg存在极值为22a,求a的值请考生在第22、23、24题中任选一题作答,若是多做,那么按所做的第一题计分,作答时写清题号22.(本小题总分值10分)选修4-1:几何证明选讲如图,在直角ABC ∆中,BC AB ⊥,D 为BC 边上异于C B ,的一点,以AB 为直径作圆O ,并别离交AD AC ,于点F E ,(1)证明:D F E C ,,,四点共圆;(2)假设D 为BC 的中点,且3=AF ,1=FD ,求AE 的长23.(本小题总分值10分)选修4-4:坐标系与参数方程选讲在平面直角坐标系xOy 中,已知直线l 的参数方程为⎩⎨⎧==ααsin cos t y t x (t 为参数,πα<<0),以原点O 为极点,以x 轴正半轴为极轴成立极坐标系,曲线C 的极坐标方程为θρcos 1-=p(0>p )(1)写出直线l 的极坐标方程和曲线C 的直角坐标方程;(2)假设直线l 与曲线C 相交于B A ,两点,求OBOA 11+的值24.(本小题总分值10分)选修4-5:不等式选讲 已知函数3)(-++=x a x x f (R a ∈)(1)当1=a 时,求不等式8)(+≥x x f 的解集; (2)假设函数)(x f 的最小值为5,求a 的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 惠州市2016届高三第一次调研考试 文科数学 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分. 考生注意: 1. 答题前,考生务必将自己的准考证号、姓名填写在答题卡上.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致. 2. 第I卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.第II卷用0.5毫米的黑色墨水签字笔在答题卡上书写作答.若在试题卷上作答,答案无效. 3. 考试结束,监考员将试题卷、答题卡一并收回.
第Ⅰ卷 一.选择题:本大题共12小题,每小题5分。在每个小题给出的四个选项中,只有一项是符合要求的。 (1)设集合1,2,3,4,2,PQxxxR,则PQ等于( ) (A)1,2,0,1,2(B)3,4(C)1 (D)1,2
(2)双曲线22132xy的焦距为( )
(A)32 (B)5 (C)25 (D)45 (3)设(是虚数单位),则( ) (A) (B)1i (C)(D)1i (4)=则中,AcbaABC,2,3,7( ) (A)30 (B)45 (C)60 (D)90
1zii22zz
1i1i 2
(5)在等比数列na中,若0na且3764aa,则5a的值为 ( )
(A)2 (B)4 (C)6 (D)8
(6)函数xxxf32cos3
2
sin)(的图象中相邻的两条对称轴间距离为 ( )
(A)32 (B)34 (C)3 (D)67
(7)已知流程图如右图所示,该程序运行后,为使输出的b值 为16,则循环体的判断框内①处应填 ( ) (A)3?a (B)3?a (C)3?a (D)3?a
(8)向量)2 , 1( a、)3 , 1( b,下列结论中,正确的是( ) (A) // ba(B) ba (C)) //( baa(D)) ( baa
(9)如右图是一个四棱锥的三视图,则该几何体的体积为( ) (A)403(B)323(C)163(D)283
(10)已知函数1),1(log1,2)(3xxxxfx,且1)(0xf,则0x( )
(A)0 (B)4 (C)0或4 (D)1或3
开始 a=1,b=1
输出b a=a+1 b=2b 结束
是
否 ① 3
(11)过抛物线24yx的焦点F作直线交抛物线于11(,)Axy、22(,)Bxy两点,如果126xx,那么
AB= ( )
(A)6(B)8(C)9(D)10 (12)对函数()fx,在使Mxf)(成立的所有常数M中,我们把M的最大值叫做函数)(xf的下确界.现已知定义在R上的偶函数)(xf满足(1)(1)fxfx,当]1,0[x时,23)(2xxf,则)(xf的下
确界为 ( ) (A)2 (B)1 (C)0 (D)1
第Ⅱ卷 注意事项: 第II卷须用黑色墨水签字笔在答题卡上书写作答,若在试题卷上作答,答案无效. 本卷包括必考题和选考题两部分。第13题~第21题为必考题,每个试题考生都必须做答。第22题~第24题为选考题,考生根据要求做答。 二.填空题:本大题共4小题,每小题5分。 (13)若3sin()25,则cos2.
(14)方程20([0,1])xxnn有实根的概率为 .
(15)已知点(,)Pxy的坐标满足条件4,,1,xyyxx点O为坐标原点,那么OP的最大值等于. (16)已知函数()1xfxaxe(aR,e为自然对数的底数),若函数()fx在点(1,(1))f处的切线平行
于x轴,则a. 4
三.解答题:解答应写出文字说明,证明过程或演算步骤。 (17)(本小题满分12分) 已知{}na为等差数列,且满足13248,12aaaa.
(I) 求数列{}na的通项公式;
(II)记{}na的前n项和为nS,若31,,kkaaS成等比数列,求正整数k的值.
(18)(本小题满分12分) 某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满
分100分)的茎叶图如图,其中甲班学生的平均分是85. (I)计算甲班7位学生成绩的方差2s
;
(II)从成绩在90分以上的学生中随机抽取两名学生, 求甲班至少有一名学生的概率.
参考公式: 方差2222121nsxxxxxxn,其中12nxxxxn.
甲 乙 8 9 7 6 8 1 1 3 9 1 1 6 0 x 5 2 6 5
(19)(本小题满分12分) 如图,矩形ABCD中,对角线BDAC、的交点为ADG,⊥平面,ABE FBCEBAEEBAE,,2为CE上的点,且CEBF.
(I)求证:AE⊥平面BCE;
(II)求三棱锥GBFC的体积.
A C D E G B F 6 (20)(本小题满分12分) 在平面直角坐标系xOy中,已知圆心在x轴上,半径为4的圆C位于y轴右侧,且与y轴相切. (I)求圆C的方程;
(II)若椭圆222125xyb的离心率为45,且左右焦点为12,FF.试探究在圆C上是否存在点P,使得12PFF为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标). 7
(21)(本小题满分12分) 已知函数323()(1)312fxxaxaxaR,.
(I)讨论函数)(xf的单调区间; (II)当3a时,若函数)(xf在区间]2,[m上的最大值为28,求m的取值范围. 8 请考生在第22、23、24题中任选一题做答。如果多做,则按所做的第一题计分.做答时请写清题号。 (22)(本小题满分10分)选修4—1:几何证明选讲 如图,AB为⊙O的直径,直线CD与⊙O相切于点E,AD垂直CD于点D,BC垂直CD于点C,EF垂直AB于点F,连接AE,BE.
证明:(Ⅰ)FEBCEB;
(Ⅱ)2
EFADBC.
(23)(本小题满分10分)选修4—4:坐标系与参数方程 在直角坐标系xOy中,直线1C的参数方程为1(2xttyt为参数),以该直角坐标系的原点O为极点,x轴的正半轴为极轴的极坐标系下,圆2C的方程为sin32cos2.
(Ⅰ)求直线1C的普通方程和圆2C的圆心的极坐标;
(Ⅱ)设直线1C和圆2C的交点为A、B,求弦AB的长.
(24)(本小题满分10分)选修4—5:不等式选讲 9
已知1m,且关于x的不等式|2|1mx的解集为[0,4]. (Ⅰ)求m的值; (Ⅱ)若a,b均为正实数,且满足abm,求22
ab的最小值.
惠州市2016届高三第一次调研考试 10 数学试题 (文科)参考答案 2015.7 一、选择题(每小题5分,共60分) 题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D C B C D A C D A C B D
1.【解析】由题意1,2PQ,故选D. 2.【解析】由双曲线定义易知2
5c,故选C.
3.【解析】由复数计算得22121ziiiz,故选B .
4.【解析】由余弦定理直接得2229471cos22322bcaAbc,且0,A,得60A,故选C. 5.【解析】由等比数列性质易知237564aaa
,且0na,则58a,故选D .
6.【解析】函数解析式化简得2()2sin()34fxx,函数的周期为2323T,由正弦函数图像可
知相邻的两条对称轴间距离为半个周期,则322T
,故选A .
7.【解析】b的值由2,4,16变化,a也由1,2,3递变,由题意易知选C. 8.【解析】由 2,1ab,则易得: ( )0aab,故选D .
9.【解析】由三视图得到其直观图(右上图所示),则体积为1140[(14)4]4323,故选A .
10.【解析】当1x时,由0
0
()21xfx得00x;当1x时,由030()log(1)1fxx得013x,
则04x
,且两者都成立,故选C.
11.【解析】由抛物线方程可知24p,得2p;又由抛物线定义可知,点A到焦点的距离等于其到准线
