2018年人教版数学选修1-1拓展资料:抛物线反射镜和汽车前灯
高中数学人教版选修1-1:2.3.2-3 抛物线的简单几何性质 课件

一、知识回顾
把直线方程代入抛物线方程
得到一元一次方程
直线与抛物线的 对称轴平行(或重合)
相交(一个交点)
得到一元二次方程 计算判别式
>0 =0 <0 相交 相切 相离
二、精典例题 例1
解:
二、精典例题 例2
(1)解:
二、精典例题 (2)证明:
二、精典例题 例3解Fra bibliotek①二、精典例题
No 伟人都是在逆境中锻炼出来的,平静的湖面不会练出出众的水手。
如果你受苦了,感谢生活,那是它给你的一份感觉;如果你受苦了,感谢上帝,说明你还活着。人们的灾祸往往成为他们的学问。
Image
② 综合①②得抛物线的标准方程为:
y2=3x或y2=-3x
三、巩固提升
补充题
如图,已知△AOB的一个顶点为抛物线 y2=2x的顶点O,A、B两点都在抛物线上, 且∠AOB=90O. (1)证明:直线AB必过一定点. (2)求△AOB面积的最小值.
能把在面前行走的机会抓住的人,十有八九都会成功。 人生的重大决定,是由心规划的,像预先计算好的框架,等待着你的星座运行。如期待改变我们的,首先要改变心的轨迹。 与其守成法,毋宁尚自然;与其求划一,毋宁展个性。——蔡元培 不要试图交到一个完美的朋友,也不要交到很多朋友。 如果不去加强并发展儿童的个人自尊感,就不能形成他的道德面貌。……教育技巧的全部诀窍就在于抓住儿童的这种上进心,这种道德上的自 勉。——苏霍姆林斯基 世界原本就不是属于你,因此你用不着抛弃,要抛弃的是一切的执著。万物皆为我所用,但非我所属。 最好的教育是以身作则。孩子们对谎言或虚伪非常敏感,极易察觉。如果他们尊重你依赖你他们就是在很小的时候也会同你合作。——甘地夫 人 当你的朋友向你倾吐胸襟的时候,你不要怕说出心中的“否”,也不要瞒住心中的“可”。 人不是坏的,只是习气罢了,每个人都有习气,只是深浅不同罢了。只要他有向善的心,能原谅的就原谅他,不要把他看做是坏人。 毁灭人只要一句话,培植一个人却要千句话,请你多口下留情。
2018学年高中数学选修1-1课件:第2章 圆锥曲线与方程2.3.2.1 精品

抛物线几何性质的应用
已知抛物线的焦点F在x轴上,直线l过F且垂直于x 轴,l与抛物线交于A,B两点,O为坐标原点,若△AOB的面积 为4,求此抛物线的标准方程.
[思路点拨] 求A,B的坐标 ―→ 求出弦长|AB| ―→ 写出△AOB的面积,利用面积列方程解
由题意,抛物线方程为 y2=2mx(m≠0),焦
解析: 抛物线 y2=10x 的焦点在 x 轴上,所以①不正确; 又抛物线 y2=10x 的准线为 x=-52,横坐标为 1 的点到焦点的距 离为:1+52=72≠6,所以③不正确;抛物线的通径长为:2p= 10≠5,所以④不正确.
设垂足为 C(2,1),则 kOC=12- -00=12,而连接垂足和焦点的斜 率为:052- -12=-2,由 2×-12=-1 可知两者垂直,适合题意.
合作探究 课堂互动
抛物线的标准方程与性质
对于顶点在原点的抛物线,给出下列条件: ①焦点在y轴上;②焦点在x轴上;③抛物线的横坐标为1 的点到焦点的距离等于6;④抛物线的通径长为5;⑤由原点向 过焦点的某条直线作垂线,垂足为(2,1). 适合抛物线y2=10x的条件是________.(要求填写合适条 件的序号) [思路点拨] 本题主要考查抛物线的简单几何性质,根据 抛物线的几何性质,用排除法解决问题.
解析: (1)焦点是 F(-8,0),准线是 x=8,表明抛物线顶点 在原点,焦点在 x 轴负半轴,故抛物线的标准方程可设为 y2=- 2px(p>0),所以 p=16.因此所求抛物线的标准方程为 y2=-32x.
(2)依题意,|OB|=8 3,∠BOy=30°. 设 B(x,y),则 x=|OB|sin 30°=4 3,y=|OB|cos 30°=12. 因为点 B(4 3,12)在 x2=2py 上, 所以(4 3)2=2p×12,解得 p=2. 故抛物线 E 的方程为 x2=4y.
2018版高中数学人教B版选修1-1学案:第二单元 2-3-2 抛物线的几何性质二 含答案 精品

2.3.2抛物线的几何性质(二)学习目标 1.掌握抛物线的几何特性.2.学会解决直线与抛物线相关的综合问题.知识点直线与抛物线的位置关系思考1直线与抛物线有哪几种位置关系?思考2若直线与抛物线只有一个交点,直线与抛物线一定相切吗?梳理(1)直线与抛物线的位置关系与公共点个数.(2)直线y-p)x+b2=0的解的个数.当k≠0时,若Δ>0,则直线与抛物线有________个不同的公共点;当Δ=0时,直线与抛物线有________个公共点;当Δ<0时,直线与抛物线________公共点.当k=0时,直线与抛物线的对称轴________________,此时直线与抛物线有________个公共点.类型一直线与抛物线的位置关系例1已知直线l:y=k(x+1)与抛物线C:y2=4x,问:k为何值时,直线l与抛物线C有两个交点,一个交点,无交点?反思与感悟 直线与抛物线交点的个数,等价于直线方程与抛物线方程联立得到的方程组解的个数.注意直线斜率不存在和得到的方程二次项系数为0的情况.跟踪训练1 平面内一动点M (x ,y )到定点F (0,1)和到定直线y =-1的距离相等,设M 的轨迹是曲线C .(1)求曲线C 的方程;(2)在曲线C 上找一点P ,使得点P 到直线y =x -2的距离最短,求出P 点的坐标; (3)设直线l :y =x +m ,问当实数m 为何值时,直线l 与曲线C 有交点?类型二 与弦长中点弦有关的问题例2 已知A ,B 为抛物线E 上不同的两点,若抛物线E 的焦点为(1,0),线段AB 恰被M (2,1)所平分.(1)求抛物线E 的方程; (2)求直线AB 的方程.反思与感悟 中点弦问题有两种解法:(1)点差法:将两个交点的坐标代入抛物线的方程,作差,由k =y 1-y 2x 1-x 2求斜率,再由点斜式求解.(2)传统法:设直线方程,并与抛物线的方程联立,消去x (或y )得关于y (或x )的一元二次方程,由根与系数的关系,得两根之和即为中点纵(或横)坐标的2倍,从而求斜率.跟踪训练2 已知抛物线y 2=6x ,过点P (4,1)引一条弦P 1P 2使它恰好被点P 平分,求这条弦所在的直线方程及|P 1P 2|.类型三 抛物线性质的综合应用命题角度1 抛物线中的定点(定值)问题例3 已知点A ,B 是抛物线y 2=2px (p >0)上的两点,且OA ⊥OB . (1)求两点的横坐标之积和纵坐标之积; (2)求证:直线AB 过定点.反思与感悟 在直线和抛物线的综合题中,经常遇到求定值、过定点问题,解决这类问题的方法很多,如斜率法、方程法、向量法、参数法等,解决这类问题的关键是代换和转化. 跟踪训练3 如图,过抛物线y 2=x 上一点A (4,2)作倾斜角互补的两条直线AB 、AC 交抛物线于B 、C 两点,求证:直线BC 的斜率是定值.命题角度2 对称问题例4 在抛物线y 2=4x 上恒有两点A ,B 关于直线y =kx +3对称,求k 的取值范围.反思与感悟 轴对称问题,一是抓住对称两点的中点在对称轴上,二是抓住两点连线的斜率与对称轴所在直线斜率的关系.跟踪训练4 已知抛物线y =-x 2+3上存在关于直线x +y =0对称的相异两点A ,B ,求A ,B 两点间的距离.1.过点P (0,1)与抛物线y 2=x 有且只有一个交点的直线有( ) A .4条 B .3条 C .2条D .1条2.已知点A (2,0),抛物线C :x 2=4y 的焦点为F ,射线F A 与抛物线C 相交于点M ,与其准线相交于点N ,则|FM |∶|MN |等于( ) A .2∶ 5 B .1∶2 C .1∶ 5D .1∶33.已知点A (-2,3)在抛物线C :y 2=2px 的准线上,过点A 的直线与C 在第一象限相切于点B ,设C 的焦点为F ,则直线BF 的斜率为( ) A.12B.23C.34D.434.过抛物线y 2=4x 的顶点O 作互相垂直的两弦OM 、ON ,则M 的横坐标x 1与N 的横坐标x 2之积为________.5.已知顶点在原点,焦点在x 轴上的抛物线截直线y =2x -4所得的弦长|AB |=35,求此抛物线的方程.求抛物线的方程常用待定系数法和定义法;直线和抛物线的弦长问题、中点弦问题及垂直、对称等可利用判别式、根与系数的关系解决;抛物线的综合问题要深刻分析条件和结论,灵活选择解题策略,对题目进行转化.答案精析问题导学 知识点思考1 三种:相离、相切、相交.思考2 不一定,当平行或重合于抛物线的对称轴的直线与抛物线相交时,也只有一个交点. 梳理 (1)有两个或一个 有且只有一个 无 (2)两 一 没有 平行或重合 一 题型探究例1 解 由方程组⎩⎪⎨⎪⎧y =k (x +1),y 2=4x ,消去y 得k 2x 2+(2k 2-4)x +k 2=0, Δ=(2k 2-4)2-4k 4=16(1-k 2). (1)若直线与抛物线有两个交点, 则k 2≠0且Δ>0, 即k 2≠0且16(1-k 2)>0, 解得k ∈(-1,0)∪(0,1). 所以当k ∈(-1,0)∪(0,1)时, 直线l 和抛物线C 有两个交点. (2)若直线与抛物线有一个交点, 则k 2=0或当k 2≠0时,Δ=0, 解得k =0或k =±1.所以当k =0或k =±1时,直线l 和抛物线C 有一个交点. (3)若直线与抛物线无交点, 则k 2≠0且Δ<0. 解得k >1或k <-1. 所以当k >1或k <-1时, 直线l 和抛物线C 无交点. 跟踪训练1 解 (1)x 2=4y . (2)设点P (x 0,x 204),点P 到直线y =x -2的距离为 |x 0-x 204-2|2=|x 204-x 0+2|2=14(x 0-2)2+12当x 0=2时,取得最小值,此时P (2,1).(3)由⎩⎪⎨⎪⎧x 2=4y ,y =x +m ,得x 2-4x -4m =0,Δ=42-4×(-4m )≥0,m ≥-1.所以当m ≥-1时,直线l 和曲线C 有交点. 例2 解 (1)由于抛物线的焦点为(1,0), 所以p2=1,p =2,所以抛物线的方程为y 2=4x . (2)设A (x 1,y 1),B (x 2,y 2), 则y 21=4x 1, ① y 22=4x 2,②且x 1+x 2=4,y 1+y 2=2. 由②-①得,(y 1+y 2)(y 2-y 1) =4(x 2-x 1), 所以y 2-y 1x 2-x 1=2.所以所求直线AB 的方程为 y -1=2(x -2), 即2x -y -3=0.跟踪训练2 解 方法一 由题意易知直线方程的斜率存在,设所求方程为y -1=k (x -4).由⎩⎪⎨⎪⎧y 2=6x ,y =kx -4k +1,得ky 2-6y -24k +6=0.当k ≠0时,Δ=62-4k (-24k +6)>0.①设弦的两端点P 1(x 1,y 1),P 2(x 2,y 2), ∴y 1+y 2=6k ,y 1y 2=6-24k k .∵P 1P 2的中点为(4,1), ∴6k =2,∴k =3,适合①式. ∴所求直线方程为y -1=3(x -4), 即3x -y -11=0,∴y 1+y 2=2,y 1·y 2=-22, ∴|P 1P 2|= 1+1k2(y 1+y 2)2-4y 1y 2 =1+1922-4×(-22)=22303. 方法二 设P 1(x 1,y 1),P 2(x 2,y 2).则y 21=6x 1,y 22=6x 2,∴y 21-y 22=6(x 1-x 2),又y 1+y 2=2,∴y 1-y 2x 1-x 2=6y 1+y 2=3, ∴所求直线的斜率k =3, 所求直线方程为y -1=3(x -4), 即3x -y -11=0.由⎩⎪⎨⎪⎧y =3x -11,y 2=6x ,得y 2-2y -22=0, ∴y 1+y 2=2,y 1y 2=-22, ∴|P 1P 2|= 1+1k2(y 1+y 2)2-4y 1y 2 = 1+19·22-4×(-22)=22303. 例3 (1)解 设点A ,B 的坐标分别为(x 1,y 1),(x 2,y 2), 则有k OA =y 1x 1,k OB =y 2x 2.因为OA ⊥OB ,所以k OA ·k OB =-1, 所以x 1x 2+y 1y 2=0.因为y 21=2px 1,y 22=2px 2, 所以y 212p ·y 222p+y 1y 2=0.因为y 1≠0,y 2≠0, 所以y 1y 2=-4p 2, 所以x 1x 2=4p 2.(2)证明 因为y 21=2px 1,y 22=2px 2,所以(y 1-y 2)(y 1+y 2)=2p (x 1-x 2), 所以y 1-y 2x 1-x 2=2p y 1+y 2,所以k AB =2py 1+y 2,故直线AB 的方程为 y -y 1=2py 1+y 2(x -x 1),所以y =2px y 1+y 2+y 1-2px 1y 1+y 2,即y =2px y 1+y 2+y 21-2px 1+y 1y 2y 1+y 2.因为y 21=2px 1,y 1y 2=-4p 2,所以y =2px y 1+y 2+-4p 2y 1+y 2,所以y =2py 1+y 2(x -2p ),即直线AB 过定点(2p,0).跟踪训练3 证明 方法一 设AB 的斜率为k ,则AC 的斜率为-k . AB :y -2=k (x -4)与y 2=x 联立得 y -2=k (y 2-4),即ky 2-y -4k +2=0. ∵y =2是此方程的一个解, ∴2y B =-4k +2k ,∴y B =1-2kk ,∴x B =y 2B =1-4k +4k 2k2, ∴B (1-4k +4k 2k 2,1-2k k ).∵k AC =-k ,∴以-k 代替k 代入B 点坐标得 C (1+4k +4k 2k 2,1+2k-k ).∴k BC =-1+2k k -1-2kk1+4k +4k 2k 2-1-4k +4k 2k 2=-14,为定值.方法二 设B (y 21,y 1),C (y 22,y 2),则k BC =y 2-y 1y 22-y 21=1y 2+y 1.∵k AB =y 1-2y 21-4=1y 1+2,k AC =y 2-2y 22-4=1y 2+2,由题意得k AB =-k AC , ∴1y 1+2=-1y 2+2,则y 1+y 2=-4, 则k BC =-14,为定值.例4 解 因为A ,B 两点关于直线y =kx +3对称, 所以可设直线AB 的方程为x =-ky +m . 设A (x 1,y 1),B (x 2,y 2),把直线AB 的方程代入抛物线方程, 得y 2+4ky -4m =0,设AB 的中点坐标为M (x 0,y 0), 则y 0=y 1+y 22=-2k ,x 0=2k 2+m .因为点M (x 0,y 0)在直线y =kx +3上, 所以-2k =k (2k 2+m )+3, 即m =-2k 3+2k +3k.因为直线AB 与抛物线y 2=4x 交于A ,B 两点, 所以Δ=16k 2+16m >0, 把m =-2k 3+2k +3k 代入,化简,得k 3+2k +3k <0,所以(k +1)·(k 2-k +3)k <0.因为k 2-k +3>0,所以k +1k <0,解得-1<k <0.跟踪训练4 解 由题意可设l :y =x +b ,把直线方程代入y =-x 2+3中, 得x 2+x +b -3=0. 设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=-1,y 1+y 2=x 1+b +x 2+b =(x 1+x 2)+2b =2b -1. 所以AB 的中点坐标为(-12,b -12),因为该点在直线x +y =0上. 所以-12+(b -12)=0,得b =1.所以|AB |=1+12|x 1-x 2| =2(x 1+x 2)2-4x 1x 2 =2(-1)2-4×(-2)=3 2. 所以A ,B 两点间的距离为3 2. 当堂训练 1.B2.C [如图所示,由抛物线定义知|MF |=|MH |,所以|MF |∶|MN |=|MH |∶|MN |. 由△MHN ∽△FOA , 则|MH ||HN |=|OF ||OA |=12, 则|MH |∶|MN |=1∶5, 即|MF |∶|MN |=1∶ 5.] 3.D 4.165.解 设所求抛物线方程为y 2=ax (a ≠0). A (x 1,y 1),B (x 2,y 2),由⎩⎪⎨⎪⎧y =2x -4,y 2=ax ,消去y ,得4x 2-(a +16)x +16=0, 由Δ=(a +16)2-256>0,得a >0或a <-32. 又∵x 1+x 2=a +164,x 1x 2=4,∴|AB |=(1+22)[(x 1+x 2)2-4x 1x 2] =35,即5[(a +164)2-16]=45,∴a =4或a =-36.∴所求抛物线的方程为y 2=4x 或y 2=-36x .。
2018年人教版数学选修1-1典型例题:抛物线的简单几何性质

2.3.2抛物线的简单几何性质【例1】(1)己知点A (-2,3)与抛物线y 2=2p x(p >0)的焦点的距离是5,则P = .(2)抛物线y 2=4x 的弦AB 垂直于x 轴,若|AB|=4,则焦点到AB 的距离为 .(3)己知直线x-y=2与抛物线y 2=4x 交于A 、B 两点,那么线段AB 的中点坐标是 .【例2】已知过抛物线y 2=2px (p >0)的焦点且斜率为1的直线交抛物线于A 、B 两点,点R 是含抛物线顶点O 的弧AB 上一点,求△RAB 的最大面积.【例3】顶点在原点,焦点在x 轴正半轴上的抛物线有一个内接直角三角形,直角顶点在原点,一条直角边O A 所在的直线方程为y =2x ,斜边AB 的长为5,求抛物线方程.33参考例1:【分析】(1)题中,由抛物线y 2=2p x 可得焦点坐标F (),由两点间距离公式得P 的方程,从而解出P 值. (2)题用到抛物线的对称性,由抛物线的对称性可设A (a,2),求出a 值即可求得点到AB 的距离.(3)题可利用直线方程与抛物线方程组成的方程组,并结合韦达定理求出AB 的中点坐标,【解】(1)由抛物线方程y 2=2p x 可得焦点坐标F (). 由题设得 又由P>0,可解得p=4.(2)由抛物线对称性,不妨设A (a,2).∴(2)2=4a.∴a=3.又抛物线y 2=4x 的焦点为F (1,0),∴焦点到AB 的距离为d=a-1=2.0,2p 30,2p .5)03()22(22=-+--p 33(3)列方程组 由①得x=2+y. ③将③代入②,可得y 2-4y-8=0. ④设A (x 1,y 1)、B (x 2,y 2),AB 中点为M (x,y ),根据韦达定理,由④得y 1+y 2=4.∴y==2,代入③得x=y+2=4.∴AB 的中点坐标为(4,2).【点拨】根据抛物线的简单几何性质求出所求题目中的未知量,原则上是越简单越好.例2:【分析】求RAB 的最大面积,因过焦点且斜率为1的弦长为定值,故可以|AB |为三角形的底,只要确定高的最大值即可.【解】设AB 所在的直线方程为y =x -. 将其代入抛物线y 2=2px ,得y 2-2py -p 2=0∴|AB |=|y 1-y 2|=·当过R 的直线l 平行于AB 且与抛物线相切时,△RAB 的面积有最大值. ⎩⎨⎧==-,4,22x y y x 221y y +2p 22p y y y y 44)(21221=-+① ②设直线l 方程为y =x +b .代入抛物线方程得y 2-2py +2pb =0由Δ=4p 2-8pb =0,得b =这时R (,p ).它到AB 的距离为h =p ∴△RAB 的最大面积为|AB |·h =p 2. 【点拨】求解抛物线中有关三角形的问题时要注意三角形的边所在直线过的特殊点,还有三角形中的定值.例3:【分析】可先设出抛物线方程,然后用待定系数法求p ,其中还要用到两点间距离公式.【解】如图所示,设抛物线方程为y 2=2px (p >0)由得:A (,p ) ∵O A ⊥O B∴直线O B 的方程为y =-x 2p 2p 22212⎩⎨⎧==px y x y 2222p 21由得:B (8p ,-4p ) ∵|AB |=5∴|AB |= ∴p = 所求抛物线方程为y 2=. 【点拨】在解决圆锥曲线方程问题时要注意应用以前学习过的平面几何的知识,使解题达到事半功倍的效果.⎪⎩⎪⎨⎧=-=pxy x y 2212335)4()28(22=++-p p p p 39132x 13394。
2018版高中数学选修1-1学案:第二章 2-4-2 抛物线的几
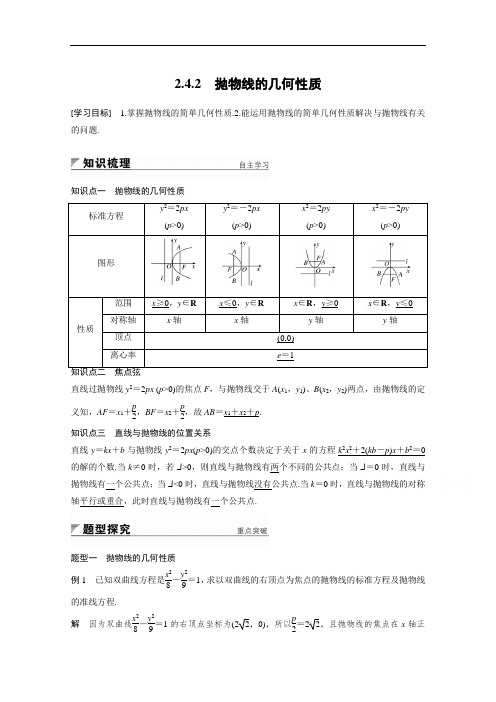
2.4.2抛物线的几何性质[学习目标] 1.掌握抛物线的简单几何性质.2.能运用抛物线的简单几何性质解决与抛物线有关的问题.知识点一抛物线的几何性质x≥0,y∈R x≤0,y∈R x∈R,y≥0x∈R,y≤0直线过抛物线y2=2px (p>0)的焦点F,与抛物线交于A(x1,y1)、B(x2,y2)两点,由抛物线的定义知,AF=x1+p2,BF=x2+p2,故AB=x1+x2+p.知识点三直线与抛物线的位置关系直线y=kx+b与抛物线y2=2px(p>0)的交点个数决定于关于x的方程k2x2+2(kb-p)x+b2=0的解的个数.当k≠0时,若Δ>0,则直线与抛物线有两个不同的公共点;当Δ=0时,直线与抛物线有一个公共点;当Δ<0时,直线与抛物线没有公共点.当k=0时,直线与抛物线的对称轴平行或重合,此时直线与抛物线有一个公共点.题型一抛物线的几何性质例1已知双曲线方程是x28-y29=1,求以双曲线的右顶点为焦点的抛物线的标准方程及抛物线的准线方程.解因为双曲线x28-y29=1的右顶点坐标为(22,0),所以p2=22,且抛物线的焦点在x轴正半轴上,所以,所求抛物线的标准方程为y 2=82x ,其准线方程为x =-2 2.反思与感悟 (1)注意抛物线各元素间的关系:抛物线的焦点始终在对称轴上,抛物线的顶点就是抛物线与对称轴的交点,抛物线的准线始终与对称轴垂直,抛物线的准线与对称轴的交点和焦点关于抛物线的顶点对称.(2)解决抛物线问题要始终把定义的应用贯彻其中,通过定义的运用,实现两个距离之间的转化,简化解题过程.跟踪训练1 已知抛物线的对称轴在坐标轴上,以原点为顶点,且经过点M (1,-2).求抛物线的标准方程和准线方程.解 (1)当抛物线的焦点在x 轴上时, 设其标准方程为y 2=mx (m ≠0). 将点M (1,-2)代入,得m =4. ∴抛物线的标准方程为y 2=4x . (2)当抛物线的焦点在y 轴上时, 设其标准方程为x 2=ny (n ≠0). 将点M (1,-2)代入,得n =-12.∴抛物线的标准方程为x 2=-12y .故所求的抛物线的标准方程为y 2=4x 或x 2=-12y .准线方程为x =-1或y =18.题型二 抛物线的焦点弦问题例2 已知抛物线方程为y 2=2px (p >0),过此抛物线的焦点的直线与抛物线交于A ,B 两点,且AB =52p ,求AB 所在的直线方程.解 由题意知焦点F ⎝⎛⎭⎫p 2,0,设A (x 1,y 1),B (x 2,y 2), 若AB ⊥x 轴,则AB =2p <52p ,不满足题意.所以直线AB 的斜率存在,设为k , 则直线AB 的方程为y =k ⎝⎛⎭⎫x -p2,k ≠0. 由⎩⎪⎨⎪⎧y =k ⎝⎛⎭⎫x -p 2,y 2=2px ,消去x ,整理得ky 2-2py -kp 2=0.由根与系数的关系得y 1+y 2=2pk,y 1y 2=-p 2. 所以AB =(x 1-x 2)2+(y 1-y 2)2 = ⎝⎛⎭⎫1+1k 2·(y 1-y 2)2 =1+1k2·(y 1+y 2)2-4y 1y 2=2p ⎝⎛⎭⎫1+1k 2=52p , 解得k =±2.所以AB 所在的直线方程为y =2⎝⎛⎭⎫x -p 2 或y =-2⎝⎛⎭⎫x -p2. 反思与感悟 (1)解决抛物线的焦点弦问题时,要注意抛物线定义在其中的应用,通过定义将焦点弦长度转化为端点的坐标问题,从而可借助根与系数的关系进行求解. (2)设直线方程时要特别注意斜率不存在的直线应单独讨论.跟踪训练2 已知直线l 经过抛物线y 2=6x 的焦点F ,且与抛物线相交于A 、B 两点. (1)若直线l 的倾斜角为60°,求AB 的值; (2)若AB =9,求线段AB 的中点M 到准线的距离. 解 (1)因为直线l 的倾斜角为60°, 所以其斜率k =tan 60°=3,又F ⎝⎛⎭⎫32,0. 所以直线l 的方程为y =3⎝⎛⎭⎫x -32. 联立⎩⎪⎨⎪⎧y 2=6x ,y =3⎝⎛⎭⎫x -32, 消去y 得x 2-5x +94=0.若设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=5, 而AB =AF +BF =x 1+p 2+x 2+p2=x 1+x 2+p . 所以AB =5+3=8.(2)设A (x 1,y 1),B (x 2,y 2),由抛物线定义知 AB =AF +BF =x 1+p 2+x 2+p2=x 1+x 2+p =x 1+x 2+3,所以x 1+x 2=6,于是线段AB 的中点M 的横坐标是3,又准线方程是x =-32,所以M 到准线的距离等于3+32=92.题型三 直线与抛物线的位置关系例3 已知直线l :y =kx +1,抛物线C :y 2=4x ,当k 为何值时,直线l 与抛物线C 有: (1)一个公共点; (2)两个公共点; (3)没有公共点.解 将直线l 和抛物线C 的方程联立得⎩⎪⎨⎪⎧y =kx +1,y 2=4x ,消去y ,得k 2x 2+(2k -4)x +1=0.(*)当k =0时,方程(*)只有一个解,为x =14,此时y =1.∴直线l 与抛物线C 只有一个公共点⎝⎛⎭⎫14,1,此时直线l 平行于x 轴. 当k ≠0时,方程(*)为一元二次方程,Δ=(2k -4)2-4k 2,①当Δ>0,即k <1且k ≠0时,直线l 与抛物线C 有两个公共点,此时直线l 与抛物线C 相交; ②当Δ=0,即k =1时,直线l 与抛物线C 有一个公共点,此时直线l 与抛物线C 相切; ③当Δ<0,即k >1时,直线l 与抛物线C 没有公共点,此时直线l 与抛物线C 相离. 综上所述,(1)当k =1或k =0时,直线l 与抛物线C 有一个公共点; (2)当k <1且k ≠0时,直线l 与抛物线C 有两个公共点; (3)当k >1时,直线l 与抛物线C 没有公共点.反思与感悟 直线与抛物线交点的个数,等价于直线方程与抛物线方程联立得到的方程组解的个数.注意直线斜率不存在和得到的方程二次项系数为0的情况.跟踪训练3 如图,过抛物线y 2=x 上一点A (4,2)作倾斜角互补的两条直线AB ,AC 交抛物线于B ,C 两点,求证:直线BC 的斜率是定值.证明 设k AB =k (k ≠0), ∵直线AB ,AC 的倾斜角互补, ∴k AC =-k (k ≠0),∴直线AB 的方程是y =k (x -4)+2.由方程组⎩⎪⎨⎪⎧y =k (x -4)+2,y 2=x ,消去y 后,整理得k 2x 2+(-8k 2+4k -1)x +16k 2-16k +4=0. ∵A (4,2),B (x B ,y B )是上述方程组的解.∴4·x B =16k 2-16k +4k 2,即x B =4k 2-4k +1k 2.以-k 代换x B 中的k ,得x C =4k 2+4k +1k 2,∴k BC =y B -y C x B -x C =k (x B -4)+2-[-k (x C -4)+2]x B -x C=k (x B +x C -8)x B -x C =k (8k 2+2k 2-8)-8kk 2=-14.∴直线BC 的斜率为定值.分类讨论思想的应用例4 已知顶点在原点,焦点在x 轴上的抛物线被直线y =2x +1截得的弦长为15,求抛物线的标准方程.分析 由于抛物线的开口有两种可能性:向左或向右,其标准方程可以设为y 2=2px (p >0)或y 2=-2px (p >0).解 设直线和抛物线相交于点A (x 1,y 1),B (x 2,y 2). (1)当抛物线开口向右时,设抛物线的标准方程为y 2=2px (p >0),则⎩⎪⎨⎪⎧y 2=2px ,y =2x +1,消去y ,得4x 2-(2p -4)x +1=0. 所以x 1+x 2=p -22,x 1x 2=14.AB =(x 1-x 2)2+[(2x 1+1)-(2x 2+1)]2 =5·(x 1-x 2)2 =5·(x 1+x 2)2-4x 1x 2 =5·(p -22)2-4×14=15, 则p 24-p =3,整理,得p 2-4p -12=0, 解得p =-2(负值舍去)或p =6, 故抛物线的标准方程为y 2=12x .(2)当抛物线开口向左时,设抛物线的标准方程为 y 2=-2p 1x (p 1>0),同理可得p 1=2,此时所求抛物线的标准方程为y 2=-4x .综上所述,抛物线的标准方程为y 2=-4x 或y 2=12x .解后反思 分类讨论思想在解决抛物线问题时经常用到,如对抛物线的开口方向进行讨论,对直线的斜率是否存在进行讨论,对判别式Δ的取值范围进行讨论等.1.以x 轴为对称轴的抛物线的通径(过焦点且与对称轴垂直的弦)长为8,若抛物线的顶点在坐标原点,则其方程为__________________. 答案 y 2=8x 或y 2=-8x解析 设抛物线y 2=2px 或y 2=-2px (p >0), 依题意得x =p2,代入y 2=2px 或y 2=-2px ,得|y |=p ,∴2|y |=2p =8,p =4. ∴抛物线方程为y 2=8x 或y 2=-8x .2.若抛物线y 2=x 上一点P 到准线的距离等于它到顶点的距离,则点P 的坐标为____________. 答案 (18,±24)解析 由题意知,点P 到焦点F 的距离等于它到顶点O 的距离,因此点P 在线段OF 的垂直平分线上,而F (14,0),所以点P 的横坐标为18,代入抛物线方程得y =±24,故点P 的坐标为(18,±24). 3.抛物线y =4x 2上一点到直线y =4x -5的距离最短,则该点坐标为__________. 答案 (12,1)解析 因为y =4x 2与y =4x -5不相交,设与y =4x -5平行的直线方程为y =4x +m .则⎩⎪⎨⎪⎧y =4x 2,y =4x +m ,⇒4x 2-4x -m =0.① 设此直线与抛物线相切,此时有Δ=0, 即Δ=16+16m =0,∴m =-1. 将m =-1代入①式,x =12,y =1,故所求点的坐标为(12,1).4.经过抛物线y 2=2x 的焦点且平行于直线3x -2y +5=0的直线l 的方程是____________. 答案 6x -4y -3=0解析 设直线l 的方程为3x -2y +c =0,抛物线y 2=2x 的焦点F (12,0),所以3×12-2×0+c=0,所以c =-32,故直线l 的方程是6x -4y -3=0.5.已知直线x -y +1=0与抛物线y =ax 2相切,则a =________. 答案 -14解析 由⎩⎪⎨⎪⎧x -y +1=0,y =ax 2,消去y 得ax 2-x -1=0, ∵直线与抛物线相切,∴a ≠0且Δ=1+4a =0. ∴a =-14.1.讨论抛物线的几何性质,一定要利用抛物线的标准方程;利用几何性质,也可以根据待定系数法求抛物线的方程.2.直线与抛物线的相交弦问题共有两类,一类是过焦点的弦,一类是不过焦点的弦.解决弦的问题,大多涉及到抛物线的弦长、弦的中点、弦的斜率.常用的办法是将直线方程与抛物线方程联立,转化为关于x 或y 的一元二次方程,然后利用根与系数的关系,这样避免求交点.尤其是弦的中点问题,还应注意“点差法”的运用.3.判断直线与抛物线位置关系的两种方法(1)几何法:利用图象,数形结合,判断直线与抛物线的位置关系,但有误差影响判断的结果. (2)代数法:设直线l 的方程为y =kx +m ,抛物线的方程为y 2=2px (p >0),将直线方程与抛物线方程联立整理成关于x (或y )的一元二次方程形式:Ax 2+Bx +C =0(或Ay 2+By +C =0).相交:①有两个交点:⎩⎪⎨⎪⎧A ≠0,Δ>0;②有一个交点:A =0(直线与抛物线的对称轴平行或重合,即相交);相切:有一个公共点,即⎩⎪⎨⎪⎧A ≠0,Δ=0;相离:没有公共点,即⎩⎪⎨⎪⎧A ≠0,Δ<0.直线与抛物线有一个交点,是直线与抛物线相切的必要不充分条件.。
人教A版选修1-1教案:抛物线的几何性质(1)(含答案)

§2.3.2 拋物線的幾何性質(1)【學情分析】:由於學生具備了曲線與方程的部分知識,掌握了研究解析幾何的基本方法,因而利用已有橢圓與雙曲線的知識,引導學生獨立發現、歸納知識,指導學生在實踐和創新意識上下工夫,訓練基本技能。
【教學目標】:(1)知識與技能:熟練掌握拋物線的範圍,對稱性,頂點,准線,離心率等幾何性質。
(2)過程與方法:重視基礎知識的教學、基本技能的訓練和能力的培養;啟發學生能夠發現問題和提出問題,善於獨立思考。
(3)情感、態度與價值觀:培養嚴謹務實,實事求是的個性品質和數學交流合作能力,以及勇於探索,勇於創新的求知意識,激發學生學習數學的興趣與熱情。
【教學重點】:熟練掌握拋物線的範圍,對稱性,頂點,准線,離心率等幾何性質。
【教學難點】:熟練掌握拋物線的範圍,對稱性,頂點,准線,離心率等幾何性質及其應用。
【課前準備】:Powerpoint或投影片三、例題講解例 1 已知拋物線的頂點在原點,對稱軸為坐標軸,且過點A(4,23),求這條拋物線的准線方程。
解:⑴若拋物線開口向右,設拋物線的標準方程為22(0)y px p=>∵()22324p=∴32p=∴拋物線的標準方程為34x=-⑵若拋物線開口向上,設拋物線的標準方程為22(0)x py p=>∵24223p=∴433p=∴拋物線的標準方程為233y=-例2 汽車前燈反射鏡與軸截面的交線是拋物線的一部分,燈口所在的圓面與反射鏡的軸垂直,燈泡位於拋物線焦點處。
已知燈口的直徑是24cm,燈深10cm,那麼燈泡與反射鏡的頂點距離是多少?讓學生運用拋物線的幾何性質,寫出符合條件的拋物線的准線方程。
三、例題講解分析:依標準方程特點和幾何性質建系,由待定係數法求解,強調方程的完備性。
解:如圖,在探照燈的軸截面所在平面內建立直角坐標系,使反光鏡的頂點(即拋物線的頂點)與原點重合,軸垂直於燈口直徑.拋物線的標準方程為22(0)y px p=>,由已知條件可得點的座標是(40,30)且在拋物線上,代入方程得:230240p=,254p=所以所求拋物線的標準方程為2452y=,焦點座標是運用拋物線的幾何性質解決現實生活中的問題,提高學生學習數學的興趣和綜合解題能力。
(新课标人教A版)选修1-1数学同步课件:2-3-1《抛物线及其标准方程》
p 方法二:设直线 l 的方程为 x=ky+2, p x=ky+ 2 得 y2-2pky-p2=0, 由 2 y =2px
2 2 2 y y y y p 1 2 1 2 则 y1· y2=-p2,x1x2= = 2p 2= . 2p 2p 4
由题意知,点 A(4,-5)在抛物线 x2=-2py(p>0)上, 16 所以 16=-2p×(-5),2p= 5 . 16 所以抛物线方程为 x =- y. 5
2
水面上涨,船面两侧与抛物线拱桥接触于 B,B′时,船 开始不能通航. 16 5 设 B(2,y′).由 2 =- 5 ×y′,所以 y′=-4.
已知抛物线的顶点在原点,对称轴为x轴,抛物线上的
点M(3,m)到焦点的距离等于5,求抛物线的方程和m的
值.
[解析] 点
p F2,0,
解法一: 设抛物线方程为 y2=2px(p>0), 则焦
m2=6p 由题设可得 p2 2 m +3-2 =5
p>0)的焦点坐标是0,-2,准
p 线方程是 y=2 .
3.过抛物线焦点的直线与抛物线相交,被抛物线所截
得的线段,称为抛物线的 焦点弦 . 4.通过抛物线的焦点作垂直于坐标轴而交抛物线于 A、 B两点的线段,称为抛物线的通径,通径|AB|的长等于 .
1 依题意有 P′(1,-1)在此抛物线上,代入得 p=2. 故得抛物线方程为 x2=-y. 又 B 在抛物线上,将 B(x,-2)代入抛物线方程得 x = 2,即|AB|= 2,则|AB|+1= 2+1, 因此所求水池的直径为 2(1+ 2)m,约为 5m, 即水池的直径至少应设计为 5m.
高中数学人教版选修1-1:2.3.2-3 抛物线的简单几何性质 课件(共8张PPT)优质课件PPT
嘲式幽默。抱一种打趣的心情来对待自己做不好的事情,一旦做起来了尽管乐在其中。所以,这次犯错,是为了下次接受挑战后,要尽量放松。在脑电波开始平和你的中枢神经系统时,你可感受到自己的内在动力在不断增加。你很快会知道自己有何
气。事过境迁,面对人生,面对社会,面对工作,一切的未来都需要自己去把握。人一定要靠自己。命运如何眷顾,都不会去怜惜一个不努力的人,更不会去同情一个懒惰的人,一切都需要自己去努力。谁都不可能一生一世的帮你,一时的享受也只
的快速发展,各行各业的疲软,再加上每年几百万毕业生涌向社会,社会生存压力太大,以至于所有稍微有点意识的年轻人都想努力提高自己。看着身边一个个同龄人那么优秀,看着朋友圈的老同学个个事业有成、买房买车,我们心急如梵,害怕被 绕着越来越多的年轻人,我们太想改变自己,太想早一日成为自己梦想中的那个自己。收藏各种技能学习资料,塞满了电脑各大硬盘;报名流行的各种付费社群,忙的人仰马翻;于是科比看四点钟的洛杉矶成为大家励志的手段,纷纷开始早起打卡行
② 综合①②得抛物线的标准方程为:
y2=3x或y2=-3x
三、巩固提升
补充题
如图,已知△AOB的一个顶点为抛物线 y2=2x的顶点O,A、B两点都在抛物线上, 且∠AOB=90O. (1)证明:直线AB必过一定点. (2)求△AOB面积的最小值.
•我们很容易遭遇逆境,也很容易被一次次的失败打垮。但是人生不容许我们停留在失败的瞬间,如果不前进,不会自我激励的话,就注定只能被这个世界抛弃。自我激励能力是人自我调节系统中重要的组成部分,主要表现在对于在压力或者困境中
2018年秋人教B版数学选修1-1 2.3.1抛物线及其标准方程练习含解析
2.3抛物线2.3.1抛物线及其标准方程课时过关·能力提升1.抛物线y2=12x的焦点坐标是()A.(12,0)B.(6,0)C.(3,0)D.(0,3)答案: C2.经过点(2,-3)且焦点在x轴正半轴上的抛物线的标准方程是()A.y.yC.y2=.y2=4x答案:B3.抛物线yA.x.xC.x=.x=答案:D4.已知圆(x-a)2+(y-b)2=r2的圆心为抛物线y2=4x的焦点,且该圆与直线3x+4y+2=0相切,则该圆的方程为()A.(x-1)2+y.x2+(y-1C.(x-1)2+y2=1D.x2+(y-1)2=1答案:C5.设点P是抛物线y2=16x上的点,它到焦点的距离h=10,则它到y轴的距离d等于()A.3B.6C.9D.12解析:设点P到抛物线y2=16x的准线的距离为l.由抛物线y2=16x.由抛物线定义知l=h,又l=d d=l-4=6.答案:B6.设定y2=2x上的点P之间的距离为d1,点P到抛物线准线l的距离为d2,则d1+d2取最小值时,点P的坐标为()A.(0,0)B.(1C.(2,2) D解析:连接PF,则d1+d2=|PM|+|PF|≥|MF|,知d1+d2的最小值是|MF|,当且仅当M,P,F三点共线时,等号成立,而直线MF的方程为y y2=2x联立求得x=2,y=2;x y=),此时,点P的坐标为(2,2).答案:C7.动点P到点F(2,0)的距离与它到直线x+2=0的距离相等,则点P的轨迹方程为.答案:y2=8x8.抛物线x=2y2的焦点坐标是.答案9. 已知y2=2px(p>0),求满足下列条件的抛物线的标准方程.(1)焦点为直线3x+4y-12=0与x轴的交点;(2)焦点到直线x=-5的距离是8.解: (1)直线与x轴的交点为(4,0),则=4,∴p=8,∴方程为y2=16x.(2)焦点在x轴上,设为,∴+5=8,解得=3,则其焦点为(3,0),∴p=6,故方程为y2=12x或y2=-52x.★10.如图,已知直线AB是抛物线y2=2px(p>0)的焦点弦,F是抛物线的焦点,点A(x1,y1),B(x2,y2),求证:(1)y1y2=-p2,x1x(2)|AB|=x1+x2+pθ为直线AB的倾斜角);(3.分析:设出直线AB的方程并与抛物线方程联立,借助一元二次方程根与系数的关系、抛物线的定义求解.证明:(1)由已知,得焦点F,当直线AB的斜率存在时,设直线AB的方程为y=k(k≠0),由消去x,得ky2-2py-kp2=0.①由一元二次方程根与系数的关系,得y1y2=-p2,y1+y2=.又由y=k,得x=y+,故x1x2=y1y2+(y1+y2)+(-p2)+.当直线AB的斜率不存在时,直线AB的方程为x=,则y1=p,y2=-p,则y1y2=-p2,x1x2=.综上,y1y2=-p2,x1x2=.(2)当直线AB的斜率存在时,由抛物线的定义知,|AF|=x1+,|BF|=x2+,∴|AB|=|AF|+|BF|=x1+x2+p.②又y=k(k≠0),∴x=y+,∴x1+x2=(y1+y2)+p.由①知y1+y2=,∴x1+x2=+p,代入②得|AB|=+2p=2p=2p.当直线AB的斜率不存在,即θ=时,A,B,|AB|=2p=+p=.综上,|AB|=x1+x2+p=.(3)=,将x1x2=,x1+x2=|AB|-p,代入上式,得.故为定值.。
2018年人教版数学选修1-1拓展资料:解析常用逻辑用语中的几个错解
解析常用逻辑用语中的几个错解本文对高中数学《常用逻辑用语》这一部分易错的几个问题的成因进行归纳和分析,整理.希望对读者的学习起一些帮助.[例1]把命题“全等三角形一定相似”写成“若p则q”的形式,并写出它的逆命题、否命题与逆否命题.错解:原命题可改写成:若两个三角形全等,则它们一定相似.逆命题:若两个三角形相似,则它们全等.否命题:若两个三角形不一定全等,则它们不一定相似.逆否命题:若两个三角形不一定相似,则它们不一定全等.错因:对“一定”的否定把握不准,“一定”的否定“一定不”,在逻辑知识中求否定相当于求补集,而“不一定”含有“一定”的意思.对这些内容的学习要多与日常生活中的例子作比较,注意结合集合知识.因而否命题与逆否命题错了.正解:否命题:若两个三角形不全等,则它们不相似.逆否命题:若两个三角形不相似,则它们不全等.[例2]将下列命题改写成“若p则q”的形式,并写出否命题.a>o时,函数y=ax+b的值随x值的增加而增加.错解:原命题改为:若a>o时,x的值增加,则函数y=ax+b的值也随着增加.错因:如果从字面上分析最简单的方法是将a>o看作条件,将“随着”看作结论,而x的值增加,y的值也增加看作研究的对象,那么原命题改为若a>o时,则函数y=ax+b的值随着x的值增加而增加,其否命题为若a o时,则函数y=ax+b的值不随x 值的增加而增加.此题错解在注意力集中在“增加”两个字上,将x 值的增加当做条件,又不把a>o 看作前提,就变成两个条件的命题,但写否命题时又没按两个条件的规则写,所以就错了.正解:原命题改为: a>o 时,若x 的值增加,则函数y=ax+b 的值也随着增加.否命题为: a>o 时,若x 的值不增加,则函数y=ax+b 的值也不增加. 原命题也可改为:当x 的值增加时,若a>o ,,则函数y=ax+b 的值也随着增加.否命题为:当x 增加时,若a ≤o ,则函数y=ax+b 的值不增加.[例3] 已知h>0,设命题甲为:两个实数a 、b 满足h b a 2<-,命题乙为:两个实数a 、b 满足h a <-|1且h b <-|1,那么A .甲是乙的充分但不必要条件B .甲是乙的必要但不充分条件C .甲是乙的充要条件D .甲是乙的既不充分也不必要条件 错解:h b a 2<-⇔h h h b a +=<---2)1()1(⇔h a <-|1|,h b <-|1|,故本题应选C.错因:(1)对充分、必要、充要条件的概念分不清,无从判断,凭猜测产生错误;(2)不能运用绝对值不等式性质作正确推理而产生错误.正解:因为,11⎪⎩⎪⎨⎧<-<-hb h a 所以,11⎩⎨⎧<-<-<-<-h b h h a h 两式相减得h b a h 22<-<- 故h b a 2<-即由命题甲成立推出命题乙成立,所以甲是乙的必要条件. 由于⎪⎩⎪⎨⎧<-<-hb h a 22 同理也可得h b a 2<-因此,命题甲成立不能确定命题乙一定成立,所以甲不是乙的充分条件,故应选B.[例4] 已知命题甲:a+b ≠4, 命题乙:a 1≠且b 3≠,则命题甲是命题乙的 .错解:由逆否命题与原命题同真同假知,若a=1且b=3则a+b=4成立,所以命题甲是命题乙的充分不必要条件.错因 :对命题的否定不正确.a 1≠且b 3≠的否定是a=1或b=3.正解:当a+b ≠4时,可选取a=1,b=5,故此时a 1≠且b 3≠不成立( a=1). 同样,a 1≠,且b 3≠时,可选取a=2,b=2,a+b=4,故此时a+b=4.因此,甲是乙的既不充分也不必要条件.注:a 1≠且b 3≠为真时,必须a 1≠,b 3≠同时成立.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
抛物线反射镜和汽车前灯
你知道吗?当把汽车的前灯开关从亮转到暗时,就有数学在起作用。具体地
说,是抛物线原理在玩花招。
如果你留心会发现,汽车前灯后面的反射镜呈抛物线的形状。事实上,它们
是抛物面(抛物线①环绕它的对称轴旋转形成的三维空间中的曲面)。明亮的光束
是由位于抛物线反射镜焦点上的光源产生的。
因此,光线沿着与抛物线的对称轴平行的方向射出。当光变暗时,光源改变
了位置。它不再在焦点上,结果光线的行进不与轴平行。现在近光只向上下射出。
向上射出的被屏蔽,所以只有向下射出的近光,射到比远光所射的距离短的地方。
抛物线是一种古老的曲线,它是梅内克缪斯(约公元前375~前325)在试图
解决用尺规作出体积为给定立方体两倍的立方体时发现的。
多少世纪以来,人类已经得到了有关抛物线的一些新的用途和发现。例如,
伽利略(1564~1642)证明抛射体的路线是抛物线。今天人们可以到五金店去买
一台高能效抛物线电热器,它只用1000瓦,但是与用1500瓦的电热器产生同样
多的热量。
注①:抛物线是平面内与称做它的焦点的定点和称做它的准线的定直线等距
离的所有点的集合。
