初中八年级的数学平行四边形、矩形、菱形.doc
初中八年级下册数学1822 菱形(第1课时)课件q

B
C 第4题图
4.如图,菱形ABCD的周长为48cm,对角线AC , BD相交于O点,
E是AD的中点,连接OE,则线段OE的长为___6_cm___.
18.2 特殊的平行四边形/
5.如图,在菱形ABCD中,点O为对角线AC与BD的交点,且在 △AOB中,OA=5,OB=12.求菱形ABCD两对边的距离h.
A
D
O
B
C
∴∠ABC= ×180°=60°,∴∠ABO= ×∠ABC=30°.
∴△ABC是等边三角形.
18.2 特殊的平行四边形/
∵菱形ABCD的周长是8cm. ∴AB=2cm. ∴OA= AB=1cm,AC=AB=2cm.
∴
.
∴BD=2OB= 2 3cm;
(2)S菱形ABCD =
1 AC•BD
2
A.24m
B.12m
C.96m
D.48m
18.2 特殊的平行四边形/
知识点 3 菱形对角线的性质 观察:将一张长方形的纸对折、再对折,然后沿图中的虚 线剪下,打开即得一个菱形.
操作:在自己剪出的菱形上画出两条折痕,折叠手中的图 形(如图),并回答以下问题:
18.2 特殊的平行四边形/
问题1 菱形是轴对称图形吗?如果是,指出它的对称轴. 是,两条对角线所在直线都是它的对称轴.
对边相等
对边相等
四边相等
对角相等 四个角都是直角 对角相等
对角线互相平分
对角线互 相平分且 相等
两条对角线互相 垂直平分,并且 每一条对角线平 分一组对角
18.2 特殊的平行四边形/
考点 1 利用菱形的性质求线段的长 如图,在菱形ABCD中,对角线AC,BD相交于点O,BD=12cm, AC=6cm,求菱形的周长. 解:∵四边形ABCD是菱形, ∴AC⊥BD,AO= AC,BO= BD. ∵AC=6cm,BD=12cm, ∴AO=3cm,BO=6cm. 在Rt△ABO中,由勾股定理,得
中考数学复习⑦ 平行四边形及矩形、菱形、正方形存在性问题探究

中考数学复习⑦ 平行四边形及矩形、菱形、正方形存在性问题探究在平行四边形的存在性问题中,常会遇到两类探究性的问题。
第一类问题是已知三点的位置,在二次函数上或在坐标平面内找一动点,使这四点构成平行四边形(简称“三定一动”)。
第二类问题是已知两个点的位置,在二次函数上或在坐标平面内找两个动点,使这四点构成平行四边形(简称“两定两动”)。
平行四边形的这四个点有可能是定序的,也有可能没有定序。
在解决这些问题时,容易出现遗漏或方法不当或错解的情况。
因此,需要分清题型并分类讨论且作图,利用几何特征计算,并灵活运用平移坐标法等解题技巧。
可以把存在性问题的基本思路叫做“三步曲”:一“分”二“作”三“算”。
对于“三定一动”,要找出平行四边形第四个顶点,则符合条件的有3个点。
这三个点的找法是以三个定点为顶点画三角形,过每个顶点画对边的平行线,三条直线两两相交,产生所要求的3个点。
对于“两定两动”,要找出平行四边形第三、四个顶点,将两个定点连成定线段,将此线段按照作为平行四边形的边或对角线两种分类讨论。
如果平行四边形的四个顶点都能用坐标来表示,则可以直接利用坐标系中平行四边形的基本特征:即对边平行且相等或对边水平距离相等和竖直距离相等列方程求解。
如果平行四边形的四个顶点中某些点不能用坐标表示,则可以利用列方程组解图形交点的方法解决。
此外,还可以灵活运用平行四边形的中心对称的性质,或者使用平移坐标法。
平移坐标法的具体步骤是先由题目条件探索三点的坐标(若只有两个定点,可设一个动点的坐标),再画出以三点为顶点的平行四边形,根据坐标平移的性质写出第四个顶点的坐标。
最后根据题目的要求(动点在什么曲线上),判断平行四边形的存在性。
除了平行四边形,矩形、菱形和正方形也有存在性问题。
对于矩形,增加对角线相等和邻边垂直的性质,还可以转化为直角三角形的存在性问题。
对于菱形,增加四边相等和对角线垂直的性质,还可以转化为直角三角形或等腰(等边)三角形的存在性问题。
八年级数学平行四边形矩形菱形
B 方案五C
B 方案六 C
过对角线交点的任一条直线都将平行四边形 返回 小结 分成面积相等的两部分
在上述问题中,小明看到菜 地中间有一水井,为了浇水 的方便,小明建议妈妈经过水井修小路, 一样可以把菜地分成面积相等的两部分, 同学们,你知道聪明的小明是怎么帮妈 妈分的吗?
A D
●
M
B
C
问题9:如图 在ABC中,AD平分∠BAC,点 M,E,F分别是AB,AD,AC上的点,四边形BEFM是平 行四边形. 求证:AF=BM
问题4:思 考 在矩形ABCD中,AB=16,BC=8.将
矩形沿AC折叠,点D落在点E处,且 CE交AB于点F,求AF的长.
D
点拨:对于折叠 C
问题,可以从折叠前 后的两个图形是全等 图形入手进行分析.
A E
F
B
如图, EF 过 ABCD 的对角 问题 5: 线AC、BD的交点O,△AOE 与△COF的面积有何关系?四边形AEFD与 四边形BCFE的面积有何关系?
证明: ∵ 四边形BEFM是平行四边形 A ∴BM=EF AB//EF
∵ AD平分∠BA F E B D C ∴∠BAD=∠CAD ∵AB//EF ∴ ∠BAD=∠AEF ∴∠CAD =∠AEF ∴ AF=EF
M
∴ AF=BM
已知:如图,AD平分∠BAC,DE∥AC 交AB于E,DF∥AB交AC于F. 求证:EF⊥AD;
看女鬼姑姑一副要找自己算后账的模样,心里招架不住,才想撒泼找由头的。此时,看陆婉娉不言语,她可不敢触这个姑姑的逆鳞。公孙 公子似乎是自来熟,并没有把自己当成外人,更没把他自己当成所谓的贵客。虽然对于这个做饭程序不太了解,但感觉自己勉强打个下手 还是可以的。以前女鬼大人独居的时候,是从来不做肉/食的,偶尔吃点海鲜,她一向是个素食主义者,可所有这一切并不代表她对肉食无 甚研究,只要她高兴,没有做不出来的满分食物。只不过,杀活物亦或是处理内脏之类的杂事儿,可从来都不曾涉及。夜叉看到肉/食连生 的都想直接吞下,若不是跟着自己时日久了,充分感觉到了吃她这个姑姑做熟的食物远比吃生的要好吃,所以也渐渐脱离了茹/毛饮血的生 活。夜叉跑开了,那剩下拨/毛处理内/脏的事儿谁来做?那位显然不太熟悉厨房工艺的公孙公子,此时却不做客人,毫不含糊地鲁胳膊挽 袖子的亲自上场,只听得一声声“撕啦撕啦”的声音响过之后。再去看,一只鸡倒是整理干净了,不过,鸡是连皮带毛的去皮除的顺带还 掠走了若干鸡/肉,内脏就更好说了,直接一掌劈开,“唏哩划啦”的,再看一整只鸡,充其量剩下的也不过一半儿,而且还是一小半儿。 陆婉娉嘴角抽抽了几下,指着那只被剥了皮的半拉生鸡,“公孙公子,地主家也不能这么浪费啊!”“呃,失误,失误,要不我再去买一 只去。”不满意夜叉的得瑟,可面对女鬼大人,这位公孙公子是没来由的腼腆。“算了,反正你也不是故意的,还不算太坏,好歹这上边 还沾着不少肉/丝,马马虎虎吧!”陆婉娉挑剔地伸手捡起那只原本肥得流油,现在跟只鸽子似的被扒了皮的肉/鸡,她是真的感觉非常之 无语了。陆婉娉虽然心情不好,也很生气,但总不能真的让公孙公子一个大男人在厨房“呼哧呼哧”的拉风箱以及给自己帮忙烧饭吧!何 况,她还很怀疑这位公孙公子拉风箱的能力,在这儿呆着只能给她添乱。于是乎,连推带搡的将他送至前厅,让黄大哈咯陪着喝茶了。陆 婉娉是从未来被孟婆大人给直接扔过来的,因着对于未来一些知识掌握的还算是得心应手。本着有些资源浪费是可耻的犯罪的原则,女鬼 大人做饭虽然没用天然气之类的原能料,用的可是比这些更高级更节能更环保的太阳能鼓风设备,用这些先进的设备替代人拉风箱,只要 适时填一把碳就OK了。一顿饭在陆婉娉的手下如变戏法一样变了出来,还未上桌,后院的夜叉就跑了出来,敢情这个吃货是闻着味儿来的。 显然,厅堂外的黄大哈咯与公孙公子二人是相谈甚欢,也不晓得二人在聊什么,总是时不时传来黄大哈咯约略有些作做的娇笑声。莫名其 妙的,陆婉娉内心里听得这样的笑声,竟然有了一丝那么她自己都不愿意承认的不快。第016章 赶
华师版八年级下册数学精品教学课件 第19章 矩形、菱形与正方形 第1课时 菱形的性质

角线互相垂直,那么能否利用对角线 C
来计算菱形 ABCD 的面积呢?
问题2 如图,四边形 ABCD 是菱形,对角线 AC,
BD 交于点 O,试用对角线表示出菱形 ABCD 的面积.
解:∵四边形 ABCD 是菱形,
A
∴AC⊥BD.
∴S菱形ABCD = S△ABC + S△ADC = 1 AC·BO + 1 AC·DO
第19章 矩形、菱形与正方形
19.2 菱形
1. 菱形的性质
第1课时 菱形的性质
情景引入 欣赏下面图片,图片中框出的图形是你熟悉的吗?
菱形的性质 前面我们学习了平行四边形和矩形,知道了矩 形是由平行四边形角的变化得到,如果平行四边 形有一个角是直角时,就成为了矩形.
平行 四边形
有一个角是直角
矩形
思考 如果从边的角度,将平行四边形特殊化,内 角大小保持不变仅改变边的长度让它有一组邻边相 等,这个特殊的平行四边形叫什么呢?
(2)菱形ABCD的面积
5. 如图,四边形 ABCD 是菱形,F 是 AB 上一点,
DF 交 AC 于 E. 求证:∠AFD = ∠CBE.
证明:∵四边形 ABCD 是菱形,
∴CB = CD, CA 平分∠BCD. ∴∠BCE = ∠DCE. 又 CE = CE, ∴△BCE≌△DCE(S.A.S.). C
O
C
同理可证∠DCA =∠BCA,
∠ADB =∠CDB,∠ABD =∠CBD.
D
归纳总结 菱形是特殊的平行四边形,它除具有平行四边形的
所有性质外,还有平行四边形所没有的特殊性质.
菱形的特殊性质
平行四边形的性质
对称性:是轴对称图形. 边:四条边都相等. 对角线:互相垂直,且每 条对角线平分一组对角.
1.3平行四边形,矩形,菱形,正方形的性质和判定2

有一个角是600的______三角形是等边三角形;
试试看
练习;课本P16:练习1;
再提高一下吧.
例三;
回头再看看
两组对边分别_____四边形叫做矩形;根据矩形
பைடு நூலகம்
的定义可知,矩形一定是______(图形名称),所 以具备这类图形的所有性质,而且必定有一个角 是_____; 性质定理一:矩形的四个角都是________; 性质定理二:矩形的对角线__________; 等边三角形的判定;
初中数学九 上册 苏科
1.3平行四边形形,矩形,菱 形,正方形的性质和判定2。
教学目标
1.复习矩形的定义;分清矩形与矩形的关系;
2.会证明矩形的性质,会利用性质解决有关的数
学问题;
动动脑,回忆一下
矩形的定义是什么? 有一个角是_____的平行四边形叫做矩形;
根据矩形的定义可知,矩形一定是______(图形
名称),所以具备这类图形的所有性质,而且必定 有一个角是_____;
再回忆一下
除了由定义得到的性质,矩形还有哪些性质? 性质定理一:矩形的四个角都是________;
性质定理二:矩形的对角线__________;
如何证明????
典型例题
例一; 例二;
等边三角形的判定
定义:三边都_____三角形叫做等边三角形; 三个角都______的三角形是等边三角形; 有两个角是_____的三角形是等边三角形;
22.3(3)_矩形、菱形的判定
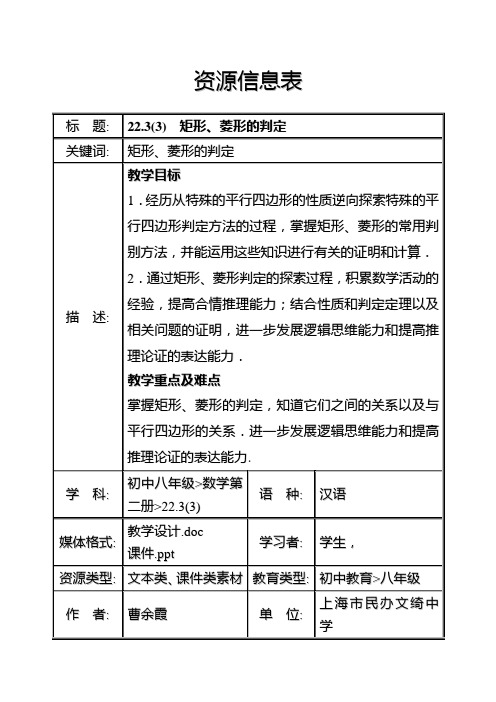
资源信息表22.3(3)矩形、菱形的判定上海市民办文绮中学曹余霞教学目标1.经历从特殊的平行四边形的性质逆向探索特殊的平行四边形判定方法的过程,掌握矩形、菱形的常用判别方法,并能运用这些知识进行有关的证明和计算.2.通过矩形、菱形判定的探索过程,积累数学活动的经验,提高合情推理能力;结合性质和判定定理以及相关问题的证明,进一步发展逻辑思维能力和提高推理论证的表达能力.教学重点及难点掌握矩形、菱形的判定,知道它们之间的关系以及与平行四边形的关系.进一步发展逻辑思维能力和提高推理论证的表达能力.教学用具准备课件教学流程教学过程设计一、温故知新1.平行四边形的判定(5个方法)2.矩形、菱形的性质复习——有别于平行四边形的特殊性质:[说明]本节课研究矩形、菱形的判定.故本环节安排平行四边形的判定复习以及矩形、菱形作为特殊的平行四边形的特殊性质回顾;便于本节课的顺利开展.二、矩形、菱形的判定探讨思考:如何从矩形、菱形特殊的性质出发,得出矩形、菱形的判定?定义可以作为第一条判定:即:有一个角是直角的平行四边形是矩形.有一组邻边相等的平行四边形是菱形.[说明]定义是作为判定的第一依据,因此,所有的定义都可以作为第一个判定方法.其他方法呢?“1)从边;2)从角;3)从对角线”的角度考虑.1.矩形:——矩形的特殊性在于直角和对角线不妨给出关于矩形判定的命题:(讨论、交流)比如:四个角是直角的四边形是矩形.三个角是直角的四边形是矩形.对角线相等的平行四边形是矩形.……分析上述给出的命题,证明讨论;得出矩形的判定定理:三个角是直角的四边形是矩形.对角线相等的平行四边形是矩形.2.菱形:——类似矩形进行讨论.并得出菱形的判定定理:四条边相等的四边形是菱形.对角线互相垂直的平行四边形是菱形.[说明]作为特殊的平行四边形,矩形、菱形在角、边、对角线方面都有特殊的性质.因此,引导学生不妨就从其特殊性开始考虑.矩形详加探究之后,对应得到菱形的判定方法.3.总结矩形菱形的判定[说明]在本环节结束时设计一个表格,将矩形的判定分别从四边形、平行四边形出发作一总结;上课时,借助PPT ,缓缓放出本课结论,有不错的效果.三、定理运用,1.例题选讲例1:如图:矩形ABCD 的对角线AC ,BD 相交于点O ,E,F,G,H 分别 在AO,BO,CO,DO 上,且AE=BF=CG=DH.求证:四边形EFGH 是矩形.分析:首先,矩形的判定方法有哪些?其次,本题可以用哪种方法? 过程说理.例2:已知如图:EF 是□ABCD 的对角线AC 的垂直平分线,EF 与边AD,BC 分别交于点E,F. 求证:四边形AECF 是菱形分析:其一:菱形的判定方法有哪些?其二:本题从何入手? 其三:过程探讨. 其四:过程说理.(菱形的三种判定方法对于本题都适用) 2.小试牛刀1.用两张等宽的长方形纸条,随意交叉放在一起,重合的部分构成四边形是什么四边形?2.如图:已知BF ,BE 分别是∠ABC 与它的邻补角的平分线,AE ⊥BEOH GF E DCBAOFEDCBA于点E ,AF ⊥BF 于点F,那么四边形AEBF 是矩形吗?为什么?[说明]所选两个例题和两个习题分别围绕矩形菱形的各三个判定, 展开多种方法的讨论;以掌握矩形、菱形的判定方法,知道它们之间的关系以及与平行四边形的关系.达到进一步发展学生逻辑思维能力和提高学生推理论证的表达能力.四、反思小结,谈谈收获1.这节课你学会了什么? ——矩形、菱形的判定 矩形:✗ 有一个角是直角的平行四边形是矩形: ✗ 有三个角是直角的四边形是矩形; ✗ 对角线相等的平行四边形是矩形. 菱形:✗ 有一组邻边相等的平行四边形是菱形; ✗ 四条边都相等的四边形是菱形; ✗ 对角线互相垂直的平行四边形是菱形.2.你还有什么疑惑吗?本节课研究的是特殊的平行四边形(矩形、菱形的判定),F ECBA注意从矩形、菱形的特殊性,熟悉它的判定方法.[说明]先请学生总结判定方法;(理清思路,分别从四边形、平行四边形出发得到的三条判定);再引导学生释疑.试图引导学生养成释疑的习惯.五、布置作业:练习册: 习题22.3(3),六、拓展思考,课外延伸习题1:以△ABC 的三边在BC 同侧分别作三个等边三角形△ABD ,△BCE ,△ACF,试回答下列问题: 1) 四边形ADEF 是什么四边形?2) 当△ABC 满足什么条件时,四边形ADEF 是矩形? 3) 当△ABC 满足什么条件时,四边形ADEF 是菱形?习题2:Rt △ABC 中,∠ACB =90°,CD 是高,AE 是角平分线,CD 、AE 交于点G ,EF ⊥AB 于点F ,试问:四边形CGFE 是什么四边形?[说明]选用两例:其一是矩形问题,结合等边三角形、三角形全等、平行四边形等问题解决,过渡到今天的矩形、菱形问题.这是一个更FEDCAG FEDCBA特殊的矩形.其二是一个经典问题:综合性很强.总之所选两题试图引导学生对于所学的各知识点达到融会贯通的目的;试图发展学生逻辑思维能力,观察能力等一些数学能力.总之,通过本课,试图带领学生学会矩形、菱形的判定方法.积累数学活动的经验,提高合情推理能力;进一步发展逻辑思维能力和提高推理论证的表达能力.。
初中数学八年级上册《平行四边形菱形矩形正方形综合复习》
北师大版初中数学八年级上册《平行四边形、菱形、矩形、正方形(综合复习1)》精品教案一. 教材分析四边形是八年级上册也是中考的重点内容,主要考查平行四边形及特殊的平行四边形,比如矩形、菱形、正方形的判定和性质,考查的形式有填空题、选择题、计算题、证明题、综合题等,考查难度中等。
二. 复习目标1. 掌握平行四边形、菱形、矩形、正方形概念,了解它们之间的关系。
2. 掌握平行四边形、菱形、矩形、正方形的有关性质,并利用其性质解决相关问题(以小型计算为主)三. 重点、难点熟练的对平行四边形、菱形、矩形、正方形的定义、性质的进行应用。
四. 复习内容:(一)基本知识回顾:1、以图表的形式引导学生回顾平行四边形、菱形、矩形、正方形概念,了解它们之间的关系。
2、引导学生用几何语言分别从边、角、对角线、对称性等方面表述平行四边形、菱形、矩形、正方形的性质。
学生相互补充订正,教师特别注意引导学生寻找它们所具有的特殊性质,比如:图形中存在的特殊三角形、全等三角形、等积三等形等,再以下面一组小练习巩固性质。
1、菱形具有而平行四边形不一定具有的性质是()A 对角线互相平分B 对角线互相垂直C 对角相等D 邻角互补2、正方形具有而菱形不具有的性质是()A 对角线互相平分B 对角线互相垂直C 对角线相等D 对角线平分一组对角3、矩形、菱形、正方形都具有的性质是()A 对角线互相平分B 对角线互相垂直C 对角线相等D 对角线平分一组对角(二)知识应用利用平行四边形、菱形、矩形、正方形的有关定义性质,解决具体问题.习题共分为三个层次:1)快速热身:以基础题为主,学生能够独立完成,正确率高2)展示自我:题目有一定的难度,给学生充足的时间,独立思考,交流订正。
教师主要进行适时点拨、方法总结,注重及时反馈。
3)勇攀高峰:题目难度增加,一题多变,使学生能举一反三。
主要针对学有余力的学生。
快速热身:1、平行四边形ABCD的周长为40cm, 两邻边AB、AD之比为2:3,则AB=_______, BC=______.2、已知如图,平行四边形ABCD,AB=_________3、正方形的边长是3,则对角线的长为______4、菱形ABCD的对角线长分别为4cm、6cm,它的边长为_______,它的面积为________5、如图,矩形ABCD的对角线相交于点O,AB=5,BD=____。
八年级数学四边形-矩形-菱形-正方形的性质和判定
如何证明????
性质定理1; 性质定理2; 性质定理3;
比比看,看谁想的快?
例一; 例二; 练习;
提升一下,锻炼大脑
小结一下吧.
ห้องสมุดไป่ตู้两组对边分别_____四边形叫做平行四边 形;
平行四边形的两组对边________; 平行四边形的两组对角________; 平行四边形的对角线__________;
形; 根据平行四边形的定义可知,平行四边形
的两组对边_______;
再努力一下
除了由定义得到的性质(两组对边分别平 行),平行四边形还有哪些性质?
平行四边形的两组对边________; 平行四边形的两组对角________; 平行四边形的对角线__________;
;舟山出海捕鱼 舟山出海捕鱼
;
文人独嗜,百姓亦胸有丘壑,尤其在一个特殊日子里,更是趋之若鹜、乐此不疲,此即九九重阳的“登高节”。 我始终认为,这是中国先民一个最浪漫、最诗意的节日。 秋高气爽,丹桂飘香,心旷神怡,菊色暴涨值此良辰,若不去登高放目、驰骋神思,实在辜负天地、有愧人生。 从“登高” 意义上说,这几乎是个绝版的节日。今人仅视为“敬老节”,无疑让它的美折损大半,伤了筋,动了骨。 登高节、重阳节、茱萸节、菊花节,乃一回事,但我尤喜“登高”之名。 九九习俗源于战国,古人将天地归于阴阳,阴即黑暗、沉寂,阳即光明、活力,奇数谓阳,偶数谓阴;九乃阳数之 首,九月初九,双阳相叠,故称重阳。加上“九”“久”谐音,重阳从一开始便是欢愉之词。曹丕《九日与钟繇书》云:“岁往月来,忽复九月九日。九为阳数,而日月并应,俗嘉其名,以为宜于长久,故以享宴高会。” 后来,重阳节又繁殖出了一串新解:除凶秽,招吉祥;延年益寿,祈福求 安。仪式也愈加丰富:饮菊花酒、贴菊叶窗、佩茱萸草、吃重阳糕、祭先祖、送寒衣但有个核心不变:登高。 登高,除赏秋,亦有惜时别离之意。九九乃秋之尾,而后草木迅速凋零,虫声偃息,万象复苏要等来年了。此时登高,将谢幕前的风景尽收眼底,将天地之恩默诵于心,颇有依依不舍和 立此存念的意思。 故有人称九月登高为“辞青”,与三月“踏青”呼应。 这种对时令的感情,除了膜拜,其他很像爱情或友谊。 眼前的欢聚与热闹,会让很多人思念远客和往事,追忆昔日的葱茏年华。最感人的,当属王维《九月九日忆山东兄弟》 “独在异乡为异客,每逢佳节倍思亲。遥知 兄弟登高处,遍插茱萸少一人。” 当然,对老百姓来说,寻欢仍是兹日最大主题。 “今日云景好,水绿秋山明。携壶酌流霞,搴菊泛寒荣。”(李白《九日》) 秋收毕,仓廪实,人心悦,少不了邀友约醉,醍醐一场。隋人孙思邈在《千金方月令》中道:“重阳日,必以糕酒登高远眺,为时宴 之游赏,以畅秋志。酒必采茱萸甘菊以泛之,即醉而归。” 辞秋,注定是一次丰盛的饯行。物质和精神,都恰逢其时。 王勃那首澎湃万丈的《滕王阁序》,即重阳宴上泼醉所致。 登高的去处,一般是山、塔、楼,所以,在一座古城,大凡能将风景揽入怀中的高处,几朝下来,皆成了名胜。对 古人来说,若城内或近郊无高,是非常败兴、非常严重的一件事,至少重阳这天没法熬,无处立足。所以,筑阁砌楼便成了古建时尚,“江南三大楼”之黄鹤楼、岳阳楼、滕王 阁,皆受驱于重阳雅集、登高揽景的欲望,一俟矗起,则声名大噪,“游必于是,宴必于是”。 某日,走在高楼大厦 的街上,我忽想:重阳那天,早年人会投奔哪儿呢?何处适于登高放目? 清《燕京岁时记》记载:“每届九月九日,则都人提壶携楹,出都登高。南则天宁寺、陶然亭、龙爪槐等处,北则蓟门烟树、清净化域等处,远则西山八处。赋诗饮酒,烤肉分糕,询一时之快乐也。”据说,除以上各处, 玉渊潭、钓鱼台也人气颇盛。而慈禧太后,去的是北海桃花山。 先人青睐这些地方,缘由莫外两点:身高和野趣。我盘点了下,清人眼里这群高丘,如今几乎皆废,或荡然无存,或只能算平地。像天宁寺、陶然亭、钓鱼台,实在既没身高,又无野趣。天宁寺畔倒是有根比它高几倍的烟囱。 昔 日的“姚明”,如今都成了小矮人。当代京民若过登高节,恐怕得去爬香山或央视转播塔了。鉴于空气清洁度,能瞅多远尚未知。 有年去福州,夜宿于山宾馆,当被告知卧榻之侧即著名的于山和白塔时,心中甚喜,顿觉夜色阑珊、地气充沛,睡得特香。翌日拉开窗帘,我大吃一惊,那传说中的 于山不过一土丘,连塔算上,高度也不及对面一栋楼。虽沮丧,但我清楚,这是心理落差所致,预期越大,失落越重。 千余年来,福州的地标即“三山两塔”,你在城里任一角落,皆可望见这三加二的全景图。历代画家绘福州,只要择五点之一摆画案,出来的全是鸟瞰图。 我想,古时九月九, “三山两塔”必是糯酒飘香、万头攒涌罢。 现在,福州人该去哪儿呢? 我看过记载,至清末,各地的“登高会”依然盛行,长沙的岳麓山、的白云山、武汉的龟山、南昌的滕王阁、西安的雁塔都是著名的雅集地。连素无丘山的,也把沪南丹凤楼及豫园大假山作为“高枝”来攀。 啰唆了这么多, 我究竟想说什么呢? 其实我想说,从前人的心目中是有“高”的,尊高、尚高、仰高,“高”对其人生步履和精神移动有股天然引力,有种欲罢不能、鬼使神差的诱惑。而且,先人所涉者,多为在野之高、山水之高、天赐之高,不仅慕之趋之,也忠实地护高、养高,捍卫身边的高物,不敢随便 削弱和降低它,不敢做有损它尊严和荣誉的事。 还有一点,即他们自然之子的秉性、灵魂里的那股酒意。 在对时季的敏感、光阴的惜怜、与自然对话的天赋及能力上,今人皆比先辈逊色得多。不仅迟钝,而且寡情。 把重阳节改成敬老节,是文明的粗暴,是生存美学的大损失。 当沥青覆盖了 旷野,当城市沦为蔽日峡谷,当石阶变成电梯,当丘山被逼得纷纷自杀,当天然之巍被夷为平地、化作砖头水泥,当世人和媒体眼中只剩下“珠峰” 登高节,只剩一个遥远的 背影。 我们刻度变了,视觉和灵魂,刻度都变了。 我们所用尺码,和欲望一样,肥大而粗陋。 我们睥睨天下,肆意 规划任何想要的海拔。 小时候,老师解释“地平线”,我马上就懂了。不久,它即出现在了我的作文里,那是日出日落的地方,那是“远方”的代名词。今天,城市的小朋友,谁见过地平线?我跑去问邻居的孩子,他拼命摇头。 在心里,我向古代那些平平仄仄、不起眼的“高”致敬,向蚂蚁 般倚石扶树、跌跌撞撞的醉客们致敬。 我还要向那漫山遍野赤裸裸的笑声致敬。 还要向一坛坛躺在深秋里的菊花酒致敬。 我醉了。恍惚看见了刘伶、嵇康、阮籍 ? 荒野的消逝? 兼致“哥本哈根气候大会”上的哭泣 ? 我们没有创造这个世界,我们正忙于削弱它。 我们需要找到如何使我们自 己变得小一些,不再是世界中心的 办法。 比尔·麦克基本 1 早上跑步,遇到件有趣的事:园子深处有一条僻径,两畔是大树和灌丛,少有人及,我跑过去时,一切正常,可原路折返时,忽眼前一晃,一条亮晶晶的丝拦住去路,我呆住,一只大蜘蛛正手忙脚乱,原来,趁我来去的间隙,它已在 两棵树之间设下埋伏。我不敢惊扰这桩阴谋,在欣赏够了这个自以为是的家伙后,我吹起口哨,绕道而行。 这给了我一天的兴奋。此后,我热爱起这个园子此前我并不欣赏她过度修饰和文明的外表,因为在那种整齐的美之下,仍活跃着一缕野性的能量,使之每个瞬间都充满未知、偶然和动荡, 尽管微弱、隐蔽,甚至被忽略不计,但在我心里,它已扭转了这园子的气质。 很显然,上述快乐并非源于邂逅蜘蛛,而是一份叫“野”的元素给的。这份“野”代表着一种诞生了亿万年的原始力量和生物激情,它在文明之外,在“时代”“社会”“人间”概念与内容之外。我亢奋的秘密在于: 我撞上了大自然的力。蜘蛛要俘获的不是我,但等来的却是我,在它眼里,我和它是平等的野物荒野的成员,我为突如其来的“平等”所晕眩 我被蜘蛛的逻辑粘住了,我被它邀请和一视同仁了,它奖励了我一个古老身份,一个和文明无关的洪荒身份 这是值得大声欢呼的。 当然,这有非分之想 的成分。在这座大城市的腹部,向一座人工园子索取更多野趣,无论如何显得矫情。 2 这个细节还激起了我对“野性”的遐想。 何谓野性呢?为何人们一边毫不犹豫清剿着身边最后一抹野趣,一边又憧憬着“可可西里”“罗布泊”式的荒凉? 美国环境学家霍尔姆斯·罗尔斯顿说:“每一条河 流,每一只海鸥,都是一次性的事件,其发生由多种力、规律与偶然因素确定例如,一只小郊狼蓄势要扑向一只松鼠时,一块岩石因冰冻膨胀而松动,并滚下山坡,这分散了狼的注意力,也使猎物警觉,于是松鼠跑掉了这些原本无关的元素撞到一起,便显示出一种野性。”我觉得,这是对野性 最好的阐述。野性之美,即大自然的动态、偶发和未知之美,它运用的是自己的逻辑,显示的是蓬勃的本能,是不受控制和未驯化的原始力量,它超越人的意志和想象,位于人类经验和见识之外。 在,有一些著名的植物景点,像香山的红叶、玉渊潭的樱花、北海的莲池、钓鱼台的银杏每年的某 个时节,报纸电视都要扮演花媒的角色,除渲染对方的妖娆,并叮嘱寻芳的路线、日程、方案等细节。比如春天,玉渊潭网站的访问量就会激增,关于早、中、晚樱的花讯,像天气预报一样准。美则美矣,但这种蜂拥而至的哄抢式消费,尤其被人工“双规” 规定时间、规定地点的计划性绽放, 再加上门票交易环节,使得这一切酷似一场演出除了印已知,除了视觉对色彩的消费,它不再给你额外惊喜。所以,这些风物我涉猎一次后,便没了再访的冲动和理由。 日子长了,诸景在人心目中,便沉淀为一种季节印象,甚至代指起了时间来,如很多文章开头会写:“当香山枫叶红了的时 候 ”“玉渊潭的樱花又开了 ”这样的花开花落,呼应的是旧闻和经验,精神上往往无动于衷。 种植型风景,本质上和庄稼、高楼大厦一样,属人类的方案产品和预定之物,乃劳动成果之一。它企图明晰、排斥意外、追求秩序和严谨,如玉渊潭樱树,每一株都被编了号,依品种、花期、色系、 比例,分配以特定区域、岗位和功能,总之,这是一套被充分预谋和策划的美学体系,像鸟巢升起的奥运焰火,其“盛世”颂语早就被一笔一画灌注在了火药配方里。一个人注视绚丽焰火和瞥见天际流星,感受截然不同,前者是工程之美,后者属野性之灿,前者你可以夸奖张艺谋,而 后者导演 是大自然,你无从感激,只会对天地油生敬意。 荒野的最大特征,即独立于人的意志之外,它和文明无关。 有一次,指导闽台合作的一档电视旅行节目,用我的话说,这是一个逃离都市的精神私奔者的系列故事。其中一期是云南,有一镜头:台湾主持人在路边摘了一朵花,兴奋地喊:野玫瑰! 我说:你若能发现一朵“不知名的花”就好了。说白了,一个带观众去远方的背包客,我希望她走得再狂野和不规则一些,能采集到大自然的一点野性,能邂逅更多的未知与陌生,如此,才堪称“在那遥远的地方”。远方的魅力和诱惑,即在于其美学方向和都市经验之相反,而“玫瑰”一词, 文气太重,香水味太呛鼻了,它顶多会让我想起情人节、酒吧或花店,它甚至扼杀想象。 3 我们眼中的“世界”
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级《特殊四边形》复习学案 (平行四边形、矩形、菱形)
知识点一:平行四边形的性质与判定:
1、如图 , 平行四边形 ABCD中 ,
∠ABC=60°,E 、F 分别在 CD、BC的延长线上 ,AE∥BD,EF
⊥ BC,DF=2,则 EF 的长为
.
2、下列条件中,能判定四边形是平行四边形的是( )
A. 一组对边相等 B. 对角线互相平分 C. 一组对角相等 D.
对角线互相垂直
3、如图所示,在 ABCD中, E、F 分别 AB、CD的中点,连结 DE、 EF、BF,则图中平行四
边形共有( )
A.2 个 B.4 个 C.6 个 D.8 个
4、下列条件中,不能判定四边形 ABCD为平行四边形的条件是
(
)
A
D
A.AB平行且等于 CD B.∠A=∠ C,∠ B=∠ D
B
C
C.AB=AD,BC=CD D. AB=CD , AD=BC
A D
5、如图,平行四边形 ABCD的对角线 AC、BD交于点
E
O,E、F 在 AC上, G、H 在 BD上, AF=CE,
BH=DG.
O H
求证: GF∥ HE.
G
F
B C
6、如图,是平行四边形的对角线上的点, ,请你猜想:线段与线
段有怎样的关系并对你的猜想加以证明。
A D
E
F
B
C
7、有一位农民有一个菜园,如图是一平行四边形,记为 □ABCD,地里有一口井,位置在
图中的 O 点,老人在临终前对两个儿子说: “这块地你们弟兄俩平均分开,但水井不能分
(不在任何一家的菜地里) ,两家公用。”老人死后,弟兄俩却不知道怎么分,你能帮助
这弟兄俩按要求分开吗
知识点二:矩形的性质与判定
◆知识讲解归纳
一、矩形的定义:有一个角是 的平行四边形叫做矩形 .
二、矩形的性质:矩形是特殊的平行四边形,它除具有一般平行四边形的性之外,还
具有( 1)矩形的四个角都是 . (2)矩形的对角线
.
三、议一议:矩形 ABCD的对角线 AC与 BD相交于点 O,那么 BO是 Rt⊿ ABC中一条怎样的
特殊线段它与 AC有怎样的大小关系为什么有这样的大小关系因此,我们得到一个性质
定理的推论:
直角三角形斜边上的中线等于 .
四、矩形的判定方法:( 1)有一个角是 的平行四边形叫做矩形
.
( 2)对角线 _________的平行四边形是矩形.(3)有三个角是 ________的四边形是矩形.
◆对应练习:
1、 一矩形两对角线之间的夹角有一个是 600 , 且这角所对的边长 5cm,
则对角线长为
( ) A. 5 cm B. 10cm C. 5
2 cm D.
无法确定
2、如图在矩形 ABCD中,对角线 AC、BD相交于点 O,则以下说
法错误的是 ( )
1
A.AB= AD
B . AC=BD
C. DAB ABC BCD CDA 90 D
. AO=OC=BO=OD
3、如图,矩形 ABCD中, AB=3,BC=4,P 是边 AD上的动点, PE⊥AC于点 E,
PF⊥BD于点 F,则 PE+PF的值为: _________。
4、矩形一个角的平分线分矩形一边成 2cm和 3cm,则这个矩形的面积为 。5、如图 , 在矩形
ABCD中, M是 BC的中点,且 MA⊥MD.?若矩形 ABCD?的周长为 48cm,?求矩形
ABCD的面积。
6、如图,在矩形 ABCD中,已知 AB=8cm,BC=10cm,折叠矩形的一边 AD,使点 D 落在
BC 边的中点 F 处,折痕为 AE,求 CE的长.
7、如图,在矩形 ABCD中, AE平分∠ BAD,∠ 1=15°.
(1) 求∠ 2 的度数. (2) 求证: BO= BE.
知识点三:菱形的性质与判定
◆知识讲解归纳
1. 菱形的概念: 一组 相等的平行四边形叫做菱形 .
2.
菱形的性质:边: ;
角: ;
对角线: 。
对称性 : 。
3.
菱形的面积:⑴ ;⑵ 。
4. 菱形的判定:(1).四条边都相等的 _____________是菱
形.(2).邻边相等的 _____________是菱
形.
(3).对角线互相垂直的 ______________是菱形
对应练习:
1、如图,边长为 6 的大正方形中有两个小正方形,若两个小正方形的面积分别为 S1,
S2,则 S1+S2 的值为(
)
A、16 B、17 C 、18 D、19
2、如图,菱形 ABCD的周长为 16,∠A=60o,则对角线 BD的长度是
( )A.2 B .2 3
C.4 D .4
3
3.菱形的边长为 5,一条对角线长为 8,那么它的另一条对角线长为 ________
4. 已知菱形的两条对角线的长分别为 4cm, 8cm,那么边长为 _________
5. 已知菱形的周长为 40cm,两条对角线的长度比为 3:4,那么两条对角线的长分别为
( )A.6cm, 8cm B. 3cm ,4cm C. 12cm ,16cm D. 24cm ,32cm
6.在下列性质中,平行四边形具有的是 _______________,菱形具有的是 _____________,
矩形具有的 是 ,正方形具有的是 。
( 1) 四条边都相等; (2)对角线互相平分; ( 3)对角线相等;( 4)对角线互相
垂直; (5)四个角都是直角; ( 6)每一条对角线平分一组对角;
( 7)对边相等
且平行;(8)有两条对称轴;
7.已知菱形的两条对角线的长分别为
10cm与 24cm,则边长为 ________,此菱形的面积
为 _________。
8.在 □ ABCD中, AC=21cm,BE⊥AC于 E,且 BE=5cm,AD=7cm,则两平行线 AD
与 BC间的距离是 ________________。
9.一个四边形边长依次是
a、b、c、d,且满足 a2+b2+c2+d2=2ac+2bd,则这个四边形为:
____________。
10.菱形有一个内角为 60°,较短的对角线长为
6cm,则菱形的边长为 ________,另一
条对角线的长为 ___________。
11. 如图,将两张长为 8,宽为 2 的矩形纸条交叉,使重叠部分是一个菱
形,容易知道当两张纸条垂直时,菱形的周长有最小值
,菱
(第 11 题图)
形周长的最大值是 .
12. 如图,在 ABCD中,O是对角线 AC的中点,过点 O作 AC的垂线与边 AD、BC分别交
于 E、 F。求证:四边形 AFCE是菱形。
13. (6 分)如图,在 □ ABCD中, BE 平分 ABC 交 AD 于点 E ,
A
ED
DF 平分 ADC 交 BC 于点 F .
求证:( 1) △ ABE ≌ CDF ;
( 2)若 BD ⊥ EF ,则判断四边形 EBFD 是什么特殊四边形,请
证明你的结论。
B F
C
