数字信号处理英文版课后答案 (9)
《数字信号处理教程》程佩青(第三版)清华大学出版社课后答案

结果 y (n ) 中变量是 n ,
∞
∞
∑ ∑ y (n ) =
x ( m )h (n − m ) =
h(m)x(n − m) ;
m = −∞
m = −∞
②分为四步 (1)翻褶( -m ),(2)移位( n ),(3)相乘,
(4)相加,求得一个 n 的 y(n) 值 ,如此可求得所有 n 值的 y(n) ;
10
T [ax1(n)+ bx2 (n)] =
n
∑
[ax1
(n
)
+
bx2
(n
)]
m = −∞
T[ax1(n) + bx2(n)] = ay1(n) + by2(n)
∴ 系统是线性系统
解:(2) y(n) =
[x(n )] 2
y1(n)
= T [x1(n)] = [x1(n)] 2
y2 (n) = T [x2 (n)] = [x2 (n)] 2
(3) y(n) = δ (n − 2) * 0.5n R3(n) = 0.5n−2 R3(n − 2) (4) x(n) = 2n u(−n −1) h(n) = 0.5n u(n)
当n ≥ 0 当n ≤ −1
∑ y(n) = −1 0.5n−m 2m = 1 ⋅ 2−n
m = −∞
3
y(n) = ∑n 0.5n−m 2m = 4 ⋅ 2n
+ 1)
−
x1 (n
+ 1)]
=
−a n
综上 i) , ii) 可知: y1 (n) = −a nu(−n − 1)
(b) 设 x(n) = δ (n − 1)
i)向 n > 0 处递推 ,
数字信号处理实验课后答案

数字信号处理实验课后答案数字信号处理实验课后答案【篇一:数字信号处理第三版课后实验程序(高西全)】txt>close all;clear all%======内容1:调用filter解差分方程,由系统对u(n)的响应判断稳定性====== a=[1,-0.9];b=[0.05,0.05]; %系统差分方程系数向量b和ax1n=[1 1 1 1 1 1 1 1 zeros(1,50)]; %产生信号x1(n)=r8(n)x2n=ones(1,128); %产生信号x2(n)=u(n)hn=impz(b,a,58); %求系统单位脉冲响应h(n)subplot(2,2,1);y=h(n);tstem(hn,y); %调用函数tstem绘图title((a) 系统单位脉冲响应h(n));box ony1n=filter(b,a,x1n); %求系统对x1(n)的响应y1(n)subplot(2,2,2);y=y1(n);tstem(y1n,y);title((b) 系统对r8(n)的响应y1(n));box ony2n=filter(b,a,x2n); %求系统对x2(n)的响应y2(n)subplot(2,2,4);y=y2(n);tstem(y2n,y);title((c) 系统对u(n)的响应y2(n));box on%===内容2:调用conv函数计算卷积============================ x1n=[1 1 1 1 1 1 1 1 ]; %产生信号x1(n)=r8(n)h1n=[ones(1,10) zeros(1,10)];h2n=[1 2.5 2.5 1 zeros(1,10)];y21n=conv(h1n,x1n);y22n=conv(h2n,x1n);figure(2)subplot(2,2,1);y=h1(n);tstem(h1n,y); %调用函数tstem绘图title((d) 系统单位脉冲响应h1(n));box onsubplot(2,2,2);y=y21(n);tstem(y21n,y);title((e) h1(n)与r8(n)的卷积y21(n));box onsubplot(2,2,3);y=h2(n);tstem(h2n,y); %调用函数tstem绘图title((f) 系统单位脉冲响应h2(n));box onsubplot(2,2,4);y=y22(n);tstem(y22n,y);title((g) h2(n)与r8(n)的卷积y22(n));box on%=========内容3:谐振器分析======================== un=ones(1,256); %产生信号u(n)n=0:255;xsin=sin(0.014*n)+sin(0.4*n); %产生正弦信号a=[1,-1.8237,0.9801];b=[1/100.49,0,-1/100.49]; %系统差分方程系数向量b和a y31n=filter(b,a,un); %谐振器对u(n)的响应y31(n) y32n=filter(b,a,xsin); %谐振器对u(n)的响应y31(n)figure(3)subplot(2,1,1);y=y31(n);tstem(y31n,y);title((h) 谐振器对u(n)的响应y31(n));box onsubplot(2,1,2);y=y32(n);tstem(y32n,y);title((i) 谐振器对正弦信号的响应y32(n));box on10.2.2 实验程序清单1 时域采样理论的验证程序清单% 时域采样理论验证程序exp2a.mtp=64/1000; %观察时间tp=64微秒%产生m长采样序列x(n)% fs=1000;t=1/fs;fs=1000;t=1/fs;m=tp*fs;n=0:m-1;a=444.128;alph=pi*50*2^0.5;omega=pi*50*2^0.5;xnt=a*exp(-alph*n*t).*sin(omega*n*t);xk=t*fft(xnt,m); %m点fft[xnt)]yn=xa(nt);subplot(3,2,1);tstem(xnt,yn); %调用自编绘图函数tstem绘制序列图box on;title((a) fs=1000hz);k=0:m-1;fk=k/tp;subplot(3,2,2);plot(fk,abs(xk));title((a) t*ft[xa(nt)],fs=1000hz);xlabel(f(hz));ylabel(幅度);axis([0,fs,0,1.2*max(abs(xk))])%===================================== ============ % fs=300hz和fs=200hz的程序与上面fs=1000hz完全相同。
数字信号处理课后答案+第3章(高西全丁美玉第三版)

k = 0, 1, ⋯, N − 1
(8) 解法一 直接计算:
1 jω 0 n x8 (n) = sin(ω0 n) ⋅ RN (n) = [e − e − jω 0 n ] R N ( n ) 2j
X 8 ( n) =
∑
n =0
N −1 kn x8 (n)WN
1 = [ e jω 0 n − e − jω 0 n ] e 2 j n =0
1− e
j(ω0 −
2π N k) 2π N −1 sin (ω0 − j(ω0 − k )( ) N 2 N 2 =e 2π sin (ω0 − k ) / 2 N
k = 0, 1, ⋯, N − 1
或
X 7 (k ) =
1 − e jω0 N
2π j(ω0 − k ) N 1− e
N −1
N −1
由于 所以
∑
n =0
N −1
n WN ( m + k )
N = 0
m= N −k m ≠ N − k , 0≤ m ≤ N − 1
DFT[X(n)]=Nx(N-k)
N −1 k =0
k=0, 1, …, N-1
5. 如果X(k)=DFT[x(n)], 证明DFT的初值定理
证: 由IDFT定义式
2π mn +θ ) N 2π mn +θ ) N ]
1 = [e 2j
j(
−e
− j(
2π = sin mn + θ N
n=0, 1, …, N-1
3. 已知长度为N=10的两个有限长序列:
1 0 ≤ n ≤ 4 x1 (n) = 0 5 ≤ n ≤ 9
数字信号处理(姚天任江太辉第三版)课后习题答案 清晰版

(2)y(n)= x(n)sin[
2 n+ ] 3 6
(3)y(n)=
k
x(k )
(4)y(n)=
k n0
x(k )
n
(5)y(n)= x(n)g(n)
解 (1)设 y 1 (n)=2x 1(n)+3,y 2 (n)=2x 2 (n)+3,由于 y(n)=2[x 1(n)+x 2 (n)]+3 ≠y 1 (n)+ y 2 (n) =2[x 1(n)+x 2 (n)]+6 故系统不是线性系统。 由于 y(n-k)=2x(n-k)+3,T[x(n-k)]=2x(n-k)+3,因而 y(n-k) = T[x(n-k)] 故该系统是非移变系统。 设|x(n)|≤M,则有 |y(n)|=|2x(n)+3|≤|2M+3|<∞ 故该系统是稳定系统。 因 y(n)只取决于现在和过去的输入 x(n),不取决于未来的输入,故该系统是因果系统。 (2)设
解 利用线性卷积公式 y(n)=
k
x ( k ) h( n k )
按照折叠、移位、相乘、相加、的作图方法,计算 y(n)的每一个取样值。 (a) y(0)=x(O)h(0)=1 y(l)=x(O)h(1)+x(1)h(O)=3 y(n)=x(O)h(n)+x(1)h(n-1)+x(2)h(n-2)=4,n≥2 (b) x(n)=2 (n)- (n-1) h(n)=- (n)+2 (n-1)+ (n-2) y(n)=-2 (n)+5 (n-1)= (n-3) (c) y(n)=
[
k
数字信号处理课后习题答案完整版

数字信号处理课后习题答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】数字信号处理(姚天任江太辉)第三版课后习题答案第二章判断下列序列是否是周期序列。
若是,请确定它的最小周期。
(1)x(n)=Acos(685ππ+n )(2)x(n)=)8(π-ne j(3)x(n)=Asin(343ππ+n )解 (1)对照正弦型序列的一般公式x(n)=Acos(ϕω+n ),得出=ω85π。
因此5162=ωπ是有理数,所以是周期序列。
最小周期等于N=)5(16516取k k =。
(2)对照复指数序列的一般公式x(n)=exp[ωσj +]n,得出81=ω。
因此πωπ162=是无理数,所以不是周期序列。
(3)对照正弦型序列的一般公式x(n)=Acos(ϕω+n ),又x(n)=Asin(343ππ+n )=Acos(-2π343ππ-n )=Acos(6143-n π),得出=ω43π。
因此382=ωπ是有理数,所以是周期序列。
最小周期等于N=)3(838取k k =在图中,x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。
计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n),并画出y(n)的图形。
解 利用线性卷积公式y(n)=∑∞-∞=-k k n h k x )()(按照折叠、移位、相乘、相加、的作图方法,计算y(n)的每一个取样值。
(a) y(0)=x(O)h(0)=1y(l)=x(O)h(1)+x(1)h(O)=3y(n)=x(O)h(n)+x(1)h(n-1)+x(2)h(n-2)=4,n ≥2 (b) x(n)=2δ(n)-δ(n-1)h(n)=-δ(n)+2δ(n-1)+ δ(n-2)y(n)=-2δ(n)+5δ(n-1)= δ(n-3) (c) y(n)=∑∞-∞=--k kn k n u k u a)()(=∑∞-∞=-k kn a=aa n --+111u(n) 计算线性线性卷积 (1) y(n)=u(n)*u(n) (2) y(n)=λn u(n)*u(n)解:(1) y(n)=∑∞-∞=-k k n u k u )()(=∑∞=-0)()(k k n u k u =(n+1),n ≥0即y(n)=(n+1)u(n) (2) y(n)=∑∞-∞=-k k k n u k u )()(λ=∑∞=-0)()(k kk n u k u λ=λλ--+111n ,n ≥0即y(n)=λλ--+111n u(n)图所示的是单位取样响应分别为h 1(n)和h 2(n)的两个线性非移变系统的级联,已知x(n)=u(n), h 1(n)=δ(n)-δ(n-4), h 2(n)=a n u(n),|a|<1,求系统的输出y(n). 解 ω(n)=x(n)*h 1(n) =∑∞-∞=k k u )([δ(n-k)-δ(n-k-4)]=u(n)-u(n-4)y(n)=ω(n)*h 2(n) =∑∞-∞=k kk u a )([u(n-k)-u(n-k-4)]=∑∞-=3n k ka,n ≥3已知一个线性非移变系统的单位取样响应为h(n)=a n -u(-n),0<a<1 用直接计算线性卷积的方法,求系统的单位阶跃响应。
数字信号处理(第三版)-课后习题答案全-(原题+答案+图)
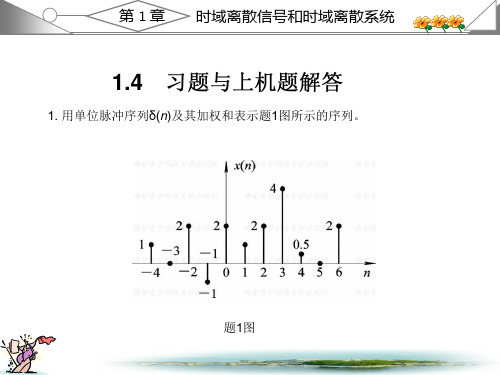
将x(n)的表示式代入上式, 得到 1 y(n)=-2δ(n+2)-δ(n+1)-0.5δ(2n)+2δ(n-1)+δ(n-2)
+4.5δ(n-3)+2δ(n-4)+δ(n-5)
第 1 章 时域离散信号和时域离散系统
8. 设线性时不变系统的单位脉冲响应h(n)和输入x(n)分别有以下三种情况,
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器, 延时器是线性非时变系统, 下面证明。 令输入为
输出为
x(n-n1)
y′(n)=x(n-n1-n0) y(n-n1)=x(n-n1-n0)=y′(n) 故延时器是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n-n0)+bx2(n-n0) =aT[x1(n)]+bT[x2(n)]
(5)y(n)=x2(n)
(6)y(n)=x(n2)
(7)y(n)=
n
(8)y(n)=x(n)sin(ωxn(m) )
m0
解: (1) 令输入为
输出为
x(n-n0)
y′(n)=x(n-n0)+2x(n-n0-1)+3x(n-n0-2) y(n-n0)=x(n-n0)+2x(n—n0—1)+3(n-n0-2)
x(m)h(n-m)
m
第 1 章 时域离散信号和时域离散系统
题7图
第 1 章 时域离散信号和时域离散系统
y(n)={-2,-1,-0.5, 2, 1, 4.5, 2, 1; n=-2, -1, 0, 1, 2, 3, 4, 5}
现代数字信号处理 课后答案(姚天任 著) 华中科技大学出版社
Q
显然,若g(z)的所有零点在单位圆 内,则c(z)为最小单位序列,否 则不是。
1 1 1 1 1 1 举例( z )( z ) z 2 ( 5 z 1)其中( z )( z )为最小相位序列, 且z 2 , ( 5 z 1)亦为最小 2 3 6 2 3 6 相位序列。
a 22 e0 a 22 E[ y 0 y1 ]E[ y1 y1 ] 1 y1 a 21 y1 e2 E[ y 2 y1 ]E[ y1 y1 ] 1 y1
T T T T
2 y1 , 故有
E[ 2 y1 ] a 22 E[ y 0 y1 ] a 21 E[ y1 y1 ] E[ y 2 y1 ] 0
x(n) 为最小相位序列,则有 z i 1,i 1, 2, 3, M。
z 由Z变换的性质Y(z) X( ),要使Y(z)为最小相位序列,即使 a
* Y(z)的所有零点 z k
zk z 1成立,即 k 1 a a
即 a max z k z M
k{1, 2 ,M }
原式 y 3
R12 R32 R22 R31) R32 R11 R21 R31 y2 y1 R22 R11 R21 R12 R22 R11 R21 R12
y 3 R31
R R32 11 R21
R12 y1 R22 y2
1、 12:解 设x(n)、y(n) 为最小相位序列,则其Z变换X(z)、Y(z)对应的所有的零点
i i Zx ,Z y 都在单位圆内,其中 i 1, 2, N,k 1, 2, M。
令 z ( n) x(n) * y(n),有Z(z) X(z)Y(z),其零点的集合
数字信号处理教程课后习题及答案
解:(1 )
n
y(n) = ∑ x(m ) m = −∞
n
y1 (n ) = T [x1 (n )] = ∑ x1 (m ) m = −∞
y2 (n ) = T [x2 (n )] =
n
∑ x2 (m )
m = −∞
n
ay1(n)+ by2 (n) = ∑[ax1(m) + bx2 (n)] m = −∞
β α
n +1
β α β =
n +1− N −n0
N−
N
α −β
y(n) = Nα n−n0 ,
(α = β )
, (α ≠ β )
如此题所示,因而要分段求解。
2 .已知线性移不变系统的输入为 x( n ) ,系统的单位抽样响应
为 h( n ) ,试求系统的输出 y( n ) ,并画图。
(1)x(n) = δ (n)
=
x(n)sin⎜⎝⎛
2π 9
+
π 7
⎟⎠⎞
ay1(n)+ by2 (n)
=
ax1(n
)
sin(
2π 9
+
π 7
)
+
bx2
(n)
sin(
2π 9
+
π 7
)
7. 试判断以下每一系统是否是(1)线性,(2)移不变的?
( ) T[x(n
−
m )] =
x(n
−
m)sin
2π 9
+
π 7
( ) y(n
− m)=
4
第一章 离散时间信号与系统
1 .直接计算下面两个序列的卷积和 y( n ) = x( n )* h( n )
《数字信号处理教程》程佩青第四版课后答案
综上 i ), ii ) 可得: y 2 (n) = a n −1u (n − 1) 由 ( a) , (b) 结果可知, x(n) 与 x 2 (n)是移一位的关系,但 y1 (n) 与 y2(n) 不是移一位的关系,所以在 y (0) = 0 条件下,系统不是移不变系统。
( 4) x ( n ) = 2 n u( − n − 1) 当n ≥ 0 当 n ≤ −1
h ( n ) = 0.5n u ( n )
y (n) = y (n) =
m = −∞ n
∑ 0.5n − m 2m = 3 ⋅ 2 − n ∑ 0.5n − m 2m = 3 ⋅ 2n
, 0 < a < 1 ,通过直接计算卷积和的办法,试确定
(3)
当 n ≥ n0 + N − 1 时 , 全重叠 y (n ) = =
m = n - N +1
∑ x ( m )h( n − m )
n m − n0
n
m = n − N +1
∑β
n
α
n −m
αn = n β
0
m = n − N +1
β ) ∑ (α
n
m
=α β
− n0
( )
β α
n − N +1
n
看作参量) ,
y (n) =
m = −∞ m = −∞ ②分为四步 (1)翻褶( -m ) , (2)移位( n ),(3)相乘, (4)相加,求得一个 n 的 y ( n ) 值 ,如此可求得所有 n 值的 y ( n ) ; ③ 一定要注意某些题中在 n 的不同时间段上求和范 围的不同
数字信号处理(第三版)_课后习题答案全_(原题+答案+图)
第 1 章
时域离散信号和时域离散系统
题2解图(一)
第 1 章
时域离散信号和时域离散系统
题2解图(二)
第 1 章
时域离散信号和时域离散系统
题2解图(三)
第 1 章
时域离散信号和时域离散系统
题2解图(四)
第 1 章
时域离散信号和时域离散系统
3. 判断下面的序列是否是周期的; 若是周期的, 确定其周期。
m 0 =aT[x1(n)]+bT[x2(n)]
m 0
第 1 章
时域离散信号和时域离散系统
(8) y(n)=x(n) sin(ωn) 令输入为
x(n-n0)
输出为 y′(n)=x(n-n0) sin(ωn) y(n-n0)=x(n-n0) sin[ω(n-n0)]≠y′(n)
故系统不是非时变系统。 由于
第 1 章
时域离散信号和时域离散系统
题4解图(一)
第 1 章
时域离散信号和时域离散系统
题4解图(二)
第 1 章
时域离散信号和时域离散系统
题4解图(三)
第 1 章
(4) 很容易证明:
时域离散信号和时域离散系统
x(n)=x1(n)=xe(n)+xo(n) 上面等式说明实序列可以分解成偶对称序列和奇对称序列。 偶对称序列可 以用题中(2)的公式计算, 奇对称序列可以用题中(3)的公式计算。 5. 设系统分别用下面的差分方程描述, x(n)与y(n)分别表示系统输入和输 出, 判断系统是否是线性非时变的。 (1)y(n)=x(n)+2x(n-1)+3x(n-2) (2)y(n)=2x(n)+3 (3)y(n)=x(n-n0) (4)y(n)=x(-n) n0为整常数
