受冲击荷载作用时构件的应力和变形计算精品PPT课件
合集下载
受冲击荷载作用时构件的应力和变形计算共51页

谢谢!
ห้องสมุดไป่ตู้
36、自己的鞋子,自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢,但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何,且尽全力做你应该做的事吧。——美华纳
受冲击荷载作用时构件的应力和变形 计算
6、法律的基础有两个,而且只有两个……公平和实用。——伯克 7、有两种和平的暴力,那就是法律和礼节。——歌德
8、法律就是秩序,有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起,可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的,因为好人用不着它们,而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
40、学而不思则罔,思而不学则殆。——孔子
机械工程基础-第三章 杆件受力变形及其应力分析-PPT课件
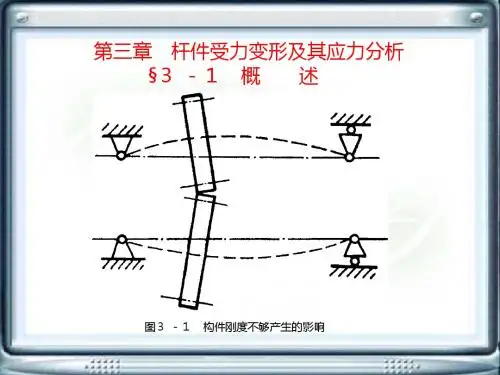
第三章 杆件受力变形及其应力分析 §3 -1 概 述
图3 -1
构件刚度不够产生的影响
图3 -2
杆件
图3 -3
杆件变形的基本形式
§3 -2
轴向拉伸和压缩
图3 -4
悬臂吊车
图3 -5
内燃机
图3 -6
截面法求轴力
图3 -7ຫໍສະໝຸດ 轴受力分析图3 -8
拉伸应力
图3 -9
拉伸试件
图3 -10
低碳钢拉伸图
图3 -43
平面弯曲
图3 -44
用截面法求梁的内力
图3 -45
弯矩的符号规定
图3 -46
简支梁受力分析
图3 -47
简支梁受均布载荷作用时的弯矩图
图3 -48
简支梁受集中力作用时的弯矩图
图3 -49
简支梁受力偶作用时的弯矩图
图3 -50
梁弯曲时的变形
图3 -51
中性层和中性轴
图3 -52
图3 -11
低碳钢Q235的σ-ε曲线
图3 -12
滑移线
图3 -13
颈缩现象
图3 -14
冷作硬化
图3 -15
灰口铸铁、玻璃钢拉伸时的σ-ε曲线
图3 -16
低碳钢压缩σ-ε曲线
图3 -17
铸铁压缩的σ-ε曲线
图3 -18
发动机连杆
图3 -19
起重吊环
图3 -20
支架受力分析
图3 -21
拉伸变形
图3 -22
杆件受力分析
§3 -3
剪
切
图3 -23
销的受力情况
图3 -24
螺栓受力情况
图3 -25
剪切
图3 -26
图3 -1
构件刚度不够产生的影响
图3 -2
杆件
图3 -3
杆件变形的基本形式
§3 -2
轴向拉伸和压缩
图3 -4
悬臂吊车
图3 -5
内燃机
图3 -6
截面法求轴力
图3 -7ຫໍສະໝຸດ 轴受力分析图3 -8
拉伸应力
图3 -9
拉伸试件
图3 -10
低碳钢拉伸图
图3 -43
平面弯曲
图3 -44
用截面法求梁的内力
图3 -45
弯矩的符号规定
图3 -46
简支梁受力分析
图3 -47
简支梁受均布载荷作用时的弯矩图
图3 -48
简支梁受集中力作用时的弯矩图
图3 -49
简支梁受力偶作用时的弯矩图
图3 -50
梁弯曲时的变形
图3 -51
中性层和中性轴
图3 -52
图3 -11
低碳钢Q235的σ-ε曲线
图3 -12
滑移线
图3 -13
颈缩现象
图3 -14
冷作硬化
图3 -15
灰口铸铁、玻璃钢拉伸时的σ-ε曲线
图3 -16
低碳钢压缩σ-ε曲线
图3 -17
铸铁压缩的σ-ε曲线
图3 -18
发动机连杆
图3 -19
起重吊环
图3 -20
支架受力分析
图3 -21
拉伸变形
图3 -22
杆件受力分析
§3 -3
剪
切
图3 -23
销的受力情况
图3 -24
螺栓受力情况
图3 -25
剪切
图3 -26
哈尔滨工程大学力学基础课件第13章解读

g
9.8
由于工字钢的自重和惯性力同向且同量级,所 以,计算动应力时应考虑自重的影响,工字钢上总 的动载荷集度
例1
求吊索和工字钢中的最大动应力。
l 12m a 5m s2 A 1.08cm2
解 qj 47.9kg m 469.42 N m
q q j a 469.42 5 239.50 N m
荷下的强度条件为
x
d max Kd j max [ ]
d max
式中 [ ]是材料在静载荷 作用下的许用应力。
o
d
( c)
例1
一长为l 12m 的28b工字钢,有横截面 积为 A 1.08cm2 的钢索AB,AC吊起,并以 等加速度a 5m s2上升(图a),求吊索和工 字钢中的最大动应力。
7800)
402
x
62700x
N
m
A
当x=0
qd 0
C
wD
600
600
B
600
当x=0.04m qd 2510 N m
qd(x )
当x=0.6m qd 37600 N m
例 3 直径为80mm,试校核AB轴及CD杆的强度。
[ ] 70MPa 7.8g cm3 w 401 s
解 CD杆危险截面D上轴力和正应力分 C
第十三章 动载荷
13、1 概 述 13、2 简单惯性力问题 13、3 构件受冲击时的应力和变形计算 13、4 提高构件抗冲击能力的措施
13.1 概 述 载荷不随时间变化(或变化极其平稳缓慢)
且使构件各部件加速度保持为零(或可忽略不 计),此类载荷为静载荷。
载荷随时间急剧变化且使构件的速度有显著 变化(系统产生惯性力),此类载荷为动载荷。
11动载荷_2冲击载荷

P
st
d
解得钢丝绳的动荷伸长
d Kd st
式中,动荷因数
l
Kd 1
v2 g
st
静荷伸长
st
Pl EA
d
P
钢丝绳内的静荷应力
st
P A
所以,钢丝绳内的动荷应力
d Kd st 1
v2 g
st
P A
1
v 2 EA gPl
P A
所以,此时轴内的最大扭转切应力
d max
Td Wt
JGIp Wt 2l
1057 MPa
◆ 相较前例,最大切应力增大了约 395 倍。在这种情况下,早 已超过了材料的许用切应力。因此,为了保证转轴的安全,在停 车时应尽量避免急刹车。
解:当滑轮被卡住,重物的速度由 v 瞬间降为零,使钢丝绳受到冲击。
此时,前面公式不再适用。
l
根据能量守恒原理,重物在冲击过程
中损失的动能和重力势能应等于钢丝
绳内增加的弹性变形能,即有
d
v
st
P
1 P v2 P
2g
d st
1 2
Fd d
1 2
Pst
P
在线弹性范围内,
Fd
◆ 与前者相比,此时的动荷应力小了很多。可见,弹簧起到了 缓冲作用,使冲击载荷大大减小。
[例3] 一正方形截面外伸梁如图,已知梁的尺寸 l = 1 m,截面边长 a = 50 mm ,弹性模量 E = 200 GPa。若一重 P = 150 N 的物体,自 高度 h = 75 mm 处自由落下,撞击梁的跨中截面 C ,试计算梁自由 端 D 的动荷挠度与梁内的动荷最大弯曲正应力。
材料力学PPT课件第十二章动载荷

7
§12—3 构件受冲击荷载作用时的动应力
一、冲 击
一个运动的物体(冲击物)以一定的速度,撞击另 一个静止的物体(被冲击构件),静止的物体在瞬间使 运动物体停止运动,这种现象叫做冲击。
二、冲击问题的分析方法:能量法
假设——
1、被冲击构件在冲击荷载的作用下服从虎克定律;
2、不考虑被冲击构件内应力波的传播
3、冲击过程只有动能、势能、变形能的转换,无其它能量损失。
4、冲击物为刚体,被冲击构件的质量忽略不计;
2021/7/13
8
三、冲击问题的简便计算方法
1、自由落体冲击 如图所示,L、A、E、Q、h 均为已知量,
求:杆所受的冲击应力。
解(1)冲击物的机械能:
Q Fd L
2021/7/13
h
TV0Q (h d)
3
§12—2 惯性力问题
一、 匀加速直线运动构件的动应力计算
如图所示,一起重机绳索以等加速度 a 提升一等截面直
杆,直杆单位体积的重量(比重、重度)为γ,横截面面积
为 A,杆长为L,不计绳索的重量。求:杆内任意横截面的 动应力、最大动应力。
F a
x
2021/7/13
解:1、动轴力的确定
FNd
Ax
实验表明:在静载荷下服从虎克定律的材料,只要应力不超 过比例极限 ,在动载荷下虎克定律仍成立且 E静 = E动。
四、动载荷问题的分类:
(1)构件作等加速直线运动和等速转动时的动应力计算; (2)构件在受冲击和作强迫振动时的动应力计算; (3)构件在交变应力作用下的疲劳破坏和疲劳强度计算。
2021/7/13
问题?
对于等截面受冲拉(压)或扭转杆件,其冲击应力与
动应力计算

E v Eh Ud 1 1 48EI E h Ph d U d Pd d 3 d d 2 2 L 3 1 48EI 2 PL 1 2 h d d Ph d 3 d 2 L 48EI 2 1 2 d st h d 2
第九章
第一节
第二节 第三节 第四节 第五节 第六节
动荷载
概述
交变应力
构件作等加速直线运动或等速转动时的 动应力计算 构件在受迫振动时的应力计算 构件在受冲击时应力和变形的计算 交变应力下材料的疲劳破坏、疲 劳极限 钢结构构件及其连接的疲劳计算
2001.07
东南大学远程教育
第一节
几个概念
概述
1.静载—①荷载增加缓慢,再从零增加到某值,保持P不变或变动很小 ②加载过程中引起构件内各质点的加速度很小而忽略 2.动载—①P随时间而改变(地震、风等、海浪冲击海浪冲击海洋平台 ②作加速运动或作匀速转动的流中构件的惯性力也是一种动载。 例如起重机吊物,机械中的飞轮 3.动应力—在动载作用下,构件内的应力
可知,杆内各点处的惯性力是 个分布力系,为此,可用线分 布力集度q d 来度量惯性力的大 小。
m
x
P
m
Nx
惯性力集度 q d为单位长度杆的质量与加速度 的乘积,即
A 1 A qd g g
2001.07 东南大学远程教育
第二节 构件作等加速直线运动 或等速转动时的动应力计算
讨论对象
作等加速直线运 动或等速转动的构件 受冲击荷载作用的构件和强迫振动的构件的动应力计算 交变应力作用下的构件的疲劳破坏和疲劳强度校核
2001.07
混凝土结构设计原理PPT课件第9章 钢筋混凝土受弯构件的应力裂缝和变形计算
cc t 0.80 f ck
si t 0.75 f sk
矩形截面
受压区混凝土边缘
t Mk x cc 0.80 f ck Icr
受拉钢筋面积的重心处
si Es
t t Mk ( hoi x ) 0.75 f sk I cr
翼板位于受压区的T形截面 判断T形截面类型:
l cr s ( 1 c / s )
M
l cr
M
ss
Es
l cr
无滑移理论
M
l cr
M
最大裂缝宽度
W f max kc
ss
Es
综合理论
W f max 2.1
sk
Es
( 1.9c 0.08
d eq
te
)
9.4.2 《公路桥规》关于最大裂缝宽度的计算方法
1 bf x 2 Es As ( h0 x ) 2
计算应力
9.4 受弯构件最大裂缝宽度的验算 裂缝产生的原因 作用的效应引起的裂缝。 由外加变形或约束引起的裂缝 钢筋锈蚀裂缝
9.4.1 受弯构件弯曲裂缝宽度计算理论 粘结滑移理论
裂缝平均宽度:
W f l cr ( s c )
ssAs
(b)
偏心受拉构件
e
e0
N se ss ) As ( h0 as
e Ns As
As
sAs C
ssAs
h0–a s(c)源自偏心受压构件es Ns nse0 As
N s ( es z ) ss As z
z [ 0.87 0.12( 1 f )(
第九章 钢筋混凝土受弯构件的应力、裂 缝和变形计算
si t 0.75 f sk
矩形截面
受压区混凝土边缘
t Mk x cc 0.80 f ck Icr
受拉钢筋面积的重心处
si Es
t t Mk ( hoi x ) 0.75 f sk I cr
翼板位于受压区的T形截面 判断T形截面类型:
l cr s ( 1 c / s )
M
l cr
M
ss
Es
l cr
无滑移理论
M
l cr
M
最大裂缝宽度
W f max kc
ss
Es
综合理论
W f max 2.1
sk
Es
( 1.9c 0.08
d eq
te
)
9.4.2 《公路桥规》关于最大裂缝宽度的计算方法
1 bf x 2 Es As ( h0 x ) 2
计算应力
9.4 受弯构件最大裂缝宽度的验算 裂缝产生的原因 作用的效应引起的裂缝。 由外加变形或约束引起的裂缝 钢筋锈蚀裂缝
9.4.1 受弯构件弯曲裂缝宽度计算理论 粘结滑移理论
裂缝平均宽度:
W f l cr ( s c )
ssAs
(b)
偏心受拉构件
e
e0
N se ss ) As ( h0 as
e Ns As
As
sAs C
ssAs
h0–a s(c)源自偏心受压构件es Ns nse0 As
N s ( es z ) ss As z
z [ 0.87 0.12( 1 f )(
第九章 钢筋混凝土受弯构件的应力、裂 缝和变形计算
材料力学性能教学课件材料在冲击载荷下的力学性能
材料力学性能教学课件材料在冲击
27
载荷下的力学性能
第三节 低温脆性
❖ 同一材料,使用同一定义方法,由于外界因素的变化 (如试样尺寸、缺口尖锐度和加载速率等),tk也要 变化,
❖ 所以在一定条件下用试样测得的tk,由于和实际结构 工况之间无直接联系,所以不能说明该材料制成的机 件一定在该温度下脆裂。
口面积的50%时的温度为tk,
记为50%FATT或FATT50、
t50。
材料力学性能教学课件材料在冲击
26
载荷下的力学性能
第三节 低温脆性
❖ 韧脆转变温度tk可用于抗脆断设计、保证机件 服役安全,但不能直接用来设计计算机件的承 载能力或截面尺寸。
❖ 机件的最低使用温度必须高于tk,两者相差越 大越安全,所以选用的材料应该具有一定的韧 性温度储备,也就是说具有一定的△值, △=t0-tk。
建造中的Titanic 号,可以看到船身上长长 的焊缝
材料力学性能教学课件材料在冲击
21
载荷下的力学性能
第三节 低温脆性
❖ 挑战者号失事了!
❖ 爆炸后的碎片在发射东南方 30km处散落了1h之久,价值 12亿美元的航天飞机,顷刻化 为乌有,7名机组人员全部遇难。 全世界为此震惊。
❖ 事故原因最终查明:起因是助 推器两个部件之间的接头因为 低温变脆破损(在航天飞机设 计准则明确规定了推进器运作 的温度应为40~90°F,而在实 际运行时,整个航天飞机系统 周围温度却是处于31~99°F的 范围。),喷出的燃气烧穿了 助推器的外壳,继而引燃外挂 燃料箱。燃料箱裂开后,液氢 在空气中剧烈燃烧爆炸造成的。
❖ 1985年以后,探险家们数次深潜到12,612英尺深的海底研究沉船,起出 遗物。1995年2月美国《科学大众》(Popular Science)杂志发表了R Gannon 的文章,标题是『What Really Sank The Titanic』,付标题是 “为什么‘不会沉没的’船在撞上一个冰山后3小时就沉没了?一项新的 科学研究回答了80年未解之谜“。
冲击应力
2H ) d st (1 1 st
2h d st (1 1 ) st
•公式推导的近似性与公式精度思考
2h Kd 1 1 st
思考1:如果h=0(突然将重物放到梁上),动载系数为多少? A P B
Kd 2
结论:突加重物时,动载系数为2,即弹性体的变形和应力均比 同值静载荷时增加一倍。 思考2:如何减少冲击对构件强度的影响? 结论:冲击载荷不仅与重物重量P和冲击高度h有关,还与相应 的静位移Δst有关。静位移Δst越大,被冲击弹性体的刚度越小, 冲击载荷越小。 进行承受冲击的构件设计时,条件允许,尽可能降低其刚 度,例如增加缓冲弹簧、加垫片等。
例1重量 P=1kN的重物从 h=40mm处自由下落,冲击在木制悬臂梁的 自由端处。l=2m,木材的E=10GPa。求梁的最大正应力及最大挠度。
解:1、计算最大静挠度
Kd 1 1
A
2h st
1000 2000 10 mm 3 120 200 3 3 10 4 12
2 20 kd 1 1 5.05 2.6
例3:已知P=500N, H=20mm, l=100mm, b=50mm, E=200GPa, 求如下两种情况下C截面挠度d和梁内的最大正应力d 。 1) 两端铰支。
P H A l/2 l/2 C b b H A l/2 l/2 C
2) 两端弹簧支持,k=100N/mm
工程简化模型的推论 冲击变形最大时,冲击 物的速度为零 冲击变形最大,被冲击 物的应力也最大 冲击物的势能转化为被 冲击物的应变能 E Vε
•最大冲击位移d与最大冲击载荷Fd公式推导
势能零点——最大变形 •机械能守恒
E V
2h d st (1 1 ) st
•公式推导的近似性与公式精度思考
2h Kd 1 1 st
思考1:如果h=0(突然将重物放到梁上),动载系数为多少? A P B
Kd 2
结论:突加重物时,动载系数为2,即弹性体的变形和应力均比 同值静载荷时增加一倍。 思考2:如何减少冲击对构件强度的影响? 结论:冲击载荷不仅与重物重量P和冲击高度h有关,还与相应 的静位移Δst有关。静位移Δst越大,被冲击弹性体的刚度越小, 冲击载荷越小。 进行承受冲击的构件设计时,条件允许,尽可能降低其刚 度,例如增加缓冲弹簧、加垫片等。
例1重量 P=1kN的重物从 h=40mm处自由下落,冲击在木制悬臂梁的 自由端处。l=2m,木材的E=10GPa。求梁的最大正应力及最大挠度。
解:1、计算最大静挠度
Kd 1 1
A
2h st
1000 2000 10 mm 3 120 200 3 3 10 4 12
2 20 kd 1 1 5.05 2.6
例3:已知P=500N, H=20mm, l=100mm, b=50mm, E=200GPa, 求如下两种情况下C截面挠度d和梁内的最大正应力d 。 1) 两端铰支。
P H A l/2 l/2 C b b H A l/2 l/2 C
2) 两端弹簧支持,k=100N/mm
工程简化模型的推论 冲击变形最大时,冲击 物的速度为零 冲击变形最大,被冲击 物的应力也最大 冲击物的势能转化为被 冲击物的应变能 E Vε
•最大冲击位移d与最大冲击载荷Fd公式推导
势能零点——最大变形 •机械能守恒
E V
材料力学-动荷载和交变应力
应变能
Ve
=
1 2
Fd d
Fd
=
EA l
d
应变能
Ve
=
1 2
Fd d
令 C= EA l
被冲击构件的 刚度系数
Fd = C d
W
vh
d
EA l
将 W 以静荷载的方式作用于冲击点处
被冲击构件沿冲击方向的静变形为 st
W = C st
C
=
W st
Fd =
W st
d
能量守恒方程
d2 - 2 st d - 2 st h = 0
对疲劳破坏的解释与构件的疲劳破坏断口是吻合的
光滑区 —— 裂纹扩展区 粗糙区 —— 最后突然
断裂形成的
构件的疲劳破坏,是在没有明显预兆的情况下 突然发生的,往往会造成严重的事故。
§13-5 交变应力的特性与疲劳极限
应力循环
应力每重复变化一次
一个应力循环
s
重复的次数 —— 循环次数
r s = min
构件中各质点以变速运动时,构件就承受动荷载 的作用。
构件由动荷载引起的应力和变形 动应力 动变形
静荷载作用下服从虎克定律的材料,在动荷载作用下, 只要动应力不超过材料的比例极限,虎克定律仍然成立。
构件内的应力随时间作周期性交替变化
交变应力
在交变应力的长期作用下: 即使是塑性很好的材料、最大工作应力远低于
仍服从虎克定律。
冲击过程中不考虑波动效应,不计声、热能损失。
一、竖向冲击问题
重为 W 的物体,从高度 h 处自由下落 到杆的顶端。
变形最大时:Fd 、d 、sd
冲击物在冲击前后动能和势能的改变 等于被冲击构件所获得的应变能。
