第4章习题及解答
第4章 汇编语言程序设计习题解答

习题4.10 习题
• 下面程序段是实现从键盘输入十个一位 进制数后 下面程序段是实现从键盘输入十个一位10进制数后 累加,最后累加和以非压缩BCD码形式存放在 码形式存放在AH 累加,最后累加和以非压缩 码形式存放在 高位) 低位) (高位)和AL (低位)中。试把程序段中所空缺 的指令填上。 的指令填上。 XOR BX ,BX ;BX清零 清零 MOV CX,10 ; 传送数据长度 LOP:MOV AH,01H;中断 中断INT 21H的01H号调用 中断 的 号调用 INT 21H ;中断调用 中断调用P172, 键入值送入 中 键入值送入AL中 中断调用 MOV AH,BH ;将BH的内容传 的内容传AH 将 的内容传 ADD AL,BL ;BL与AL的值相加 结果在 中 的值相加,结果在 与 的值相加 结果在AL中 AAA ;非压缩 非压缩BCD码加法调整 非压缩 码加法调整 MOV BX,AX ;累加结果送 累加结果送BX 累加结果送 LOOP LOP ;CX-1→CX,判断 判断CX≠0,下列要求在数据段中依次书写各数据定义语句: 试按下列要求在数据段中依次书写各数据定义语句: 为首字节的连续存储单元中存放20H个重 (1)以DA1为首字节的连续存储单元中存放 ) 为首字节的连续存储单元中存放 个重 复的数据序列: , , 个 ,一个7。 复的数据序列:2,3,10个4,一个 。 为字符串变量, (2)DA2为字符串变量,用字变量(DW)设置一字 ) 为字符串变量 用字变量( ) 符串; 符串;‘STUDENTS’(按次顺序存放在各单元中)。 (按次顺序存放在各单元中)。 赋值以DA1为首地址 (3)用等值语句给符号 )用等值语句给符号COUNT赋值以 赋值以 为首地址 的数据区共占有的字节数, 的数据区共占有的字节数,此等值语句必须放在最 后一语句。 后一语句。 解答: 解答: ),7) (1)DA1 DB 20H DUP(2,3,10 DUP(4), ) ) ( , , ( ), (2)DA2 DW ‘TS’, ‘DU’,‘NE’,’ST’, ) , , , , (3) COUNT EQU DA2- DA1 )
微机原理及接口第四章习题答案

“微机系统原理与接口技术”第四章习题解答1.判断以下说法能否正确,若有错,请说明原由并更正。
(1)伪指令在汇编过程中不会产生二进制代码。
(2)宏和过程的同样之处是都可用于简化源程序书写、精简目标代码。
(3)在计算机中,高级语言往常需要变换为汇编语言后才能履行。
(4)汇编语言程序上机一般包含编写、汇编、链接和调试几个步骤。
答:( 1)正确。
(2)错误。
宏不可以精简目标代码。
(3)错误。
高级语言程序经编译或解说后直接变换为目标代码。
(4)正确。
2.已知数据和符号定义A1DB?A2DB8K1EQU 100判断以下指令的正误,并说明错误指令的原由。
(1) MOVK1, AX(2) MOVA2, AH(3) MOVBX, K1MOV [BX] , DX(4) CMPA1, A2( 5) K1EQU 200答:( 1)错误。
K1 是符号常数,在此处相当于立刻数100 ,故不可以做目的操作数。
(2)正确。
(3)正确。
(4)错误。
A1、 A2 都是字节变量,相当于两个储存器单元,故不可以同时出现在一条指令中直接进行比较。
( 5)错误。
用EQU定义的符号不可以从头赋值,除非已用PURGE排除了原值。
3.若数据段中有定义NUM1EQU 23HNUM2DW0则指令MOV NUM2, NUM1 的源、目操作数的寻址方式以及指令履行后NUM2+ 1 单元的内容分别是什么?答:指令 MOV NUM2,NUM1的源操作数使用立刻数寻址,目的操作数使用直接寻址。
指令履行后NUM2+ 1 单元的内容是0。
4.设 DS=6000H, BX=8432H,SS=5000H,SP=3258H,内存 69632H~ 69635H 单元的内容挨次是 00H、11H、22H、33H。
4 字节指令 CALL DWORDPTR[BX+1200H] 自己位于 2000H:3250H处的双字单元中。
当8086 履行该指令后转移至子程序进口时,CS、IP 、 SS、SP 各寄存器以及栈顶 2 个字单元的内容分别是多少?答:履行结果为CS=3322H,IP=1100H ,SS=5000H,SP=3254H,栈顶的两个字即断点地点,为2000H: 3254H。
第四章习题解答

第四章习题解4-3 已知调制信号()cos(2000)cos(4000)m t t t ππ=+,载波为4cos10t π,进行单边带调制,试确定该单边带信号的表示式,并画出频谱图。
[解]首先计算()m t 的希尔伯特变换,ˆ()sin(2000)sin(4000)mt t t ππ=+, 然后分别计算上边带与下边带的单边带调制信号。
上边带信号:44444411ˆ()()cos(10)()sin(10)221{[cos(2000)cos(10)sin(2000)sin(10)]2[cos(4000)cos(10)sin(4000)sin(10)]}1[cos(12000)cos(14000)]2U s t m t t mt t t t t t t t t t t t ππππππππππππ=−=−+−=+ 类似地,下边带信号为:1()[cos(8000)cos(6000)]2D s t t t ππ=+。
频谱图:实线为上边带信号,虚线为下边带信号。
4-6 某调制系统如图P4-6所示,为了在输出端同时得到f 1(t )和f 2(t ),试确定接收端的c 1(t)和c (t)f 1(t f 2(t f 1(t )f 2(t )[解] 1020()()cos 2()sin 2s t f t f t f t f t ππ=⋅+如果 10()cos 2c t f t π=,20()sin 2c t f t π= 则11020111()()cos4()sin 4222g t f t f t f t f t ππ⎡⎤=++⋅⎢⎥⎣⎦21020111()()sin 4()cos 4222g t f t f t f t f t ππ⎡⎤=⋅+−⎢⎥⎣⎦通过低通滤波器则输出正好是)(211t f 和)(212t f 。
(相干解调)4-7 设某信道具有均匀的双边噪声功率谱密度()n P f =0.5×10−3W/Hz ,在该信道中传输抑制载波的双边带信号,并设调制信号()m t 的频带限制在5kHz ,而载波为100kHz ,已调信号的功率为10kW 。
第4章 习题答案

50������-2 = 0
������������������������ = -0.5 +
������������
解得 L=10(已舍去负值)
且
������2������������������ ������������2
=
-100������-3<0
所以,当劳动投入量 L=10 时,劳动的
第四章 生产论 3. 已知生产函数 Q=f(L,K)=2KL-0.5L2 -0.5K2, 假定厂商目前处于短期生产,且 K =10。
(1)写出在短期生产中该厂商关于劳动的 总产量 TPL 函数、劳动的平均产量 APL 函数 和劳动的边际产量 MPL 函数。
(2)分别计算当劳动的总产量 TPL、劳动 的平均产量 APL 和劳动的边际产量 MPL 各自 达到最大值时的厂商的劳动投入量。
有 MP=0,于是,有 35+16L-3L2=0。
解得������ = − 5
3
和
L=7。������
=
-
5 3
不合
理,舍去,故取 L=7。
由此可得,生产要素 L 投入量的合理区 间为[4,7]。因此,企业对生产要素 L 的使用 量为 6 是处于短期生产的合理区间的。
11. 已知生产函数 Q=AL1/3K2/3。 判断:(1)在长期生产中,该生产函数的规模 报酬属于哪一种类型?
50 劳动的平均产量函数:
APL=
TPL =20-0.5L- 50
������
������
劳动的边际产量函数:
MPL=
������������������������ ������������
=20-L
(2)关于总产量的最大值:
何子述信号与系统习题解答第4章连续时间傅里叶分析(2012新)

2 2 3j 1
F δ t 1 δ
n
j t
F
n
再由傅里叶变换的线性,可得 h t 为
h t 2 t 3¢ t t
(c)同理可得
j Y 6Y j F 2 j F 3F
何子述
高等教育出版社
h t
题 4.8 解:
sin 1t πt
δ t
sin 2 t πt
该题中的单边带通滤波器的频率响应可看成是一个截止频率为 c 的低通滤波器的 频率响应在频谱上的一个搬移,搬移量为 3c ,由第三章傅里叶变化的频移特性知,信 号在时域乘以一个复指数信号 e j0t 后,其傅里叶变换在频域上平移 0 。 由主教材式(4.2.2)知,低通滤波器的冲激响应为
h t
由上可知,一定存在一个信号 g t ,使得
sin c t t
h t
且 g t 为
sin c t πt
g t
g t e j3c t
题 4.9 解: 由主教材式(4.2.1)知,理想低通滤波器的频率响应为
1, H 0,
由主教材式(4.2.2)知,其冲激响应为
c c
h t
sin c t πt
由主教材式(4.1.3)知,系统频率响应 H 可表示为
H H e jH
(a)由上式知,该滤波器对应的频率响应为
H1 H e
0 c c 0 其他
上式可看成截止频率为 c / 2 的低通滤波器被频移至 c / 2 和 c / 2 ,并分别乘上幅度 j 和 j ,且截止频率为 c / 2 的低通滤波器可表示为 H 2 ,所以 H 3 可表示为
第4章_组合逻辑电路习题解答
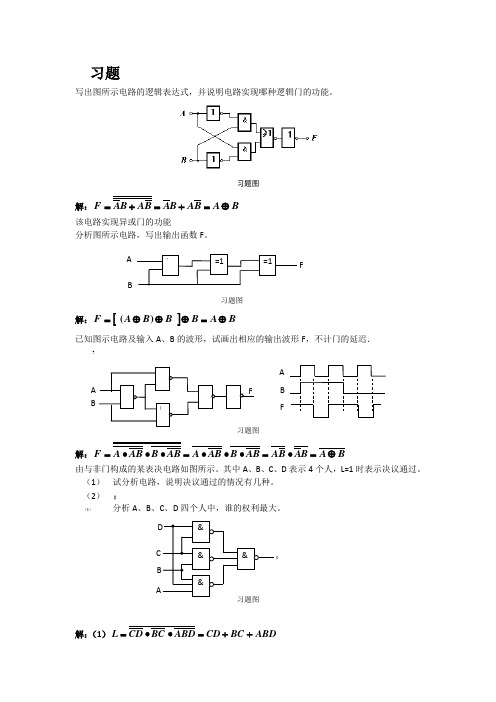
习题写出图所示电路的逻辑表达式,并说明电路实现哪种逻辑门的功能。
习题图解:B A B A B A B A B A F ⊕=+=+= 该电路实现异或门的功能分析图所示电路,写出输出函数F 。
习题图 解:[]B A B BB A F ⊕=⊕⊕⊕=)(已知图示电路及输入A 、B 的波形,试画出相应的输出波形F ,不计门的延迟.?解:B A B A B A AB B AB A AB B AB A F ⊕=•=•••=•••=由与非门构成的某表决电路如图所示。
其中A 、B 、C 、D 表示4个人,L=1时表示决议通过。
(1) 试分析电路,说明决议通过的情况有几种。
(2) 【 (3) 分析A 、B 、C 、D 四个人中,谁的权利最大。
习题图解:(1)ABD BC CD ABD BC CD L ++=••=C & && & D $ L B A " =1=1 =1FFA B[FB A(2)(3)根据真值表可知,四个人当中C 的权利最大。
分析图所示逻辑电路,已知S 1﹑S 0为功能控制输入,A ﹑B 为输入信号,L 为输出,求电路所具有的功能。
&习题图解:(1)011011)(S S B S A S S B S A L ⊕⊕+⊕=⊕⊕•⊕= (2)(3)当S 1S 0=00和S 1S 0=11时,该电路实现两输入或门,当S 1S 0=01时,该电路实现两输入或非门,当S 1S 0=10时,该电路实现两输入与非门。
(2)1¥电路逻辑功能为:“判输入ABC 是否相同”电路。
已知某组合电路的输入A 、B 、C 和输出F 的波形如下图所示,试写出F 的最简与或表达式。
习题图:解:(1)根据波形图得到真值表:,(2)由真值表得到逻辑表达式为C AB BC A C B A F ++=、设∑=)14,12,10,9,8,4,2(),,,(m D C B A F ,要求用最简单的方法,实现的电路最简单。
激光原理第四章习题解答
1 静止氖原子的4223P S →谱线中心波长为632.8纳米,设氖原子分别以0.1C 、O.4C 、O.8C 的速度向着观察者运动,问其表观中心波长分别变为多少? 解答:根据公式(激光原理P136) 由以上两个式子联立可得:代入不同速度,分别得到表观中心波长为:nm C 4.5721.0=λ,nm C 26.4144.0=λ,nm C 9.2109.0=λ解答完毕(验证过)2 设有一台麦克尔逊干涉仪,其光源波长为λ,试用多普勒原理证明,当可动反射镜移动距离L 时,接收屏上的干涉光强周期性的变化L 2次。
证明:对于迈氏干涉仪的两个臂对应两个光路,其中一个光路上的镜是不变的,因此在这个光路中不存在多普勒效应,另一个光路的镜是以速度υ移动,存在多普勒效应。
在经过两个光路返回到半透镜后,这两路光分别保持本来频率和多普勒效应后的频率被观察者观察到(从半透境到观察者两个频率都不变),观察者感受的是光强的变化,光强和振幅有关。
以上是分析内容,具体解答如下:无多普勒效应的光场:()t E E ⋅=πνν2cos 0 产生多普勒效应光场:()t E E ⋅=''02cos ''πνν在产生多普勒效应的光路中,光从半透经到动镜产生一次多普勒效应,从动镜回到半透镜又产生一次多普勒效应(是在第一次多普勒效应的基础上) 第一次多普勒效应:⎪⎭⎫⎝⎛+=c υνν1'第二次多普勒效应:⎪⎭⎫⎝⎛+≈⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+=c c c υνυνυνν21112'''在观察者处:()⎪⎭⎫ ⎝⎛⋅⋅⎪⎭⎫ ⎝⎛⋅+⋅==⎭⎬⎫⎩⎨⎧⎪⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛++⋅=+=t c t c t E t c t E E E E πνυπνυπνυπνπν2cos 22cos 2212cos 2cos 0021观察者感受到的光强:⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡⋅⎪⎭⎫ ⎝⎛⋅+=t c I I υνπ22cos 12显然,光强是以频率cυν⋅2为频率周期变化的。
计算机系统结构第四章(习题解答)
1. 假设一条指令的执行过程分为“取指令”、“分析”和“执行”三段,每一段的时间分别是△t 、2△t 和3△t 。
在下列各种情况下,分别写出连续执行n 条指令所需要的时间表达式。
⑴ 顺序执行方式。
⑵ 仅“取指令”和“执行”重叠。
⑶ “取指令”、“分析”和“执行”重叠。
答:⑴ 顺序执行方式12 ......1 2 12T =∑=++n1i i i i )t t t (执行分析取址=n(△t +2△t +3△t)=6n △t⑵ 仅“取指令”和“执行”重叠12 ......1 212T =6△t +∑=+1-n 1i i i )t t (执行分析=6△t +(n-1)(2△t +3△t)=(5n +1)△t⑶ “取指令”、“分析”和“执行”重叠12 34 ......1 2 3 41234△t2△t3△t△t2△t3△t△t2△t3△tT =6△t +∑=1-n 1i i )t (执行=6△t +(n-1)(3△t)=(3n +3)△t2. 一条线性流水线有4个功能段组成,每个功能段的延迟时间都相等,都为△t 。
开始5个任务,每间隔一个△t 向流水线输入一个任务,然后停顿2个△t ,如此重复。
求流水线的实际吞吐率、加速比和效率。
答:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15...1 2 3 4 5 6 7 8 9 10 11 12 13 14 151 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 56 7 8 9 10 11 12 13 14 151 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23我们可以看出,在(7n+1)Δt 的时间内,可以输出5n 个结果,如果指令的序列足够长(n →∞),并且指令间不存在相关,那么,吞吐率可以认为满足:)n (t75t )n /17(5t )1n 7(n 5TP ∞→∆=∆+=∆+=加速比为:)n (720n /17201n 7n 20t )1n 7(t 4n 5S ∞→=+=+=∆+∆⨯=从上面的时空图很容易看出,效率为:)n (75n /1751n 7n 5t )1n 7(4t 4n 5E ∞→=+=+=∆+⨯∆⨯=3. 用一条5个功能段的浮点加法器流水线计算∑==101i i A F 。
[分享]第四章刚体的转动问题与习题解答
第四章 刚体的转动 问题与习题解答问题:4-2、4-5、4-94-2如果一个刚体所受合外力为零,其合力矩是否也一定为零?如果刚体所受合外力矩为零,其合外力是否也一定为零?答:一个刚体所受合外力为零,其合力矩不一定为零,如图a 所示。
刚体所受合外力矩为零,其合外力不一定为零,例如图b 所示情形。
4-5为什么质点系动能的改变不仅与外力有关,而且也与内力有关,而刚体绕定轴转动动能的改变只与外力矩有关,而与内力矩无关?答:因为合外力对质点所作的功,等于质点动能的增量;而质点系中内力一般也做功,故内力对质点系的动能的增量有贡献。
而在刚体作定轴转动时,任何一对内力对转轴的力矩皆为一对大小相等、方向相反的力矩,且因定轴转动时刚体转过的角度d θ都一样,故其一对内力矩所作的功()0inij ij ji ij ji W M d M d M M d θθθ=+=+=,其内力功总和也为零,因而根据刚体定轴转动的动能定理可知:内力矩对其转动动能的增量无贡献。
4-9一人坐在角速度为0ω的转台上,手持一个旋转的飞轮,其转轴垂直地面,角速度为ω'。
如果突然使飞轮的转轴倒转,将会发生什么情况?设转台和人的转动惯量为J ,飞轮的转动惯量为J '。
答:(假设人坐在转台中央,且飞轮的转轴与转台的转轴重合)视转台、人和飞轮为同一系统。
(1)如开始时飞轮的转向与转台相同,则系统相对于中心轴的角动量为:10L J J ωω''=+飞轮转轴快速倒转后,飞轮的角速度大小还是ω',但方向与原来相反;如设转台此时的角速度为1ω,则系统的角动量为:21L J J ωω''=-在以上过程中,外力矩为零,系统的角动量守恒,所以有:10J J J J ωωωω''''-=+即 102J Jωωω''=+,转台的转速变大了。
(2)如开始时飞轮的转向与转台相反,则系统相对于中心轴的角动量为:10L J J ωω''=-飞轮转轴快速倒转后,飞轮的角速度大小还是ω',但方向与原来相反;如设转台此时的角速度为1ω,则系统的F 1F 3ab角动量为:21L J J ωω''=+在以上过程中,外力矩为零,系统的角动量守恒,所以有:10J J J J ωωωω''''+=-即 102J Jωωω''=-,转台的转速变慢了。
机械原理总复习题及解答第四章
机械原理总复习题及解答第四章第4章凸轮机构及其设计4.1填空题4.1.1.设计滚⼦从动件盘形凸轮机构时,滚⼦中⼼的轨迹称为凸轮的廓线;与滚⼦相包络的凸轮廓线称为廓线。
4.1.2.盘形凸轮的基圆半径是上距凸轮转动中⼼的最⼩向径。
4.1.3.根据图4.1的??22d d s 运动线图,可判断从动件的推程运动是_____________,从动件的回程运动是______________。
图4.1题4.1.9图4.1.4.在设计滚⼦从动件盘形凸轮轮廓曲线中,若出现时,会发⽣从动件运动失真现象。
此时,可采⽤⽅法避免从动件的运动失真。
4.2判断题4.2.1..偏置直动尖顶从动件盘形凸轮机构中,其推程运动⾓等于凸轮对应推程廓线所对中⼼⾓;其回程运动⾓等于凸轮对应回程廓线所对中⼼⾓。
( )4.2.2.在直动从动件盘形凸轮机构中进⾏合理的偏置,是为了同时减⼩推程压⼒⾓和回程压⼒⾓。
( )4.2.3.当凸轮机构的压⼒⾓的最⼤值超过许⽤值时,就必然出现⾃琐现象。
()4.2.4.凸轮机构中,滚⼦从动件使⽤最多,因为它是三种从动件中的最基本形式。
()4.2.5.直动平底从动件盘形凸轮机构⼯作中,其压⼒⾓始终不变。
()4.2.6.滚⼦从动件盘形凸轮机构中,基圆半径和压⼒⾓应在凸轮的实际廓线上来度量。
()4.2.7.滚⼦从动件盘形凸轮的实际轮廓曲线是理论轮廓曲线的等距曲线。
因此,只要将理论廓线上各点的向径减去滚⼦半径,便可得到实际轮廓曲线上相应点的向径。
()4.2.8.从动件按等加速等减速运动规律运动时,推程的始点、中点及终点存在柔性冲击。
因此,这种运动规律只适⽤于中速重载的凸轮机构中。
()4.2.9.从动件按等加速等减速运动规律运动是指从动件在推程中按等加速运动,⽽在回程中则按等减速运动,且它们的绝对值相等。
()4.2.10.从动件按等速运动规律运动时,推程起始点存在刚性冲击,因此常⽤于低速的凸轮机构中。
()4.2.11.在对⼼直动尖顶从动件盘形凸轮机构中,当从动件按等速运动规律运动时,对应的凸轮廓线是⼀条阿⽶德螺旋线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 多项式 4.1习题 ,()(),..(-)-(-)()()-(-)()--(-)(-)ZacadbcqZstadbcqacacbdabcdadbcacbdabcdacqacbdqabcd1. 设a,b,c,d已知(a-c)(ad+bc),求证(a-c)(ab+cd)证明:
又由 () 得 ()() 即 ,,-()()bdqZbdqZacabcd 即有
121212
,65(-3)13,65(-2)5,65-,65(-3)13(-2)571865-(6528)65(-65)-2828mmmmrccmcmcccmmr2. 一个整数被5除余3,被13除余2,求它被65除的余数解:设所求数为由题知 即 有 令 ,, 则有 故有
1723582957,581-143,-143202,0231414ababababbababa3. 对于下列的整数,分别求出以除所得的商和余数: (1), (2), (3), (4)解:)由带余除法,可表示为 故商为,余数为; )同理得 故商为,余数为; )由 知商为,余数为; 49595ba )由 知商为,余数为。
.()001ababbaqqZbqbaqqab4. 证明:若ab,b0,则证明:由 可得 又
又
1,)1.b11 1115. 设a,b是不全为零的整数,且a=da,b=db,d,a,bZ.证明d是a与b的一个最大公因数的充分必要条件是(a 1111111111
[]4.1.3,,..01(,)1[](,)1''1''1,''uvZstuavbdudavdbdduavbababuavbabuvuavbddd证明:根据定理得 即 又
故有
即 则有 综上所述,结论得证 6.(,)1,(,)1.,(1),,..()()(1),,1,1abababababddZduvZstuabvabduauvabduvaZuvaZab 证明:若则 证明:反证 假设() 且
故 ()与 () 矛盾 ,17.1..,()(),,.abababpabpapbppmnabkkZpabpbbkpapbpkmbmkmknbnknkp () 设是一个大于的整数且具有以下性质: 对于任意整数,,若,则或 证明是一个素数 证明:令 又
当 不整除,有,不整除 又有,不整除或; 不整除或 若为合数,那,mknkppkpbp么由可知必为素数,否则 同理可证当不整除时,也必为素数
4.2习题 224324321.,,(21)(1)251\2(2)(21)()12521-2,1,31khmxhxxkxxxmxxxkhxhkxhkxhkhkmkhmhk 求使
解:对于左边
即有 解之得
432322.()242,()254.()(),()(),()().fxxxxxgxxxxfxgxfxgxfxgx 设
计算 4324432700765432()()4292()()6()0254()()()23913131868kk
ikikifxgxxxxxfxgxxxgxxxxxfxgxabxxxxxxxx
解:由题得
令
323122
22
3.()59-73,()(53),()().-15-50[()()]3691()()04.()0().()0()()()fxxxxgxxxfxgxfxgxxfxgxsfxfxfxfxfxfx 设求乘积 的次数及其系数和解:根据 得 令 则有 的系数和 证明:当时,是偶次多项式证明: 又有 根据定理24.2.12()()()()(),()()2fxfxfxfxfxnnNfxn的()知 ()()() 再令 () 结论得证
2225.(),(),()..()()(),()()()0.(),(),()1221222132212fxgxhxfxxgxxhxfxgxhxgxgfxfhxhghfgghfhghfgf 设是实数域上的多项式证明如下 若是 则 证明:令 () () () 当 时,有 当 时,有 当 时,有 或 2222214()(),(),()(),(),()()()()06.(),(),()()0(),()1()0(),()hfxfxgxhxfxgxhxfxgxhxfxgxhxfxgxihxfxxgxxxhxx
又由题可知 是偶次多项式,又由于是实数域上的多项式 故 的次数不存在 即 求一组满足上题结论的不全为零的复系数多项式解:令 , 即 , 222()()0()()0(),()1xgxxhxfxfxgxihx
满足条件 即 ,
4.3 习题 3221.()321,()321,()()()().fxxxxgxxxgxfxqxrx设求用除
所得的商式和余数 23232
22
17393213212133751337147399299172(),()3999()()()()xxxxxxxxxxxxxxxqxxrxfxgxqxrx解:
故 即
24323224
1212112212
2.,,(1)()?012,1(1)()3.()(()()),()(()()),:()(()()()()),(),()mpqxmxxpxqpmmmrqmpmmqmxmxxpxqgxfxfxgxfxfxgxuxfxuxfxuxuxFx在适合什么条件时,解:由题知当余式时有 即当 时 有 设证明其中为中任意两个12121212121211()(()()),()(()())()(()()()())()(()()()())()(),()()3()()(igxfxfxgxfxfxgxfxfxfxfxgxfxfxfxfxgxfxgxfxuxFxi多项式 证明:
即 根据多项式整除性质)可知 1122112221,2)..()()(),()()()2()()(1,2)..()(()()()())4.(1)(),(1)(),(1)().11(1)(),(1)(iostgxuxfxgxuxfxuxFxistgxuxfxuxfxxfxxfxxfxxxfxxf 再根据性质)得
若则证明: 1212)(),()[]()()(1)(1)()()(1)(2)xuxuxFxfxuxxfxuxx
221
()()(1)(-1)-(2)(1)()(-1)()2uxuxxxfxx 得
212
()()()[]2(-1)()21-1()0ouxuxuxFxxfxxxfx 故
即 或时,可得出 同样结论成立
12121212
212
1212
5.(1)()(()()),()()()()(2)()()(),()()()()1(),()1,()1()(()())()()()gxfxfxgxfxgxfxgxfxfxgxfxgxfxgxxfxxfxxgxfxfxgxfxfx 若则且对吗? 若则或对吗?解:()不对 如 :令 可见 而 不整除 和 (21212122()-1,()1,()1()()()()()()gxxfxxfxxgxfxfxgxfxfx)不对 如 :令 可见 而 不整除 和
(1)(2)6.(1)(1),.,1()1(1)(1),(1)(1).(1)(1)(0),1(1)1,(1)(1)(1)(dnndqdqdqddndnnqdrdqrrdndxxdndndnnqdxxxxxxxxxnqdrrdxxxxxxxx
证明:的充分必要条件是(这里是正整数)证明 设 ,即 则 即 设,令则
且212121)(1)(1)0,0.7.()110220()32.(),()[]..(1)()10()(1)(2)()2dqdrxxxrdrdnfxxxfxxxuxuxFxstxuxfxxux ,又 故 ,即 设被除的余式为,被除的余式为, 求被 除的余式解:设 , 23120()(2)()[]..()32(3)(1)(2)-(2)(1)()32--10(1)434-10(1)fxuxFxstfxxxurxxfxxxuuxrx 又 , () 有 ()() () 由(),()可得
习题4.4
