九年级数学上册章末复习(三)图形的相似测试题湘教版
湘教版九年级数学上册第3章 图形的相似练习题

湘教版九年级数学上册第3章 图形的相似练习题1.2021·兰州2x =3y (y ≠0),那么下面结论成立的是( )A.x y =32B.x 3=2yC.x y =23D.x 2=y 32.2021·永州如图3-Y -1,以下条件不能判定△ADB ∽△ABC 的是( )图3-Y -1A .∠ABD =∠ACBB .∠ADB =∠ABCC .AB 2=AD ·ACD.AD AB =AB BC3.2021·重庆△ABC ∽△DEF ,且相似比为1∶2,那么△ABC 与△DEF 的面积比为( )A .1∶4B .4∶1C .1∶2D .2∶14.2021·张家界如图3-Y -2,D ,E 区分是△ABC 的边AB ,AC 的中点,假设△ADE 的周长是6,那么△ABC 的周长是( )A .6B .12C .18D .243-Y -23-Y -35.2021·枣庄如图3-Y -3,在△ABC 中,∠A =78°,AB =4,AC =6,将△ABC 沿图3-Y -4中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )图3-Y -4图3-Y -56.2021·哈尔滨如图3-Y -5,在△ABC 中,D ,E 区分为AB ,AC 边上的点,DE ∥BC ,F 为BC 边上一点,衔接AF 交DE 于点G ,那么以下结论中一定正确的选项是( )A.AD AB =AE ECB.AG GF =AE BDC.BD AD =CE AED.AG AF =AC EC7.2021·株洲如图3-Y -6,假定△ABC 内一点P 满足∠P AC =∠PBA =∠PCB ,那么点P 为△ABC 的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle ,1780—1855)于1816年终次发现,但他的发现并未被事先的人们所留意,1875年,布洛卡点被一个数学喜好者法国军官布洛卡(Brocard ,1845—1922)重新发现,并用他的名字命名.效果:在等腰直角三角形DEF 中,∠EDF =90°,假定点Q 为△DEF 的布洛卡点,DQ =1,那么EQ +FQ 等于( )A .5B .4C .3+ 2D .2+ 2图3-Y -6图3-Y -78.2021·湘潭如图3-Y -7,在△ABC 中,D ,E 区分是边AB ,AC 的中点,那么△ADE 与△ABC 的面积比S △ADE ∶S △ABC =________.9.2021·长春如图3-Y -8,直线a ∥b ∥c ,直线l 1,l 2与这三条平行线区分交于点A ,B ,C 和点D ,E ,F .假定AB ∶BC =1∶2,DE =3,那么EF 的长为________.图3-Y -8图3-Y -910.2021·娄底如图3-Y -9,∠A =∠D ,要使△ABC ∽△DEF ,还需添加一个条件,你添加的条件是________.(只需写一个条件,不添加辅佐线和字母)11.2021·长沙如图3-Y -10,△ABO 三个顶点的坐标区分为A (2,4),B (6,0),O (0,0),以原点O 为位似中心,把这个三角形增加为原来的12,可以失掉△A ′B ′O ,点B ′的坐标是(3,0),那么点A ′的坐标是________.图3-Y -10图3-Y -11.2021·吉林如图3-Y -11,数学活动小组为了测量学校旗杆AB 的高度,运用长为2 m 的竹竿CD 作为测量工具.移动竹竿,使竹竿顶端的影子与旗杆顶端的影子在空中O 处重合,测得OD =4 m ,BD =14 m ,那么旗杆AB 的高为________m.13.2021·凉山州如图3-Y -12,在边长为1的正方形网格中树立平面直角坐标系,△ABC 三个顶点的坐标区分为A (-1,2),B (2,1),C (4,5).(1)画出△ABC 关于x 轴对称的△A 1B 1C 1;(2)以原点O 为位似中心,在x 轴的上方画出△A 2B 2C 2,使△A 2B 2C 2与△ABC 位似,且位似比为2,并求出△A 2B 2C 2的面积.图3-Y -1214.2021·株洲如图3-Y -13所示,正方形ABCD 的顶点A 在等腰直角三角形DEF 的斜边EF 上,EF 与BC 相交于点G ,衔接CF .(1)求证:△DAE ≌△DCF ;(2)求证:△ABG ∽△CFG .图3-Y -1315.2021·怀化如图3-Y -14,△ABC 为锐角三角形,AD 是BC 边上的高,正方形EFGH 的一边FG 在BC 上,顶点E ,H 区分在AB ,AC 上.BC =40 cm ,AD =30 cm.(1)求证:△AEH ∽△ABC ;(2)求这个正方形的边长与面积.图3-Y -1416.2021·常德如图3-Y -15,直角三角形ABC 中,∠BAC =90°,D 在BC 上,衔接AD ,作BF ⊥AD 区分交AD 于点E ,交AC 于点F .(1)如图①,假定BD =BA ,求证:△ABE ≌△DBE .(2)如图②,假定BD =4DC ,取AB 的中点G ,衔接CG 交AD 于点M ,求证:①GM =2MC ;②AG 2=AF ·AC .图3-Y -15详解详析1.A [解析] 选项A ,两边都除以2y ,得x y =32,故A 契合题意;选项B ,两边除以不同的整式,故B 不契合题意;选项C ,两边都除以2y ,得x y =32,故C 不契合题意;选项D ,两边除以不同的整式,故D 不契合题意.应选A.2.D [解析] 选项A 中,∵∠ABD =∠ACB ,∠A =∠A ,∴△ADB ∽△ABC ,故此选项不合题意;选项B 中,∵∠ADB =∠ABC ,∠A =∠A ,∴△ADB ∽△ABC ,故此选项不合题意;选项C 中,∵AB 2=AD ·AC ,∴AB AC =AD AB, 又∵∠A =∠A ,∴△ADB ∽△ABC ,故此选项不合题意;选项D 中,由AD AB =AB BC不能判定△ADB ∽△ABC ,故此选项契合题意.3.A [解析] ∵△ABC ∽△DEF ,且相似比为1∶2,∴△ABC 与△DEF 的面积比为1∶4.4.B [解析] ∵D ,E 区分是AB ,AC 的中点,∴AD =12AB ,AE =12AC ,DE =12BC ,∴△ABC 的周长=AB +AC +BC =2AD +2AE +2DE =2(AD +AE +DE )=2×6=12.应选B.5.C [解析] A .阴影局部的三角形与原三角形有两个角相等,故两个三角形相似,故本选项不契合题意;B.阴影局部的三角形与原三角形有两个角相等,故两个三角形相似,故本选项不契合题意;C.两个三角形的对应边不成比例,故两个三角形不相似,故本选项契合题意;D.两个三角形对应边成比例且夹角相等,故两个三角形相似,故本选项不契合题意.应选C.6.C [解析] A .∵DE ∥BC ,∴△ADE ∽△ABC ,∴AD AB =AE AC,故A 错误;B.∵DE ∥BC ,∴AG GF =AE EC ,故B 错误;C.∵DE ∥BC ,∴BD AD =CE AE ,故C 正确;D.∵DE ∥BC ,∴△AGE ∽△AFC ,∴AG AF =AE AC,故D 错误.应选C. 7.D [解析] 如图,在等腰直角三角形△DEF 中,∠EDF =90°,DE =DF ,∠1=∠2=∠3.∵∠1+∠QEF =∠3+∠DFQ =45°,∴∠QEF =∠DFQ .又∵∠2=∠3,∴△DQF ∽△FQE ,∴DQ FQ =FQ QE =DF EF =12.∵DQ =1,∴FQ =2,EQ =2,∴EQ +FQ =2+2.应选D.8.1∶4 [解析] ∵D ,E 区分是边AB ,AC 的中点,∴DE ∥BC ,DE =12BC ,∴△ADE ∽△ABC ,∴S △ADE ∶S △ABC =(DE BC )2=14.故答案为1∶4. 9.6 [解析] ∵a ∥b ∥c ,∴AB BC =DE EF ,∴12=3EF,∴EF =6.故答案为6. 10.答案不独一,如AB ∥DE11.(1,2) [解析] ∵点A 的坐标为(2,4),以原点O 为位似中心,把这个三角形增加为原来的12,∴点A ′的坐标是(2×12,4×12),即(1,2).故答案为(1,2). 12.9 [解析] ∵OD =4 m ,BD =14 m ,∴OB =OD +BD =18 m .由题意可知∠ODC =∠OBA ,且∠O 为公共角,∴△OCD ∽△OAB ,∴OD OB =CD AB ,即418=2AB,解得AB =9(m),即旗杆AB 的高为9 m. 13.解:(1)如下图,△A 1B 1C 1就是所求作三角形.(2)如下图,△A 2B 2C 2就是所求作三角形.如图,区分过点A 2,C 2作y 轴的平行线,过点B 2作x 轴的平行线,交点区分为E ,F . ∵A (-1,2),B (2,1),C (4,5),△A 2B 2C 2与△ABC 位似,且位似比为2, ∴A 2(-2,4),B 2(4,2),C 2(8,10),∴S △A 2B 2C 2=8×10-12×6×2-12×4×8-12×6×10=28. 14.证明:(1)∵四边形ABCD 是正方形,△DEF 是等腰直角三角形,∴∠ADC =∠EDF =90°,AD =CD ,DE =DF ,∴∠ADE +∠ADF =∠ADF +∠CDF ,∴∠ADE =∠CDF .在△ADE 和△CDF 中,⎩⎪⎨⎪⎧DE =DF ,∠ADE =∠CDF ,AD =CD ,∴△ADE ≌△CDF .(2)延伸BA ,交ED 于点M ,∵△ADE ≌△CDF ,∴∠EAD =∠FCD ,即∠EAM +∠MAD =∠BCD +∠BCF .∵∠MAD =∠BCD =90°,∴∠EAM =∠BCF .∵∠EAM =∠BAG ,∴∠BAG =∠BCF .又∵∠AGB =∠CGF ,∴△ABG ∽△CFG .15.解:(1)证明:∵四边形EFGH 是正方形,∴EH ∥FG ,∴△AEH ∽△ABC .(2)如图,设EH 与AD 交于点P ,由(1)知△AEH ∽△ABC ,∴EH BC =AP AD. ∵AD 是BC 边上的高,四边形EFGH 是正方形,∴EF =FG =GH =EH ,四边形EFDP 是矩形,∴PD =EF ,∴AP =AD -PD =AD -EF =AD -EH ,∴EH 40=30-EH 30,解得EH =1207(cm),∴EH 2=(1207)2=1440049(cm 2),∴这个正方形的边长为1207 cm ,面积为1440049cm 2. 16.证明:(1)在Rt △ABE 和Rt △DBE 中,⎩⎪⎨⎪⎧BA =BD ,BE =BE , ∴Rt △ABE ≌Rt △DBE .(2)①过点G 作GH ∥AD 交BC 于点H ,∵AG =BG ,∴BH =DH .∵BD =4DC ,∴设DC =1,那么BD =4,∴BH =DH =2.∵GH ∥AD ,∴GM MC =HD DC =21, ∴GM =2MC .②过点C 作CN ⊥AC 交AD 的延伸线于点N ,那么CN ∥AG ,∴△AGM ∽△NCM ,∴AG NC =GM MC. 由①知GM =2MC ,∴2NC =AG .∵∠BAC =∠AEB =90°,∴∠ABF =∠CAN =90°-∠BAE ,∴△ACN ∽△BAF ,∴AF CN =AB AC. ∵AB =2AG , ∴AF CN =2AG AC , ∴2CN ·AG =AF ·AC ,∴AG 2=AF ·AC .。
湘教版数学九年级上册第三章图形的相似测试题

初中数学试卷九年级上数学第三章图形的相像测试题(时限: 100 分钟总分: 100 分)班级姓名总分一、 选择题 (此题共 8 小题,每题 3 分,共 24 分 )1. 已知ab c 0 ,则a b的值为 ( )23 4cA.4B.5D.15422. 如图, DE ∥BC ,在以下比率式中,不可以建立的是()AD = AEDE AEA.ECB.=DBBC ECAB =ACDB ABC.AED. =ADECAC3. 以下说法正确的选项是()A .两个正方形必定相像B .两个菱形必定相像C .两个等腰梯形必定相像D .两个直角梯形必定相像金戈铁制卷4. 如图,已知 1 2,那么增添以下一个条件后,仍没法 ..判断△ABC ∽△ADE 的是()A .B D B .C AEDD2A1C .ABAC D .ABBC AD AEAD DEB E C5. 如图,小正方形边长均为 1 ,则以下图中三角形 (暗影部分) 与△ABC 相像的是()A B C D6. 在平面直角坐标系中,已知 A ( 6 ,3 ),B ( 6 ,0)两点,以坐标原点 O 为位似中心,位似比为 1 ,把线段 AB 减小到线段 A ' B ' ,则 A ' B '的长度等于()3bDC7. 如图,用两根等长的钢条AC 和 BD 交错构成一个卡钳,能够用来丈量工作内槽的宽度 .设OAOB m ,且量得 CD b ,OOCOD则内槽的宽 AB 等于()ABbB.mbD. mbA.bC.m 1m8. 如图, P 为线段 AB 上一点, AD 与 BC 交于 E ,DC∠CPD =∠A =∠B , BC 交 PD 于 F , AD 交 PCEFG于 G ,则图中相像三角形有()APB金戈铁制卷A.1 对B.2 对C.3 对D.4 对二、填空题 (此题共 8 小题,每题 3 分,共 24 分 )9. 假如a= 2 ,那么 a ______ .b 3 a b10. 在比率尺是 1:8000 的某市地图上,若一条路的长度约25cm ,则它的实质长度约为______;对于地图上3cm ×5cm 的矩形广场相应的实质占地面积为_____平方千米 .11.如图,在△ ABC中,点D在AB上,请你再增添一个 A适合的条件,使△ ADC∽△ACB,那么要增添的条件是DB C________ 注(:只要添写一个知足要求的条件即可) .12. 在 Rt △ABC,若CD是 Rt △ABC斜边AB上的高,AD =3, CD=4,则 BC = _______.13. 顶角为 36 °的等腰三角形称为黄金三角形 .如图△ABC,△BDC,△DEC 都是黄金三角形.已知 AB=1,则 DE = _______.14. 张明同学想利用树影丈量校园内的树高,他在某一时辰测得小树高为 1.5m 时,其影长为 1.2m ,当他丈量教课楼旁的一棵大树影长时,因大树凑近教课楼,有一部分影子在墙上.经丈量,地面部分影长为 6.4m ,墙上影长为 1.4m ,那么这棵大树高约________m金戈铁制卷15.如图, DE 是ABC的中位线, M 是 DE 的中点,那么S NDM= .S NBC16 .在平面直角坐标系中,正方形ABCD 的地点如右图所示,点 A 的坐标为(1,0),点 D 的坐标为(0,2).延伸CB 交x 轴于点A1,作正方形A1 B1 C1C;延伸C1B1交x 轴于点A2,作正方形第 2013 A2B2C2C1,按这样的规律进行下去,个正方形的面积为.三、解答题 (共 52 分 )17.( 本小题满分 10 分 )如图,图中的小方格都是边长为 1 的正方形,△ABC与△A′B′C′是对于点O为位似中心的位似图形,它们的极点都在小正方形的极点上.(1 )画出位似中心点O;(2 )求出△ABC与△A′B′C′的位似比;(3 )以点O为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于 1.5 .金戈铁制卷ANDM湘教版数学九年级上册第三章图形的相似测试题A 18. ( 本小题满分 6 分 )如图,在△ ABC 中, D、 E 分别是 AC、 AB 边上的点,EDAED= C,AB=6, AD =4, AC=5, 求 AE 的长. B C19.( 本小题满分 6 分)如图,在边长为 1 的小正方形构成的网格中,△ABC 和△DEF 的极点都在格点上,判断△ABC 和△DEF 能否相像,并说明原因.金戈铁制卷湘教版数学九年级上册第三章图形的相似测试题20.( 本小题满分 6 分)如图,在平面直角坐标系中,△ABC 和△A'B'C '是以坐标原点O为位似中心的位似图形,且点B(3,1), B′(6,2).( 1 )若点 A(5, 3 ),则A′的坐标为;2( 2 )若△ABC 的面积为 m ,则△A′B′C′的面积=.21.(本小题满分 12 分 )已知:如图,在菱形ABCD 中,E为BC边上一点,∠AED= ∠ .B(1 )求证:△ABE∽△DEA;(2 )若AB =4 ,求AE DE的值.22.( 本小题满分 12 分 )小明想利用太阳光丈量楼高.他带着皮尺到达一栋楼下,发现对面墙上有这栋楼的影yA'AC'CB子,针对这类状况,他设计了一种丈量方案,详细丈量状况以下:如表示图,小明边O 1yA' 挪动边察看,发现站到点 E 处时,能够使自己落在墙上的影子与这栋楼落在墙上的影A金戈铁制卷C'CBO 1子重叠,且高度恰巧同样.此时,测得小明落在墙上的影子高度CD = 1.2m , CE=0.8m ,CA =30m (点A、E、C在同向来线上).已知小明的身高EF 是,请你帮小明求出楼高 AB (结果精准到0.1m ).BFDA E C九年级数学第三章图形的相像测试题参照答案一、选择题:; 2.B ;3.A ; 4.D ; 5.A ; 6. A ;7.D ;二、填空题: 9. 210. 2 千米, 0.096 ;11.ADC ACB 等;20 ;12.;5 3 3 5 1 9 201213. 2 ;14. 9.4 ;15.16;16. 5 ( 4) .三、解答题:金戈铁制卷17.略 .18.AE 10.319.解:△ABC 和△DEF 相像.由勾股定理,得AB 2 5,AC 5,BC=5 ,AB AC BC 5 QDF EF 2 ,DE22∴△ABC∽△DEF.20.( 1)( 5 , 6 );(2 ) 4 m .21. ( 1)证明:∵ 四边形ABCD是菱形,∴AD∥BC.∴AEB DAE .又∵∠B=∠AED,∴△ABE∽△DEA .(2 )解:∵△ABE∽△DEA,∴AE AB.∴ AE DE AB DA.DA DE∵四边形 ABCD 是菱形, AB = 4 ,∴ AB=DA =4.∴ AE DE AB2 16 .22. 18.8m.金戈铁制卷。
湘教版九年级数学上册 第三章 图形的相似 单元测试题(无答案)

第三章图形的相似单元测试题(满分120分;时间:120分钟)真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!题号一二三总分得分一、选择题(本题共计10 小题,每题3 分,共计30分,)1. 下列图形不是相似图形的是()A.所有的正三角形B.所有的矩形C.所有的正方形D.所有的圆2. 已知线段a,b,c,d,且满足ab =cd,下列等式中不一定成立的是()A.b a =dcB.b−aa=d−ccC.ba+b=cc+dD.a+cb+d=cd3. 已知△ABC∼△DEF,若△ABC与△DEF的相似比为2:3,△ABC的面积为40,则△DEF的面积为()A.60B.70C.80D.904. 如图,△AOB缩小后得△COD,△AOB与△COD的相似比是3,若点C坐标为(1, 2),则点A的坐标为()A.(2, 4)B.(2, 6)C.(3, 6)D.(3, 4)5. 已知两个相似多边形的相似比是3:4,其中较小多边形的周长为36cm,则较大多边形的周长为()A.48cmB.54cmC.56cmD.64cm6. 如图,在△ABC中,AF:FC=1:2,G是BF的中点,AG的延长线交BC于E,那么BE:EC的值为()A.1:4B.1:2C.2:5D.1:37. 下列条件中,能判定△ABC与△DEF相似的是()A.∠A=∠D,ACDF =BCEFB.∠A=∠C,ABDE=BCEFC.∠A=∠D=90∘,ABDE =BCEFD.∠A=∠D=90∘,∠C=55∘,∠F=25∘8. 如图:在△ABC中,点D、E分别在AB、AC上,根据下列给定的条件,不能判断DE 与BC平行的是()A.AD DB =AEECB.ADAB=AEACC.ADAE=ABACD.DEBC=AEAC9. 商家通常依据“乐观系数准则”确定商品销售价格,即根据商品的最低销售限价a,最高销售限价b(b>a)以及实数x(0<x<1)确定实际销售价格c=a+x(b−a),这里x被称为乐观系数.经验表明,最佳乐观系数x恰好使得b−ac−a =c−ab−c,据此可得,最佳乐观系数x的值等于()A.1 2B.√54C.√5+12D.√5−1210. 某班在布置新年联欢会会场时,需要将直角三角形彩纸裁成长度不等的矩形彩条.如图,在Rt△ABC中,∠C=90∘,AC=30cm,AB=50cm,依次裁下宽为1cm的矩形纸条a1,a2,…,a n.若使裁得的矩形纸条的长不小于5cm,则每张直角三角形彩纸能裁成的矩形纸条的总数为()A.24B.25C.26D.27二、填空题(本题共计10 小题,每题3 分,共计30分,)11. 已知:ab =23,则a−ba+b=________.12. 如图,由24个边长为1的正方形组成4×6的网格.若△A′B′C′∽△ABC(相似比不是1),且△A′B′C′,△ABC的顶点都是网格内正方形的顶点,则△A′B′C′的面积是________.13. 如图,△ABC中,DE // BC,AD=5,AB=10,AE=4,则AC的长为________.14. 如图,点都在网格线交点处的三角形叫做格点三角形,已知图中的每个小正方形的边长都是1个单位,在图中选择适当的位似中心,画一个与格点△DEF位似且位似比不等于1的格点三角形________.15. 如图,AC、BD相交于点O,要使△AOB∽△DOC,则要补充的条件可以是________.16. 张华同学的身高为1.6米,某一时刻他在阳光下的影长为2米,与他邻近的一棵树的影长为6米,则这棵树的高为________米.17. 在比例尺为1:500000的地图上,量得甲、乙两地的距离约为5厘米,则甲、乙两地的实际距离约为________千米.18. 若1x :1y=12,则x:y=________.19. 如图,△ABC顶角是36∘的等腰三角形(底与腰的比为√5−12的三角形是黄金三角形),若△ABC、△BDC、△DEC都是黄金三角形,已知AB=4,则DE=________.20. 如图,正方形ABCD的边长为4,AE=EB,MN=2,线段MN的两端在CB、CD上滑动,当CM=________时,△ADE与△CMN相似.三、解答题(本题共计6 小题,共计60分,)21. 已知梯形ABCD中,AD // BC,EF // BC,AE=FC,EB=634,DF=513,求AE长.22. 如图,图中小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形顶点上.(1)画出位似中心点O;(2)△ABC与△A′B′C′的位似比为________;(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的位似为1:2.23. 如图,在▱ABCD中,AC与BD交于点O,点F,E,M,N分别是AO,BO,CO,DO 的中点,这样形成一个▱FEMN,你能证明▱ABCD∽▱FEMN吗?24. 如图,A、B两点被池塘隔开,在AB外任选一点C,连接AC、BC分别取其三等分点M、N量得MN=38m.求AB的长.25. 要设计一座2m高的维纳斯女神雕像(如图),使雕像的上部AC(肚脐以上)与下部BC(肚脐以下)的高度比,等于下部与全部的高度比,即点C(肚脐)就叫做线段AB的黄金分割点,这个比值叫做黄金分割比.试求出雕像下部设计的高度以及这个黄金分割比?(结果精确到0.001)26. 已知P为△ABC内任意一点,连AP,BP,CP并延长分别交对边于D,E,F.求证:(1)PDAD +PEBE+PFCF=1(2)APAD ,BPPE,CPPF三者中,至少有一个不大于2,也至少有一个不少于2.。
九年级上册数学单元测试卷-第3章 图形的相似-湘教版(含答案)
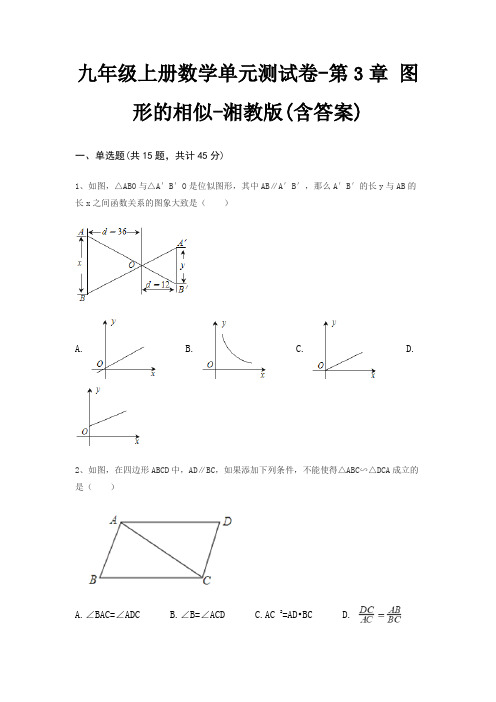
九年级上册数学单元测试卷-第3章图形的相似-湘教版(含答案)一、单选题(共15题,共计45分)1、如图,△ABO与△A′B′O是位似图形,其中AB∥A′B′,那么A′B′的长y与AB的长x之间函数关系的图象大致是()A. B. C. D.2、如图,在四边形ABCD中,AD∥BC,如果添加下列条件,不能使得△ABC∽△DCA成立的是()A.∠BAC=∠ADCB.∠B=∠ACDC.AC 2=AD•BCD.3、若△ABC∽△A′B′C′,相似比为2:3,则△ABC与△A′B′C′的周长的比为()A.2:3B.4:9C.3:2D. :4、如图所示为农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏板DE长为1米,支撑点A到踏脚D的距离为0.6米,原来捣头点E着地,现在踏脚D着地,则捣头点E上升了()A.0.5米B.0.6米C.0.3米D.0.9米5、如图,在矩形ABCD中,DE⊥AC于E,∠EDC∶∠EDA=1∶3,且AC=10,则DE的长度是()A.3B.5C.D.6、下面四个图案:不等边三角形、等边三角形、正方形和矩形,其中每个图案花边的宽度都相同,那么每个图形中花边的内外边缘所围成的几何图形不相似的个数有()A.4个B.3个C.2个D.1个7、如图,A,B两点分别在反比例函数和的图像上,连接OA,OB,若OA ⊥OB,OB=2OA,则k的值为()A.-2B.2C.-4D.48、如图,在△中,D,E两点分别在边, 上,∥.若,则为()A. B. C. D.9、如图,Rt△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D,按下列步骤作图:步骤1:分别以点C和点D为圆心,大于CD的长为半径作弧,两弧相交于M,N两点;步骤2:作直线MN,分别交AC,BC于点E,F;步骤3:连接DE,DF。
若AC=4,BC=2,则线段DE的长为()A. B. C. D.10、如图,直线与双曲线(k>0,x>0)交于点A,将直线向上平移4个单位长度后,与y轴交于点C,与双曲线(k>0,x>0)交于点B,若OA=3BC,则k的值为( )A.3B.6C.D.11、如图,在平面直角坐标系中,已知点,,以原点为位似中心,相似比为,把缩小,则点的对应点的坐标是()A. 或B.C.D. 或12、如图,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,若AD=1,BC=3,则的值为( )A. B. C. D.13、如图,Rt△BOA与Rt△COA的斜边在x轴上,BA=6,A(10,0),AC与OB相交于点E,且CA=CO,连接BC,下列判断一定正确的是()①△ABE∽△OCE;②C(5,5);③BC=;④S△ABC=3.A.①③B.②④C.①②③D.①②③④14、如图,下列条件中不能判定△ACD∽△ABC的是()A.∠ADC=∠ACBB.C.∠ACD=∠BD.AC 2=AD•AB15、如图,在△ABC中,D、E、F分别是边AB、AC、BC上的点,连接EF,CD相交于点G,若四边形BDEF是平行四边形,则下列说法不正确的是()A. B. C. D.二、填空题(共10题,共计30分)16、在平面直角坐标系中,将以点为位似中心,为位似比作位似变换,得到.已知,则点的坐标是________.17、两个相似三角形的相似比为1:3,则它们周长的比为________.18、如图,铁道路口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高为________.(杆的宽度忽略不计)19、如果= ,那么的值等于________.20、有一块三角形的草地,它的一条边长为25m.在图纸上,这条边的长为5cm,其他两条边的长都为4cm,则其他两边的实际长度都是________m.21、正方形DEFG是的内接正方形,AM⊥BC于M,交DG于H,若AM=4cmcm,BC 长6cm, 则正方形DEFG的边长是________cm。
【湘教版】九年级数学上册:第三章《图形的相似》单元测试(含答案)

形上的顶点坐标为()A. (-2^, 一26)B. (2乞 2方)C. (—2b, —2a )D. (— 2&,—方)7. 如图,下列各式不能说明AMCs △血於的是()A. ZADE=ZBB. ZAED^ZC C AD _ AED A 。
_ DE '~AB~~AC • ~AB~~BC8. 如图,将△宓的三边缩小为原来的丄,下列说法: 2①ZXMC 与△必F 是位似图形;②△宓与△化尸是相似图形;③AMC 与△加7的周长之比为2 : 1;④ZXMC 与济'的而积之比 为4 : 1.其中正确的个数是()(第8题) (第11题) (第12题) 二.填空题(本大题共6个小题,每小题3分,共18分) 9. 己皿ABC S 'DEF,且兰=丄,则 S“r : S SF = _______ . DE 2 10. 已知- = 则-=. a + b 5 b 11. 如图,在DABCD 中,尸是肋延长线上一点,连接矿交%于点E,在 不添加辅助线的情况下,请写出图中一对相似三角 形: 个1±A.B C12. 如图,甲,乙两楼相距20米,甲楼高20米小明站在距甲楼10米的S 处目测得点力与甲,乙楼顶B. C 刚好在同一直线上,若小明的身 高忽略不计,则乙楼的高度是 ____ 米.13. 若△ ABCsM ff C',且 —=-,^\ABC 的周长为12阿则A'B' 4△才B' C'的周长为 _______ c m.14. 如图,△宓与△才B' C 是位似图形,且顶点都在格点上,则位 似中心的坐标是 _______ .三•解答题(共58分)15. (10分)如图所示,矩形力磁与矩形加/相似吗?若相似,请加以 证明,并求出相似比;若不相似,请说明理由.16. (12分)如图,以点0为位似中心,位似比为2,画岀△遊 的位似 △才B lC・2 cm B 4 cm1.3 cm17.(12 分)如图,在△遊中、DE〃BC、EF〃AB、求证:\ADEs\E仏18.(12分)如图,ZC=90°,点〃是初的中点,质丄丽于点0交氏于点E,若肋=30,胚=18,求图中四边形血疗C的而积.19.(12分)如图,路灯(尸点)距地面8米,身高1.6米的小明从距路灯的底部(0点)20米的A点,沿创所在的直线行走14米到方点时,身影的长度是变长了还是变短了?变长或变短了多少米?\/9O B N A .W参考答案l.A 2.D 3.B 4. A 5.B 6.力1.D 8. D9.- 10. - 11.答案不唯一,如△加12. 60 13. 164214.(9, 0)15.矩形初仞与矩形加/相似,相似比为20 : 13,理由:.. AB BC CD AD20 □・——= ——= ——= ——= ——,且EF FG GH EH13・•・矩形個g矩形日沏16.图略.17.9:DE//BC y :.又、:EF"AB,:・乙姑乙F氏.:.'ADE S'EFZ、]& 在Rt'ABC中,BC=yjAB2-AC2 =24.•・•点刀是肋的中点,:.BD=丄M=15.2•:乙BDE= ZC=9X , ZB= ZA・•・△宓s△朗,.・・竺=竺,.・・%=兰DE CA 45㈣边形Q£C= Sggc —丄X 18 X 24 —— X — X 15 —131 — .2 2 4 819.变短了.V , ZAM(=ZOMP y・•・\MACs3OP.・••也=竺,即MA = 口.解得畅二5.MO OP 20 + MA 8同理由△*劭“△用"可求得NB=1. 5.JHA-NB=5-1. 5=3. 5(米).即小明的身影变短了3. 5米.。
湘教版九年级数学上册第3章 图形的相似测试题

湘教版九年级数学上册第3章 图形的相似测试题一、选择题(本大题共7小题,每题4分,共28分)1.5x =6y ,那么x y等于( ) A .5 B .6 C.56 D.652.C 是线段AB 的黄金联系点,且AB =6 cm ,那么BC 的长为( )A .(3 5-3)cmB .(9-3 5)cmC .(3 5-3)cm 或(9-3 5)cmD .(9-3 5)cm 或(6 5-6)cm3.如图3-Z -1,在四边形ABCD 中,AD ∥BC ,对角线AC ,BD 相交于点O ,AD =1,BC =4,那么△AOD 与△BOC 的面积之比等于( )A.12B.14C.18D.1164.以下选项中能判定△ABC ∽△DEF 的是( )A .∠A =45°,∠B =55°;∠D =45°,∠F =75°B .AB =5,BC =4,∠A =45°;DE =10,EF =8,∠D =45°C .AB =6,BC =5,∠B =40°;DE =5,EF =4,∠E =40°D .BC =4,AC =6,AB =9;DE =18,EF =8,DF =12图3-Z -1图3-Z -25.如图3-Z -2,线段AB 两个端点的坐标区分为A (6,6),B (8,2),以原点O 为位似中心,在第一象限内将线段AB 增加为原来的12后失掉线段CD ,那么端点C 的坐标为( ) A .(3,3) B .(4,3)C .(3,1)D .(4,1)6.如图3-Z -3,在△ABC 中,中线BE ,CD 相交于点O ,衔接DE ,以下结论:①DE BC=12;②S △DOE S △COB =12;③AD AB =OE OB ;④S △DOE S △ADE =13.其中正确的有( ) A .1个 B .2个 C .3个 D .4个图3-Z -3图3-Z -47.如图3-Z -4,在Rt △ABC 中,∠ABC =90°,AB =6,BC =8,∠BAC ,∠ACB 的平分线相交于点E ,过点E 作EF ∥BC 交AC 于点F ,那么EF 的长为( )A.52B.83C.103D.154二、填空题(本大题共4小题,每题4分,共16分)8.在比例尺为1∶40000的地图上,某条路途的长为7 cm ,那么该路途的实践长度是________ km.9.如图3-Z -5,在△ABC 中,MN ∥BC 区分交AB ,AC 于点M ,N .假定AM =1,MB =2,BC =3,那么MN 的长为________.10.在△ABC 中,AB =6,AC =5,点D 在边AB 上,且AD =2,点E 在边AC 上,当AE =________时,以A ,D ,E 为顶点的三角形与△ABC 相似.图3-Z -5图3-Z -611.如图3-Z -6,铁路道口的栏杆短臂长1 m ,长臂长16 m .当短臂端点下降0.5 m 时,长臂端点降低________m .(杆的宽度疏忽不计)三、解答题(本大题共5小题,共56分)12.(10分)如图3-Z -7所示,AD ,BE 区分是钝角三角形ABC 的边BC ,AC 上的高,求证:AD BE =AC BC. 图3-Z -713.(10分)如图3-Z -8,四边形ABCD 中,E ,F ,G 区分在AD ,BD ,CD 上,且EF ∥AB ,FG ∥BC .求证:△DEG ∽△DAC .图3-Z -814.(10分)如图3-Z -9,在10×10的正方形网格中,点A ,B ,C ,D 均在格点上,以点A 为位似中心画四边形AB ′C ′D ′,使它与四边形ABCD 位似,且位似比为2.(1)在图中画出四边形AB ′C ′D ′;(2)填空:△AC ′D ′是________三角形.图3-Z -915.(12分)为测量操场上旗杆的高度,设计的测量方案如图3-Z -10所示,标杆高度CD =3 m ,标杆与旗杆的水平距离BD =15 m ,人的眼睛距空中的高度EF =1.6 m ,人与标杆CD 的水平距离DF =2 m ,E ,C ,A 三点共线,求旗杆AB 的高度.图3-Z -1016.(14分)如图3-Z -11,四边形ABCD 中,AB =AC =AD ,AC 平分∠BAD ,点P 是AC 延伸线上一点,且PD ⊥AD .(1)证明:∠BDC =∠PDC ;(2)假定AC 与BD 相交于点E ,AB =1,CE ∶CP =2∶3,求AE 的长.图3-Z -11详解详析1.D2.C [解析] ∵C 是线段AB 的黄金联系点,且AB =6 cm ,∴BC =5-12AB =(3 5-3)cm 或BC =3-52AB =(9-3 5)cm.应选C.3.D [解析] 在梯形ABCD 中,AD ∥BC ,所以△AOD ∽△COB .又由AD =1,BC =4,依据相似三角形的面积比等于相似比的平方,即可求得△AOD 与△BOC 的面积之比.4.D 5.A6.C [解析] 由BE ,CD 均为△ABC 的中线可知,DE 为△ABC 的中位线,所以DE =12BC ,DE ∥BC ,所以DE BC =12,故①正确; 由DE ∥BC 可得△DOE ∽△COB ,所以S △DOE S △COB =(DE BC)2=14,故②错误;由DE ∥BC 可得AD AB =DE BC ,DE BC =OE OB ,所以AD AB =OE OB ,故③正确;由于DE ∥BC ,所以△ADE ∽△ABC ,所以S △ADE S △ABC =(DE BC )2=14,设△DOE 的高OH 为h ,DE =a ,那么BC =2a ,△BOC 的高为2h ,△ABC 的高为6h ,△ADE 的高为3h ,所以S △DOE S △ADE =12ah 12·a ·3h =13,故④正确.应选择C. 7.C [解析] 延伸FE 交AB 于点D ,作EG ⊥BC 于点G ,作EH ⊥AC 于点H ,∵EF ∥BC ,∠ABC =90°,∴FD ⊥AB .又∵EG ⊥BC ,∴四边形BDEG 是矩形.∵AE 平分∠BAC ,CE 平分∠ACB ,∴ED =EH =EG ,∠DAE =∠HAE ,∴四边形BDEG 是正方形.在△DAE 和△HAE中,∵⎩⎪⎨⎪⎧∠DAE =∠HAE ,∠ADE =∠AHE ,AE =AE ,∴△DAE ≌△HAE (AAS),∴AD =AH .同理△CGE ≌△CHE ,∴CG =CH .设BD =BG =x ,那么AD =AH =6-x ,CG =CH =8-x .∵AC =AB 2+BC 2=62+82=10,∴6-x +8-x =10,解得x =2,∴BD =DE =2,AD =4.∵DF ∥BC ,∴△ADF ∽△ABC ,∴AD AB =DF BC ,即46=DF 8,解得DF =163, 那么EF =DF -DE =163-2=103.应选C. 8.2.8 [解析] 设这条路途的实践长度为x ,那么140000=7x,解得x =280000 cm =2.8 km. 9.1 [解析] ∵MN ∥BC ,∴△AMN ∽△ABC ,∴AM AB =MN BC, 即11+2=MN 3,∴MN =1. 10.125或53 [解析] 当AE AD =AB AC时, ∵∠A =∠A ,∴△AED ∽△ABC ,此时AE =AB ·AD AC =6×25=125;当AD AE =AB AC时,∵∠A =∠A , ∴△ADE ∽△ABC ,此时AE =AC ·AD AB =5×26=53. 故答案为125或53. 11.812.证明:∵AD ,BE 是钝角三角形ABC 的高,∴∠ADC =∠BEC =90°.又∵∠DCA =∠BCE ,∴△DAC ∽△EBC ,∴AD BE =AC BC. 13.证明:∵EF ∥AB ,∴DE DA =DF DB. ∵FG ∥BC ,∴DG DC =DF DB , ∴DE DA =DG DC. 又∵∠EDG =∠ADC ,∴△DEG ∽△DAC .14.解:(1)如图,四边形AB ′C ′D ′即为所求作图形.(2)依据网格的特点,应用勾股定理可以求出AD ′=C ′D ′=210,应用勾股定理的逆定理可以得出∠AD ′C ′=90°,故△AC ′D ′是等腰直角三角形.15.解:如图,过点E 作EH ⊥AB 于点H ,交CD 于点G ,那么EF =DG =BH =1.6 m ,GH =BD =15 m ,EG =DF =2 m ,∴CG =CD -DG =3-1.6=1.4(m).∵CG ∥AH ,∴△ECG ∽△EAH ,∴CG AH =EG EH , 即1.4AH =22+15, 解得AH =11.9(m),∴AB =AH +BH =11.9+1.6=13.5(m).答:旗杆AB 的高度为13.5 m.16.解:(1)证明:∵AB =AD ,AC 平分∠BAD ,∴AC ⊥BD ,∴∠ACD +∠BDC =90°.∵AC =AD ,∴∠ACD =∠ADC ,∴∠ADC +∠BDC =90°.∵PD ⊥AD ,∴∠ADC +∠PDC =90°,∴∠BDC =∠PDC .(2)过点C 作CM ⊥PD 于点M , ∵∠BDC =∠PDC ,∴CE =CM .∵∠CMP =∠ADP =90°,∠P =∠P , ∴△CPM ∽△APD ,∴CM AD =PC P A. 设CM =CE =x .∵CE ∶CP =2∶3,∴PC =32x . ∵AB =AD =AC =1,∴x 1=32x 32x +1, 解得x =13(x =0不合题意,舍去), 故AE =1-13=23.。
湘教版九年级上《第三章图形的相似》单元检测试题(有答案)
2018-2019学年度第一学期湘教版九年级数学上册_第三章_ 图形的相似_ 单元检测试题考试总分: 120 分考试时间: 120 分钟学校:__________ 班级:__________ 姓名:__________ 考号:__________ 一、选择题(共 10 小题,每小题 3 分,共 30 分)1.已知ab+c =bc+a=cb+a=k,则k的取值为()A.1 2B.−1C.12或−1 D.−12或−12.下面四组线段中不能成比例线段的是()A.3、6、2、4B.4、6、5、10C.1、√2、√3、√6D.2√5、√15、4、2√33.已知△ABC∽△DEF,若对应边AB:DE=1:2,则它们的周长比等于()A.1:2B.1:4C.2:1D.4:14.如图,在三角形ABC中,E,F分别是AB,AC边上的点,且有EF // BC,如果EBAB =45,则ACFC=( )A.9 4B.59C.54D.955.如图所示,顶角为36∘的等腰三角形,其底边与腰之比等于k,这样的三角形叫做黄金三角形.已知AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2014个黄金三角形的周长为()A.k2012B.k2013C.k2013(2+k)D.k20132+k6.如图,在△ABC中,点D在AB上,在下列四个条件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=AD⋅AB;④AB⋅CD=AD⋅CB,能满足△ADC与△ACB相似的条件是()A.①、②、③B.①、③、④C.②、③、④D.①、②、④7.如图,直线a // b // c,直线m、n与a、b、c分别交于点A、C、E和B、D、F,若AC=4,AE=10,BF=152,则DF的长为()A.9 2B.10C.3D.728.如图,直角梯形ABCD中,AB // CD,∠C=90∘,∠BDA=90∘,AB=a,BD=b,CD=c,BC=d,AD=e,则下列等式成立的是()A.b2=acB.b2=ceC.be=acD.bd=ae9.若两个相似三角形的面积之比为a:b,则它们的周长之比为()A.a2:b2B.a:bC.√a:√bD.无法确定10.△ABC与△DEF的相似比为1:4,则△DEF与△ABC的相似比为()A.1:2B.1:3C.4:1D.1:16二、填空题(共 10 小题,每小题 3 分,共 30 分)11.如图,在Rt△ABC中,∠C=90∘,CD⊥AB于D.若AD=2cm,DB=6cm,则CD=________.12.如图,在△ABC中,D是AB边上一点,连接CD,要使△ADC与△ABC相似,应添加的条件是________.13.已知两个位似图形的位似比为2:1,则这两个位似图形的面积比为________.14.如图,在△ABC中,DE // BC,若AD=1,DE=2,BD=3,则BC=________.15.已知P是线段AB上一点,且APPB =25,则APAB=________.16.如图,在△ABC中,D、E两点分别在边BC、AC上,AE:EC=CD:BD= 1:2,AD与BE相交于点F,若△ABC的面积为21,则△ABF的面积为________.17.如图,在梯形ABCD中,AD // BC,AC平分∠BCD,∠BAC=∠D,若AD=4,BC=10,则AC=________.18.在同一时刻物高与影长成比例,小莉量得综合楼的影长为6米,同一时刻他量得身高1.6米的同学的影长为0.6米,则综合楼高为________米.19.如图是圆桌正上方的灯泡O发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径为1.2m,桌面距离地面1m,若灯泡O距离地面3m,则地面上阴影部分的面积为________m2.20.若两个相似三角形的面积之比为1:16,则它们的周长之比为________.三、解答题(共 6 小题,每小题 10 分,共 60 分)21.如图,在△ABC中,∠ACB=90∘,CD⊥AB于点D,AC=6√3,BD=3.(1)求∠A的度数;(2)求BC的长及△ABC的面积.22.如图,在△ABC中,D为AC边上一点,∠DBC=∠A.(1)求证:△ACD∽△ABC;(2)如果BC=√6,AC=3,求CD的长.23.路边有两根相距4m的电线杆AB,CD,分别在高为3m的A处和高为6m的C处用铁丝将两电线杆固定(1)求铁丝AD与铁丝BC的交点M离地面的高度MH;(2)若电线杆AB与CD的长分别为a,b,请猜想高度MH与a,b间的关系.24.小明想测量在太阳光下一栋楼高,他设计了一种测量方案如下:如图,小明站到点E处时,刚好使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,小明测得落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上),已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).25.如图,小明站在竖立的电线杆AB前D处时的影子长为3m,他向电线杆走了4m到达E处时的影子长为1m.若小明的身高为1.8m.(1)求电线杆的长;(2)找出△ABF的位似图形,并指出位似中心.26.如图,已知:△ABC中,M为BC边的中点,O为AM上一点,BO的延长线交AC于点D,CO延长线交AB于点E,PQ // BC,且PQ过点O与AB、AC分别交于P 和点Q,求证:(1)PO=OQ;(2)DE // BC.答案1.C2.B3.A4.C5.C6.A7.A8.A9.C10.C11.2√3cm12.∠ACD=∠B,∠ADC=∠ACB,ADAC =ACAB13.4:114.815.2716.617.2√1018.1619.0.81π20.1:421.解:(1)∵∠ACB=90∘,CD⊥AB于点D,∴AC2=AD⋅AB,即(6√3)2=AD⋅(AD+3),整理得AD2+3AD−108=0,解得AD=9或AD=−12(舍去),在Rt△ACD中,∵cosA=ADAC =6√3=√32,∴∠A=30∘;(2)∵AB=AD+BD=9+3=12,而∠A=30∘,∴BC=12AB=6,∴S△ABC=12⋅AC⋅BC=12⋅6√3⋅6=18√3.22.(1)证明:∵∠DBC=∠A,∠C=∠C,∴△ACD∽△ABC;(2)解:∵△ACD∽△ABC,∴BC AC =CDBC,∴√6 3=√6,∴CD=2.23.铁丝AD与铁丝BC的交点M离地面的高度MH为2m;(2)猜想:MH=a2b.∵AB // CD,∴△ABM∽△DCM,∴AB CD =ab,∵MH // AB,∴△MDH∽△ADB,∴MH AB =DHBD=ab,即MHa=ab,∴MH=a2b.24.楼高AB约为20.0米.25.解:(1)在△ABF和△HEF中.∠B=∠HEF=90∘,∠BFA=∠EFH,则△ABF∽△HEF,∴AB HE =BFEF,即ABHE =BE+11①,在△ABC和△GDC中,∠B=∠GDC=90∘,∠C=∠C,则△ABC∽△GDC,∴AB GD =BCDC,即ABGD =BE+4+33②,而HE=GD③,由①、②、③可得BE+1=BE+73,解得BE=2.把BE=2代入①中,得AB=(2+1)HE=1.8×3=5.4(m);(2)△ABF的位似图形是△HEF.位似中心是点F.说明:以上各题若用其它做法可参照此标准评分.26.证明:(1)∵PQ // BC,PO // BM,OQ // MC,∴PO:MB=AO:AM,OQ:MC=AO:AM,∴OP:BM=OQ:CM,∵MB=MC,∴PO=OQ.(2)∵PO // BC,OQ // BC,∴PO:BC=EO:EC,OQ:BC=DO:BD,∴EO:EC=DO:BD,∴DE // BC.。
湘教版九年级数学上册作业课件 第3章 图形的相似 章末复习(三)
第3章 图形的相似
章末复习(三)
知识点一 平行线分线段成比例
1.如图,在横格作业纸(横线等距)上画一条直线,
与横格线交于 A,B,C 三点,则 BC∶AC 等于
(C ) A.2∶3
B.2∶5
C.3∶4
D.3∶5
第1题图
2.如图,在△ABC 中,点 D 在 BC 边上,连接 AD,点 G 在线段 AD 上,GE∥BD,且交 AB 于点 E,GF∥AC,且交 CD 于点 F,则下列结 论一定正确的是( D )
=AC=
2 2
BC=
2 2
×3
2 =3.∴AQ=CQ-
AC=92 -3=32 ,AP=AB-BP=3-1=2.在 Rt
△APQ 中,PQ= AQ2+AP2 = (32)2+22
=52 .
4.如图,在△ABC中,DE∥BC,AD=5,BD=10, AE=4,AC=( D ) A.8 B.9 C.10 D.12
第4题图
5.(天心区校级月考)如图,在三角形 ABC 中, D 为 BC 的中点,AF=2BF,CE=3AE,连接 CF 交 DE 于 P 点,则DEPP 的值为__3___.
的面积比为( D )
A.13
B.14
C.15
D.16
第7题图
8.如图所示,在正方形ABCD中,G为CD边中点,连接AG并延长交 BC边的延长线于E点,对角线BD交AG于F点.已知FG=2,则线段AE的 长度为( D )
A.6 B.8 C.10 D.12
第8题图
9.(武陵区校级期末)如图.在▱ABCD中,E是BC上一点.BE∶EC= 2∶3,AE交BD于点F,则S△BEF∶S△BCD=__4_∶__3_5_____.
第三章《图形的相似》复习课(总复习3))(湘教版)
1.8
B
A
2.7 E D
8.7
C
4、如图,正方形ABCD中,AB=4,G为DC中 点,E在BC边上运动,(E点与点B、点C不重合) 设BE=x,过E作GA平行线交AB于F,设AFEG 面积为y,写出y与x的函数关系式,并指出自变 量x的取值范围。 A D G F B E C
例补2、如图,正方形ABCD的边长为4cm, 点P是BC边上不与点B、C重合的任意一点, 连结AP,过点P作PQ⊥AP交DC于点Q,设 BP的长为xcm,CQ的长为ycm. (1)求点P在BC上运动的过程中y的最大值; (2)当y =
(1)图中有全等三角形吗?找出来并证明. (2)图中有相似三角形吗?找出来并证明. (3)BD2=AD· DF吗?请说明理由.
二 .学以致用 5、如图,在△ABC中,∠BAC=90°,AB=6,BC=12, 点P从A点出发向B以1m/s的速度移动,点Q从B点出发向 C点以2m/s的速度移动,如果P、Q分别从A、B两地同 时出发,几秒后△ PBQ与原三角形相似?
2.△ABC中,AB>AC,过AB上一点D作直线DE 交另一边于E,使所得三角形与原三角形相似, 画出满足条件的图形. A A A A E
D
B CB
D
E CB
D
E CB
D
E C
一试身手
1.如图,阳光通过窗户照到室内,在地面上留 下2.7m宽的亮区,已知亮区一边到窗口下的 墙角距离EC=8.7m,窗口高AB=1.8m,那么窗 口底边离地面的高BC是多少呢?
C
Q
B
P
A
二 .学以致用
一块直角三角形木板的一条直角边AB长1.5m, 面积为1.5m2。要把它加工成一个面积最大的 正方形桌面,甲、乙两人的加工方法分别如 图1和图2所示,你能用所学过的知识说明谁 的加工方法符合要求吗?(加工损耗忽略不 计,计算结果保留分数) B B
湘教版九年级数学上册第3章 图形的相似 测试题
第3章 图形的相似一、选择题(本大题共7小题,每小题4分,共28分)1.若ab =cd ≠0,则下列式子正确的是( )A.a d =c bB.a c =b dC.a b =c dD.d c =b a2.已知△ABC △△A ′B ′C ′,AD ,A ′D ′分别是对应边BC ,B ′C ′上的高,且BC =10 cm ,B ′C ′=6 cm ,AD =7 cm ,则A ′D ′等于( )A.163cm B .12 cm C.215cm D .以上都不正确 3.如图3-Z -1,在△ABC 中,D 是AB 边上的一点,若△ACD =△B ,AD =a ,AC =2,△ADC 的面积为1,则△BCD 的面积为( )图3-Z -1A .aB .2aC .3aD .4a4.下列说法:△所有等腰三角形都相似;△有一个底角相等的两个等腰三角形相似;△有一个角相等的等腰三角形相似;△有一个角为60°的两个直角三角形相似.其中正确的说法是( )A .②④B .①③C .①②④D .②③④5.宽与长的比是5-12(约0.618)的矩形叫作黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:作正方形ABCD ,分别取AD ,BC 的中点E ,F ,连接EF .以点F 为圆心,以FD 为半径画弧,交BC 的延长线于点G .作GH △AD ,交AD 的延长线于点H ,则图中下列矩形是黄金矩形的是( )图3-Z -2A .矩形ABFEB .矩形EFCDC .矩形EFGHD .矩形DCGH6.如图3-Z -3,已知△ABC ,任取一点O ,连接AO ,BO ,CO ,并取它们的中点D ,E ,F ,得△DEF ,则下列说法正确的个数是( )①△ABC 与△DEF 是位似图形;△△ABC 与△DEF 是相似图形;△△ABC 与△DEF 的周长比为1△2;△△ABC 与△DEF 的面积比为4∶1.图3-Z -3A .1B .2C .3D .47.为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理.她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E ,标记好脚掌中心位置为B ,测得脚掌中心位置B 到镜面中心C 的距离是50 cm ,镜面中心C 距离旗杆底部D 的距离为4 m ,如图3-Z -4所示.已知小丽同学的身高是1.54 m ,眼睛位置A 距离小丽头顶的距离是4 cm ,则旗杆DE 的高度等于( )图3-Z -4A .10 mB .12 mC .12.4 mD .12.32 m二、填空题(本大题共7小题,每小题5分,共35分)8.已知a b =3,则a -b b=________. 9.在△ABC 中,AB =6,AC =8,在△DEF 中,DE =4,DF =3,要使△ABC 与△DEF 相似,需添加一个条件是________.(写出一种情况即可)10.如图3-Z -5,以点O 为位似中心,将△ABC 缩小得到△A ′B ′C ′,若AA ′=2OA ′,则△ABC 与△A ′B ′C ′的周长比为________.图3-Z -511.如图3-Z -6,在△ABC 中,D 为AC 上一点,且CD AD =12,过点D 作DE △BC 交AB 于点E ,连接CE ,过点D 作DF △CE 交AB 于点F .若AB =15,则EF =________.图3-Z -612.如图3-Z -7,在直角坐标系中,每个小方格的边长均为1,△AOB 与△A ′OB ′是以原点O 为位似中心的位似图形,且OA OA ′=32,点A ,B 都在格点上,则点B ′的坐标是________.图3-Z-713.如图3-Z-8,为了测量一水塔的高度,小强用2 m长的竹竿做测量工具,移动竹竿,使竹竿、水塔的顶端的影子恰好落在地面上的同一点.此时,竹竿与这一点相距8 m,与水塔相距32 m,则水塔的高度为________m.图3-Z-814.如图3-Z-9,△OPQ在边长为1个单位的方格纸中,它们的顶点在小正方形的顶点位置,点A,B,C,D,E也是小正方形的顶点,从点A,B,C,D,E中选取三个点所构成的三角形与△OPQ相似,那么这个三角形是________.图3-Z-9三、解答题(本大题共3小题,共37分)15.(10分)如图3-Z-10,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.(1)画出位似中心点O;(2)求出△ABC与△A′B′C′的位似比;(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的位似比为3△2.图3-Z-1016.(13分)如图3-Z-11(示意图),小明把手臂水平向前伸直,手持长为a的小尺竖直,瞄准小尺的两端E,F,不断调整站立的位置,使站在点D处正好看到旗杆的底部和顶部.如果小明的手臂长l=40 cm,小尺的长a=20 cm,点D到旗杆底部的距离AD=25 m,求旗杆AB的高度.图3-Z-1117.(14分)如图3-Z-12,正方形ABCD中,M为BC上一点,F是AM的中点,EF ⊥AM,垂足为F,EF交AD的延长线于点E,交DC于点N.(1)求证:△ABM△△EF A;(2)若AB=12,BM=5,求DE的长.图3-Z-121.[答案] A2.[答案] C∴△ACD ∽△ABC ,∴S △ADC S △ABC =(AD AC)2=14. ∵S △ADC =a ,∴S △ABC =4a ,S △BCD =S △ABC -S △ADC =3a .故选C.4.[解析] A △中等腰三角形的角不确定,所以△错;△中有一个底角相等即所有角都对应相等,所以△对;△中可能是一底角和一顶角相等,所以△错;△中两个角对应相等,所以相似,④对.故选A.5.[解析] D 设正方形的边长为2,则CD =2,CF =1,在直角三角形DCF 中,DF =CF 2+CD 2=12+22=5,∴FG =5,∴CG =5-1,∴CG CD =5-12,∴矩形DCGH 为黄金矩形.故选D.6.[解析] C 根据位似的性质得出△△ABC 与△DEF 是位似图形,②△ABC 与△DEF 是相似图形.△△DEF 是将△ABC 的三边缩小为原来的12得到的,∴△ABC 与△DEF 的周长比为2△1,故△错误.根据面积比等于相似比的平方,可知④△ABC 与△DEF 的面积比为4△1.故选C.7.[解析] B 由题意可得AB =1.5 m ,BC =0.5 m ,DC =4 m ,△ABC ∽△EDC ,则AB DE =BC DC ,即1.5DE =0.54,解得DE =12(m),故选B. 8.[答案] 29.[答案] △A =△D (答案不唯一)10.[答案] 3△1[解析] 由题意可知△ABC △△A ′B ′C ′,∵AA ′=2OA ′,∴OA =3OA ′,∴AC A ′C ′=OA O ′A ′=31,∴C △ABC C △A ′B ′C ′=AC A ′C ′=31. 故答案为3△1.11.[答案] 103∵CD ∶AD =1△2,∴AD ∶AC =2△3,即AE △AB =2△3.∵AB =15,∴AE =10.∵DF ∥CE ,∴AF ∶AE =AD △AC ,即AF △10=2△3,解得AF =203, 则EF =AE -AF =10-203=103. 12.[答案] (-2,43) [解析] 由题意得OA OA ′=32,又△B (3,-2),∴点B ′的坐标是[3×(-23),-2×(-23)],即点B ′的坐标是(-2,43).故答案为(-2,43). 13.[答案] 1014.[答案] △CDB[解析] 与△OPQ 相似的是△BCD .理由如下:连接BC ,BD ,如图所示,则△BCD =90°+45°=135°=△QOP .由勾股定理得OP =BC =2,∵OQ =2,CD =1,∴OP CD =QO BC =21,∴△OPQ ∽△CDB .故答案为△CDB .15.解:(1)略.(2)位似比为1△2.(3)略.16.解:过点C 作CH △AB 于点H ,交EF 于点P ,则CH =DA =25 m ,CP =40 cm =0.4 m ,EF =20 cm =0.2 m.∵EF ∥AB ,∴△CEF ∽△CBA , ∴EF BA =CP CH, 即0.2BA =0.425,解得AB =12.5(m). 答:旗杆AB 的高度为12.5 m.17.解:(1)证明:△四边形ABCD 是正方形,∴AD ∥BC ,∴∠AMB =△EAF .又△EF △AM ,∴∠AFE =90°,∴∠B =△AFE ,∴△ABM ∽△EF A .(2)△△B =90°,AB =12,BM =5,∴AM =122+52=13,AD =12.△F 是AM 的中点,∴AF =FM =6.5.△△ABM △△EF A ,∴BM F A = AM EA ,即56.5=13EA,∴AE =16.9,∴DE =AE -AD =4.9.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
章末复习(三) 图形的相似
01 基础题
知识点1 比例及比例线段
1.下列各线段的长度成比例的是(D)
A.2 cm,5 cm,6 cm,8 cm
B.1 cm,2 cm,3 cm,4 cm
C.3 cm,6 cm,7 cm,9 cm
D.3 cm,6 cm,9 cm,18 cm
2.已知5x-8y=0,则x∶y=8∶5.
知识点2 平行线分线段成比例
3.如图,已知AB∥CD∥EF,BD∶DF=2∶5,那么下列结论正确的是(D)
A.AC∶AE=2∶5
B.AB∶CD=2∶5
C.CD∶EF=2∶5
D.CE∶EA=5∶7
知识点3 相似图形和位似图形
4.如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相
似比为13,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为(A)
A.(3,2)
B.(3,1)
C.(2,2)
D.(4,2)
5.如图所示,它们是两个相似的平行四边形,根据条件可知,∠α=125°,m=12.
2
知识点4 相似三角形的判定
6.如图,在▱ABCD中,E为AD的三等分点,AE=23AD,连接BE,交AC于点F,AC=12,则AF为(B)
A.4 B.4.8
C.5.2 D.6
7.(海南中考)如图,点D在△ABC的边AC上,要判断△ADB与△ABC相似,添加一个条件,不正确
的是(C)
A.∠ABD=∠C B.∠ADB=∠ABC
C.ABBD=CBCD D.ADAB=ABAC
知识点5 相似三角形的性质
8.(云南中考)如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B,如果△ABD的面积为
15,那么△ACD的面积为(D)
A.15 B.10
C.152 D.5
9.如图,Rt△ABC中,∠C=90°,D是AC边上一点,AB=5,AC=4,若△ABC∽△BDC,则CD=(D)
A.2 B.32
C.43 D.94
知识点6 相似三角形的应用
3
10.如图,甲,乙两楼相距20米,甲楼高20米,小明站在距甲楼10米的A处目测得点A与甲,乙
楼顶B、C刚好在同一直线上,若小明的身高忽略不计,则乙楼的高度是60米.
11.如图,为了测量水塘边A、B两点之间的距离,在可以看到的A、B的点E处,取AE、BE延长线
上的C、D两点,使得CD∥AB,若测得CD=5 m,AD=15 m,ED=3 m,则A、B两点间的距离为20m.
02 中档题
12.如图,锐角△ABC的高CD和BE相交于点O,图中与△ODB相似的三角形有(B)
A.4个 B.3个
C.2个 D.1个
13.(安顺中考)如图,矩形EFGH内接于△ABC,且边FG落在BC上,AD⊥BC,BC=3,AD=2,EF=
2
3
EH,那么EH的长为32.
14.在△ABC中,∠B=25°,AD是BC边上的高,并且AD2=BD·DC,则∠BCA的度数为65°或115°.
15.如图,已知四边形ABCD中,∠A=90°,AD∥BC.
(1)请你补充一个条件,使△ABD∽△DCB,并证明你补充的条件符合要求;
4
(2)在(1)的条件下,如果AD=6,BD=43,求DC的长.
解:(1)补充条件为:∠BDC=90°.
证明:∵AD∥BC,
∴∠ADB=∠DBC.
∵∠A=∠BDC=90°,
∴△ABD∽△DCB.
(2)∵△ABD∽△DCB,
∴ADDB=BDCB,即643=43BC.解得BC=8.
在Rt△BDC中,DC=BC2-BD2=4.
16.晚饭后,小聪和小军在社区广场散步.小聪问小军:“你有多高?”小军一时语塞.小聪思考
片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,
如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正
好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为
0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,
求出小军身高BE的长.(结果精确到0.01米)
解:由题意得∠CAD=∠MND=90°,∠CDA=∠MDN.
∴△CAD∽△MND.
∴CAMN=ADND.
∴1.6MN=1×0.8(5+1)×0.8.
∴MN=9.6.
又∵∠EBF=∠MNF=90°,∠EFB=∠MFN,
∴△EBF∽△MNF.∴EBMN=BFNF.
5
∴EB9.6=2×0.8(2+9)×0.8.
∴EB≈1.75.
答:小军的身高约为1.75米.
03 综合题
17.(益阳中考改编)如图,在△ABC中,AB=AC,BD=CD,CE⊥AB 于E.BE=2,BC=6.
(1)求证:△ABD∽△CBE;
(2)求AE的长度;
(3)设AD与CE交于F,求△CFD的面积.
解:(1)证明:在△ABC中,AB=AC,BD=CD,∴AD⊥BC.
∵CE⊥AB,
∴∠ADB=∠CEB=90°.
又∵∠B=∠B,
∴△ABD∽△CBE.
(2)∵△ABD∽△CBE,
∴AB∶CB=BD∶BE.
∴AB∶6=3∶2.解得AB=9.
∴AE=7.
(3)在Rt△BEC中,由勾股定理得CE=42.
∵∠ADC=∠CEB=90°,∠ECB=∠ECB,
∴△CDF∽△CEB.
∴CD∶CE=DF∶EB.
∴3∶42=DF∶2.解得DF=342.
∴S△CFD=12×342×3=982.
