2016~2017学年度第一学期期末联合体七年级答案

合集下载

2016-2017学年初一上期末数学试卷含答案

2016-2017学年临沂市七年级（上）期末数学试卷一、选择题：每小题3分，共42分，将唯一正确答案的代号字母填在下面的方格内．1．（3分）a，b为有理数，下列说法正确的是（）A．|a+b|的值一定是正数B．a2+1的值一定是正数C．当a＜b时，a2＜b2D．当a＞b时，|a|＞|b|2．（3分）如图，M是线段EF的中点，N是线段MF上一点，如果EF=2a，NF=b，那么下面结论中错误的是（）A．MN=a﹣b B．MN= a C．EM=a D．EN=2a﹣b3．（3分）下列说法正确的是（）A．画射线OA=3cmB．线段AB和线段BA不是同一条线段C．点A和直线l的位置关系有两种D．三条直线相交有3个交点4．（3分）已知某种型号的纸100张的厚度约为1cm，那么这种型号的纸13亿张的厚度约为（）A．1.3×105km B．1.3×104km C．1.3×103km D．1.3×102km5．（3分）下列说法中正确的个数是（）（1）﹣a表示负数；（2）多项式﹣3a2b+7a2b2﹣2ab+l的次数是3；（3）单项式﹣的系数为﹣2；（4）若|x|=﹣x，则x＜0．A．0个B．1个C．2个D．3个6．（3分）若x、y为有理数，且|x+2|+（y﹣2）2=0，则（）2017的值为（）A．1 B．﹣1 C．2017 D．﹣20177．（3分）在解方程=1﹣时要先去分母，则下列去分母中正确的是（）A．2﹣4x=1﹣3x+1 B．2（1﹣2x）=1﹣（3x+1）C．2﹣4x=6﹣3x+1 D．2（1﹣2x）=6﹣（3x+1）8．（3分）当x=1时，代数式px3+qx+1的值为2018，则当x=﹣1时，代数式px3+qx+1的值为（）A．2016 B．﹣2017 C．﹣2016 D．20179．（3分）刘谦的魔术表演风靡全国，小明同学也学起了刘谦发明了一个魔术盒，当任意有理数对（a，b）进入其中时，会得到一个新的有理数：a2+b﹣1．例如把（3，﹣2）放入其中，就会得到32+（﹣2）﹣1=6．现将有理数对（﹣1，﹣2）放入其中，则会得到（）A．﹣1 B．﹣2 C．﹣3 D．210．（3分）a是两位数，b是三位数，如果把a放在b的左边，那么所成的五位数可表示为（）A．1000a+10b B．1000a+b C．ab D．a+b11．（3分）由四舍五入法得到的近似数5.6×103，则下列说法中正确的是（）A．精确到十分位B．精确到个位 C．精确到百位 D．精确到千位12．（3分）如图，下列说法中错误的是（）A．OA方向是北偏东30°B．OB方向是北偏西15°C．OC方向是南偏西25°D．OD方向是东南方向13．（3分）两个角，它们的比是7：3，差为36°，则这两个角的关系是（）A．互余B．互补C．既不互余也不互补D．不确定14．（3分）妈妈为今年参加中考的女儿小红制作了一个正方体礼品盒（如图），六个面上各有一个字，连起来就是“预祝中考成功”，其中“祝”的对面是“考”，“成”的对面是“功”，则它的平面展开图可能是（）A．B．C．D．二、填空题：每题3分，共15分．15．（3分）若单项式xy2m﹣1与单项式﹣52x2y2的次数相同，则m= ．16．（3分）如图所示，用含a、b字母的代数式表示图中阴影部分的面积为．17．（3分）若实数x，y满足x+y﹣7=0和3x﹣5y+3=0，则式子3（x+y）﹣（3x﹣5y）的值是．18．（3分）小明将两块都含45°的三角板按如图所示放置，小明用量角器测得∠AOD=150°，则∠COB的度数为．19．（3分）若“@”表示为一种运算符号，并且有：4@2=28；6@3=218；8@2=416，那么：9@3= ．三、解答题20．（5分）计算：﹣14+[4﹣（+﹣）×24]÷5．21．（6分）．22．（7分）已知x=1是方程2﹣（a﹣x）=2x的解，求关于y的方程a（y﹣5）﹣2=a（2y﹣3）的解．23．（8分）如图，四点A、B、C、D，按照下列语句画出图形；（1）直线AC和线段DB相交于点O；（2）延长线段AD至E，使AD=DE；（3）画射线BA；（4）反向延长线段BC．24．（11分）如图，已知O为直线AB上一点，过点O向直线AB上方引三条射线OC、OD、OE，且OC平分∠AOD，∠BOE=3∠DOE，∠COE=70°．求：（1）∠BOE的度数；（2）∠AOC的度数．25．（12分）请根据图中提供的信息，回答下列问题：（1）一个暖瓶与一个水杯分别是多少元？（只填写结果）一个暖瓶元；一个水杯元．（2）甲、乙两家商场同时出售同样的暖瓶和水杯，为了迎接新年，两家商场都在搞促销活动，甲商场规定：这两种商品都打九折；乙商场规定：买一个暖瓶赠送二个水杯，单独买水杯不优惠．若某单位想要买4个暖瓶和15个水杯，请问选择哪家商场购买更合算，并说明理由．（3）若必须买5个暖瓶，则当买多少个水杯时到两家商城一样合算．26．（14分）A、B、C为数轴上的三点，动点A、B同时从原点出发，动点A每秒运动x个单位，动点B每秒运动y个单位，且动点A运动到的位置对应的数记为a，动点B运动到的位置对应的数记为b，定点C对应的数为8．（1）若2秒后，a、b满足|a+8|+（b﹣2）2=0，则x= ，y= ，并请在数轴上标出A、B两点的位置．（2）若动点A、B在（1）运动后的位置上保持原来的速度，且同时向正方向运动z秒后使得|a|=|b|，使得z= ．（3）若动点A、B在（1）运动后的位置上都以每秒2个单位向正方向运动继续运动t秒，点A 与点C之间的距离表示为AC，点B与点C之间的距离表示为BC，点A与点B之间的距离为AB，且AC+BC=1.5AB，则t= ．2016-2017学年山东省临沂市莒南县七年级（上）期末数学试卷参考答案与试题解析一、选择题：每小题3分，共42分，将唯一正确答案的代号字母填在下面的方格内．1．（3分）a，b为有理数，下列说法正确的是（）A．|a+b|的值一定是正数B．a2+1的值一定是正数C．当a＜b时，a2＜b2D．当a＞b时，|a|＞|b|【解答】解：A、当a+b=0时，|a+b|=0，不是正数，故选项错误；B、a2≥0，则a2+1＞0，则a2+1一定是正数，选项正确；C、当x=﹣2，b=1时，a＜b，而a2＞b2，故选项错误；D、当a=1，b=﹣2时，a＞b，而|a|＜|b|，选项错误．故选B．2．（3分）如图，M是线段EF的中点，N是线段MF上一点，如果EF=2a，NF=b，那么下面结论中错误的是（）A．MN=a﹣b B．MN= a C．EM=a D．EN=2a﹣b【解答】解：∵M是线段EF的中点，EF=2a，∴MF=EF=a，∴MN=MF﹣NF=a﹣b，EM=EF=a，EN=EF﹣NF=2a﹣b．故选B．3．（3分）下列说法正确的是（）A．画射线OA=3cmB．线段AB和线段BA不是同一条线段C．点A和直线l的位置关系有两种D．三条直线相交有3个交点【解答】解：A、射线没有长度，故本选项错误；B、线段AB和线段BA是同一条线段，故本选项错误；C、点A和直线l的位置关系有两种，在直线上或在直线外，故本选项正确；D、三条直线相交可能有1个或2个或3个交点，故本选项错误．故选C．4．（3分）已知某种型号的纸100张的厚度约为1cm，那么这种型号的纸13亿张的厚度约为（）A．1.3×105km B．1.3×104km C．1.3×103km D．1.3×102km【解答】解：根据题意得： 13×108÷100÷105=1.3×102（km），故选D5．（3分）下列说法中正确的个数是（）（1）﹣a表示负数；（2）多项式﹣3a2b+7a2b2﹣2ab+l的次数是3；（3）单项式﹣的系数为﹣2；（4）若|x|=﹣x，则x＜0．A．0个B．1个C．2个D．3个【解答】解：（1）小于0的数是负数，故（1）说法错误；（2）多项式﹣3a2b+7a2b2﹣2ab+l的次数是4，故（2）说法错误；（3）单项式﹣的系数为﹣，故（3）说法错误；（4）若|x|=﹣x，x≤0，故（4）说法错误，故选：A．6．（3分）若x、y为有理数，且|x+2|+（y﹣2）2=0，则（）2017的值为（）A．1 B．﹣1 C．2017 D．﹣2017【解答】解：由题意得，x+2=0，y﹣2=0，解得，x=﹣2，y=2，则（）2017=﹣1，故选：B．7．（3分）在解方程=1﹣时要先去分母，则下列去分母中正确的是（）A．2﹣4x=1﹣3x+1 B．2（1﹣2x）=1﹣（3x+1）C．2﹣4x=6﹣3x+1 D．2（1﹣2x）=6﹣（3x+1）【解答】解：去分母得：2（1﹣2x）=6﹣（3x+1），故选D8．（3分）当x=1时，代数式px3+qx+1的值为2018，则当x=﹣1时，代数式px3+qx+1的值为（）A．2016 B．﹣2017 C．﹣2016 D．2017【解答】解：将x=1代入px3+qx+1∴p+q+1=2018∴p+q=2017将x=﹣1代入px3+qx+1∴﹣p﹣q+1=﹣（p+q）+1=﹣2017+1=﹣2016故选（C）9．（3分）刘谦的魔术表演风靡全国，小明同学也学起了刘谦发明了一个魔术盒，当任意有理数对（a，b）进入其中时，会得到一个新的有理数：a2+b﹣1．例如把（3，﹣2）放入其中，就会得到32+（﹣2）﹣1=6．现将有理数对（﹣1，﹣2）放入其中，则会得到（）A．﹣1 B．﹣2 C．﹣3 D．2【解答】解：把实数对（﹣1，﹣2）代入a2+b﹣1=2中得：（﹣1）2﹣2﹣1=1﹣2﹣1=﹣2．故选B．10．（3分）a是两位数，b是三位数，如果把a放在b的左边，那么所成的五位数可表示为（）A．1000a+10b B．1000a+b C．ab D．a+b【解答】解：∵a放在b的左边，b一个三位数，∴b的大小不变，a扩大了1000倍，∴所成的五位数是1000a+b，故选B．11．（3分）由四舍五入法得到的近似数5.6×103，则下列说法中正确的是（）A．精确到十分位B．精确到个位 C．精确到百位 D．精确到千位【解答】解：5.6×103=5600，精确到了百位，故选C．12．（3分）如图，下列说法中错误的是（）A．OA方向是北偏东30°B．OB方向是北偏西15°C．OC方向是南偏西25°D．OD方向是东南方向【解答】解：A、OA方向是北偏东60°，此选项错误；B、OB方向是北偏西15°，此选项正确；C、OC方向是南偏西25°，此选项正确；D、OD方向是东南方向，此选项正确．错误的只有A．故选：A．13．（3分）两个角，它们的比是7：3，差为36°，则这两个角的关系是（）A．互余B．互补C．既不互余也不互补D．不确定【解答】解：设一个角为7x，则另一个角为3x，则有7x﹣3x=36°，∴x=9°，则这两个角分别为63°，27°，而63°+27°=90°∴这两个角的关系为互余．故选A．14．（3分）妈妈为今年参加中考的女儿小红制作了一个正方体礼品盒（如图），六个面上各有一个字，连起来就是“预祝中考成功”，其中“祝”的对面是“考”，“成”的对面是“功”，则它的平面展开图可能是（）A．B．C．D．【解答】解：A、“祝”的对面是“成”，故本选项错误；B、“祝”的对面是“成”，故本选项错误；C、三个汉字的位置不对应，故本选项错误；D、符合，故本选项正确．故选D．二、填空题：每题3分，共15分．15．（3分）若单项式xy2m﹣1与单项式﹣52x2y2的次数相同，则m= 2 ．【解答】解：由题意可知：1+2m﹣1=2+2，解得：m=2故答案为：2（3分）如图所示，用含a、b字母的代数式表示图中阴影部分的面积为．16．【解答】解：由图可得，阴影部分的面积是：（a+b）a﹣=，故答案为：．17．（3分）若实数x，y满足x+y﹣7=0和3x﹣5y+3=0，则式子3（x+y）﹣（3x﹣5y）的值是24 ．【解答】解：由题意得：x+y=7，3x﹣5y=﹣3，则原式=21+3=24，故答案为：2418．（3分）小明将两块都含45°的三角板按如图所示放置，小明用量角器测得∠AOD=150°，则∠COB的度数为30°．【解答】解：∵∠AOC=∠AOD﹣∠COD，∴∠AOC=150°﹣90°=60°，∵∠COB=∠AOB﹣∠AOC，∴∠COB=90°﹣60°=30°．故答案为：30°．19．（3分）若“@”表示为一种运算符号，并且有：4@2=28；6@3=218；8@2=416，那么：9@3= 327 ．【解答】解：根据题中的新定义得：原式=（9÷3）×100+9×3=300+27=327，故答案为：327．三、解答题20．（5分）计算：﹣14+[4﹣（+﹣）×24]÷5．【解答】解：﹣14+[4﹣（+﹣）×24]÷5=﹣1+[4﹣×24﹣×24+×24]÷5=﹣1+[4﹣9﹣4+18]÷5=﹣1+9÷5=﹣1+1. 8=0.821．（6分）．【解答】解：去分母得：3x﹣9﹣15=5x﹣20，移项得：3x﹣5x=﹣20+9+15，合并同类项得：﹣2x=4，系数化1得：x=﹣2．22．（7分）已知x=1是方程2﹣（a﹣x）=2x的解，求关于y的方程a（y﹣5）﹣2=a（2y﹣3）的解．【解答】解：把x=1代入方程得：2﹣（a﹣1）=2，解得：a=1，代入方程a（y﹣5）﹣2=a（2y﹣3）得：（y﹣5）﹣2=2y﹣3，解得：y=﹣4．23．（8分）如图，四点A、B、C、D，按照下列语句画出图形；（1）直线AC和线段DB相交于点O；（2）延长线段AD至E，使AD=DE；（3）画射线BA；（4）反向延长线段BC．[来源:]【解答】解：（1）如图所示，直线AC，线段DB以及点O即为所求；（2）如图所示，点E即为所求；（3）如图所示，射线BA即为所求；（4）如图所示，射线CB即为所求．24．（11分）如图，已知O为直线AB上一点，过点O向直线AB上方引三条射线OC、OD、OE，且OC平分∠AOD，∠BOE=3∠DOE，∠COE=70°．求：（1）∠BOE的度数；（2）∠AOC的度数．【解答】解：设∠BOE=x，则∠DOE=x，∵∠BOD=∠BOE+∠EOD=x，∵∠AOD=180°﹣∠BOD=180°﹣x．∵OC平分∠AOD，∴∠AOC=∠COD=∠AOD=（180°﹣x）=90°﹣x．∵∠COE=∠COD+∠DOE=90°﹣x+x=70°，解得x=60°，∴∠BOE=60°；（2）∵∠AOC=90°﹣x，∴∠AOC=50°．25．（12分）请根据图中提供的信息，回答下列问题：（1）一个暖瓶与一个水杯分别是多少元？（只填写结果）一个暖瓶32 元；一个水杯 2 元．（2）甲、乙两家商场同时出售同样的暖瓶和水杯，为了迎接新年，两家商场都在搞促销活动，甲商场规定：这两种商品都打九折；乙商场规定：买一个暖瓶赠送二个水杯，单独买水杯不优惠．若某单位想要买4个暖瓶和15个水杯，请问选择哪家商场购买更合算，并说明理由．（3）若必须买5个暖瓶，则当买多少个水杯时到两家商城一样合算．【解答】解：（1）设一个暖瓶的价格为m元，一个水杯的价格为n元，根据题意得：，解得：．故答案为：32；2．（2）甲商城的费用（4×32+15×2）×0.9=142.2（元）；乙商城的费用4×32+（15﹣4×2）×2=142（元）．∵142.2＞142，∴到乙商城购买合算．（3）设购买x个水杯时到两家商场一样合算，根据题意得：（5×32+2x）×0.9=5×32+（x﹣10）×2，解得：x=20．答：当买20个水杯时到两家商场一样合算．26．（14分）A、B、C为数轴上的三点，动点A、B同时从原点出发，动点A每秒运动x个单位，动点B每秒运动y个单位，且动点A运动到的位置对应的数记为a，动点B运动到的位置对应的数记为b，定点C对应的数为8．（1）若2秒后，a、b满足|a+8|+（b﹣2）2=0，则x= 4 ，y= 1 ，并请在数轴上标出A、B 两点的位置．（2）若动点A、B在（1）运动后的位置上保持原来的速度，且同时向正方向运动z秒后使得|a|=|b|，使得z= ．（3）若动点A、B在（1）运动后的位置上都以每秒2个单位向正方向运动继续运动t秒，点A 与点C之间的距离表示为AC，点B与点C之间的距离表示为BC，点A与点B之间的距离为AB，且AC+BC=1.5AB，则t= ．【解答】解：（1）∵|a+8|+（b﹣2）2=0，∴a+8=0，b﹣2=0，即a=﹣8，b=2，则x=|﹣8|÷2=4，y=2÷2=1（2）动点A、B在（1）运动后的位置上保持原来的速度，且同时向正方向运动z秒后a=﹣8+4z，b=2+z，∵|a|=|b|，∴|﹣8+4z|=2+z，解得；（3）若动点A、B在（1）运动后的位置上都以每秒2个单位向正方向运动继续运动t秒后点A表示：﹣8+2t，点B表示：2+2t，点C表示：8，∴AC=|﹣8+2t﹣8|=|2t﹣16|，BC=|2+2t﹣8|=|2t﹣6|，AB=|﹣8+2t﹣（2+2t）|=10，∵AC+BC=1.5AB∴|2t﹣16|+|2t﹣6|=1.5×10，解得；。

2016-2017学年江苏省徐州市七年级(上)期末数学试题含答案

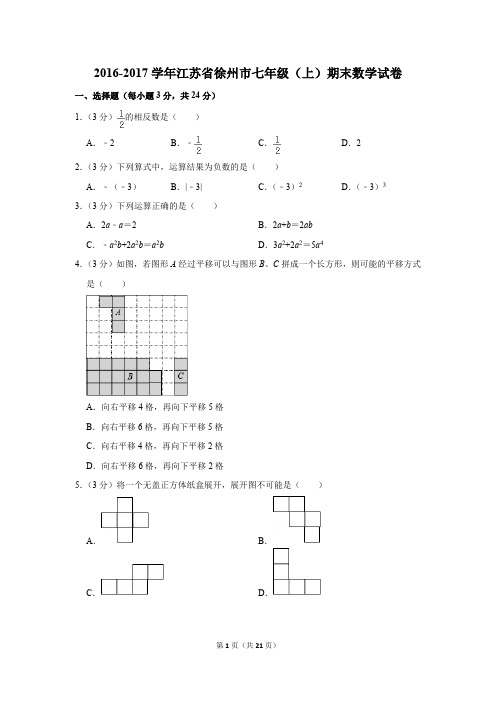
2016-2017学年江苏省徐州市七年级（上）期末数学试卷一、选择题（每小题3分，共24分）1．（3分）的相反数是（）A．﹣2B．﹣C．D．22．（3分）下列算式中，运算结果为负数的是（）A．﹣（﹣3）B．|﹣3|C．（﹣3）2D．（﹣3）33．（3分）下列运算正确的是（）A．2a﹣a＝2B．2a+b＝2abC．﹣a2b+2a2b＝a2b D．3a2+2a2＝5a44．（3分）如图，若图形A经过平移可以与图形B、C拼成一个长方形，则可能的平移方式是（）A．向右平移4格，再向下平移5格B．向右平移6格，再向下平移5格C．向右平移4格，再向下平移2格D．向右平移6格，再向下平移2格5．（3分）将一个无盖正方体纸盒展开，展开图不可能是（）A．B．C．D．6．（3分）如图，BC＝AB，D为AC的中点，若DC＝3，则AB的长是（）A．3B．4C．5D．67．（3分）已知射线OC在∠AOB的内部，下列关系式①∠AOC＝∠BOC；②∠AOC+∠BOC＝∠AOB；③∠AOB＝2∠AOC；④∠BOC＝∠AOB．其中，能说明OC为∠AOB的平分线的有（）A．1个B．2个C．3个D．4个8．（3分）观察下列图形，照此规律，第5个图形中白色三角形的个数是（）A．81B．121C．161D．201二、填空题（本题共8小题，每小题3分，共24分）9．（3分）计算：﹣3﹣1＝．10．（3分）多项式3a2+2b3的次数是．11．（3分）2017年春运期间，徐州铁路两站预计发送旅客2430000人次，该数据用科学记数法可表示为人次．12．（3分）若m+2n＝1，则代数式3﹣m﹣2n的值是．13．（3分）数学课上，小丽把一副三角板按如图所示的位置摆放（其中一个三角板的直角顶点在另一个三角板的直角边上），如果∠α＝28°，那么∠β＝ °．14．（3分）建筑工人在砌墙时，经常在两个墙角分别立一根标志杆，在两根标志杆之间拉一条线，沿这条线就可以砌出直的墙了，其中的数学道理是．15．（3分）当x＝﹣2时，代数式kx+5的值为﹣1，则k的值为．16．（3分）若输入整数a，按照下列程序，计算将无限进行下去且不会输出，则a所有可能取到的值为．三、解答题（本题共9小题，共72分）17．（10分）计算（1）|﹣4|+23+3×（﹣5）（2）﹣12016﹣×[4﹣（﹣3）2]．18．（6分）先化简，再求值：5（3a2b﹣ab2）﹣4（3a2b﹣ab2），其中a＝2，b＝﹣3．19．（8分）解下列方程（1）4﹣x＝3（2﹣x）（2）＝2﹣．20．（6分）如图是由6个棱长都为1cm的小正方体搭成的几何体．（1）该几何体的主视图如图所示，请在下面方格纸中高分别画出它的左视图和俯视图；（2）该几何体的表面积为 cm2．21．（8分）为实施“学讲计划”，某班学生计划分成若干个学习小组，若每组5人，则多出4人，若每组6人，则有一组只有2人，该班共有多少名学生？22．（8分）如图，在方格纸中，点A、B、C是三个格点（网格线的交点叫做格点）（1）过点C画AB的垂线，垂足为D；（2）将点D沿BC翻折，得到点E，作直线CE；（3）直线CE与直线AB的位置关系是；（4）判断：∠ACB ∠ACE．（填“＞”、“＜”或“＝”23．（8分）如图，直线AB与CD相交于O，OE是∠AOC的平分线，OF⊥CD，OG⊥OE，∠BOD＝52°．（1）求∠AOF的度数；（2）求∠EOF与∠BOG是否相等？请说明理由．。

2016-2017学年第一学期七年级期末数学试卷打印2

七年级期末数学复习一、选择题7．如图所示，有理数a、b在数轴上的位置如图，则下列说法错误的是（）A．b﹣a＞0 B．a+b＜0 C．ab＜0 D．b＜a二、填空题12．若（a﹣1）2+|b+2|=0，则（a+b）5=13．若﹣5x n y4与12x3y2-m是同类项，则m+n= ．15．如图，AB，CD相交于点O，OE⊥AB，垂足为O，∠COE=44°，则∠AOD=．16、17、三、解答题18．（8分）计算：（1）10+（﹣5）×2﹣（﹣9）．（2）．19．（6分）计算：．20．（6分）合并同类项：5x2﹣7xy+3x2+6xy﹣4x2．21．（6分）先化简，再求值：，其中，．\20．已知（x+2）2+|y﹣|=0，求5x2y﹣[2x2y﹣（xy2﹣2x2y）﹣4]﹣2xy2的值．23．某市出租车的收费标准是：行程不超过3千米起步价为10元，超过3千米后每千米增收1.8元．某乘客出租车x千米．（1）试用关于x的代数式分情况表示该乘客的付费．（2）如果该乘客坐了8千米，应付费多少元？（3）如果该乘客付费26.2元，他坐了多少千米？24．如图，OM是∠AOC的平分线，ON是∠BOC的平分线．（1）如图1，当∠AOB=90°，∠BOC=60°时，∠MON的度数是多少？写出理由（2）如图2，当∠AOB=70°，∠BOC=60°时，∠MON=（3）如图3，当∠AOB=α，∠BOC=β时，∠MON= 25．如图，已知数轴上点A表示的数为8，B是数轴上的一点，AB=12，动点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．（1）写出数轴上点B表示的数，点P表示的数（用含t的代数式表示）；（2）动点Q从点B出发，以每秒4个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时追上点Q？2016-2017学年第一学期新人教版七年级期末数学试卷参考答案一、选择题（共10小题，每小题3分，满分30分）1．B．2．D．3．D．4．A．5．C．6．C．7．A．8．D．9．C．10．B．二、填空题（共6小题，每小题4分，满分24分）11．﹣6%．12．-113．4．14．4．15．134°．16．（）n a 三、解答题（共9小题，满分66分）17．计算：﹣12014﹣6÷（﹣2）×|﹣|．解：原式=﹣1+6××=﹣1+1=0．18．【解答】解：如图所示．19．【解答】解：去分母，得3（y+1）=24﹣4（2y﹣1），去括号，得9y+3=24﹣8y+4，移项，得9y+8y=24+4﹣3，合并同类项，得17y=25，系数化为1，得y=．20．【解答】解：∵（x+2）2+|y﹣|=0，∴x=﹣2，y=，则原式=5x2y﹣2x2y+xy2﹣2x2y+4﹣2xy2=x2y﹣xy2+4=2++4=6．21．【解答】解：设到雷锋纪念馆的人数为x人，则到毛泽东纪念馆的人数为（589﹣x）人，由题意得，2x+56=589﹣x，解得x=178．答：到雷锋纪念馆参观的人数有178人．22．【解答】解：（1）7﹣（﹣10）=17（辆）；（2）100×7+（﹣1+3﹣2+4+7﹣5﹣10）=696（辆），答：（1）生产量最多的一天比生产量最少的一天多生产17辆；（2）本周总生产量是696辆，比原计划减少了4辆．23．【解答】解：（1）当行程不超过3千米即x≤3时时，收费10元；当行程超过3千米即x＞3时，收费为：10+（x﹣3）×1.8=1.8x+4.6（元）．（2）当x=8时，1.8x+4.6=1.8×8+4.6=19（元）．答：乘客坐了8千米，应付费19元；（3）设他坐了x千米，由题意得：10+（x﹣3）×1.8=26.2，解得x=12．答：他乘坐了12千米．24．【解答】解：（1）如图1，∵∠AOB=90°，∠BOC=60°，∴∠AOC=90°+60°=150°，∵OM平分∠AOC，ON平分∠BOC，∴∠MOC=∠AOC=75°，∠NOC=∠BOC=30°∴∠MON=∠MOC﹣∠NOC=45°．（2）如图2，∵∠AOB=70°，∠BOC=60°，∴∠AOC=70°+60°=130°，∵OM平分∠AOC，ON平分∠BOC，∴∠MOC=∠AOC=65°，∠NOC=∠BOC=30°∴∠MON=∠MOC﹣∠NOC=65°﹣30°=35°．故答案为：35°．（3）如图3，∠MON=α，与β的大小无关．理由：∵∠AOB=α，∠BOC=β，∴∠AOC=α+β．∵OM是∠AOC的平分线，ON是∠BOC的平分线，∴∠MOC=∠AOC=（α+β），∠NOC=∠BOC=β，∴∠AON=∠AOC﹣∠NOC=α+β﹣β=α+β．∴∠MON=∠MOC﹣∠NOC=（α+β）﹣β=α即∠MON=α．故答案为：α．25．【解答】解：（1）∵AB=12，AO=8，∴BO=4，∴点B在数轴上表示的数为﹣4，点P从点A出发，以每秒6个单位长度的速度沿数轴向左匀速运动，则AP=6t，∴点P表示的数为8﹣6t；故答案为﹣4，8﹣6t；（2）设x秒后P点追上Q点，则6t﹣4t=12，解得：t=6；（3）①点P在AB中间，∵AM=PM，BN=PN，∴MN=AB=6；②点P在B点左侧，PM=PA=（PB+AB），PN=PB，∴MN=PM﹣PN=PA﹣PB=AB=6，综上所述，MN在点P运用过程中长度无变化．。

人教版 2016-2017学年七年级上册初一数学期末考试卷及答案

人教版 2016-2017学年七年级上册初一数学期末考试卷及答案2016-2017学年度第一学期期末数学试题七年级数学一、选择题（共20分）1.零不属于（）A。

正数集合 B。

有理数集合 C。

整数集合 D。

非正有理数集合2.已知下列各数-8，2.1，3，0，-2.5，10，-1中，其中非负数的个数是（）A。

2个 B。

3个 C。

4个 D。

5个3.下列各组数中，互为相反数的是（）A。

|3|和-3 B。

|1|和-3 C。

|3|和3 D。

|1|和14.甲、乙、丙三地的海拔高度为20米，-15米，-10米，那么最高的地方比最低的地方高（）A。

10米 B。

25米 C。

35米 D。

5米5.质检员抽查某零件的质量，超过规定尺寸的记为正数，不足规定尺寸的记为负数，结果第一个.13mm，第二个-0.12mm，第三个0.15mm，第四个0.11mm，则质量最好的零件是（）A。

第一个 B。

第二个 C。

第三个 D。

第四个6.绝对值相等的两数在数轴上对应两点的距离为8，则这两个数为（）A。

±8 B。

0和-8 C。

0和8 D。

4和-47.下列判断正确的是（）A。

比正数小的数一定是负数 B。

零是最小的有理数 C。

有最大的负整数和最小的正整数 D。

一个有理数所对应的点离开原点越远，则它越大8.一个数的平方仍然得这个数，则此数是（）A。

0 B。

±1 C。

±1和0 D。

1和-19.圆柱的侧面展开图是（）A。

圆形 B。

扇形 C。

三角形 D。

四边形10.下列说法正确的是（）A。

两点之间的距离是两点间的线段；B。

同一平面内，过一点有且只有一条直线与已知直线平行；C。

同一平面内，过一点有且只有一条直线与已知直线垂直；D。

与同一条直线垂直的两条直线也垂直。

二、填空（共24分）1.六棱柱有 8 个顶点，12 个面。

2.如果运进72吨记作+72吨，那么运出56吨记作-56吨。

3.任意写出5个正数，5个负数，并且分别填入所属集合里，正数集合{1.2.3.4.5}，负数集合{-1.-2.-3.-4.-5}。

秦皇岛市抚宁区2016-2017年七年级上期末数学试卷含答案解析【精品期末】

2016-2017学年河北省秦皇岛市抚宁区七年级（上）期末数学试卷一、选择题：本大题共12小题，每小题3分，共36分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．如果水库的水位高于正常水位2m时，记作+2m，那么低于正常水位3m时，应记作（）A．+3mB．﹣3m C．+m D．﹣m2．下列说法正确的是（）A．有最小的正数B．有最小的自然数C．有最大的有理数D．无最大的负整数3．下面说法正确的是（）A．的系数是B．的系数是C．﹣5x2的系数是5D．3x2的系数是34．原产量n吨，增产30%之后的产量应为（）A．（1﹣30%）n吨B．（1+30%）n吨C．n+30%吨D．30%n吨5．下列方程变形中，正确的是（）A．方程3x﹣2=2x+1，移项，得3x﹣2x=﹣1+2B．方程3﹣x=2﹣5（x﹣1），去括号，得3﹣x=2﹣5x﹣1C．方程t=，未知数系数化为1，得t=1D．方程﹣=1化成3x=66．下列四个生活、生产现象中，其中可用“两点之间，线段最短”来解释的现象有（）①用两个钉子就可以把木条固定在墙上②植树时，只要定出两棵树的位置，就能确定同一行树所在的直线③从A地到B地架设电线，总是尽可能沿着直线架设④把弯曲的公路改直，就能缩短路程．A．①②B．①③C．②④D．③④7．如图，将一副三角尺按不同位置摆放，摆放方式中∠α与∠β互余的是（）A．B．C．D．8．若|2a|=﹣2a，则a一定是（）A．正数B．负数C．正数或零D．负数或零9．一个多项式与x2﹣2x+1的和是3x﹣2，则这个多项式为（）A．x2﹣5x+3B．﹣x2+x﹣1C．﹣x2+5x﹣3D．x2﹣5x﹣1310．小华在做解方程作业时，不小心将方程中的一个常数污染了看不清楚，被污染的方程是y﹣=y﹣■，怎么办呢？小明想了想，便翻看了书后的答案，此方程的解是：y=﹣6，小华很快补好了这个常数，并迅速完成了作业．这个常数是（）A．﹣4B．3C．﹣4D．411．若∠1=40.4°，∠2=40°4′，则∠1与∠2的关系是（）A．∠1=∠2B．∠1＞∠2C．∠1＜∠2D．以上都不对12．如图所示，把一个正方形对折两次后沿虚线剪下，展开后所得的图形是（）A．B．C．D．二、填空题：本大题共6小题，每小题3分，共18分，把答案写在题中横线上．13．的相反数是，绝对值是，倒数是．14．若多项式2x2+3x+7的值为10，则多项式6x2+9x﹣7的值为．15．一个角的补角是这个角余角的3倍，则这个角是度．16．一艘船从甲码头到乙码头顺流行驶，用了2个小时，从乙码头返回甲码头逆流行驶，用了2.5小时，已知水流的速度是3千米/时，则船在静水中的速度是千米/时．17．若（a+3）2+|b﹣2|=0，则（a+b）2011=．18．观察下列算式：12﹣02=1+0=1；22﹣12=2+1=3；32﹣22=3+2=5；42﹣32=4+3=7；52﹣42=5+4=9；…若字母n表示自然数，请你观察到的规律用含n式子表示出来：．三、解答题：本大题共7小题，共66分，解答应写出文字说明、证明过程或演算步骤．19．计算题：（1）6﹣（+3）﹣（﹣7）+（﹣2）；（2）（﹣2）2﹣22﹣|﹣|×（﹣10）2；（3）（+﹣）÷（﹣）；（4）﹣12012﹣[2﹣（1﹣×0.5）]×[32﹣（﹣2）2]．20．先化简，再求值．x﹣2（x﹣y2）+（﹣x+y2），其中x=﹣2，y=．21．解方程：（1）x﹣4=2x+3﹣x；（2）y﹣=2﹣．22．一项工程，甲单独做要10天完成，乙单独做要15天完成，两人合做4天后，剩下的部分由乙单独做，还需要几天完成？23．已知，如图，B，C两点把线段AD分成2：5：3三部分，M为AD的中点，BM=6cm，求CM 和AD的长．24．如图，直线AB、CD交于O点，且∠BOC=80°，OE平分∠BOC，OF为OE的反向延长线．（1）求∠2和∠3的度数；（2）OF平分∠AOD吗？为什么？25．如图所示，点C在线段AB上，AC=8cm，CB=6cm，点M、N分别是AC、BC的中点．（1）求线段MN的长．（2）若C为线段AB上任意一点，满足AC+CB=acm，其他条件不变，你能猜想出MN的长度吗？并说明理由．（3）若C在线段AB的延长线上，且满足AC﹣CB=bcm，M、N分别为AC、BC的中点，你能猜想出MN的长度吗？请画出图形，写出你的结论，并说明理由．2016-2017学年河北省秦皇岛市抚宁区七年级（上）期末数学试卷参考答案与试题解析一、选择题：本大题共12小题，每小题3分，共36分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．如果水库的水位高于正常水位2m时，记作+2m，那么低于正常水位3m时，应记作（）A．+3mB．﹣3m C．+m D．﹣m【考点】正数和负数．【分析】根据正数和负数表示相反意义的量，可得答案．【解答】解：水库的水位高于正常水位2m时，记作+2m，那么低于正常水位3m时，应记作﹣3m，故选：B．2．下列说法正确的是（）A．有最小的正数B．有最小的自然数C．有最大的有理数D．无最大的负整数【考点】有理数．【分析】根据有理数的分类，利用排除法求解．【解答】解：既没有最大的也没有最小的正数，A错误；最小的自然数是0，B正确；有理数既没有最大也没有最小，C错误；最大的负整数是﹣1，D错误；故选B．3．下面说法正确的是（）A．的系数是B．的系数是C．﹣5x2的系数是5D．3x2的系数是3【考点】单项式．【分析】根据单项式系数的定义求解．【解答】解：A、的系数是π，故本选项错误；B、的系数是，故本选项错误；C、﹣5x2的系数是﹣5，故本选项错误；D、3x2的系数是3，故本选项正确．故选D．4．原产量n吨，增产30%之后的产量应为（）A．（1﹣30%）n吨B．（1+30%）n吨C．n+30%吨D．30%n吨【考点】列代数式．【分析】原产量n吨，增产30%之后的产量为n+n×30%，再进行化简即可．【解答】解：由题意得，增产30%之后的产量为n+n×30%=n（1+30%）吨．故选B．5．下列方程变形中，正确的是（）A．方程3x﹣2=2x+1，移项，得3x﹣2x=﹣1+2B．方程3﹣x=2﹣5（x﹣1），去括号，得3﹣x=2﹣5x﹣1C．方程t=，未知数系数化为1，得t=1D．方程﹣=1化成3x=6【考点】解一元一次方程．【分析】根据解一元一次方程的一般步骤对各选项进行逐一分析即可．【解答】解：A、方程3x﹣2=2x+1，移项，得3x﹣2x=1+2，故本选项错误；B、方程3﹣x=2﹣5（x﹣1），去括号，得3﹣x=2﹣5x+5，故本选项错误；C、方程t=，未知数系数化为1，得t=，故本选项错误；D、方程﹣=1化成3x=6，故本选项正确．故选D．6．下列四个生活、生产现象中，其中可用“两点之间，线段最短”来解释的现象有（）①用两个钉子就可以把木条固定在墙上②植树时，只要定出两棵树的位置，就能确定同一行树所在的直线③从A地到B地架设电线，总是尽可能沿着直线架设④把弯曲的公路改直，就能缩短路程．A．①②B．①③C．②④D．③④【考点】线段的性质：两点之间线段最短．【分析】分别利用直线的性质以及线段的性质分析得出答案．【解答】解：①用两个钉子就可以把木条固定在墙上，是两点确定一条之间，故此选项错误；②植树时，只要定出两棵树的位置，就能确定同一行树所在的直线，是两点确定一条之间，故此选项错误；③从A地到B地架设电线，总是尽可能沿着直线架设，是两点之间，线段最短，故此选项正确；④把弯曲的公路改直，就能缩短路程，是两点之间，线段最短，故此选项正确；故选：D．7．如图，将一副三角尺按不同位置摆放，摆放方式中∠α与∠β互余的是（）A．B．C．D．【考点】余角和补角．【分析】根据图形，结合互余的定义判断即可．【解答】解：A、∠α与∠β不互余，故本选项错误；B、∠α与∠β不互余，故本选项错误；C、∠α与∠β互余，故本选项正确；D、∠α与∠β不互余，∠α和∠β互补，故本选项错误；故选C．8．若|2a|=﹣2a，则a一定是（）A．正数B．负数C．正数或零D．负数或零【考点】绝对值．【分析】根据绝对值的定义，绝对值等于它的相反数的数是负数或零．【解答】解：∵2a的相反数是﹣2a，且|2a|=﹣2a，∴a一定是负数或零．故选D．9．一个多项式与x2﹣2x+1的和是3x﹣2，则这个多项式为（）A．x2﹣5x+3B．﹣x2+x﹣1C．﹣x2+5x﹣3D．x2﹣5x﹣13【考点】整式的加减．【分析】由题意可得被减式为3x﹣2，减式为x2﹣2x+1，根据差=被减式﹣减式可得出这个多项式．【解答】解：由题意得：这个多项式=3x﹣2﹣（x2﹣2x+1），=3x﹣2﹣x2+2x﹣1，=﹣x2+5x﹣3．故选C．10．小华在做解方程作业时，不小心将方程中的一个常数污染了看不清楚，被污染的方程是y﹣=y﹣■，怎么办呢？小明想了想，便翻看了书后的答案，此方程的解是：y=﹣6，小华很快补好了这个常数，并迅速完成了作业．这个常数是（）A．﹣4B．3C．﹣4D．4【考点】一元一次方程的解．【分析】设这个常数为m，将y=﹣6代入被污染的方程，可得出m的值．【解答】解：设这个常数为m，则被污染的方程是y﹣=y﹣m，将y=﹣6代入可得：﹣6﹣=×（﹣6）﹣m，解得：m=4．故选D．11．若∠1=40.4°，∠2=40°4′，则∠1与∠2的关系是（）A．∠1=∠2B．∠1＞∠2C．∠1＜∠2D．以上都不对【考点】角的大小比较；度分秒的换算．【分析】首先同一单位，利用1°=60′，把∠α=40.4°=40°24′，再进一步与∠β比较得出答案即可．【解答】解：∵∠1=40.4°=40°24′，∠2=40°4′，∴∠1＞∠2．故选：B．12．如图所示，把一个正方形对折两次后沿虚线剪下，展开后所得的图形是（）A．B．C．D．【考点】剪纸问题．【分析】此类问题只有动手操作一下，按照题意的顺序折叠，剪开，观察所得的图形，可得正确的选项．【解答】解：按照题意，动手操作一下，可知展开后所得的图形是选项B．故选B．二、填空题：本大题共6小题，每小题3分，共18分，把答案写在题中横线上．13．的相反数是，绝对值是，倒数是﹣．【考点】相反数；绝对值；倒数．【分析】根据相反数的定义，只有符号不同的两个数是互为相反数，的相反数是；根据绝对值的定义，一个数的绝对值等于表示这个数的点到原点的距离，的绝对值是根据倒数的定义，互为倒数的两数乘积为1，﹣×（﹣）=1．【解答】解：根据相反数、绝对值和倒数的定义得：的相反数是；的绝对值是；的倒数是﹣．14．若多项式2x2+3x+7的值为10，则多项式6x2+9x﹣7的值为2．【考点】整式的加减—化简求值．【分析】由题意得2x2+3x=3，将6x2+9x﹣7变形为3（2x2+3x）﹣7可得出其值．【解答】解：由题意得：2x2+3x=36x2+9x﹣7=3（2x2+3x）﹣7=2．15．一个角的补角是这个角余角的3倍，则这个角是45度．【考点】余角和补角．【分析】设这个角为x，根据余角和补角的概念、结合题意列出方程，解方程即可．【解答】解：设这个角为x，由题意得，180°﹣x=3（90°﹣x），解得x=45°，则这个角是45°，故答案为：45．16．一艘船从甲码头到乙码头顺流行驶，用了2个小时，从乙码头返回甲码头逆流行驶，用了2.5小时，已知水流的速度是3千米/时，则船在静水中的速度是27千米/时．【考点】一元一次方程的应用．【分析】设船在静水中的速度是x，则顺流时的速度为（x+3）km/h，逆流时的速度为（x﹣3）km/h，根据往返的路程相等，可得出方程，解出即可．【解答】解：设船在静水中的速度是x，则顺流时的速度为（x+3）km/h，逆流时的速度为（x﹣3）km/h，由题意得，2（x+3）=2.5（x﹣3），解得：x=27，即船在静水中的速度是27千米/时．故答案为：27．17．若（a+3）2+|b﹣2|=0，则（a+b）2011=﹣1．【考点】非负数的性质：偶次方；非负数的性质：绝对值．【分析】根据非负数的性质列出方程求出a、b的值，代入所求代数式计算即可．【解答】解：根据题意得：，解得：，则（a+b）2011=﹣1．故答案是：﹣1．18．观察下列算式：12﹣02=1+0=1；22﹣12=2+1=3；32﹣22=3+2=5；42﹣32=4+3=7；52﹣42=5+4=9；…若字母n表示自然数，请你观察到的规律用含n式子表示出来：（n+1）2﹣n2=2n+1．【考点】规律型：数字的变化类．【分析】根据题意，分析可得：（0+1）2﹣02=1+2×0=1；（1+1）2﹣12=2×1+1=3；（1+2）2﹣22=2×2+1=5；…进而发现规律，用n表示可得答案．【解答】解：根据题意，分析可得：（0+1）2﹣02=1+2×0=1；（1+1）2﹣12=2×1+1=3；（1+2）2﹣22=2×2+1=5；…若字母n表示自然数，则有：n2﹣（n﹣1）2=2n﹣1；故答案为（n+1）2﹣n2=2n+1．三、解答题：本大题共7小题，共66分，解答应写出文字说明、证明过程或演算步骤．19．计算题：（1）6﹣（+3）﹣（﹣7）+（﹣2）；（2）（﹣2）2﹣22﹣|﹣|×（﹣10）2；（3）（+﹣）÷（﹣）；（4）﹣12012﹣[2﹣（1﹣×0.5）]×[32﹣（﹣2）2]．【考点】有理数的混合运算．【分析】（1）原式利用减法法则变形，计算即可得到结果；（2）原式先计算乘方及绝对值运算，再计算乘法运算，最后算加减运算即可得到结果；（3）原式利用除法法则变形，再利用乘法分配律计算即可得到结果；（4）原式先计算乘方运算，再计算乘法运算，最后算加减运算即可得到结果．【解答】解：（1）原式=6﹣3+7﹣2=13﹣5=8；（2）原式=4﹣4﹣×100=4﹣4﹣25=﹣25；（3）原式=（+﹣）×（﹣60）=﹣45﹣35+50=﹣80+50=﹣30；（4）原式=﹣1﹣（2﹣1+）×5=﹣1﹣5﹣=﹣．20．先化简，再求值．x﹣2（x﹣y2）+（﹣x+y2），其中x=﹣2，y=．【考点】整式的加减—化简求值．【分析】原式去括号合并得到最简结果，把x与y的值代入计算即可求出值．【解答】解：原式=x﹣2x+y2﹣x+y2=﹣3x+y2，当x=﹣2，y=时，原式=6．21．解方程：（1）x﹣4=2x+3﹣x；（2）y﹣=2﹣．【考点】解一元一次方程．【分析】根据一元一次方程的解法即可求出答案【解答】解：（1）x﹣8=4x+6﹣5xx﹣8=﹣x+62x=14x=7（2）6y﹣3（y﹣1）=12﹣（y+2）6y﹣3y+3=12﹣y﹣23y+3=10﹣y4y=7y=22．一项工程，甲单独做要10天完成，乙单独做要15天完成，两人合做4天后，剩下的部分由乙单独做，还需要几天完成？【考点】一元一次方程的应用．【分析】设工作量为1，根据甲单独做需要10天完成，乙单独做需要15天完成，即可求出甲乙的效率；等量关系为：甲的工作量+乙的工作量=1，列出方程，再求解即可．【解答】解：设乙还需x天完成，由题意得4×（+）+=1，解得x=5．答：乙还需5天完成．23．已知，如图，B，C两点把线段AD分成2：5：3三部分，M为AD的中点，BM=6cm，求CM 和AD的长．【考点】两点间的距离．【分析】由已知B，C两点把线段AD分成2：5：3三部分，所以设AB=2xcm，BC=5xcm，CD=3xcm，根据已知分别用x表示出AD，MD，从而得出BM，继而求出x，则求出CM和AD的长．【解答】解：设AB=2xcm，BC=5xcm，CD=3xcm所以AD=AB+BC+CD=10xcm因为M是AD的中点所以AM=MD=AD=5xcm所以BM=AM﹣AB=5x﹣2x=3xcm因为BM=6cm，所以3x=6，x=2故CM=MD﹣CD=5x﹣3x=2x=2×2=4cm，AD=10x=10×2=20cm．24．如图，直线AB、CD交于O点，且∠BOC=80°，OE平分∠BOC，OF为OE的反向延长线．（1）求∠2和∠3的度数；（2）OF平分∠AOD吗？为什么？【考点】对顶角、邻补角；角平分线的定义．【分析】（1）根据邻补角的定义，即可求得∠2的度数，根据角平分线的定义和平角的定义即可求得∠3的度数；（2）根据OF分∠AOD的两部分角的度数即可说明．【解答】解：（1）∵∠BOC+∠2=180°，∠BOC=80°，∴∠2=180°﹣80°=100°；∵OE是∠BOC的角平分线，∴∠1=40°．∵∠1+∠2+∠3=180°，∴∠3=180°﹣∠1﹣∠2=180°﹣40°﹣100°=40°．（2）∵∠2+∠3+∠AOF=180°，∴∠AOF=180°﹣∠2﹣∠3=180°﹣100°﹣40°=40°．∴∠AOF=∠3=40°，∴OF平分∠AOD．25．如图所示，点C在线段AB上，AC=8cm，CB=6cm，点M、N分别是AC、BC的中点．（1）求线段MN的长．（2）若C为线段AB上任意一点，满足AC+CB=acm，其他条件不变，你能猜想出MN的长度吗？并说明理由．（3）若C在线段AB的延长线上，且满足AC﹣CB=bcm，M、N分别为AC、BC的中点，你能猜想出MN的长度吗？请画出图形，写出你的结论，并说明理由．【考点】两点间的距离．【分析】（1）根据线段中点的定义得到MC=AC=4cm，NC=BC=3cm，然后利用MN=MC+NC进行计算；（2）根据线段中点的定义得到MC=AC，NC=BC，然后利用MN=MC+NC得到MN=acm；（3）先画图，再根据线段中点的定义得MC=AC，NC=BC，然后利用MN=MC﹣NC得到MN=bcm．【解答】解：（1）∵点M、N分别是AC、BC的中点，∴MC=AC=×8cm=4cm，NC=BC=×6cm=3cm，∴MN=MC+NC=4cm+3cm=7cm；（2）MN=acm．理由如下：∵点M、N分别是AC、BC的中点，∴MC=AC，NC=BC，∴MN=MC+NC=AC+BC=AB=acm；（3）解：如图，∵点M、N分别是AC、BC的中点，∴MC=AC，NC=BC，∴MN=MC﹣NC=AC﹣BC=（AC﹣BC）=bcm．2017年2月4日。

精品解析：江苏省南京师范大学附属中学2016-2017学年七年级上学期期末考试数学试题(解析版)

2016-2017学年度（上）期末测试卷七年级数学一、选择题1.3-的倒数是（）A. 3B. 13C.13- D. 3-【答案】C【解析】【分析】由互为倒数的两数之积为1，即可求解．【详解】∵1313⎛⎫-⨯-= ⎪⎝⎭，∴3-的倒数是13-. 故选C 2.将一副三角板按如图所示位置摆放，其中∠α与∠β一定互余的是（）A. B. C.D.【答案】C【解析】【分析】先根据图形结合互余的定义进行一一判断，然后综合即可得出符合题意的选项. 【详解】解：A、∠α与∠β不一定互余，故本选项错误；B、∠α与∠β不互余，故本选项错误；C、∠α与∠β互余，故本选项正确；D、∠α与∠β不互余，∠α和∠β互补，故本选项错误；故选：C．【点睛】本题考查的知识点是对顶角、余角和补角.解题关键是熟记“互余的两个角的和等于90°”.3.若|a﹣1|=a﹣1，则a的取值范围是（）A. a≥1B. a≤1C. a＜1D. a＞1【答案】A【解析】试题分析：由绝对值性质可得：一个正数的绝对值是它本身，一个负数的绝对值是它的相反数，0的绝对值是0．因为|a﹣1|=a﹣1，所以a﹣1≥0，所以a≥1．选A．考点：绝对值的性质．【此处有视频，请去附件查看】4.如图是一个正方体的平面展开图，把展开图折叠成正方体后，“祝”字一面对面的字是（）A. 新B. 年C. 快D. 乐【答案】D【解析】试题分析：正方体的平面展开图的特征：相对面展开后间隔一个正方形.由图可得“祝”字对面的字是“快”，故选：D.点睛：本题属于基础应用题，只需学生熟练掌握正方体的平面展开图的特征，即可完成.5.下列说法不正确的是（）A. 过任意一点可作已知直线的一条平行线B. 在同一平面内两条不相交的直线是平行线C. 在同一平面内，过直线外一点只能画一条直线与已知直线垂直D. 直线外一点与直线上各点连接的所有线段中，垂线段最短【答案】A【解析】试题分析：平面内，过直线外一点有且只有一条直线与已知直线平行，故A 不正确；在同一平面内两条不相交的直线是平行线，这是平行线的概念，故B 正确；在同一平面内，过直线外一点只能画一条直线与已知直线垂直，故C 正确；直线外一点与直线上各点连接的所有线段中，垂线段最短，故D 正确；故选：A.6. 如图，下列图案均是长度相同的火柴按一定的规律拼搭而成：第1个图案需7根火柴，第2个图案需13根火柴，…，依此规律，第11个图案需（）根火柴．A. 156B. 157C. 158D. 159【答案】B【解析】根据第1个图案需7根火柴，7=1×（1+3）+3，第2个图案需13根火柴，13=2×（2+3）+3，第3个图案需21根火柴，21=3×（3+3）+3，得出规律第n 个图案需n （n+3）+3根火柴，再把11代入即可求出答案．解：根据题意可知：第1个图案需7根火柴，7=1×（1+3）+3，第2个图案需13根火柴，13=2×（2+3）+3，第3个图案需21根火柴，21=3×（3+3）+3，…，第n 个图案需n （n+3）+3根火柴，则第11个图案需：11×（11+3）+3=157（根）；故选B ．“点睛”此题主要考查图形的变化类，关键是根据题目中给出的图形，通过观察思考，归纳总结出规律，再利用规律解决问题，难度一般偏大，属于难题.【此处有视频，请去附件查看】二、填空题7.温度由1℃下降10℃后是________℃.【答案】-9【解析】试题分析：根据温度的关系，利用有理数的加减可得1-10=-9.故答案：9.8.大家翘首以盼的南京地铁4号线将于2017年春节前开通，它从龙江站到仙林湖站线路长度33.8千米.则数据33.8用科学记数法表示为___________.【答案】3.38×10【解析】试题分析：由科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n 是正数；当原数的绝对值＜1时，n 是负数．因此33.8= 3.38×10.9.若23m n +=-，则842m n --的值是________.【答案】14【解析】试题分析：根据整体思想，先提公因式，整体代入即可得8-4m-2n=8-2（2m+n ）=8-2×（-3）=14.10.如果一个角是2015'︒，那么这个角的余角是___________︒.【答案】69.75【解析】试题分析：根据互余两角的和为90°，可求解余角为90°-20°15′=69°45′=69.75°.故答案为：60.7511.某商品的进价为每件100元，按标价打八折售出后每件可获利20元，则该商品的标价为每件____元. 【答案】150【解析】设该商品的标价为每件x元，由题意得：80%x﹣100=20，解得：x=150，故答案为150．12.如图是一个数值运算的程序，若输出y的值为5，则输入的值为_______.【答案】±4【解析】试题分析：根据运算程序，可知运算的关系式为（x2-1）÷3，代入可得（x2-1）÷3=5，解方程可得x=±4.13.小明想度量图中点C到三角形ABC的边AB的距离，在老师的指导下小明完成了画图，那么____就是点C到直线AB的距离.【答案】线段CD的长度【解析】试题分析：根据点到直线的距离为点到直线的垂线段的长度，可知CD的长度为点C到AB的距离.故答案为：CD的长度互补的角是14.如图，直线AB与CD相交于O，OE与AB、OF与CD分别相交成直角.图中与COE________.【答案】EOD ∠和BOF ∠【解析】试题分析：根据对顶角相等可知∠AOC=∠B OD ，∠DOF=90°，可根据和为180°的两角互为补角，可知∠COE 的补角为∠EOD 何∠BOF.15.如图，已知数轴上点A 、B 、C 所表示的数分别为a 、b 、c ，点C 是线段AB 的中点，且2AB =，如果原点O 的位置在线段AC 上，那么2a b c +-=________.【答案】0 【解析】试题分析：由题意及数轴上点的位置得：（a+b ）÷2=c，即a+b=2c ，则2a b c +-==0．故答案为0点睛：此题考查了有理数的混合运算，数轴，以及绝对值，熟练掌握运算法则是解本题的关键．16.线段1AB =，1C 是AB 的中点，2C 是1C B 的中点，3C 是2C B 的中点，4C 是3C B 的中点，依此类推……，线段2015AC 的长为____.【答案】2015112⎛⎫- ⎪⎝⎭【解析】试题分析：根据中点的意义，可知:1 C B =12AB ，2C B =121 C B =12×12AB ，…… 由此可知其规律为：n C B =1()2n 1n C B -，因此可知12015C B =20151()2AB ，因此可求得2015AC =2015112⎛⎫- ⎪⎝⎭.故答案为：2015112⎛⎫- ⎪⎝⎭.三、解答题17.计算：（1）()()322453⎡⎤-÷⨯--⎣⎦；（2）()157242612⎛⎫+-⨯- ⎪⎝⎭【答案】（1）8 （2）18-【解析】试题分析：根据有理数的混合运算，先算乘方，再算乘除，最后算加减，如果有括号先算括号里面的，然后结合乘方运算求解即可.试题解析：（1）()()322453⎡⎤-÷⨯--⎣⎦=-8÷4×[5-9]=-2×（-4）=8（2）()157242612⎛⎫+-⨯- ⎪⎝⎭=157(24)(24)(24)2612⨯-+⨯--⨯- =-12-20+14=-1818.解方程：（1）()432x x -=-；（2）223146x x +--= 【答案】（1）1x = （2）0x =【解析】试题分析：根据一元一次方程的解法，去分母，去括号，移项，合并同类项，系数化为1，解方程即可. 试题解析：（1）4-x=3（2-x ）4-x=6-3x-x+3x=6-42x=2x=1（2）223146x x +--=3（x+2）-2（2x-3）=123x+6-4x+6=123x+4x=12-6-67x=0x=019.化简求值：()()2222274523a b a b ab a b ab +-+--，其中1a =-，2b =.【答案】228a b ab +，-30【解析】试题分析：根据去括号法则和合并同类项法则化简，然后代入求值即可.试题解析：原式228a b ab =+其中1a =-，2b =，代入得：原式()()2212812=-⨯+⨯-⨯=30-20. 如图，是由若干个完全相同的小正方体组成的一个几何体．（1）请画出这个几何体的三视图；（2）如果在这个几何体上再添加一些相同的小正方体，并保持这个几何体的主视图和俯视图不变，那么最多可以再添加______个小正方体.【答案】（1）作图见解析（2）2【解析】试题分析：（1）根据题目中图形可知：主视图共3列，从左到右，第一列有3个小正方形，第二列有2个小正方形，第三列有1个小正方形，左视图共2列，从左到右，第一列有3个小正方形，第二列有1个小正方形，俯视图共2列，从左到右，第一列有2个小正方形，第二列有1个小正方形，第三列有1个小正方形.（2）可在第二层第一列第一行加一个，第三层第一列加一个，共2个.试题解析：（1）如图;（2）可在第二层第一列第一行加一个，第三层第一列加一个，共2个.考点：几何体的三视图.∠=∠，在射线AE上取一点D，使21.如图，利用直尺和圆规，在三角形ABC的边AC上方作EAC ACBAD BC=，连接CD.观察并回答所画的四边形是什么特殊的四边形？（尺规作图要求保留作图痕迹，不写作法）【答案】作图见解析【解析】试题分析：根据基本作图-做一个角等于一只角，结合题意画图，然后判断即可. 试题解析：如下图所画的四边形为：平行四边形22.如图，90AOB ∠=︒，在AOB ∠的内部有一条射线OC .（1）画射线.OD OC ⊥（2）写出此时AOD ∠与BOC ∠的数量关系，并说明理由.【答案】（1）作图见解析（2）（1）AOD BOC ∠=∠或180AOD BOC ∠+∠=︒【解析】试题分析：（1）根据基本作图—做已知直线的垂线即可；（2）通过图形判断即可.试题解析：（1）画图，如下图（2）AOD BOC ∠=∠或180AOD BOC ∠+∠=︒23.已知关于m 的方程12 (m －16)＝－5的解也是关于x 的方程2 (x －3)－n ＝3的解． (1) 求m 、n 的值； (2) 已知线段AB ＝m ，在射线AB 上取一点P ，恰好使AP PB＝n ，点Q 为线段PB 的中点，求AQ 的长．【答案】（1）m =6，n =3；（2）AQ =214或152 【解析】【分析】（1）先利用解一元一次方程的方法解出 12 (m -16)=-5中m 的值；因为两个方程同解，代入()233x n --=解出n 的值即可.（2）因为点P 的位置不能确定,故应分点P 在线段AB 上时,先根据比值求出AP ,PB 的长度,再根据中点定义求出PQ 的长度,相加即可求出AQ 的长度;当点P 在线段AB 的延长线上时,根据比值求出BP 的长度,再根据中点定义求出BQ 的长度,相加即可求出AQ 的长度.【详解】解：()()111652m -=-， 1610m -=-，6m =，Q 关于m 的方程()12651m -=-的解也是关于x 的方程()233x n --=的解． x m ∴=，将6m =，代入方程()233x n --=得：()2633n --=，解得：3n =，故63m n ==，；()2由()1知：63AP AB PB==，， ①当点P 在线段AB 上时，如图所示：63AP AB PB ==Q ，， 9322AP BP ∴==，， Q 点Q 为PB 的中点，1324PQ BQ BP ∴===， 9321244AQ AP PQ ∴=+=+=； ②当点P 在线段AB 的延长线上时，如图所示：63AP AB PB==Q ，， 3PB ∴=，Q 点Q 为PB 的中点，32PQ BQ ∴==， 315622AQ AB BQ ∴=+=+=．故214AQ =或152． 24.图是一根可伸缩的鱼竿，鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩，完全收缩后，鱼竿长度即为第1节套管的长度(如图1所示)；使用时，可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这根鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50 cm ，第2节套管长46 cm ，以此类推，每一节套管均比前一节套管少4 cm.完全拉伸时，为了使相邻两节套管连接并固定，每相邻两节套管间均有相同长度的重叠，设其长度为x cm.(1)请直接写出第5节套管的长度；(2)当这根鱼竿完全拉伸时，其长度为311 cm ，求x 的值.【答案】（1）34cm ；（2）每相邻两节套管间重叠的长度为1 cm.【解析】试题分析：（1）根据“第n 节套管的长度=第1节套管的长度﹣4×（n ﹣1）”，代入数据即可得出结论；（2）同（1）的方法求出第10节套管重叠的长度，设每相邻两节套管间的长度为xcm ，根据“鱼竿长度=每节套管长度相加﹣（10﹣1）×相邻两节套管间的长度”，得出关于x 的一元一次方程，解方程即可得出结论．试题解析：（1）第5节套管的长度为：50﹣4×（5﹣1）=34（cm ）．（2）第10节套管的长度为：50﹣4×（10﹣1）=14（cm ），设每相邻两节套管间重叠的长度为xcm ，根据题意得：（50+46+42+…+14）﹣9x=311，即：320﹣9x=311，解得：x=1．答：每相邻两节套管间重叠的长度为1cm ．考点：一元一次方程的应用．25.如图（1），点O 为线段AB 上一点，过点D 作射线OC ，使:1:2AOC BOC ∠∠=，将一直角三角板的直角顶点放在点O 处，一边OM 在射线OB 上，另一边ON 在线段AB 的下方.（1）将图（1）中的直角三角板绕点O 按逆时针方向旋转，使ON 落在射线OB 上（如图（2）），则三角板旋转的角度为____度；（2）继续将图2中的直角三角板绕点O 按逆时针方向旋转，使ON 在AOC ∠的内部（如图3）.试求AOM ∠与NOC ∠度数的差；（3）若图1中的直角三角板绕点O 按逆时针方向旋转一周，在此过程中：①当直角边OM 所在直线恰好垂直于OC 时，AOM ∠的度数是________；②设直角三角板绕点O 按每秒15︒的速度旋转，当直角边ON 所在直线恰好平分AOC ∠时，求三角板绕点O 旋转时间t 的值.【答案】（1）90︒（2）30AOM NOC ∠-∠=︒（3）①150AOM ∠=︒或30°②4t =或()16s【解析】试题分析：（1）根据旋转的性质可知，旋转角是∠MON.（2）如图3，利用角平分线的定义，结合已知条件，求得∠AOC=60°，然后根据直角的性质、图中角与角间的数量关系推出结论；（3）①根据旋转的定义，画图，然后根据周角和已知角求解；②根据速度和角平分线的性质，分逆时针和顺时针计算即可.试题解析：（1）90︒（2）30AOM NOC ∠-∠=︒（3）①150AOM ∠=︒或30︒②4t =或()16s26.数轴上有A 、B 、C 三点，分别表示有理数26-、10-、20，动点P 从A 出发，以每秒1个单位的速度向右移动，当P 点运动到C 点时运动停止，设点P 移动时间为t 秒.（1）用含t 的代数式表示P 点对应的数：_________；（2）当P 点运动到B 点时，点Q 从A 点出发，以每秒2个单位的速度向C 点运动， Q 点到达C 点后，再立即以同样的速度返回A 点.①用含t 的代数式表示Q 点在由A 到C 过程中对应的数：_________；②当t =______时，动点P 、Q 到达同一位置（即相遇）；③当3PQ =时，求t 的值.【答案】（1）26t -+；（2）①258t -；②32或1243；③3t =， 29， 35， 1213， 1273. 【解析】【分析】（1）根据题意可得P 点对应的数；（2）①P 因为点从A 运动到B 点所花的时间为16秒，Q 点从A 运动到C 点所花的时间为23秒所以Q 点在由A 到C 过程中对应的数()26216258t t -+-=-为；②分为返回前相遇和返回后相遇两种情况：返回前相遇，P 的路程等于Q 的路程等于Q 的路程减去16；而返回后相遇，则是二者走的总路程是Q 到C 的路程的2倍，分别列式子求解.【详解】（1）P 点所对应的数为：26t -+（2）①258t -②P 点从A 运动到B 点所花的时间为16秒，Q 点从A 运动到C 点所花的时间为23秒当1639t ≤≤时，P ：26t -+，Q ：()26216258t t -+-=-26258t t -+=-，解之得32t =当3946t ≤≤时，P ：26t -+，Q ：()20239982t t --=-26982t t -+=-，解之得1243t =③3t =，29，35，1213，1273 【点睛】考核知识点：一元一次方程应用.理解定义，列出方程关键.。

2016~2017学年度第一学期期末溧水区七年级答案

2016～2017学年度第一学期期末质量调研测试七年级数学答案一、选择题：（每小题2分，共16分）二、填空题（每小题2分，共20分）9． -4 10．2.10975×104 11．3 12．小于 13．111.7 14．1.5 15． 1 16．15.09 17．800 18．64三、解答题(共64分）19．（1）解：原式= —1－(2－9) ……………………………2分= —1+7 ………………………………………3分= 6 …………………………………………4分（2）解：原式=（–34）⨯（–24）+116⨯（–24）–78⨯（–24）…………………2分（写对两个得1分，写对三个得两分）= 18 – 44+21…………………………… ……3分= – 5……………………………………………4分20．（1）解：原式=a +5a －3b －2a +4b …………………… 2分=4a +b …………………………………… 4分解：原式=ab ab a ab a 218221222-⎪⎭⎫⎝⎛++-……………… 1分 =ab ab a ab a 218221222---- ……………… 2分 =－9ab ……………… 3分当a ＝－12，b ＝时，原式=－9×（－12 ）×（－23）=－3 ………………4分21．（1）解：4x －4=8 ………………………………………1分4x =8+4……………………………………………2分4x =12……………………………………………3分x =3……………………………………………4分（2）解：6x -3(x -1)=12-2(x +2) …………………………1分6x -3x +3=12-2x -4………………………………2分5x =5……………………………………………3分x =1…………………………………………… 4分22．解：①当点C 在点M 的右边时：因为M 为AB 的中点，所以AM ＝ 21AB 因为AB ＝4cm ，所以AM ＝ 2cm …………………………1分因为AM ＝ 2cm ，MC ＝0.4cm所以AC ＝ AM +MC ＝ 2.4cm ……………………………2分因为N 为AC 的中点，所以AN ＝21AC ＝ 1.2cm …………3分所以MN ＝ AM －AN ＝ 0.8cm ……………………………4分②当点C 在点M 的左边时：因为M 为AB 的中点，所以AM ＝21AB 因为AB ＝4cm ，所以AM ＝ 2cm因为AM ＝ 2cm ，MC ＝0.4cm所以AC ＝ AM －MC ＝ 1.6cm ………………………………5分因为N 为AC 的中点，所以AN ＝21AC ＝ 0.8cm ……………6分所以MN ＝ AM －AN ＝ 1.2cm …………………………………7分由①②可知，MN 的长为0.8cm 或1.2cm ．23．画图每小题1分，大小关系CE ＜CA 1分，理由垂线段最短1分，共4分24．三种视图每个1分，表面积32.56cm 2 1分，花费1628元1分，共5分25．解：（1）因为∠AOE =120°，OF 平分∠AOE所以∠AOF =∠EOF =21∠AOE=60° …………………1分因为OF 垂直于OD所以∠COF =∠DOF =90°………………………………2分所以∠AOC ＝∠COF －∠AOF=30°， ………………3分所以∠DOB=∠AOC ＝30° …………………………4分（2）因为OF 平分∠AOE ，所以∠AOF =∠EOF =21∠AOE …………5分又因为OF 垂直于OD ，所以∠COF =∠DOF =90°所以∠AOC +∠AOF =∠DOE +∠EOF =90°,所以∠AOC =∠DOE ，………6分又因为∠DOB=∠AOC所以∠DOB =∠DOE 即OD 平分∠BOE ……………………………………7分26．解：(1)如果按普通电价付电费0.5×500=250元………………………1分如果按峰谷电价付电费0.56×200＋0.36×300=220元………………2分 250－220=30元答：小明家按照峰谷电价方式付电费比较省钱，能省250－220=30元…3分(2)设峰时电量为x 度，谷时电量为(500-x )度 …………………4分由题意，可得： 250＝0.56x +0.36(500-x )，…………………………5分解得x ＝350．………………………………………………………6分答：峰时电量为350度时，两种方式所付的电费相等………………………7分27．解：(1)20 ………………………………………………………………2分(2) 设OM 与ON 的夹角是10°时的旋转时间为x 秒.当OM 与OA 成180°之前，OM 在ON 左边时，根据题意得：30+x -6x =10，解得：x=4；……………………4分OM 与ON 右边时，根据题意得：6x -（30+x ）=10，解得：x=8；……………………6分当OM 与OA 成180°之后，OM与ON右边时，根据题意得：30+x+10+（6x-180）=180，解得：x=3207；…………………8分OM在ON左边时，根据题意得：30+x+（6x-180-10）=180，解得：x=3407.……………………10分答：OM与ON的夹角是10°时的旋转时间为4秒、8秒、3207秒或3407秒。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

参考答案与评分标准
一、选择题（本大题共6题，每小题2分，共12分）
题号
1 2 3 4 5 6
答案
C B D B D C
二、填空题（本题共10小题，每题2分，共20分）
7. 答案不唯一，如等 8.1.7×105 9．—5； 10.6 11. ＞；
12.18 13. 56； 14. 2或4 15.1 16.100
三. 解答题（本大题共9题，共68分）
17.（1）原式＝－4＋3＋6 „„„„„3分（每个1分）
＝5 „„„„„4分

（2）原式＝－1－0.5×13×（2－9） „„„„„3分（每个1分）

＝16 „„„„„ 5分
18. （1）去括号得：2x＋2＝1－x－3 „„„„„2分
移项合并得：3x＝－4 „„„„„ 3分

解得：x＝43 „„„„„ 4分

（2）)13(312)75(2xx „„„„„„„2分
39121410xx
„„„„„„„3分

12143910xx
„„„„„4分

1x
„„„„„„„„5分

19．原式＝—x+6y2－4x－8x+4y2 „„„„„„„2分
＝—11x+10y2 „„„„„4分
当1 2yx时

原式＝2110211）（ ＝－12„„„„„„„„6分
20. （1）画图正确 „„„„„2分
（2）画图正确 „„„„„ 4分
（3）20 „„„„„6分
21. （1）24 „„„„„2分
（2）

„„„„„6分
22. 设窗的宽是x米，则高为（x＋0.5）米，由题意得：
3x＋2（x＋0.5）＝6， „„„„„3分
解得：x＝1． „„„„„5分
则x＋0.5＝1.5．1×1.5＝1.5
答：窗户的透光面积1.5平方米． „„„„„7分
23．（1）如∠DOF=∠BOF； „„„„„2分
（2）∵OE⊥CD，∴∠COE=90°，
∴∠AOC=∠COE﹣∠AOE=90°﹣26°=64°，
∵∠AOC=∠BOD，∴∠BOD=64°， „„„„„5分
又∵OF平分∠BOD，

∴∠DOF=∠BOD=×64°=32°，
∴∠COF=180°﹣∠DOF=180°﹣32°=148°．„„„„„8分
24．解：参考问题1：汽车在普通公路上的行驶时间是多少h？„„„„„2分
设汽车在普通公路上的行驶时间是xh．根据题意，得„„„„„3分

)4(90503xx
„„„„„„„„„„„„„„„„„5分

解得5.1x „„„„„„„„„„„„„„7分
答：汽车在普通公路上的行驶时间是1.5h．
参考问题2：汽车在普通公路上的行驶路程是多少 km？
设汽车在普通公路上的行驶路程是xkm．

490350
xx
，解得75x，答：略．

（其它问题参照给分，如汽车在高速公路上的行驶时间是2.5h，在高速公路上的行驶路
程是225km，总路程是300km）
25．解：（1）是； „„„„„„„„„„„„„„„„„„„„„1分
（2）31，21，32；（写出1个或两个给1分，写出三个给2分） „„„„„3分（3）

如图①，当∠MPN=2∠QPM时，60)6010(2t，解得9t；
如图②，当∠QPN=2∠QPM或2∠MPN时，60210t，解得12t；
如图③，当∠QPM=2∠MPN时，6026010t．解得18t；
所以，当t的值为9，12，18时，射线PM是∠QPN的“巧分线”．„„„„„„„6分

（4）4.2t，4t，
6t
„„„„„„„„„„„„„„„„„„„„„„„„„„„10分

（提示：∠QPN=t10，∠QPM=tt10605建立三个方程）