直棱柱的概念
湘教版九年级数学下册课件:3.2 直棱柱、圆锥的侧面展开图(共29张PPT)

A.(30+5 29)π m2 C.(30+5 21)π m2
B.40π m2 D.55π m2
【解析】设底面圆的半径为 R,则πR2=25π,解
得 R=5,圆锥的母线长= 22+52= 29,∴圆锥的侧面
积=π×5× 29=5 29π,圆柱的侧面积=2π×5×3 =30π,∴需要毛毡的面积=(30+5 29)π m2.
得:3π 4 =2πr,
∴r=38 .∴h=
12-382=
55 8
cm.
15. 如图,在正方形网格图中建立一直角坐标系, 一条圆弧经过网格点 A,B,C,请在网格中进行下列操 作:
(1)请在图中确定该圆弧所在圆心 D 点的位置,D 点 坐标为 ;
(2)连接 AD,CD,求⊙D 的半径及扇形 DAC 的圆心 角度数;
(1)求扇形 CEF 的面积; (2)用扇形 CEF 做成圆锥的侧面,求圆锥的高.
解:(1)连接 CG, ∴CG⊥AB, ∵∠B=45°, BC= 2,∴CG=1, ∴S 扇 CEF=135·36π0·12=38π;
(2)设圆锥的底面半径为 r,
E︵F的弧长=135×18π0 ×1=3π 4 ,由题意,
图① A.面 CDHE C.面 ABFG
图② B.面 BCEF D.面 ADHG
•9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。2021/9/82021/9/8Wednesday, September 08, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/9/82021/9/82021/9/89/8/2021 6:01:46 PM •11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/9/82021/9/82021/9/8Sep-218-Sep-21 •12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/9/82021/9/82021/9/8Wednesday, September 08, 2021
3.1认识直棱柱

2n
n+2
3n
n
面数 +顶点数-2=棱数
留意你身边的每 一物,你定能发 现许多有用知识!
要认真完成课 后作业哦!
多 面 体
我们知道:长方体又作为一种特殊的直棱柱。 请大家考虑这样 一个问题! 请同学们进一步说明 立方体、长方体、 直四棱柱、
让 我 们 把 四棱柱 和棱柱的相互关系? 注 (指出下列图示中的数字序号所表示的相应几何体类型) 意 力 重 新 直 直 拉 棱 四 长 四 ③ 棱 ① 立方体 ② 柱 棱 回 棱 方 柱 柱 柱 体 到 长 方 体
⒉侧面都是长方形(含正方形)。 直五棱柱 直四棱柱 直六棱柱 直三棱柱
底面 下面,请同学们把注意力集中到 直棱柱的侧棱 直三棱柱 我们规定: 侧 借助动画观察: 由侧棱 的多少来 棱 相邻两条侧棱之间的 长度和位置关系。 定义不同的直棱柱 侧面 。。。。。。
直棱柱的相邻两条侧棱互相平行
且长度相等。 直棱柱的高与侧棱的长度 相等。
七面体 八面体
五面体
讨论与合作
第一组 仔细观察,你能发现第二组几何 第二组与第一组的不同点: 直棱柱的基本特征: 体与第一组几何体有什么不同吗? ⒈都有上下两个底面,底面是平面 第二组 图形中的多边形,且彼此全等; ⒉侧面都是长方形(含正方形)。
①
②棱柱的基本特征:
⒈都有上下两个底面,底面是平面 图形中的多边形,且彼此全等;
7个平面 七面体
四面体 4个平面
随着面数的不同,我们自然很容易 【规定】 对许多几何体进行定义。 由若干个平面组成的几何体叫做多面体;
多面体上相邻两个面之间的交线叫做该多面体的棱; 几个面的公共顶点叫做多面体的顶点。
顶点
棱
棱柱与棱锥的认识与分类

棱柱与棱锥的认识与分类棱柱和棱锥是几何图形中的重要概念。
它们是立体几何中常见的形状,具有不同的特征和属性。
本文将对棱柱和棱锥进行认识与分类的介绍,帮助读者更好地理解这两种几何形状。
一、棱柱的认识与分类棱柱是由两个相似的多边形底面和连接这两个底面的矩形侧面组成的立体。
它的特点是侧面是平行于底面的矩形,并且棱柱的顶点到底面的距离都相等。
我们可以根据棱柱底面的形状来对棱柱进行分类。
1. 正棱柱:当底面为正多边形(如正三角形、正方形等)时,棱柱称为正棱柱。
正棱柱的特点是底面的边和侧面的高线垂直,并且侧面也是正多边形。
2. 直棱柱:当底面为任意多边形时,棱柱称为直棱柱。
直棱柱的特点是底面的边和侧面的高线不一定垂直,而是可以偏离垂直方向。
3. 斜棱柱:如果棱柱的侧面倾斜,则称为斜棱柱。
斜棱柱的特点是底面的边和侧面的高线不垂直,而是有倾斜的角度。
二、棱锥的认识与分类棱锥是由一个多边形底面和连接底面每个顶点至一个共同点(顶点)的三角形侧面组成的立体。
棱锥的特点是它只有一个顶点,而其它顶点都在该顶点到底面的连线上。
我们可以根据底面的形状来对棱锥进行分类。
1. 正棱锥:当底面为正多边形时,棱锥称为正棱锥。
正棱锥的特点是底面的边和侧面的斜高线垂直,并且侧面也是正多边形。
2. 直棱锥:当底面为任意多边形时,棱锥称为直棱锥。
直棱锥的特点是底面的边和侧面的斜高线不一定垂直,而是可以偏离垂直方向。
3. 斜棱锥:如果棱锥的侧面倾斜,则称为斜棱锥。
斜棱锥的特点是底面的边和侧面的斜高线不垂直,而是有倾斜的角度。
三、棱柱与棱锥的区别与联系棱柱和棱锥在形状上有一定的类似之处,都是由底面和侧面组成的立体。
但是它们的区别主要体现在以下几个方面:1. 顶点数量:棱柱有两个底面,而棱锥只有一个底面,顶点是唯一的。
2. 侧面形状:棱柱的侧面是矩形,而棱锥的侧面是三角形。
棱柱的侧面可以是正多边形或任意多边形,而棱锥的侧面也可以是正多边形或任意多边形。
直棱柱和正棱柱的区别

直棱柱和正棱柱的区别
正棱柱比直棱柱的要求高,正棱柱一定是直棱柱,而直棱柱
不一定是正棱锥。直棱柱每条侧棱垂直底面,正棱柱的底面
是正多边形,正棱柱侧面的每个面全等。长方体如果有两个
相对的面为正方形的话就是正棱柱,否则是直棱柱,正方体
是正棱柱。
直棱柱和正棱柱的区别
1什么是直棱柱
直棱柱的上下底面可以是三角形、四边形、五边形、六边形
等多边形,侧面都是长方形(含正方形)。根据底面图形的
边数,我们称它为直三棱柱、直四棱柱(长方体和立方体都
是直四棱柱)、直五棱柱、直六棱柱。
直棱柱的所有侧棱都面且各棱相互平行,上下两个面沿竖直
方向平移可重叠。但是斜棱柱的侧棱不垂直与底面,与底面
成一定的夹角,各棱都相互平行,上下两个底面沿竖直方向
平移不可重叠。
2什么是正棱柱
底面是正多边形的直棱柱叫做正棱柱。正棱柱是侧棱都垂直
于底面,且底面是正多边形的棱柱。
特别注意:底面为正多边形,侧棱垂直于底面,但是侧棱和
底面边长不一定相等。而直棱柱侧棱也是垂直于底面,侧棱
和底面边长不一定相等,而且底面多边形形状也不确定。
八年级数学上册 第3章直三棱柱复习课件 浙教版2

田凹不能有。
第九页,编辑于星期五:六点 三分。
口诀
一
四
一
“一四一〞 “一三二〞,
型
“一〞在同层可任意;
“三个二〞成阶梯,
一
“二个三〞,“日〞状连;
三
二
异层必有“日〞
型
整体没有“田〞
三 个 二 型
第十页,编辑于星期五:六点 三分。
1、以下平面图形能折叠成正方体吗?
×
√
×
×
“一四一〞 “一三二〞, “一〞在同层可任意;
直棱柱侧面积=底面周长×高
直棱柱外表积=侧面积+上下两底面面积
7、由三视图描述几何体
1、三视图中有两个长方体必是柱体,底面 是圆,那么是圆柱。底面是几边形,那么 是几棱柱。
2、三视图中有两个三角形的是锥体,底 面是圆,那么是圆锥,底面是几边形,那 么是几棱锥。
第二十七页,编辑于星期五:六点 三分。
第二十八页,编辑于星期五:六点 三分。
〔3〕如图,粗线表示嵌在一个立方体玻璃器具内的一根铁丝 ,请画出该立方体玻璃器具的三视图。
主视图 左视图 俯视图
第三十一页,编辑于星期五:六点 三分。
小组合作交流
这节课你有何收获, 能与大家分享、交流你的感受吗?
第三十二页,编辑于星期五:六点 三分。
第二十二页,编辑于星期五:六点 三分。
4cm
请同学们将事先准备好的立方体纸盒,沿某些
棱剪开,且使六个面连在一起,然后铺平,你
们能得到怎样的图形?
第二十三页,编辑于星期五:六点 三分。
4cm
C 〞〔C〕
C B
C ’〔C〕
A
那将“立方体的铁丝框〞改成“立方体的纸 盒〞,上述两题结论又该如何呢?
直棱柱

直棱柱
直棱柱的定义:
侧棱与底面垂直的棱柱称为直棱柱.
直棱柱的性质
1,侧棱与底面垂直
2,侧棱长(最长的一条)与高相等
3,侧面与对角面都是矩形
4,侧面展开图是矩形
5,侧面积=底面周长×侧棱长
6,体积=底面积×侧棱长
7.表面积=侧面积+两个底面积
8.直棱柱相邻两条侧棱互相平行且相等
规律:
直N棱柱
面N+2
棱3N
点2N
题:棱柱成为直棱柱的一个必要不充分条件为( )
A,有一侧棱与底面垂直
B,有一侧棱与底面两边垂直
C,有一侧面为正方形且与底面垂直
D,有两个不相邻的侧面互相垂直
答:B
正棱柱
定义
底面是正多边形的直棱柱叫做正棱柱。
正棱柱是侧棱都垂直于底面,且底面是正多边形的棱柱。
特别注意:底面为正多边形,侧棱垂直于底面,但是侧棱和底面边长不一定相等。
而直棱柱侧棱也是垂直于底面,侧棱和底面边长不一定相等,而且底面多边形形状也不确定。
性质
(1)正棱柱的侧棱垂直于底面。
(2)正棱柱的侧面于底面相互垂直。
(3)正棱柱的侧面为矩形,但不一定是正方形。
1-复习:1、棱柱的分类

A' B'
A
D' C'
D
AA1⊥A1C1
B A'
B' A
B
C D'
C' D
C
BB1⊥B1D1
AA1⊥B1D1
AA1∥BB1
AA1⊥平面A1B1C1D1
AA1⊥A1B1 AA1⊥A1D1
同理A1B1⊥A1D1 平行六面体ABCD-A1B1C1D1是长方体
课堂总结
1平行六面体 直平行六面体 长方体 正方体
动 画
等于一个顶点上三条棱长的平方和。
音
乐 已知:长方体AC’中,AC’是一条对角线(如图)
求证:AC'2=AB2+AD2+AA'2
首 页
即:l 2 = a 2 + b 2 + c 2
上
A'
D'
页
下 页
小
B' c aA
l
C'
b
D
结
B
C
结
束
8
结论
A'
D'
动 画
长方体AC‘中,AC’是
音 它的一条对角线,则
首
页 (1)侧棱都相等,侧面都是平行四边形。
上 页
直棱柱的各个侧面都是矩形;
正棱柱的各个侧面都是全等的矩形。
下
页
(2)两个底面与平行底面的平面的截面
小
结 是全等的多边形。
结
束 〔3)不相邻的两条侧棱的截面是平行四
边形。
2
动 画
音 乐
首 页
上 页
下 页
第4讲 直棱柱
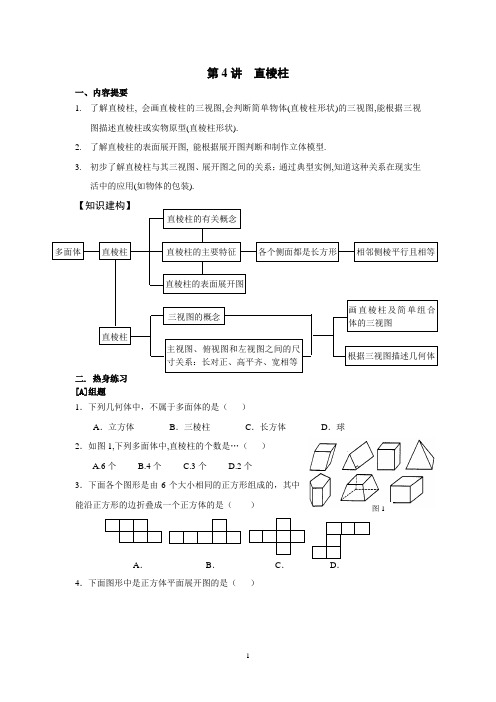
第4讲 直棱柱一、内容提要1. 了解直棱柱, 会画直棱柱的三视图,会判断简单物体(直棱柱形状)的三视图,能根据三视图描述直棱柱或实物原型(直棱柱形状).2. 了解直棱柱的表面展开图, 能根据展开图判断和制作立体模型.3. 初步了解直棱柱与其三视图、展开图之间的关系;通过典型实例,知道这种关系在现实生活中的应用(如物体的包装).二. 热身练习[A]组题1.下列几何体中,不属于多面体的是( )A.立方体 B .三棱柱C .长方体D .球 2.如图1,下列多面体中,直棱柱的个数是…( )A.6个B.4个C.3个D.2个3.下面各个图形是由6个大小相同的正方形组成的,其中能沿正方形的边折叠成一个正方体的是( )4.下面图形中是正方体平面展开图的是( )图图1A .B .C .D .5.下面简单几何体的左视图是( )6.一物体的主视图是长方形,则该物体不可能是()A. 圆柱体B. 长方体C. 三棱锥D. 直棱柱 7.如图是一些立体图形的三视图,请根据视图说出这些立体图形的名称:(1)(2)名称: 名称:8.如图2是某品牌牙膏的软包装盒,其尺寸如图所标(单位:cm ),请画出这种包装盒的表面展开图,并计算这个包装盒的表面积.三. 例题分析例1、一个直棱柱有12个顶点,它是几棱柱?有多少条棱?多少个面?例2、把图1折成正方体后,如果相对面所对应的值相等,那么x 的平方根与y 的算术平方根之积为 .A .B .C .D .A .B .C .D .正面图12145图2例3、如图3是由几个小立方块所搭几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数.请画出这个几何体的主视图、左视图.★★例4、已知一个几何体的三视图如图4所示,描述该几何体的形状,并根据图中数据计算它的表面积.(结果精确到1cm 2)★★例5、 如图,长方体的长为15cm ,宽为10cm ,高为20cm ,点B 在棱CD 上,CB=5cm. 一只壁虎要沿长方休的表面从A 点爬到B 点,需要爬行的最短路径是多少cm?四. 思维提升 [B]组题1.下列实物的形状中,是直棱柱的是( )A. B. C. D.2.直棱柱的棱数,一定是下列某自然数的倍数( )A.2B.3C.5D.73.如图1所示,八棱柱模型的底面边长都是4cm ,侧棱长为4cm . 下列说法,错误的是( )A .每个面都是正方形B .侧面积为128cm 2C .共有16个顶点D .共有24条棱32211图3图 5图14.一个直三棱柱(如图4甲)顺着侧棱的方向切一刀,可以得到一个直三棱柱和一个直四棱柱(如图4乙).(1) 对图3甲用同样的方法切一刀, 能否得到两个直三棱柱?如何切?(2) 一个直四棱柱用同样的方法切一刀,得到一个直n 棱柱和一个直m 棱柱, 写出m , n 所有可能的值.5.如图6是一个食品包装盒的侧面展开图.(1) 请写出这个包装盒的多面体形状的名称;(2) 请根据图中所标的尺寸,计算这个多面体的侧面积.7.图7表示一个由相同小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,那么该几何体的主视图为( )★★8。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直棱柱的概念
直棱柱的概念
直棱柱是一种几何体,它具有六个矩形面和八个顶点,每个顶点都连接着三条边。
直棱柱的特点是其两个底面平行且相等,侧面为矩形。
直棱柱在数学中被广泛应用,在工程学、建筑学、物理学和化学等领域也有重要的应用。
一、基本结构
1.1 底面
直棱柱的底面是一个矩形,它有两条相等的长边和两条相等的短边。
底面上方有一条平行于底面的上底面。
1.2 侧面
直棱柱的侧面是由四个矩形组成,这四个矩形都是相等的。
每个侧面都有一个长边和一个短边,并且所有侧面都平行于彼此。
1.3 顶点
直棱柱共有8个顶点,每个顶点连接着三条边。
其中4个顶点位于底部,4个顶点位于上部。
二、性质
2.1 面积和体积
直棱柱的表面积可以通过将两个底面和四个侧面的表面积相加得到。
直棱柱的体积可以通过将底面积与高相乘得到。
2.2 对称性
直棱柱具有对称性,即它可以被分成两个完全相同的部分。
这是因为直棱柱的两个底面和所有侧面都是相等的。
2.3 直角性
如果直棱柱的底面是正方形,那么每个顶点都是一个直角。
如果底面是矩形,则只有在矩形边长比例为1:√2时,每个顶点才是一个直角。
三、应用
3.1 工程学
在工程学中,直棱柱被广泛应用于建筑和机械设计中。
例如,在建筑设计中,直棱柱可以被用作支撑结构或墙体材料。
在机械设计中,直棱柱可以被用作机器外壳或支撑结构。
3.2 物理学
在物理学中,直棱柱被用作模型来研究光线、声波和电场等现象。
例如,在光学实验中,一些实验室使用高度精确的直棱柱来控制光线传播方向和强度。
3.3 化学
在化学领域中,直棱柱被用作反应器和储存容器。
直棱柱的形状和结构使它们非常适合于储存液体和气体,并且可以轻松地进行加热或冷却。
四、总结
直棱柱是一种具有六个矩形面和八个顶点的几何体,它具有两个底面平行且相等,侧面为矩形。
直棱柱在数学中被广泛应用,在工程学、建筑学、物理学和化学等领域也有重要的应用。
直棱柱具有对称性和
直角性,可以被用作支撑结构、墙体材料、机器外壳、反应器和储存容器等。
