缓和曲线计算公式概要
(整理)高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
圆曲线、缓和曲线计算方法

● 圆曲线方法一:sin (1cos )180i i i i i i x R y R l R ϕϕϕπ⎧⎪=⎪=-⎨⎪︒⎪=⋅⎩——i l 为待定点i P 至起点间的弧长i ϕ为i l 所对的圆心角R 为曲线半径方法二:11802l A R π︒=⋅⋅ 2sin l R A =⋅00cos(/)sin(/)x x l A y y l A =+⋅+-⎧⎨=+⋅+-⎩起点方位角左减右加起点方位角左减右加——00(,)x y 为圆曲线起点坐标方法三:180l A R π︒=⋅ 00cos(/)sin(/)x x R B A y y R B A =+⋅+-⎧⎨=+⋅+-⎩——l 为圆曲线上任意一点距起点距离00(,)x y 为圆曲线圆心坐标B 为圆心到圆曲线起点的方位角,A 为任意点对应的圆心角● 缓和曲线522030406l x l R l ly Rl ⎧=-⎪⎪⎨⎪=⎪⎩——l 为曲线上任一点至起点的曲线长R 曲线半径0l 为缓和曲线全长圆曲线、缓和曲线计算方法1、直线段:先由JD1以及JD2的坐标算出JD1到JD2的方位角,即直线段方位角A ,故可算出HZ 、ZH 坐标及其直线段各点坐标。
2、缓和曲线:以HZ 、ZH 为起点,缓和曲线上任意一点离HZ 、ZH 距离为l ,利用公式522003040()6l x l R l l R ly Rl ⎧=-⎪⎪⎨⎪=⎪⎩为缓和曲线全长,为圆曲线半径算出该点的相对起点坐标,利用arctan y x算出该点相对起点的方位角B ,再根据线路走向及直线段方位角可算出该点的方位角C (顺时针加,逆时针减),用可求出该点相对起点的距离D ,最后用00cos sin x x D C y y D C =+⎧⎨=+⎩可求出该点的坐标。
(00(,)x y 为缓和曲线起点的坐标)3、圆曲线:用上述方法求出圆曲线两端点HY 、YH 坐标,算出HY 到YH 的方位角F ,以及两点间的距离E ,用12arccos ER可算出两端点连线与起点到圆心连线的夹角G ,根据线路走向求出起点到圆心的方位角H (H=F+/-G ),00(,)x y 圆曲线为起点坐标,根据00cos sin x x R H y y R H=+⎧⎨=+⎩,求出圆心坐标。
缓和曲线、竖曲线、圆曲线、匝道(计算公式)

一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:xy②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x0时sgn(x)=1,当x=0时sgn(x)=0。
公路缓和曲线原理及缓和曲线计算公式

一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车4)与圆曲线配合得当,增加线形美观2.缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A2/ρ(A:与汽车有关的参数)ρ=C/sC=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R,l h=s 则 l h=A2/R4.缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ρ,a s=Δa/t≤0.62)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
发布日期:2012-01-31 作者:李秋生浏览次数:1494)从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
线路工程测量-缓和曲线

根据象限角判断方位角
边长S 线路里程:
S Xi2.i1yi2.i1
计算中桩点 相对坐标:
中桩坐标:将曲线各点相对坐标转换成国家大地坐标
已知
A' arctgYi1Yi
公路中线逐桩坐标X X i1
i 直线段中桩坐标
计算
JD(Xj,Yj)
i(m,n)
A
--桩点至起点的里程之差
X‘
已知
ZD(X0,Y0) 1(50,0) ZH(m,n) D X Y
一、困难条件下的曲线测设
(一)曲线控制点遇障碍
3、曲线起终点不能置镜——如ZH点在沟中 1)测设A点:计算A点坐标(xA、yA) 2)外业:在切线上设P点,量P-JD距离
3)计算: xp TPJD
r arct(g yA ) xp xA
AP yA 2(xpxA)2
4)测设: (1)置镜P点,后视JD点,拨角后 测设A点 (2)置镜A点,后视P点反拨角 r+βA定向,得A点切线方向
5、曲线与坐标系反向
Y‘
时 y坐标按负值计算
X‘ (X,Y) P(x1,y1)
Y
全站仪测设公路中 线
导线控制测量
附合导线:与国家高 级控制点联测,进行 导线闭合
一.困难条件下曲线的测设 二.控制点(JD、ZH、HZ)无法置镜——在JD、HY、YH、切线上任一点、曲线上任一点置镜测设 三.曲线遇障碍时的测设——切线方向 四.复杂曲线的测设 五.复曲线——曲线要素的计算 六.回头曲线 七.中桩坐标的计算——坐标转换
αA、 αB , 如何测?
4)测设: (1)根据AB点测设ZY、YZ点 (2)根据M点测设QZ点
一、困难条件下的曲线测设
(一)曲线控制点遇障碍
圆曲线及缓及曲线坐标推算公式附带例题
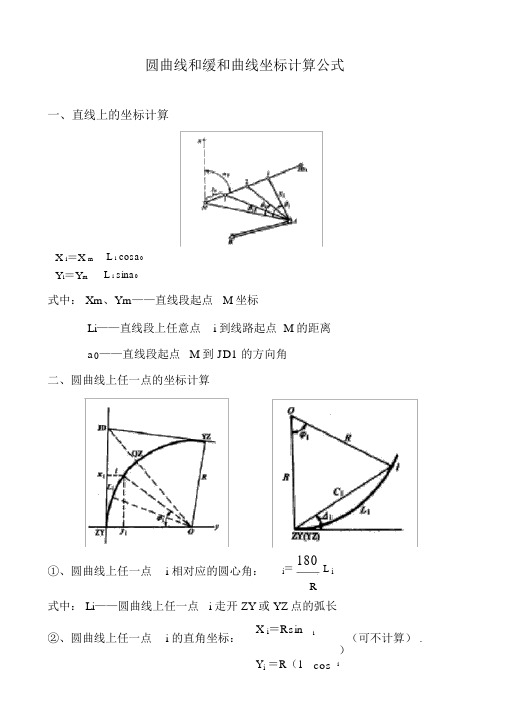
圆曲线和缓和曲线坐标计算公式一、直线上的坐标计算X i=X m L i cosa0Y i=Y m L i sina0式中: Xm、Ym——直线段起点M 坐标Li——直线段上任意点i 到线路起点 M 的距离a0——直线段起点M 到 JD1 的方向角二、圆曲线上任一点的坐标计算①、圆曲线上任一点i 相对应的圆心角:i=180L iR式中: Li——圆曲线上任一点 i 走开 ZY或 YZ点的弧长②、圆曲线上任一点i 的直角坐标:X i=Rsin i(可不计算) . Y i=R(1 cos i)③、圆曲线 ZY 或 YZ 点到任一点 i 的偏角: i = i=90L i2R④、圆曲线 ZY 或 YZ 点到任一点 i 的弦长: C i =2Rsin( i ) 2R sin( i )2 ⑤、圆曲线 ZY 或 YZ 点到任一点 i 的弦长的方向角: a i = a zy jd 或 y z jdiX i =X ZY 或 YZ C i cosa i⑥、所以圆曲线上任意点 i 的坐标为:C i sina iY i=YZY 或YZ例题:已知一段圆曲线 ,R=3500m ,Ls =553.1m ,交点里程 K50+154.734, ZY 点到 JD 方向方向角为 A=129° 23′ 18.3″,右偏 9° 3′ 15.8″, ZY 点里程K49+877.607, YZ 点里程 K50+430.707,起点坐标为 x =389823.196, y =507787.251,求 K50+200 处中点坐标及左右各偏 12.5m 的坐标。
解: K50+200 处的曲线长度为 Li = 322.393mK50+200 相对应的方向角: a =180L i = 180322.393=5 16 39.52R3500 K50+200 相对应的偏角:i =i = 90L i =90 322.393=2 38 19.762 R3500K50+200 到 zy 点的弦长: C i =2Rsin i =2 3500 sin2 38 19.76 =322.279m zy 点到 K50+200 中桩的方向角: a i = a zyjdi =129 23 18 .3 2 38 19 .76 =132 1 38 .06K50+200 左、右偏 12.5m 的方向角:a 左= A i a90 =134 39 57.82 90 =44 39 57.82 a 右=A i a90 =134 39 57.82 90 =134 39 57.82所以 K50+200 处的坐标为:X i =X ZY C i cosa i =389823.196 322.279 cos132 1 38.06 =389607.4354 Y i =Y ZY C i sina i =507787.251 322.279 sin132 1 38.06 =508026.6484K50+200 左偏 12.5m 的坐标为:X 左=X i=12.5 cos44 39 57.82=12.5cosa左389607.4354 389616.3256 =Y i=12.5=Y左12.5sina左508026.6484 sin44 39 57.82 508035.4656 K50+200 右偏 12.5m 的坐标为:X 右=X i=389607.4354 12.5 cos134 39 57.82=389598.648212.5cosa右=Y i=12.5=Y右12.5sina右508026.6484 sin134 39 57.82 508035.5386 三、缓和曲线上任一点的坐标计算2切线角:i=Li180缓和曲线上任意点i 的偏角:i =i=L2i 1803 6RL s缓和曲线 ZH 或 HZ 点到任意点i 的方向角为: a i=a ZH jd或 HZ jd ix i=L iL5i 40R2 L2s缓和曲线上任意点 i 的坐标为: 3y i=L i6RL s缓和曲线 ZH 或 HZ 点到任意点 i 的弦长:C i=x2 y2所以缓和曲线上任意点 i 的坐标为:X i=X ZH或HZ C i cosa i Yi=YZH或 HZ C i sina i例题:已知一段缓和曲线, ZH 点到 JD 方向方向角为 A=183°17′08.9″,线路左偏 43° 31′02″,ZH 点里程为 K52+001.615,ZH 点坐标 x =388071.927,y= 508789.089, R =960m ,Ls =120m ,求 K52+100 处的中点坐标及左右各偏 12.5m 的坐标。
圆曲线带有缓和曲线的曲线元素计算原理

圆曲线带有缓和曲线的曲线元素计算原理圆曲线带有缓和曲线的曲线元素计算原理1、缓和曲线的概念汽车在直线上行驶时,离心力为零;在曲线上行驶,就会产生离心力,如果某路线的直线段与圆曲线直接连接时,汽车从直线进入圆曲线那一瞬间就会突然产生离心力,驶出圆曲线又立即消失。
同时驾驶员在直线进入圆曲线或回到直线时迅速改变行车方向,造成驾驶操纵紧张,因而造成行成不安全、乘客不舒适。
汽车在以高速进入较小半径圆曲线时,这种现象尤为明显。
为了缓和行车方向的突然变化及离心力的突然产生和消失,确保高速行车的安全和舒适,需要在直线段和圆曲线之间插入一段曲率半径由无穷大逐渐变化到圆曲线半径的过渡性曲线,这种曲线就叫做缓和曲线。
缓和曲线的作用是使汽车在不降低车速的情况下能均匀徐缓转向,由直线段逐渐过渡到圆曲线或曲圆曲线逐渐过渡到直线段,从而保证行车平稳、旅客舒适。
在设有超高和加宽时,缓和曲线也作为逐步超高及加宽的部分。
2、数学模型字母含义:(1)、曲线主要桩点名称简称汉语拼音缩写英语缩写交点交点JD IP转点转点ZD TP第一缓和曲线起点直缓点ZH TS第一缓和曲线终点缓圆点HY SC 曲线中点曲中点QZ MC第二缓和曲线起点圆缓点YH CS第二缓和曲线终点缓直点HZ ST(2)、曲线已知参数:R:圆曲线半径Ls:缓和曲线长度α:转向角(3)、曲线要素计算:β0:切线角(缓和曲线角);δ0:缓和曲线总偏角;b0:缓和曲线反偏角;P:内移值;q:切垂距(切线增值);T H:切线长;L H:曲线总长(两段缓和曲线+圆曲线的长度);Ly:圆曲线长度;E H:外矢距;D H:切曲差;X0:以ZH点或HZ点为坐标原点,ZH或HZ的切线为X轴,ZH 或HZ的法线方向为Y 轴,缓和曲线终点(HY点或YH点)的X坐标增量;Y0:以ZH点或HZ点为坐标原点,ZH或HZ的切线为X轴,ZH 或HZ的法线方向为Y轴,缓和曲线终点(HY点或YH点)的Y坐标增量;(4)、待求点字母含义:L:待求点至ZH点或HZ的曲线长度;:以ZH点或HZ点为坐标原点,ZH或HZ的切线为X轴,ZH或HZ的法线方向为Y 轴,待求点的X坐标增量;:以ZH点或HZ点为坐标原点,ZH或HZ的切线为X轴,ZH或HZ的法线方向为Y轴,待求点的Y坐标增量;二、缓和曲线公式1、基本公式如上图所示,缓和曲线的半径随着曲线长度的增大而成反比地均匀减小,即在缓和曲线上任一点的曲率半径ρ与曲线的长度L呈反比关系。
缓和曲线要素及公式介绍

为了保障车辆行驶安全,在直线与圆曲线之间加入一段半径由∞逐渐变化到R的曲线,这种曲线称为缓和曲线。
目前常用的缓和曲线多为螺旋线,它有一个特性,曲率半径ρ与曲线长度l成反比。
数学表达为:ρ∝1/l 或ρ·l = k ( k为常数)若缓和曲线长度为l0,与它相连的圆曲线半径为R,则有:ρ·l = R·l0 = k目前我国公路采用k = (V为车速,单位为km/h),铁路采用k = ,则公路缓和曲线的长度为l0 = R ,铁路缓和曲线的长度为:l0 = R 。
11.2.2 带缓和曲线的圆曲线的主点及主元素的计算带缓和曲线的圆曲线的主点有直缓点ZH、缓圆点HY、曲中点QZ、圆缓点YH、缓直点HZ 。
带缓和曲线的圆曲线的主元素及计算公式:切线长 T h = q+(R+p)·tan(α/2)曲线长 L h = 2l0+R·(α-2β0)·π/180°外矢距 E h = (R+p)·sec(α/2)-R切线加长 q = l0/2-l03/(240R2)圆曲线相对切线内移量 p = l02/(24R)切曲差 D h = 2T h -L h式中:α 为线路转向角;β0为缓和曲线角;其中q、p、β0缓和曲线参数。
11.2.3 缓和曲线参数推导dβ = dl/ρ = l/k·dl两边分别积分,得:β= l2/(2k) = l/(2ρ)当ρ = R时,则β =β0β0 = l0/(2R)若选用点为ZH原点,切线方向为X轴,垂直切线的方向为Y轴,建立坐标系,则:dx = dl·cosβ = cos[l2/(2k)]·dldy = dl·sinβ = sin[l2/(2k)]·dl考虑β很小,sinβ和cosβ即sin(l2/(2k))和cos(l2/(2k))可以用级数展开,等式两边分别积分,并把k = R·l0代入,得以曲线长度l为参数的缓和曲线方程式:X = l-l5/(40R2l02)+……Y = l3/(6Rl0)+……通常应用上式时,只取前一、二项,即:X = l-l5/(40R2l02)Y = l3/(6Rl0)另外,由图可知,q = X HY-R·sinβ0p = Y HY-R(1-cosβ0)以β0= l0/(2R)代入,并对sin[l0/(2R)]、cos[l0/(2R)]进行级数展开,取前一、二项整理可得:q = l0/2-l03/(240R2)p = l02/(24R)若仍用上述坐标系,对于圆曲线上任意一点i,则i点的坐标X i、Y i可以表示为:Xi = R·sinψi+qYi = R·(1-cosψi)+p11.2.4 带缓和曲线的圆曲线的主点桩号计算及检核ZH桩号 = JD桩号-T hHY桩号 = ZH桩号+l0QZ桩号 = HY桩号+L/2YH桩号 = QZ桩号+L/2 = HY桩号+L = ZH桩号+l0+LHZ桩号 = YH桩号+l0 = ZH桩号+L hJD桩号 = ZY桩号-T h+D h(检核)11.2.5 带缓和曲线的圆曲线的主点的测设过程:(1)在JD点安置经纬仪(对中、整平),用盘左瞄准直圆方向,将水平度盘的读数配到0°00′00″,在此方向量取T h,定出ZH点;(2)从JD沿切线方向量取T h-X HY,然后再从此点沿切线垂直方向量取Y HY , 定出HY点;(3)倒转望远镜,转动照准部到度盘读数为α,量取T h,定出HZ点;(4)从JD沿切线方向量取T h-X HY,然后再从此点沿切线垂直方向量取Y HY , 定出YH点;(5)继续转动照准部到度盘读数为(α+180°)/2,量取E h,定出QZ点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、缓和曲线上的点坐标计算
已知:①缓和曲线上任一点离ZH点的长度:l
②圆曲线的半径:R
③缓和曲线的长度:l0
④转向角系数:K(1或-1
⑤过ZH点的切线方位角:α
⑥点ZH的坐标:xZ,yZ
计算过程:
说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:
当计算第二缓和曲线上的点坐标时,则:
l为到点HZ的长度
α为过点HZ的切线方位角再加上180°
K值与计算第一缓和曲线时相反
xZ,yZ为点HZ的坐标
切线角计算公式:
二、圆曲线上的点坐标计算
已知:①圆曲线上任一点离ZH点的长度:l
②圆曲线的半径:R
③缓和曲线的长度:l0
④转向角系数:K(1或-1
⑤过ZH点的切线方位角:α
⑥点ZH的坐标:xZ,yZ
计算过程:
说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:
当只知道HZ点的坐标时,则:
l为到点HZ的长度
α为过点HZ的切线方位角再加上180°
K值与知道ZH点坐标时相反
xZ,yZ为点HZ的坐标
三、曲线要素计算公式
公式中各符号说明:
l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)
l1——第一缓和曲线长度
l2——第二缓和曲线长度
l0——对应的缓和曲线长度
R——圆曲线半径
R1——曲线起点处的半径
R2——曲线终点处的半径
P1——曲线起点处的曲率
P2——曲线终点处的曲率
α——曲线转角值
四、竖曲线上高程计算
已知:①第一坡度:i1(上坡为“+”,下坡为“-”
②第二坡度:i2(上坡为“+”,下坡为“-”
③变坡点桩号:SZ
④变坡点高程:HZ
⑤竖曲线的切线长度:T
⑥待求点桩号:S
计算过程:
五、超高缓和过渡段的横坡计算
已知:如图,
第一横坡:i1
第二横坡:i2
过渡段长度:L
待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i
解:d=x/L
i=(i2-i1(1-3d2+2d3+i1
六、匝道坐标计算
已知:①待求点桩号:K
②曲线起点桩号:K0
③曲线终点桩号:K1
④曲线起点坐标:x0,y0
⑤曲线起点切线方位角:α0
⑥曲线起点处曲率:P0(左转为“-”,右转为“+”
⑦曲线终点处曲率:P1(左转为“-”,右转为“+”求:①线路匝道上点的坐标:x,y
②待求点的切线方位角:αT
计算过程:。
