缓和曲线计算原理
缓和曲线坐标计算原理

坐标转换的公式为:
应当注意的问题:
在运用式(10-49)计算时,当曲线为左转角,应以yi=一yi代入。
13
三、YH点至HZ点之间的中桩坐标计算(第二缓和 曲线)
此段为第二缓和曲线,仍可按切线支距法公式 (10-27)和(10-33)先算出局部坐标x、y,再按下 式转换为统一坐标:
利用上式计算时,尤其要注意线路的偏转方向, 当曲线为右转角时,应以yi=一yi代入。
缓和曲线参数:
l0 0 2R
2 l0 P 24 R
加设缓和曲线 后使切线增长 的距离:
HY点或YH点的 缓和曲线角度
加设缓和曲线后 圆曲线相对于切 7 线的内移量
3.缓和曲线的计算方法(分段计算): 如下图所示,是一段加设缓和曲线的圆曲线,从(ZH)到(HZ) 间是一段完整的对称缓和曲线的圆曲线。这种缓和曲线的布设方式就 是京沪高铁的曲线特征。 在选定各圆曲线半径R和缓和曲线长度ls后,根据各桩的里程桩号, 按下述方法即可算出相应的坐标值(X,Y)。
在选定各圆曲线半径R和缓和曲线长度ls后,根据各桩的 里程桩号,按下述方法即可算出相应的坐Z点(包括路线起点)至ZH点之间的坐标 计算(直线段)
如上图,此段为直线,桩点的坐标按下式计算:
上式中:Ai-1, i为路线导线JDi-1至JDi的坐标方位 角;Di为桩点至HZi-1点的距离,即桩点里程与HZi1点里程之差;XHZi-1、 YHZi-1 为HZi-1点的坐标, 由下式计算:
14
中桩坐标算例
已知:
求:中桩坐标
15
解:计算步骤如下: 1.计算路线转角:
缓和曲线超高计算

公路缓和曲线知识与计算公式未知2010-04-04 17:34:42 本站一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形 , 是道路平面线形要素之一。
1 .缓和曲线的作用1 )便于驾驶员操纵方向盘2 )乘客的舒适与稳定,减小离心力变化3 )满足超高、加宽缓和段的过渡,利于平稳行车4 )与圆曲线配合得当,增加线形美观2 .缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的 0 °均匀地增加到圆曲线上。
S=A2/ρ( A :与汽车有关的参数)ρ=C/s C=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3 .回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R , l h=s 则 l h=A2/R4 .缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1 )根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ ρ ,a s= Δ a/t ≤ 0.62 )依驾驶员操纵方向盘所需时间求缓和曲线长度 (t=3s)3 )根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
4 )从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在 3°—— 29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5 .直角坐标及要素计算1 )回旋线切线角( 1 )缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
缓和曲线公式
用回旋线(放射螺旋型)作为缓和曲线。
回旋线是一种曲率随曲线长度成比例变化的曲线,不仅可以使线形更加美观,而且与驾驶员匀速转动方向盘由圆曲线驶入直线或者由直线驶入圆曲线的轨迹线相符合。
其基本公式为:rl=A2;其中:r—回旋线上某点曲率半径(m);l—回旋线上其点到原点的曲线长(m);A—回旋线参数;由于rl是长度的二次方,故令C=A2,A表征曲率变化的缓急程度,因此在缓和曲线上,r随l的变化而变化,在缓和曲线的终点处,l=L s,r=R,RL s=A2,即A=√(RL s);其中:R—回旋线所连接的圆曲线半径;L s—回旋线形的缓和曲线长度。
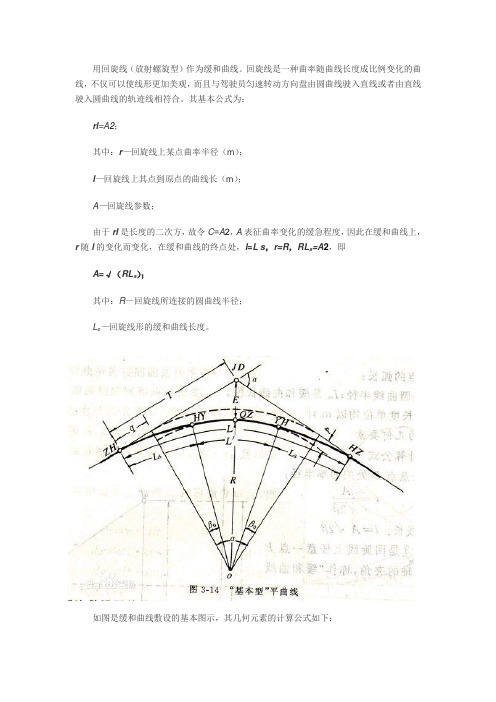
如图是缓和曲线敷设的基本图示,其几何元素的计算公式如下:q =L s/2-L s3/(240×R2) (m);p=L s2/(24R)-L s4/(2384×R3) (m);β=28.6479L s/R(。
);T=(R+p)tan(α/2)+q(m);L=(α-2β)πR/180+2Ls(m);E=(R+p)/cos(α/2) -R(m);J=2T-L(m);其中:α—路线转角(。
);β—圆曲线对应角度(。
);q—偏移值(m);p—原曲线与直线偏移值(m);T—切线长(m);E—外移值(m);J—里程差(m);[式中α为路线设计参数,R值对于设计道路可查相关规范][1-2]缓和曲线的作用:p(1)曲率连续变化,便于车辆遵循。
(2)离心加速度逐渐变化,旅客感觉舒适。
(3)超高横坡度及加宽逐渐变化,行车更加稳定。
(4)与圆曲线配合,增加线形美观。
缓和曲线和圆曲线的有关计算

缓和曲线和圆曲线的计算与测设一、缓和曲线的性质缓和曲线是直线与圆曲线间的一种过渡曲线。
它与直线分界处半径为∞,与圆曲线相接处半径与圆曲线半径R 相等。
缓和曲线上任一点的曲率半径ρ∝l1 或ρl=C式中,C 变更率。
当l =0l 时,ρ=R ,所以0Rl =C式中,0l 为缓和曲线总长。
ρl=C 是缓和曲线的必要条件,实用中能满足这一条件的曲线可以作为缓和曲线,如辐射螺旋线、三次抛物线等。
我国缓和曲线均采用辐射螺旋线。
二、缓和曲线方程式按照ρl=C 为必要条件导出的缓和曲线方程为:X=l -2540C l +493456C l +…Y=Cl 63-37336C l +51142240C l + (1)根据测设要求的精度,实际应用中可将高次项舍去,并顾及到0Rl =C ,则上式变为X=l -202540l R lY=036Rl l -3037336l R l (2)式中,x 、y 为缓和曲线上任一点的直角坐标,坐标原点为直缓点(ZH )或缓直点(HZ );通过该点的缓和曲线切线为x 轴,如图2:l 为缓和曲线上任一点P 到ZH (或HZ )的曲线长;0l 为缓和曲线总长度。
当l =0l 时,x=x 0,y=y 0,代入式(2)得:X 0=0l -23040R lY 0=Rl 62-340336Rl (3)式中,x 0 、y 0 为缓圆点(HY )或圆缓点(YH )的坐标。
三、缓和曲线常数计算β0、δ0、m 、p 、 x 0、y 0 等称为缓和曲线常数。
其物理意义及几何关系由下图,图3可得知:β0——缓和曲线的切线角,即HY (或YH )点的切线与ZH (或HZ )点切线的交角;亦即圆曲线一端延长部分所对应的圆心角。
δ0——缓和曲线的总偏角;m —切垂距,即ZH (或HZ )到由圆心O 向切线所作垂线垂足的距离; p —圆曲线内移量,为垂线长与圆曲线半径R 之差。
常数计算公式如下:X 0=0l -23040R lY 0=Rl 62-340336Rlβ0=π18020R lδ0=031β=π 18060R lm=2l -230240R lp=24R l 20-3402688Rl ≈24Rl 20 (4) 下面我们推证常数β0、δ0 、m 、p 、x 0、y 0。
《缓和曲线》课件

目录 Contents
• 引言 • 缓和曲线的数学原理 • 缓和曲线在实际中的应用 • 缓和曲线的绘制方法 • 缓和曲线的优化设计 • 案例分析
01
引言
什么是缓和曲线
缓和曲线是道路设计中的一个重要元 素,是指在直线和圆曲线之间或圆曲 线与圆曲线之间设置的曲率连续变化 的曲线。
某大型桥梁设计案例
总结词:创新性
详细描述:该案例介绍了一座大型桥梁的设计过程,设计团队通过运用缓和曲线的理念,创造出了既实用又美观的桥梁造型 ,为桥梁设计领域带来了新的思路和启示。
某高档住宅区景观设计案例
总结词:综合性
详细描述:该案例展示了一个高档住宅区的景观设计,设计中充分融入了缓和曲线的元素,打造出了 一个和谐、自然、舒适的居住环境,体现了缓和曲线在景观设计中的综合应用价值。
曲率突变的影响
曲率突变会导致车辆在行驶过程中出现急转弯或 急变向的情况,影响行车安全。因此,需要对曲 率突变进行控制和优化。
曲率连续性的实现方法
通过合理设置缓和曲线参数,如曲率半径、缓和 曲线长度等,来保证曲率的连续性和平滑性。
曲线长度优化
曲线长度与行车安全
缓和曲线的长度是影响车辆行驶安全的重要因素。过短的 缓和曲线会导致车辆在转弯过程中出现急转弯或急变向的 情况,影响行车安全。
曲线美观性的实现方法
通过合理选择缓和曲线的线形、参数和材料等,来提高缓和曲线的美观性。同 时,还需考虑周围环境和建筑风格,使缓和曲线与周围环境相协调。
06
案例分析
某城市道路设计案例
总结词:典型性
详细描述:该案例选取了某城市的道路设计作为研究对象,这条道路在设计中充 分运用了缓和曲线的理念,使得道路在满足交通功能的同时,也具备良好的景观 效果和舒适度。
圆曲线、缓和曲线计算方法

● 圆曲线方法一:sin (1cos )180i i i i i i x R y R l R ϕϕϕπ⎧⎪=⎪=-⎨⎪︒⎪=⋅⎩——i l 为待定点i P 至起点间的弧长i ϕ为i l 所对的圆心角R 为曲线半径方法二:11802l A R π︒=⋅⋅ 2sin l R A =⋅00cos(/)sin(/)x x l A y y l A =+⋅+-⎧⎨=+⋅+-⎩起点方位角左减右加起点方位角左减右加——00(,)x y 为圆曲线起点坐标方法三:180l A R π︒=⋅ 00cos(/)sin(/)x x R B A y y R B A =+⋅+-⎧⎨=+⋅+-⎩——l 为圆曲线上任意一点距起点距离00(,)x y 为圆曲线圆心坐标B 为圆心到圆曲线起点的方位角,A 为任意点对应的圆心角● 缓和曲线522030406l x l R l ly Rl ⎧=-⎪⎪⎨⎪=⎪⎩——l 为曲线上任一点至起点的曲线长R 曲线半径0l 为缓和曲线全长圆曲线、缓和曲线计算方法1、直线段:先由JD1以及JD2的坐标算出JD1到JD2的方位角,即直线段方位角A ,故可算出HZ 、ZH 坐标及其直线段各点坐标。
2、缓和曲线:以HZ 、ZH 为起点,缓和曲线上任意一点离HZ 、ZH 距离为l ,利用公式522003040()6l x l R l l R ly Rl ⎧=-⎪⎪⎨⎪=⎪⎩为缓和曲线全长,为圆曲线半径算出该点的相对起点坐标,利用arctan y x算出该点相对起点的方位角B ,再根据线路走向及直线段方位角可算出该点的方位角C (顺时针加,逆时针减),用可求出该点相对起点的距离D ,最后用00cos sin x x D C y y D C =+⎧⎨=+⎩可求出该点的坐标。
(00(,)x y 为缓和曲线起点的坐标)3、圆曲线:用上述方法求出圆曲线两端点HY 、YH 坐标,算出HY 到YH 的方位角F ,以及两点间的距离E ,用12arccos ER可算出两端点连线与起点到圆心连线的夹角G ,根据线路走向求出起点到圆心的方位角H (H=F+/-G ),00(,)x y 圆曲线为起点坐标,根据00cos sin x x R H y y R H=+⎧⎨=+⎩,求出圆心坐标。
公路缓和曲线段原理及缓和曲线计算公式

程序使用说明Fx9750、9860系列程序包含内容介绍:程序共有24个,分别是:1、0XZJSCX2、1QXJSFY3、2GCJSFY4、3ZDJSFY5、4ZDGCJS6、5SPJSFY7、5ZDSPFY8、5ZXSPFY9、6ZPJSFY 10、7ZBZFS 11、8JLHFJH 12、9DBXMJJS13、9DXPCJS 14、9SZPCJS 15、GC-PQX 16、GC-SQX17、PQX-FS 18、PQX-ZS 19、ZD-FS 20、ZD-PQX21、ZD-SQX 22、ZD-ZS 23、ZDSP-SJK 24、ZXSP-SJK其中,程序2-14为主程序,程序15-24为子程序。
每个主程序都可以单独运算并得到结果,子程序不能单独运行,它是配合主程序运行所必需的程序。
刷坡数据库未采用串列,因为知道了窍门,数据库看起很多,其实很少。
程序1为调度2-8程序;程序2为交点法主线路(含不对称曲线)中边桩坐标正反计算及极坐标放样程序;程序3为主线路中边桩高程计算及路基抄平程序;程序4为线元法匝道中边桩坐标正反计算及极坐标放样程序;程序5为匝道线路中边桩高程计算及路基抄平程序;程序6为任意线型开口线及填筑边线计算放样程序;程序7专为主线路开口线及填筑边线计算放样程序,只需测量任意一点三维数据,即可马上计算出该点相对于中桩法线上的偏移量;程序8专为匝道线路开口线及填筑边线计算放样程序,只需测量任意一点三维数据,即可马上计算出该点相对于中桩法线上的偏移量;程序9为桥台锥坡计算放样程序;程序10为计算两点间的坐标正反算程序;程序11为距离后方交会计算测站坐标程序;程序12为任意多边形面积周长计算程序;程序13为导线近似平差计算程序;程序14为水准近似平差计算程序;程序2-8所用数据库采用的串列,匝道用的File 1;主线用的File 2。
第一步:先用Excel按照文字说明输入完整条线路对应数据;第二步:保存为CSV格式,然后设置单元格格式、数字格式、科学计数、小数位数设置10位以上并保存;第三步:用FA-124导入,匝道数据列表文件选择“File 1”,主线数据列表文件选择“File 2”。
圆曲线带有缓和曲线的曲线元素计算原理

圆曲线带有缓和曲线的曲线元素计算原理圆曲线带有缓和曲线的曲线元素计算原理1、缓和曲线的概念汽车在直线上行驶时,离心力为零;在曲线上行驶,就会产生离心力,如果某路线的直线段与圆曲线直接连接时,汽车从直线进入圆曲线那一瞬间就会突然产生离心力,驶出圆曲线又立即消失。
同时驾驶员在直线进入圆曲线或回到直线时迅速改变行车方向,造成驾驶操纵紧张,因而造成行成不安全、乘客不舒适。
汽车在以高速进入较小半径圆曲线时,这种现象尤为明显。
为了缓和行车方向的突然变化及离心力的突然产生和消失,确保高速行车的安全和舒适,需要在直线段和圆曲线之间插入一段曲率半径由无穷大逐渐变化到圆曲线半径的过渡性曲线,这种曲线就叫做缓和曲线。
缓和曲线的作用是使汽车在不降低车速的情况下能均匀徐缓转向,由直线段逐渐过渡到圆曲线或曲圆曲线逐渐过渡到直线段,从而保证行车平稳、旅客舒适。
在设有超高和加宽时,缓和曲线也作为逐步超高及加宽的部分。
2、数学模型字母含义:(1)、曲线主要桩点名称简称汉语拼音缩写英语缩写交点交点JD IP转点转点ZD TP第一缓和曲线起点直缓点ZH TS第一缓和曲线终点缓圆点HY SC 曲线中点曲中点QZ MC第二缓和曲线起点圆缓点YH CS第二缓和曲线终点缓直点HZ ST(2)、曲线已知参数:R:圆曲线半径Ls:缓和曲线长度α:转向角(3)、曲线要素计算:β0:切线角(缓和曲线角);δ0:缓和曲线总偏角;b0:缓和曲线反偏角;P:内移值;q:切垂距(切线增值);T H:切线长;L H:曲线总长(两段缓和曲线+圆曲线的长度);Ly:圆曲线长度;E H:外矢距;D H:切曲差;X0:以ZH点或HZ点为坐标原点,ZH或HZ的切线为X轴,ZH 或HZ的法线方向为Y 轴,缓和曲线终点(HY点或YH点)的X坐标增量;Y0:以ZH点或HZ点为坐标原点,ZH或HZ的切线为X轴,ZH 或HZ的法线方向为Y轴,缓和曲线终点(HY点或YH点)的Y坐标增量;(4)、待求点字母含义:L:待求点至ZH点或HZ的曲线长度;:以ZH点或HZ点为坐标原点,ZH或HZ的切线为X轴,ZH或HZ的法线方向为Y 轴,待求点的X坐标增量;:以ZH点或HZ点为坐标原点,ZH或HZ的切线为X轴,ZH或HZ的法线方向为Y轴,待求点的Y坐标增量;二、缓和曲线公式1、基本公式如上图所示,缓和曲线的半径随着曲线长度的增大而成反比地均匀减小,即在缓和曲线上任一点的曲率半径ρ与曲线的长度L呈反比关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.2道路线形的基本介绍道路运输在整个国民经济生活中起着重要作用。
道路的新建和改建,测量工作必须先行,所以公路施工测量所承担的任务也是非常大的,为了更好的进行道路施工工作,下面就道路线形进行一下简单的介绍。
一般所说的路线,是指道路中线的空间位置。
中线在水平面上的投影称作路线的平面;沿中线竖直剖切再行展开则是路线的纵断面;中线上任一点法向切面是道路在该点的横断面。
无论是铁路、公路还是地铁隧道和轻轨,由于受到地形、地物、地质及其他因素的限制,经常要改变线路前进的方向。
当线路方向改变时,在转向处需用曲线将两直线连接起来。
因此,线路工程总是由直线和曲线所组成。
曲线按其线形可分为:圆曲线、缓和曲线、复曲线和竖曲线等。
公路中线应满足的几何条件是:线形连续平滑;线形曲率连续(中线上任一点不出现两个曲率值);线形曲率变化率连续(中线上任一点不出现两个曲率变化值)。
考虑上述几何条件,顾及计算与敷设方便,现代公路平面线形要素由直线、圆曲线和缓和曲线构成,称之为平面线形三要素。
其中缓和曲线的曲率半径是从∞逐渐变到圆曲线半径R 的变量。
在与直线连接处半径为∞,与圆曲线连接处半径为R ,曲线上任一点的曲率半径与该点至起点的曲线长成反比。
目前公路线形设计已开始使用非对称线形(成为非对称平曲线)设计,特别是在互通立交匝道和山区高速高速公路线形设计中,这种线形设计使用得较多。
非对称线形分为完全非对称线形和非对称非完整线形两种,所谓“完全非对称曲线”的含义就是第一缓和曲线和第二缓和曲线起点处(ZH 或HZ )的半径为∞,圆半径为R ,第一缓和曲线长1s l ,第二缓和曲线长为2s l ,12s s l l ≠。
所谓“非完整”的含义是第一缓和曲线和第二缓和曲线的半径不是∞,而是1R 、2R 。
而坐标法成为高速公路放样的主要方法,坐标法放样线路中线的这个操作过程中,最重要的一部就是计算线路放样点的坐标。
2 路线中桩坐标计算原理在实际工程中,线路的设计由专门的设计方完成,在线路完成设计得到审批后设计方便把所设计线路的线路要素(或者称为曲线要素)提供给施工方。
所提供的曲线要素一般包括:线路中各曲线段的起点坐标、起点里程、起点半径、终点坐标、终点里程、终点半径、交点坐标、曲线参数、转角(包括用一定的符号表示左右转)、两条切线长(起点与终点各所对应的两条切线)、曲线长。
当然不同的工程项目所提供的曲线要素也不一样,以上所述的要素是大多数设计方会提供的,有的设计方在提供上述要素的前提下,还提供曲线段的外距、中点坐标、弦长或者走向方位角等要素,供施工方在计算施工坐标时予以相互检核。
所以,为了保证原理的通用性,我们需要用最少的、最通用的、最有利于使用、最有利于推算的条件来讲解。
通过对多份实际工程中用到的曲线元素的分析,得出了计算最复杂曲线(非完整缓和曲线)的中、边桩坐标及中桩→边桩坐标方位角的最少条件。
中桩,指的是为表示中线位置和线形等,沿路线中线所设置的编有桩号的桩或标志。
中桩测设是指沿着直线或曲线详细测设中桩,是工程中放样测量的重要组成部分。
中桩的放样方法有多种,但随着测量仪器的日益先进,测量手段也开始发生变化且趋向于简单,测量的结果也日益精确,当然所要求的放样元素也由所变化。
现在工程中实际用到的放样仪器主要是全站仪、GPS-RTK ,这就决定我们在计算线路的放样元素时,得出的主要对象是桩位在总体坐标系中的二维坐标(高程放样是在其单独的高程坐标系中单独进行的)。
经过总结,发现进行中桩坐标计算时,无论其是何种曲线段只要给出下述条件即可进行相应的计算。
条件:线路中各曲线段的起点坐标1x 1y 、起点里程1s 、起点半径1r 、终点坐标2x 2y 、终点里程2s 、终点半径2r 、交点坐标3x 3y 、曲线参数A 、转向(-1或1)。
由于在圆曲线、完整缓和曲线段及非完整缓和曲线段中桩、边桩坐标计算过程中,需要先建立局部坐标系然后进行二维坐标之间的转换,所以下面首先对二维坐标系之间的转换进行讲解:2.1二维直角坐标系的转换两个直角坐标系(如右图)进行相互转换的旋转角称为欧勒角,对于二维直角坐标系两个坐标系之间的夹角大小等于其欧勒角。
对于二维直角坐标系已知P 点在局部坐标系中的坐标,()P P A B ,局部坐标系原点0,()x y 以及局部坐标系相对于总体坐标系的坐标方位角,则P 在总体坐标系中的坐标为:00cos sin sin cos p P P p x x A y y B θθθθ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦- 将矩阵换算为方程式的形式为:00cos sin sin cos pppPPpx x A B yy A B θθθθ=+-⎫⎪⎬=++⎪⎭式中0x 0y 与θ值可由计算人员提供。
B同样,若已知P 点在总体坐标系中的坐标,()P Px y ,可按下式将其换算为在局部坐标系中的坐标,()P PA B :00()()()()cos sin sin cos PPP PPP y y x x A y y x x B θθθθ⎫=-+-⎪⎬=--+-⎪⎭在前期的预备知识了解后,下面就工程中可能遇到的十一种路段,如何进行中桩坐标的计算逐一的进行详细的讲解。
2.2直线段中桩坐标计算原理首先说清的一点是,直线段不具有交点坐标。
在进行中桩坐标计算时,首先根据起点坐标1x 1y 与终点坐标2x 2y 计算起点至终点的坐标方位角jdjz :2121arctany y jdjz x x-=-在得到计算起点至终点的坐标方位角jdjz 后,即可计算该直线段上任意里程s 的坐标,计算方式为:1111()()cos sin jdjz x x s s y y jdjzs s =+-=+- 这样,直线段的任意要求里程的中桩坐标就求出来了。
2.2圆曲线段中桩坐标计算原理现在的铁路公路为了顾及到车辆行驶的安全性,防止使驾驶员的产生视觉疲劳,经常布设圆曲线,圆曲线是一种比较简单的线形,但因圆曲线段的线路走向较直线段较为复杂,所以在计算中桩过程中,为了坐标的计算方便以及后续的坐标系转换,须建立单独的坐标系,首先在局部坐标中计算各个桩号的中桩坐标,然后再根据局部坐标系原点在全局坐标系中的坐标以及局部坐标系X 轴方向在全局坐标系中的坐标方位角进行坐标转换。
2.2.1 圆曲线段中桩坐标计算通用原理由于路线的转向不同,局部坐标系的建立方式也有所不同,这里先讲述圆曲线段中桩坐标计算的通用原理。
如右图所示,以曲线起点ZY 为坐标原点,以顺着线路方向的切线为X 轴,以切线的垂线方向为Y 轴,两个轴构成测量坐标系。
则该圆曲线段上任意里程的中桩在局部坐标系中的坐标为:sin 1cos180R x y R S R Rϕϕϕ=⎡⎤=⎣⎦⋅-=式中s 为曲线段距离,即曲线段桩号差值。
在计算出桩位在局部坐标系中的坐标后,就必须进行坐标系之间的转换:00cos sin sin cos pppPPpx x A B yy A B θθθθ=+-⎫⎪⎬=++⎪⎭这里叙述的两个轴的定义只是为了叙述原理方便所定义的,并不代表全部情况,随着线路转向不同的而不同,当然x ,y 的计算公式也因坐标系的不同而不同,实际线路计算时需灵活处理。
同时顾及坐标计算的方便以及后续坐标系的转换,这里建议在建立坐标系时建立测量坐标系而不是数学坐标系。
2.2.1 圆曲线段左、右转的处理方式圆曲线段之所以要讨论左、右转的问题,主要是顾及到在局部坐标系中的坐标保证是正值,同时保证为了后期的坐标转换的方便,很容易通过图形来表示:通过我们也可以很容易的总结出桩位在各自的局部坐标系中的坐标,中()式为线路左转时的局部坐标的计算公式,()式为线路右转时的局部坐标的计算公式:sin 1cos 180R x y R S R R ϕϕϕ=⎡⎤=⎣⎦⋅-= sin 1cos 180R x y R S R Rϕϕϕ=⎡⎤=⎣⎦⋅-=无论线路是左转还是右转,在计算完桩位在局部坐标系中坐标后都需要进行坐标系的转换,公式不再赘述,公式中的各个量得含义也不变。
2.3完整缓和曲线段中桩坐标计算原理直线的半径为无穷大;进入圆曲线时,则半径为R ,所以从直线段过渡到圆曲线时,汽车的行驶曲率半径是不断变化,这一变化路段即为缓和曲线段。
2.3.1 完整缓和曲线段中桩坐标计算通用原理由于缓和曲线段没有统一的曲率半径,所以计算桩位坐标的过程是比较困难比较繁式中p l 将cos β、sin β按级数展开:48224400263300111838411248P P PP P P P Pdl l l dl R l R l dl l l dl Rl R l ⎫⎛⎫⎫-=-+-⎪ ⎪⎪⎭⎝⎭⎪⎬⎛⎫⎫⎪-=-+ ⎪⎪⎪⎭⎝⎭⎭积分得:在计算出桩位在局部坐标系中的坐标后,就必须进行坐标系之间的转换:00cos sin sin cos pppPPpx x A B yy A B θθθθ=+-⎫⎪⎬=++⎪⎭这里叙述的两个轴的定义只是为了叙述原理方便所定义的,并不代表全部情况,随着线路转向不同的而不同,当然x ,y 的计算公式也因坐标系的不同而不同,实际线路计算时需灵活处理。
同时顾及坐标计算的方便以及后续坐标系的转换,这里建议在建立坐标系时建立测量坐标系而不是数学坐标系,这样有利于坐标系的统一。
2.3.2 完整缓和曲线段不同过渡方式的左、右转的处理方式这里之所以要强调不同过渡方式的不同,是因为不同的过渡方式附带的不同转向所导致的坐标系的建立方式不同以及坐标计算公式不同,但坐标系建立的原则就是保证x 值与y均保证为正值,方便后期的坐标转换。
现在就不同的过渡方式以及不同的转向进行逐一讨论:1.线路是由大半径过渡到校半径,转向是左转这里为了计算出的中桩坐标都是正值,而且为了后期的坐标系的转换的方便这里建议建立坐标系的方式为:原点位于QD(起点),X轴经过原点正向垂直于ZH→JD切线的方向,Y轴经过过原点正向指向与于ZH→JD切线的方向一致。
这样各个桩位在局部坐标系总的值为:式中l为所求桩位距离QD的曲线长即为里程差,0l为完整的缓和曲线长度,R为终点半径。
P2.线路是由大半径过渡到校半径,转向是右转这里建议建立坐标系的方式为:原点位于QD(起点),X轴经过原点正向指向ZH →JD切线的方向,Y轴经过过原点正向垂直于ZH→JD切线方向,构成测量坐标系。
这样各个桩位在局部坐标系总的值为:式中各字母的含义与前面所述一样,在此不再赘述。
3.线路是由小半径过渡到大半径,转向是左转这里建议建立坐标系的方式为:原点位于ZD(终点),X轴经过原点正向指向ZD →JD切线的方向,Y轴经过原点正向垂直于ZD→JD切线方向,构成测量坐标系。
