缓和曲线长度及平曲线计算
道路勘测设计 第二章道路平面设计3
R
0
]
y P R {1 cos[( LP LS 2) 180 R]}
基本形单曲线回旋线要素计算
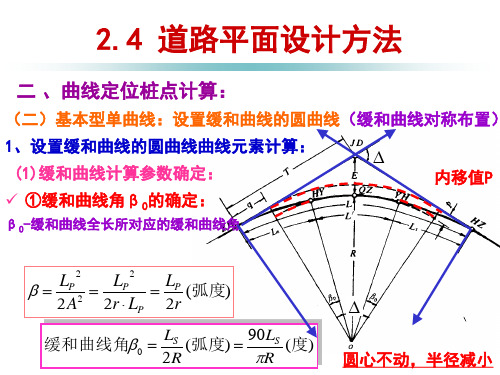
（二）设置缓和曲线的圆曲线：基本型单曲线 3、加密桩点坐标计算： （1）缓和曲线段内坐标计算： 切线支距法：
LP x LP 2 40 R 2 LS
L y P 6 RLS
2.4 道路平面设计方法
三、平面设计一般规定与基本步骤
道路平面布置设计的步骤：
（1）根据道路的技术等级，根据《标准》JTG B01-2003和《规范》 JTG D20-2006查出设计速度、最小半径、缓和曲线最小长度、直线 段的最大最小长度等主要技术标准的规定值
（2）根据地形、地物条件确定控制因素
（三）复曲线设计：
3、卵形复曲线：
实际工程中，应尽量避免采用这种曲线
（三）复曲线设计：
3、卵形复曲线：
①复中设置缓和曲线的特点： 缓和曲线段两端点的 曲率半径分别与相应 圆的圆曲线半径一致
曲线定位桩点计算
FZ
较小半径圆曲线相对 于大半径圆曲线内移 一段距离
即复曲线中间缓和曲 线段被原公切点中分 缓和曲线段中点(FZ 点)通过内移距离(内 移值之差PF)的中心
Eh B
切线支距法： x q R sin
Lh
y P R (1 cos )
LP LS 180 [
LS 90 LS 0 (弧度) (度) 2R R
θ
LP LS / 2180
R
x q R sin[( LP LS 2) 180 R]
Eh ( R P) sec R(m) 2
Lh ( 2 0 )
各种曲线类型的缓和曲线的判断及起点、终点曲率半径的计算方法
各种曲线类型的缓和曲线的判断及起点、终点曲率半径的计算方法看到这个标题是有点绕口啊！总结任何曲线类型都是由自然段组合而成，所谓自然段统指直线、缓和曲线、圆曲线。
圆曲线又分单圆曲线和复曲线。
单圆曲线就是单一半径的曲线。
具有两个半径或以上不同半径的曲线称复曲线。
在此一般平曲线不在说了，第一缓和曲线、圆曲线、第二缓和曲线。
目前在坐标计算中经常遇到缓和曲线，实际中相信有很多测友选择用积木法或叫线元法正反算程序进行线路坐标计算，这就牵涉到线元的起点终点曲率半径判断的问题，一般的直线元，圆曲线元的起点终点半径判断，比较容易，可能令大家感觉麻烦的就是缓和曲线起点终点半径判断问题，缓和曲线有时候判断算对了，有时候却坐标算不对，究其原因，问题就出于该缓和曲线是否是完整缓和曲线。
目前公路线性有非对称线性的设计，特别是在互通立交匝道和山区高速公路线性设计中。
非对称线性又分为完全非对称线性和非对称非完整线性两种。
所谓“完全非对称曲线”的含义就是第一缓和曲线长和第二缓和曲线长不等，而第一缓和曲线和第二缓和曲线起点处的半径为无穷大。
所谓“非完整”的含义就是第一缓和曲线和第二缓和曲线的半径不是无穷大，而是有半径的。
关于这点，一般课本教材上没有明确的讲述，查找网上对此问题的解释也是散见于不同的论文著作中，对于测量新手来说，线元法程序是非常适用上手的，但却往往因为遇到不完整缓和曲线的起点或终点的半径判断计算不出来导致坐标计算错误，的确是件令人恼火的事情，在此我就把自己的判断经验做一论述，给用线元法程序的测友们一同分享，当然高手们请一笑而过，也可留下你的经验与大家一起分享交流学习。
先说说完整缓和曲线和不完整缓和曲线以及不对称缓和曲线与对称缓和曲线的概念问题，以免混为一谈.当对于单独一段缓和曲线从其完整与否来讲是分为完整与不完整两类；当对于一个单交点内的两段缓和曲线（即常说的第一缓和曲线和第二缓和曲线而言）又有对称缓和曲线与不对称缓和曲线之分。
不等长缓和曲线的平曲线计算
事路桥 市政项 目设 计管理 与研究 ； 卫 国 （９ ８一） 栗 １６ ， 男， 广西龙 胜 人 ， 总 ， 工 ， 事 公路 工 程 施 工 设 副 高 从 计 、 理与研究 。 管
如 图 ｌ所 示 ，由 于 平 曲 线 两 端 的 缓 和 曲线 不 等 长 ，因而 两边 切 线亦 不 等 长 ，需 分别 进行 计 算 。 当计
ｍ ｅｈ ｄ ｂ ｓ ｈ ｏ ｉ ｎ ａ ｕ ｖ ａｉ ｏ ｈ ｒｎ ｉｉｎ ｃ ｒ ｅｗｉ ｉ ｅ ｅ ｅ ｇ ｈ． ｔ ｏ ｙ ｕ ｉ ｔ ｅｈ ｒ ｏ ｔｌ ｒ ｅｂ ｓｓ ｆｔ ｅｔａ ｓｔ ｕ ｔ ｄｆ ｒｄ ｌｎ ｔ ｇ ｎ ｚ ｃ ｏ ｖ ｈ ｆ
不等 长缓 和 曲线的平 曲线 计算
刘 洁 ，粟 卫 国２
（． １ 桂林市市政 综合设计 院 ，广西 摘 桂林 ５ １０ ；２ 桂林 公路管理局 ４０ １ ． 广西 桂林 ５ １０ ） ４ ０ ２
要 ：讨论 公路与城 市道路设计 中常用不 等长缓和 曲线 的平 曲线 ，以及利用 不 等长缓 和 曲线平 曲线 要素 的坐 标计 算
些 原理 。
２ 不 等长 缓 和 曲线 的 平 曲线 各 要素 计算
如图 ｌ 所示 ，Ｊ 为平 曲线交点 ，Ｌ １ Ｌ ２ Ｄ 与 不等
收稿 日期 ：０ ２ ７—９ ２ ０ 一Ｏ
作者简介 ： 刘
洁 （９０ ， ， １７ 一） 女 广西桂 林市 人 ， 工程 师 ， 主要从
图 １ 切 线长的计算 图
ｌ 引 言
长 ，假 设 Ｌ ２ ， 由于 平 曲 线 两 端 的缓 和 曲线 不 ＞Ｌ １ 等 长 ，因而 在计 算 平 曲线 各 要素 时 ，就 不 能简 单 的套 用 等 长缓 和 曲线 的计算 公 式 。 （ ）切 线长 的计 算 １
平曲线计算
表1一2一1已知工程数据
返回
图1一2一1带缓和曲线的曲线要索
返回
图1一2一2偏角法测设曲线
返回
图1
返回
图1 -2 -5输入已知数据
返回
图1一2一6结算结果显示
返回
图1一2一7选定单元格
返回
图1一2一8拉动结果
返回
图1一2一9计算显示
切线增长值
下一页 返回
学习情景一平曲线计算的专业知识
切线长 曲线长 或者 其中，圆曲线长 外距 切曲差
上一页 下一页 返回
学习情景一平曲线计算的专业知识
2.曲线主点里程计算 直缓点 缓圆点 曲中点 圆缓点 缓直点 交点
上一页 下一页 返回
学习情景一平曲线计算的专业知识
二、圆曲线带有缓和曲线的测设方法
下一页 返回
学习情景二Excel编写的计算过程
5.拉动单元格 将鼠标放在选定单元格的右下角，使其变成“+”号，然后向下
拉动，拉动过程中，单元格中会出现错误，可以不必理会。如图1一2 一8所示。 6.填写已知条件
填写已知条件JD桩号、半径R、缓和曲线长度LS ,曲线偏角PJ， 就可计算出相应的曲线要素和主点桩号，如图1 -2 -9所示
任务二平曲线计算
学习情景一平曲线计算的专业知识 学习情景二Excel编写的计算过程 实践教学情景Excel工程应用一
学习情景一平曲线计算的专业知识
一、曲线要素的计算
以单交点平曲线为例，如图1 -2一1所示，只设一个JD点的平 曲线成为单交点平曲线，主要计算要素已经给定，但是为方便进行平 曲线的计算，下面先进行复习。 1.曲线要素的计算 已知条件:JD桩号、半径R,偏角PJ、缓和曲线LS 求解:切线长T,曲线长L，外距E，切曲差D, ZH, HY, QZ, YH, HZ 计算公式如下: 内移值
浅析路线设计缓和曲线合理长度取值范围
浅析路线设计缓和曲线合理长度取值范围0 引言缓和曲线是公路平面线形设计中采用的最常用的线形之一。
缓和曲线是在直线和圆曲线之间插入一段曲率半径由+∞逐步渐变为R的回旋线，不仅符合汽车转弯时的行车轨迹，而且使公路的平面线形顺适美观，具有良好的视觉效果和心理作用感。
在缓和曲线设计中，缓和曲线缓和段长度的取值是影响道路平面线形视觉质量的重要因素之一。
如果缓和曲线缓和段长度取值太短，不仅不能起到曲率渐变的作用，而且缓和段与剩余圆曲线的衔接和搭配极不协调，行车视觉效果比较差；如果缓和曲线缓和段长度取值太长，无论从线形组合效果还是弯道超高和加宽设计方面都存在着较大的不足。
因此，合理确定和设计缓和曲线缓和段的长度，是平面缓和曲线线形设计需要解决的重要问题之一。
目前无论是专业参考资料，还是公路线形设计使用的设计软件中，都没有给出合理确定缓和段长度的计算方法，只是按照《公路工程技术标准》（以下简称《标准》）的设计要求，取大于或等于缓和曲线最小缓和段长度即可，而没有考虑不同平曲线半径条件下缓和曲线缓和段长度的合理取值。
缓和段长度对平面线形质量的影响分析在平面缓和曲线设计中，缓和曲线缓和段长度的取值将直接影响到平面线形的视觉质量和行车效果。
道路平面线形由由直线和曲线组合而成，曲线又分为曲率半径为常数的圆曲线和曲率半径为变数的缓和曲线两种。
对于缓和曲线的取值范围，公路相关规范中均只有最小值的界定，而对于最大值，规范并没有明确，本文根据驾驶员反应操作3s行程、离心加速度变化、考虑超高缓和率所需长度、考虑视觉和线形美学所需长度及公路路线设计规范及平纵组合等原则进行最值拟定，为公路设计提供一定的理论价值。
1 缓和曲线的设置设置缓和曲线的目的在于通过曲率的逐渐变化，适应汽车转向操作的行使轨迹及路线的顺畅，缓和行车方向的突变和离心力的突然产生；使离心加速度逐渐变化，不致产生侧向冲击，并缓和超高，作为超高变化的过渡段，来减少行车震荡。
缓和曲线设置
一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间，由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1．缓和曲线的作用1）便于驾驶员操纵方向盘2）乘客的舒适与稳定，减小离心力变化3）满足超高、加宽缓和段的过渡，利于平稳行车4）与圆曲线配合得当，增加线形美观2．缓和曲线的性质为简便可作两个假定：一是汽车作匀速行驶；二是驾驶员操作方向盘作匀角速转动，即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A2/ρ（A：与汽车有关的参数）ρ=C/sC=A2由上式可以看出，汽车行驶轨迹半径随其行驶距离递减，即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比，此方程即回旋线方程。
3．回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令：ρ=R，l h=s 则 l h=A2/R4．缓和曲线最小长度缓和曲线越长，其缓和效果就越好；但太长的缓和曲线也是没有必要的，因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定：1）根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性，就需控制离心力的变化率。
a1=0,a2=v2/ρ,a s=Δa/t≤0.62）依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3）根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡（即超高渐变率）是指在缓和曲线上设置超高缓和段后，因路基外侧由双向横坡逐渐变成单向超高横坡，所产生的附加纵坡。
4）从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间，视觉效果好。
《公路工程技术标准》规定：按行车速度来求缓和曲线最小长度，同时考虑行车时间和附加纵坡的要求。
5．直角坐标及要素计算1）回旋线切线角（1）缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
βx=s2/2Rl h（2）缓和曲线的总切线角β=l h/2R.180/л2）缓和曲线直角坐标任意一点P处取一微分弧段ds，其所对应的中心角为dβx dx=dscosβxdy=dssinβx3）缓和曲线常数（1）主曲线的内移值p及切线增长值q内移值：p=Y h-R(1-cosβh)=l h2/24R切线增长值：q=X h-Rsinβh=l h/2-lh3/240R2（2）缓和曲线的总偏角及总弦长总偏角：βh=l h/2R总弦长：C h=l h-l h3/90R2O为圆曲线的圆心，圆曲线所对圆心角（等于公路偏角）。
线路工程测量-缓和曲线
小结
1、困难条件下曲线的测设 1）控制点（JD、ZH、HZ）无法置 镜——在JD、HY、YH、切线上任 一点、曲线上任一点置镜测设 2）曲线遇障碍时的测设——切线方向
2、复杂曲线的测设 1）复曲线——曲线要素的计算 2）回头曲线
3、中桩坐标的计算——坐标转换
34
思考题
1、在HY点置镜前测圆曲线如何确定切线方向？ 2、副交点有二个，能否有三个呢？ 3、什么是复曲线？ 4、已知：交点里程为K2+849.27，圆曲线半径
17
思考题
1、缓和曲线任意点的半径？ 2、缓和曲线常数？ 3、缓和曲线要素计算公式？ 4、加入缓和曲线后圆曲线与曲线有什么变化？ 5、已知：交点里程为K2+849.27，圆曲线半径
R=400m，缓和曲线长70m,转向角为 27°45′08″， 计算：1）缓和曲线常数、要素
2）缓和曲线主点里程 3）按整桩号法计算各中桩坐标 4）按整桩号法计算各中桩偏角和弦长
（2）置镜A点，后视P点反拨角r+βA 定向，得A点切线方向
A点在缓和曲线：
A
l
2 A
2Rl
A点在圆曲线：
A
l 2R
lA l R
21
一、困难条件下的曲线测设
（二）曲线上遇障碍时的测设
1、等量偏角法 1）测至3点后，4点不通视 2）置镜于3点，照准0点，度盘读数设为1800，转动望远镜为00时，视线在0~3方向上， 读数为δ3视线在3点的切线上 3）拨4、5点偏角，视线就在点4、5的方向上 4）测至6点后，视线受阻 5）置镜于5点，照准3点，度盘读数设为1800 + δ3 ，转动望远镜为00时，视线在0~5方向 上，读数为δ5视线在5点的切线上 6）读数为δ6视线在6点的切线，向前测设
道路工程测量课件第8章第4节 缓和曲线测设
的曲线，这种曲线称为缓和曲线，如图所示。
程
三、缓和曲线参
数
四、利用手机软
件进行道路中桩
坐标计算
五、利用计算机
计算缓和曲线
六、利用手机计
算缓和曲线
缓和曲线
新形态一体化
《道路工程测量》
第8章 道路中线测量
第4节 缓和曲线测设
根据《城市道路工程设计规范》（CJJ 37-2012）中
6.2.4的规定，直线与圆曲线或大半径圆曲线与小半径圆曲线
=2527528.374+146.563×cos55°43′18″-12.023×sin55°43′18″
=2527600.986m
YQZ=YZH+ x ×sinαZH-JD1+ y ×cosαZH-JD1
=521645.357+146.563×sin55°43′18″+12.023×cos55°43′18″
第8章 道路中线测量
第4节 缓和曲线测设
（7）选择“程序”，点击“批量计算”，勾选“全线”，
输入“桩间距如20”，选择中桩“计算”，结果排序“左中
右隧或中左右”，如果要计算边桩，则左边桩选择“手动输
入”，输入“左偏距如20”，同理，输入“右偏距如20”（
如果不计算边桩，则不需要输入）；勾选“整桩”、“主点
=2527528.374+79.949×cos55°43′18″-2.132×sin55°43′18″
=2527571.641m
YHY=YZH+ x ×sinαZH-JD1+ y ×cosαZH-JD1
=521645.357+79.949×sin55°43′18″+2.132×cos55°43′18″
(完整版)平曲线要素计算.doc
一、路线转角、交点间距的计算（一）在地形图上量出路线起终点及各路线交点的坐标：QD 23810,27180 、JD1 23996，26977 、JD 2 24684，26591 、 JD3 248480，25885 、JD4 25350，25204 、ZD 2606225783，（二）计算公式及方法设起点坐标为 QD X0 ,Y0，第 i 个交点坐标为 JD i X i ,Y i , i 1,2,3,4, 则坐标增量 DX X i X i 1, DY Y i Y i 1交点间距 D (DX )22 DY象限角arctanDYDX方位角 A 是由象限角推算的：象限DX DY A 象限DX DY A Ⅰ+ + A Ⅲ- - A 180o Ⅱ- + A 180o Ⅳ+ - A 360o转角i A i Ai 11.QD与 JD1之间：坐标增量 DX X1 X 0 =23966 23810=186 0DY Y1 Y0 26977 27180 203 0交点间距 D (DX )2 DY 21862 2032275.33m象限角arctan DY arctan 203 47.502 oDX 186方位角 A0 360o 360o 47.502o 312.498o 2.JD1与 JD 2之间：坐标增量 DX X 2 X1 =24684 23966=688 0DY Y2 Y1 26591 26977 386 0交点间距 D 2 222象限角arctanDYarctan 386 29.294 oDX 688 方位角 A 1 360o360o29.294o 330.706o转角 1 =A 1 A 0 330.706o 312.498o 18.208o3. JD 2 与JD 3之间：坐标增量 DXX 3 X 2 =24840 24684=156 0 DYY 3 Y 2 25885 26591706 0交点间距 D(DX )221562 706 2DY 723.03m象限角arctanDYarctan70677.54oDX156方位角 A 2 360o360o 77.54o 282.46o转角 2 =A 2 A 1 282.46o 330.706o 48.246 o4. JD 3与 JD 4 之间：坐标增量 DXX 4 X 3 =25350 24840=510 0DY Y 4 Y 3 25204 25885681 0交点间距 D(DX )225102681 2DY850.8m象限角arctan DYarctan 510 53.171oDX 681方位角 A 3 360o360o 53.171o306.829o转角 3 =A 3 A 2 306.829 282.46 24.369o5. JD 4 与 ZD 之间：坐标增量 DXX X 4 =26062 25350=712 0DYYY 4 2578325204 579 0 交点间距 D (DX )2 27122 5792 917.706mDY 象限角arctanDYarctan57939.118 oDX712方位角 A 039.118o转角o o o二、各平曲线要素的计算( 一) JD 1曲线要素计算取R 800m ,设计速度为 60km/ h ,JD1桩号为K0+275.33，转角1.缓和曲线长度 L S，则：L SV 30.0366030.036 9.72(m)R 800L SV 603 50(m)33.63.6L S R~ R 800 ~ 800 88.89 ~ 800(m) 9 9取整数，采用缓和曲线长120m（《公路工程技术标准》规定：V 最小缓和曲线长度为50m ）.2.圆曲线内移值 RL2S L4S 1202 120 40.75(m)R2688 (R)3 24 800 2688 (800) 324R3.总切线长T hL S L3S 120 120359.989(m)先求 q240R2 2 240 80022所以 T h (R R) tan q (800 18.208 59.989 188.31(m)0.75) tan2 24.曲线总长度 L hL S =0.0752RL h ( 2 ) R 2L S ? R+L S 374.22(m)180 1805.五个基本桩号JD 1 K0+274.33) T h 188.31ZH K 0+087.02 18.208o60 km h 时，) L SHY1) ( L h 2L S )YH1) L SHZ 11L h) 2QZ1120.00K0+207.02134.22 K0+341.24120.00 K0+461.24187.11 K0+274.13E h ( R R)sec R (800 0.75sec 18.208800 10.97(m)2 2超距 D 2T L h 2 188.31 374.22 2.4(m) 。
平曲线超高与缓和曲线
·7 ·
现 。确定缓和曲线长度的主要因素是曲率缓和与超 高缓和 ,而加宽缓和不作为缓和曲线长度的控制因 素 。《标准》3. 0. 13 条“缓和曲线中”规定 “: 缓和曲 线采用回旋线 ,缓和曲线的长度应根据计算行车速 度求算 ,并尽量采用大于表 3. 0. 13 所列数值 。”标准 中规定的缓和曲线的最小长度主要从曲率缓和考 虑 ,以保证驾驶员从容行驾驶和乘车舒适为目的 ,用 3s 行程作为缓和曲线最低限度的控制值 。该值只 有在地形 、地物受到严格限制时才予采用 。在一般 情况下 ,当圆曲线部分需设置超高时 ,缓和曲线还应 满足超高过渡的要求 ,缓和曲线的长度至少能完全 包括超高缓和段的长度 ,但如果按超高渐变率求出 的缓和段长度比缓和曲线还要长时 ,则必须延长缓 和曲线路段 。通常情况下缓和曲线是能满足超高缓 和要求的 。但采用缓和曲线最小长度连接小半径曲 线时 ,由于行车道外边缘相对坡度的变化受行车道 宽度的限制 ,缓和曲线长度能否满足超高缓和段的 要求 ,应进行复核验算 。在实际设计工作中 ,缓和曲 线并不单纯作为曲率和超高变化的缓和段 ,而应作 为在视觉上获得圆滑线形的条件 。为了满足视觉条 件的要求 ,应在圆曲线半径 1 - 1/ 3 范围内选取回旋 曲线的参数 A ,缓和曲线长度随着圆曲线半径的增 大而增长 ,以利于视觉和线形美学上的要求 ,使线形 美观协调 。 6 设计方法
1 前言 公路几何线形是将路线平面 、纵断面 、横断面结
合在一起的三维立体线形 ,设计时应综合考虑 ,保证 路线总体的均衡连续性 。设计公路线形时 ,在保证
ቤተ መጻሕፍቲ ባይዱ
汽车行驶的安全性 、舒适性和经济性的同时 ,还应考 虑线形与地形 、地物 、景观等自然条件相协调以及技 术和经济的合理性 。缓和曲线和超高设计是公路几 何线形的重要组成部分 ,对于保证线形的顺适 、流
平曲线认识
第三讲公路平面坐标计算1、平曲线认识道路是一个三维空间的工程结构物，它的中线是一个空间曲线，叫路线，其在水平面的投影就是平面线形。
道路平面线形由于受到沿线地形、地质、水文、气候等自然条件和人为条件的制约而改变方向。
在路线平面方向的转折处为满足行车要求，需要用适当的曲线把前、后直线连接起来，这种曲线称为平曲线。
平曲线包括圆曲线和缓和曲线。
①圆曲线要素主点桩号计算：ZY点里程=JD点里程-TQZ点里程=ZY点里程+L/2 YZ点里程=ZY点里程+LJD里程=QZ里程+D/2（校核）②缓和曲线要素切线长： 外距：曲线长：()s s 18022180l aR l a R L h +=+-=πβπ切线加长：q =/2－3/(240R2)圆曲线相对切线内移量：p = 2/(24R)切曲差 Dh = 2T －Lh上式中：α 为线路转向角；β0为缓和曲线角； 其中q 、p 、β0缓和曲线参数。
ZH 桩号 = JD 桩号－T HY 桩号 = ZH 桩号＋QZ 桩号 = HY 桩号＋L/2YH 桩号 = QZ 桩号＋L/2 = HY 桩号＋L = ZH 桩号＋＋LHZ 桩号 = YH 桩号＋= ZH 桩号＋LhJD 桩号 = ZY 桩号－Th ＋Dh （检核）m)2)(（q tgp R T ++=α）（m 2sec)(R p R E -+=αLs Ls Ls Ls Ls Ls注意：上面计算需要大家掌握主点桩号计算，五大主点：ZH、HY、QZ、YH、HZ，还会遇到一些特殊点例如起点QD、终点ZD、公切点GQ。
可以判断下图即可。
重点知识必须掌握（线元法基础）：直线：曲率为0，起终点半径无穷大。
圆曲线：具有一定曲率半径的圆弧，半径为固定值。
缓和曲线：在直线与圆曲线之间或两个不同半径的圆曲线之间设置的曲率连续变化的曲线（指从直线上半径无穷大到圆曲线的定值之间曲率半径逐渐变化的过渡段），我国公路缓和曲线的形式采用回旋线。
（曲率为半径的倒数）A1,A2——缓和曲线参数R——圆曲线半径Ls1,Ls2——缓和曲线长度一段完整缓和曲线满足公式：A²=R x Ls1，A²=R x Ls2入缓和曲线：从ZH点到HY点，A固定不变，随着Ls1的增大，半径从∞减小到R出缓和曲线：从YH点到HZ点，A固定不变，随着Ls2的减小，半径从R增大到∞如果A²≠R x Ls，那么这段缓和曲线是不完整的，叫做不完整缓和曲线。
缓和段曲线参数及超高、加宽计算
第三节 缓和段一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间，由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1．缓和曲线的作用 1）便于驾驶员操纵方向盘2）乘客的舒适与稳定，减小离心力变化3）满足超高、加宽缓和段的过渡，利于平稳行车 4）与圆曲线配合得当，增加线形美观 2．缓和曲线的性质为简便可作两个假定：一是汽车作匀速行驶；二是驾驶员操作方向盘作匀角速转动，即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A 2/ρ（A ：与汽车有关的参数）ρ=C/s C=A 2由上式可以看出，汽车行驶轨迹半径随其行驶距离递减，即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比，此方程即回旋线方程。
3．回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令：ρ=R ，l h =s 则 l h =A 2/R4．缓和曲线最小长度缓和曲线越长，其缓和效果就越好；但太长的缓和曲线也是没有必要的，因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定：1）根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性，就需控制离心力的变化率。
a 1=0,a 2=v 2/ρ,a s =Δa/t ≤0.6 RVl h 3035.0≥2）依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s) 2.16.3V t V vt l h ===3）根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡（即超高渐变率）是指在缓和曲线上设置超高缓和段后，因路基外侧由双向横坡逐渐变成单向超高横坡，所产生的附加纵坡。
ph l c h ≥4）从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间，视觉效果好。
《公路工程技术标准》规定：按行车速度来求缓和曲线最小长度，同时考虑行车时间和附加纵坡的要求。
5．直角坐标及要素计算 1）回旋线切线角（1）缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
道路工程测量(圆曲线缓和曲线计算公式)
道路工程测量( 圆曲线缓和曲线计算公式)内容：理解线路勘测设计阶段的主要测量工作 (初测控制测量、带状地形图测绘、中线测设和纵横断面测量)；掌握路线交点、转点、转角、里程桩的概念和测设方法；掌握圆曲线的要素计算和主点测设方法；掌握圆曲线的切线支距法和偏角法的计算公式和测设方法；了解虚交的概念和处理方法；掌握缓和曲线的要素计算和主点测设方法；理解缓和曲线的切线支距法和偏角法的计算公式和测设方法；掌握路线纵断面的基平、中平测量和横断面测量方；了解全站仪中线测设和断面测量方法。
重点：圆曲线、缓和曲线的要素计算和主点测设方法；切线支距法和偏角法的计算公式和测设方法；路线纵断面的基平、中平测量和横断面测量方法—难点：缓和曲线的要素计算和主点测设方法；缓和曲线的切线支距法和偏角法的计算公式和测设方法。
§ 9.1交点转点转角及里程桩的测设一、道路工程测量概述 6 x:分为：路线勘测设计测量(route reconnaissance and design survey) 和道路施工测量(road construction survey) 。
(一)勘测设计测量(route reconnaissance and design survey)分为：初测(preliminary survey) 和定测(location survey)1 、初测内容：控制测量(control survey) 、测带状地形图(topographical map of a zone)和纵断面图(profile) 、收集沿线地质水文资料、作纸上定线或现场定线，编制比较方案，为初步设计提供依据。
2、2、定测内容：在选定设计方案的路线上进行路线中线测量(center line survey) 、测纵断面图(profile) 、横断面图(cross-section profile) 及桥涵、路线交叉、沿线设施、环境保护等测量和资料调查，为施工图设计提供资料。
缓和曲线设置
一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间，由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1．缓和曲线的作用1）便于驾驶员操纵方向盘2）乘客的舒适与稳定，减小离心力变化3）满足超高、加宽缓和段的过渡，利于平稳行车4）与圆曲线配合得当，增加线形美观2．缓和曲线的性质为简便可作两个假定：一是汽车作匀速行驶；二是驾驶员操作方向盘作匀角速转动，即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A2/ρ（A：与汽车有关的参数）ρ=C/sC=A2由上式可以看出，汽车行驶轨迹半径随其行驶距离递减，即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比，此方程即回旋线方程。
3．回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令：ρ=R，l h=s 则 l h=A2/R4．缓和曲线最小长度缓和曲线越长，其缓和效果就越好；但太长的缓和曲线也是没有必要的，因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定：1）根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性，就需控制离心力的变化率。
a1=0,a2=v2/ρ,a s=Δa/t≤0.62）依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3）根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡（即超高渐变率）是指在缓和曲线上设置超高缓和段后，因路基外侧由双向横坡逐渐变成单向超高横坡，所产生的附加纵坡。
4）从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间，视觉效果好。
《公路工程技术标准》规定：按行车速度来求缓和曲线最小长度，同时考虑行车时间和附加纵坡的要求。
5．直角坐标及要素计算1）回旋线切线角（1）缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
βx=s2/2Rl h（2）缓和曲线的总切线角β=l h/2R.180/л2）缓和曲线直角坐标任意一点P处取一微分弧段ds，其所对应的中心角为dβx dx=dscosβxdy=dssinβx3）缓和曲线常数（1）主曲线的内移值p及切线增长值q内移值：p=Y h-R(1-cosβh)=l h2/24R切线增长值：q=X h-Rsinβh=l h/2-lh3/240R2（2）缓和曲线的总偏角及总弦长总偏角：βh=l h/2R总弦长：C h=l h-l h3/90R2O为圆曲线的圆心，圆曲线所对圆心角（等于公路偏角）。
缓和曲线
在此引入一个“虚拟延伸”的观点，让这段这不完整的缓和曲线延伸成一段完整的缓和
曲线至 HZ′（桩号 K40＋440.720，注意这点不在设计线路上）
知β＝（90×33.5302）/(190×π×63.530)= 2°40′5.89″
B?
484443.327 EXE
Y=484448.4151
EXE
I=222.6015582
在圆曲线段，你正反算都可以，所要注意是起始方位角的不同，半径正负号的变化。
以上讨论了基本曲线的六种情况的中桩坐标计算，应该说上面两套程序都可以解决了，
如果对于不对称的缓和曲线所组成的基本曲线以上程序完全适用。
以上都是讨论的完整的缓和曲线，如果对于一段不完整的缓和曲线（在卵形曲线中经常
-39703.767 EXE
R？
以上同理
35 EXE
M？
30 EXE
N？
191°52′45″－180 EXE
I＝15.81260512 注意这是反向方位角
EXE
A?
3103847.328 EXE
T?
36.497 EXE
X=3103823.3
EXE
B?
484443.327 EXE
Y=484438.5534.
L5 I=N+( L-K-M/2)×180/R/ π◢
L6 GOTO 0 R——曲线半径 L——待求点桩号 K——ZH 点桩号 M——缓和曲线长
姚永庆
N——起始方位角
T——切线长
I——待求点切线方位角
第 L3，L4 行太长太复杂，仔细看一下它有好多相同的计算语段，只要多用几个存储键
就行了。
操作
显示
说明
缓和曲线
§11-6 虚交点的测设 11一、单圆曲线虚交的测设 1．圆外基线法
a T ′ = Rtg 4
测设时由ZY和YZ点分别沿切线 量出T’得M点和N点，再由M点或N 点沿MN或NM方向量T’即得QZ点。 曲线主点定出后，即可用切线 切线 支距法或偏角法进行曲线详细测设。 支距法或偏角法
§11-6 虚交点的测设 11一、单圆曲线虚交的测设
①在ZH点安置经纬仪（对中、整平），用盘左瞄准JD，将水 ZH点安置经纬仪（对中、整平），用盘左瞄准JD， 点安置经纬仪 ），用盘左瞄准JD 平度盘的读数配到0 00′00″； 平度盘的读数配到0°00′00″； ②转动照准部到度盘读数为δ1，从ZH点量取分段弦长C，定 转动照准部到度盘读数为δ1， ZH点量取分段弦长C δ1 点量取分段弦长 出1点； δi，从第i ③转动照准部到度盘读数为 δi，从第i－1点量取分段弦长 与此方向交出第i C，与此方向交出第i点； ④另一半缓和曲线在HZ点上按同样方法测设。 另一半缓和曲线在HZ点上按同样方法测设。 HZ点上按同样方法测设
dx = dl ⋅ cos β dy = dl ⋅ sin β
l5 x =l − 2 2 40R ls 3 l y= 6Rls
dy x dx
§11-5 带有缓和曲线的平曲线测设 11一、缓和曲线
2．回旋线型缓和曲线公式 (3) 缓和曲线的参数方程
l5 x =l − 40R2ls2 l3 y= 6Rls
3 ls x0 = ls − 40R2 2 l y0 = s 6R
y
y0 x0 x
§11-5 带有缓和曲线的平曲线测设 11二、带有缓和曲线的平曲线主点测设 内移值p与切线增值q 1．内移值p与切线增值q的计算
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
➢3. 缓和曲线数学表达式
3.4 缓和曲线
3.4.3 缓和曲线的最小长度
1．离心加速度的变化率
▪ 离心加速度的变化率as： （离心加速度随时间的变化率）
as
a t
ቤተ መጻሕፍቲ ባይዱ
v2 Rt
在等速行驶的情况下： t Ls v
as
v3 RLs
0.0214
V3 RLs
满足乘车舒适感的缓和曲线最小长度 ：
Lsmin
0.0214
x
x = q + R sinm (m) y = p + R (1 - cosm) (m)
式中：
m
δ
0
28.6479(
2lm R
Ls
)
()
δl—m———lm圆所曲对线应上的任圆意心点角m（至ra缓d）和，曲δ线终lRm点的弧。长（m）；
例题：已知平原区某二级公路有一弯道， JD=K2+536.48，
一般认为当p≤0.10时，即可忽略缓和曲线。如按3s行程计算缓和曲 线长度时，若取p=0.10，则不设缓和曲线的临界半径为：
Rh
Ls 2 24 p
1 24
1 0.10
( V )2 1.2
0.289V
2
设计速度
3.4.4 缓和曲线的省略
在直线和圆曲线间设置缓和曲线后，圆曲线产生了内移，其位移值为p， p Ls2 24R
3.4.4 切线支距法敷设曲线计算方法
1. 敷设回旋线公式：
O
x
l
l5 40 A4
l
l5 40 R 2 L2S
β
HZ
0
β00δ
p R(1-cosφ )
y
l3 6 A2
l7 336 A6
l3 6RLS
φ
R
YH
M
式中：l——回旋线上任意点m至缓和曲线终Z点H 的弧长（mHY）y。
αn
q
Rsinφ
n
2. 敷设带有回旋线的圆曲线公式：
➢ 偏角α右=15°28′30″，半径R=250m，缓和曲线长度Ls=70m ➢ 要求：（1）计算曲线主点里程桩号；
①小圆曲线按规定设置相当于最小回旋线长的回旋线时，其大圆与小圆 的内移值之差不超过0.10m。
②设计速度≥80km/h时，大圆半径（R1）与小圆半径(R2)之比小于1.5。 ③设计速度<80km/h时，大圆半径（R1）与小圆半径(R2)之比小于2。
例3-1：某平原区二级公路上有一平曲线，半径为420m。试设计计算该平 曲线的最小缓和曲线长度。
▪由《规范》表7.5.3（5.4.6）查得： i ib 0.06
▪由《规范》表7.5.4（5.4.7）查得：p=1/150
Ls min
Bi p
7.5 0.06 1 / 150
67.50
（4）按视觉条件计算
Ls min
R 9
420 9
46.67
▪ LS = R = 420 ▪ 综合以上各项得：Lsmin = 67.50m， ▪ 最终取5的整倍数得到70m。
0.289V
2
《标准》规定：当公路的平曲线半径小于不设超高的最小半径时，应设 缓和曲线。
四级公路可不设缓和曲线。
《规范》规定可不设缓和曲线的情况： （1）在直线和圆曲线间，当圆曲线半径大于或等于《标准》规定的 “不设超高的最小半径”时； （2）半径不同的同向圆曲线间，当小圆半径大于或等于“不设超高 的最小半径”时； （3）小圆半径大于表3.5.1中所列半径，且符合下列条件之一时：
V3 as R
我国公路计算规范一般建议as≤0.6
V3 Lsmin 0.036 R
2．驾驶员的操作及反应时间
缓和曲线不管其参数如何，都不可使车辆在缓和曲线上的行驶时间过短 而使司机驾驶操纵过于匆忙。
一般认为汽车在缓和曲线上的行驶时间至少应有3s
V Lsmin 1.2
《标准》按行驶时间不小于3s的要求制定了各级公路缓和曲线最小长度。
3.4 缓和曲线
（第3讲）
教学内容：
➢1. 缓和曲线的最小长度确定 ➢2. 回旋线参数A ➢3. 缓和曲线的省略 ➢4.切线支距法敷设曲线
重点解决的问题：
怎样确定缓和曲线长度（或回旋线参数A）？
什么情况下可以不设置缓和曲线？
上次课内容回顾：
怎样计算带缓和曲线的平曲线的里程桩号➢及1.切缓线和支曲距线值作？用 ➢2. 缓和曲线线形
R2 A2 R2 9
R 9
LS
R
回旋线过长β大于29°时，圆曲线与回旋线不能很好协调。
适宜的缓和曲线角是β0=3°～29°。
3.4.4 缓和曲线的省略
在直线和圆曲线间设置缓和曲线后，圆曲线产生了内移，其位移值为p， p Ls2 24R
在Ls一定的情况下，p与圆曲线半径成反比，当R大到一定程度时，p 值将会很小。这时缓和曲线的设置与否，线形上已经没有多大差异。
在Ls一定的情况下，p与圆曲线半径成反比，当R大到一定程度时，p值 将会很小。这时缓和曲线的设置与否，线形上已经没有多大差异。
一般认为当p≤0.10时，即可忽略缓和曲线。如按3s行程计算缓和曲线 长度时，若取p=0.10，则不设缓和曲线的临界半径为：
Rh
Ls 2 24 p
1 24
1 0.10
( V )2 1.2
▪解：（1）按离心加速度的变化率计算 ▪ 由《标准》表2.0.5查得=80km/h
V3
803
Ls min 0.036
R
0.036 43.89 420
▪（2）按驾驶员的操作及反应时间计算
Ls min
V 1.2
80 1.2
66.67
▪（3）按超高渐变率计算
▪由《标准》表3.0.2（5.2.1）可得：B=2×3.75=7.50m；
4. 视觉条件
在一般情况下，特别是当圆曲线半径较大时，车速较高时，应该使用 更长的缓和曲线。
回旋线参数表达式： A2 = R·Ls
根据国外经验，当使用回旋线作为缓和曲线时，回旋线参数A和所连接 的圆曲线应保持的关系式一般为：R/3≤A≤R
根据经验, 当R在100m 左右时, 通常取 A=R；如果R小于100m, 则选择A 等于R或大于R。反之, 在圆曲线较大时, 可选择A在R/3左右, 如R超过了 3000m, A可以小于R/3。
《城规》制定了城市道路的最小缓和曲线长度，如表3-7。
3．超高渐变率
超高渐变率——在超高过渡段上，路面外侧逐渐抬高, 将在外侧形成一 个附加坡度, 这个附加坡度称为超高渐变率。
当圆曲线上的超高值一定时, 这个附加坡度就取决于缓和段的长度。
p Bi Lc
Lsmin
Bi p
式中：B——旋转轴至行车道（设路缘带时为路缘带）外侧边缘的宽度； Δi——超高坡度与路拱坡度代数差（%）； p ——超高渐变率，即旋转轴线与行车道外侧边缘线之间的相对坡度。