缓和曲线、圆曲线测设计算例题

带有缓和曲线的圆曲线逐桩坐标计算例题

带有缓与曲线的圆曲线逐桩坐标计算例题:某山岭区二级公路,已知交点的坐标分别为JD1(40961、914,91066、103)、JD2(40433、528,91250、097)、JD3(40547、416,91810、392),JD2里程为K2+200、000,R=150m,缓与曲线长度为40m,计算带有缓与曲线的圆曲线的逐桩坐标。

(《工程测量》第202页36题)解:(1)转角、缓与曲线角、曲线常数、曲线要素、主点里程、主点坐标计算方法一:偏角法(坐标正算)(2)第一缓与段坐标计算 228370'''= β 308416012'''= α(3)圆曲线段坐标计算 1490153-'''==βαα(4)第二缓与段坐标计算 228370=桩号弧长里程里程桩点ZY -=i l偏角0231β⎪⎪⎭⎫ ⎝⎛=∆S i i L l 方位角 i c i ∆-=12αα (左转) 弦长22590Sii i L R l l c -= Xi i c i ZH i c X X αcos +=Yiic i ZH i c Y Y αsin +=ZH:K2+048、5620 160 48 03 40576、543 91200、296 +060 11、438 0 12 30 160 35 33 11、438 40565、754 91204、097 +080 31、438 1 34 23 159 13 40 31、438 40547、149 92211、446 HY K2+088、562402 32 47 158 15 1639、96840539、41991215、104桩号弧长里程里程桩点HY -=i l偏角π︒=∆90R l i i方位角(左转) i JD ZY c i∆=---0βαα弦长ii R c ∆=sin 2X i c i HY i c X X αcos += Yici HY i c Y Y αsin +=HY: K2+088、5620βαα-=-JD ZY 切线153 09 41 40539、419 91215、104 +100 11、438 2 11 04 150 58 37 11、435 40529、420 91220、652 +120 31、438 6 00 15 147 09 26 31、38040513、055 91232、122+140 51、438 9 49 26 143 20 15 +16071、438 13 38 37 139 31 04QZ:K2+176、28087、718 16 45 10136 24 3186、47340476、789 91274、728+180 91、438 +200 111、438 +220 131、438 +240 151、438 +260171、438YH:K2+263、998175、43633 30 21119 39 20165、60640457、480 91359、018桩号弧长里程里程桩点-Z H l i =偏角0231β⎪⎪⎭⎫⎝⎛=∆S i i L l 方位角i c i∆+=32αα(左转)弦长22590Si i i L R l l c -=X ii c i i c X X αcos HZ +=Y ii c i HZ i c Y Y αsin +=方法二:切线支距法(坐标系转换)(2)第一缓与段坐标计算308416012'''= α1212sin cos ααy x X X ZH i ++= 1212cos sin ααy x Y Y ZH i -+=(本题为左转曲线)228370'''= β p = 0.444m q = 19.988m308416012'''= α ZH (40576、543 , 91200、296) sin cos ααy x X X ++= cos sin ααy x Y Y -+=YH: K2+263、99840 2 32 47 261 03 24 39、968 40457、480 91359、018 +280 23、998 0 55 00 259 25 37 23、996 40459、290 91374、911 +300 3、998 0 01 32258 30 373、998 40462、89791394、582HZ K2+303、99832α258 30 3740463、693 91398、500桩号里程里程桩点ZY -=i l 22540s L R l l x -=33733366SS L R l RL l y -= X iY iZH: K2+048、5620 40576、543 91200、296 +060 11、438 11、438 0、042 40565、755 91204、096 +080 31、438 31、417 0、863 40547、156 92211、446 HYK2+088、5624039、9291、77840539、41991215、104桩号里程里程桩点HY -=i l0180βπϕ+=Rl i q R x +=ϕsin P ()p R y +-=ϕcos 1PX i Y iHY:K2+088、56240539、419 91215、10473037812'''= α2323sin cos ααy x X X HZ i +-= 2323cos sin ααy x Y Y HZ i --=(本题为左转曲线)。

带有缓和曲线的圆曲线逐桩坐标计算例题

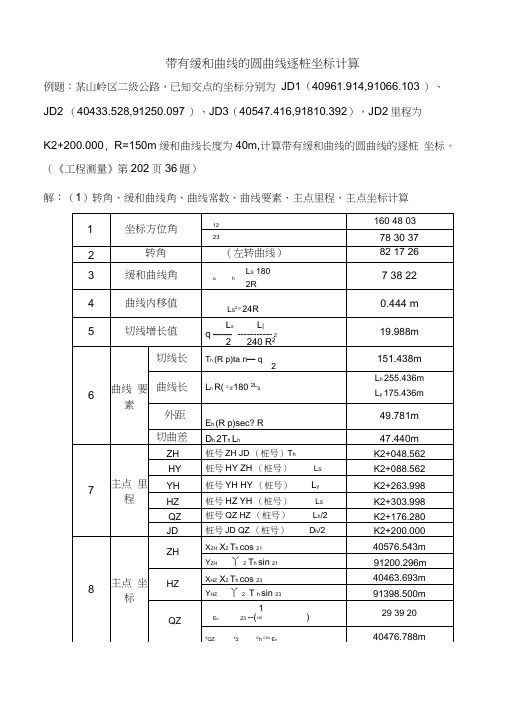
带有缓和曲线的圆曲线逐桩坐标计算例题：某山岭区二级公路，已知交点的坐标分别为JD1（40961.914,91066.103 ）、JD2 （40433.528,91250.097 ）、JD3（40547.416,91810.392），JD2里程为K2+200.000, R=150m缓和曲线长度为40m,计算带有缓和曲线的圆曲线的逐桩坐标。

（《工程测量》第202页36题）解：（1）转角、缓和曲线角、曲线常数、曲线要素、主点里程、主点坐标计算方法一：偏角法（坐标正算）（2）第一缓和段坐标计算°7382212160 48 03桩号弧长l i 桩点里程-ZY 里程偏角21 l ii3 LS方位角C i12i（左转）弦长 c I 丄90R 2L 2XiXiXZHqCOS C iYiY Y ZH C i sin c iZH: K2+048.562160 48 0340576.543 91200.296 +060 11.438 0 12 30 160 35 33 11.438 40565.754 91204.097 +080 31.438 1 34 23 159 13 40 31.438 40547.149 92211.446 HY K2+088.562402 32 47158 15 1639.96840539.41991215.104（3）圆曲线段坐标计算切线 ZYJD - o153 09 41桩号弧长li桩点里程-HY里程偏角1 90iiR方位角（左转）弦长C i 2Rsi n iXX X HY C i cos cYY Y HYc ；sin cciZY JD -0 -iHY: K2+088.562切线 153 ZY JD 009 4140539.41991215.104 +100 11.438 2 11 04 150 58 37 11.435 40529.420 91220.652 +120 31.438 6 00 15 147 09 26 31.38040513.05591232.122+140 51.438 9 49 26 143 20 15+16071.438 13 38 37 139 31 04QZ: K2+176.28087.71816 45 10136 24 3186.47340476.78991274.728+180 91.438+200 111.438+220 131.438+240 151.438+260171.438YH:K2+263.998175.43633 30 21 119 39 20 165.606 40457.480 91359.018(4)第二缓和段坐标计算7 38 22方法二：切线支距法(坐标系转换) (2)第一缓和段坐标计算12160 48 03X i X ZH xcos 12 ysin 伐Y Y ZH xsin 12 ycos 12 (本题为左转曲线)(3) 圆曲线段坐标计算7 38 22 p = 0.444m q = 19.988m160 48 03 ZH( 40576.543 , 91200.296)12X i X ZH xcos 12 ysin 12Y Y ZH xsin 12 ycos 12(4)第二缓和段坐标计算1278 30 37X i X HZ XCOS 23 ysin 23 Y Y HZ xsin 23 ycos 23 (本题为左转曲线)。

带有缓和曲线的圆曲线逐桩坐标计算例题

带有缓和曲线的圆曲线逐桩坐标计算
例题：某山岭区二级公路，已知交点的坐标分别为JD1（40961.914,91066.103 ）、JD2 （40433.528,91250.097 ）、JD3（40547.416,91810.392），JD2里程为
K2+200.000, R=150m缓和曲线长度为40m,计算带有缓和曲线的圆曲线的逐桩坐标。

（《工程测量》第202页36题）
解：（1）转角、缓和曲线角、曲线常数、曲线要素、主点里程、主点坐标计算
方法一：偏角法（坐标正算）
（2）第一缓和段坐标计算-0=7 3822 5 = 160 48 03
X Y
(4)第二缓和段坐标计算.0 = 7 38 22
方法二：切线支距法（坐标系转换）
（2）第一缓和段坐标计算
：-12 =160 48 03
X j =X Z H+ xcosot12+ y si n%2X=X ZH+ xs in a12 - yco^t12（本题为左转曲线）
(3) 圆曲线段坐标计算
0=73822 p = 0.444m q = 19.988m
12 =160 48 03 ZH( 40576.543 , 91200.296)
X i = X ZH xcos：12 ysin：12 Y =Y ZH xsin：12一ycos：12
:12=78 30 37
X i =X HZ—xcosc(23 +ysin o(23 Y =Y HZ— xsin53 _yco^t23 (本题为左转曲线)。

缓和曲线计算题集(第二篇)

缓和曲线计算题集2一、已知某道路曲线第一切线上控制点ZD1和JD1，ZD1坐标为：（3162630.051，39389768.043），JD1坐标为（3162606.831，39390001.897）该曲线设计半径R=1000m，缓和曲线长L0=100m，JD1里程为DK0+275.004，转向角α左=23°03′38″。

请计算道路曲线主点ZH、HY、QZ点坐标，及第一缓和曲线和圆曲线上中桩点K0+100、K0+180的坐标，共计算5个点。

解：转角：23 03 38 方位角：275 40 14曲线五大桩里程和坐标一、直缓桩号ZH=00+020.9205 ,坐标X=3162581.7254 , 坐标Y=39390254.7371二、缓圆桩号HY=00+120.9205 ,坐标X=3162593.262 , 坐标Y=39390155.416 ,三、曲中桩号QZ=00+272.1618 ,坐标X=3162626.9124 , 坐标Y=39390008.1136 ,四、圆缓桩号YH=00+423.4031 ,坐标X=3162682.3721 , 坐标Y=39389867.5625 ,五、缓直桩号HZ=00+523.4031 ,坐标X=3162728.9689 , 坐标Y=39389779.0949 ,曲线要素表切线长T1=254.0835 切线角βo1=2.8648外失距E=21.0217 内移量p1=0.4166 曲线长L=502.4826 切垂距q1=49.9958 切曲差Dh=5.6844里程坐标X 坐标YK1+100 3162590.3585 39390176.1337K1+180 3162603.7508 39390097.2838L=80m，二、某平原区二级公路上，有一弯道R=250m，缓和曲线S交点桩号为JD=K17+568.38，偏角α=38°30′00″。

求曲线要素和桩点里程。

公路工程测量放线圆曲线、缓和曲线(完整缓和曲线、非完整缓和曲线)计算解析

公路工程测量放线圆曲线、缓和曲线(包括完整缓和曲线、非完整缓和曲线）计算解析例：某道路桥梁中，A匝道线路。

已知交点桩号及坐标：SP,K9+000(2957714。

490，485768。

924）；JD1，K9+154。

745(2957811。

298，485889.647）；EP，K9+408.993（2957786。

391，486158.713）。

SP-JD1方位角：51°16′25″;转角：右44°00′54.06″；JD1—EP方位角：95°17′20″.由上面“A匝道直线、曲线及转角表”得知：K9+000—K9+116.282处于第一段圆曲线上，半径为385.75m；K9+116.282—K9+151.282处于第一段缓和曲线上，K9+151。

282的半径为300m，缓和曲线要素A1=217.335，Ls1=35m；K9+151.282-K9+216。

134处于第二段圆曲线上，半径为300m；K9+216。

134—K9+251.134处于第二段缓和曲线上，K9+251。

134的半径为1979.5,缓和曲线要素A2=111。

245，Ls2=35m；1 / 11K9+251。

134—K9+408.933处于第三段圆曲线上，半径为1979。

5m。

求：K9+130、K9+200、K9+230、K9+300的中桩坐标，切线方位角,左5米边桩的坐标，右10米边桩的坐标。

解：首先，我们知道要求一个未知点的坐标，必须知道起算点坐标，起算点至未知点的方位角，起算点至未知点的直线距离,然后利用坐标正算的计算公式，就可以直接求出未知点的坐标.那么，关于圆曲线和缓和曲线（包括完整缓和曲线和非完整缓和曲线）的计算，我们需要知道如何求出起算点至圆曲线或缓和曲线上某点的方位角和直线距离.下面，先列出关于圆曲线和缓和曲线中角度和距离计算的相关公式。

2 / 113 / 11y 轴。

过圆曲线上任意点P 的切线与ZY-JD 相交，夹角（切线角）为β，ZY-P 与ZY —JD 的夹角（弦切角）为α，ZY-P 的弧长为L ，ZY —P 的直线距离为d,圆曲线的半径为R 。

圆曲线和缓和曲线坐标推算公式(附带例题)

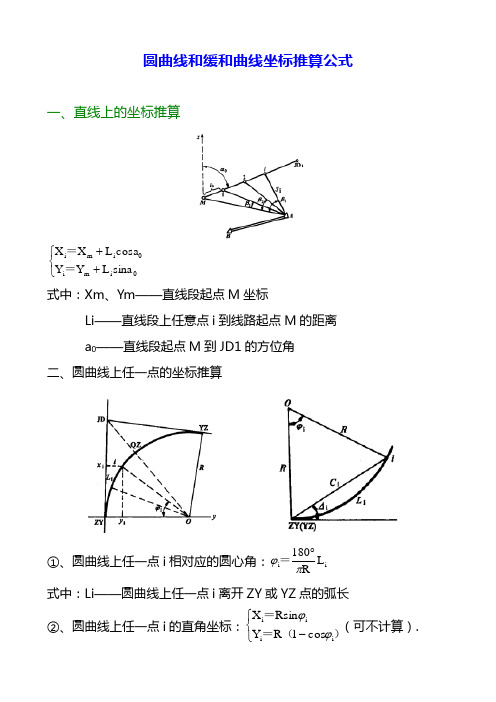
圆曲线和缓和曲线坐标推算公式一、直线上的坐标推算⎩⎨⎧++0i m i0i m i sina L Y Y cosa L X X ＝＝式中：Xm 、Ym ——直线段起点M 坐标Li ——直线段上任意点i 到线路起点M 的距离 a 0——直线段起点M 到JD1的方位角二、圆曲线上任一点的坐标推算①、圆曲线上任一点i 相对应的圆心角：i i L R180πϕ︒＝式中：Li ——圆曲线上任一点i 离开ZY 或YZ 点的弧长②、圆曲线上任一点i 的直角坐标：⎩⎨⎧-）（＝＝i iii cos 1R Y Rsin X ϕϕ（可不计算）.③、圆曲线ZY 或YZ 点到任一点i 的偏角：i ii L R902πϕ︒∆＝＝④、圆曲线ZY 或YZ 点到任一点i 的弦长：)sin(2)2sin(2C i i iR R ∆=ϕ＝⑤、圆曲线ZY 或YZ 点到任一点i 的弦长的方位角：i jd y z jd zy i a a ∆±→→或＝⑥、所以圆曲线上任意点i 的坐标为：⎩⎨⎧++i i YZ ZY iii YZ ZY i sina C Y Y cosa C X X 或或＝＝例题：已知一段圆曲线,R=3500m ，Ls ＝553.1m ，交点里程K50+154.734，ZY 点到JD 方向方位角为A=129°23′18.3″，右偏9°3′15.8″，ZY 点里程K49+877.607，YZ 点里程K50+430.707，起点坐标为x ＝389823.196，y ＝507787.251，求K50+200处中点坐标及左右各偏12.5m 的坐标。

解：K50+200处的曲线长度为Li ＝322.393mK50+200相对应的方位角："'︒⨯⨯︒︒52.39165393.3223500180L R 180i ＝＝＝ππa K50+200相对应的偏角："'︒⨯⨯︒︒∆76.19382393.322350090L R 902i ii ＝＝＝＝ππϕ K50+200到zy 点的弦长：m 279.32276.19382sin 35002Rsin 2C i i ＝＝＝"'︒⨯⨯∆ zy 点到K50+200中桩的方位角："'︒"'︒+"'︒∆+→06.38113276.193823.1823129a a i jd zy i ＝＝＝K50+200左、右偏12.5m 的方位角："'︒︒-"'︒︒-+82.5739449082.573913490a a ＝＝＝左i A "'︒︒+"'︒︒++82.57391349082.573913490a a ＝＝＝右i A所以K50+200处的坐标为：⎩⎨⎧"'︒⨯++"'︒⨯++6484.50802606.381132sin 279.322251.507787sina C Y Y 4354.38960706.381132cos 279.322196.389823cosa C X X i i ZY ii i ZY i ＝＝＝＝＝＝K50+200左偏12.5m 的坐标为：⎩⎨⎧"'︒⨯++"'︒⨯++4656.50803582.573944sin 5.126484.508026sina 5.21Y Y 3256.38961682.573944cos 5.124354.389607cosa 5.21X X i i ＝＝＝＝＝＝左左左左 K50+200右偏12.5m 的坐标为：⎩⎨⎧"'︒⨯++"'︒⨯++5386.50803582.5739341sin 5.126484.508026sina 5.21Y Y 6482.38959882.5739341cos 5.124354.389607cosa 5.21X X i i ＝＝＝＝＝＝右右右右三、缓和曲线上任一点的坐标推算切线角：πβ︒⨯1802RL L s 2i i ＝缓和曲线上任意点i 的偏角：πβδ︒⨯180RL 6L 3s 2i ii ＝＝缓和曲线ZH 或HZ 点到任意点i 的方位角为：i jd HZ jd ZH a a i δ±→→或＝缓和曲线上任意点i 的坐标为：⎪⎪⎩⎪⎪⎨⎧-s 3ii 2s 25i i i 6RL L y L 40R L L x ＝＝缓和曲线ZH 或HZ 点到任意点i 的弦长：22i yx C +＝所以缓和曲线上任意点i 的坐标为：⎩⎨⎧++i i HZ ZH iii HZ ZH i sina C Y Y cosa C X X 或或＝＝例题：已知一段缓和曲线，ZH 点到JD 方向方位角为A=183°17′08.9″，线路左偏43°31′02″，ZH 点里程为K52+001.615，ZH 点坐标x ＝388071.927，y ＝508789.089，R ＝960m ，Ls ＝120m ，求K52+100处的中点坐标及左右各偏12.5m 的坐标。

带有缓和曲线的圆曲线逐桩坐标计算例题

带有缓和曲线的圆曲线逐桩坐标计算例题：某山岭区二级公路，已知交点的坐标分别为JD1（40961.914,91066.103）、 JD2（40433.528,91250.097）、JD3（40547.416,91810.392），JD2里程为K2+200.000，R=150m,缓和曲线长度为40m,计算带有缓和曲线的圆曲线的逐桩坐标。

（《工程测量》第202页36题）解：（1）转角、缓和曲线角、曲线常数、曲线要素、主点里程、主点坐标计算1 坐标方位角12α3084160'''23α730378''' 2 转角 α（左转曲线）627182'''3 缓和曲线角 πββ1802⨯==R L S h o22837'''4 曲线内移值 RL p S242=m 444.05切线增长值232402R L L q SS -=m 988.196曲线要素切线长 q p R T h ++=2tan )(αm 438.151曲线长 S h L R L 2180)2(0+-=πβαm 436.255=h L m 436.175y =L外距 R p R E h -+=2sec )(αm 781.49切曲差 h h h L T D -=2m 440.477主点里程ZH 桩号JD ZH =（桩号）h T - K2+048.562 HY桩号ZH HY =（桩号）S L + K2+088.562 YH 桩号HY YH =（桩号）y L + K2+263.998 HZ 桩号YH HZ =（桩号）S L + K2+303.998 QZ 桩号HZ QZ =（桩号）2/h L - K2+176.280 JD 桩号QZ JD =（桩号）2/h D + K2+200.0008主点坐标ZH 212cos αh ZH T X X +=m 543.40576 212sin αh ZH T Y Y += m 296.91200HZ232cos αh HZ T X X +=m 693.40463 232sin αh HZ T Y Y +=m 500.91398QZ)180(21-23ααα-︒=hE 029329'''h E h QZE X X αcos 2+=m 788.40476h E h QZ E Y Y αsin 2+=m 728.91274方法一：偏角法（坐标正算）（2）第一缓和段坐标计算 228370'''= β 308416012'''= α（3）圆曲线段坐标计算 1490153-0'''==-βααJD ZY 切线桩号弧长里程里程桩点ZY -=i l偏角 0231β⎪⎪⎭⎫ ⎝⎛=∆S i i L l 方位角 i c i ∆-=12αα (左转) 弦长22590Sii i L R l l c -= Xi i c i ZH i c X X αcos +=Yiic i ZH i c Y Y αsin +=ZH:K2+048.5620 160 48 03 40576.543 91200.296 +060 11.438 0 12 30 160 35 33 11.438 40565.754 91204.097 +080 31.438 1 34 23 159 13 40 31.438 40547.149 92211.446 HYK2+088.562 402 32 47 158 15 1639.96840539.41991215.104桩号弧长里程里程桩点HY -=i l偏角π︒=∆90R l ii方位角(左转) i JD ZY c i∆=---0βαα弦长ii R c ∆=sin 2Xic i HY i c X X αcos +=Yi c i HY i c Y Y αsin +=HY: K2+088.5620βαα-=-JD ZY 切线153 09 41 40539.419 91215.104 +100 11.438 2 11 04 150 58 37 11.435 40529.420 91220.652 +120 31.438 6 00 15 147 09 26 31.380 40513.05591232.122+140 51.438 9 49 26 143 20 15 +16071.438 13 38 37 139 31 04 QZ: K2+176.28087.718 16 45 10136 24 3186.473 40476.78991274.728+180 91.438 +200 111.438 +220 131.438 +240 151.438 +260171.438 YH:K2+263.998175.43633 30 21119 39 20165.60640457.48091359.018（4）第二缓和段坐标计算 228370'''= β桩号弧长里程里程桩点-Z H l i =偏角0231β⎪⎪⎭⎫⎝⎛=∆S i i L l 方位角i c i∆+=32αα(左转) 弦长22590Si i i L R l l c -=X ii c i i c X X αcos HZ +=Y ii c i HZ i c Y Y αsin +=YH: K2+263.99840 2 32 47 261 03 24 39.968 40457.480 91359.018 +280 23.998 0 55 00 259 25 37 23.996 40459.290 91374.911 +300 3.998 0 01 32258 30 373.998 40462.89791394.582HZ K2+303.99832α258 30 3740463.693 91398.500方法二：切线支距法（坐标系转换）（2）第一缓和段坐标计算308416012'''= α1212sin cos ααy x X X ZH i ++= 1212cos sin ααy x Y Y ZH i -+=（本题为左转曲线）（3）圆曲线段坐标计算228370'''= β p = 0.444m q = 19.988m 308416012'''= α ZH （40576.543 , 91200.296） 1212sin cos ααy x X X ZH i ++= 1212cos sin ααy x Y Y ZH i -+=桩号里程里程桩点ZY -=i l 22540s L R l l x -= 33733366SS L R l RL l y -= X iY iZH: K2+048.5620 40576.543 91200.296 +060 11.438 11.438 0.042 40565.755 91204.096 +080 31.438 31.417 0.863 40547.156 92211.446 HY K2+088.562 4039.9291.77840539.41991215.104桩号里程里程桩点HY -=i l0180βπϕ+=Rl i q R x +=ϕsin P ()p R y +-=ϕcos 1PX i Y i HY: K2+088.56240539.419 91215.104 +100 11.438 12 00 30 51.196 3.726 40529.419 91220.651 +120 31.438 19 38 52 70.4249.177 40513.05291232.122+140 51.438 27 17 14 +16071.438 34 55 36 QZ: K2+176.28087.718 41 08 43 118.68437.48740476.78891274.728+180 91.438 42 33 58+200 111.438 +220 131.438 +240 151.438 +260171.438 YH:K2+263.998175.43674 39 04164.638110.74040457.47991359.018（4）第二缓和段坐标计算 73037812'''= α2323sin cos ααy x X X HZ i +-= 2323cos sin ααy x Y Y HZ i --=（本题为左转曲线）桩号里程里程桩点ZY -=i l 22540s L R l l x -=33733366SS L R l RL l y -= X iY iYH: K2+263.99840 39.929 1.778 40457.482 91359.017 +280 23.998 23.992 0.384 40459.290 91374.912 +300 3.998 3.998 0.002 40462.89891394.582HZ K2+303.99840463.693 91398.500。

坐标计算实例(缓和曲线)(1)

缓和曲线逐桩坐标计算（转载）摘要：利用一缓和曲线算例，通过数学分析，推导出缓和曲线逐桩坐标计算公式，此公式可作为道路测设中的范例来运用，有很强的指导意义。

关键词：缓和曲线、公式、逐桩坐标一、引言道路建设中，由于受地形或地质影响，经常需要改变线路方向，为满足行车要求，往往要用曲线把两条直线连接起来。

曲线的构成形式无外乎圆曲线和缓和曲线，本文以河北省沿海高速某曲线段为例推导出缓和曲线的逐桩坐标计算公式，以方便图纸的审核，满足施工放样的需求。

本公式具有良好的操作性，方便施工、提高精度，可作为道路测设中的范例运用。

二、公式推导1 、实例数据河北省沿海高速公路一缓和曲线（如图）：AB 段为缓和曲线段，A 为ZH 点，B 为HY 点，R B=800m ；A 点里程为NK0+080 ，切线方位角为θA=100 ° 00 ′ 24.1 ″，坐标为X A=4355189.493,Y A=476976.267 ；B 点里程为NK0+158.125 ，切线方位角为θB=102 ° 48 ′ 15.6 ″，坐标为X B=4355174.669 ，Y B=477052.964 ，推求此曲线段内任意点坐标。

2 、公式推导及实例计算方法一：弦线偏角法1 ）公式推导由坐标增量的计算方法我们不难理解，求一点坐标可以根据其所在直线的方位角以及直线上另一点的坐标和距待求点的距离。

所以我们可以利用ZH 点，只要知道待求点距ZH 点的距离（弦长S ）和此弦与ZH 点切线方位角的夹角（转角a ），即可求出该点坐标。

根据回旋线方程C=RL ，用B 点数据推导出回旋线参数：C=RL S=800*78.125=62500 （L S为B 点至ZH 点的距离）设待求点距ZH 点距离为L因回旋线上任意点的偏角β0=L2/2RL S, 且转角a=β0/3 ，可得该点转角a 。

（曲线左转时a 代负值）。

根据缓和曲线上的弧弦关系S=L-L5/90R2L S2，可以求出待求点至ZH 点的弦长。

缓和曲线连同圆曲线测设

缓和曲线连同圆曲线测设
实习报告
班级：
组别：
姓名：
学号：
指导教师：
年月日
前言
1、曲线元素计算
（1）设计元素
R=缓和曲线长l0= 转向角α
JD里程：DK+
（2）转向角测量
日期：年月日仪器Байду номын сангаас号仪器编号
班级组别观测者记录者
置镜点
盘位
目标
水平度盘读数
（° ′ ″）
半测回角值
（° ′ ″）
一测回角值
（° ′ ″）
JD
L
ZD1
ZD2
R
ZD2
ZD1
（3）缓和曲线常数
（4）曲线综合要素
2、曲线主要点里程推算
（1）里程推算
JD DK +
-T
ZH DK +
+l0
HY DK +
+（L-2l0）/2
QZ DK +
+（L-2l0）/2
YH DK +
+l0
HZ
（2）计算检核
ZH DK +
+2T
DK +
-q
HZ DK +
3、分弦偏角计算（圆曲线段不足20米的破弦）
NO
分弦（m）
分弦偏角（°′″）
δ1
δ2
δ3
δ4
δ5
3、偏角法测设曲线资料计算
日期：年月日仪器型号仪器编号
班级组别观测者记录者
点号
里程
正反拨
偏角（°′″）
平盘读数（°′″）
备注
ZH（0）

圆曲线和缓和曲线坐标推算公式(附带例题)

圆曲线和缓和曲线坐标推算公式一、直线上的坐标推算⎩⎨⎧++0i m i0i m i sina L Y Y cosa L X X ＝＝式中：Xm 、Ym ——直线段起点M 坐标Li ——直线段上任意点i 到线路起点M 的距离 a 0——直线段起点M 到JD1的方位角二、圆曲线上任一点的坐标推算①、圆曲线上任一点i 相对应的圆心角：i i L R180πϕ︒＝式中：Li ——圆曲线上任一点i 离开ZY 或YZ 点的弧长②、圆曲线上任一点i 的直角坐标：⎩⎨⎧-）（＝＝i iii cos 1R Y Rsin X ϕϕ（可不计算）.③、圆曲线ZY 或YZ 点到任一点i 的偏角：i ii L R902πϕ︒∆＝＝④、圆曲线ZY 或YZ 点到任一点i 的弦长：)sin(2)2sin(2C i i iR R ∆=ϕ＝⑤、圆曲线ZY 或YZ 点到任一点i 的弦长的方位角：i jd yz jd zy i a a ∆±→→或＝⑥、所以圆曲线上任意点i 的坐标为：⎩⎨⎧++i i YZ ZY iii YZ ZY i sina C Y Y cosa C X X 或或＝＝例题：已知一段圆曲线,R=3500m ，Ls ＝553.1m ，交点里程K50+154.734，ZY 点到JD 方向方位角为A=129°23′18.3″，右偏9°3′15.8″，ZY 点里程K49+877.607，YZ 点里程K50+430.707，起点坐标为x ＝389823.196，y ＝507787.251，求K50+200处中点坐标及左右各偏12.5m 的坐标。

解：K50+200处的曲线长度为Li ＝322.393mK50+200相对应的方位角："'︒⨯⨯︒︒52.39165393.3223500180L R 180i ＝＝＝ππa K50+200相对应的偏角："'︒⨯⨯︒︒∆76.19382393.322350090L R 902i ii ＝＝＝＝ππϕ K50+200到zy 点的弦长：m 279.32276.19382sin 35002Rsin 2C i i ＝＝＝"'︒⨯⨯∆ zy 点到K50+200中桩的方位角："'︒"'︒+"'︒∆+→06.38113276.193823.1823129a a i jd zy i ＝＝＝K50+200左、右偏12.5m 的方位角："'︒︒-"'︒︒-+82.5739449082.573913490a a ＝＝＝左i A "'︒︒+"'︒︒++82.57391349082.573913490a a ＝＝＝右i A 所以K50+200处的坐标为：⎩⎨⎧"'︒⨯++"'︒⨯++6484.50802606.381132sin 279.322251.507787sina C Y Y 4354.38960706.381132cos 279.322196.389823cosa C X X i i ZY ii i ZY i ＝＝＝＝＝＝K50+200左偏12.5m 的坐标为：⎩⎨⎧"'︒⨯++"'︒⨯++4656.50803582.573944sin 5.126484.508026sina 5.21Y Y 3256.38961682.573944cos 5.124354.389607cosa 5.21X X i i ＝＝＝＝＝＝左左左左 K50+200右偏12.5m 的坐标为：⎩⎨⎧"'︒⨯++"'︒⨯++5386.50803582.5739341sin 5.126484.508026sina 5.21Y Y 6482.38959882.5739341cos 5.124354.389607cosa 5.21X X i i ＝＝＝＝＝＝右右右右三、缓和曲线上任一点的坐标推算切线角：πβ︒⨯1802RL L s 2i i＝缓和曲线上任意点i 的偏角：πβδ︒⨯180RL 6L 3s 2i ii ＝＝缓和曲线ZH 或HZ 点到任意点i 的方位角为：i jd H Z jd ZH a a i δ±→→或＝缓和曲线上任意点i 的坐标为：⎪⎪⎩⎪⎪⎨⎧-s 3ii 2s 25i i i 6RL L y L 40R L L x ＝＝缓和曲线ZH 或HZ 点到任意点i 的弦长：22i yx C +＝所以缓和曲线上任意点i 的坐标为：⎩⎨⎧++i i HZ ZH iii HZ ZH i sina C Y Y cosa C X X 或或＝＝例题：已知一段缓和曲线，ZH 点到JD 方向方位角为A=183°17′08.9″，线路左偏43°31′02″，ZH 点里程为K52+001.615，ZH 点坐标x ＝388071.927，y ＝508789.089，R ＝960m ，Ls ＝120m ，求K52+100处的中点坐标及左右各偏12.5m 的坐标。

圆曲线、缓和曲线计算例题《精选》

圆曲线坐标计算公式β=180°/π×L/R（L= βπ R/180°）弧长公式β为圆心角△X=sinβ×R△Y=(1-cosβ)×RC= 弦长X=X1+cos (α ±β/2)×CY=Y1+sin (α ±β/2)×Cβ代表偏角,（既弧上任一点所对的圆心角）。

β/2是所谓的偏角（弦长与切线的夹角）△X、△Y代表增量值。

X、Y代表准备求的坐标。

X1、Y1代表起算点坐标值。

α代表起算点的方位角。

R 代表曲线半径缓和曲线坐标计算公式β= L2/2RLS ×180°/πC= L - L5/90R2LS2X=X1+cos (α ±β/3)×CY=Y1+sin (α ±β/3)×CL代表起算点到准备算的距离。

LS代表缓和曲线总长。

X1、Y1代表起算点坐标值。

直线坐标计算公式X=X1+cosα×L Y=Y1+sinα×LX1、Y1代表起算点坐标值α代表直线段方位角。

L代表起算点到准备算的距离。

左右边桩计算方法X边=X中+cos（α±90°)×LY边=Y中+sin（α±90°)×L在计算左右边桩时，先求出中桩坐标，在用此公式求左右边桩。

如果在线路方向左侧用中桩方位角减去90°，线路右侧加90°，乘以准备算的左右宽度。

例题:直线坐标计算方法α(方位角)=18°21′47″X1=84817.831 Y1=352.177 起始里程DK184+714.029求DK186+421.02里程坐标解:根据公式X=X1+cosα×LX=84817.831+COS18°21′47″×(86421.02—84714.029)=86437.901Y=Y1+sinα×LY=352.177+sin18°21′47″×(86421.02—84714.029)=889.943求DK186+421.02里程左右边桩,左侧3.75m,右侧7.05m.解:根据公式线路左侧计算:X边=X中+cos（α±90°)×LX边=86437.901+cos(18°21′47″- 90°)×3.75=86439.082Y边=Y中+sin（α±90°)×LY边=889.943+sin(18°21′47″- 90°)×3.75=886.384线路右侧计算: X边=X中+cos（α±90°)×LX边=86437.901+cos(18°21′47″+ 90°)×7.05=86435.680 Y边=Y中+sin（α±90°)×L Y边=889.943+sin(18°21′47″+90°)×7.05=896.634例题:缓和曲线坐标计算方法α(ZH点起始方位角)=18°21′47″X1=86437.901 Y1=889.941起始里程DK186+421.02曲线半径2500缓和曲线长120m求HY点坐标,也可以求ZH点到HY点任意坐标解:根据公式β=L2/2RLS×180°/πβ=｛1202/(2×2500×120)｝×(180°/π)= 1°22′30.36″C=L-L5/90R2LS2C=120-1205/(90×25002×1202)=119.997X=X1+cos(α±β/3)×CX=86437.901+cos(18°21′47″-1°22′30.36″/3)×119.997=86552.086Y=Y1+sin(α±β/3)×CY=889.941+sin(18°21′47″-1°22′30.36″/3)×119.997=926.832求DK186+541.02里程左右边桩,左侧3.75m,右侧7.05m.解:根据公式线路左侧计算:X边=X中+cos（α±90°)×LX边=86552.086+cos｛(18°21′47″-1°22′30.36″)- 90°｝×3.75=86553.182Y边=Y中+sin（α±90°)×LY边=926.832+sin｛(18°21′47″-1°22′30.36″)- 90°｝×3.75=923.246线路右侧计算: X边=X中+cos（α±90°)×LX边=86552.086+cos｛(18°21′47″-1°22′30.36″)+ 90°｝×7.05=86550.026Y边=Y中+sin（α±90°)×LY边=926.832+sin｛(18°21′47″-1°22′30.36″)+ 90°｝×7.05=933.574缓和曲线方位角计算方法α=(起始方位角±β偏角)= 18°21′47″-1°22′30.36″=16°59′16.64″注:缓和曲线在计算坐标时,此公式只能从两头往中间推,只能从ZH点往HY点推,HZ点往YH 点推算,如果YH往HZ点推算坐标,公式里的β为β2/3.例题:圆曲线坐标计算方法α(HY点起始方位角)= 16°59′16.64″X1=86552.086Y1=926.832 曲线半径2500曲线长748.75起始里程DK186+541.02求YH点坐标,也可以求QZ点坐标或任意圆曲线一点坐标.解:根据公式β=180°/π×L/Rβ= 180°/π×748.75/2500=17°09′36.31″△X=sinβ×R△X=sin17°09′36.31″×2500=737.606△Y=(1-cosβ)×R△Y=(1-cos17°09′36.31″)×2500=111.290C=弦长C=745.954X=X1+cos(α±β/2)×CX= 86552.086 +cos(16°59′16.64″+360°-17°09′36.31″/2) ×745.954=87290.023Y=Y1+sin(α±β/2)×CY=926.832+ sin(16°59′16.64″+360°-17°09′36.31″/2) ×745.954=1035.905圆曲线方位角计算方法α=(起始方位角±β偏角)= 16°59′16.64″+360°-17°09′36.31″=359°49′40.33″求DK187+289.77里程左右边桩,左侧3.75m,右侧7.05m.解:根据公式线路左侧计算: X边=X中+cos（α±90°)×LX边=87290.023+cos(359°49′40.33″-90°)×3.75=87290.012Y边=Y中+sin（α±90°)×LY边=1035.905+sin(359°49′40.33″-90°)×3.75=1032.155线路右侧计算: X边=X中+cos（α±90°)×LX边=87290.023+cos(359°49′40.33″+90°)×7.05=87290.044Y边=Y中+sin（α±90°)×LY边=1035.905+sin(359°49′40.33″+90°)×7.05=1042.955。

(完整版)缓和曲线、圆曲线测设计算例题

已知曲线半径R=6000，缓和曲线长度l 0=280，交点JD27坐标及相邻方位角已在图中给出，ZH 点里程为DK2+100。

请计算：1、曲线要素中的切线长T 、曲线长L 、外矢距E ；2、HY 、QZ 、YH 、HZ 的里程；3、ZH 点坐标及其左边桩3米的坐标；4、DK2+180的坐标及右边桩2米的坐标；5、DK2+660的坐标及右边桩35米的坐标。

永州α=225-17-08.0JD27(D K 2+100)(1000.000,1000.000)α=232-35-13.9H Z Q ZHZ H Y YH附公式：m 为缓和曲线切垂距，m= l 0/2- l 03/（240R 2）p 为缓和曲线内移距，P= l 02/（24R ）- l 04/（2688R 3）缓和曲线方程式：X=h - h 5/（40R 2l 2）+ h 9/（3456 R 4l 4）Y=h 3/（6Rl ）- h 7/（336 R 3l 3）+ h 11/（42240 R 5l 5）解：1、转向角α=α2-α1=7°18′05.9″切线长T=（R+P ）tg （α/2）+m = 522.863曲线长L=（R απ）/180+l 0= 1044.626外矢距E=（R+P ）sec （α/2）-R=12.746式中m 为缓和曲线切垂距，m= l 0/2- l 03/（240R 2）=139.9974p 为缓和曲线内移距，P= l 02/（24R ）- l 04/（2688R 3）=0.54442、HY 点里程为DK2+100+280=DK2+380；QZ 点里程为DK2+100+1044.626/2=DK2+622.313；HZ 点里程为DK2+100+1044.626=DK3+144.626；YH 点里程为DK3+144.626-280=DK2+864.6263、JD27到ZH 点的方位角αJD27-ZH =232°35′13.9″-180=52°35′13.9″ JD27到ZH 点的坐标增量为：△x =T ×cos αJD27-ZH =317.667m△y =T ×sin αJD27-ZH =-415.299m于是ZH 点坐标为X ZH = x JD27+ △x = 1317.667my ZH = Y JD27+△y =1415.299mZH点到左边桩3米的方位角αZH-左边桩= 232°35′13.9″-90=142°35′13.9″左边桩3米的坐标为：X左= x ZH+ 3×cosαZH-左边桩= 1315.284mY左= y ZH +3×sinαZH-左边桩=1417.122m4、DK2+180的坐标及右边桩2米的坐标:DK2+180在缓和曲线上，计算过程为：ZH点到JD27的方位角αZH-JD1= =232°35′13.9″DK2+180到ZH点的缓和曲线长度h为180-100=80根据缓和曲线方程式：X=h - h5/（40R2l2）+ h9/（3456 R4l4）=80.000Y=h3/（6Rl）- h7/（336 R3l3）+ h11/（42240 R5l5）=0.0508由X和Y可以求出DK5+900与ZH的距离D和它的偏角δ：D=√（X2+ Y2）=80.000δ=arctg（Y/ X）=0°02′11.0″于是DK2+180的坐标（X1，Y1）为：X1= 1317.667+Dcos（232°35′13.9″-δ）=1269.022Y1 = 1415.299+Dsin（232°35′13.9″-δ）=1351.788DK2+300右边桩2米的坐标（X2，Y2）为：X2= 1269.022+2×cos（232°35′13.9″-3δ+90）=1270.608Y2= 1351.788+2×sin（232°35′13.9″-3δ+90）=1350.5705、圆曲线点DK2+660计算过程为：曲中点QZ的里程推算为DK2+622.313, DK2+660到QZ的圆曲线长度为660-622.313=37.687,所对应的圆心角为O′=（180*37.687）/（πR）=0°21′35.6″， JD27到圆心O的方位角αJD27-O=225°17′08.0″-（180-7°18′05.9″）/2=138°56′10.95″圆心O的坐标为：X3 =1000+（E+R）cos（138°56′10.95″）=-3533.494Y3= 1000+（E+R）sin（138°56′10.95″）=4949.753DK2+660的坐标（X4，Y4）为：X4= X3++ R cos（138°56′10.95″+180- O′）=965.544Y4 = Y3+Rsin（138°56′10.95″+180- O′）=980.035DK2+660右边桩35米的坐标（X5，Y5）为：X5= X3++ （R+35）×cos（138°56′10.95″+180- O′）=991.788Y5= Y3+（R+35）×sin（138°56′10.95″+180- O′）=956.878。

缓和曲线计算题集

缓和曲线计算题集题目一：已知某道路曲线第一切线上控制点JD1（750，750），ZD1(100,100),该曲线设计半径R=500m，缓和曲线长L0=50m，JD1里程为DK1+300，转向角α右=23°30′08″。

请按要求计算道路曲线主点ZH、HY、QZ、YH、HZ点的里程及道路曲线主点ZH、HY、QZ点坐标，第一缓和曲线和圆曲线上中桩点K1+115、K1+250的坐标，共计算5个点。

题目一参考答案及结果7个曲线要素桩号坐标q=24.998 ZH DK1+170.948 ZH (658.7468 ,658.7468)p=0.208 HY DK1+220.948 HY (693.5041,694.6824)β=2°51′53.2″ QZ DK1+298.496 QZ (740.8707,755.9852)T=129.052 YH DK1+376.044 YH (778.199,823.869)L=255.096 HZ DK1+426.044 HZ (797.2929,870.0736)E=10.916 K1+115 (643.934,643.934)J=3.008 K1+250 (712.3576,716.7199)题目二设某公路的交点JD桩号为K1+50它的坐标是（100，100），ZD1(40,40),右转角α=60°。

曲线设计半径R=100m，缓和曲线长Ls=10m，请按要求计算道路曲线主点ZH、HY、QZ、YH、HZ点的里程及道路曲线主点ZH、HY点坐标及桩点K0+988、K1+000的坐标。

(示意图略)问题：请计算出7个曲线要素，5个主点里程，4个点的坐标。

题目二参考答案及结果7个曲线要素桩号坐标q=4.998 ZH K0+987.241 ZH (坐标X=55.6229 , 坐标Y=55.6229) p=0.042 HY K0+997.241 HY (坐标X=62.5744 , 坐标Y=62.8101) β=2°51′53.2″QZ K1+44.601 QZ (坐标X=85.0106 , 坐标Y=104.0164) T=62.759 YH K1+91.961 YH (坐标X=86.1834 , 坐标Y=150.9202) L=114.72 HZ K1+101.961 HZ (坐标X=83.7569 , 坐标Y=160.6202) E=15.519J=10.798。

圆曲线和缓和曲线坐标推算公式(附带例题)

圆曲线和缓和曲线坐标推算公式一、直线上的坐标推算⎩⎨⎧++0i m i0i m i sina L Y Y cosa L X X ＝＝式中：Xm 、Ym ——直线段起点M 坐标Li ——直线段上任意点i 到线路起点M 的距离 a 0——直线段起点M 到JD1的方位角二、圆曲线上任一点的坐标推算①、圆曲线上任一点i 相对应的圆心角：i i L R180πϕ︒＝式中：Li ——圆曲线上任一点i 离开ZY 或YZ 点的弧长②、圆曲线上任一点i 的直角坐标：⎩⎨⎧-）（＝＝i iii cos 1R Y Rsin X ϕϕ（可不计算）.③、圆曲线ZY 或YZ 点到任一点i 的偏角：i ii L R902πϕ︒∆＝＝④、圆曲线ZY 或YZ 点到任一点i 的弦长：)sin(2)2sin(2C i i iR R ∆=ϕ＝⑤、圆曲线ZY 或YZ 点到任一点i 的弦长的方位角：i jd yz jd zy i a a ∆±→→或＝⑥、所以圆曲线上任意点i 的坐标为：⎩⎨⎧++i i YZ ZY iii YZ ZY i sina C Y Y cosa C X X 或或＝＝例题：已知一段圆曲线,R=3500m ，Ls ＝553.1m ，交点里程K50+154.734，ZY 点到JD 方向方位角为A=129°23′18.3″，右偏9°3′15.8″，ZY 点里程K49+877.607，YZ 点里程K50+430.707，起点坐标为x ＝389823.196，y ＝507787.251，求K50+200处中点坐标及左右各偏12.5m 的坐标。

解：K50+200处的曲线长度为Li ＝322.393mK50+200相对应的方位角："'︒⨯⨯︒︒52.39165393.3223500180L R 180i ＝＝＝ππa K50+200相对应的偏角："'︒⨯⨯︒︒∆76.19382393.322350090L R 902i ii ＝＝＝＝ππϕ K50+200到zy 点的弦长：m 279.32276.19382sin 35002Rsin 2C i i ＝＝＝"'︒⨯⨯∆ zy 点到K50+200中桩的方位角："'︒"'︒+"'︒∆+→06.38113276.193823.1823129a a i jd zy i ＝＝＝K50+200左、右偏12.5m 的方位角："'︒︒-"'︒︒-+82.5739449082.573913490a a ＝＝＝左i A "'︒︒+"'︒︒++82.57391349082.573913490a a ＝＝＝右i A 所以K50+200处的坐标为：⎩⎨⎧"'︒⨯++"'︒⨯++6484.50802606.381132sin 279.322251.507787sina C Y Y 4354.38960706.381132cos 279.322196.389823cosa C X X i i ZY ii i ZY i ＝＝＝＝＝＝K50+200左偏12.5m 的坐标为：⎩⎨⎧"'︒⨯++"'︒⨯++4656.50803582.573944sin 5.126484.508026sina 5.21Y Y 3256.38961682.573944cos 5.124354.389607cosa 5.21X X i i ＝＝＝＝＝＝左左左左 K50+200右偏12.5m 的坐标为：⎩⎨⎧"'︒⨯++"'︒⨯++5386.50803582.5739341sin 5.126484.508026sina 5.21Y Y 6482.38959882.5739341cos 5.124354.389607cosa 5.21X X i i ＝＝＝＝＝＝右右右右三、缓和曲线上任一点的坐标推算切线角：πβ︒⨯1802RL L s 2i i＝缓和曲线上任意点i 的偏角：πβδ︒⨯180RL 6L 3s 2i ii ＝＝缓和曲线ZH 或HZ 点到任意点i 的方位角为：i jd H Z jd ZH a a i δ±→→或＝缓和曲线上任意点i 的坐标为：⎪⎪⎩⎪⎪⎨⎧-s 3ii 2s 25i i i 6RL L y L 40R L L x ＝＝缓和曲线ZH 或HZ 点到任意点i 的弦长：22i yx C +＝所以缓和曲线上任意点i 的坐标为：⎩⎨⎧++i i HZ ZH iii HZ ZH i sina C Y Y cosa C X X 或或＝＝例题：已知一段缓和曲线，ZH 点到JD 方向方位角为A=183°17′08.9″，线路左偏43°31′02″，ZH 点里程为K52+001.615，ZH 点坐标x ＝388071.927，y ＝508789.089，R ＝960m ，Ls ＝120m ，求K52+100处的中点坐标及左右各偏12.5m 的坐标。

带有缓和曲线的圆曲线逐桩坐标计算例题

带有缓和曲线的圆曲线逐桩坐标计算例题：某山岭区二级公路，已知交点的坐标分别为JD1（40961.914,91066.103）、 JD2（40433.528,91250.097）、JD3（40547.416,91810.392），JD2里程为K2+200.000，R=150m,缓和曲线长度为40m,计算带有缓和曲线的圆曲线的逐桩坐标。

（《工程测量》第202页36题）解：（1）转角、缓和曲线角、曲线常数、曲线要素、主点里程、主点坐标计算1 坐标方位角12α3084160'''23α730378''' 2 转角 α（左转曲线）627182'''3 缓和曲线角 πββ1802⨯==R L S h o22837'''4 曲线内移值 RL p S242=m 444.05切线增长值232402R L L q SS -=m 988.196曲线要素切线长 q p R T h ++=2tan )(αm 438.151曲线长 S h L R L 2180)2(0+-=πβαm 436.255=h L m 436.175y =L外距 R p R E h -+=2sec )(αm 781.49切曲差 h h h L T D -=2m 440.477主点里程ZH 桩号JD ZH =（桩号）h T - K2+048.562 HY桩号ZH HY =（桩号）S L + K2+088.562 YH 桩号HY YH =（桩号）y L + K2+263.998 HZ 桩号YH HZ =（桩号）S L + K2+303.998 QZ 桩号HZ QZ =（桩号）2/h L - K2+176.280 JD 桩号QZ JD =（桩号）2/h D + K2+200.0008主点坐标ZH 212cos αh ZH T X X +=m 543.40576 212sin αh ZH T Y Y += m 296.91200HZ232cos αh HZ T X X +=m 693.40463 232sin αh HZ T Y Y +=m 500.91398QZ)180(21-23ααα-︒=hE 029329'''h E h QZE X X αcos 2+=m 788.40476h E h QZ E Y Y αsin 2+=m 728.91274方法一：偏角法（坐标正算）（2）第一缓和段坐标计算 228370'''= β 308416012'''= α（3）圆曲线段坐标计算 1490153-0'''==-βααJD ZY 切线桩号弧长里程里程桩点ZY -=i l偏角 0231β⎪⎪⎭⎫ ⎝⎛=∆S i i L l 方位角 i c i ∆-=12αα (左转) 弦长22590Sii i L R l l c -= Xi i c i ZH i c X X αcos +=Yiic i ZH i c Y Y αsin +=ZH:K2+048.5620 160 48 03 40576.543 91200.296 +060 11.438 0 12 30 160 35 33 11.438 40565.754 91204.097 +080 31.438 1 34 23 159 13 40 31.438 40547.149 92211.446 HYK2+088.562 402 32 47 158 15 1639.96840539.41991215.104桩号弧长里程里程桩点HY -=i l偏角π︒=∆90R l ii方位角(左转) i JD ZY c i∆=---0βαα弦长ii R c ∆=sin 2Xic i HY i c X X αcos +=Yi c i HY i c Y Y αsin +=HY: K2+088.5620βαα-=-JD ZY 切线153 09 41 40539.419 91215.104 +100 11.438 2 11 04 150 58 37 11.435 40529.420 91220.652 +120 31.438 6 00 15 147 09 26 31.380 40513.05591232.122+140 51.438 9 49 26 143 20 15 +16071.438 13 38 37 139 31 04 QZ: K2+176.28087.718 16 45 10136 24 3186.473 40476.78991274.728+180 91.438 +200 111.438 +220 131.438 +240 151.438 +260171.438 YH:K2+263.998175.43633 30 21119 39 20165.60640457.48091359.018（4）第二缓和段坐标计算 228370'''= β桩号弧长里程里程桩点-Z H l i =偏角0231β⎪⎪⎭⎫⎝⎛=∆S i i L l 方位角i c i∆+=32αα(左转) 弦长22590Si i i L R l l c -=X ii c i i c X X αcos HZ +=Y ii c i HZ i c Y Y αsin +=YH: K2+263.99840 2 32 47 261 03 24 39.968 40457.480 91359.018 +280 23.998 0 55 00 259 25 37 23.996 40459.290 91374.911 +300 3.998 0 01 32258 30 373.998 40462.89791394.582HZ K2+303.99832α258 30 3740463.693 91398.500方法二：切线支距法（坐标系转换）（2）第一缓和段坐标计算308416012'''= α1212sin cos ααy x X X ZH i ++= 1212cos sin ααy x Y Y ZH i -+=（本题为左转曲线）（3）圆曲线段坐标计算228370'''= β p = 0.444m q = 19.988m 308416012'''= α ZH （40576.543 , 91200.296） 1212sin cos ααy x X X ZH i ++= 1212cos sin ααy x Y Y ZH i -+=桩号里程里程桩点ZY -=i l 22540s L R l l x -= 33733366SS L R l RL l y -= X iY iZH: K2+048.5620 40576.543 91200.296 +060 11.438 11.438 0.042 40565.755 91204.096 +080 31.438 31.417 0.863 40547.156 92211.446 HY K2+088.562 4039.9291.77840539.41991215.104桩号里程里程桩点HY -=i l0180βπϕ+=Rl i q R x +=ϕsin P ()p R y +-=ϕcos 1PX i Y i HY: K2+088.56240539.419 91215.104 +100 11.438 12 00 30 51.196 3.726 40529.419 91220.651 +120 31.438 19 38 52 70.4249.177 40513.05291232.122+140 51.438 27 17 14 +16071.438 34 55 36 QZ: K2+176.28087.718 41 08 43 118.68437.48740476.78891274.728+180 91.438 42 33 58+200 111.438 +220 131.438 +240 151.438 +260171.438 YH:K2+263.998175.43674 39 04164.638110.74040457.47991359.018（4）第二缓和段坐标计算 73037812'''= α2323sin cos ααy x X X HZ i +-= 2323cos sin ααy x Y Y HZ i --=（本题为左转曲线）桩号里程里程桩点ZY -=i l 22540s L R l l x -=33733366SS L R l RL l y -= X iY iYH: K2+263.99840 39.929 1.778 40457.482 91359.017 +280 23.998 23.992 0.384 40459.290 91374.912 +300 3.998 3.998 0.002 40462.89891394.582HZ K2+303.99840463.693 91398.500。

缓和曲线计算题集

缓和曲线计算题集题目一：已知某道路曲线第一切线上控制点JD1（750，750），ZD1(100,100),该曲线设计半径R=500m，缓和曲线长L0=50m，JD1里程为DK1+300，转向角α右=23°30′08″。

请按要求计算道路曲线主点ZH、HY、QZ、YH、HZ点的里程及道路曲线主点ZH、HY、QZ点坐标，第一缓和曲线和圆曲线上中桩点K1+115、K1+250的坐标，共计算5个点。

题目一参考答案及结果7个曲线要素桩号坐标q=24.998 ZH DK1+170.948 ZH (658.7468 ,658.7468)p=0.208 HY DK1+220.948 HY (693.5041,694.6824)β=2°51′53.2″ QZ DK1+298.496 QZ (740.8707,755.9852)T=129.052 YH DK1+376.044 YH (778.199,823.869)L=255.096 HZ DK1+426.044 HZ (797.2929,870.0736)E=10.916 K1+115 (643.934,643.934)J=3.008 K1+250 (712.3576,716.7199)题目二设某公路的交点JD桩号为K1+50它的坐标是（100，100），ZD1(40,40),右转角α=60°。

曲线设计半径R=100m，缓和曲线长Ls=10m，请按要求计算道路曲线主点ZH、HY、QZ、YH、HZ点的里程及道路曲线主点ZH、HY点坐标及桩点K0+988、K1+000的坐标。

(示意图略)问题：请计算出7个曲线要素，5个主点里程，4个点的坐标。

题目二参考答案及结果7个曲线要素桩号坐标q=4.998 ZH K0+987.241 ZH (坐标X=55.6229 , 坐标Y=55.6229) p=0.042 HY K0+997.241 HY (坐标X=62.5744 , 坐标Y=62.8101) β=2°51′53.2″QZ K1+44.601 QZ (坐标X=85.0106 , 坐标Y=104.0164) T=62.759 YH K1+91.961 YH (坐标X=86.1834 , 坐标Y=150.9202) L=114.72 HZ K1+101.961 HZ (坐标X=83.7569 , 坐标Y=160.6202) E=15.519J=10.798。

道路工程测量(圆曲线缓和曲线计算)

内容：理解线路勘测设计阶段的主要测量工作（初测控制测量、带状地形图测绘、中线测设和纵横断面测量）；掌握路线交点、转点、转角、里程桩的概念和测设方法；掌握圆曲线的要素计算和主点测设方法；掌握圆曲线的切线支距法和偏角法的计算公式和测设方法；了解虚交的概念和处理方法；掌握缓和曲线的要素计算和主点测设方法；理解缓和曲线的切线支距法和偏角法的计算公式和测设方法；掌握路线纵断面的基平、中平测量和横断面测量方；了解全站仪中线测设和断面测量方法。

重点：圆曲线、缓和曲线的要素计算和主点测设方法；切线支距法和偏角法的计算公式和测设方法；路线纵断面的基平、中平测量和横断面测量方法难点：缓和曲线的要素计算和主点测设方法；缓和曲线的切线支距法和偏角法的计算公式和测设方法。

§9.1交点转点转角及里程桩的测设一、道路工程测量概述分为：路线勘测设计测量(routereconnaissanceanddesignsurvey)和道路施工测量(roadconstructionsurvey)。

（一）勘测设计测量(routereconnaissanceanddesignsurvey)分为：初测(preliminarysurvey)和定测(locationsurvey)1、初测内容：控制测量(controlsurvey)、测带状地形图(topographicalmapofazone)和纵断面图(profile)、收集沿线地质水文资料、作纸上定线或现场定线，编制比较方案，为初步设计提供依据。

2、定测内容：在选定设计方案的路线上进行路线中线测量(centerlinesurvey)、测纵断面图(profile)、横断面图(cross-sectionprofile)及桥涵、路线交叉、沿线设施、环境保护等测量和资料调查，为施工图设计提供资料。

（二）道路施工测量(roadconstructionsurvey)按照设计图纸恢复道路中线、测设路基边桩和竖曲线、工程竣工验收测量。