立体几何证明平行的方法及专题训练
高考数学复习—立体几何:(二)空间直线平面关系判断与证明—平行与垂直关系证明(试题版)
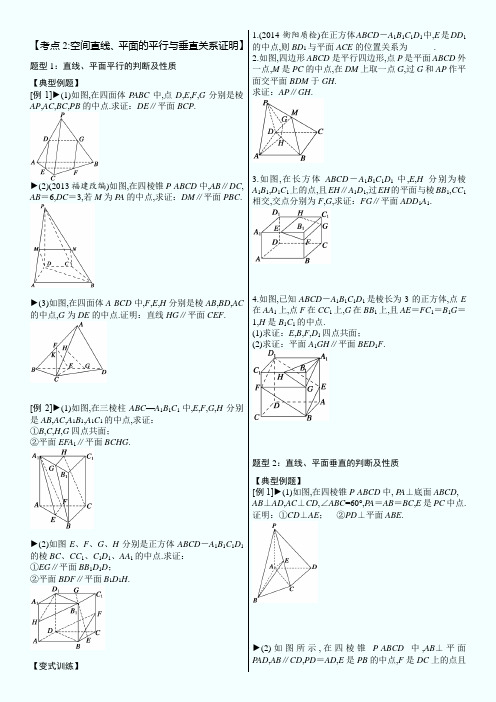
【考点2:空间直线、平面的平行与垂直关系证明】题型1:直线、平面平行的判断及性质【典型例题】[例1]►(1)如图,在四面体P ABC中,点D,E,F,G分别是棱AP,AC,BC,PB的中点.求证:DE∥平面BCP .►(2)(2013福建改编)如图,在四棱锥P-ABCD中,AB∥DC, AB=6,DC=3,若M为P A的中点,求证:DM∥平面PBC . ►(3)如图,在四面体A-BCD中,F,E,H分别是棱AB,BD,AC 的中点,G为DE的中点.证明:直线HG∥平面CEF .[例2]►(1)如图,在三棱柱ABC—A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:①B,C,H,G四点共面;②平面EF A1∥平面BCHG .►(2)如图E、F、G、H分别是正方体ABCD-A1B1C1D1的棱BC、CC1、C1D1、AA1的中点.求证:①EG∥平面BB1D1D;②平面BDF∥平面B1D1H .【变式训练】1.(2014·衡阳质检)在正方体ABCD-A1B1C1D1中,E是DD1的中点,则BD1与平面ACE的位置关系为______.2.如图,四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:AP∥GH .3.如图,在长方体ABCD-A1B1C1D1中,E,H分别为棱A1B1,D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G,求证:FG∥平面ADD1A1.4.如图,已知ABCD-A1B1C1D1是棱长为3的正方体,点E 在AA1上,点F在CC1上,G在BB1上,且AE=FC1=B1G=1,H是B1C1的中点.(1)求证:E,B,F,D1四点共面;(2)求证:平面A1GH∥平面BED1F .题型2:直线、平面垂直的判断及性质【典型例题】[例1]►(1)如图,在四棱锥P-ABCD中, P A⊥底面ABCD, AB⊥AD,AC⊥CD,∠ABC=60°,P A=AB=BC,E是PC中点. 证明:①CD⊥AE;②PD⊥平面ABE .►(2)如图所示,在四棱锥P-ABCD中,AB⊥平面P AD,AB∥CD,PD=AD,E是PB的中点,F是DC上的点且DF=12AB,PH为△P AD中AD边上的高.①证明:PH⊥平面ABCD;②证明:EF⊥平面P AB.[例2]►(1)[2014·辽宁文]如图所示,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F,G分别为AC,DC,AD的中点.(I)求证:EF⊥平面BCG;(II)求三棱锥D -BCG的体积.►(2)(2012·课标全国)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA1,D是棱AA1的中点.(I)证明:平面BDC1⊥平面BDC;(II)平面BDC1分此棱柱为两部分,求这两部分体积的比.►(3)(2015·大庆质检) 如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.①求证:PC⊥BC;②求点A到平面PBC的距离.【变式训练】1.如图,四棱锥P—ABCD中,P A⊥底面ABCD,AB⊥AD,点E 在线段AD上,且CE∥AB. (1)求证:CE⊥平面P AD;(2)若P A=AB=1,AD=3,CD=2,∠CDA=45°,求四棱锥P-ABCD的体积.2.[2014·福建文]如图所示,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.(1)求证:CD⊥平面ABD;(2)若AB=BD=CD=1,M为AD中点,求三棱锥A -MBC的体积.3.(2015·唐山统考)如图,在三棱锥P-ABC中,P A=PB=AB =BC,∠PBC=90°,D为AC的中点,AB⊥PD.(1)求证:平面P AB⊥平面ABC;(2)如果三棱锥P-BCD的体积为3,求P A.4.[2014·课标Ⅰ文]如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.(1)证明:B1C⊥AB;(2)若AC⊥AB1,∠CBB1=60°,BC=1,求三棱柱ABC-A1B1C1的高.☆题型3:直线、平面平行与垂直关系的综合【典型例题】[例1]►(1)已知l,m是两条不同的直线,α,β是两个不同的平面,下列命题中真命题是(写出序号).①若l⊂α,m⊂α,l∥β,m∥β,则α∥β;②若l⊂α,l∥β,α∩β=m,则l∥m;③若α∥β,l∥α,则l∥β;④若l⊥α,m∥l,α∥β,则m⊥β.►(2)(2014·辽宁)已知m,n表示两条不同直线,α表示平面.下列说法正确的是()A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥α►(3)(2015·江西七校联考)已知直线a和平面α,β,α∩β=l,a⊄α,a⊄β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是()A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面►(4)(2013·课标Ⅱ)已知m,n为异面直线,m⊥平面α,n⊥平面β,直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则()A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l►(5)(2016·课标Ⅱ)α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有________.(填写所有正确命题的编号) [例2]►(1)(2014·北京)如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别为A1C1,BC的中点.(I)求证:平面ABE⊥平面B1BCC1;(II)求证:C1F∥平面ABE;(III)求三棱锥E-ABC的体积.►(2)[2014江苏文]如图,三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知P A⊥AC,P A=6,BC=8,DF=5. 求证:(I)直线P A∥平面DEF;(II)平面BDE⊥平面ABC.[例3]►(1)[2014·陕西文]四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.(I)求四面体ABCD的体积;(II)证明:四边形EFGH是矩形.►(2)(2012·北京)如图1,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点.将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.(I)求证:DE∥平面A1CB;(II)求证:A1F⊥BE;(III)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.【变式训练】1.(2016·浙江联考)已知a,b,c为三条不同的直线,α,β是空间两个平面,且a⊂α,b⊂β,α∩β=c.给出下列命题:①若a与b是异面直线,则c至少与a,b中的一条相交;②若a不垂直于c,则a与b一定不垂直;③若a∥b,则必有a∥c;④若a⊥b,a⊥c,则必有α⊥β. 其中正确命题的个数是()A.0B.1C.2D.32.(2012·四川)下列命题正确的是()A.若两直线和同一平面所成的角相等,则这两条直线平行B.若一平面内有三点到另一平面的距离相等,则这两平面平行C.若一直线平行于两相交平面,则这条直线与这两平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行3.(2015·福建)若l,m是两条不同的直线,m垂直于平面α,则“l⊥m”是“l∥α”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.(2016·山东济南一模)设m,n是两条不同的直线,α,β是两个不同的平面.()A.若m⊥n,n∥α,则m⊥αB.若m∥β,β⊥α,则m⊥αC.若m⊥β,n⊥β,n⊥α,则m⊥αD.若m⊥n,n⊥β,β⊥α,则m⊥α5.(2016·浙江温州联考)关于直线a,b,l及平面α,β,下列命题中正确的是()A.若a∥α,b∥α,则a∥bB.若a∥α,b⊥a,则b⊥αC.若a ⊂α,b ⊂α,且l ⊥a ,l ⊥b ,则l ⊥αD.若a ⊥α,a ∥β,则α⊥β 6.(2015·山东二模)设m ,n 是空间两条直线,α,β是空间两个平面,则下列命题中不正确的是( ) A.当n ⊥α时,“n ⊥β”是“α∥β”的充要条件B.当m ⊂α时,“m ⊥β”是“α⊥β”的充分不必要条件C.当m ⊂α时,“n ∥α”是“m ∥n ”的必要不充分条件D.当m ⊂α时,“n ⊥α”是“m ⊥n ”的充分不必要条件 7.(2016·浙江)已知互相垂直的平面α,β交于直线l ,若直线m ,n 满足m ∥α,n ⊥β,则( )A.m ∥lB.m ∥nC.n ⊥lD.m ⊥n 8.(2013北京)如图,四棱锥P -ABCD 中,AB ∥CD ,AB ⊥AD ,CD =2AB ,平面P AD ⊥底面ABCD ,P A ⊥AD .E 和F 分别是CD 和PC 的中点.求证: (1)P A ⊥底面ABCD ; (2)BE ∥平面P AD ;(3)平面BEF ⊥平面PCD .9.[2014·山东文]如图,四棱锥P -ABCD 中,AP ⊥平面PCD , AD ∥BC ,AB =BC=12AD ,E ,F 分别为线段AD ,PC 的中点. (1)求证:AP ∥平面BEF ; (2)求证:BE ⊥平面P AC .10.(2013全国Ⅱ文)如图,直三棱柱ABC -A 1B 1C 1中,D ,E 分别是AB ,BB 1的中点.(Ⅰ)证明:BC 1∥平面A 1CD ;(Ⅱ)设AA 1=AC =CB =2,AB =22,求三棱锥C -A 1DE 的体积.11.(2013·辽宁)如图,AB 是圆O 的直径,P A 垂直圆O 所在的平面,C 是圆O 上的点. (1)求证:BC ⊥平面P AC ; (2)设Q 为P A 的中点,G 为△AOC 的重心,求证:QG ∥平面PBC .12.[2014·课标Ⅱ文]如图,四棱锥P -ABCD 中,底面ABCD 为矩形,P A ⊥平面ABCD ,E 为PD 的中点. (1)证明:PB ∥平面AEC ;(2)设AP =1,AD =3,三棱锥P - ABD 的体积V =34,求A到平面PBC 的距离.13.(2015江苏)如图,在直三棱柱ABC -A 1B 1C 1中,已知AC ⊥BC ,BC =CC 1.设AB 1的中点为D ,B 1C ∩BC 1=E . 求证:(1)DE ∥平面AA 1C 1C ; (2)BC 1⊥AB 1.14.(2015广东文)如图,三角形PDC 所在的平面与长方形ABCD 所在的平面垂直,PD =PC =4,AB =6,BC =3. (1)证明:BC ∥平面PDA ; (2)证明:BC ⊥PD ;(3)求点C 到平面PDA 的距离.15.(2015课标Ⅱ)如图,长方体ABCD -A 1B 1C 1D 1中,AB =16, BC =10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E =D 1F =4.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由); (2)求平面α把该长方体分成的两部分体积的比值.16.(2015陕西)如图,直角梯形ABCD 中,AD ∥B C,∠BAD =π2, AB =BC =12AD =a ,E 是AD 的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到如图2中△A 1BE 的位置,得到四棱锥A 1﹣BCDE . (Ⅰ)证明:CD ⊥平面A 1OC ;(Ⅱ)当平面A 1BE ⊥平面BCDE 时,四棱锥A 1﹣BCDE 的体积为362,求a 的值.17.(2016·课标Ⅱ文)如图,菱形ABCD 的对角线AC 与BD 交于点O ,点E ,F 分别在AD ,CD 上,AE =CF ,EF 交BD 于点H ,将△DEF 沿EF 折到△D ′EF 的位置. (1)证明:AC ⊥HD ′(2)若AB =5,AC =6,AE =54,OD ′=22,求五棱锥D ′ABCFE 的体积.18.(2016·课标Ⅲ文)如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,AD ∥BC ,AB =AD =AC =3,P A =BC =4,M 为线段AD 上一点,AM =2MD ,N 为PC 的中点. (1)证明MN ∥平面P AB ;(2)求四面体N -BCM 的体积.19.[2017全国I 文]如图,在四棱锥P-ABCD 中,AB//CD ,且∠BAP =∠CDP =90°.(1)证明:平面PAB ⊥平面PAD ; (2)若PA =PD =AB =DC ,∠ADP =90°,且四棱锥P-ABCD 的体积为83,求该四棱锥的侧面积.20.[2017全国II 文]如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD ,AB =BC =12AD , ∠BAD =∠ABC =90°.(1)证明:直线BC ∥平面PAD ;(2)若△PCD 面积为27,求四棱锥P-ABCD 的体积.21.[2017全国III 文]在正方体ABCD-A 1B 1C 1D 1中,E 为棱CD 的中点,则( )A.A 1E ⊥DC 1B.A 1E ⊥BDC.A 1E ⊥BC 1D.A 1E ⊥AC22.[2017全国III 文]如图,四面体ABCD 中,△ABC 是正三角形,AD =CD .(1)证明:AC ⊥BD ;(2)已知△ACD 是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比.。
完整版)立体几何中平行与垂直证明方法归纳

完整版)立体几何中平行与垂直证明方法归纳本文系统总结了立体几何中平行与垂直证明方法,适合高三总复时学生构建知识网络、探求解题思路、归纳梳理解题方法。
以下是常见证明方法:一、“平行关系”常见证明方法一)直线与直线平行的证明1.利用平行四边形的对边互相平行的特性;2.利用三角形中位线性质;3.利用空间平行线的传递性(即公理4);4.利用直线与平面平行的性质定理;5.利用平面与平面平行的性质定理;6.利用直线与平面垂直的性质定理;7.利用平面内直线与直线垂直的性质;8.利用定义:在同一个平面内且两条直线没有公共点。
二)直线与平面平行的证明1.利用直线与平面平行的判定定理;2.利用平面与平面平行的性质推论;3.利用定义:直线在平面外,且直线与平面没有公共点。
三)平面与平面平行的证明1.利用平面与平面平行的判定定理;2.利用某些空间几何体的特性;3.利用定义:两个平面没有公共点。
二、“垂直关系”常见证明方法一)直线与直线垂直的证明1.利用直角三角形的两条直角边互相垂直的特性;2.看夹角:两条共(异)面直线的夹角为90°,则两直线互相垂直;3.利用直线与平面垂直的性质:如果一条直线与一个平面垂直,则这条直线垂直于此平面内的所有直线。
1.利用空间几何体的特性:例如长方体侧棱垂直于底面。
2.观察直线与平面所成角度:若直线与平面所成角为90度,则该直线垂直于平面。
3.利用直线与平面垂直的判定定理:若一条直线与一个平面内的两条相交直线垂直,则该直线垂直于此平面。
4.利用平面与平面垂直的性质定理:若两个平面互相垂直,则在这两个平面内分别作垂直于交线的直线,则这两条直线互相垂直。
5.利用常用结论:例如若一条直线平行于一个平面的垂线,则该直线也垂直于此平面。
高中数学立体几何中的线线平行、线面平行、面面平行专题总结练习
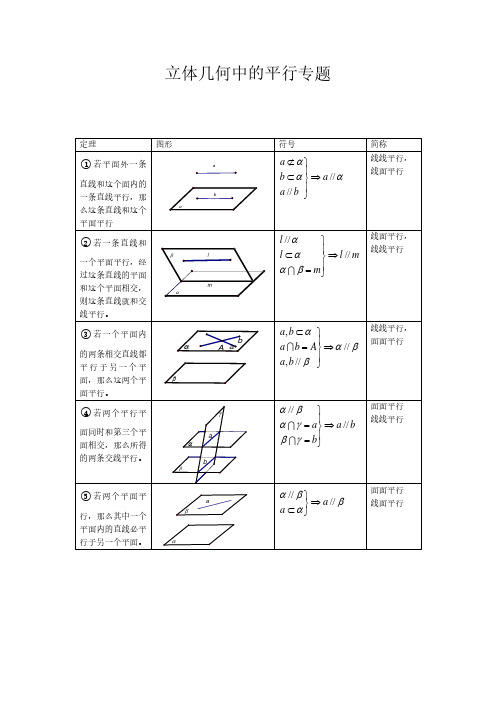
立体几何中的平行专题m β⎪=⎭,//b A b β⎪=⇒⎬⎪⎭a b γγ⎪=⇒⎬⎪=⎭//β⎫一、线线平行1.在同一平面内没有公共点的两条直线平行,如内错角相等、同位角相等、同旁内角互补、三角形中位线、平行四边形对边平行2.利用线面平行的性质定理:如果一条直线和一个平面平行,则经过这条直线的一个平面与这个平面相交,那么这条直线和交线平行。
3.平行的传递性:如果两直线都平行于第三条直线,那么这两条直线互相平行。
4.面面平行的性质定理:如果两个平行平面分别和第三个平面相交,则它们的交线平行。
5.线面垂直的性质:如果两条直线垂直于同一个平面,那么这两条直线平行。
6.用向量证明二、线面平行1.线面平行的判定定理:平面外的一条直线,如果和这个平面内的一条直线平行,那么这条直线就和这个平面平行(线面平行的判定定理)。
2.面面平行的性质定理:如果两个平面相互平行,那么在一个平面内的任何一条直线都平行于另一个平面.3.向量法−中,ABCD是平行四边形,M,N分别是AB,PC的中1. 如图,在四棱锥P ABCD点.求证:MN//平面PAD.2、如图,两个正方形ABCD 和ABEF 所在的平面相交于AB,M,N 分别是对角线AC,BF 上的点,AM=FN ,求证:MN//平面BCE.3、在正方体中,O 为面ABCD 的中心, 求证:111//.AO B CD 平面4、已知:点是平行四边形ABCD 所在平面外一点, Q 是PA 的中点,求证:PC//平面BQD.D EC DB1B 1A 1CBA5.如图,在长方体''''D C B A ABCD −中,'''''//,,ACD EF C B B A F E 平面的中点,求证:分别是棱6.在四棱锥P —ABCD 中,底面ABCD 是矩形,M ,N 分别是AB ,PC 的中点. 求证:MN ∥平面PAD ;D ABCEFPA BCDMN7.正四棱锥S ABCD −中,E 是侧棱SC的中点.求证:直线SA //平面BDE8、如图,在正方体1111ABCD A B C D −中,E 是1AA 的中点,求证: 1//A C 平面BDE 。
立体几何中线面平行的方法题附详细解答

(基本方法)立体几何中证明线面平行或面面平行都可转化为线线平行,而证明线线平行一般有以下的一些方法:(1)通过“平移”。
⑵利用三角形中位线的性质。
(3)利用平行四边形的性质。
⑷利用对应线段成比例。
(5)利用面面平行,等等。
(1)通过“平移”再利用平行四边形的性质1.如图,四棱锥 P— ABCD的底面是平行四边形,点 E、F分另I」为棱AB PD 的中点.求证:AF//平面PCE分析:取PC的中点G连EG.,FG贝踢证AEGF是平行四边形 2、如图,已知直角梯形 ABCD中, AB// CD AB丄BC AB=1, BO 2, C01+ 3,(第1题过A作AE!CD 垂足为E, G F分别为AD CE的中点,现将△ ADE沿AE折叠, 使得DEL EC.(I)求证:BC L面 CDE (U)求证:FG//面 BCD高中立体几何证明平行分析:取DB的中点H,连GH,HC贝易证D 3、已知直三棱柱 ABC— A1B1C1中,D, E, FGHC是平行四边形DE F CM为BE的中点,AC L BE.求证: 分别为AA, CC1, AB/的AC(I) CD丄BC (U) CD//平面B1FM.分析:连EA,易证GEAD是平行四边形,于是MF BA AD,CD AD, EB//平面 PAD E F G MAD CD BD BC AM EFG 求证:C1PFDAECB1 1 AB ABEF ABCD ABEF ABCD BAD FAB 90°, BC 〃 —AD BE 〃 - AF G,H2 2求证: DO ^E 为PD 中点 求证:AE//平面PBC 2 分析:取PC 的中点F,连EF 则易证ABFE 是平行四边形 11、在如图所示的几何体中,四边形 AEBABCD 为平行四边形,/ ACB 90 ,EA 丄平面ABCD, EF /AB,FG/BC,EG/AC . AB =2EF .(I)若M是线段AD 的中点,求证:GM //平面ABFE(U)若AC = BC =2AE ,求二面角A-BF-C的大小. (I) 证法 EF ACB EGF FG 1 BC2 BN P ND 90 0ABCD AM90 , ABC 〔BC FA 2 AM SM M AB F PA AF 2FP (1)求证:BE (2)求证:CM //平面BEF ; ABC PB ABC BCA 90“为EFG. GM平面PAC D分析:取AF 的中点N,连CN MN 易证平面CMN1C a, b,c , a//b a// ,b a// ,b// C ABCD M,N AB,CD MN 1 AC BC MN2ECCE PC 八EMABFr:N 『/\ EQ, 训\ -_F\XCb a//c,b//c a //1AC BC MN2AC BCMN1 -AC 2BC8.如下图所示,四个正方体中, P 分别为其所在棱的中点底面边长是2,侧棱长是 『3,D 是AC 的中点.求证:B 1C//平面A 1BD .11.如图,在平行六面体 ABCDABCD 中,E ,M ,N, G 分别是AA ,CD CB CC 的 中点,求证:(1)MN参考答案一、选择题 1 . D 【提示】当I 时,内有无数多条直线与交线I 平行,同时这些直线也与平面 平行.故A, B ,C 均是错误的 2. C【提示】棱AC, BD 与平面EFG 平行,共2条. 3. C【提示】a 〃 ,b,则a//b 或a,b 异面;所以A 错误;a 〃,b 〃 ,则a//b 或a, b 异面或a,b 相交,所以B 错误;a//,口 b,则a//b 或a, b 异面,所以D 错误;a//c,b//c , 则a//b ,这是公理4,所以C 正确. 4. B【提示】若直线 m 不平行于平面 ,且m ,则直线m 于平面 相交, 内不存 在与m 平行的图,正三棱柱ABCA 1B 1C 1 的A B 为正方体的两个顶点, ,能得到M N,直线.5. B【提示】②③④错误•②过平面外一点有且只有一个平面和这个平面平行,有无数多条直线与它平行•③过直线外一点有无数个平面和这条直线平行④平行于同一条直线的两条直线和同一平面平行或其中一条在平面上6. D【提示】本题可利用空间中的平行关系,构造三角形的两边之和大于第三边二、填空题7.平面ABC平面ABD【提示】连接AM并延长,交CD于 E,连结BN并延长交CD于F,由重心性质可知,E、F重合为一点,且该点为 CD的中点E,由EM=EN=1得MN/ AB因此,MN/平MA NB 2面ABC且MN/平面ABD8.①③【提示】对于①,面 MNP T③,MP9平行【提示】连接BD交AC于0,连OE二0曰B D,,OEC平面 ACE二B D1//平面ACE.三、解答题10.证明:设AB1与A i B相交于点P,连接PD,则P为AB i中点,D为 AC中点,PD B i C A i B B1CA1B 明:(1) M、N分别是 CD CB的中点,MN //所以 BDMNQ QC QAC 面 EBD,E0 面 EBD,所以 AGg// AG 面AHC,所以 AG// // // 所以 BD BD DG=G 面 EBD// 面 BDG。
立体几何平行判定与性质定理专题突破训练含详解

立体几何平行判定与性质定理专题突破训练一、单选题1.如图所示,P 为矩形ABCD 所在平面外一点,矩形对角线交点为O ,M 为PB 的中点,下列结论正确的个数为( )①//OM 平面PBC ②//OM 平面PCD ③//OM 平面PDA ④//OM 平面PBA A .1个B .2个C .3个D .4个2.a 、b 、l 是直线,α是平面,则下列说法正确的是( ) A .l 平行于α内的无数条直线,则//l α B .a 不在面α,则//a α C .若//a b ,b α⊂,则//a αD .若//a b ,b α⊂,则a 平行于α内的无数条直线3.若l ,m 是平面α外的两条不同直线,且//m α,则“//l m ”是“//l α”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件4.在以下四个命题中:①直线与平面没有公共点,则直线与平面平行;②直线与平面内的任意一条直线都不相交,则直线与平面平行;③直线与平面内的无数条直线不相交,则直线与平面平行;④平面外的一条直线与平面内的一条直线平行,则直线与平面不相交.正确的命题是( ) A .①②B .①②③C .①③④D .①②④5.已知两条不同直线,m n 和平面α,下列判断正确的是( ) A .若//,//,m n αα则//m n B .若,,m n αα⊥⊥则m n ⊥ C .若//,//,m m n α则//n α D .若,//,m m n α⊥则n α⊥6.下列命题正确的是( )A .一个平面内两条直线都平行于另一个平面,那么这两个平面平行B .如果一个平面内任何一条直线都平行于另一个平面,那么这两个平面平行C .平行于同一直线的两个平面一定相互平行D .如果一个平面内的无数条直线都平行于另一个平面,那么这两个平面平行 7.已知α,β是不同的平面,m ,n 是不同的直线,则下列命题不正确的是( ) A .若m ⊥α,m ∥n ,n ⊂β,则α⊥β B .若m ∥n ,α∩β=m ,则n ∥α,n ∥β C .若m ∥n ,m ⊥α,则n ⊥α D .若m ⊥α,m ⊥β,则α∥β8.下列命题中:(1)平行于同一直线的两个平面平行;(2)平行于同一平面的两个平面平行;(3)垂直于同一直线的两直线平行;(4)垂直于同一平面的两直线平行.其中正确的个数有( ) A .1B .2C .3D .49.如图,在四棱锥P-ABCD 中,M ,N 分别为AC ,PC 上的点,且MN ∥平面P AD ,则( )A .MN ∥PDB .MN ∥P AC .MN ∥AD D .以上均有可能10.如图,在三棱锥P —ABC 中,点D ,E 分别为棱PB ,BC 的中点.若点F 在线段AC 上,且满足AD //平面PEF ,则AFFC的值为( )A .1B .2C .12D .2311.在正方体1111ABCD A B C D -中,M 是1AA 的中点,过M 在平面11ACC A 内作直线MN 交11A C 于N ,若//MN 平面1BC D ,则111A NA C =( ) A .14B .13C .12D.2二、多选题12.如图所示,P 为矩形ABCD 所在平面外一点,矩形对角线的交点为O ,M 为PB 的中点,给出以下结论,其中正确的是( )A .OM ∥PDB .OM ∥平面P AC C .OM ∥平面PDAD .OM ∥平面PBA13.设a ,b 为两条直线,α,β为两个平面,下列四个命题中,错误的命题是 A .若a ,b 与α所成的角相等,则//a b B .若//a α,b β//,//αβ,则//a b C .若a α⊂,b β⊂,//b α,则//αβ D .若a α⊥,b β⊥,αβ⊥,是a b ⊥14.如图,在棱长为2的正方体1111ABCD A B C D -中,O 为正方体的中心,M 为1DD 的中点,F 为侧面正方形11AA D D 内一动点,且满足1//B F 平面1BC M ,则( )A .若P 为正方体表面上一点,则满足OPA 的面积为2的点有12个 B .动点F 的轨迹是一条线段C .三棱锥1F BC M -的体积是随点F 的运动而变化的D .若过A ,M ,1C 三点作正方体的截面Ω,Q 为截面Ω上一点,则线段1A Q 长度的取值范围为⎣ 15.如图,在四棱锥P ABCD -中,M 、N 分别为AC 、PC 上的点,且//MN 平面PAD ,则( )A .//MN PDB .//MN 平面PABC .//MN AD D .//MN PA三、双空题16.如图,在棱长为1的正方体1111ABCD A B C D -,点E ,F 分别是棱BC ,1CC 的中点,P 是侧面11BCC B 内一点(含边界),若1//A P 平面AEF ,点P 的轨迹长度为________,三棱锥P AEF -的体积为________.17.已知正方体1111ABCD A B C D -的棱长为2,点,M N 分别是棱1,BC CC 的中点,则异面直线AN 与BC 所成角的余弦值为___________;若动点P 在正方形11BCC B (包括边界)内运动,且1PA //平面AMN ,则线段1PA 的长度范围是___________.18.如图,直三棱柱111ABC A B C -的所有棱长都为4,P Q R 、、分别在棱111AA AB B C 、、上,123AP AQ B R ===,,过P Q R 、、三点的平面截三棱柱所得的截面是________边形,该截面的面积是___________.19.如图,已知斜三棱柱111ABC A B C -中,点D ,1D 分别为11,AC A C 上的点.若1//BC 平面11AB D ,则1111A D D C =________;若平面1//BC D 平面11AB D ,则AD DC=_______.20.已知四棱锥P ABCD -的底面ABCD 是边长为3的正方形,PD ⊥平面ABCD ,6PD =,E 为PD 中点,过EB 作平面α分别与线段P A 、PC 交于点M ,N ,且//AC α,则PMPA=________;四边形EMBN 的面积为________.四、解答题21.已知四棱锥P ABCD -中,//CD AB ,取PA 的中点M ,BC 的中点N ,求证://MN 平面PDC .22.如图,四棱锥P ABCD -中,点M 、N 分别为直线,PB PD 上的点,且满足PM PNPB PD=,求证://MN 平面ABCD.23.如图,在三棱柱111ABC A B C -中,1AA AC ⊥且1AA AC =,点E ,F 分别为11B C 和BC 的中点,1B A 与1A B 相交于点G .(1)证明:平面//EFG 平面11A ACC ; (2)求异面直线GE 和AC 所成角的大小.24.如图,在正方体1111ABCD A B C D -中,S 是B 1D 1的中点,E ,F ,G 分别是BC ,CD ,SC 的中点,求证:(1)EG ∥平面BDD 1B 1; (2)平面EFG ∥平面BDD 1B 1.25.如图,长方体ABCD -A 1B 1C 1D 1中,AB =AD =1,AA 1=2,点P 为DD 1的中点.(1)求证:直线BD 1∥平面P AC ; (2)求异面直线BD 1与AP 所成角的大小.26.如图,AB 是圆O 的直径.C 是圆O 上的点,P 为平面ABC 外一点.设Q 为P A 的中点,G 为AOC △的重心,求证://QG 平面PBC .27.如图,已知//αβ,点P 是平面,αβ外的一点,直线PA 和PC 分别与β相交于B 和D .(1)求证://AC BD ;(2)已知4cm,5cm,3cm PA AB PC ===,求PD 的长.28.如图所示,已知α,β,γ都是平面,且////αβγ,两条直线l ,m 分别与平面α,β,γ相交于点A ,B ,C 和点D ,E ,F . 求证:AB DEBC EF=.29.如图所示,两条异面直线,AB CD 与三个平行平面,,αβγ分别相交于,,A E B 及 ,,C F D 又AD BC 、与平面β的交点为,H G .求证:四边形EHFG 为平行四边形.30.如图,在四棱锥O ABCD -中,底面ABCD 是矩形.(1)设M 为OA 上靠近A 的三等分点,N 为BC 上靠近B 的三等分点.求证://MN 平面OCD .(2)设E 是OD 上靠近点D 的一个三等分点,试问:在OD 上是否存在一点F ,使//BF 平面ACE 成立?若存在,请予以证明;若不存在,说明理由.31.如图,已知在直三棱柱111ABC A B C -中,,,,M N P Q 分别是1111,,,AA BB AB B C 的中点.(1)在图中画出过,,M N Q 三点的截面,并说出截面图形的形状(不必说明画法与理由); (2)求证:1PC //平面MNQ .32.如图,在三棱柱111ABC A B C -中,点D ,1D 分别为AC ,11A C 上的动点,若平面1//BC D 平面11AB D ,请问ADDC是否为定值.若为定值求出该值,若不是定值,说明理由.33.(如图1)在直角梯形ABCD 中,//AB DC ,90BAD ∠=︒,4AB =,2AD =,3DC =,点E 在CD 上,且2DE =.将ADE 沿AE 折起,使得平面ADE ⊥平面ABCE (如图2).(1)求证:BE AD ;(2)在线段BD 上是否存在点P ,使得//CP 平面ADE ?若存在,求:PD BP 的值;若不存在,请说明理由.参考答案1.B【分析】证明//OM PD ,即可证明②③正确;M ∈平面PBC ,故①错误,M ∈平面PAB ,故④错误.【详解】对于①,M ∈平面PBC ,故①错误;对于②,由于O 为BD 的中点,M 为PB 的中点,则//OM PD , OM ⊂平面PCD ,PD ⊂平面PCD ,则//OM 平面PCD ,故②正确;对于③,由于//OM PD ,OM ⊂平面PAD ,PD ⊂平面PAD ,则//OM 平面PAD ,故③正确;对于④,由于M ∈平面PAB ,故④错误.故选:B2.D【分析】利用线面平行的判定定理和性质定理逐个分析判断即可【详解】对于A ,当l 平行于α内的无数条直线,若l α⊂,则l 与α不平行,所以A 错误, 对于B ,当a 不在面α时,a 与α有可能相交,所以B 错误,对于C ,当//a b ,b α⊂时,若a α⊂,则a 与α不平行,所以C 错误,对于D ,当//a b ,b α⊂时,由线面平行的性质可知a 平行于α内的无数条直线,所以D 正确,故选:D3.A【分析】根据线线、线面的平行关系,结合条件间的推出关系,判断“//l m ”、“//l α”之间的充分、必要关系.【详解】∵l ,m 是平面α外的两条不同的直线,//m α,∴若//l m ,则推出“//l α”;若//l α,则//l m 或l 与m 相交;∴若l ,m 是平面α外的两条不同直线,且//m α,则“//l m ”是“//l α”的充分不必要条件. 故选:A.4.D【分析】根据线面平行的定义及判定定理可判断.【详解】定义:一条直线与一个平面无公共点(不相交),称为直线与平面平行.可知①②正确;线面平行的判定定理:平面外的一条直线与平面内的一条直线平行,则该直线与此平面平行. 可知④正确;当线在面内时,直线与平面内的无数条直线不相交(平行时),所以③不正确.故选:D.5.D【分析】根据线线、线面、面面的平行与垂直的位置关系即可判断.【详解】解:对于选项A :若//,//m n αα,则m 与n 可能平行,可能相交,可能异面,故选项A 错误;对于选项B :若,m n αα⊥⊥,则//m n ,故选项B 错误;对于选项C :当n ⊂α时不满足//n α,故选项C 错误;综上,可知选项D 正确.故选:D.6.B【分析】根据面面平行的知识对选项逐一分析,由此确定正确选项.【详解】对于A 选项,这两个平面可能相交,故A 选项错误.对于B 选项,如果一个平面内任何一条直线都平行于另一个平面,那么这两个平面平行,正确,故B 选项正确.对于C 选项,这两个平面可能相交,故C 选项错误.对于D 选项,这两个平面可能相交,故D 选项错误.故选:B7.B【分析】根据空间垂直、平行逐项讨论,即可得出结论.【详解】选项A:m ⊥α,m ∥n ,可得n ⊥α,n ⊂β,则α⊥β,该选项正确;选项B:m ∥n ,α∩β=m ,直线n 可能在α或β内,该选项不正确;选项C:是线面垂直的判定,故正确;选项D:是面面平行的判定,故正确.故选:B【点睛】本题考查有关空间线面平行、垂直性质和判定定理,属于基础题.8.B【分析】举特例说明可判断命题(1),(3);利用面面平行的传递性可判断(2);利用线面垂直的性质可判断(4)即可得解.【详解】对于命题(1),长方体1111ABCD A B C D -中,平面ABCD 与平面11ABB A 都与直线11C D 平行,而这两个平面却相交,(1)不正确;对于命题(2),由平面与平面平行的传递性知,平行于同一平面的两个平面平行是正确的,(2)正确;对于命题(3),长方体1111ABCD A B C D -中,棱AB ,AD 都垂直于棱AA 1,而AB 与AD 相交,(3)不正确;对于(4),由直线与平面垂直的性质知,垂直于同一平面的两直线平行是正确的,(4)正确, 所以命题(2),(4)都正确,有2个.故选:B9.B【分析】直接利用线面平行的性质分析解答.【详解】∵MN ∥平面P AD ,MN ⊂平面P AC ,平面P AD ∩平面P AC=P A ,∴MN ∥P A.故选:B10.C【分析】连接CD ,交PE 于G ,连接FG ,由//AD 平面PEF ,得到//AD FG ,由点D ,E 分别为棱PB ,BC 的中点,得到G 是PBC 的重心,由此能求出结果.【详解】解:连接CD ,交PE 于G ,连接FG ,如图,//AD 平面PEF ,平面ADC平面PEF FG =,//AD FG ∴, 点D ,E 分别为棱PB ,BC 的中点.G ∴是PBC 的重心, ∴12AF DG FC GC ==. 故选:C .11.A【分析】连接AC 、BD ,AC BD E =,连接1C E ,取11A C 的中点F ,连接AF ,根据正方体的性质可得1//AF EC ,再由线面平行的性质得到1//MN C E ,从而得到//MN AF ,即可得解;解:连接AC 、BD ,AC BD E =,连接1C E ,取11A C 的中点F ,连接AF ,在正方体1111ABCD A B C D -中1AE C F =,1//AE C F ,所以四边形1AEC F 为平行四边形,所以1//AF EC ,又//MN 平面1BC D ,MN ⊂平面11ACC A ,平面11ACC A 平面11BC D C E =,所以1//MN C E ,所以//MN AF ,因为M 是1AA 的中点,所以N 为1A F 的中点,所以11114A N AC =,即11114A N A C = 故选:A12.AC【分析】根据已知条件,利用三角形中位线定理判定A 正确;利用线面平行的判定定理判定C 正确;根据线面平行的定义——没有公共点,判定BD 错误.【详解】因为矩形对角线的交点为O ,所以O 是BD 的中点, 又M 为PB 的中点,OM ∴为△PBD 的中位线,//OM PD ∴,又OM ⊄平面PAD ,PD ⊂平面PAD ,所以OM ∥平面PDA ,故AC 正确;OM 与平面PAC 有公共点O ,与平面PBA 有公共点M ,故BD 错误.故选:AC .13.ABC根据题意,依次分析选项,A 、用直线的位置关系判断.B 、用长方体中的线线,线面,面面关系验证.C 、用长方体中的线线,线面,面面关系验证.D 、由a α⊥,αβ⊥,可得到a β⊂或//a β,再由b β⊥得到结论.【详解】解:A 、直线a ,b 的方向相同时才平行,不正确;B 、用长方体验证.如图,设11A B 为a ,平面AC 为α,BC 为b ,平面11A C 为β,显然有//a α,b β//,//αβ,但得不到//a b ,不正确;C 、可设11A B 为a ,平面1AB 为α,CD 为b ,平面AC 为β,满足选项C 的条件却得不到//αβ,不正确;D 、a α⊥,αβ⊥,a β∴⊂或//a β又b β⊥,a b ∴⊥,D 正确故选:ABC【点睛】本题考查线线平行与垂直、线面平行的判定.把线面关系放到长方体中有助于问题解决,是解题中是常用的方法;本题是基础题.14.BD【分析】选项A :设O '为底面正方形ABCD 的中心,根据OO A '的面积为12AO OO ''⋅=,由此可判断选项A ;选项B :分别取1AA ,11A D 的中点H ,G ,连接1B G ,GH ,1HB ,1AD ;证明平面1B GH ∥平面1BC M ,从而得到点F 的轨迹为线段GH .选项C :根据选项B 可得出GH ∥平面1BC M ,从而得到点F 到平面1BC M 的距离为定值,再结合1BC M 的面积也为定值,从而可得到三棱锥1F BC M -的体积为定值.选项D :设N 为1BB 的中点,从而根据面面平行的性质定理可得到截面Ω即为面1AMC N ,从而线段1A Q 长度的最大值为线段11A C 的长,最小值为四棱锥11A AMC N -以1A 为顶点的高.【详解】对于A :设O '为底面正方形ABCD 的中心,连接AO ,AO ',OO ',则12AO AC '=1112OO AA '==,所以OO A '的面积为11122AO OO ''⋅== 所以在底面ABCD 上点P 与点O '必重合,同理正方形11ABB A 的中心,正方形11ADD A 的中心都满足题意.又当点P 为正方体各条棱的中点时也满足OPA A 不正确; 对于B :如图①,分别取1AA ,11A D 的中点H ,G ,连接1B G ,GH ,1HB ,1AD . 因为11B H C M ∥,1GH BC ∥,1B H ⊂平面BHG ,1C M ⊂平面1BC M ,GH ⊂平面BHG ,1C B ⊂面1BC M ,111BC C M C ⋂=,所以平面1B GH ∥平面1BC M ,而1B F ∥平面1BC M ,所以1B F ⊂平面1B GH ,所以点F 的轨迹为线段GH ,故B 正确; 对于C :由选项B 可知,点F 的轨迹为线段GH ,因为GH ∥平面1BC M ,则点F 到平面1BC M 的距离为定值,同时1BC M 的面积也为定值,则三棱锥1F BC M -的体积为定值,故C 不正确; 对于D :如图②,设平面Ω与平面11AA B B 交于AN ,N 在1BB 上.因为截面Ω⋂平面11AA D D AM =,平面11AA D D ∥平面11BB C C ,所以1AM C N ∥.同理可证1AN C M ∥,所以截面1AMC N 为平行四边形,所以点N 为1BB 的中点.在四棱锥11A AMC N -中,侧棱11A C 最长,且11AC =设棱锥11A AMC N -的高为h ,因为1AM C M ==1AMC N 为菱形,所以1AMC 的边1AC 1AC =则112AMC S =⨯△1111111142223323C AA M AA M V SD C -=⋅=⨯⨯⨯⨯=△,所以111111433A AMC AMC C AA M V S h V --=⋅===△,解得h =.综上,可知1A Q 长度的取值范围是⎣,故D 正确.故选:BD .15.BD【分析】利用线面平行的性质结合线面平行的判定可得出结论.【详解】因为//MN 平面PAD ,MN ⊂平面PAC ,平面PAC 平面PAD PA =,//MN PA ∴, PA ⊂平面PAB ,MN ⊄平面PAB ,因此,//MN 平面PAB .故选:BD.16 112 【分析】分别取棱1BB ,11B C 的中点M ,N ,连接1A M ,1A N ,MN ,1BC ,NE ,推导出//MN 平面AEF ,1//A N 平面AEF ,得到平面1//A MN 平面AEF ,由此得以点P 的轨迹是线段MN , 借助等积变换可得三棱锥P AEF -的体积.【详解】解:如图,分别取棱1BB ,11B C 的中点M ,N ,连接1A M ,1A N ,MN ,1BC ,NE , M ,N ,E ,F 分别是其所在棱的中点,1//MN BC ∴,1//EF BC ,//MN EF ∴,MN ⊂/平面AEF ,EF ⊂平面AEF ,//MN ∴平面AEF ,1//AA NE ,1AA NE =,∴四边形1AENA 为平行四边形,1//A N AE ∴,1A N ⊂/平面AEF ,AE ⊂平面AEF ,1//A N ∴平面AEF ,1A N M N N =,∴平面1//A MN 平面AEF , P 是侧面11BCC B 内一点,且1//A P 平面AEF ,∴点P 必在线段MN 上,∴点P 的轨迹长度为112MN BC =∵//MN 平面AEF , ∴1111133412P AEF N AEF A NE NE F F V V V S AB ---===⋅=⨯⨯= .112.17.23 【分析】异面直线AN 与BC 所成的角就是∠DAN ,计算得3AN =,所以2cos 3DAN ∠=;由面面平行的性质得点P 在1BB 与11B C 中点的连线EF 上,设EF 中点为H ,则1A H 最短,1A E 或1A F同时最大,所以所求范围是. 【详解】 因为BC ∥AD, 异面直线AN 与BC 所成的角就是直线AN 与AD 所成的角,即∠DAN 为异面直线AN 与BC 所成的角,3AC AN == 所以2cos 3AD DAN AN ∠==; 取11B C 的中点E ,1BB 的中点F ,连接1A E ,1A F ,EF ,取EF 中点O ,连接1A O ,点M ,N 分别是棱长为2的正方体1111ABCD A B C D -中棱BC ,1CC 的中点,1//AM A E ∴,//MN EF , AM M N M =,1A E EF E =,∴平面//AMN 平面1A EF ,动点P 在正方形11BCC B (包括边界)内运动,且1//PA 面AMN ,∴点P 的轨迹是线段EF ,11A E A F ====EF1AO EF ∴⊥,∴当P 与O 重合时,1PA 的长度取最小值1A O =,当P 与E (或)F 重合时,1PA 的长度取最大值为11A E A F ==1PA ∴的长度范围为. 故答案为:23;. 【点睛】求异面直线的夹角一般要通过平行转换成平面角,第二个问题中动点的轨迹要点是求出直线的轨迹,是通过面面平行的思想转换的,做题时可以通过单独画截面图求解.18.五【分析】延长PQ 和1B B 交于M ,连RM 交BC 于E ,连QE ,延长QP 和11B A 交于N ,连RN 交11A C 于F ,连FP ,则过P Q R 、、三点的平面截三棱柱所得的截面是五边形PQERF ,通过计算可得ME EQ ⊥,RF MR ⊥,利用大直角三角形的面积减去两个小三角形的面积可得结果.【详解】如图:延长PQ 和1B B 交于M ,连RM 交BC 于E ,连QE ,延长QP 和11B A 交于N ,连RN 交11A C 于F ,连FP ,则过P Q R 、、三点的平面截三棱柱所得的截面是五边形PQERF , 依题意可知,P Q 为1,AA AB 的中点,所以PAQ △与MBQ 全等,所以2MB PA ==, 因为1//BE B R ,所以11BE MB B R MB =,所以2316BE ⨯==,所以ME因为QE ==MQ所以222ME EQ MQ +=,所以ME EQ ⊥,因为平面MRN 与两平行平面ABC 和111A B C 的交线为EQ 和RF ,所以//EQ RF ,所以RF MR ⊥,MR =MN =所以RN因为22211RN B R B N +=,所以1NR B R ⊥,又13FC R π∠=,所以1122FC RC ==,所以FR ==NF RN FR =-==cos RN FNP MN ∠===sin FNP ∠==所以12NPF S =⨯=△12MEQ S ==△又1122MRN S MR RN =⨯=⨯=△,所以截面面积为MNR NPF MEQ S S S --==△△△故答案为:五;.【点睛】关键点点睛:利用平面的基本性质作出截面是解题关键.19.1 1【分析】连接1A B 交1AB 于点O ,连接1OD ,由1//BC 平面11AB D 得性质定理得到11//BC OD ,又在11A BC 中,O 为1A B 的中点,可知1D 为11A C 的中点,即可求得结果;根据平面1//BC D 平面11AB D 的性质定理可知11//BC OD ,同理11//AD DC ,再根据比例关系即可求得结果.【详解】如图,连接1A B 交1AB 于点O ,由三棱柱性质知,O 为1A B 的中点,连接1OD1//BC 平面11AB D ,1BC ⊂平面11A BC ,平面11A BC ⋂平面111AB D OD =,11//BC OD ∴,又在11A BC 中,O 为1A B 的中点,故1D 为11A C 的中点,所以11111A D D C = 若平面1//BC D 平面11AB D , 又平面11A BC ⋂平面11BDC BC =,平面11A BC ⋂平面111AB D OD =,11//BC OD ∴,同理11//AD DC ,11111A D A O D C OB ∴=,1111A D D C DC AD= 又11AO OB =,1DC AD=,则1AD DC =【点睛】关键点睛:本题考查线面平行,及面面平行的性质定理,解题的关键是熟记线面平行证线线平行的性质定理,及面面平行证线线平行的性质定理,考查学生的逻辑推理能力与空间想象能力,属于中档题.20.23【分析】延伸平面α,交AC 所在的平面ABCD 于RS ,即平面α平面ABCD RS =,可得//AC RS ,在三角形PAD △和RED 中,利用平面几何三角形全等和平行线中的比例关系可得PM PA;至于四边形EMBN 的面积,连接MN ,BD ,可证明MN BE ⊥,求出,MN BE 的长度,通过面积公式12MN EB ⋅可得答案. 【详解】延伸平面α,交AC 所在的平面ABCD 于RS ,即平面α平面ABCD RS =,又B ∈平面α平面ABCD , B RS ∴∈,即,,R S B 三点共线,又//AC α,由线面平行的性质定理可得//AC RS ,则4ARB ABR π∠=∠=,即AR AB =,∴点A 为RD 的中点,又E 为PD 中点, 则6,3,2PD RD DA DE PDA ADP π====∠=∠=,PAD RED ∴≅,MPE MRA ∴∠=∠,又,PME RMA PE RA ∠=∠=,PME RMA ∴≅,则ME MA =,过M 作MK PD ⊥交PD 于点K ,222PM MK MK ME MA PA AD DR RE PA∴==⋅=⋅=⋅, 则2PM MA =,2233PM MA PA MA ∴==; 连接MN ,BD 由23PM PA =同理可得23PN PC =, //MN AC ∴,又PD ⊥平面ABCD ,AC ⊂平面ABCD ,PD AC ∴⊥,又,BD AC BD PD D ⊥=,AC ∴⊥面PBD ,又BE ⊂面PBD ,AC BE ∴⊥,MN BE ∴⊥,23MN PM AC PA ==, 2233MN AC ∴==⨯又EB ==所以四边形EMBN 的面积为1122MN EB ⋅=⨯=故答案为:23;【点睛】本题考查空间线面平行的判定和性质,考查空间线面垂直的判定和性质,关键是利用线面平行的性质合理作出图像,考查学生的作图能力和计算能力,是中档题.21.证明见解析【分析】如图,连接AN并延长,交DC的延长线于点E,连接PE,可得N为AE的中点,再由三角形中位线定理可得MN∥PE,然后由线面平行的判定定理可证得结论【详解】证明:如图,连接AN并延长,交DC的延长线于点E,连接PE.因为CD∥AB,N为BC的中点,所以N为AE的中点.因为M为PA的中点,所以MN∥PE.因为MN⊄平面PDC,PE⊂平面PDC,所以MN∥平面PDC.22.证明见解析【分析】MN平面ABCD.通过线线平行来证得//【详解】连接BD , ∵PM PN PB PD=,∴//MN BD , ∵MN ⊄平面ABCD ,BD ⊂平面ABCD ,∴//MN 平面ABCD .23.(1)证明见解析;(2)45︒【分析】(1)连接11,A C AC ,通过证明//FG 平面11A ACC 与//EG 平面11A ACC ,可得平面//EFG 平面11A ACC ;(2)找到1C AC ∠为异面直线GE 和AC 所成角,求1C AC ∠即可.【详解】证明:(1)由题意可得,点,F G 分别是BC 和1BA 的中点,连接11,A C AC ,1//FG A C ∴,又FG ⊄平面111,A ACC A C ⊂平面11A ACC ,//FG ∴平面11A ACC ,同理:1//EF C C ,则 //EF 平面11A ACC ,又,FG EF F FG =⊂平面,EFG EF ⊂平面EFG ,∴平面//EFG 平面11A ACC ;(2)点,G E 分别是1B A 和11B C 的中点,1//GE AC ∴,1C AC ∴∠为异面直线GE 和AC 所成角,由题意知,四边形11ACC A 为正方形,所以145C AC ︒∠=,即GE 和AC 所成角为45︒.【点睛】本题考查通过线面平行证明面面平行,考查异面直线所成的角,是基础题.24.(1)证明见解析;(2)证明见解析.【分析】(1)连接SB ,得到EG ∥SB ,结合线面平行的判定定理,即可证得EG ∥平面BDD 1B 1. (2)连接SD ,得到FG ∥SD ,证得FG ∥平面BDD 1B 1,再由EG ∥平面BDD 1B 1,面面平行的判定定理,即可证得平面EFG ∥平面BDD 1B 1.【详解】(1)如图所示,连接SB ,因为E ,G 分别是BC ,SC 的中点,所以EG ∥SB ,又因为SB ⊂平面BDD 1B 1,且EG ⊄平面BDD 1B 1,所以直线EG ∥平面BDD 1B 1.(2)如图所示,连接SD ,因为F ,G 分别是CD ,SC 的中点,所以FG ∥SD , 又因为SD ⊂平面BDD 1B 1,且FG ⊄平面BDD 1B 1,所以FG ∥平面BDD 1B 1,又由EG ∥平面BDD 1B 1,EG ⊂平面EFG ,FG ⊂平面EFG ,EG ∩FG =G ,所以平面EFG ∥平面BDD 1B 1.25.(1)证明见解析(2)30︒【分析】(1)连结PO ,先证线线平行,再证线面平行即可;(2)由(1)知,1PO BD ∥,所以APO ∠即为异面直线1BD 与AP 所成的角,然后再解三角形即可.(1)证明:设AC 和BD 交于点O ,则O 为BD 的中点.连结PO ,又因为P 是1DD 的中点,所以1PO BD ∥.又因为PO ⊂平面1,PAC BD ⊄平面PAC所以直线1BD ∥平面PAC .(2)由(1)知,1PO BD ∥,所以APO ∠即为异面直线1BD 与AP 所成的角.在ADP △中可得PA =因为12PA PC AO AC ===且PO AO ⊥,所以1sin2AO APO AP ∠===. 又090APO ︒︒<∠≤,所以30APO ︒∠=故异面直线1BD 与AP 所成角的大小为30︒.26.证明见解析【分析】连接OG 并延长,交AC 于点M ,连接QM ,QO ,由已知可得M 为AC 的中点,//QM PC ,//OM BC ,可证//QM 平面PBC ,//OM 平面PBC ,从而平面//QMO 平面PBC , 即可证明结论.【详解】证明:如图,连接OG 并延长,交AC 于点M ,连接QM ,QO .由G 为AOC △的重心,得M 为AC 的中点.由Q 为M 的中点,得//QM PC ,PC ⊂平面PBC ,QM ⊄平面PBC ,所以//QM 平面PBC ,又O 为AB 的中点,所以//OM BC .同理可证//OM 平面PBC ,因为QM MO M ⋂=,QM ⊂平面QMO ,MO ⊂平面QMO ,所以平面//QMO 平面PBC .因为QG ⊂平面QMO ,所以//QG 平面PBC .【点睛】本题考查利用面面平行的性质定理证明线面平行,属于基础题.27.(1)证明见解析;(2)274 【分析】(1)由面面平行的性质定理得证线线平行;(2)由平行线的性质可求得线段长.【详解】(1)PB PD P =,所以,PB PD 确定一个平面PBD ,由题意平面PBD AC α=,平面PBD BD β=,//αβ所以//AC BD ;(2)由(1)//AC BD ,所以PA PC AB CD =,所以351544PC AB CD PA ⋅⨯===, 所以1527344PD PC CD =+=+=. 28.证明见解析【分析】连接DC ,设DC 与平面β相交于点G ,连,BG GE ,根据面面平行的性质定理,可得//BG AD ,利用三角形相似关系,即可证明结论.【详解】证明:连接DC ,设DC 与平面β相交于点G ,则平面ACD 与平面α,β分别相交于直线AD ,BG ,平面DCF 与平面β,γ分别相交于直线GE ,CF .因为//αβ,所以//BG AD ,因此CBG CAD ,因此AB DG BC GC=.同理可得DG DE GC EF =.因此AB DE BC EF =. 【点睛】本题考查根据面面平行的性质定理,以及线线平行的性质,属于基础题.29.证明见解析.【分析】由αβ∥得到AC EG HF ,同理得到BD EH GF ,所以四边形EHFG 为平行四边形.【详解】证明:∵平面ABC平面AC α=, 平面ABC平面BC β=,且αβ∥AC EG ∴. 同理可证AC HF .EG HF ∴.同理可证∥EH FG .∴四边形EHFG 为平行四边形.【点睛】本题考查面面平行的性质,属于简单题.30.(1)证明见解析;(2)在OD 上是存在OE 中点F ,使//BF 平面ACE 成立,证明见解析.【分析】(1)取AD 上靠近A 的三等分点G ,连接MG NG ,,可得//MG OD ,进而证明//MG 平面OCD ,同理证明//NG 平面OCD ,得出面//MNG 平面OCD 即可证明;(2)存在OE 中点F ,连BF BD ,,使=BD AC P ⋂,连PE ,得出//PE BF 即可证明. 【详解】(1)如图,取AD 上靠近A 的三等分点G ,连接MG NG ,,AOD △中,:1:2:=1:2AM MO AG GD =,, 则//MG OD ,又MG ⊄平面OCD ,OD ⊂平面OCD ,//MG ∴平面OCD ,同理,//NG 平面OCD ,又=MG NG G ⋂,∴平面//MNG 平面OCD ,又MN ⊂平面MNG ,∴//MN 平面OCD .(2)存在OE 中点F ,使//BF 平面ACE 成立.取OE 中点F ,连BF BD ,,使=BD AC P ⋂,连PE .ABCD 是矩形,P ∴是BD 的中点,又E 是OD 上靠近点D 的一个三等分点,且F 是OE 中点,E ∴是FD 的中点,BDF ∴中,//PE BF ,又PE ⊂平面ACE ,BF ⊄平面ACE ,//BF ∴平面ACE ,故在OD 上是存在OE 中点F ,使//BF 平面ACE 成立.【点睛】关键点睛:本题考查线面平行的证明,解题的关键是正确理解线面平行的判定定理以及面面平行的性质.31.(1)MHQN 是过,,M N Q 三点的截面,梯形;(2)证明见解析.【分析】(1)取11A C 中点H ,连接 HQ QN ,, NM ,MH ,即可得出结果; (2)连接11,BC AC ,根据面面平行的判定定理,得到平面//MNQ 平面1ABC ,进而可得线面平行.【详解】(1)取11A C 中点H ,连接 HQ QN ,, NM ,MH ,则梯形MHQN 是过,,M N Q 三点的截面,如图所示.(2)连接11,BC AC .∵三棱柱111ABC A B C -是直三棱柱,∴四边形11ABB A 是矩形.∵,M N 分别是11,AA BB 的中点,∴//MN AB .在11B C B 中,,Q N 分别是111,B C BB 的中点,∴1//NQ BC .又∵1,AB BC B MN NQ N ⋂=⋂=,∴平面//MNQ 平面1ABC .又∵P 是AB 的中点,∴1PC ⊂平面1ABC ,∴1//PC 平面MNQ .【点睛】本题主要考查几何体过点的截面图形,以及证明线面平行,熟记面面平行的判定定理与性质定理即可,属于常考题型.32.是定值1,理由见解析.【分析】连接1A B 交1AB 于点O ,连接1OD ,由平面1BC D ∥平面11AB D ,得到1BC ∥1OD ,1AD ∥1DC ,则四边形11ADC D 是平行四边形,根据111112C D AC =,得到11111122AD C D AC AC ===,从而可得1AD DC = 【详解】解:如图,连接1A B 交1AB 于点O ,连接1OD ,由棱柱的性质,可知四边形11A ABB 为平行四边形,所以O 为1A B 的中点,因为平面1BC D ∥平面11AB D ,且平面11A BC ⋂平面111AB D D O =,平面11A BC ⋂平面11BC D BC =,所以1BC ∥1OD ,所以1D 为线段11A C 的中点,所以111112C D AC =, 因为平面1BC D ∥平面11AB D ,平面11AAC C平面11BDC DC =,平面11AAC C 平面111AB D AD =, 所以1AD ∥1DC ,因为AD ∥11C D ,所以四边形11ADC D 是平行四边形, 所以11111122AD C D AC AC ===, 所以1AD DC =,33.(1)证明见解析;(2)存在,13=PD BP . 【分析】 (1)首先根据题意易证AE EB ⊥,再根据面面垂直的性质得到EB ⊥平面AED ,从而得到EB AD ⊥.(2)首先在AB 上取一点的F ,满足14AF AB =,在BD 上取一点的P ,满足14DP DB =,连接,,PF PC FC ,易证//PF 平面ADE ,//PF 平面ADE ,从而得到平面//PFC 平面ADE ,再利用面面平行的性质得到//PC 平面ADE ,从而得到13=PD BP . 【详解】(1)在梯形ABCE 中,取AB 的中点H ,连接EH ,BE ,如图所示所以AE ==BE == 又因为4AB =,所以222AE BE AB +=,即AE EB ⊥. 在图2中,因为平面ADE ⊥平面ABCE AE =,AE EB ⊥,所以EB ⊥平面AED .又因为AD ⊂平面AED ,所以EB AD ⊥.(2)在AB 上取一点的F ,满足14AF AB =, 在BD 上取一点的P ,满足14DP DB =,连接,,PF PC FC ,如图所示:因为//AF EC ,AF EC =,所以四边形AFCE 为平行四边形, 所以//FC AE .又因为AE ⊂平面ADE ,⊄FC 平面ADE ,所以//FC 平面ADE , 因为34BF BP BA BD ==,所以//PF AD . 又因为AD ⊂平面ADE ,PF ⊄平面ADE ,所以//PF 平面ADE , 又因为PF ⊂平面PFC ,PC ⊂平面PFC ,FCPF F =, 所以平面//PFC 平面ADE .又因为PC ⊂平面PFC ,所以//PC 平面ADE . 所以13=PD BP .。
立体几何平行问题证明方法秘笈:

DE B 1A 1C 1CABFM PEDC B A立体几何平行问题证明方法秘笈:专题一:线线平行与线面平行:1、两直线平行的判定方法:①定义:在同一个平面内,且没有公共点的两条直线平行.②如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行,③平行于同一直线的两直线平行.④垂直于同一平面的两直线平行⑤两平行平面与同一个平面相交,那么两条交线平行。
2、直线与平面平行的判定方法:①定义:若一条直线和平面没有公共点,则这直线与这个平面平行.②如果平面外一条直线和这个平面内的一条直线平行,则这条直线与这个平面平行.③两个平面平行,其中一个平面内的直线平行于另一个平面.方法1、做平行四边形 1.如图,四棱锥P -ABCD 的底面是平行四边形,点E 、F 分别为棱AB 、 PD 的中点.求证:AF ∥平面PCE ;2、已知直三棱柱ABC -A 1B 1C 1中,D, E, F 分别为AA 1, CC 1, AB 的中点,M 为BE 的中点, 求证:C 1D ∥平面B 1FM.3、如图所示, 四棱锥P ABCD 底面是直角梯形, CD=2AB, E 为PC 的中点, 证明: ;4.正方体ABCD —A 1B 1C 1D 1中O 为正方形ABCD 的中心,求证: D 1O//平面A 1BC 15、在四棱锥P-ABCD 中,AB ∥CD ,AB=DC ,.求证:AE ∥平面PBC ;6、如图,平面平面,四边形与都是直角梯形,,,分别为的中点 证明:CH//面ABEF方法2、利用三角形中位线的性质。
1、如图,已知、、、分别是四面体的棱、、、的中点,求证:∥平面。
-,,AD CD AD BA ⊥⊥//EB PAD 平面21中点为PD E ABEF ⊥ABCD ABEF ABCD 090,BAD FAB BC∠=∠=//=12AD BE //=12AF ,G H ,FA FD E F G M AD CD BD BC AM EFG EFACDP(第1题2、如图,ABCD 是正方形,E 是PC 的中点。
立体几何证明平行专题
立体几何证明平行专题训练命题:***1. 如图,四棱锥P—ABCD勺底面是平行四边形,点E、F分别为棱AB PD的中点. 求证:AF//平面PCE(第1题图)2、如图,已知直角梯形ABCD中, AB// CD AB丄BC AB= 1 , BC= 2, CD= 1 + J3 , 过A作AE!CD垂足为E, G F分别为AD CE的中点,现将△ ADE沿AE折叠,使得DEL EC.(I)求证:FG//面BCD (H)求证:BC L面CDEABC- A1B1C1 中,D, E, F 分别为AA, CC1, AB 的中点,M为BE的中点,AC L BE.求证:(I) C1D// 平面BFM.4、如图所示,四棱锥P ABCD底面是直角梯形,BA AD,CD AD, CD=2AB, E为PC的中点,3、已知直三棱柱(H) GDI BC求证:EB //平面PAD ;已知E 、F 、G 、M 分别是四面体的棱 AD 、CD 、BD 、BC 的中点,求证:AM //平面EFG 。
ABCD 是正方形,0是正方形的中心, E 是PC 的中点。
PA //平面 BDE 5、如图,6、如图,求证:7.如图,求 三棱柱 ABC-A 1B 1C 1中,D 为AC 的中点. 证12、如图,三棱锥中,底面,,PB =BC =CA 为的中点,为的中点,点在上,且(1) 求证:平面;(2) 求证:平面;AB ABEF ABCD ABEF ABCD BAD FAB 900,B(A 〃 BC//平面DHG C,D, F,E i C 1 E 为PD 中点 求证:AE//平面P B Q 」—AF/G,H FA,FD 211、如图:S 是平行四边形ABCD 平面外一点,M N 分别是 SA BD 上的点,且 ^A M =-BN , SM ND 求证:MIN/平面SDCDB C P提示:1. 分析:取PC的中点G,连EG., FG,则易证AEGF是平行四边形2. 分析:取DB的中点H,连GH,HC则易证FGHC是平行四边形3. 分析:连EA易证GEAD是平行四边形,于是MF分析::取PD的中点F,连EF,AF则易证ABEF是平行四边形5. 分析:连MD交GF于H,易证EH是厶AMD的中位线6. 分析:连接EO即为三角形中位线7. 分析:连BC交BG于点E,易证ED是厶B i AC的中位线8. 分析:证四边形BCHG 是平行四边形9. 分析:连Di B i交A i C i于O点,易证四边形OBBO是平行四边形10. 分析:取PC的中点F,连EF则易证ABFE是平行四边形11. 分析:过M作ME分析:取AF的中点N,连CN MN|易证平面CMN//EFB。
立体几何中证明线线平行的方法
立体几何中证明线线平行的方法
在立体几何中,证明两条线平行的方法通常有以下几种:
1. 利用平行线的性质:如果可以证明两条线分别与同一条第三条线平行,则可以推断这两条线平行。
这可以通过使用平行线的定理或者平行线的判定条件来证明。
2. 利用等角定理:如果可以证明两条线与另一条线之间形成的对应角度相等,则可以推断这两条线平行。
这可以通过使用等角定理(如同位角、内错角等)来证明。
3. 利用平行四边形的性质:如果可以证明两条线分别是平行四边形的对角线,或者两条线分别平分平行四边形的两个对角线角度,则可以推断这两条线平行。
4.利用向量的性质:如果可以证明两条线的方向向量相等,则可以推断这两条线平行。
这可以通过计算两条线的方向向量并比较它们来证明。
需要注意的是,每种方法都需要根据具体问题的情况选择合适的方法,有时可能需要结合多种方法来证明两条线平行。
在证明过程中,也需要合理运用已知的几何定理和性质,并且注意推理的逻辑性和严密性。
高中数学课件-立体几何复习——平行、垂直证明
(1) 证明 如图所示,取线段 BC 的中点 F, 连接 EF、FD.
在△PBC 中,E、F 分别为 PC、CB 的中点, ∴EF∥PB. 在直角梯形 ABCD 中,F 为 CB 的中点, ∴BF=12BC=1. 又∵AD∥BC,且 AD=1, ∴AD // BF. ∴四边形 ABFD 是平行四边形, ∴FD∥AB. 又∵EF∩FD=F,PB∩BA=B, ∴平面 EFD∥平面 PAB. 又∵DE⊂平面 EFD,∴DE∥平面 PAB.
F
构造平面法
(1) 证明 如图所示,取线段 PB 的中点 H, 连接 EH、AH.
在△PBC 中,E、H和分别为 PC、PB 的中点, ∴EH // BC. 在直角梯形 ABCD 中, ∵AD∥BC,且 AD=1,BC=2 ∴AD // 12BC. ∴AD // EH. ∴四边形 ABFD 是平行四边形, ∴ED∥AH.
β
a
αlHale Waihona Puke a all
a
☺ 简称:面面垂直,线面垂直.
归纳小结
1.垂直关系的转化 在证明两平面垂直时一般先从现有的直线中寻找平面的垂线,若 这样的直线图中不存在,则可通过作辅助线来解决.如有平面垂 直时,一般要用性质定理,在一个平面内作交线的垂线,使之转 化为线面垂直,然后进一步转化为线线垂直.故熟练掌握“线线 垂直”、“面面垂直”间的转化条件是解决这类问题的关键.
➳性质:如果两个平行平面同时和第三个平面相交 ,那么它们的交线平行.
//
a
a // b
b
☺ 简称:面面平行,线线平行.
定理应用
空间中的平行
1.长方体ABCD-A1B1C1D1中,点E, F分别是BA1,BC1的中点。 求证:EF // 平面ABCD
北师大版必修第二册第六章立体几何初步(直线和平面平行证明技法)课件
∴ AE//平面DC1
点评
优点:招式本身的关键在于平行四边行,同学
们比较熟悉,因此接受起来比较快。
缺点:找平行四边形的思维过程中可能的情况
比较多,要一个一个去排除,需要一定的逻辑
思维能力。再有,招式本身不能解决所有题目
要注意变招。
体验
如图,已知三棱柱 − 1 1 1 中,E为
B1C1的中点,F为AA1的中点,求证:EA1//
平面B1CF
环节三
转为面面平行
如图,四棱锥 − ,底面ABC
D为正方形,E,F,G分别为
PC,PD,BC中点,求证:PA//平面
EFG
点拨
面面平行到线面平行的方法中,寻找与平面EFG平行的平面是解题
的关键,而寻找平行平面遵循一定的方法其实是很容易找到的。
证明:连结BD与AC交于点O,连结OE、E,O分别为
DD1、BD中点, ∴ //1
又 ⊂ 平面, 1 ⊄ 平面
BD1//平面AEC
优点: 招式简洁,证明过程简易。
缺点:与平面的交点若不是特殊点,会出现能
找出平行线,但难于证明的情况。再有就是平
面的另一面可能在题目中难以找到第三点。
体验
如图,已知四棱锥p-ABCD的底面ABCD是菱形,
点F为PC中点,求证:PA//平面BFD
环节二
构造平行四边形
例2:如图,正方体E为A,B −
1 1 1 1 , 1 1 上任意一点,求证:AE//平面DC1
点拨
通过平行四边行找平行线是高中立体几何中的常
见手段。若能够找到平行四边行的相邻两边,则
2.构造平行四边形
3.升格为面面平行
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何证明平行的方法及专题训练
罗虎胜
立体几何中证明线面平行或面面平行都可转化为线线平行,而证明线线平行一般有以下的一些方法:(1)通过“平移”。
(2)利用三角形中位线的性质。
(3)利用平行四边形的性质。
(4)利用对应线段成比例。
(5)利用面面平行的性质,等等。
(1) 通过“平移”再利用平行四边形的性质
1.如图,四棱锥P-ABCD的底面是平行四边Array形,点E、F 分别为棱AB、 PD的中点.求
证:AF∥平面PCE;
分析:取PC的中点G,连EG.,FG,则易证AEGF
D
B
A 1
A
F
是平行四边形
2、如图,已知直角梯形ABCD 中,AB∥CD,AB⊥BC,AB =1,BC =2,CD =1+3,
过A 作AE⊥CD,垂足为E ,G 、F 分别为AD 、CE 的中点,现将△ADE 沿AE 折叠,使得DE⊥EC.
(Ⅰ)求证:BC⊥面CDE ; (Ⅱ)求证:FG∥面BCD ; 分析:取DB 的中点H ,连GH,HC 则易证FGHC
3、已知直三棱柱ABC -A 1B 1C 1中,D, E, F 分别为AA
1点,
M 为BE 的中点, AC⊥BE . 求证:
(Ⅰ)C 1D⊥BC; (Ⅱ)C 1D∥平面B 1FM.
E
分析:连EA ,易证C 1EAD 是平行四边形,于是MF -,,AD CD AD BA ⊥⊥//EB PAD 平面E F
G M AD CD BD BC AM EFG AM EFG ///ABC A B C -90BAC ∠=2,
AB AC ==/A B //B C MN //A ACC 1C 求证:AB 11C 明: BC 11C 证:AP ∥GH .
分析:连结AC 交BD 于O 点,连结OM ,
易证OM ∥PA
从而PA ∥平面DBM,再根据直线与平面平行的性质得AP ∥GH .
(.3) 利用平行四边形的性质
10.正方体ABCD —A 1B 1C 1D 1中O 为正方形ABCD 的中心,求证: D 1O 2
1
中点为PD E 求证:AE ∥平面PBC ;
分析:取PC 的中点F ,连EF 则易证ABFE 是平行四边形
12、在如图所示的几何体中,四边形ABCD 为平行四边形,∠ ACB=90︒,EA⊥平面ABCD,EF ∥AB,FG∥BC,EG∥AC.AB=2EF.
(Ⅰ)若M是线段AD的中点,求证:GM∥平面ABFE; (Ⅱ)若AC=BC=2AE,求二面角A-BF-C的大小.
(I )证法一: 因
为
EF 90ACB ∠=︒90,EGF ABC ∠=︒∆.
EFG ∆BC FG 21=
ABCD BC AM 21=FA ⊂GM ⊄SM AM ND BN AM DN
SM BN
=ABC P -E PC M AB F
PA 2AF FP = 求证://CM 平面BEF ;
分析: 取AF 的中点N ,连CN 、MN ,
(1) 易
证平面
CMN 111ABC A B C -3AC =4BC =5
AB =14AA =D AB 1AC BC ⊥1
1CDB //平面AC
N
M
B 1
C 1
D 1
A 1
D
C
B
A
P N
M
B 1
C 1
D 1
A 1
D
C
B
A
11C CDB -1C 11CDB //平面AC 1111ABCD A B C D -11,2AB BC AA ===M BC
N 1AA 求证: //MN 平面1A CD ;
(2) 过,,N C D 三点的平面把长方体1111ABCD A B C D -截成
两部分几何体, 求所截成的两部分几何体的体积的比值.
(1)证法1:设点P 为AD 的中点,连接,MP NP . ∵ 点M 是BC 的中点, ∴ //MP CD .
∵ CD ⊂平面1A CD ,MP ⊄平面1A CD ,
∴ //MP 平面1A CD . …2分 ∵ 点N 是1AA 的中点, ∴ 1//NP A D .
∵ 1A D ⊂平面1A CD ,NP ⊄平面1A CD , ∴
//
NP 平面
1A CD
.
P
N
M
B 1
C 1
D 1
A 1D
C
B
A
…4分
∵ MP NP P =,MP ⊂平面MNP ,NP ⊂平面MNP , ∴ 平面//MNP 平面1A CD . ∵ MN ⊂平面MNP , ∴
//
MN 平面
1A CD
.
…6分
证法2: 连接AM 并延长AM 与DC 的延长线交于点P , 连接1
A P , ∵ 点M 是BC 的中点, ∴ BM MC =.
∵ BMA CMP ∠=∠, 90MBA MCP ︒∠=∠=,
∴ Rt MBA ≅Rt MCP . …2分
∴ AM MP =.
∵ 点N 是1AA 的中点,
Q
N
M
B 1
C 1
D 1
A 1D
C
B
A
∴ 1MN //A P . …4分
∵ 1A P ⊂平面1A CD ,MN ⊄平面1A CD ,
∴ //MN 平面1A CD . …6分
(2) 解: 取1BB 的中点Q , 连接NQ ,CQ , ∵ 点N 是1AA 的中点, ∴ //NQ AB . ∵ //AB CD , ∴ //NQ CD .
∴ 过,,N C D 三点的平面NQCD 把长方体1111ABCD A B C D -截成两部分几何体,
其中一部分几何体为直三棱柱QBC -NAD , 另一部分几何体为直四棱柱1111B QCC A NDD -. …8分 ∴ 111
11222
QBC S QB BC ∆==⨯⨯=, ∴
直三棱柱
QBC -NAD
的体积
11
2
QBC V S AB ∆==
, (10)
分
∵ 长方体1111ABCD A B C D -的体积112V =⨯⨯2=, ∴
直四棱柱
1111
B QC
C A ND
D -体积
213
2
V V V =-=
. …12分 ∴ 12
V V =1232
=1
3.
∴ 所截成的两部分几何体的体积的比值为
1
3
. …14分。
