高等流体力学第5讲
流体力学5

复速度
复速度和共轭复速度
平面势流的流动复势已知时,便可以对复势求导, 若复势 W ( z ) i
对 z 进行微分,得
dW i i u iv dz x x y y
O y u+iv v u-iv 图5 .2 复 速度 x
复势导数的实部是 轴向的速度分量 , 导数的虚部是y轴向的速度分量 的负值, 如图5.2所示。
对于 W1 ( z) A ln z 是强度为m 2 πA的源(汇)放置于 (0,0)点的复势; 对于 W2 ( z) Bi ln z ,则是强度为 2 πB的点涡放置于 (0,0)点的复势。(当 B 0 时,点涡为顺时针方向 旋转,反之则为逆时针方向旋转)
流动图形的分析 :
W ( z) ( A Bi)ln z ( A Bi)ln rei ( A ln r B ) i( A B ln r )
第五章
平面势流理论
要点:平面势流的复势(平面势流理论)、奇 点分布法、镜像法、共形映射法、机翼理论、 作用在物体上的力和力矩。 难点:求解平面势流的计算和应用,奇点分布 法的运动分析、共形映射法的图形转换(保角 变换) 、儒可夫基升力计算。
在不可压缩理想流体中,当流动无旋时, 称为势流,若又可简化为平面流动时,这种流 动称为二维势流,也称平面势流。在平面势流 中不仅存在速度势 ,同时存在流函数 。它们 均满足拉普拉斯方程,由于拉普拉斯方程是二 阶线性方程,可以应用叠加原理,利用已有的 一些解的叠加,以寻求满足给定边界条件和初 始条件下具有实际背景的许多问题的解答。
x
实部 φ (x,y)和虚部 ψ(x,y)在(x,y)处可微; φ (x,y)和 ψ(x,y)满足柯西-黎曼条件(简称 C-R 方程)
流体力学 第5章 圆管流动..

第5章圆管流动一.学习目的和任务1.本章学习目的(1)掌握流体流动的两种状态与雷诺数之间的关系;(2)切实掌握计算阻力损失的知识,为管路计算打基础。
2.本章学习任务了解雷诺实验过程及层流、紊流的流态特点,熟练掌握流态判别标准;掌握圆管层流基本规律,了解紊流的机理和脉动、时均化以及混合长度理论;了解尼古拉兹实验和莫迪图的使用,掌握阻力系数的确定方法;理解流动阻力的两种形式,掌握管路沿程损失和局部损失的计算;了解边界层概念、边界层分离和绕流阻力。
二.重点、难点重点:雷诺数及流态判别,圆管层流运动规律,沿程阻力系数的确定,沿程损失和局部损失计算。
难点:紊流流速分布和紊流阻力分析。
由于实际流体存在黏性,流体在圆管中流动会受到阻力的作用,从而引起流体能量的损失。
本章将主要讨论实际流体在圆管内流动的情况和能量损失的计算。
5.1 雷诺(Osborne Reynolds)实验和流态判据5.1.1 雷诺实验1883年,英国科学家雷诺通过实验发现,流体在流动时存在两种不同的状态,对应的流体微团运动呈现完全不同的规律。
这就是著名的雷诺实验,它是流体力学中最重要实验之一。
105如图5-1所示为雷诺实验的装置。
其中的阀门T1保持水箱A 内的水位不变,使流动处在恒定流状态;水管B 上相距为l 处分别装有一根测压管,用来测量两处的沿程损失f h ,管末端装有一个调节流量的阀门T3,容器C 用来计量流量;容器D 盛有颜色液体,T2控制其流量。
进行实验时,先微开阀门T3,使水管中保持小速度稳定水流,然后打开颜色液体阀门T2放出连续的细流,可以观察到水管内颜色液体成一条直的流线,如图5-2(a )所示;从这一现象可以看出,在管中流速较小时,它与水流不相混和,管中的液体质点均保持直线运动,水流层与层间互不干扰,这种流动称为层流(Laminar flow )。
比如,实际中黏性较大的液体在极缓慢流动时,属层流运动。
随后,逐渐开大阀门T3,增大管中液体流速,流速达到一定速度时,管内颜色液体开始抖动,具有波形轮廓,如图5-2(b )所示。
流体力学:第5章势流理论-上

c1
c2
5.2.1 复势的可叠加性 解析函数 W1(z) 1 i1 W2 (的z) 线性2 组i合2 ,
W (z) W1(z) W2 (z)
仍然是解析函数,仍然代表某一种流动的复势。简单 流动组合成复杂流动——叠加法
5.3 平面势流的基本解
目的:求解最简单的流动,为解决复杂势流奠定基础。 内容:均匀流、点源、点涡、偶极。
v 0 (R )
5.1.3 初始条件(initial condition)
初始时刻 t0速度势 (或 )在流 体域内
或边界上满足的条件。
例5-1 半径为R 的固定大球壳中充满不可压缩理想流体,半径为a
的小球以速度V(t) 在其中运动。试建立速度势定解问题。
解 : 取静坐标系o - xyz
z
2 0 (在流体中)
势流问题的数学描述—— Mathematical Model
5.1.1 基本方程——Laplace Equition
v 0
v
0
v
2 0 (in fluid)
Laplace方程是线性方程。要使 解唯一,需给出边界条件、初
v
p(x, y, z,t)
始条件。
R( M )
5.1.2 边界条件(Boundary Condition)
借助复变函数数学工具解平面势流问题。
平面势流:φ和ψ都是调和函数, 2 0, ,且2满足0
x y
y x
(C-R 条件)
5.2.1 复势与复速度(复平面)
1)复势函数:W (z) (x, y) i (x, y)
解析函数
平面势流
2)复速度(导数)与流体速度的关系:
z x iy
dW W W i i u iv Vei
高等流体力学PPT课件

2
aij ijkk
uD S r
表示由于流体微团变形而产生的 M 点相对于M点 的速度变化。
uR
1 ur
2
表示由于流体微团绕瞬时轴旋转而产生的 对于M 点的速度变化。
M 点相
26
26
欧拉和拉格朗日参考系中的时间导数
欧拉参考系:
u t x,y,z
u
u(x,
y,
z,
t)
某一空间点上的流体速度随时间的变化,称当地导 数或局部导数。
拉格朗日参考系:u u(x0, y0, z0,t)
u
t
x0 , y0 ,z0
流体质点速度随时间的变化,即加速度。
在欧拉参考系下用 Du 表示流体质点的速度变化。
25
速度分解定理,应变率张量和旋转率张量
速度分解定理
ui
ui x j
xj
1 2
ui x j
u j xi
1 2
ui x j
u j xi
xj
sij x j aij x j S r A r
Sr 1 ur
2
u uD uR
aij x j ijk x jk r
物质导数
以矢量和张量下标形式表示的物质导数
D
Dt
t
uk
xk
D
Dt
t
u
t
u
算符
u
ui vj wk
i
x
j
y
k
z
u v w x y z
13
13
物质导数物理意义
D Dt t uk xk
D 物质导数,质点导数,随体导数;
Dt
欧拉参考系中的时间导数,称局部导数或就地导数,表示空
流体力学第五章 圆管流动

进一步分析时均流速与脉动速度 内流经△ 的流量 取△A,时间 内流经△A的流量 ,时间T内流经
u ⋅ ∆A⋅ T = ∫ u∆Adt = ∫ (u ± u′)∆Adt 0
T 0
T
1 1 T 1 T u = ∫ udt ± ∫ u′dt = u ± T 0 T 0 T ∴ T 1 u = ∫ udt T o 1 T u′ = ∫ u′dt = 0 T 0
第五章 圆管流动
5.1 5.2 5.4 5.5 5.6 5.7 5.8 5.9 层流、 层流、紊流和雷诺实验 圆管层流 圆管中的流体的湍流运动 流体流动的两种流动阻力 圆管湍流流动的沿程损失 管流局部损失 复杂管路计算 压力管路中的水锤
5.1 层流、紊流和雷诺判据 层流、
1、雷诺实验 、 流体的阻力特性直接影响到流体流动时的能量损失,为探索流体摩擦阻力 的规律,人们进行了长期研究。1883年,雷诺(Osborne Reynolds)通过大量 实验,终于发现了液体在管道中流动时有着两种不同的流动状态,阻力特性也 不相同。这种现象可用图5-1所示的雷诺实验装置观测出来。
粗糙区
Re > 1 9 1 .2 d ( ) ∆ λ ∆ 有 关 ,阻 力 平 方 区 d
λ与 Re 无 关 ,和 λ=
(2lg 1
γ
∆
+ 1 .7 4 ) 2
4. 莫迪 莫迪(Moody)图 图
的镀锌钢管, 例1. 长度 . 长度l=1000m,内径 ,内径d=200mm的镀锌钢管,用以输送运 的镀锌钢管 动粘度 ν = 35.5×10−6 m2 / s(即ν = 35.5cSt) 的油液 ,测得流量 Q=38L/s。确定沿程损失? 。确定沿程损失? 解:(1)确定流速及流态 :( ) 管中u为 管中 为 雷诺数Re为 雷诺数 为
第五章 流体力学不可压缩粘流的精确解

第五章 不可压缩粘流的精确解自从建立了流体运动基本方程组,人们就开始致力于寻求在各种情况下流体运动的精确解。
流体运动的精确解一方面对认识和分析流体运动的规律具有重要的意义,另一方面又可为检验各类数值方法的可靠性和精确度提供重要依据。
不可压缩粘流的控制方程是于N S -方程,由于它的的非线性,使得求流动精确解问题常常成为一件非常困难的工作。
在一些特殊边界条件下形成的流动,比如平行剪切流问题,N S -方程的非线性项为零。
求这一类问题的精确解,数学上处理起来比较容易。
对定常流而言,常归结为解二阶常微分方程;在非定常流的情况下,常归结为扩散型方程等常见的数学物理方程,从而可以使用分离变量法、积分变换法或其它数学方法求解。
本章将给出不同类型流动精确解的一些例子。
5.1 平行平板间的定常平面流考虑粘性流体在相距2h 的两块无限大平行平板间的流动,建立如图 5.1 所示的直角坐标系。
流体运动源于沿x 方向的已知压力梯度的板壁运动。
这里下板固定,上板以U 运动。
当dx /dp 和U 不随时间变化时,流动是定常的。
考虑到速度只有沿x 方向的一个分量,并且只是坐标y 的函数,由于流线相互平行,称为平行剪切流。
在S N -方程()∂∂ρνV t V V p V f +⋅∇=-∇+∇+12(3.3.12)中,非线性项()0=⎪⎭⎫⎝⎛∂∂=∇⋅u x u V V是所有平行剪切流的特点,S N -方程在x 方向的投影简化为22dyud dx dp μ= (5.1.1)因压力梯度dpdx是一个常数,上式满足边界条件()0=-h u 和()U h u =的解为 ⎪⎭⎫⎝⎛++⎪⎪⎭⎫ ⎝⎛--=h y U h y dx dp h u 1212222μ (5.1.2)由速度分布求出单位宽度平板间的体积流量Uh dx dph udy Q hh+-==⎰-μ323(5.1.3)平均流速是y图5.1 平行平板间的流动U dx dp h Q h u 213212+-==μ(5.1.4)进一步求出切应力h Udx dp y y u yx 2μ∂∂μτ+=⎪⎪⎭⎫ ⎝⎛= (5.1.5)当dp dx /<0时,切应力的最大值和最小值分别在下板面和上板面处出现。
流体力学_第五章_1-3节
Re vd ——雷诺数(无量纲)
12
层流
紊流
层流
紊流
上临界雷诺数ReC
Re
12000-40000
Re
ReC 2300 下临界雷诺数
Re<Rec 层流 实用上以下临界雷诺数为准
Re>Rec 紊流(包括层流向紊流的临界区2000~4000)
Re=Rec 临界流
Rec 2000或2300
仅针对圆管
p2
g
wl gA
23
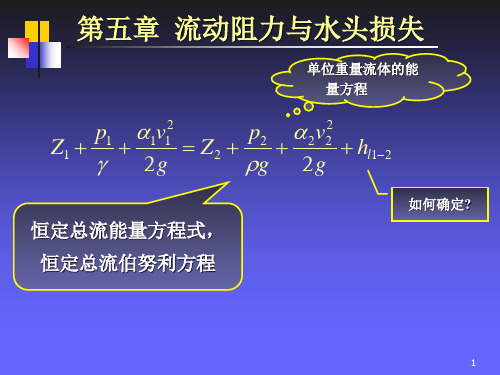
第三节 圆管层流
对截面1-1和2-2列出伯努利方程
1 2 1
Z1
p1
g
1
v12 2g
Z2
p2
g
2
v22 2g
hl1-2
在等直径圆管中 v1 v2
hl hf
hf
Z1
p1
g
Z
2
p2
g
又
Z1
p1
g
Z2
p2
g
wl gA
R A
hf
层流 hf k1v1.0 v1.0
OA段
紊流
hf
k v1.75~2.0 2
v1.75~2.0
AC、BD段斜率大于2
CDE段 结论:流态不同,沿程损失规律不同
11
流态的判别准则 —— 临界雷诺数
圆管流雷诺数
vc d
vc Rec d
Re c
vc d
vcd
临界雷诺数
Re c ——下临界雷诺数,临界雷诺数(2000左右或2300)
hf
1 R
R A
水力半径R是一个基本上能反映 过流断面大小、形状对沿程 损失综合影响的物理量
流体力学第五章课件

(5-4)
27
第五章
能量损失和有压管流
例. 密度ρ=850kg/m3、粘性系数μ=1.53×10-2kg/m· s的油, 在管径为10cm的管内流动,流量为0.05l/s。试求管轴心 即r=2cm处的速度、沿程损失系数λ 、管壁及r=2cm处切 应力、单位管长的能量损失。 解:由例5-1知道,该流动属于层流,故 umax 2v 12.7cm / s 因为 u umax kr 2 ,当r=r0=5cm,u=0代入得
6
第五章
能量损失和有压管流
实验结果表明:当 流速非常小时,流动成 为层流,沿程损失与速 度一次方成正比,逐渐 加大速度,流动由层流 转变为紊流,曲线突然 变陡,沿BC向上。在紊 流时,沿程损失hf与流 速vn成正比,根据管道 内壁的相对粗糙情况, n值在1.75~2.0范围内。
7
第五章
能量损失和有压管流
能量损失和有压管流
二、层流中的沿程损失 从式(5-8)可以得到 32 L 32L hf 2v v 2 g d gd
这就是圆管层流的沿程损失公式,也称为哈根—泊肃 叶定理(Hagen-Poiseulle Law)。 上式说明,层流的能量损失与速度的一次方成正比, 雷诺实验结果也证明了这一点。同式(5-4)比较,可得 层流的沿程损失系数λ为:
第五章 能量损失和有压管流
第五章 能量损失和有压管流
本章介绍粘性流体的流动状态,分析流动阻力 的产生机理及特征,研究不可压缩粘性流体在管道 中流动的能量损失以及有压管流的计算方法。
1
第五章 能量损失和有压管流
§5-1 沿程损失和局部损失
粘性流体在流动过程中,由于流体之间的相对运动而 产生切应力以及流体与固体壁面之间产生摩擦阻力,这些阻 力的形成将使流动流体的部分机械能不可逆转地转化为热能, 引起流体机械能损失,简称能量损失。由于引起能量损失的 阻力与固体边界条件直接相关,故将根据固体边界的变化情 况,把能量损失分为两类:沿程损失和局部损失。 一、沿程损失 当限制流体流动的固体边壁沿程不变化(如均匀流)或 者变化微小(缓变流)时,过流断面上的速度分布沿程变 化缓慢,则流体内部以及流体与固体边壁之间产生沿程不 变的阻力,由沿程阻力引起的机械能损失称为沿程能量损 失,简称沿程损失,用hf表示。很明显hf与管段的长度成正 比。 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五讲 气动函数及压力波一、 气流参数(一)滞止参数如果按照一定的过程将气流速度滞止到零,此时气流的参数就叫做滞止参数。
滞止状态的概念可以很形象地用图5-1来表示。
它是假想把某一点处的气流引入一个容积很大的贮气箱,使其速度滞止到零。
根据一元稳定绝能流动的能量方程式2211221122h v h v +=+ 可知气体的焓值随气流速度的减小而增大。
如果把气流由速度v 1=v (焓h 1=h )绝能地滞止到v 2=0,此时所对应的焓值h 2就称为滞止焓,用符号h *表示,则*212h h v =+如果研究的是定热比容的完全气体,h =c p T ,则式(9一22)可改p c v T T /212*+= (5-1) 式中 T *称为滞止温度,它是把气流速度绝能滞止到零时的温度。
将式(5—1)两边同除以T ,则有2*2221111/1/()12212p kR k v T T v c T v T k c -=+=+=+- 所以*211Ma 2k T T -=+(5-2) 前面得到了滞止温度与温度的比与Ma 数的关系式,下面我们来推导一下其它滞止参数的表达式。
完全气体的状态方程和滞止状态的状态方程可表示为p =ρRT 和p *=ρRT * ,两者相除则有 ***()()p p ρρT T =。
(a ) 对等熵流动有p */ ρ*k =常数,p / ρk =常数,两者相比,则有**()k p p ρρ=。
(b ) 由式(a )和(b )可得**2111()(1Ma )2k kk k k p p T T ---==+ (5-3)图5-1 滞止参数模型11**2111()(1Ma )2k k k ρρT T ---==+ (5-4)由式(9-2、3、4)可知,气流参数与其滞止参数的比值只是气流Ma 数的函数。
这种函数关系是分析和计算气体流动的基础,在气体动力学中占有非常重要地位。
这里应强调的是,在气体动力学中,引进滞止状态的概念是把它作为一个参考状态。
对一元流动来讲,每个截面都对应有自己的滞止状态,而与实际流动中的过程无关。
也就是说,滞止参数是一个点函数。
引入滞止焓后,一元稳定流动的能量方程可表式为*1*2h h w q s -=- (5-5)对绝能流动而言,有**21h h =或*h =常数。
由此可知:一元稳定绝能流动的滞止焓沿流程为一常数,同佯对完全气体,因为h *=c p T *,所以其滞止温度也保持不变。
通过进一步的理论分析可证明,在绝能等熵流动中,所有的滞止参数沿流程都不变。
(二)临界状态参数将c 2=kRT 及c *2=kRT *引入到绝能等熵的能量方程后,则有22*121c v kRT k k +==--常数 (5-6) 由上式可知,c 与v 的关系函数满足椭圆方程,关系曲线如图5-2所示。
从中可以看出,在气流由滞止状态绝能地向最大流速状态的变化过程中,必然要经历这样一种状态.即v =c 或Ma=1的状态。
气体动力学中称这种状态为临界状态,所对应的气流参数称为气流的临界状态参数,并标以下标cr ,如p cr 、T cr 、v cr 和c cr 等。
显然,v cr =c cr 。
在式(5-6)中令c =v =c cr ,则可得 cr c =(5-7) max /cr v c =。
(5-8) 利用Ma 数的定义、式(5-2)、(5-3)和(5-4),可得*/2/(1)cr T T k =+, (5-9)*1/[2/(1)]k k cr p p k -=+, (5-10) 1*1/[2/(1)]k cr ρρk -=+。
(5-11)对空气,k =1.4,则有p cr /p *=0.5283。
应该指出,在一元流动的每一个截面上,都有相应于该截面的临界参数,如同在气流的每一个截面上都有相应的滞止参数一样。
如果气流在某个截面上的Ma 数恰好等于1,则该截面上的气流状态就是临界状态,该截面上气流的参数就是临界参数,该截面叫做临界截面。
图5-2 c v 曲线c在绝能等熵流动过程中,因为沿流道所有滞止参数保持不变,所以所有的临界参数也保持不变。
(三)速度系数在气体动力学中,除了用马赫数作为无量纲参数以外,往往也用气流速度与临界声速 之比作为无量纲速度,称为速度系数,并用符号λ来表示,即cr λv c = (5-12)与Ma 数相比,应用λ数的最大好处是,在绝能流动中,当气体速度趋于v max 时,c 下降为零,Ma 数趋于无穷大,这样在作图时v =v max 附近的情况就无法表示出来。
而max max cr λv == (5-13) 这样就消除了上述困难。
2221Ma 211Ma 2k λk +=-+ (5-14) 或22221Ma 111λk k λk +=--+ (5-15)上述关系可以作成如图5-3所示的图线。
可见,当 Ma=0时,λ=0;当 Ma<1时,λ<1 (亚声速); 当 Ma=1时,λ=1;当 Ma>1时,λ>1 (超声速);当Ma→∞时,max λλ== 因此,λ数和Ma 数一样也是表示亚声速或超声速气流的一个简单标志。
另外,气流参数与滞止参数的比也可以用λ数来表示,把式(5-14)代入式(5-2、3、4),得到*21(1)1k T λk -=-+ (5-16) *211(1)1kk k p p λk --=-+ (5-17)1*211(1)1k k ρρλk --=-+ (5-18)二、气体动力学函数及其应用从前面的分析中可以看出,气流滞止参数与气流参数之比可以用气流的Ma 数或λ数的函数来表示。
后面还将会看到,流量公式和动量方程式也可以用Ma 数或λ数的函数表示出来。
这些Ma 数或λ数的函数叫做气体动力学函数。
λ图5-3λ~Ma 曲线(一)函数τ(λ)、π(λ)和ε(λ)、在气体动力学中,令*21()11k τλT λk -==-+ (5-19) *211()(1)1kk k πλp p λk --==-+ (5-20)1*211()(1)1k k ελρρλk --==-+ (5-21)对空气(k =1.4)来说,函数τ(λ)、π(λ)和ε(λ)随λ数的变化如图5-4a 所示,这三个函数均为单减函数。
另外,这三个函数也可用Ma 数表示如下:*21(Ma)1/(1Ma )2k τT T -==+(5-22) *211(Ma)1/(1Ma )2kk k πp p --==+ (5-23)1*211(Ma)1/(1Ma )2k k ερρ--==+ (5-24)函数τ(Ma)、π(Ma)和ε(Ma)随Ma 的变化如图5-4所示。
例5-3 用风速管测得空气流中一点的总压p *=9.81×104Pa ,静压p =8.44×104Pa ,用热电偶测得该点空气流的总温T *=400K ,试求该点气流的速度v 。
解:由式(5-22)可得4*48.4410()0.869.8110πλp p ⨯===⨯。
由气动函数表(k =1.4)查得λ=0.5025,则气流速度为cr v λc ==0.5025187m/s ==。
(二)流量函数气动计算中往往是先给定气流的滞止参数和λ数(或Ma 数),如果直接按公式m ρAv =来计算流量,则π(λ), ε( λ), τ(λ) λ0.4 0.8 1.2 1.6 2.0 τ(λ)ε( λ) π(λ)0.2 0.4 0.6 0.8 1.0 (a)2.4图5-4 函数π, ε, τ曲线Ma0.5 1.0 1.5 2.02.53.0 3.5(b)τ(Ma) ε (Ma) π(Ma)0.20.0.0.8 1.0 π(Ma), ε(Ma),必须先根据给定的滞止参数和λ数求出v 和ρ。
但这佯计算是很麻烦的,下面我们就来寻求用λ函数表示的流量公式。
由流量公式可得()cr cr cr crρvm ρAv ρv A ρv ==,11*211*/11(1)(1)11/k k cr cr cr ρv ρρk k λλλk k ρv ρρ----==--++,1121111()(1)21k k k k λλk --+-=-+。
将上式用q (λ)表示,并称为流量函数,即1121111()()(1)21k k k k q λλλk --+-=-+ (5-25)则有()cr cr m q λρv A =。
式中ρcr 和c vr 均可表示为11**11*22()()11k k cr p ρρk RT k --==++,cr cr v c ==所以有**()p m KAq Tλ= (5-26)其中1112-+⎪⎭⎫ ⎝⎛+=k k k R k K 。
对空气, k =1.4, R =287.4J/(kg·K),则K =0.0404。
q (λ)随λ数的变化如图5-5a所示。
当λ=0时,q (λ)=0;当λ=1时,q (λ)=1,取最大值;当λ=λmax 时,q (λ)=0。
由此可见,q (λ)在临界截面处取最大值。
流量函数q (λ)也可以表示成Ma 数的函数q (Ma),q (Ma)随Ma 数的变化如图5-5b 所示。
引入流量函数后,一元稳定流动的连续方程又可表示为0.6 0.4 1.0 0.2 Ma0.8 00.81.62.4 λy (λ)q (λ) (a)1.02.03.00.20.40.60.8 1.0q (Ma) (b) y (λ)q (λ)图5-5 函数q 曲线**()p m KλT==常数 (5-27)由式(9-54),在绝能等熵流动的条件下,由于p *和T *保持不变,则有()Aq λ=常数 (5-28) 由此可以得出下列重要结论:1.当气流为亚声速(λ<1)时,由图5-5可见,随λ数的增大,q (λ)也随之增大,因此,相应的流管截面积必须减小。
所以,对亚声速流动讲,流管截面积减小时流速增大;流管截面积增大时则流速减小。
2.当气流为超声速(λ>1)时,随λ数的增大,q (λ)却减小,因此,相应的流管截面积必须增大。
所以,对超声速流动,流管截面积增大时,流速增大;流管截面积减小时,则流速减小。
3.当λ=1时,q (λ)达到最大值,相应的截面积应该是流管的最小截面积。
即对绝能等熵流动而言,临界面必是流管中的最小截面。
但这只是必要条件,也就是说流管的最小截面并不一定是临界截面。
从上述结论可以知道,要将气流绝能等熵地由亚声速流动加速为超声速流动,管道必须做成先收缩后扩张的形状,即拉伐尔喷管,如图9-11所示。
关于这个问题的细节将在后面讨论。
有时候已知条件不是气流的滞止压力而是气流压力,此时流量公式中的q (λ)可用另一个气动函数y (λ)来代替。
*()()()p q λm K y λπλT ==, (5-29)在图5-5a 中也给出了y (λ)随λ数的变化情况。
