全国大学生数学竞赛
历届全国大学生数学竞赛初赛试卷

全国大学生数学竞赛初赛试卷(非数学类)2021年 第一届全国大学生数学竞赛初赛试卷(非数学类)一、填空题(每小题5分,共20分)1.计算()ln(1)d yx y x y ++=⎰⎰____________,其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.2.设)(x f 是持续函数,且知足220()3()d 2f x x f x x =--⎰,则()f x =____________.3.曲面2222x z y =+-平行平面022=-+z y x 的切平面方程是__________.4.设函数)(x y y =由方程29ln )(y y f e xe =肯定,其中f 具有二阶导数,且1≠'f ,则=22d d xy________________. 二、(5分)求极限xenx x x x ne e e )(lim 20+++→ ,其中n 是给定的正整数. 三、(15分)设函数)(x f 持续,10()()g x f xt dt =⎰,且A xx f x =→)(lim,A 为常数,求()g x '并讨论)(x g '在0=x 处的持续性.四、(15分)已知平面区域}0,0|),{(ππ≤≤≤≤=y x y x D ,L 为D 的正向边界,试证:(1)⎰⎰-=---Lx y Lx yx ye y xe x ye y xed d d d sin sin sin sin ;(2)2sin sin 25d d π⎰≥--Ly yx ye y xe.五、(10分)已知xxe xe y 21+=,xxexe y -+=2,xx x e e xe y --+=23是某二阶常系数线性非齐次微分方程的三个解,试求此微分方程.六、(10分)设抛物线c bx ax y ln 22++=过原点.当10≤≤x 时,0≥y ,又已知该抛物线与x 轴及直线1=x 所围图形的面积为31.试肯定c b a ,,,使此图形绕x 轴旋转一周而成的旋转体的体积V 最小.七、(15分)已知)(x u n 知足1()()1,2,n x nn u x u x x e n -'=+=,且neu n =)1(,求函数项级数∑∞=1)(n nx u之和.八、(10分)求-→1x 时,与∑∞=02n n x 等价的无穷大量.2021年 第二届全国大学生数学竞赛初赛试卷(非数学类)一、(25分,每小题5分) (1)设22(1)(1)(1)nn x a a a =+++,其中||1,a <求lim .n n x →∞(2)求21lim 1x xx ex -→∞⎛⎫+ ⎪⎝⎭. (3)设0s >,求0(1,2,)sx n n I e x dx n ∞-==⎰.(4)设函数()f t有二阶持续导数,1(,)r g x y f r ⎛⎫== ⎪⎝⎭,求2222g g x y ∂∂+∂∂.(5)求直线10:0x y l z -=⎧⎨=⎩与直线2213:421x y z l ---==--的距离. 二、(15分)设函数()f x 在(,)-∞+∞上具有二阶导数,而且()0f x ''>,lim ()0x f x α→+∞'=>,lim ()0x f x β→-∞'=<,且存在一点0x ,使得0()0f x <. 证明:方程()0f x =在(,)-∞+∞恰有两个实根.三、(15分)设函数()y f x =由参数方程22(1)()x t t t y t ψ⎧=+>-⎨=⎩所肯定,且22d 3d 4(1)y x t =+,其中()t ψ具有二阶导数,曲线()y t ψ=与22132t u y e du e-=+⎰在1t =出相切,求函数()t ψ. 四、(15分)设10,nn n kk a S a=>=∑,证明:(1)当1α>时,级数1nn na S α+∞=∑收敛;(2)当1α≤且()n s n →∞→∞时,级数1nn na S α+∞=∑发散. 五、(15分)设l 是过原点、方向为(,,)αβγ,(其中2221)αβγ++=的直线,均匀椭球2222221x y z a b c++≤(其中0c b a <<<,密度为1)绕l 旋转. (1)求其转动惯量;(2)求其转动惯量关于方向(,,)αβγ的最大值和最小值.六、(15分)设函数()x ϕ具有持续的导数,在围绕原点的任意滑腻的简单闭曲线C 上,曲线积分422d ()d 0L xy x x yx y ϕ+=+⎰的值为常数.(1)设L 为正向闭曲线22(2)1x y -+=,证明422d ()d 0L xy x x yx y ϕ+=+⎰;(2)求函数()x ϕ;(3)设C 是围绕原点的滑腻简单正向闭曲线,求422d ()d C xy x x y x y ϕ++⎰.2021年 第三届全国大学生数学竞赛初赛试卷(非数学类)一、计算下列各题(本题共3小题,每小题各5分,共15分)(1)求11cos 0sin lim xx x x -→⎛⎫⎪⎝⎭;(2).求111lim ...12n n n n n →∞⎛⎫+++ ⎪+++⎝⎭; (3)已知()2ln 1arctan tt x e y t e⎧=+⎪⎨=-⎪⎩,求22d d y x .二、(本题10分)求方程()()24d 1d 0x y x x y y +-++-=的通解.三、(本题15分)设函数()f x 在0x =的某邻域内具有二阶持续导数,且()()()0,0,0f f f '''均不为0,证明:存在唯一一组实数123,,k k k ,使得()()()()12320230lim0h k f h k f h k f h f h →++-=.四、(本题17分)设2221222:1x y z a b c ∑++=,其中0a b c >>>,2222:z x y ∑=+,Γ为1∑与2∑的交线,求椭球面1∑在Γ上各点的切平面到原点距离的最大值和最小值.五、(本题16分)已知S 是空间曲线2231x y z ⎧+=⎨=⎩绕y 轴旋转形成的椭球面的上半部份(0z ≥)(取上侧),∏是S 在(,,)P x y z 点处的切平面,(,,)x y z ρ是原点到切平面∏的距离,,,λμν表示S 的正法向的方向余弦. 计算:(1)()d ,,SzS x y z ρ⎰⎰;(2)()3d S z x y z S λμν++⎰⎰ 六、(本题12分)设()f x 是在(,)-∞+∞内的可微函数,且()()f x mf x '<,其中01m <<,任取实数0a ,概念1ln (),1,2,...n n a f a n -==,证明:11()n n n a a ∞-=-∑绝对收敛.七、(本题15分)是不是存在区间[]0,2上的持续可微函数()f x ,知足(0)(2)1f f ==,()1f x '≤,2()d 1f x x ≤⎰?请说明理由.2021年 第四届全国大学生数学竞赛初赛试卷(非数学类)一、(本大题共5小题,每小题6分,共30分)解答下列各题(要求写出重要步骤). (1)求极限21lim(!)n n n →∞.(2)求通过直线2320:55430x y z l x y z +-+=⎧⎨+-+=⎩的两个彼此垂直的平面1π和2π,使其中一个平面过点(4,3,1)-.(3)已知函数(,)ax byz u x y e+=,且20ux y∂=∂∂. 肯定常数a 和b ,使函数(,)z z x y =知足方程20z z zz x y x y∂∂∂--+=∂∂∂∂. (4)设函数()u u x =持续可微,(2)1u =,且3(2)d ()d Lx y u x x u u y +++⎰在右半平面与路径无关,求(,)u x y .(5)求极限1limx xx t +.二、(本题10分)计算20sin d x e x x +∞-⎰.三、(本题10分)求方程21sin 2501x x x=-的近似解,精准到0.001.四、(本题12分)设函数()y f x =二阶可导,且()0f x ''>,(0)0f =,(0)0f '=,求330()lim ()sin x x f u f x u→,其中u 是曲线()y f x =上点(,())P x f x 处的切线在x 轴上的截距.五、(本题12分)求最小实数C ,使得知足10()d 1f x x =⎰的持续函数()f x 都有10f dx C ≤⎰.六、(本题12分)设()f x 为持续函数,0t >. 区域Ω是由抛物面22z x y =+和球面 2222x y z t ++=(0)z >所围起来的部份. 概念三重积分222()()d F t f x y z v Ω=++⎰⎰⎰,求()F t 的导数()F t ''.七、(本题14分)设1n n a ∞=∑与1n n b ∞=∑为正项级数,证明:(1)若()111lim 0n n n n n a a b b →∞++->,则级数1n n a ∞=∑收敛;(2)若()111lim 0n n n n n a a b b →∞++-<,且级数1n n b ∞=∑发散,则级数1n n a ∞=∑发散.2021年 第五届全国大学生数学竞赛初赛试卷(非数学类)一、解答下列各题(每小题6分,共24分,要求写出重要步骤) 1.求极限(lim 1sin nn →∞+.2.证明广义积分0sin d xx x+∞⎰不是绝对收敛的. 3.设函数()y y x =由323322x x y y +-=肯定,求()y x 的极值.4.过曲线0)y x ≥上的点A 作切线,使该切线与曲线及x 轴所围成的平面图形的面积为34,求点A 的坐标. 二、(满分12分)计算定积分2sin arctan d 1cos xx x e I x xππ-⋅=+⎰.三、(满分12分)设()f x 在0x =处存在二阶导数(0)f '',且()lim0x f x x→=.证明:级数11n f n ∞=⎛⎫⎪⎝⎭∑收敛. 四、(满分12分)设(),()0()f x f x m a x b π'≤≥>≤≤,证明2sin ()d baf x x m≤⎰. 五、(满分14分)设∑是一个滑腻封锁曲面,方向朝外.给定第二型的曲面积分()()()333d d 2d d 3d d I x x y z y y z x z z x y ∑=-+-+-⎰⎰.试肯定曲面∑,使积分I 的值最小,并求该最小值.六、(满分14分)设22d d ()()a a C y x x yI r x y -=+⎰,其中a 为常数,曲线C 为椭圆222x xy y r ++=,取正向.求极限lim ()a r I r →+∞.七、(满分14分)判断级数()()1111212n n n n ∞=+++++∑的敛散性,若收敛,求其和.2021年 第六届全国大学生数学竞赛初赛试卷(非数学类)一、填空题(共有5小题,每题6分,共30分)1.已知1x y e =和1x y xe =是齐次二阶常系数线性微分方程的解,则该方程是 .2.设有曲面22:2S z x y =+和平面022:=++z y x L . 则与L 平行的S 的切平面方程是 .3.设函数()y y x =由方程21sin d 4y x t x t π-⎛⎫= ⎪⎝⎭⎰所肯定.求d d x y x == .4.设1(1)!nn k kx k ==+∑,则=∞→n n x lim .5.已知130()lim 1xx f x x e x →⎛⎫++= ⎪⎝⎭,则=→20)(lim x x f x . 二、(本题12分)设n 为正整数,计算21d 1cos ln d d ne I x x x π-⎛⎫= ⎪⎝⎭⎰. 三、(本题14分)设函数()f x 在]1,0[上有二阶导数,且有正常数,A B 使得()f x A ≤,|"()|f x B ≤. 证明:对任意]1,0[∈x ,有22|)('|BA x f +≤. 四、(本题14分)(1)设一球缺高为h ,所在球半径为R . 证明该球缺体积为2)3(3h h R -π,球冠面积为Rh π2;(2)设球体12)1()1()1(222≤-+-+-z y x 被平面6:=++z y x P 所截的小球缺为Ω,记球缺上的球冠为∑,方向指向球外,求第二型曲面积分d d d d d d I x y z y z x z x y ∑=++⎰⎰.五、(本题15分)设f 在],[b a 上非负持续,严格单增,且存在],[b a x n ∈,使得⎰-=b an nn dx x f a b x f )]([1)]([.求n n x ∞→lim . 六、(本题15分)设2222212n n nnA n n n n =++++++,求⎪⎭⎫ ⎝⎛-∞→n n A n 4lim π.2021年 第七届全国大学生数学竞赛初赛试卷(非数学类)一、填空题(每小题6分,共5小题,满分30分)(1)极限2222sin sin sin lim 12n n nn n n n n πππ→∞⎛⎫ ⎪+++= ⎪+++ ⎪⎝⎭. (2)设函数(),z z x y =由方程,0z z F x y y x ⎛⎫++= ⎪⎝⎭所决定,其中(),F u v 具有持续偏导数,且0u v xF yF +≠则z zxy x y∂∂+=∂∂ . (3)曲面221z x y =++在点()1,1,3M -的切平面与曲面所围区域的体积是 . (4)函数()[)[)3,5,00,0,5x f x x ⎧∈-⎪=⎨∈⎪⎩在(]5,5-的傅立叶级数在0x =收敛的是 . (5)设区间()0,+∞上的函数()u x 概念域为()2xt u x e dt +∞-=⎰,则()u x 的初等函数表达式是 .二、(12分)设M 是以三个正半轴为母线的半圆锥面,求其方程.三、(12分)设()f x 在(),a b 内二次可导,且存在常数,αβ,使得对于(),x a b ∀∈,有()()()f x f x f x αβ'=+,则()f x 在(),a b 内无穷次可导.四、(14分)求幂级数()()30211!nn n x n ∞=+-+∑的收敛域及其和函数.五、(16分)设函数()f x 在[]0,1上持续,且()()110,1f x dx xf x dx ==⎰⎰. 试证:(1)[]00,1x ∃∈使()04f x >; (2)[]10,1x ∃∈使()14f x =.五、(16分)设(),f x y 在221x y +≤上有持续的二阶偏导数,且2222xx xy yy f f f M ++≤. 若()()()0,00,0,00,00x y f f f ===,证明:()221,4x y f x y dxdy +≤≤⎰⎰.2021年 第八届全国大学生数学竞赛初赛试卷(非数学类)一、填空题(每小题5分,满分30分) 1、若()f x 在点x a =可导,且()0f a ≠,则()1lim nn f a n f a →∞⎛⎫⎛⎫+ ⎪⎪⎝⎭⎪= ⎪⎪⎝⎭__________. 2、若()10f =,()1f '存在,求极限()()220sin cos tan3lim1sin x x f x x xI ex→+=-.3、设()f x 有持续导数,且()12f =,记()2x z f e y =,若zz x∂=∂,求()f x 在0x >的表达式.4、设()sin 2x f x e x =,求02n a π<<,()()40f .5、求曲面22 2x z y =+平行于平面220x y z +-=的切平面方程.二、(14分)设()f x 在[]0,1上可导,()00f =,且当()0,1x ∈,()01f x '<<,试证当()0,1a ∈,()()()230d d aaf x xf x x >⎰⎰.三、(14分)某物体所在的空间区域为222:22x y z x y z Ω++≤++,密度函数为222x y z ++,求质量()222d d d M x y z x y z Ω=++⎰⎰⎰.四、(14分)设函数()f x 在闭区间[]0,1上具有持续导数,()00f =,()11f =, 证明:()10111lim 2n n k k n f x dx fn n →∞=⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭∑⎰. 五、(14分)设函数()f x 在闭区间[]0,1上持续,且()1d 0I f x x =≠⎰,证明:在()0,1内存在不同的两点12,x x ,使得()()12112f x f x I+=. 六、(14分)设()f x 在(),-∞+∞可导,且()()(2f x f x f x =+=.用Fourier 级数理论证明()f x 为常数.2021年 第九届全国大学生数学竞赛初赛试卷(非数学类)一、1. 已知可导函数f (x )知足⎰+=+xx tdt t f x xf 01sin )(2)(cos cosxf(x)+2∫f(t)sintdt x0=x +1,则()f x =_________.2. 求⎪⎭⎫ ⎝⎛+∞→n n n 22sin lim π.3. 设(,)w f u v =具有二阶持续偏导数,且==+u x cy v x cy -,,其中c 为非零常数. 则21xx yy w w c-=_________. 4. 设()f x 有二阶导数持续,且(0)'(0)0,"(0)6f f f ===,则240(sin )lim x f x x→=____. 5. 不定积分sin 2sin 2(1sin )x e xI dx x -=-⎰=________. 6. 记曲面222z x y =+和z =围成空间区域为V ,则三重积分Vzdxdydz ⎰⎰⎰=___________.二、(本题满分14分) 设二元函数(,)f x y 在平面上有持续的二阶偏导数. 对任何角度α,概念一元函数()(cos ,sin )g t f t t =ααα.若对任何α都有(0)0dg dtα=且22(0)0d g dt α>. 证明)0,0(f 是(,)f x y 的极小值. 三、(本题满分14分) 设曲线Γ为在2221x y z ++=,1x z +=,0,0,0x y z ≥≥≥上从(1,0,0)A 到(0,0,1)B 的一段. 求曲线积分⎰Γ++=xdz zdy ydx I .四、(本题满分15分) 设函数()0f x >且在实轴上持续,若对任意实数t ,有||()1t x e f x dx +∞---∞≤⎰,则,()a b a b ∀<,2()2b a b a f x dx -+≤⎰. 五、(本题满分15分) 设{}n a 为一个数列,p 为固定的正整数。
全国大学生数学竞赛上海赛区获奖名单

全国大学生数学竞赛上海赛区获奖名单近日,第15届全国大学生数学竞赛上海赛区比赛结束。
本次比赛由上海市教育委员会主办,上海市教育发展基金会、上海市市场监督管理局、上海师范大学数学科学学院和上海市科学技术协会共同承办。
全国大学生数学竞赛是国家教育部高等教育司、教育部高等学校数学与统计学科教学指导委员会组织的一项大型综合性教学竞赛活动,旨在激发学生数学科学研究热情、培养学生数学分析解题能力,增强学生创新意识和实践能力,以及促进全国大学生数学科学教育的发展。
本次比赛共招募上海市全部大学393所,参赛选手达2.7万余人,参赛队伍达1.5万支。
本次比赛考察了数学共性知识和数学基本运算能力,以及初等函数、初等数论、线性代数、概率论、微积分初级、数据结构、计算机科学等方面的数学科学素养。
比赛结果非常平均,参赛者高水平表现得到了表彰。
此次评选活动,上海赛区共推荐400余人,获奖名单如下:一等奖:胡佳(上海外国语大学)、林颖(华东理工大学)、钟航(上海大学)二等奖:张嘉怡(上海理工大学)、吴钥(上海财经大学)、卫妍(华东师范大学)三等奖:李杰(上海师范大学)、黄韵(华东政法大学)、陈云(上海交通大学)优胜奖:刘昊(上海外国语大学)、苏柯泽(同济大学)、陈弈(上海大学)参赛者获奖名单中,不仅有来自上海各大学的学子,还有一些来自全国各个城市的参赛者。
他们在精心准备、认真训练的基础上,都以极高的水平参赛,出色地完成了比赛,获得了各自的成绩,受到了广泛的肯定与关注。
从本次比赛中可以看到,大学生们在探索与学习数学的道路上,拥有良好的心态、高度的热情与进取的气概,并取得了突出的成绩,这鼓舞着我们更加致力于深入探索数学之美,努力提高数学水平。
随着社会对科技创新和创业能力的日益需求,数学作为基础科学,其研究与发展所带来的重要性和意义有增无减,未来科技创新的成功必将离不开数学的支撑。
期望本次比赛为学生架起一座桥梁,让他们在比赛的过程中深入探究和发现数学之美,不断提升技能,实现潜能发挥,以及团结协作的品质,为今后的科技创新打下更加坚实的基础。
2020年第十二届全国大学生数学竞赛--初赛《数学类A卷》试题(含参考答案)

(2) 求点 A1, B1,C1 三点的坐标; (3) 给定点A(1, 1, 0), B(1, 1, 0),C(1, 1, 0) ,求四面体 NA1B1C1 的体积. 【参考解答】:(1) 由直线的两点式方程,直接可得过 N, A 两点的直线方程为
(2) 直线 NA 的参数方程为
x y z 1
.
a1 a2 1
1 k
趋于
0,故
lim
n
yn
1
yn
0.
所以
bn an yn yn1 0, n
从而可知 an , bn 的极限相等,从而 yn 收敛. 最后,由 的连续性可得 xn 收
敛.
六、(20
分)对于有界区间
a,
b
的划分
P : a x0 x1 xn1 b
其范数定义为||
P
||
max xk1
1
0
2021
1
代入极限式得I
.
2021
【思路二】 由 Stolz 公式,得
lim 1 12020 22020 n2020
n n 2021
lim
n 2020
1
n n2021 (n 1)2021 2021
12020 22020 n 2020
1
故 ln
有界. 故I .
n 2021
x a1t, y a2t, z 1 t
将其代入球面方程,得
2
a1t
2
a2t
(1 t)2
1
2
解得参数值为t
a12
a22
或t 1
0.
从容可得 A1 的坐标为
A1
a12
2a1 a22
全国第七届大学生数学竞赛获奖名单
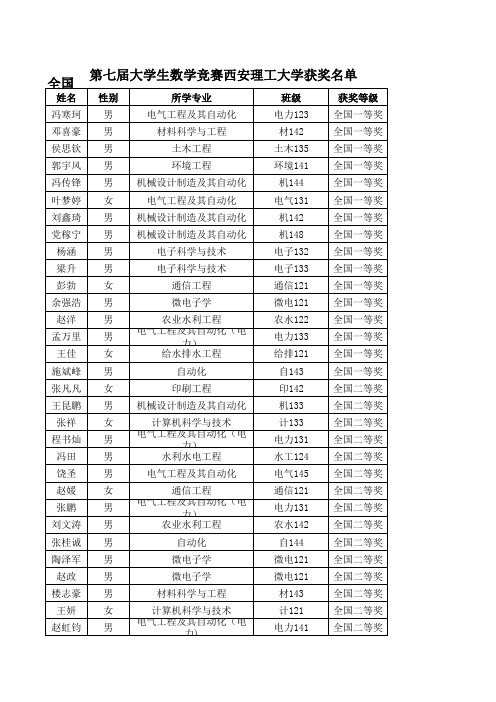
赵洋
男
农业水利工程
孟万里
男
电气工程及其自动化(电 力)
王佳
女
给水排水工程
农水122 电力133 给排121
全国一等奖 全国一等奖 全国一等奖
施斌峰 男
自动化
自143
全国一等奖
张凡凡 女
印刷工程
印142
全国二等奖
王昆鹏 男 机械设计制造及其自动化
机133
全国二等奖
张祥
女
计算机科学与技术
程书灿
男
电气工程及其自动化(电 力)
原景鑫 男
自动化
周汝豪 男
材料物理
张必燊 男
城市地下空间工程
念路鹏 张沛
男 男
电气工程及其自动化(电 电气工程及力其)自动化(电
力)
高盎然 女
给排水科学与工程
崔凯旋 女
金融学
刘国玥 男
微电子学
马春艺 女
自动化
张钦琪 男
材料成型及控制工程
魏蓓
女
热能与动力工程
常志洋 男
热能与动力工程
赵青青 女
电子信息工程
叶梦婷 女
电气工程及其自动化
电气131 全国一等奖
刘鑫琦 男 机械设计制造及其自动化
机142
全国一等奖
党稼宁 男 机械设计制造及其自动化
机148
全国一等奖
杨涵
男
电子科学与技术
电子132 全国一等奖
梁升
男
电子科学与技术
电子133 全国一等奖
彭勃
女
通信工程
通信121 全国一等奖
余强浩 男
微电子学
微电121 全国一等奖
全国大学生数学竞赛考纲概要

全国大学生数学竞赛大纲(非数学专业类为了进一步推动高等学校数学课程的改革和建设,提高大学数学课程的教学水平,激励大学生学习数学的兴趣,发现和选拔数学创新人才,更好地实现“中国大学生数学竞赛”的目标,特制订本大纲。
一、竞赛的性质和参赛对象“中国大学生数学竞赛”的目的是:激励大学生学习数学的兴趣,进一步推动高等学校数学课程的改革和建设,提高大学数学课程的教学水平,发现和选拔数学创新人才。
“中国大学生数学竞赛”的参赛对象为大学本科二年级及二年级以上的在校大学生。
二、竞赛的内容中国大学生数学竞赛(非数学专业类竞赛内容为大学本科理工科专业高等数学课程的教学内容,具体内容如下:一、函数、极限、连续1.函数的概念及表示法、简单应用问题的函数关系的建立.2.函数的性质:有界性、单调性、周期性和奇偶性.3.复合函数、反函数、分段函数和隐函数、基本初等函数的性质及其图形、初等函数.4.数列极限与函数极限的定义及其性质、函数的左极限与右极限.5.无穷小和无穷大的概念及其关系、无穷小的性质及无穷小的比较.6.极限的四则运算、极限存在的单调有界准则和夹逼准则、两个重要极限.7.函数的连续性(含左连续与右连续、函数间断点的类型.8.连续函数的性质和初等函数的连续性.9.闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理.二、一元函数微分学1. 导数和微分的概念、导数的几何意义和物理意义、函数的可导性与连续性之间的关系、平面曲线的切线和法线.2. 基本初等函数的导数、导数和微分的四则运算、一阶微分形式的不变性.3. 复合函数、反函数、隐函数以及参数方程所确定的函数的微分法.4. 高阶导数的概念、分段函数的二阶导数、某些简单函数的n阶导数.5. 微分中值定理,包括罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理.6. 洛必达(L’Hospital法则与求未定式极限.7. 函数的极值、函数单调性、函数图形的凹凸性、拐点及渐近线(水平、铅直和斜渐近线、函数图形的描绘.8. 函数最大值和最小值及其简单应用.9. 弧微分、曲率、曲率半径.三、一元函数积分学1. 原函数和不定积分的概念.2. 不定积分的基本性质、基本积分公式.3. 定积分的概念和基本性质、定积分中值定理、变上限定积分确定的函数及其导数、牛顿-莱布尼茨(Newton-Leibniz公式.4. 不定积分和定积分的换元积分法与分部积分法.5. 有理函数、三角函数的有理式和简单无理函数的积分.6. 广义积分.7. 定积分的应用:平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力及函数的平均值.四.常微分方程1. 常微分方程的基本概念:微分方程及其解、阶、通解、初始条件和特解等.2. 变量可分离的微分方程、齐次微分方程、一阶线性微分方程、伯努利(Bernoulli方程、全微分方程.3. 可用简单的变量代换求解的某些微分方程、可降阶的高阶微分方程:.4. 线性微分方程解的性质及解的结构定理.5. 二阶常系数齐次线性微分方程、高于二阶的某些常系数齐次线性微分方程.6. 简单的二阶常系数非齐次线性微分方程:自由项为多项式、指数函数、正弦函数、余弦函数,以及它们的和与积7. 欧拉(Euler方程.8. 微分方程的简单应用五、向量代数和空间解析几何1. 向量的概念、向量的线性运算、向量的数量积和向量积、向量的混合积.2. 两向量垂直、平行的条件、两向量的夹角.3. 向量的坐标表达式及其运算、单位向量、方向数与方向余弦.4. 曲面方程和空间曲线方程的概念、平面方程、直线方程.5. 平面与平面、平面与直线、直线与直线的夹角以及平行、垂直的条件、点到平面和点到直线的距离.6. 球面、母线平行于坐标轴的柱面、旋转轴为坐标轴的旋转曲面的方程、常用的二次曲面方程及其图形.7. 空间曲线的参数方程和一般方程、空间曲线在坐标面上的投影曲线方程.六、多元函数微分学1. 多元函数的概念、二元函数的几何意义.2. 二元函数的极限和连续的概念、有界闭区域上多元连续函数的性质.3. 多元函数偏导数和全微分、全微分存在的必要条件和充分条件.4. 多元复合函数、隐函数的求导法.5. 二阶偏导数、方向导数和梯度.6. 空间曲线的切线和法平面、曲面的切平面和法线.7. 二元函数的二阶泰勒公式.8. 多元函数极值和条件极值、拉格朗日乘数法、多元函数的最大值、最小值及其简单应用.七、多元函数积分学1. 二重积分和三重积分的概念及性质、二重积分的计算(直角坐标、极坐标、三重积分的计算(直角坐标、柱面坐标、球面坐标.2. 两类曲线积分的概念、性质及计算、两类曲线积分的关系.3. 格林(Green公式、平面曲线积分与路径无关的条件、已知二元函数全微分求原函数.4. 两类曲面积分的概念、性质及计算、两类曲面积分的关系.5. 高斯(Gauss公式、斯托克斯(Stokes公式、散度和旋度的概念及计算.6. 重积分、曲线积分和曲面积分的应用(平面图形的面积、立体图形的体积、曲面面积、弧长、质量、质心、转动惯量、引力、功及流量等八、无穷级数1. 常数项级数的收敛与发散、收敛级数的和、级数的基本性质与收敛的必要条件.2. 几何级数与p级数及其收敛性、正项级数收敛性的判别法、交错级数与莱布尼茨(Leibniz判别法.3. 任意项级数的绝对收敛与条件收敛.4. 函数项级数的收敛域与和函数的概念.5. 幂级数及其收敛半径、收敛区间(指开区间、收敛域与和函数.6. 幂级数在其收敛区间内的基本性质(和函数的连续性、逐项求导和逐项积分、简单幂级数的和函数的求法.7. 初等函数的幂级数展开式.8. 函数的傅里叶(Fourier系数与傅里叶级数、狄利克雷(Dirichlei定理、函数在[-l,l]上的傅里叶级数、函数在[0,l]上的正弦级数和余弦级数。
十四届中国大学生数学竞赛获奖名单

十四届中国大学生数学竞赛获奖名单一、全国一等奖1.康宁,辽宁大学;2.陈思涛,北京大学;3.杨睿,清华大学;4.张浩然,复旦大学;5.林易,浙江大学;6.郑泽南,南京大学;7.郑浩,西安交通大学;8.郑文杰,武汉大学;9.蒋一帆,中南大学;10.熊昷,厦门大学;11.郑立灿,南开大学;12.贺雨桐,东南大学;13.马翔宇,太原理工大学;14.王云瀚,同济大学;15.李晗,电子科技大学;16.刘宇凡,中山大学;17. 郑小平,重庆邮电大学。
二、全国二等奖1.童维,西北工业大学;2.付新,西安电子科技大学;3.谭羽佳,南京航空航天大学;4.张涛,中国农业大学;5.杨汉龙,东北大学;6.谢嘉玮,上海交通大学;7.王峥然,中国科学技术大学;8.刘钰,哈尔滨工业大学;9.沈明雄,华东师范大学;10.孙名字,华中科技大学;11.许亮,南京农业大学;12.杨瑞昊,浙江师范大学;13.陶炜龙,合肥工业大学;14.张璇,北京师范大学;15.黄晓渝,中央民族大学;16.魏琪,苏州大学;17.周杨,北京交通大学;18.黄珩庆,中国人民大学;19.赵士卿,山东大学;20.李新,吉林大学。
三、全国三等奖1.马跃,北京航空航天大学;2.范苓,南京理工大学;3.张迪,湖南大学;4.罗家乐,深圳大学;5.李洋,大连理工大学;6.马艳秋,山东大学威海分校;7.丁耀,广西大学;8.王敏,安徽大学;9.马超,湖北大学;10.金鑫,西南大学;11.张俊宁,西安理工大学;12.马茹,西安科技大学;13.黄莎莎,中国矿业大学徐州校区;14.陈志伟,四川大学;15.孙健,武汉理工大学;16.赵洋,兰州大学;17.刘憬,深圳大学;18.李健,东北林业大学;19.崔传洁,河北工业大学;20.李益,北京科技大学。
四、特别奖1.郑凡,华南师范大学;2.刘磊,山西大学;3.张轩,西南民族大学;4.邓昊,四川师范大学;5.范妍,河南师范大学;6.李楠,江苏大学;7.丁晨,宁夏大学;8.陈江萁,云南大学;9.庞宗涛,福建师范大学;10.张志萍,山西农业大学;11.朱洋,西北农林科技大学;12.庞俊涛,浙江财经大学;13.张玉梅,青海大学;14.白赫,新疆师范大学;15.马昕,云南师范大学;16.刘浩,湖北中医药大学;17.曹舒,四川农业大学;18.李林,大连科技学院;19.张定祥,青岛大学;20.高雪琪,中国地质大学(武汉)。
2022十四届全国大学生数学竞赛广东赛区获奖名单

2022十四届全国大学生数学竞赛广东赛区获奖名单2022,我国在广东省举办了十四届全国大学生数学竞赛,这场比赛由中国数学会,中国科学院数学与系统科学研究院,大学数学与应用数学教育与科研协会和中国校外教育网络协会共同发起和主办,是一次全国性大型数学竞赛,聚集大批青少年人才,包括多门数学类学科,涉及国际国内高校专业层次的参赛人员,是一次系统的数学知识竞技活动。
此次全国数学竞赛,广东省吸引了众多参赛者,来自全国多地的青少年参加了此次比赛,参赛人员多达1000多人,他们来自不同的地区、学校、专业和年龄,许多参赛队伍走访了比赛现场,为比赛增添了趣味和活力。
在激烈的比赛中,比赛最终宣布了众多优秀成绩,在竞赛中取得优异成绩的参赛者被授予了相应的荣誉和奖励。
总而言之,广东省的十四届全国大学生数学竞赛获奖名单如下:一等奖:吴泰铭,华南师范大学;二等奖:何玉杰,中山大学;三等奖:阮景晨,广东外语外贸大学;特等奖:李成启,深圳大学;优秀奖:胡瑞琴,深圳职业技术学院;优秀奖:张竹山,广东工业大学;广东省青少年班获奖者:杨嘉荣,黄鹤英语学校,罗敬元,汕头市第一中学,朱家熙,汕头师范学院附属中学,许睿彦,汕头市第三中学,陈浩,汕头市第九中学,陈泽,汕头市第五中学,熊攀,汕头市第十中学,胡峰,汕头市第二中学,苏家宁,汕头市第六中学,罗家熙,汕头市第四中学,彭小森,汕头市第八中学。
此次全国大学生数学竞赛的诞生,为我国的社会发展带来了无限可能。
在未来,将青少年数学竞赛塑造为一个活跃而有意义的文化性活动,引领大学生从接受教育到社会实践,从个人实现到国家发展改革,这将是一条新的发展道路。
从本次大学生数学竞赛中,我们可以看到,在困难与机遇并存的环境中,即使手头条件不太好,也能发挥自身的潜能,取得优异成绩,这是学习数学的精神,也是这次数学竞赛的精神。
数学的奥秘正在等着我们来探索,中国的数学教育也正在发展,大学生数学竞赛为青少年提供了一个平台,让他们可以探索数学之美,取得更好的成绩。
第4届全国大学生数学竞赛决赛试卷(数学类)

专业:考生座位号:线所在院校:封密准考证号:姓名:第四届全国大学生数学竞赛决赛试卷(数学类,2013)考试形式: 闭卷 考试时间: 150 分钟 满分: 100 分.注意:1、所有答题都须写在此试卷纸密封线右边,写在其它纸上一律无效. 2、密封线左边请勿答题,密封线外不得有姓名及相关标记. 3、如当题空白不够,可写在当页背面,并标明题号.一、(本题15分)设A 为正常数,直线L 与双曲线222(0)x y x -=>所围的有限部分的面积为A . 证明:(i) 上述L 被双曲线222(0)xy x -=>所截线段的中点的轨迹为双曲线.(ii) L 总是(i)中轨迹曲线的切线.二、(本题15分)设函数()f x 满足条件: 1) ()a f x b -∞<≤≤<+∞, a x b ≤≤;2) 对任意不同的x,y a,b 有()(),其中f x f y L x y L ⎡⎤∈-<-⎣⎦是大于0小于1的常数.设1,,x a b ⎡⎤∈⎣⎦令11(),1,2, (2)n n n x x f x n +⎡⎤=+=⎣⎦ . 证明lim n n x x→∞=存在,且().f x x =专业:考生编号:线所在院校:封密准考证号:姓名:三、(本题15分)设实n 阶方阵A 的每个元素的绝对值为2. 证明:当n ≥3时,112!3n A n +≤.四、(本题15分)设()f x 为区间(),a b 上的可导函数. 对()0,x a b ∈,若存在0x 的邻域U 使得任意的{}0\x U x ∈有'000()()()()f x f x f x x x >+-,则称0x 为()f x 的凹点. 类似地,若存在0x 的邻域U 使得任意的{}0\x U x ∈有'000()()()()f x f x f x x x <+-,则称0x 为()f x 的凸点.求证:若()f x 是区间(),a b 上的可导函数且不是一次函数,则()f x 一定存在凹点或凸点..专业: 考生编号:线所在院校:封密准考证号:姓名:五、(本题20分)设111213212223313233a a a A a a a a a a ⎛⎫ ⎪= ⎪ ⎪⎝⎭为实对称矩阵, *A 为A 的伴随矩阵. 记212342111213123432122234313233(,,,)x x x x x a a a f x x x x x a a a x a a a -=--. 若A 的行列式为12-, A 的所有特征值的和为1, 且(1,0,2)T -为*(4)0A I x -=一个解. 试给出一正交变换11223344x y x y Q x y x y ⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭使得1234(,,,)f x x x x 化为标准型.六、(本题20分)令R 为实数域, n 为给定的正整数,A 表示所有n 次首一实系数多项式组成的集合.证明:1,0,()()inf0b cbn b c P x AP x dx c++∈>∈>⎰R .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全国大学生数学竞赛
全国大学生数学竞赛是一项全国范围内的学术竞赛活动,旨在提高大学生的数学素养和解决实际问题的能力。
该竞赛由教育部主办,每年都吸引着全国各高校的优秀学子参与。
作为数学竞赛的顶级赛事之一,全国大学生数学竞赛具
有较高的知名度和影响力。
这项竞赛分为理论赛和应用赛两个阶段。
理论赛主要考察学生对数学基础知识的掌握和理论推导能力,题目涵盖了数学的各个分支,如代数、几何、概率与统计等。
而应用赛则侧重于学生解决实际问题的能力,要求学生运用数学方法分析和解决现实问题。
参加全国大学生数学竞赛对学生来说是一次宝贵的经历。
通过参与竞赛,学生可以锻炼自己的逻辑思维和分析问题的能力,提高数学知识的应用水平。
此外,竞赛中的交流和互动也有助于学生之间的学习和成长,激发出更多的数学热情。
全国大学生数学竞赛对于学习数学的大学生们而言意义
重大。
通过参加竞赛,学生能够接触到一些高难度的数学问题,加深对数学知识的理解和掌握。
竞赛过程中的挑战和压力也能够帮助学生提升解决问题的能力和应对压力的能力。
为了取得好成绩,在备赛期间,学生们需要充分利用学
校和社会资源,积极参加数学辅导班和讲座,深入学习数学知识,扩展数学视野。
同时,解题能力的提高也需要大量的题目练习和思考。
通过分析解题思路和解题技巧,学生们能够更好地应对竞赛中的各种题目。
总的来说,参加全国大学生数学竞赛对于大学生的数学
学习和个人发展有着积极的影响。
它不仅能够提高学生的数学素养和解决实际问题的能力,还能够培养学生的逻辑思维和分析能力。
因此,我鼓励更多的大学生积极参与全国大学生数学竞赛,不断挑战自我,提高自己的数学能力。
