人教版小学五年级数学上册 组合图形的面积练习题及答案
人教版数学 五年级上册 组合图形的面积 课后练习题

一、选择题1. 估计一下,下图不规则土地的面积约是()。
A.B.C.2. 如图,每个小正方形的面积是1cm2,曲线所围成的图形面积约是()。
A.30cm2B.40cm2C.50cm2D.70cm23. 下面图形中不可以密铺的是()。
A.正五边形B.正六边形C.正三角形4. 在下边的梯形中,甲、乙两个三角形的面积().A.相等B.不相等C.无法确定5. 如图所示,每个小方格的面积是1cm2,估计图中涂色部分的面积约为()cm2。
A.10 B.20 C.30 D.40二、填空题6. 用24个边长1厘米正方形拼成长方形,有()种不同的拼法,周长最短的是()厘米。
(请在下表中列举不同的拼法)长/cm宽/cm周长/cm7. 一个大长方形被分成三个小长方形S1、S2、S3和一个正方形S,已知S1与S2的面积和为13,S2与S3的面积和为33,每个小长方形的长和宽都是正整数,且正方形的面积比小长方形S1、S2、S3的面积都大,则正方形的面积为.8. 直角三角形的两直角边的长都是整厘米数,面积为59.5平方厘米.每次取四个同样的三角形围成(不重叠,不剪裁)含有两个正方形图案的图形(如图),在围成的所有正方形图案中,最小的正方形的面积是_____平方厘米,最大的正方形的面积是_____平方厘米.9. 图中长方形的面积是10平方厘米,则阴影部分的面积一共是( )平方厘米。
10. 两个长方形如图摆放,M为AD的中点,阴影部分的面积=.三、解答题11. (1)观察下图,用数对表示各个点的位置。
A(4,8) B(,) C(,) D(,) E(,)(2)如果每个小方格的面积为1cm2。
请你求出下面这个图形的面积。
12. 如图是一个大正方形和一个小正方形拼成的,已知小正方形边长4cm,阴影部分面积28cm2,求空白部分面积.13. 一台收割机,作业宽度是1.8米.每小时5千米,多少小时可以收割完右面这块地?14. 在如图中,阴影部分A的面积比阴影部分B的面积大10.5平方厘米,求线段BC的长度?。
五年级数学上册组合图形面积应用题面积解答题附解析

组合图形面积应用1.计算下面图形中阴影部分的面积。
(单位:厘米)解:25×16-(9+11)×6÷2=25×16-20×6÷2=400-120÷2=400-60=340(平方厘米)答:阴影部分的面积为340平方厘米。
2.求面积是多少?解:[(200-140)+100]×(200-80)÷2+200×140=160×120÷2+28000=9600+28000=37600(平方米)答:面积是37600平方米。
3.计算下图阴影部分的面积。
解:阴影部分的面积=(10+15)×10÷2-10×10÷2 =25×10÷2-100÷2=250÷2-50=125-50=75(平方米)。
4.计算阴影部分的面积。
(单位:cm)解:60×40-60×40÷2=2400-2400÷2=2400-1200=1200(平方厘米)5.求下面组合图形的面积。
(单位:cm)解:8×4+8×4÷2=32+32÷2=32+16=48(平方厘米)6.计算下面阴影部分的面积。
(1)(2)(1)解:阴影部分的面积=14×12÷2=168÷2=84(平方厘米)(2)解:阴影部分的面积=12×10-12×6÷2=120-72÷2=120-36=84(平方分米)(2)阴影部分的面积=平行四边形的面积-三角形的面积,平行四边形的底是20dm,高是10dm;三角形的底是20dm,高是6dm,再根据平行四边形的面积=底×高,三角形的面积=底×高÷2,代入数值计算即可。
7.计算下面图形的面积。
2020年人教版五年级上册数学六、4.组合图形的面积附答案

六、4.组合图形的面积一、填空乐园1.在一个上底是6厘米、下底是9厘米、高是4厘米的梯形中剪去一个最大的三角形,剩下的部分面积是( )平方厘米。
2.一个平行四边形,面积是54平方分米,如果高缩小到原来的21,要使面积不变,底应该( )。
3.三角形的底扩大a 倍,高扩大b 倍,面积扩大( )倍。
4.如图,要使三角形ABE 的面积是梯形AECD 面积的一半.BE 的长应是( )。
5.下面平行四边形的面积是15平方厘米,阴影部分的面积是( )平方厘米。
6.如图,现有6x6的方格,每个小方格的边长都是1,那么图中阴影部分的面积的总和等于( )。
7.如图,每两个相邻点之间的距离都是1厘米,三角形ABG 的面积是( ),梯形CDEF 的面积是( ),这个图形的面积是( )。
8.如图,每两个相邻的点之间的距离都是1厘米,平行四边形ABCE 的面积为( ),梯形ABDE 的面积为( )。
9.如图,若每个小正方形的面积都是1平方厘米,那么图中阴影部分的面积是( )平方厘米。
10.如图.每相邻三个点所形成的三角形都是面积为1的正三角形,则三角形ABC的面积为( )。
11.如图,平行四边形ABCD的底边DC长5 cm,直角三角形DCE的直角边EC长4厘米。
已知两块阴影部分的面积和比三角形EFG的面积大5平方厘米,则CF=( )厘米。
12.将一个正方形的一组对边各延长4厘米后,就成了一个长方形,这个长方形的面积比原来正方形的面积多32平方厘米,这个长方形的面积是原来正方形面积的( )倍。
二、判断快车1.两个等底等高的三角形都能拼成一个平行四边形。
( )2.在平行四边形内画一个三角形,三角形的面积一定等于平行四边形面积的一半。
( ) 3.两个面积相等的梯形,形状也一定相同。
( )4.梯形只有一条高,三角形有三条高。
( )5.两个完全一样的直角梯形可以拼成一个等腰梯形。
( )6.周长相等的两个平行四边形的面积不一定相等。
( )7.把一个长方形木框拉成平行四边形后,它的面积一定与原来长方形的面积相等。
五年级上册数学《组合图形面积》应用题

《组合图形面积》应用题1、一个果园形状如图,一棵果树占地5m²,这个果园一共可以种多少棵树?30×10+(30-16)×(20-10)÷2=300+14×10÷2=300+70=370(平方米)370÷5=74(棵)2、李大爷家有一块菜地(如图),这块菜地的面积有多少平方米?(19+9)×9+(21-9)×9=28×9+12×9=252+108=360(平方米)答:这块菜地的面积有360平方米.3、下面的组合图形你一定很熟悉吧,那就请你动起手来,试一试吧如图阴影部分是梯形,左面长方形长4厘米,宽3厘米,A为宽中点.求阴影部分的面积?3×4-3×(4÷2)÷2=12-3×2÷2=12-3=9(平方厘米)答:阴影部分的面积是9平方厘米《组合图形面积》应用题4、学校要油漆60扇教室的门的外面(门的形状如图,单位:米).(1)需要油漆的面积一共是多少?0.8×2-0.4×0.3=1.6-0.12=1.48(平方米)1.48×60=88.8(平方米)答:需要油漆的面积一共是88.8平方米.(2)如果油漆每平方米需要花费10元,那么学校一共要花费多少元?88.8×10=888(元)答:学校一共要花费888元.5、王爷爷家有一块地,他分别用来种植高粱、土豆和玉米(如下图).其中土豆和玉米的种植面积相等,都是21m².请计算出王爷爷家这块地的面积.21×2÷6=7(米)(9.3+9.3+6+6)×7÷2=30.6×7÷2=107.1(平方米)答:王爷爷家这块地的面积是107.1平方米.。
数学五年级上册《组合图形的面积》同步训练(含答案)
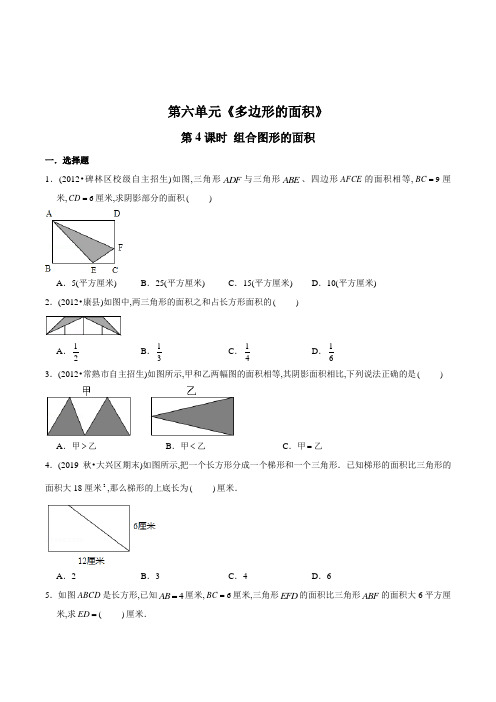
第六单元《多边形的面积》第4课时组合图形的面积一.选择题1.(2012•碑林区校级自主招生)如图,三角形ADF与三角形ABE、四边形AFCE的面积相等,9BC=厘米,6CD=厘米,求阴影部分的面积()A.5(平方厘米)B.25(平方厘米)C.15(平方厘米)D.10(平方厘米)2.(2012•康县)如图中,两三角形的面积之和占长方形面积的()A.12B.13C.14D.163.(2012•常熟市自主招生)如图所示,甲和乙两幅图的面积相等,其阴影面积相比,下列说法正确的是()A.甲>乙B.甲<乙C.甲=乙4.(2019秋•大兴区期末)如图所示,把一个长方形分成一个梯形和一个三角形.已知梯形的面积比三角形的面积大18厘米2,那么梯形的上底长为()厘米.A.2B.3C.4D.65.如图ABCD是长方形,已知4AB=厘米,6BC=厘米,三角形EFD的面积比三角形ABF的面积大6平方厘米,求(ED=)厘米.A.9B.7C.8D.6二.填空题6.(2019春•海淀区月考)如图,有一块长方形场地,长62=,从A、B两处入口的小路宽都AD mAB m=,宽41是1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为2m.7.(2019春•静安区月考)如图的三角形分成两部分,甲的面积是210cm,乙的面积是2cm.8.(2019•徐州)如图中,阴影部分的面积占大长方形的.9.(2019春•湖北月考)如图,梯形的面积是.10.(2019•长沙县)如图,D是BC的三等分点,E是AC的四等分点,三角形ABC的面积是三角形ADE的面积的 倍.11.(2019春•杨浦区月考)如图,已知AE EC =,:2:3BD DC =,AFE ∆的面积比BFD ∆的面积多2,则ABC ∆的面积是12.(1999•广州自主招生)一个宽是3厘米的长方形,如果将长和宽都增加3厘米,那么面积增加81平方厘米;如果将长和宽都减少2厘米,那么面积减少 平方厘米.三.判断题13.如图所示,梯形的上底长等于下底长的一半,空白面积也等于阴影部分面积的一半. (判断对错)四.计算题14.(2018秋•环江县期末)计算下面图中阴影部分的面积.(单位:分米)15.(2019•武侯区)计算下面图形的面积.(单位:)cm16.(2017•西安模拟)求图中阴影部分的面积(单位:厘米) 17.(2015秋•徐州月考)求下列各图形面积18.(2017秋•栖霞区校级期中)求阴影部分面积.19.(2016秋•贵州月考)计算如图各图形的面积.20.计算下面图形中阴影部分的面积.(单位:分米)五.应用题21.(2019春•无棣县期末)在一块长方形地上,种上三种不同的蔬菜,如图.(1)黄瓜地的周长是多少米?(2)西红柿地的面积是多少?22.(2017•武汉模拟)如图,在直角三角形ABC里面裁剪一个正方形CDEF,剩下两个三角形,已知=,则图中阴影部分的面积是多少平方厘米?BE cm=,43AE cm23.(2017秋•巴南区期中)有一块长方形的地如图,中间有两条2m宽的水泥小路,其余部分为草坪,求草坪的面积?24.实验小学评比“卫生文明班级”需要制作一些流动红旗(如图)。
五年级上册数学-思维训练 组合图形的面积(直线图形)汇总(含答案)人教新课标

小学数学思维训练5-5.组合图形的面积(直线图形)一、知识要点(一)常用的面积公式及其联系图(二)几种常见的解题方法对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。
常用的基本方法有:1. 直接求面积:这种方法是根据已知条件,从整体出发直接求出不规则图形面积。
例1:求下图阴影部分的面积(单位:厘米)。
解答:通过分析发现它就是一个底是2、高是4的三角形,其面积直接可求为:×2×4=4(平方厘米)2.相加、相减求面积:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加或相减求出所求图形的面积。
例2:正方形甲的边长是5厘米,正方形乙的边长是4厘米,阴影部分的面积是多少?解答:两个正方形的面积:+=41(平方厘米)三个空白三角形的面积和:(5+4)×5÷2+4×4÷2+5×(5-4)÷2=33(平方厘米)阴影部分的面积:41-33=8(平方厘米)3.等量代换求面积:一个图形可以用与它相等的另一个图形替换,如果甲乙大小相等,那么求出乙的大小,就知道甲的大小;两个图形同时增加或减少相同的面积,它们的差不变。
例3:平行四边形ABCD的边BC长8厘米,直角三角形ECB的直角边EC长为6厘米。
已知阴影部分的总面积比三角形EFG的面积大8平方厘米,平行四边形ABCD的面积是多少?解答:阴影部分的总面积比三角形EFG的面积大8平方厘米,分别加上梯形FBCG,得出的平行四边形ABCD比三角形EBC的面积大8平方厘米。
平行四边形ABCD的面积:8×6÷2+8=32(平方厘米4.借助辅助线求面积:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法求面积。
例4:下图中,CA=AB=4厘米,三角形ABE比三角形CDE的面积大2平方厘米,CD的长是多少?解答:结合已知条件看图,很难有思路,连接DA,就可以发现:三角形ABE比三角形CDE 的面积大2平方厘米,分别加上三角形DAE得到的三角形ABD比三角形CDA的面积大2平方厘米。
数学五年级上册组合图形的面积解决问题复习测试题(含答案)

6.4组合图形的面积1.双龙兴村有一个长35米的长方形喷水池,后来设计师又将长增加了6米,于是喷水池面积增加了180平方米,现在扩建后的面积是多少?2.按照下页图的样子,在一平行四边形纸片上割去了甲、乙两个直角三角形.已知甲三角形两条直角边分别为4厘米和8厘米,乙三角形两条直角边分别为6厘米和12厘米.求阴影部分的面积.3.长方形ABCD周长为16米,在它的每条边上各画一个以该边为边长的正方形,已知这四个正方形的面积之和是68平方米,求长方形ABCD的面积.(已将辅助图形画好)4.如图是某OK厅的广告牌,每个小方格为1平方分米,请你算一算广告牌上“OK”的面积.5.粉刷一间教室的一面墙(如图),如果每平方米用涂料0.2kg,除去窗户,粉刷需多少千克涂料?如果每千克涂料花费4元,共需多少元?6.学校有一块劳动基地,如下图所示,其中(1)部分种玉米,(2)部分种花生,(3)部分种棉花.①种玉米的面积是10平方米,种花生的面积是多少平方米?②如果每平方米种棉花2棵,那么在(3)部分可以种棉花多少棵?7.学校粉刷这面墙,每平方米用涂料0.15千克,一共用涂料多少千克?8.学校艺术节课本剧表演需要一堵道具墙(如下图).请你算一算,至少需要纸板多少平方米?9.有一天,爷爷打算在院落里种上蔬菜,已知院落为东西长32米,南北宽21米的长方形,为了行走方便要修筑同样宽的三条道路:东西两条,南北一条,南北道路垂直于东西道路(如图阴影部分),余下的部分要种上西红柿,设道路宽为0.5米,爷爷让小明算一下,用于种菜的面积是多少?10.测测你的综合能力(1)如图所示是两个相同的直角梯形重叠在一起,求阴影部分的面积.(单位:厘米)(2)某学校学生外出游玩坐船,如果每条船坐8人,还剩9人.每条船坐9人,还剩1条船空着没有同学坐.问有几个人?有几条船?11.一个正方形的硬纸板,先沿着它的一条边剪去宽4厘米的长方形,再沿着它的另一条边也剪去宽4厘米的长方形,面积比原来的正方形减去了96平方厘米.原来正方形的面积是多少平方厘米?12.一个长方形操场,长80米,宽60米,现在要扩建这个场地,长增加25米,宽增加15米.扩建后的面积增加了多少平方米?(试着用两种方法计算)13.一个正方形的边长增加10厘米后,面积增加了220平方厘米,求原来正方形的面积是多少平方厘米?14.在一个正方形金鱼池(图中的空白部分)的周围铺了一圈草坪,草坪的宽度是2米,面积是136平方米.求金鱼池的边长.15.有一天,爷爷打算在院落里种上蔬菜,已知院落为东西长32米,南北宽21米的长方形,为了行走方便要修筑同样宽的三条道路:东西两条,南北一条,南北道路垂直于东西道路(如图阴影部分),余下的部分要种上西红柿,设道路宽为0.5米,爷爷让小明算一下,用于种菜的面积是多少?16.一个长方形操场,长80米,宽60米,现在要扩建这个场地,长增加25米,宽增加15米.扩建后的面积增加了多少平方米?(试着用两种方法计算)17.在一张长30厘米、宽18厘米的长方形纸的一端剪掉一个最大的正方形,在剩下的长方形纸的一端再剪掉一个最大的正方形.最后剩下部分是什么图形?它的面积是多少平方厘米?18.[化整为零].如图,正方形ABCD和正方形EFGH分别内接于同一个等腰直角三角形MBN(这里的内接指正方形的四个顶点全部在三角形的边上).已知正方形ABCD的面积是72平方厘米,那么正方形EFGH的面积是多少平方厘米?19.如图,有一面墙,粉刷这面墙每平方米需用0.15千克涂料.一共要用多少千克涂料?20.有一块铁皮,形状如图.如果要油饰这块铁皮的一面,每平方米用油漆0.6千克,刷完这块铁皮需要多少千克油漆?21.解答下面各题.(1)计算阴影部分的面积.(单位:厘米)(2)货车和客车同时从甲城开往乙城.货车每小时行40千米,客车每小时行60千米,客车在中途停留两小时,但仍比货车早到30分.甲、乙两城相距多少千米?22.有一块长方形菜地,长16米,宽8米.菜地中间留了两条2米宽的路,把菜地平均分成4块,每块地的面积是多少平方米?(单位:米)23.如图是一块长方形草地,长是20米,宽是12米,中间有两条石子路,一条是底是2米的平行四边形,一条是2米的长方形.求草地的面积.24.如图是一块红领巾实验基地(每小格代表1㎡),如果在这块地里种牡丹,每棵大约占地0.2㎡,每棵卖14元,这块地里种的牡丹大约能收入多少元?25.一个梯形上底是5厘米,下底是8.2厘米,高是4.5厘米,如果在这个梯形中剪去一个最大的三角形,剩下的面积是多少平方厘米?参考答案1.35×(180÷6)+180=35×30+180=1050+180=1230(平方米)答:现在扩建后的面积是1230平方米.2.解:将甲、乙分别平移到如图位置,则平行四边形的面积就是两个长方形的面积之和,8×6+4×12﹣8×4÷2﹣12×6÷2,=48+48﹣16﹣36,=96﹣52,=44(平方厘米);答:阴影部分的面积是44平方厘米.3.因为大正方形BC1EA1的边长BC1=BC+CC1=BC+CD=×16=8(米),所以大正方形BC1EA1的面积=8×8=64(平方米);又因正方形ADD1A1的面积+正方形CC1E1D的面积=68÷2=34(平方米),而长方形ABCD和长方形DE1ED1的面积相等,所以长方形ABCD的面积为(64﹣34)÷2=15(平方米);答:长方形ABCD的面积为15平方米.4.根据题干分析可得:“OK”所在的方格一共有:12+10=22(个),22×1=22(平方分米),答:它的面积是22平方分米.5.8×6+8×1.2÷2﹣2.4×1.2)×0.2,=(48+4.8﹣2.88)×0.2,=49.92×0.2,=9.984(千克);9.984×4=39.936(元);答:粉刷需9.984千克涂料,如果每千克涂料花费4元,共需39.936元.6.①10×2÷2.5=8(米),5×8=40(平方米),答:种花生的面积40平方米②2×(6.5+3.5)×8÷2=2×10×4,=80(棵);答:在(3)部分可以种棉花80棵.7.解:0.15×(10×1.6÷2+10×4),=0.15×(8+40),=0.15×48,=7.2(千克);答:一共用涂料7.2千克.8.2÷2=1(米),3.14×12÷2+2×1.5=1.57+3=4.57(平方米)答:至少需要纸板4.57平方米.9.用于种菜的面积就是长为31.5米,宽为20米的长方形的面积,31.5×20=630(平方米);答:用于种菜的面积是630平方米.10.(1)(20﹣5+20)×8÷2,=35×8÷2,=280÷2,=140(平方厘米);答:阴影部分的面积是140平方厘米.(2)设有x条船,8x+9=9(x﹣1),8x+9=9x﹣9,9x﹣8x=18,x=18;8×18+9,=144+9,=153(人);答:有153人,18条船.11.图①的面积是:10×10=100(平方米);图②、图③每个长方形的面积:(900﹣100)÷2,=800÷2,=400(平方米);原来正方形的边长:400÷10=40(米);原来这个操场的面积是:40×40=1600(平方米);答:原来这个操场的面积是1600平方米.12.第一种方法:(80+25)×(60+15),=105×75,=7875(平方米),7875﹣60×80=3075(平方米).答:扩建后的面积增加了3075平方米.第二种方法:25×60+(80+25)×15,=1500+1575,=3075(平方米).答:扩建后的面积增加了3075平方米.13.原来正方形的边长是:(220﹣10×10)÷2÷10,,=(220﹣100)÷2÷10,=120÷2÷10,=6(厘米),原来的面积是:6×6=36(平方厘米);答:原来正方形的面积是36平方厘米.14.解:(136﹣2×2×4)÷4÷2,=120÷4÷2,=30÷2,=15(米),答:这个正方形鱼池的边长是15米.15.用于种菜的面积就是长为31.5米,宽为20米的长方形的面积,31.5×20=630(平方米);答:用于种菜的面积是630平方米.16.第一种方法:(80+25)×(60+15),=105×75,=7875(平方米),7875﹣60×80=3075(平方米).答:扩建后的面积增加了3075平方米.第二种方法:25×60+(80+25)×15,=1500+1575,=3075(平方米).答:扩建后的面积增加了3075平方米.17.(30﹣18)×(18﹣12),=12×6,=72(平方厘米),答:剩下的是一个长方形,面积是72平方厘米.18.72×2=144(平方厘米),则===64(平方厘米),答:正方形EFGH的面积是64平方厘米.19.10×1.6÷2+10×4,=8+40,=48(平方米);48×0.15=7.2(千克);答:一共要用7.2千克涂料.20.(3×1.2÷2+5×2.4)×0.6,=(1.8+12)×0.6,=13.8×0.6,=8.28(千克);答:刷完这块铁皮需要8.28千克油漆.21.(1)3×4÷2×2÷5,=12÷5,=2.4(厘米),(5+8)×2.4÷2﹣3×4÷2,=13×2.4÷2﹣6,=15.6﹣6,=9.6(平方厘米);答:阴影部分的面积是9.6平方厘米.(2)60×[(60×2.5)÷(60﹣40)﹣2.5], =60×[7.5﹣2.5]=60×5,=300(千米).答:甲乙两城相距300千米.22.(16﹣2 )×(8﹣2)÷4,=14×6÷4,=84÷4,=21(平方米),答:每块地的面积是21平方米.23.(20﹣2)×(12﹣2),=18×10,=180(平方米).答:草地的面积是180平方米.24.实验基地的面积:63+(9÷2﹣1),=63+(4.5﹣1),=63+3.5,=66.5(平方米);牡丹总棵树:66.5÷0.2=332.5≈333(棵);牡丹总售价:333×14=4662(元);答:这块地里种的牡丹大约能收入4662元.25.剪去一个最大的三角形,必须以梯形的下底作为三角形的底,梯形的高作为三角形的高,所以三角形的面积:8.2×4.5÷2=18.45(平方厘米),梯形的面积:(5+8.2)×4.5÷2=29.7(平方厘米),剩下的面积:29.7﹣18.45=11.25(平方厘米).答:剩下的面积是11.25平方厘米.。
五年级数学上册求组合图形面积阴影应用题面积解答题附解析
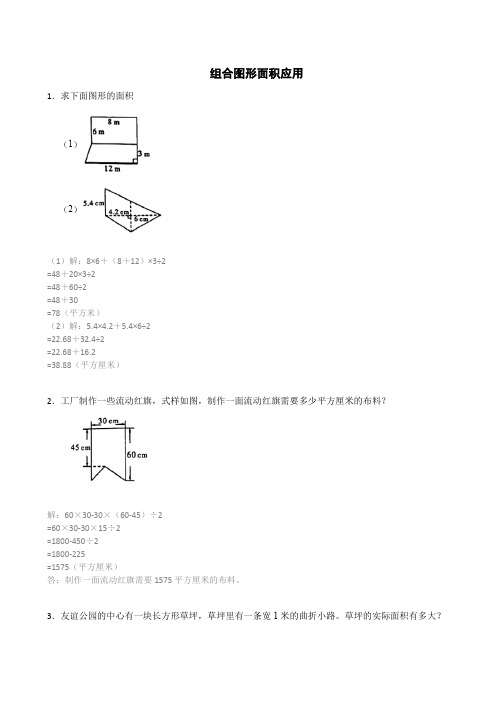
组合图形面积应用1.求下面图形的面积(1)(2)(1)解:8×6+(8+12)×3÷2=48+20×3÷2=48+60÷2=48+30=78(平方米)(2)解:5.4×4.2+5.4×6÷2=22.68+32.4÷2=22.68+16.2=38.88(平方厘米)2.工厂制作一些流动红旗,式样如图,制作一面流动红旗需要多少平方厘米的布料?解:60×30-30×(60-45)÷2=60×30-30×15÷2=1800-450÷2=1800-225=1575(平方厘米)答:制作一面流动红旗需要1575平方厘米的布料。
3.友谊公园的中心有一块长方形草坪,草坪里有一条宽1米的曲折小路。
草坪的实际面积有多大?解:(12-1)×(10-1)=11×9=99(平方米)答:草坪的实际面积有99平方米。
4.李叔叔家原来有一块边长12米的正方形菜地,今年他将这块菜地进行了扩建(如图中的涂色部分)。
(1)原来这块菜地的面积是多少平方米?(2)李叔叔今年扩建了多少平方米的菜地?(1)解:12×12=144(平方米)答:原来这块菜地的面积是144平方米。
(2)解:(12+7)×(12+2)-144=19×14-144=266-144=122(平方米)答:李叔叔今年扩建了122平方米的菜地。
5.求出下面图形的面积。
(1)如图,已知梯形的面积是60米2,那么,阴影部分(三角形)的面积是多少米"?(2)求出下面组合图形的面积。
(单位:厘米)(1)解:(60×2)÷(8+12)=120÷20=6(米)8×6÷2=48÷2=24(平方米)答:阴影部分(三角形)的面积是24平方米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
组合图形的面积
1.组合图形的面积
(1)下面组合图形的面积是______平方厘米。
(2)下面组合图形是由一个正方形和有一个平行四边形组成,它的面积是______平方厘米。
(3)下面组合图形的面积是______平方厘米。
(4)下面组合图形的面积是______平方厘米。
(5)下图阴影部分的面积是______平方厘米。
(单位:厘米)
(6)下图阴影部分的面积是______平方分米。
(单位:分米)
2.替换法求三角形或梯形的面积
(1)三角形ABC与三角形DFE是两个完全相同的直角三角形,把它们的一部分叠放在一起,如下图所示,阴影部分的面积是_____平方厘米。
(单位:cm)
(2)如右图,三角形ABC与三角形DFE是两个完全相同的直角三角形,把它们的一部分叠放在一起,如下图所示,阴影部分的面积
是_____平方厘米。
(单位:cm)
(3)三角形ABC与三角形EFD是两个完全相同的直角三角形,把它们的一部分叠放在一起,如下图所示,阴影部分的面积是______
平方厘米。
(单位:cm)
(4)如下图所示,两个完全相同的梯形重叠放在一起,阴影部分的面积是______平方厘米。
(单位:cm)
(5)如下图所示,两个完全相同的梯形重叠放在一起,阴影部分的面积是______平方厘米。
(单位:cm)
(6)如右图所示,两个完全相同的梯形重叠放在一起,阴
影部分的面积是______平方厘米。
(单位:cm)
3.面积差不变-线段围成的图形
(1)已知长方形的长为6厘米,宽为2.5厘米,三角形的底边长为6厘米,高为2厘米,这两个图形有一小部分重合了,则它们没有重合的部分的面积相差______平方厘米
(2)边长为5厘米和4厘米的两个正方形有一小部分重合,
则它们没有重合的部分的面积相差______平方厘米
(3)已知梯形的上底长4厘米,下底长为7厘米,高为3厘米,
这个梯形与一个边长为3厘米的正方形有一小部分重合
了,则它们没有重合的部分的面积相差______平方厘米
(4)已知三角形ABC的底边BC长为4厘米,高为3厘米,三角形DEF的底边EF 长为5厘米,高为6厘米,这两个三角形有一小部分重合了,则它们没有重合的部分的面积相差______平方厘米
(5)已知平行四边形的底边长为7厘米,高为3厘米,
三角形的底边长为6厘米,高为5厘米,这两个图
形有一小部分重合了,则它们没有重合的部分的
面积相差______平方厘米
(6)图中甲的面积比乙的面积大4平方厘米,三角形ABC的
底边长为4厘米,高为2.5厘米,那么三角形DEF的面
积是______平方厘米
(7)图中甲的面积比乙的面积小5平方厘米,正方形ABCD的边长为5厘米,那么三角形ABF的面积是______平方厘米
4.有关直角梯形的面积
(1)如图所示,直角梯形ABCD的高AB长26厘米,AD长24
厘米,△DEF的面积是175.5平方厘米,EF的长度是BC
的二分之一,梯形ABCD的面积是______平方厘米。
(2)如图所示,直角梯形ABFD的高AB长25厘米,AD
长25厘米,△DEC的面积是200平方厘米,EC的
长度是BF的三分之一,梯形ABFD的面积是______
平方厘米。
(3)如图所示,直角梯形ABCD的高AB长10厘米,BC
长8厘米,△CEF的面积是20平方厘米,EF的长
度是AD的四分之一,梯形ABCD的面积是______平
方厘米。
(4)右图是一个直角梯形(单位:厘米)。
阴影部
分的面积是______平方厘米。
(5)下图是一个直角梯形(单位:厘米)。
AB=20cm,CF=16cm,BC=18.5cm,阴影部分的面积是______平方厘米。
(6)下图是一个直角梯形(单位:米)。
AB=6m,CF=4m,BC=10m,阴影部分的面积是______平方米。
5.正方形组合成不规则图形的面积
(1)下图是由一个边长15cm的大正方形和一个边长为8cm的小正方形组成的,图中阴影部分的面积是______平方厘米。
(2)下图是由一个边长30cm的大正方形和一个边长为24cm的小正方形组成的,图中涂色部分的面积是______平方厘米。
(3)下图是由一个边长6cm的大正方形和一个边长为4cm的小正方形组成的,图中阴影部分的面积是______平方厘米。
(4)下图是由一个边长10m的大正方形和一个边长为6m的小正方形组成的,图中阴影部分的面积是______平方米。
(5)下图是由一个边长10cm的大正方形和一个边长为6cm的小正方形组成的,图中阴影部分的面积是______平方厘米。
(6)下图是由一个边长6cm的大正方形和一个边长为4cm的小正方形组成的,图中涂色部分的面积是______平方厘米。
(7)下图是由一个边长5cm的大正方形和一个边长为3cm的小正方形组成的,图中涂色部分的面积是______平方厘米。
(8)下图是由一个边长12cm的大正方形和一个边长为8cm的小正方形组成的,图中涂色部分的面积是______平方厘米。
【答案】
1.(1)65,分别求出平行四边形和三角形的面积,再相加求和;
(2)96,分别求出正方形和平行四边形的面积,再相加即可;
(3)199,分别求出三角形、梯形和平行四边形的面积,再相加即可;
(4)66,分别求出平行四边形和梯形的面积,再相加即可;
(5)24,用梯形面积减去平行四边形面积,可得图中的阴影部分面积;
(6)354,用梯形的面积减去直角三角形的面积,可得图中的阴影部分面积。
2.(1)539,运用转化法把求阴影部分的面积转化为求梯形ACGD的面积即可解答;
如下图:因为三角形ABC与三角形DFE是两个完全相同的直角三角形,
则:面积1+面积2=阴影部分的面积+面积2;
面积1=阴影部分的面积;
(2)243;(3)7;(5)63;(6)84;
(4)396,运用转化法把求阴影部分的面积转化为求梯形DHGI的
面积即可解答。
如右图:梯形ABCD的面积=梯形EFGH的面积,
则:面积1+面积2=阴影部分的面积+面积2;
面积1=阴影部分的面积;
3.(1)9,如右图:长方形的面积=面积1+面积2,三角形的面积=面积3+面积2;
根据等式的性质:
长方形的面积-三角形的面积=面积1+面积2-面积3
-面积2
长方形的面积-三角形的面积=面积1-面积3
所以它们没有重合的部分的面积差就是长方形和三角形的面积差,依此即可解答(2)9;(3)7.5;(4)9;(5)6;(6)9,由题可得:甲的面积=乙的面积+4,根据等式的性质:则甲的面积+空白面积=乙的面积+4+空白面积,三角形DEF的面积=三角形ABC的面积+4,列式为:4×2.5÷2+4=9(平方厘米);(7)30;
4.(1)663,先根据△DEF的面积,求出底边EF的长度;再求出BC的长度;最后根据梯
形的面积公式,求出直角梯形ABCD的面积;
(2)912.5;(3)120;(4)△ABC与△DBC同底等高,
所以面积相等;进一步分析得出阴影部分面积与△ABE的
面积的关系,即可求解;(5)148;(6)20;
5.(1)92,把阴影部分分割成左右两个三角形,分别求出两个三角形的面积再相加即可;
(2)378,阴影部分的面积=两个正方形的面积和-空白部分两个三角形的面积;
(3)22,阴影部分的面积=两个正方形的面积和-空白部分大三角形的面积;
(4)18,阴影部分的面积=两个正方形的面积和-空白部分三个三角形的面积;
(5)68,阴影部分的面积=两个正方形的面积和-空白部分两个三角形的面积;
(6)16,方法一:可先算出图形下半部分直角梯形的面积再减去空白的小正方形和大三角形的面积。
方法二:可用分割法,将阴影部分分成两个钝角三角形,分别求出两个三角形的面积;最后相加即可;
(7)15,可先算出图形下半部分直角梯形的面积再减去左下角和右下角两个空白的三角形的面积,即为阴影部分面积;
(8)104,整个图形可以分割成左边的正方形和右边的梯形,据此求出总面积,再减去空白的三角形面积即为阴影部分面积。
