江苏省徐州市王杰中学高中数学必修二132空间几何体的体积导学案

合集下载

江苏省徐州市贾汪区建平中学人教版高中数学必修二：1.3.2 空间几何体的体积教案

合作交流，启发式.
教学辅助手段
多媒体
专用教室
教学过程设计
教
学
二次备课
一、问题情境：
1.复习回顾：
①侧面积
②表面积（全面积）
填写下列公式：
S直棱柱侧＝S正棱锥侧＝
S正棱台侧＝S圆柱侧＝
S圆柱侧＝S圆台侧＝
2.已知几何体体积公式(S为底面积，h为高)
V长方体＝
V圆柱体＝
V圆锥体＝
二、数学建构(预习祖暅原理，填写下列公式)
分析：六角螺帽的体积是一个正六棱柱的体积与一个圆柱的体积的差，再由密度算出一个六角螺帽的质量．
四、要点归纳与方法小结
本节课学习了以下内容
1.柱、锥、台的体积公式，能运用公式求解有关体积计算问题
2．柱体、锥体、台体之间的关系；
1.用一张长12cm、宽8cm的矩形铁皮围成圆柱形的侧面，求这个圆柱的体积。
V柱体＝
V椎体＝
V台体＝
复习上节课内容：
默写公式
思考：两个底面积相等、高也相等的棱柱（圆柱）的体积如何？
思考：
柱体、椎体、台体的体积公式有何区别与联系？
教学过程设计
教
学
二次备课
三、数学运用
例1．正三棱锥底面边长为2，侧面均为直角三角形，求此三棱锥的体积。
例2有一堆规格相同的铁制（铁的密度是7.8g/cm3)六角螺帽共重6kg，已知底面是正六边形，边长为12mm,内孔直径为10mm，高为10mm，问这堆螺帽大约有多少个（π取3．14，可用计算器）？
2.已知一个铜质的五棱柱的底面积为16cm2，高为4cm，现将它溶化后铸成一个正方体的铜块，那么铜块的棱长是多少？
3.若一个六棱锥的高为10cm，底面是边长为6cm的正六边形，求这个六棱锥的体积。

江苏省徐州经济技术开发区高级中学苏教版高中数学二1.3.2空间几何体的体积教案1

空间几何体的体积教学目标:1.了解柱、锥、台的体积公式，能运用公式求解有关体积计算问题1;2。

了解柱体、锥体、台体空间结构的内在联系;3.培养学生空见想象能力、理性思维能力以及观察能力．教学过程：一、复习回顾1.直棱柱、正棱锥和正棱台的侧面积公式：S，其中c指的=直棱柱侧是．S,其中h'指的=正棱锥侧是．S=正棱台侧．2。

圆柱、圆锥和圆台的侧面积公式：=S=．圆柱侧=S=．圆台侧=S=．圆锥侧3。

情境：回忆初中学过的计算长方体的体积公式．_________________或_______________．4.问题：两个底面积相等、高也相等的棱柱，它们的体积有什么关系？取一摞书堆放在桌面上，组成一个长方体，然后改变一下形状，比较改变形状前后这摞书的体积．二、建构数学1。

祖暅原理：两等高的几何体若在所有等高处的水平截面的面积相等，则这两个几何体的体积等． 2。

柱体的体积：棱柱（圆柱）可由多边形（圆）沿某一方向得到，因此，两个底面积相等、高也相等的棱柱(圆柱）应该具有相等的体积。

底面积相等，高也相等的柱体的体积也相等。

V 柱体=sh3.锥体的体积:类似的，底面积相等,高也相等的两个锥体的体积也相等.Sh V 31=锥体(S 为底面积,h 为高。

） 4。

台体的体积．上下底面积分别是s /,s ，高是h,则)''(31S SS S h V ++=台体5。

柱体、锥体、台体的体积公式之间关系Sh V S SS S h V Sh V S S S 31)''(310''=−−→−++=−−−←===锥体台体柱体6。

运用祖暅原理类似的方法我们还能证实这样一个结论：①一个底面半径和高都等于R 的圆柱，挖去一个以上底面为底面，下底面圆心为顶点的圆锥后，用沙粒充满后，再将其所容纳的沙粒倒入一个半径为R 的半球内,结果刚好也能充满半球．说明两者体积相等．一个底面半径和高都等于R 的圆柱，挖去一个以上底面为底面,下底面圆心为顶点的圆锥后，所得几何体的体积与一个半径为R 的半球的体积相等．由此得到322323121R R R R R V πππ=⨯-⨯=球，所以343V R π=球． ②运用极限思想求球的表面积设想一个球由许多顶点在球心，底面都在球面上的“准锥体"组成，这些“准锥体"的底面并不是真正的多边形,但只要这些“准锥体”的底面足够地小，就可以把它们近似地看成棱锥．这时，这些“准锥体”的高趋向于球半径R ，底面积123,,,S S S ……的和趋向于球面积，所有这些“准锥体”的体积的和趋向于球的体积，因此312341113333R V RS RS RS π==+++球 (13)RS =球面,所以24S R π=球面．三、数学运用：例1.有一堆相同规格的六角螺帽毛坯(如图）共重kg 6．已知毛坯底面正六边形边长是mm 12,高是mm 10，内孔直径是mm 10．那么这堆毛坯约有多少个？（铁的密度是3/8.7cm g ）。

高一数学必修2教案：1.3.2空间几何体的表面积和体积(教学设计)Word版

探究几种方法，找出形成归纳、
公式背后的理论依
猜想和证
据
明的科学
思维习惯
圆台的上、下底面半径分别为 r，r′，母线为 l，其表面积 S＝ __________________.
根据台体的特征，如何求台体的体积？由于圆台 ( 棱台 ) 是由圆锥 ( 棱锥 ) 截成的，因此可以利用两个锥体的体积差．得到圆台 ( 棱台 ) 的体积公式．
2 A．3
B．2
3 C． 2
1 D．2
环节四：归纳总结 , 知识回顾
棱台的侧面展开是什么图形？圆台的侧面展示是什么图形？棱台和圆台的侧面积和体积公式
环节五：作业与测试
练习与测试
学生整理反思，深化认识
独立完成作业限时完成测试
通过作业与测试巩固知识提升应用能力
类比得出圆台的体积
环节二：例题讲解
例 1 、已知一正四棱台的上底边长为 8cm，高为 3cm，求其体积。
4cm，下底边长为
例 2．如图，一个圆台形花盆盆口直径 20cm，盆底直径
为 15cm，底部渗水圆孔直径为 1.5cm，盆壁长 15cm．为
了美化花盆的外观，需要涂油漆．已知每平方米用
100
1.3 空间几何体的表面积和体积（第二课时）
【教学过程】
教学流程
教师活动
环节一：问题导入
类比棱柱、棱锥，思考：棱台也是由多个平面图形围成的几何体，什么？如何计算它的表面积？
它的展开图是
学生活动结合已有知识进行思考，引出新知识
设计意图新旧知识建立联系
环节二：探棱台侧面展开图究过程
忆，加强应用方面的
A． 81π C． 14π

高中数学必修二《空间几何体》1.3.1 导学案设计(含答案)

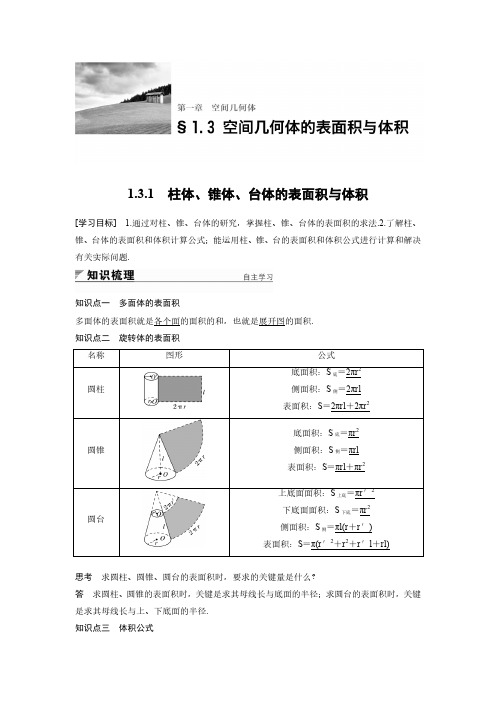
1.3.1柱体、锥体、台体的表面积与体积[学习目标] 1.通过对柱、锥、台体的研究，掌握柱、锥、台体的表面积的求法.2.了解柱、锥、台体的表面积和体积计算公式；能运用柱、锥、台的表面积和体积公式进行计算和解决有关实际问题.知识点一多面体的表面积多面体的表面积就是各个面的面积的和，也就是展开图的面积.知识点二旋转体的表面积思考求圆柱、圆锥、圆台的表面积时，要求的关键量是什么？答求圆柱、圆锥的表面积时，关键是求其母线长与底面的半径；求圆台的表面积时，关键是求其母线长与上、下底面的半径.知识点三体积公式1.柱体：柱体的底面面积为S，高为h，则V＝Sh.2.锥体：锥体的底面面积为S，高为h，则V＝13Sh.3.台体：台体的上、下底面面积分别为S′、S，高为h，则V3思考简单组合体分割成几个几何体，其表面积如何变化？其体积呢？答表面积变大了，体积不变.题型一空间几何体的表面积例1圆台的母线长为8 cm，母线与底面成60°角，轴截面两条对角线互相垂直，求圆台的表面积.解如图所示的是圆台的轴截面ABB1A1，其中∠A1AB＝60°，过A1作A1H⊥AB于H，则O1O＝A1H＝A1A·sin 60°＝43(cm)，AH＝A1A·cos 60°＝4(cm)，即r2－r1＝AH＝4.①设A1B与AB1的交点为M，则A1M＝B1M.又∵A1B⊥AB1，∴∠A1MO1＝∠B1MO1＝45°.∴O1M＝O1A1＝r1.同理OM＝OA＝r2.∴O1O＝O1M＋OM＝r1＋r2＝43，②由①②可得r1＝2(3－1)，r2＝2(3＋1).∴S表＝πr21＋πr22＋π(r1＋r2)l＝32(1＋3)π(cm2).反思与感悟 1.圆柱、圆锥、圆台的相关几何量都集中体现在轴截面上，因此准确把握轴截面中的相关量是求解旋转体表面积的关键.2.棱锥及棱台的表面积计算常借助斜高、侧棱及其在底面的射影与高、底面边长等构成的直角三角形(或梯形)求解.跟踪训练1已知棱长为a，各面均为等边三角形的四面体SABC(即正四面体SABC)，求其表面积.解由于四面体SABC的四个面是全等的等边三角形，所以四面体的表面积等于其中任何一个面面积的4倍.先求△SBC的面积，过点S作SD⊥BC，交BC于点D，如图所示.因为BC ＝a ，SD ＝SB 2－BD 2＝a 2－⎝⎛⎭⎫a 22＝32a ，所以S △SBC ＝12BC ·SD ＝12a ×32a ＝34a 2.因此，四面体SABC 的表面积为S ＝4×34a 2＝3a 2. 题型二空间几何体的体积例2 在Rt △ABC 中，AB ＝3，BC ＝4，∠ABC ＝90°，把△ABC 绕其斜边AC 所在的直线旋转一周后，所形成的几何体的体积是多少？解如图所示，两个圆锥的底面半径为斜边上的高BD ，且BD ＝AB ·BC AC ＝125，两个圆锥的高分别为AD 和DC ，所以V ＝V 1＋V 2＝13πBD 2·AD ＋13πBD 2·CD ＝13πBD 2·(AD ＋CD )＝13πBD 2·AC ＝13π×⎝⎛⎭⎫1252×5＝485π. 故所形成的几何体的体积是485π. 反思与感悟求几何体体积的常用方法跟踪训练2 如图，在棱长为a 的正方体ABCD －A 1B 1C 1D 1中，求A 到平面A 1BD 的距离d .解在三棱锥A 1－ABD 中，AA 1⊥平面ABD ，AB ＝AD ＝AA 1＝a ，A 1B ＝BD ＝A 1D ＝2a ， ∵11--=，A ABD A A BD V V∴13×12a 2·a ＝13×12×2a ×32·2a ·d . ∴d ＝33a .∴A 到平面A 1BD 的距离为33a . 题型三与三视图有关的表面积、体积问题例3 (1)某几何体的三视图如图所示(单位：cm)，则该几何体的表面积等于( ) A.8π cm 2 B.7π cm 2 C.(5＋3)π cm 2D.6π cm 2(2)一个几何体的三视图如图所示(单位：m)，则该几何体的体积为________m 3.答案 (1)B (2)6＋π解析 (1)此几何体是由一个底面半径为1，高为2的圆柱与一个底面半径为1，母线长为2的圆锥组合而成的，故S 表＝S 圆柱侧＋S 圆锥侧＋S 底＝2π×1×2＋π×1×2＋π×12＝7π. (2)由三视图可知该几何体是组合体.下面是长方体，长、宽、高分别为3,2,1；上面是一个圆锥，底面圆半径为1，高为3，所以该几何体的体积为3×2×1＋13π×12×3＝(6＋π) m 3.反思与感悟 1.解答此类问题的关键是先由三视图还原作出直观图，然后根据三视图中的数据在直观图中求出计算体积所需要的数据.2.若由三视图还原的几何体的直观图由几部分组成，求几何体的体积时，依据需要先将几何体分割分别求解，最后求和.跟踪训练3 某几何体的三视图如图所示，则该几何体的体积是________.答案 16π－16解析由三视图可知该几何体是一个圆柱内部挖去一个正四棱柱，圆柱底面圆半径为2，高为4，故体积为16π；正四棱柱底面边长为2，高为4，故体积为16，故题中几何体的体积为16π－16.分割转化求体积例4 如图所示，已知ABCD －A 1B 1C 1D 1是棱长为a 的正方体，E ，F 分别为AA 1，CC 1的中点，求四棱锥A 1－EBFD 1的体积.分析本题若直接求解较为困难，这里利用“割”的思想，将四棱锥的体积转化为两个等底的三棱锥的体积之和，从而简化求解步骤. 解因为EB ＝BF ＝FD 1＝D 1E ＝ a 2＋⎝⎛⎭⎫a 22＝52a ，D 1F ∥EB ，所以四边形EBFD 1是菱形. 连接EF ，则△EFB ≌△EFD 1.易知三棱锥A 1－EFB 与三棱锥A 1－EFD 1的高相等，故111122---==.A EBFD A EFB F EBA V V V 又因为1∆EBA S ＝12EA 1·AB ＝14a 2，则1-F EBA V ＝112a 3，所以111122---==A EBFD A EFB F EBA V V V ＝16a 3.解后反思本题首先利用分割的方法，把四棱锥分割为两个全等的三棱锥，然后利用等积转换法，针对三棱锥的几何特点，变换顶点，体积不变，将不容易求体积的三棱锥转化为容易求体积的三棱锥，从而使问题获解.圆柱体积的求解例5 把长、宽分别为4,2的矩形卷成一个圆柱的侧面，求这个圆柱的体积. 分析利用底面的周长，求得底面半径，利用圆柱的体积公式求解. 解设圆柱的底面半径为r ，母线长为l ，高为h .如图①所示，当2πr ＝4，l ＝2时，r ＝2π，h ＝l ＝2，所以V 圆柱＝πr 2h ＝8π；如图②所示，当2πr ＝2，l ＝4时，r ＝1π，h ＝l ＝4；所以，此时V 圆柱＝πr 2h ＝4π.解后反思圆柱的侧面展开图为矩形，但一个矩形对应的圆柱并不惟一.应该对以哪个边为母线进行分类讨论.1.一个圆柱的侧面展开图是一个正方形，则这个圆柱的表面积与侧面积的比是( ) A.1＋2π2π B.1＋2π4π C.1＋2ππ D.1＋4π2π 答案 A解析设底面圆半径为r ，母线长为h ，∴h ＝2πr ，则S 表S 侧＝2πr 2＋2πrh 2πrh ＝r ＋h h ＝r ＋2πr 2πr ＝1＋2π2π.2.如图，一个底面半径为2的圆柱被一平面所截，截得的几何体的最短和最长母线长分别为2和3，则该几何体的体积为( )A.5πB.6πC.20πD.10π 答案 D解析用一个完全相同的几何体把题中几何体补成一个圆柱，如图，则圆柱的体积为π×22×5＝20π，故所求几何体的体积为10π.3.一个几何体的三视图及其尺寸如图(单位：cm)，则该几何体的表面积为( )A.12πB.18πC.24πD.36π 答案 C解析由三视图知该几何体为圆锥，底面半径r ＝3，母线l ＝5，∴S 表＝πrl ＋πr 2＝24π.故选C.4.一个六棱锥的体积为23，其底面是边长为2的正六边形，侧棱长都相等，则该六棱锥的侧面积为________. 答案 12解析设正六棱锥的高为h ，侧面的斜高为h ′.由题意，得13×6×12×2×2×32×h ＝23，∴h ＝1.∴斜高h ′＝12＋⎝⎛⎭⎫2×322＝2，∴S 侧＝6×12×2×2＝12.5.如图，在上、下底面对应边的比为1∶2的三棱台中，过上底面一边作一个平行于棱CC 1的平面A 1B 1EF ，这个平面分三棱台成两部分，这两部分的体积之比为________. 答案 3∶4(或4∶3)解析设三棱台的上底面面积为S 0，则下底面面积为4S 0，111-A B C ABC V 三棱柱＝S 0h .111-ABC A B C V 三棱台＝73S 0h .设剩余的几何体的体积为V ，则V ＝73S 0h －S 0h ＝43S 0h ，体积之比为3∶4或4∶3.1.圆柱、圆锥、圆台的侧面积分别是它们侧面展开图的面积，因此弄清侧面展开图的形状及侧面展开图中各线段与原旋转体的关系，是掌握它们的侧面积公式及解有关问题的关键.2.计算柱体、锥体和台体的体积，关键是根据条件找出相应的底面面积和高，要充分运用多面体的有关截面及旋转体的轴截面，将空间问题转化为平面问题.3.在几何体的体积计算中，注意体会“分割思想”、“补体思想”及“等价转化思想”.一、选择题1.将边长为1的正方形以其一边所在直线为旋转轴旋转一周，所得几何体的侧面积是( ) A.4π B.3π C.2π D.π 答案 C解析底面圆半径为1，高为1，侧面积S ＝2πrh ＝2π×1×1＝2π.故选C.2.已知高为3的直棱柱ABC －A 1B 1C 1的底面是边长为1的正三角形，则三棱锥B 1－ABC 的体积为( )A.14B.12C.36D.34 答案 D解析 S 底＝12×1×1－⎝⎛⎭⎫122＝34，所以1B ABC V －三棱锥＝13S 底·h ＝13×34×3＝34. 3.若一个圆锥的轴截面是等边三角形，其面积为3，则这个圆锥的表面积是( ) A.3π B.33π C.2π D.9π 答案 A解析设圆锥底面的半径为R ，则由12×2R ×3R ＝3，得R ＝1.所以S 圆锥表＝πRl ＋πR 2＝π×1×2＋π＝3π.4.在一个长方体中，过一个顶点的三条棱长的比是1∶2∶3，它的体对角线长是214，则这个长方体的体积是( ) A.6 B.12 C.24 D.48 答案 D解析设长方体的三条棱长分别为a,2a,3a ，那么a 2＋(2a )2＋(3a )2＝214.解得a ＝2，长方体的体积为V ＝2×4×6＝48.5.一个多面体的三视图如图所示，则该多面体的表面积为( )A.21＋ 3B.18＋ 3C.21D.18 答案 A解析由三视图可知，该多面体为一个边长为2的正方体在左下角与右上角各切去一个三棱锥，因此该多面体的表面积为6×⎝⎛⎭⎫4－12＋12×2×62×2＝21＋ 3. 6.体积为52的圆台，一个底面积是另一个底面积的9倍，那么截得这个圆台的圆锥的体积是( )A.54B.54πC.58D.58π 答案 A解析设上底面半径为r ，则由题意求得下底面半径为3r ，设圆台高为h 1，则52＝13πh 1(r 2＋9r 2＋3r ·r )，∴πr 2h 1＝12.令原圆锥的高为h ，由相似知识得r 3r ＝h －h 1h ，∴h ＝32h 1， ∴V 原圆锥＝13π(3r )2×h ＝3πr 2×32h 1＝92×12＝54.7.某三棱锥的三视图如图所示，则该三棱锥的体积是( )A.16B.13C.23 D.1 答案 B解析如图，三棱锥的底面是一个直角边长为1的等腰直角三角形，有一条侧棱和底面垂直，且其长度为2，故三棱锥的高为2，故其体积V ＝13×12×1×1×2＝13，故选B. 二、填空题8.一个圆柱和一个圆锥的轴截面分别是边长为a 的正方形和正三角形，则它们的表面积之比为________. 答案 2∶1解析 S 圆柱＝2·π⎝⎛⎭⎫a 22＋2π·a 2·a ＝32πa 2， S 圆锥＝π⎝⎛⎭⎫a 22＋π·a 2·a ＝34πa 2， ∴S 圆柱∶S 圆锥＝2∶1.9.现有橡皮泥制作的底面半径为5，高为4的圆锥和底面半径为2，高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变，但底面半径相同的新的圆锥和圆柱各一个，则新的底面半径为________. 答案7解析设新的底面半径为r ，则有13×πr 2×4＋πr 2×8＝13×π×52×4＋π×22×8，解得r ＝7. 10.一个几何体的三视图如图所示(单位：m)，则该几何体的体积为________m 3.答案 83π解析由三视图可知原几何体是由两个圆锥和一个圆柱组成的，它们有共同的底面，且底面半径为1，圆柱的高为2，每个圆锥的高均为1，所以体积为2×13π×12×1＋π×12×2＝8π3(m 3).11.设甲、乙两个圆柱的底面积分别为S 1，S 2，体积分别为V 1，V 2.若它们的侧面积相等，且S 1S 2＝94，则V 1V 2的值是________. 答案 32解析设两个圆柱的底面半径和高分别为r 1，r 2和h 1，h 2.由S 1S 2＝94，得πr 21πr 22＝94，∴r 1r 2＝32. 由圆柱的侧面积相等，得2πr 1h 1＝2πr 2h 2，即r 1h 1＝r 2h 2.∴V 1V 2＝πr 21h 1πr 22h 2＝r 1r 2＝32. 三、解答题12.已知某几何体的俯视图是如图所示的矩形，正视图是一个底边长为8、高为4的等腰三角形，侧视图是一个底边长为6、高为4的等腰三角形.(1)求该几何体的体积V ；(2)求该几何体的侧面积S .解由已知可得该几何体是一个底面为矩形、高为4、顶点在底面的投影是矩形中心的四棱锥V -ABCD .(1)V ＝13×(8×6)×4＝64.(2)该四棱锥的两个侧面VAD ，VBC 是全等的等腰三角形，且BC 边上的高为h 1＝ 42＋⎝⎛⎭⎫822＝42，另两个侧面VAB ，VCD 也是全等的等腰三角形，AB 边上的高为h 2＝ 42＋⎝⎛⎭⎫622＝5.因此S 侧＝2⎝⎛⎭⎫12×6×42＋12×8×5＝40＋24 2. 13.已知底面半径为 3 cm ，母线长为 6 cm 的圆柱，挖去一个以圆柱上底面圆心为顶点，下底面为底面的圆锥，求所得几何体的表面积及体积.解作轴截面如图，设挖去的圆锥的母线长为l ，底面半径为r ，则l ＝(6)2＋(3)2＝9＝3(cm).故几何体的表面积为S ＝πrl ＋πr 2＋2πr ·AD＝π×3×3＋π×(3)2＋2π×3× 6＝33π＋3π＋62π＝(33＋3＋62)π(cm2). 几何体的体积为V＝V圆柱－V圆锥＝π·r2·AD－13πr2AD＝π×3×6－13×π×3× 6＝26π(cm3).。

苏教版高中数学必修二空间几何体的表面积和体积教案

空间几何体的表面积和体积预习提纲1．平面展开图2．概念：直棱柱：正棱柱：正棱锥：正棱台：3．面积公式：S直棱柱侧＝S正棱锥侧＝S正棱台侧＝S圆柱侧＝＝S圆锥侧＝＝S圆台侧＝＝S球面＝相互间的关系：4．体积公式：V长方体＝＝V柱体＝V锥体＝V台体＝V球＝相互间的关系：空间几何体的表面积和体积教案例1：已知直三棱柱底面各边的比为17∶10∶9，侧棱长为16 cm，全面积为1440 cm2，求底面各边之长.例2：正三棱锥底面边长为a，侧棱与底面成45°角，求此棱锥的侧面积与全面积.例3：从一个正方体中，如图那样截去4个三棱锥后，得到一个正三棱锥A—BCD，求它的体积是正方体体积的几分之几？例4：假设正棱锥的底面边长为a ，侧棱长为2a ，求对角面的面积和侧面积.例5：如图，圆柱的底面直径与高都等于球的直径，求证：（1）球的表面积等于圆柱的侧面积；（2）球的表面积等于圆柱全面积的23例6：有三个球，第一个球内切于正方体的六个面，第二个球与这个正方体各条棱都相切，第三个球过这个正方体的各顶点，求这三个球的表面积之比.例7：已知圆锥的全面积是它内切球表面积的2倍，求圆锥侧面积与底面积之比.练习：1.已知球面上A、B、C三点的截面和球心的距离等于球的半径的一半，且AB=BC=CA=2，求球的体积.2.一个体积为8的正方体的各个顶点都在球面上，求此球的体积.例8：求球与它的外切圆柱、外切等边圆锥的体积之比.例9：半径为R的球的内接四面体内有一内切球，求这两球的体积比？空间几何体的表面积和体积教案例1：已知直三棱柱底面各边的比为17∶10∶9，侧棱长为16 cm ，全面积为1440 cm 2，求底面各边之长.分析：这是一道跟直棱柱侧面积有关的问题，从结论出发，欲求底面各边之长，而各边之比已知，可分别设为17a 、10a 、 9a ，故只须求出参数a 即可，那么如何利用已知条件去求 a 呢？［生］设底面三边长分别是17a 、10a 、9a , S 侧＝（17a ＋10a ＋9a ）·16＝576a 设17a 所对三角形内角α，则cos α＝（10a ）2＋（9a ）2－（17a ）22×10a ×9a ＝－35 ，sin α＝45S 底＝12 ·10a ·9a ·45＝36a 2∴576a ＋72a 2＝1440 解得：a ＝2 ∴三边长分别为34 cm ，20 cm ，18 cm.［师］此题中先设出参数a ，再消去参数，很有特色. 例2：正三棱锥底面边长为a ，侧棱与底面成45°角，求此棱锥的侧面积与全面积. 分析：可根据正棱锥的侧面积与全面积公式求得.解：如图所示，设正三棱锥S —ABC 的高为SO ，斜高为SD ，在Rt △SAO 中，∴AO ＝SA ·cos45°∵AO ＝23 AD ＝23 32a ∴SA ＝63a在Rt △SBD 中 SD ＝a a a 615)21()36(22=- ∴S 侧＝12 ·3a ·SD ＝154a 2. ∵S 底＝34a 2∴S 全＝（154＋34）a 2 例3：从一个正方体中，如图那样截去4个三棱锥后，得到一个正三棱锥A —BCD ，求它的体积是正方体体积的几分之几？分析：在准确识图的基础上，求出所截得的每个三棱锥的体积和正三棱锥A —BCD 的体积即可.解：设正方体体积为Sh ,则每个截去的三棱锥的体积为 13 ·12 Sh ＝16 Sh . ∵三棱锥A —BCD 的体积为 Sh －4·16 Sh ＝13Sh .∴正三棱锥A —BCD 的体积是正方体体积的13 .例4：假设正棱锥的底面边长为a ，侧棱长为2a ，求对角面的面积和侧面积. 解：如图所示，在正四棱锥P —ABCD 中，AB ＝a ，PB ＝2a ，作PO ⊥底面ABCD 于O .连结BD ，则O ∈BD ，且PO ⊥BC ，由AB ＝a ，得BD ＝ 2 a ，在Rt △P AB 中， PO 2＝PB 2－BO 2＝（2a ）2－（22a ）2∴PO ＝142a ，S 对角面＝12 PO ·BD ＝72a 2. 又作PE ⊥BC 于E ，这时E 是BC 的中点 ∴PE 2＝PB 2－BE 2＝（2a ）2－（12 a ）2∴PE ＝152a ∴S 侧＝4×21PE ·BC ＝15 a 2 ∴对角面面积为72a 2,侧面积为 15 a 2. 例5：如图，圆柱的底面直径与高都等于球的直径，求证：（1）球的表面积等于圆柱的侧面积；（2）球的表面积等于圆柱全面积的23证明：（1）设球的半径为R ，则圆柱的底面半径为R ，高为2R ，得S 球＝4πR 2，S 圆柱侧＝2πR ·2R ＝4πR 2 ∴S 球＝S 圆柱侧（2）∵S 圆柱全＝4πR 2+2πR 2＝6πR 2 S 球＝4πR 2 ∴S 球＝23S 圆柱全例6：有三个球，第一个球内切于正方体的六个面，第二个球与这个正方体各条棱都相切，第三个球过这个正方体的各顶点，求这三个球的表面积之比.解：设正方体的棱长为a ，则第一个球的半径为 a 2 ，第二个球的半径是22a ，第三个球的半径为32a . ∴r 1∶r 2∶r 3＝1∶ 2 ∶ 3 ∴S 1∶S 2∶S 3＝1∶2∶3例7：已知圆锥的全面积是它内切球表面积的2倍，求圆锥侧面积与底面积之比.解：过圆锥的轴作截面截圆锥和内切球分别得轴截面SAB 和球的大圆⊙O ，且⊙O 为 △SAB 的内切圆.设圆锥底面半径为r ,母线长为l ;内切圆半径为R ，则S 锥全＝πr 2＋πrl ，S 球＝4πR 2，∴r 2＋rl ＝8R 2① 又∵△SOE ∽△S A O 1∴r l rl rl r l r R +-=--=22 ②由②得：R 2＝r 2·r l r l +-代入①得：r 2＋rl ＝8r 2·rl rl +-，得： l ＝3r ∴32===rlr rl S S ππ底锥侧 ∴圆锥侧面积与底面积之比为3∶1. 练习：1.已知球面上A 、B 、C 三点的截面和球心的距离等于球的半径的一半，且AB =BC =CA =2，求球的体积.2.一个体积为8的正方体的各个顶点都在球面上，求此球的体积. 例8：求球与它的外切圆柱、外切等边圆锥的体积之比.解：如图所示，等边△SAB 为圆锥的轴截面，此截面截圆柱得正方形C 1CDD 1，截球面得球的大圆圆O 1.设球的半径O 1O ＝R ，则它的外切圆柱的高为2R ，底面半径为R ，则有OB ＝O 1O ·cot30°＝ 3 R SO ＝OB ·tan60°＝ 3 R ·3 ＝3R ∴V 球＝43 πR 3,V 柱＝πR 2·2R ＝2πR 3V 锥＝13π（ 3 R ）2·3R ＝3πR 3∴V 球∶V 柱∶V 锥＝ 4∶6∶9［师］以上题目，通过作球及外切圆柱、等边圆锥的公共截面暴露这些几何体之间的相互关系.让我们继续体会有关球的相接切问题.例9：半径为R 的球的内接四面体内有一内切球，求这两球的体积比？解：如图所示，大球O 的半径为R ；设正四面体 A —BCD 的棱长为a ，它的内切球半径为r ，依题意BO 1＝23 32a ＝33a ，AO 1＝AB 2－BO 12 ＝a 2－（33a ）2 ＝63a 又∵BO 2＝BO 12＋OO 12，∴R 2＝（22)36()33R a a -+ ∴a ＝362R 连结OA ，OB ，OC ，OD ，内切球球心到正四面体各面距离为r , V O —BCD ＝V O —ABC ＋V O —ACD ＋V O —AOB ＋V O —BCD ∴r S AO S BCD BCD ⋅⋅⋅=⋅⋅∆∆314311 ∴r ＝41AO∴r ＝R R a 31362126126=⋅= ∴V 小球∶V 大球＝34π·（31R ）3∶34π·R 3＝1∶27∴内切球与外接球的体积比为1∶27.。

江苏省徐州市王杰中学高二数学下册《2.3.2双曲线的几何性质》导学案[ 高考]

双曲线的几何性质导学案一、自学准备与知识导学1．椭圆有哪些几何性质，是如何探讨的？2．双曲线的两种标准方程是什么？3．类比联想得出性质(范围、对称性、顶点)，完成下列关于椭圆与双曲线性质的表格。

4.双曲线的范围在以直线by xa=和by xa=-为边界的平面区域内，那么从x、y的变化趋势看，双曲线22221x ya b-=与直线by xa=±具有怎样的关系呢？根据对称性，可以先研究双曲线在第一象限的部分与直线by xa=的关系。

定义：直线__________叫做双曲线22221x y a b -=的渐近线；直线________叫做双曲线22221y x a b-=的渐近线。

例如：画双曲线2212516x y -=，先作渐近线_________，再描几个点，就可以随后画出比较精确的双曲线。

5.双曲线的离心率：双曲线的焦距与实轴的比_________叫做双曲线的离心率，且离心率的范围__________。

变形：由于b a = 二、学习交流与问题探讨例1求双曲线22143x y -=的实轴长和虚轴长、焦点的坐标、离心率、渐近线方程．例2：已知双曲线的中心在原点，焦点在y 轴上，焦距为16，离心率为43，求双曲线的标准方程。

例3：求与双曲线221169x y -=共渐近线，且经过()3A -点的双曲线的标准方及离心率．变形：求双曲线22916144y x -=的实半轴长和虚半轴长、焦点的坐标、离心率、渐近线方程．例4 ：如图，设(),M x y 与定点()5,0F 的距离和它到直线l ：165x =的距离的比是常数54，求点M 的轨迹方程．例5：双曲线型冷却塔的外形，是双曲线的一部分绕其虚轴旋转所成的曲面如图（1），它的最小半径为12m ，上口半径为13m ，下口半径为25m ，高为55m ．试选择适当的坐标系，求出双曲线的方程（各长度量精确到1m ）．三、练习检测与拓展延伸1．已知双曲线方程如下，求它们的两个焦点、离心率e 和渐近线方程．⑴22169144x y -=； ⑵22169144x y -=-2．求双曲线的标准方程：⑴实轴的长是10，虚轴长是8，焦点在x 轴上； ⑵焦距是10，虚轴长是8，焦点在y 轴上；⑶离心率e =()5,3M -； ⑷两条渐近线的方程是23y x =±，经过点9,12M ⎛⎫- ⎪⎝⎭。

苏教版高中数学必修二空间几何体的表面积与体积表面积教案

普通高中课程标准实验教科书—数学必修Ⅱ[苏教版]空间几何体的表面积教学目标（1）了解平面展开图的概念，会识别一些简单多面体的平面展开图；（2）了解直棱柱、正棱锥、正棱台的表面积的计算公式；（3）会求一些简单几何体的表面积．教学重点多面体的平面展开图,求简单几何体的表面积．教学难点多面体的平面展开图．教学过程一、问题情境1．情景：通过演示一些多面体的平面展开图的过程，让学生了解平面展开图的概念． 2．问题：哪些图形是空间图形的平面展开图？二、学生活动仔细观察这些平面图形，说说它们是哪些空间图形的平面展开图？三、建构数学1．多面体的平面展开图的概念一些简单多面体沿着它的某些棱剪开而形成的平面图形叫做该多面体的平面展开图． 2．直棱柱、正棱柱、正棱锥、正棱台（1）侧棱垂直于底面的棱柱叫直棱柱．把直棱柱的侧面沿一条侧棱剪开后展在一个平面上，展开图的面积就是棱柱的侧面积．直棱柱的侧面展开图是矩形,这个矩形的长等于直棱柱的底面周长c ，宽等于直棱柱的高h ，因此直棱柱的侧面积是S ch =直棱柱侧．（2）底面为正多边形的直棱柱叫正棱柱．（3）底面是正多边形，顶点在底面的正投影是底面多边形的中心的棱锥叫做正棱锥．如果正棱锥的底面周长为c ，斜高为h '，由图可知它的侧面积是12S ch '=侧．（4）正棱锥被平行于底面的平面所截，截面和底面之间的部分叫做正棱台．与正棱锥的侧面积公式类似,若设正棱台的上、下底面的周长分别为,c c '，斜高为h '，则其侧面积是1()2S c c h ''=+侧．项目名称直棱柱正棱柱正棱锥正棱台定义侧棱垂直于底面的棱柱叫直棱柱底面为正多边形的直棱柱叫正棱柱底面是正多边形，顶点在底面的正投影是底面多边形的中心的棱锥叫做正棱锥正棱锥被平行于底面的平面所截，截面和底面之间的部分叫做正棱台侧面积的计算公式,S ch =侧c 为底面的周长，h为棱柱的高1,2S ch c '=侧为底面周长，h '是斜高（侧面等腰三角形底边上的高）1(),2S c c h c '''=+侧为上底面周长，c 为下底面周长，h '是斜高（侧面等腰梯形的高）性质每个侧面都是矩形，底面是多边形每个侧面都是矩形，底面是正多边行侧面是全等的等腰三角形，底面是正多边形，每条侧棱都相等侧面是全等的等腰梯形，底面是正多边形，每条侧棱都相等说明：（1）当且仅当正棱锥，正棱台时才有斜高．（2）正棱柱，正棱锥，正棱台的侧面积公式之间的关系可用下图表示：练习：如图是正方体纸盒的展开图，那么直线AB 、CD 在原来正方体中所成的角是多少？提示：把平面展开图还原为正方体。

江苏省徐州市贾汪区建平中学高中数学必修二：1-3 空间几何体的体积2学案精品

空间几何体的体积(2)学案 2017.10
主备审核
教学目标：
１．理解球的表面积公式的推导。

2.会求一些球的组合体中的面积与体积的问题.
一、知识要点：
球的表面积公式：．
球的体积公式：．
推导：
1.关于球的体积的有趣结论：一个底面半径和高都等于R的圆柱，挖去一个等底等高的圆锥，所得体积等于一个半径为R的半球的体积。

2.等体积法与“积分”思想探求球的表面积。

二、数学应用
例：求棱长为2的正方体的外接球的表面积和体积。

课堂练习：
1、钢球由于热膨胀二使半径增加千分之一，那么它的表面积和体积分别增加几分之几？
2、计算地球的表面积与体积（地球半径为6370km，保留4位有效数字）
３．三个球的半径的比是1 : 2 : 3 , 求证: 其中最大的一个球的体积是另两个球的体积之和的3倍
4、长方体的一个顶点上的三条棱长分别为3，4，5，且它的八个顶点都在同一个球面上，求这个球的表面积和体积。

5.表面积为324π的球，其内接正四棱柱的高是14，求这个正四棱柱的表面积．
课堂小结：１．球的体积和表面积公式
２．长方体的外接球
课后作业：p64 第6题。

苏教版高中数学必修二空间几何体的表面积与体积体积教案

课题：空间几何体的体积
一、教学目标：
⒈知识目标：掌握棱柱、圆柱、棱锥、圆锥的体积的推导方法，理解祖暅原理，会应用棱柱、圆柱、棱锥、圆锥的体积公式。

⒉能力目标：通过学习祖暅原理，理解祖暅原理的内涵，体验空间与平面问题互相转化的方法，体会到复杂的体积问题怎样转化为简单的体积问题而得到解决，从而提高学生的数学思维能力。

⒊德育目标：学生通过学习祖暅原理，了解我国古代数学家在这方面作出的突出成就，受到爱国主义教育，提高学习数学的兴趣。

二、教学重点与难点：
重点是棱柱、圆柱、棱锥、圆锥的体积公式的推导方法。

难点是对祖暅原理的理解和棱柱、圆柱、棱锥、圆锥的体积公式的应用。

三、教学方法与教学手段：
教学方法：本节课的课型为“新授课”。

虽然学生初中已经学习了圆柱、圆锥的体积的公式，但用的是实验验证的方法，并没有从根本上理解圆柱、圆锥的体积公式的由来，本课采用推导的方法，以长方体的体积公式和祖暅原理为基础推导出几种几何体的体积公式，通过不同形式的探究过程，让学生积极参与到教学活动中来，并且始终处于积极的问题探究和辨析思考的学习气氛中。

教学手段：采用多媒体辅助教学，增强直观性，增大课堂容量，提高效率。

四、教学过程：。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

空间几何体的体积(一)导学案
章节与课题第一章第1.3.2节空间几何体的体积1 课时安排 7课时
主备人常丽雅审核人梁龙云
使用人使用日期或周次第三周
本课时学习目标或
学习任务
了解柱、锥、台、球体积的计算公式．

本课时重点难点或
学习建议
柱、锥、台、球体积计算公式的运用．

本课时教学资源的
使用
导学案

学习过程
一、自学准备与知识导学
1．圆锥形烟囱的底面半径是cm40，高是cm30．已知每平方米需要油漆g150，油漆
100个这样的烟囱帽的外表面，共需油漆多少千克？（取14.3
，精确到kg1.0）

2．某长方体纸盒的长、宽、高分别为cm7，cm5，cm4，则每层有57个单位正方体，
共有4层，因此它的体积为______________________．
设长方体的长、宽、高分别为a，b，c，那么它的体积为__________或___________．
3．柱体、锥体、台体、球的体积公式：

柱体V
____________________________________________．

锥体V
____________________________________________．

台体V
____________________________________________．

球V
_____________________________________________．

4．球面被经过球心的平面截得的圆叫做球的大圆，大圆的半径等于球半径．

球的表面积公式为______________________；这表明球的表面积是球大圆面积的4倍．

二、学习交流与问题探讨
例1 有一堆相同规格的六角螺帽毛坯（如图）共重kg6．已知毛坯底面正六边形边长
是mm12，高是mm10，内孔直径是mm10．那么这堆毛坯约有多少个？
（铁的密度是3/8.7cmg）
例2 下图是一个奖杯的三视图（单位：cm），试画出它的直观图，
并计算这个奖杯的体积（精确到301.0cm）．

三、练习检测与拓展延伸
1．用一张长cm12、宽cm8的矩形铁皮围成圆柱形的侧面，求这个圆柱的体积．

2．已知一个铜质的五棱柱的底面积为216cm，高为cm4，现将它熔化后铸成一个正方
体铜块，那么铸成的铜块的棱长为多少（不计损耗）？

3．若一个六棱锥的高为cm10，底面是边长为cm6的正六边形，求这个六棱锥的体积．

四、小结与提高
空间几何体的体积(二)导学案
章节与课题第一章第1.3.2节空间几何体的体积2 课时安排 8课时
主备人常丽雅审核人梁龙云
使用人使用日期或周次第三周
本课时学习目标
或学习任务
初步掌握求体积的常规方法，例如割补法，等积转换等．

本课时重点难点
或学习建议
割补法，等积转换等方法的运用．

本课时教学资源
的使用
导学案

学习过程
一、自学准备与知识导学
1．如图，在三棱锥ABCP中，已知BCPA，lBCPA，EDPA，

EDBC，且hED．求证：三棱锥ABCP
的体积为hlV261．

2．一个圆锥形的空杯子上面放着一个半球形的冰淇淋，如果将冰淇淋全部放入杯中，
能放下吗？

A
B
D
C

P
E
二、学习交流与问题探讨
例1 将半径分别为cm1、cm2、cm3的三个锡球熔成一个大锡球，
求这个大锡球的表面积．

三、练习检测与拓展延伸
1．两个球的体积之比为27:8，则这两个球的表面积之比是_____________________．
2．若两个球的表面积之差为48，两球面上两个大圆周长之和为12，则这两球

的半径之差为_____________________________．
3．如果一个圆柱和一个圆锥的底面直径和高都与球的直径相等．
求证：圆柱、球、圆锥体积的比是1:2:3．

四、小结与提高