太阳能小屋的设计毕业设计论文
论文XI
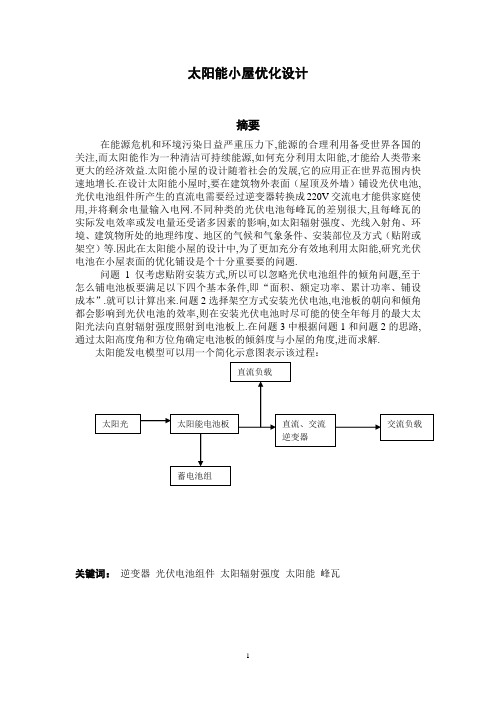
太阳能小屋优化设计摘要在能源危机和环境污染日益严重压力下,能源的合理利用备受世界各国的关注,而太阳能作为一种清洁可持续能源,如何充分利用太阳能,才能给人类带来更大的经济效益.太阳能小屋的设计随着社会的发展,它的应用正在世界范围内快速地增长.在设计太阳能小屋时,要在建筑物外表面(屋顶及外墙)铺设光伏电池,光伏电池组件所产生的直流电需要经过逆变器转换成220V交流电才能供家庭使用,并将剩余电量输入电网.不同种类的光伏电池每峰瓦的差别很大,且每峰瓦的实际发电效率或发电量还受诸多因素的影响,如太阳辐射强度、光线入射角、环境、建筑物所处的地理纬度、地区的气候和气象条件、安装部位及方式(贴附或架空)等.因此在太阳能小屋的设计中,为了更加充分有效地利用太阳能,研究光伏电池在小屋表面的优化铺设是个十分重要要的问题.问题1仅考虑贴附安装方式,所以可以忽略光伏电池组件的倾角问题,至于怎么铺电池板要满足以下四个基本条件,即“面积、额定功率、累计功率、铺设成本”.就可以计算出来.问题2选择架空方式安装光伏电池,电池板的朝向和倾角都会影响到光伏电池的效率,则在安装光伏电池时尽可能的使全年每月的最大太阳光法向直射辐射强度照射到电池板上.在问题3中根据问题1和问题2的思路,通过太阳高度角和方位角确定电池板的倾斜度与小屋的角度,进而求解.太阳能发电模型可以用一个简化示意图表示该过程:关键词:逆变器光伏电池组件太阳辐射强度太阳能峰瓦问题重述:对于问题1,题目给定地理位置为山西大同,安装方式为贴附安装,选定光伏电池组件,对小屋(见附件2)的部分外表面进行铺设,并根据电池组件分组数量和容量,选配相应的逆变器的容量和数量.对于问题2,电池板的朝向与倾角均会影响到光伏电池的工作效率,,题目要求选择架空方式安装光伏电池,重新考虑问题1.对于问题3,根据附件7给出的小屋建筑要求,题目要求为大同市重新设计一个小屋,要求画出小屋的外形图,并对所设计小屋的外表面优化铺设光伏电池,给出铺设及分组连接方式,选配逆变器,计算相应结果.附件1:光伏电池组件的分组及逆变器选择的要求附件2:给定小屋的外观尺寸图附件3:三种类型的光伏电池(A单晶硅、B多晶硅、C非晶硅薄膜)组件设计参数和市场价格附件4:大同典型气象年气象数据。
数学建模——太阳能小屋的设计模型

(1)根据山西省大同市的气象数据,仅考虑贴附安装方式,选定光伏电池组件,对小屋的部分外表面进行铺设,并根据电池组件分组数量和容量,选配相应的逆变器的容量和数量。
(2):电池板的朝向与倾角均会影响到光伏电池的工作效率,请选择架空方式安装光伏电池,重新考虑问题1。
(3):根据附件7给出的小屋建筑要求,为大同市重新设计一个小屋,要求画出小屋的外形图,并对所设计小屋的外表面优化铺设光伏电池,给出铺设及分组连接方式,选配逆变器,计算相应结果。
二、问题分析
对于在绿色小屋上铺设太能电池板最优解的问题,我们可以设定为是多因素限制的一个多变量的规划问题。
太阳能电池由电池板和逆变器构成,两个相互影响,只允许相同型号的光伏组件进行串联,不同型号的光伏组件只能并联。电池板本身大小固定,很难完全铺设,这些都是限制因素,都要在模型中加以考虑。
根据逆变器的参数调整设计电池组件分组阵列串并联的方式以满足相应的输出电压和总功率,研究电池板型号对应于逆变器的关系来确定电池板的组件;
最后,对所建模型进行评价和改进,并且就太阳能小屋的设计和建造问题给出了具体的建议。
关键词:光伏电池优先因子贪婪算法非线性优化最佳倾角
一、问题重述
在设计太阳能小屋时,需在建筑物外表面(屋顶及外墙)铺设光伏电池,光伏电池组件所产生的直流电需要经过逆变器转换成220V交流电才能供家庭使用,并将剩余电量输入电网。不同种类的光伏电池每峰瓦的价格差别很大,且每峰瓦的实际发电效率或发电量还受诸多因素的影响,如太阳辐射强度、光线入射角、环境、建筑物所处的地理纬度、地区的气候与气象条件、安装部位及方式(贴附或架空)等。因此,在太阳能小屋的设计中,研究光伏电池在小屋外表面的优化铺设是很重要的问题。
太阳能小屋的设计_数学建模竞赛B题 精品

太阳能小屋的设计摘要本文讨论在经济效益最优情况下太阳能电池的铺设设计。
经济效益为发电收益与发电成本的差值,当发电量越大,发电成本越小时,经济收益越可观。
问题一中,本文先选出各个墙面经济效益最好的几种电池板,使用效益最好的电池板结合光伏电池组件的分组及逆变器选择的要求进行调整,得出最优铺设方案。
但北面墙各种电池均呈亏损状况,因此在北面不进行铺设。
经过计算得:小屋在35年内的总发电量为:560453.969 kWh,总经济效益为:75955.765元,回收年限为:23.80年。
问题二中,由于太阳能电池板的倾斜角与方位角会影响到其接受总辐射量的大小,进而影响到其盈利状况。
本文使用Matlab编程求出电池板的最佳倾斜角与最佳方位角分别为:34.56°与22.63°。
重新计算出各个墙面将接受到的总辐射量,利用问题一中的方法对各面墙重新铺设,优化之后的小屋在35年内的总发电量为:609242.125 kWh,总经济效益为:98886.199元,回收年限为:21.80年。
问题三中,自行设计的小屋朝向调整为最佳方位角,并将小屋的受光面积作为目标函数,小屋的建筑条件最为约束条件使用Lingo软件进行优化得到小屋的各建筑条件。
之后使用问题一中的方法对小屋进行铺设,求得小屋在35年内的总发电量为:968749.058 ,总经济效益为:152901.657,回收年限为:22.14年。
[关键词]:Matlab软件光伏电池线性约束优化Lingo软件一、问题的重述在设计太阳能小屋时,需在建筑物外表面(屋顶及外墙)铺设光伏电池,光伏电池组件所产生的直流电需要经过逆变器转换成220V交流电才能供家庭使用,并将剩余电量输入电网。
不同种类的光伏电池每峰瓦的价格差别很大,且每峰瓦的实际发电效率或发电量还受诸多因素的影响,如太阳辐射强度、光线入射角、环境、建筑物所处的地理纬度、地区的气候与气象条件、安装部位及方式(贴附或架空)等。
太阳能小屋的优化模型新

太阳能小屋的优化模型摘要本文通过分析太阳能小屋光伏电池和逆变器等设备把太阳能转换为电能,但光伏电池在小屋外表面的优化铺设很重要。
本论文就太阳辐射强度,光线入射角,建筑物的地理纬度,安装部位及方式(贴附或架空)等因素考虑,得出电池的最优铺设。
对于问题一,题中给出了大同市的气象数据;三种类型的光伏电池组件的相关信息及逆变器的参数,房屋东、西、南、北面的具体面积,按照要求选用最优规划模型,利用房子的面积,光伏电池的转化率等约束条件,寻求东、西、南、北及顶面的光伏电池的最优铺设方式。
具体结果见表1:根据最优方案,算出小屋光伏电池经济效益为7882922.43元,投资的回收年限为3年。
对于问题二,电池板的朝向与倾角会影响到光伏电池的工作效率,贴附安装会损失一定的太阳辐射能,用架空方式安装光伏电池,我们建立倾斜面太阳总辐射强度与赤尾角、时角、太阳高度角等之间的关系式:2c o s )(s i n c o s 2βρραθH D H B T I I I I I -++=。
用EXCEL 软件对每个时刻太阳辐射量求和,比较得出在13时太阳水平面总辐射强度、水平面散射辐射强度、法向直射辐射强度均为最大,则单位面积受到的辐射强度最大,算出此时的最佳倾斜角γ与最佳方位角A 分别为32.01、45.8,再由问题一的最优化模型,算出小屋光伏电池经济效益为210457.61元,投资的回收年限为15年。
对于问题三,在前两问的基础上,为大同市重新设计小屋,由题给小屋建筑的要求,我们考虑平顶的小房屋,这样小屋受到的光照面积大,更加有利于对太阳辐射的吸收。
关键字:太阳能电池 最佳铺设方式 最优化模型 倾斜太阳辐射三.模型假设1.假设题中所给数值均有效;2.要计算35年寿命周期内光伏电池发电总量,假设在35年内太阳辐射的总量是稳定的;3.假设在以后的各年中,小屋所受光照辐射量保持恒定;四.模型建立与求解模型一:对于问题一,我们只考虑贴附安装方式,即光伏电池安在墙壁上对小屋的外表面进行铺设,但考虑到小屋全年太阳能光伏发电总量尽可能大而单位发电量的费用尽可能小,由题给关系我们从最优化考虑,建立发电量和费用的最优化问题,根据约束条件,用LINGO 软件求出小屋的外表面部分铺设量,得出电池组件分组数量和容量,及相应逆变器的容量和数量。
太阳能小屋的优化设计与研究

辐射强度 > 8 0 W 的日 照时间
3 5 6 1
23 . 45 s i n
( 2 z ( 2 3 8 6 4 5 + n ) 1
为了选择 优秀的电池板材料 ,我们定义 电池板 的性价 比 转换效率/ 价格 ,根据 不同电池板 的性价 比确定小屋各个面的 选择情况 。
阳高度是指太 阳光 的入射方 向和地平面之间的夹 角 ,对 于地球上的某个地点 ,专业上讲太 阳高度角是指某地太 阳光线 与该地作垂直于地心的地表切线 的夹角 ,这是 以太 阳视盘面 的
MJ / mz 。
其 中, P表示输 出功率 ; t 表示 日照时 间; W表示输 出电能 。
Y = × 0 . 5元 / k W ・ h ( 3)
( 4)
其 中 y表示收益。
Y =1 0 0 0× 叩×x j / X S
倾斜 面接 收到 的辐射一般采用 K l i e n t 和T h e i l a c h e r 提出的 倾斜 面月辐射量计算模型 :
域 继续 取 5个等分倾角点 ,以此类推 ,不 断缩小 区域范 围,直 至满 足所要求的精度为止 。
6 新 设计太 阳 能小屋 长 、宽 、高 的计 算
根 据附件 7的建筑要求 ,以及上述两 问中对于小屋总发 电 量 的求解可 以得 出结论 :当小屋的顶面积越大时 ,对太 阳能 的 吸收越 大 ,进而转化为的 电能就越大 ,采用线性规划模型 ,令 屋 顶面积 C:ma x x / ( 5 . 4 一 ) z +y 2 . ,可列出下列关 系式对小屋 长 、宽 、高进行 约束限制 :
太阳能小屋的优化设计

太阳能小屋的优化设计方倩玉;陆晓玲;陈丹婷【期刊名称】《南通职业大学学报》【年(卷),期】2014(000)001【摘要】讨论太阳能小屋的设计问题。
建立以全年太阳能发电总量最大及单位发电量费用最小的双目标规划模型,解决小屋表面的选定和光伏电池的选配,并利用CAD画图软件实现光伏电池的铺设方案。
针对架空方式安装光伏电池,添加使顶面光照辐射量最大的目标函数,求得最佳架空倾斜角,进而设计新的太阳能小屋,使小屋的方位角和外观尺寸达到最优。
%This paper discusses about the design of solar energy lodge. It sets up a double goal design model with maximum power generation and minimum cost per unit. It also solves cabin surfaces and selected option-al photovoltaic cells and the use of CAD drawing software program for photovoltaic cell layout. Photovoltaic cells are installed overhead to add light radiation so that the top surface can obtain the largest objective func-tion we calculate the optimal tilt angle overhead, and then design new solar energy lodge to optimize azimuth and the appearance of size.【总页数】5页(P59-63)【作者】方倩玉;陆晓玲;陈丹婷【作者单位】南京邮电大学,南京 210023;南京邮电大学,南京 210023;南京邮电大学,南京 210023【正文语种】中文【中图分类】O29【相关文献】1.太阳能小屋的优化设计 [J], 王名扬;李民2.基于数学模型的太阳能小屋优化设计 [J], 张朝伦;杨尚安;谭笑;刘洋3.太阳能小屋的优化设计 [J], 后敏;陈利娟;唐倩;王海月;胡定刚4.太阳能小屋的优化设计与研究 [J], 郑十5.论太阳能小屋的优化设计方法 [J], 冯登因版权原因,仅展示原文概要,查看原文内容请购买。
太阳能小屋设计
太阳能小屋的设计摘要:太阳能小屋是利用太阳能发电的新热点,具有节约占用地,减少由于输电的线路投资和损失等优点。
在设计太阳能小屋时,铺设在建筑外表面的光伏电池发电量受诸多因素的影响。
因此,研究光伏电池在小屋外表面的优化铺设是光伏电池产业发展的一个实际课题。
问题1:根据要求,小屋的全年太阳能光伏电池发电量尽可能大,单位发电量的费用尽可能小。
我们通过35年经济效益最大化来实现上述两个量的选择,在实现最优化的过程中我们引进两个原则:(1)逆变器的选择方式通过单位功率价格来优先选择,计算结果显示,功率大的逆变器较为划算,同时当逆变器选定后,电池的增加不会增加电池的相应单位发电量的成本,为了使逆变器对应的单位发电量费用降低,应尽可能让逆变器满载。
(2)电池的选择通过单位面积效益来选定。
通过电池的单位面积效益我们选出较优的电池。
同时考虑并联的光伏组件端电压相差不应超过10%的正常工作条件约束、选配的逆变器的容量应大于等于光伏电池组件分组安装的容量的安全约束,建立多目标规划模型。
通过软件求解,最后只有南顶面要铺电池, 35年的发电量为.6度,经济效益为4422.3元,回报年限为33年问题2:题目要求考虑电池板的朝向和倾角均会影响光伏电池的工作效率,选择架空的方式进行铺设,该问可视为第一问的模型优化。
非水平面上晴天实际日射强度的计算公式,根据实际情况,公式化简为:n ',(1cos) cos sin2ADQ s s αααα+=++┻,s通过使坡面一年的辐射能量最大,利用C语言进行求解,求出当架空面的倾角为α=41时,坡顶面接收到的辐射总能量是最大。
关键词:光伏电池、逆变器、辐射强度、多目标规划、excel一问题的重述在设计太阳能小屋时,需在建筑物外表面(屋顶及外墙)铺设光伏电池,光伏电池组件所产生的直流电需要经过逆变器转换成220V交流电才能供家庭使用,并将剩余电量输入电网。
不同种类的光伏电池每峰瓦的价格差别很大,且每峰瓦的实际发电效率或发电量还受诸多因素的影响,如太阳辐射强度、光线入射角、环境、建筑物所处的地理纬度、地区的气候与气象条件、安装部位及方式(贴附或架空)等。
太阳能小屋的优化设计
太阳能小屋的优化设计模型摘 要本文首先对所给数据进行初始筛选,计算出电池板的价格,然后将适合每种电池版的有效辐射强度进行年度求和,最后判别出各个墙面的铺设方案。
问题一,根据约束条件建立了双目标规划模型,即使小屋的全年太阳能光伏发电总量尽可能大,而单位发电量的费用尽可能小,并使用Lingo 软件进行求解。
考虑到逆变器的价格,额定电流以及输入电压范围,选择合适的电池组,得到35年的投入产出比为2.00743394091.99188883.3=,回收年限为P K N /==8.67年。
问题二,参考附录4山西大同典型气象年逐时参数及各方向辐射强度计算出太阳高度角,将顶棚的电池板竖起一个角度,是电池板在辐射强度最大的时候与太阳光垂直,屋顶南面倾角为10.6度,电池板需与水平面的角度为37.5度,则在屋顶上的角度为26.9度,此时顶棚收益为96.871942*1530034.66*5012.3478*33=-+=z回收年限为8.23年。
问题三,设计小屋仍然为长方形小屋,根据第二问的答案,设计屋顶的角度为37.5度,空间最低净空高度距地面高度为2.8m ,则屋顶最高处与房檐高度为2.6m ,以采光加权面积最大没目标函数,求取最大值,因为不是线性规划采用c++程序进行求解,解得小屋的长为12.872m ,宽为5.7489m ,此时根据线性规划对铺设方案进行求解,得由此35年的投入产出比为2.1223,回收年限为7.98年。
关键词: 多目标规划 加权平均 投入产出比一、问题重述21世纪是世界能源结构发生巨大变革的世纪。
由于传统能源(如煤、石油、天然气等)的供给已出现严重短缺局面,人类开始将目光转向可再生能源的发展。
大规模地开发利用可再生洁净能源,以资源无限、清洁干净的可再生能源为主的多样性的能源结构代替以资源有限、污染严重的石化能源为主的能源结构已成为人们关注的焦点。
太阳能作为一种新型的绿色可再生能源,与其他新能源相比利用最大,是最理想的可再生能源。
太阳能小屋的设计
承
诺
书
我们仔细阅读了中国大学生数学建模竞赛的竞赛规则. 我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网 上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。 我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的 资料(包括网上查到的资料) ,必须按照规定的参考文献的表述方式在正文引用处和参 考文献中明确列出。 我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。如有违反竞赛规 则的行为,我们将受到严肃处理。 我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展 示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等) 。
2
3.参数设置
为了叙述的方便,我们把题中所用的变量用下列参数来代替: 符号 说明 Voc 电池板的开路电压 Isc 电池板的短路电流 电池板将太阳能转化为电能的转换效率 电池板的性价比 E 太阳能转化的直流电量 Q 总辐射强度 Sij i 类电池板 j 的面积, i A, B, C , j 1, 2,3, P 电池板的输出功率 日照时间 t Y 太阳能小屋 n 年之后的收益 yij i 类电池板 j 的价格, i A, B, C , j 1, 2,3, ts 太阳时 时角 赤纬角 太阳高度角 当地的纬度(大同的纬度为 40.1°) A 太阳的方位角 Di 第 i 个月中辐射量等于月均辐射量的日期 当月的平均辐射量 H i 日出时角 ' 日落时角 i hi 太阳高度角 H Oj 地外水平面辐射量 H b 0 j 地表水平面上的直接辐射量 H d 0 j 散射辐射量 I b. j 地表法线方向直接辐射 Id. j 散射强度 s 太阳板与屋顶的倾角 单位 V A % / kWh W / m2 m2 W h 元 元/Wp 小时 度 度 度 度 度 / W / m2 度 度 度 W / m2 W / m2 W / m2 W / m2 W / m2
2012年全国大学生数学建模大赛B题--论文
2012年全国大学生数学建模大赛B题--论文太阳能小屋的设计摘要:在太阳能小屋的设计中为实现太阳能光伏板最佳朝向、倾角及排布阵列设计及优化,通过建立倾斜放置的光伏板表面接收太阳辐射能模型,计算到达光伏板上的太阳辐射能量,推导出光伏板的最佳朝向及倾角。
为使光伏板最大限度地接收太阳辐射的能量,在选择合适的朝向及倾角的基础上,对光伏电池排布阵列,建立目标规划,并通过与实际逆变器的相互匹配,不断对目标进行优化,最终得到一组最优解。
通过上述研究,结合山西大同市本地情况,重新设计出一个更加适合当地地理及气象条件的太阳能光能房屋并为其选择最优的阵列排布方案。
针对问题一:电池板只是铺设房屋的表面,没有涉及到电池板放的角度问题,先求算出房屋的角度为10.62度,再根据角度,建立模型算出光伏板上太阳能辐射量。
并用目标规划阵列排列方案计算出电池的排布。
再通过排布计算出经济效益,最后得出35年之内无法收回成本。
针对问题二:通过对角度建立模型,计算得出最佳角度44.66度,通过排布计算出电池板排布最佳方案,建立模型计算出经济效益,在28.5年收回成本。
如考虑货币时间价值,35年的经济效益是亏损的。
针对问题三:要通过目标构建一个产电量尽量大,而成本尽量小的理想模型。
假设小屋无挑檐、挑雨棚(即房顶的边投影与房体的长宽投影相等),建立模型计算出最佳的图形,并画出模型图。
关键字:太阳能太阳能辐射模型最佳倾角电池模型目标规划一.阐述问题太阳能作为迄今人类所认识的最清洁的可再生能源,其与建筑一体化将在建筑节能中起到十分重要的作用。
屋顶在建筑外围结构中所接受的日照时间最长,接受的太阳辐射量也最大,具有利用太阳辐射的优越条件,同时,屋顶较开阔,便于大面积连续布置太阳能设备,因此,在城市中,建筑屋顶是太阳能利用的最佳场所。
目前,许多国家已纷纷实施和推广“太阳能屋顶计划”,如有德国十万屋顶计划、美国百万屋顶计划以及日本的新阳光计划等。
我国属于太阳能利用条件较好的地区,尤其是青藏高原地区太阳能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 太阳能小屋的设计 摘要 本文主要研究太阳能小屋的设计和外表面合理铺设光伏电池的问题,不仅要使小屋的全年太阳能光伏发电总量尽可能大,而且要考虑到效益问题,即安装了太阳能电池后,在给定的年限中盈利而不能亏损。在考虑大同气象数据的基础上,对所提供的电池型号和逆变器型号进行选择和安排铺设。 针对问题一,首先对气象数据按季度进行处理,利用MATLAB求出四季度每一时段各面光照的平均值,可将一年的光照强度模型简化为四组数据。电池有三种类型,各类之间的差别比较大,由于光照强度以一年为循环周期,对于不同的光照强度类型,可以根据产电量将三类电池进行优先选择顺序排序。同类型的不同型号电池中,太阳能转换效率略有差别,考虑到最大发电量,同类型的电池中优先选择转换效率大的型号,由此建立选择电池型号的模型。然后根据尺寸限制对各面进行初步铺设并选择最佳的逆变器。由于要考虑到经济效益问题,需要对以上建立的模型修正,对各个面中各型号的电池进行收益计算,去掉那些在给定年限中无法收回成本的电池型号,由此建立发电量尽量大且收益又大的模型。由所建模型可知仅对前顶面铺设A3型号,南面铺设C2型号电池,其他面不铺设,成本回收年限为26.98年,在35年的净收益为45925.71元。 针对问题二,在考虑电池板的朝向与倾角均会影响到光伏电池的工作效率的情况下,选择架空方式安装光伏电池,重新考虑问题一。解决此问题的关键是找出大同市的最佳电池板朝向角和倾角。对最佳朝向角和倾斜角建立适当模型后得出最佳朝向角为12度,最佳倾角为40度。用架空的方式铺设屋顶的电池板使其朝向角和倾角满足最佳角度,同时考虑到前屋顶加上倾角后面积增加进而可以增加电池板的数量,利用经验公式得出此时的辐射强度并重新计算,得到成本回年限为17.75年,35年的净收益为247500.69元。 对于问题三,由前两问的结论可知,对于小屋电池板的铺设,只需铺设南面和前顶面,同时小屋的屋顶朝向满足电池板的最优朝向。由于前顶面发电量最大,在建立小屋尺寸模型时,应在满足小屋的设计要求的前提下,使前顶面面积最大。其次是,合理安排门和窗户的位置,使南面可以安装电池板的面积最大,同时考虑电池板的最优倾角,建立适当小屋模型,可以使该小屋在满足舒适性的要求下,可以获得的效益也最大。在所建的小屋模型中,成本回年限为15.84年,35年的净收益为306127.06元。
关键字:太阳能小屋 光伏电池 最佳朝向角和倾角 光照强度 2
一、 问题重述 1.1 问题背景 在设计太阳能小屋时,需在建筑物外表面铺设光伏电池,光伏电池组件所产生的直流电需要经过逆变器转换成220V交流电才能供家庭使用,并将剩余电量输入电网。不同种类的光伏电池每峰瓦的价格差别很大,且每峰瓦的实际发电效率或发电量还受诸多因素的影响,如太阳辐射强度、光线入射角、环境、建筑物所处的地理纬度、地区的气候与气象条件、安装部位及方式等。因此,在太阳能小屋的设计中,研究光伏电池在小屋外表面的优化铺设是很重要的问题。 在同一表面采用两种或两种以上类型的光伏电池组件时,同一型号的电池板可串联,而不同型号的电池不可串联。在不同表面上,即使是相同型号的电池也不能进行串、并联连接。应注意分组连接方式及逆变器的选配。 1.2 问题讨论 根据题意,讨论下列三个问题,分别给出小屋外表面光伏电池的铺设方案,使小屋的全年太阳能光伏发电总量尽可能大,而单位发电量的费用尽可能小,并计算出小屋光伏电池35年寿命期内的发电总量、经济效益及投资的回收年限。给出小屋各外表面电池组件铺设图形及连接方式示意图,给出电池组件分组阵列容量及选配逆变器规格列表。 1、根据山西省大同市的气象数据,在仅考虑贴附安装方式的前提下,选定光伏电池组件,对小屋的部分外表面进行铺设,并根据电池组件分组数量和容量,选配相应的逆变器的容量和数量。 2、电池板的朝向与倾角均会影响到光伏电池的工作效率,选择架空方式安装光伏电池,重新讨论问题1。 3、据小屋建筑要求,为大同市重新设计一个小屋,画出小屋的外形图,并对所设计小屋的外表面优化铺设光伏电池,讨论出铺设及分组连接方式,选配逆变器,计算相应结果。 二、 问题分析
对于问题一,根据大同的气象数据,可以得知每天早上八点到下午五点的光照可以用于太阳能电板发电;对于全年而言,由于太阳的辐射强度随季节周期性变化比较明显,于是可以将全年的数据按照季节分为四组,对每一个季节的每一时刻的数据求平均值,得到各个季节早上八时到下午五时每时刻阳光照射的平均值。 A、B、C三类电池的性能差别比较大,并且小屋的每个表面阳光强度也不相同,由此可知小屋的不同表面应选择不同的电池类型。在对小屋每个表面选定电池组铺设的时候,应使小屋的全年太阳能光伏发电总量尽可能大,在暂时不考虑逆变器成本的情况下,建立单位面积上发电收益最大模型,进而初步得出每个表面应优先用的电池类型。结合所求得的每季度的平均光照强度,在各个面分别选择A,B,C类型电池,求得各类型电池单位面积上发电数量,比较其大小,进而选出各个面所应选择的电池种类。在此基础上对各个面进行电池排放,最后在所剩的空缺面积上考虑电池尺寸大小,选择合适的电池,使得空间利用率最高。 为了使单位发电量的费用尽可能小,可以在选择逆变器时,合理安排电池组的串并联顺序,使其在满足逆变器要求的基础上单位发电量费用降低,进而达到利润最大。 针对问题二,在第一问的基础上,考虑到电池板的朝向与倾角均会影响到光伏电池的工作效率,需要选择架空方式安装光伏电池,对于小屋四周的太阳能电板,由于考虑 3
到实际其情况,四周的电池板不能进行架空安装,而小屋屋顶有一定的安装角度,可以结合赤纬角与太阳高度角合理选择屋顶的太阳能电板安装角度。加入时角算出每时刻的阳光利用率,进而求解出发电总量。 对于问题三,在一、二讨论的基础上,首先设计好倾角以及转角,再根据顶面和南面面积优先最大化进行设计尺寸。在此只需铺设南面和前顶面,将小屋的朝向适当向西偏离正南朝向以满足电池板的最优朝向问题。合理安排门和窗户的位置,使南面可以安装电池板的面积最大,同时考虑电池板的最优倾角,建立适当小屋模型,可以使该小屋在满足舒适性的要求下,可以获得的效益也最大。
三、 模型假设 1、假设电费不变,即保持为0.5元/kWh 2、假设山西省三十年内气候变化保持平稳,不会有大的气候波动 3、假设所转化的电全部备用,即全被出售 4、假设忽略架空价,电板安装等的成本 5、假设不考虑资金的时间价值 6、假设小屋周围没有高楼、大树等物体的遮挡 7、假设逆变器全部放在屋内
四、 符号说明 a 实际光照强度
ij 第j类第i种光伏电池组件的转化效率
t 时间长度
L 电价
jl 第j类光伏电池的每峰瓦的价格
b 标准辐射度
W 利润
Q 发电量
c 经过转化后的电量
P 电池的额定功率
ix i类逆变器的单位售价
1 后屋顶与水平面的夹角
2 前屋顶与水平面的夹角
当地地理纬度
倾斜角度 4
时角
赤纬角
M 倾斜面光伏阵列面上的太阳能总辐射量
D 散射辐射量
五、 模型建立及求解 5.1 问题一:在仅考虑贴附的情况下,对小屋的部分表面进行铺设 太阳能小屋的是在利润最大的基础上建立的,在此我们可以假设电费在最近几十年内保持不变为一个定值L,利润公式W=销售额C-成本R,由于电价一定,为使利润最大,故使小屋的建造成本最小即可,即光伏电池组件和逆变器最优组合。 5.1.1 模型建立 根据大同的气象数据得出:对于一年而言,有效光照时间基本上是从早上八时到下午五时。在一年中,太阳的辐射随季节周期性变化比较明显,但对于一个季节内各月,光照强度差异不是很大,因此在此可以用季节的平均光照强度代替每天的光照强度,即:
178mmnnaat 式中ma表示m时刻的辐射强度,nt表示第n季节的天数。 利用MATLAB[1]将附表四中每一季度早上八时到下午五时的光照平均值求出。整理得出表格:(编程见附录) 表1:各季度每时段平均辐射值
时刻 水平面总辐射强度 东向总辐射 强度 南向总辐射 强度 西向总辐射 强度 北向总辐射 强度 第一季度每天的平均光照 8 10.31 10.28 5.2 4.6 4.6 9 73.27 87.99 46.91 24.95 24.95 10 200.06 228.81 180.39 50.16 50.16 11 335.37 285.41 343.16 63.17 52.17 12 438.21 226.85 458.36 69.7 69.71 13 483.36 103.35 499.26 73.92 73.92 14 494.22 74.71 519.47 189.86 74.7 15 445.01 66.85 487.65 324.14 66.85 16 357.59 49.04 430.68 446.01 49.04 17 237.04 26.07 362.36 571.17 26.07 第二季度每天的平均光照 8 282.78 317.53 76.79 61.2 61.2 9 423.62 355.52 146.5 78.07 78.07 10 557.17 332.65 226.57 97.27 97.27 11 624.93 240.41 266.68 95.98 95.98
