数电习题答案(第五版)
电子技术基础(数字部分)第五版答案康华光

第一章数字逻辑习题1.1数字电路与数字信号1.1.2 图形代表的二进制数01011010011.4一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSBLSB0 1 2 11 12 (ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms频率为周期的倒数,f=1/T=1/0.01s=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%1.2数制1.2.2将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于42.(2)127 (4)2.718解:(2)(127)D=-1=(10000000)B-1=(1111111)B=(177)O=(7F)H 72(4)(2.718)D=(10.1011)B=(2.54)O=(2.B)H1.4二进制代码1.4.1将下列十进制数转换为8421BCD码:(1)43 (3)254.25解:(43)D=(01000011)BCD1.4.3试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+ (2)@ (3)you (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASCⅡ码为0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为1000000,(01000000)B=(40)H(3)you的ASCⅡ码为本1111001,1101111,1110101,对应的十六进制数分别为79,6F,75(4)43的ASCⅡ码为0110100,0110011,对应的十六紧张数分别为34,331.6逻辑函数及其表示方法1.6.1在图题1. 6.1中,已知输入信号A,B`的波形,画出各门电路输出L的波形。
解: (a)为与非,(b)为同或非,即异或第二章逻辑代数习题解答2.1.1 用真值表证明下列恒等式(3)ABABAB⊕=+(A⊕B)=AB+AB解:真值表如下ABAB⊕AB AB AB⊕AB+AB 0111111111111由最右边2栏可知,与AB+AB的真值表完全相同。
数电答案

习 题1题1.1 数字信号的波形如图题1.1.1图所示,若波形的高,低电平用正逻辑赋值。
试用二进制数序列表示该脉冲波形(每一时间段用一位二进制数表示)。
解:从时间段1~8的数字序列为:10011011。
题1.2 若用正逻辑赋值。
高电平等于3伏,低电平等于0.3伏,将下述二进制数序列用脉冲波形表示(一位二进制数用每一相等的时间段表示)。
(a ) 110110101 (b ) 1011001 (c ) 10101011 (d ) 10001110解:对于各个数字序列,用脉冲波形表示如图1.1(a)、(b)、(c)、(d)所示。
题1.3 有一脉冲信号,脉冲信号的高电平维持时间为0.1μS,低电平维持时间为0.4μS 求信号的脉冲周期T ,占空比q 。
解:脉冲周期T=高电平维持时间+低电平维持时间=0.1μS+0.4μS =0.5μS ;占空比q =高电平维持时间/脉冲周期T=0.1/0.5=0.2。
题1.4 有一正弦模拟信号,u(t)=9sinωt 伏,若以0.5伏作为基本转换单位,试问在t=T/4,T/2,3T/4,T/6时,将该模拟量的瞬时值转换数字量,则数字量为多大?解:在t=T/4,T/2,3T/4,T/6时,u(t)=9sinωt 伏的瞬时值分别为:9V ,0V ,-9V ,7.94V ,采用四舍五入进行量化:则数字量分别为:18,0,-18,16。
题1.5 将下述十进制数转换成为八进制数(保留小数点后二位),再转换成为二进制数。
(a ) 658.95D (b ) 135.16D (c ) 63.24D (d ) 1027.67D解:658D =1×83+2×82+2×81+2×80,而 0.95×8=7.6,0.6×8=4.8,所以: 658.95D =1222.74O =1010010010.1111B ;同理:135.16D =207.12O =10000111.00101B ;63.24D =77.17O =111111.001111B ;1027.67D =2003.52O =10000000011.10101B ;题1.6 将下述十进制数转换成为十六进制数(保留小数点后二位),再转换成为二进制数。
数字电子技术基础-康华光第五版答案

数字电子技术基础-康华光第五版答案(总36页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一章数字逻辑习题1.1 数字电路与数字信号图形代表的二进制数1.1.4 一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0 1 2 11 12 (ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%数制将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于2−4(2)127 (4)解:(2)(127)D= 27 -1=()B-1=(1111111)B=(177)O=(7F)H(4)()D=B=O=H二进制代码将下列十进制数转换为 8421BCD 码:(1)43 (3)解:(43)D=(01000011)BCD试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+ (2)@ (3)you (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASCⅡ码为 0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为 1000000,(01000000)B=(40)H(3)you 的ASCⅡ码为本 1111001,1101111,1110101,对应的十六进制数分别为 79,6F,75(4)43 的ASCⅡ码为 0110100,0110011,对应的十六紧张数分别为 34,33逻辑函数及其表示方法在图题 1. 中,已知输入信号 A,B`的波形,画出各门电路输出 L 的波形。
解: (a)为与非, (b)为同或非,即异或第二章逻辑代数习题解答用真值表证明下列恒等式(3)A⊕ =B AB AB+ (A⊕B)=AB+AB由最右边2栏可知,A⊕B与AB+AB的真值表完全相同。
《电子技术基础》第五版(数字部分)高教版课后答案

1.1 数字电路与数字信号第一章 数字逻辑习题1.1.2 图形代表的二进制数MSBLSB 0 1 211 12(ms )解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10% 数制1.2.2 将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于 2 (2)127 (4)解:(2)(127)D=27-1=()B-1=(1111111)B =(177)O=(7F )H (4)()D=B=O=H 二进制代码1.4.1 将下列十进制数转换为 8421BCD 码: (1)43 (3) 解:(43)D=(01000011)BCD1.4.3 试用十六进制写书下列字符繁荣 ASC Ⅱ码的表示:P28 (1)+ (2)@ (3)yo u (4)43解:首先查出每个字符所对应的二进制表示的 ASC Ⅱ码,然后将二进制码转换为十六进制 数表示。
(1)“+”的 ASC Ⅱ码为 0101011,则(00101011)B=(2B )H (2)@的 ASC Ⅱ码为 1000000,(01000000)B=(40)H(3)you 的 ASC Ⅱ码为本 1111001,1101111,1110101,对应的十六进制数分别为79,6F,75 (4)43 的 ASC Ⅱ码为 0110100,0110011,对应的十六紧张数分别为 34,33 逻辑函数及其表示方法解: (a)为与非, (b)为同或非,即异或第二章逻辑代数习题解答2.1.1 用真值表证明下列恒等式(3) A⊕B AB AB(A⊕B)=AB+AB解:真值表如下A B A⊕BAB AB A⊕BAB+AB0 0 1 11111111111A (1BC ) ACDCDEA ACDCDEACD CDEACD E2.1.4 用代数法化简下列各式(3) ABC B C)A⋅B A⋅B(A B)(A B)1BAB ABABBABAB(9) ABC DABD BC D ABCBD BC解: ABC DABDBC DABCBD BCB ( ACD )L D ( AC)2(3)(L AB)(C D)2.2.2 已知函数 L(A,B,C,D)的卡诺图如图所示,试写出函数 L 的最简与或表达式解:L( A, B, C, D) BC D BCD B C D ABD2.2.3 用卡诺图化简下列个式(1)ABCD ABCD AB AD ABC3解:ABCD ABCD AB AD ABCABCD ABCD AB CC DDAD B B CCABC D D)()()()()(ABCD ABCD ABC D ABCD ABC D ABC D ABC D(6)L( A, B, C, D ) ∑m解:(0, 2, 4, 6,9,13)∑d(1, 3, 5, 7,11,15)L AD(7)L( A, B, C , D )∑m 解: (0,13,14,15)∑d(1, 2, 3, 9,10,11)L AD AC AB42.2.4 已知逻辑函数L AB BC C A,试用真值表,卡诺图和逻辑图(限用非门和与非门)表示解:1>由逻辑函数写出真值表A11112>由真值表画出卡诺图B1111C1111L1111113>由卡诺图,得逻辑表达式L AB BC AC 用摩根定理将与或化为与非表达式L AB BC AC AB⋅B C⋅AC4>由已知函数的与非-与非表达式画出逻辑图5第三章习题MOS逻辑门电路3.1.1 根据表题所列的三种逻辑门电路的技术参数,试选择一种最合适工作在高噪声环境下的门电路。
阎石《数字电子技术基础》(第5版)(课后习题 数-模和模-数转换)【圣才出品】
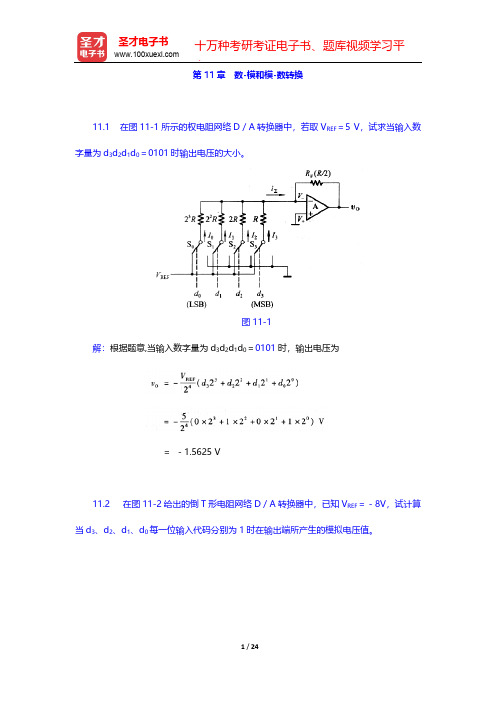
第11章 数-模和模-数转换11.1 在图11-1所示的权电阻网络D/A转换器中,若取V REF=5 V,试求当输入数字量为d3d2d1d0=0101时输出电压的大小。
图11-1解:根据题意,当输入数字量为d3d2d1d0=0101时,输出电压为=-1.5625 V11.2 在图11-2给出的倒T形电阻网络D/A转换器中,已知V REF=-8V,试计算当d3、d2、d1、d0每一位输入代码分别为1时在输出端所产生的模拟电压值。
图11-2解:由题意可得因此,当31d =时,O 4v V =;当21d =时,O v 2V =;当11d =时,O 1v V =;当01d =时,O 05v .V =。
11.3 在图11-3所示的D /A 转换电路中,给定V REF =5V ,试计算(1)输入数字量的d 9~d 0每一位为1时在输出端产生的电压值。
(2)输入为全1、全0和1000000000时对应的输出电压值。
图11-3解:由题意可得因此,题(1)、(2)的结果如表11-1所示。
表11-111.4 在图11-3由CB7520所组成的D /A 转换器中,已知V REF =-10V ,试计算当输入数字量从全0变到全1时输出电压的变化范围。
如果想把输出电压的变化范围缩小一半,可以采取哪些方法?解:由题意可得当输入全为0时,有0O min v V =;当输入全为1时,有()1010219992REF O max V v .V =--=。
因此,电压变化范围为0~9.99 V 。
如果想把输出电压的变化范围缩小一半,可以采取以下方法:①令参考电压REF V 的绝对值减半;②令求和放大器的放大倍数减少一半。
即在out I 与放大器输出端O v 之间外接一个大小等于2R 的反馈电阻。
11.5 图11-4所示电路是用CB7520和同步十六进制计数器74LS161组成的波形发生器电路。
已知CB7520的V REF =-10V ,试画出输出电压O v的波形,并标出波形图上各点电压的幅度。
电子技术基础数电部分课后答案(第五版康华光--

反馈延迟环节( RC电路):利用RC电路的充放电特路 的输出状态,以获得脉冲波形输出。
RC延时环节
开 关 电 路
8.3.1 由CMOS门电路组成的多谐振荡器
1. 电路组成
υo1与υo 反相,电容接在υo与υI之间:
C
0
t
2. 工作原理
(2)第二暂稳态电容放电,电路自动翻转到第一暂稳态
电容放电
vC
vI
当 v I =VTH 时,
vI
v O1
D1
vI
D2
G1
TP D3
vO1
TN
D4
R
v O 迅速使得G1截止、G2导通
υ O1 =1υ O =0 电路返回第一暂稳态
G2 VDD TP
vI VDD
VDD+V+
放电
VTH
导通
不变
3、555定时器功能表
阈值输入 (VI1)
×
2 3 VCC
2 3 VCC
2 3 VCC
输入
输出
触发输入
(VI2)
×
1 3 VCC
1 3 VCC
1 3 VCC
复位(RD) 0 1 1 1
输出 (VO)
0 1
0
不变
放电管 T
导通 截止
导通
不变
8.4.2 用555定时器组成施密特触发器
555
双555型号的最后几位数码
556
7555 7556
优点
驱动能力较大 低功耗、高输入阻抗
电源电压工作范围
5~16V
3~18V
负载电流
可达200mA
可达4mA
8.4.1 555定时器
电子技术基础(数字部分)第五版答案康华光
第一章数字逻辑习题1.1 数字电路与数字信号1.1.2 图形代表的二进制数0101101001.1.4 一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSBLSB0 1 2 11 12 (ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/0.01s=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%1.2 数制1.2.2 将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于42. (2)127 (4)2.718解:(2)(127)D=-1=(10000000)B-1=(1111111)B=(177)O=(7F)H 72(4)(2.718 )D=(10.1011)B=(2.54)O=(2.B)H1.4 二进制代码1.4.1 将下列十进制数转换为8421BCD码:(1)43 (3)254.25解:(43)D=(01000011)BCD1.4.3 试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+ (2)@(3)you (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
...4>由已知函数的与非-与非表达式画出逻辑图...4>由已知函数的与非-与非表达式画出逻辑图4>由已知函数的与非-与非表达式画出逻辑图4>由已知函数的与非-与非表达式画出逻辑图...OLV=0.1V, ILV=1.5V, 因此有:(1) =0< ViILV=1.5V, 属于逻辑门0(2) <1.5V=ViILV, 属于逻辑门0(3) <0.1<ViILV=1.5V, 属于逻辑门0(4) 由于CMOS管的栅极电流非常小, 通常小于1uA,在10kΩ电阻上产生的压降小于10mV即...OLV=0.1V, ILV=1.5V, 因此有:(1) =0< ViILV=1.5V, 属于逻辑门0(2) <1.5V=ViILV, 属于逻辑门0(3) <0.1<ViILV=1.5V, 属于逻辑门0(4) 由于CMOS管的栅极电流非常小, 通常小于1uA,在10kΩ电阻上产生的压降小于10mV即OLV=0.1V, ILV=1.5V, 因此有:(1) =0< ViILV=1.5V, 属于逻辑门0(2) <1.5V=ViILV, 属于逻辑门0(3) <0.1<ViILV=1.5V, 属于逻辑门0(4) 由于CMOS管的栅极电流非常小, 通常小于1uA,在10kΩ电阻上产生的压降小于10mV即...高阻113.1.12 (a)AL11...高阻113.1.12 (a)AL11高阻113.1.12 (a)AL11高阻113.1.12 (a)AL11高阻113.1.12 (a)AL11高阻113.1.12 (a)AL11...1.1.3vmA..≈444Ω...1.1.4vmA..≈444Ω...1111111111110 1 0 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 1 1 10 1 0 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 1 1 11 0 0 0 1 1 1 1 1 0 0 0 0 1 0 0 1 1 1 0 111112 )由真值表画卡诺图11112 )由真值表画卡诺图11112 )由真值表画卡诺图11112 )由真值表画卡诺图11112 )由真值表画卡诺图11112 )由真值表画卡诺图...输入输出ABCLL=C1111__LC=...输入输出ABCLL=C 01111__ LC=输入输出ABCLL=C 01111__ LC=输入输出ABCLL=C 01111__ LC=第六章习题答案1.1.5已知某时序电路的状态表如表题6.1,6所示,输人为A,试画出它的状态图。
电子技术基础数字部分第五版康光华主编第4章习题答案
第四章习题答案4.1.4 试分析图题4.1.4所示逻辑电路的功能。
解:(1)根据逻辑电路写出逻辑表达式:()()L A B C D =⊕⊕⊕ (2)根据逻辑表达式列出真值表:由真值表可知,当输入变量ABCD中有奇数个1时,输出L=1,当输入变量中有偶数个1时,输出L=0。
因此该电路为奇校验电路。
4.2.5 试设计一个组合逻辑电路,能够对输入的4位二进制数进行求反加1 的运算。
可以用任何门电路来实现。
解:(1)设输入变量为A、B、C、D,输出变量为L3、L2、L1、L0。
(2)根据题意列真值表:(3)由真值表画卡诺图(4)由卡诺图化简求得各输出逻辑表达式()()()3L AB A C AD ABCD A B C D A B C D AB C D =+++=+++++=⊕++()()()2L BC BD BCD B C D B C D B C D =++=+++=⊕+ 1L CD CD C D =+=⊕0L D =(5)根据上述逻辑表达式用或门和异或门实现电路,画出逻辑图如下:A B CDL 3L 2L 1L 04.3.1判断下列函数是否有可能产生竞争冒险,如果有应如何消除。
(2)(,,,)(,,,,,,,)2578910111315L A B C D m =∑ (4)(,,,)(,,,,,,,)4024612131415L A B C D m =∑解:根据逻辑表达式画出各卡诺图如下:(2)2L AB BD =+,在卡诺图上两个卡诺圈相切,有可能产生竞争冒险。
消除办法:在卡诺图上增加卡诺圈(虚线)包围相切部分最小项,使2L AB BD AD =++,可消除竞争冒险。
(4)4L AB AD =+,在卡诺图上两个卡诺圈相切,有可能产生竞争冒险。
消除办法:在卡诺图上增加卡诺圈(虚线)包围相切部分最小项,使4L AB AD BD =++,可消除竞争冒险。
4.3.4 画出下列逻辑函数的逻辑图,电路在什么情况下产生竞争冒险,怎样修改电路能消除竞争冒险。
电子技术基础数字部分第五版康光华主编第6章习题答案
第六章作业答案解:根据状态表作出对应的状态图如下:6.1.3 已知状态图如题图6.1.3所示,试列出其状态表。
00/010/06.1.8已知状态表如表题6.1.8所示,若电路的初始状态为Q 1Q 0=00,输入信号A 的波形如图题6.1.8所示,输出信号为Z ,试画出Q 1Q 0的波形(设触发器对下降沿敏感)。
解:根据已知的状态表及输入信号A=011001,该电路将从初始状态Q1Q0=00开始,按照下图所示的顺序改变状态:Q1Q0的波形图如下:CPAQQ16.2.1试分析图题6.2.1(a)所示时序电路,画出其状态表和状态图。
设电路的初始状态为0,试画出在图题6.2.1(b)所示波形的作用下,Q和Z的波形图。
CP AZ解:由电路图可写出该电路的状态方程和输出方程分别为:1n n Q A Q Z AQ+=⊕=状态图如下所示:0/1Q 和Z 的波形如下所示:CP A Q Z6.2.4分析图题6.2.4所示电路,写出它的激励方程组、状态方程组和输出方程,画出状态表和状态图。
A CPZ解:电路的激励方程组为:10101011J Q K AQ J Q K ==== 状态方程组为:()11101101100nn n nnnnnn n Q Q Q QQ Q AQ Q Q Q A ++==+=+输出方程为: 10Z AQ Q =根据状态方程组和输出方程可列出状态表如下:状态图如下:6.3.2 某同步时序电路的状态图如图题6.3.2所示,试写出用D 触发器设计时的最简激励方程组。
解:由状态图可知,要实现该时序电路需要用3个D 触发器。
(2)画出各激励信号的卡诺图,在状态转换真值表中未包含的状态为不可能出现的,可作无关项处理。
(3)由卡诺图得到各激励信号的最简方程如下:22110nnnD Q D Q D Q === 6.3.5试用下降沿触发的JK 触发器和最少的门电路实现图6.3.5所示的Z 1和Z 2输出波形。
Z Z解:从Z 1和Z 2输出波形可以看出,对于每一个Z 1或Z 2周期,均可等分为4段时间间隔相等的状态,即Z 2 Z 1=00、Z 2 Z 1=01、Z 2 Z 1=11和Z 2 Z 1=01,因此要设计的时序电路可以有4个状态,分别用00、01、10、11来表示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高级肖特基 TTL,低功耗和高级低功耗肖特基 TTL 高,强,小 (c) (b) (c) 多 强 (a) (a) (b) 高级肖特基 TTL (c)
习题
2.1 与,或, 与 2.2 与门, 或门, 与门 2.3 (a)F=A+B, F=AB (b)F=A+B+C, F=ABC (c)F=A+B+C+D, F=ABCD 2.4 (a)0 (b)1 (c)0 (d)0 2.5 (a)0 (b)0 (c)1 (d)0 2.6 (a)1 (b)1 (c)1 (d)1 2.7 (a)4 (b)8 (c)16 (d)32 2.8 (a)3 (b)4 (c)5 (d)6 2.9 (a)
1.2.8. 1.2.9. 1.2.10.
(c) (b) (b)
1.2.11. (b)
1.2.12. (a) 1.2.13. (c)
1.2.14. (c)
1.2.15. (c)
1.2.16. 1001001
1.2.17. 11
1.2.18. 110010
1.2.19. 1.2.20. 1.2.21.
1.21 010100 原= 010100 补, 101011 原= 110101 补, 110010 原= 101110 补, 100001 原 =
111111 补
1.22 1310 = 00001101 补, 11010 = 01101110 补, -2510 = 11100111 补, -90 = 1
F = A⋅B (b) 高
2.2.4. 32 2.2.5. 16,5
2.2.6. 1 2.2.7. 串联
2.2.8. 2.2.9. 2.2.10. 2.2.11.
(d) 不相同 高 相同
2.2.12. (a)
2.2.13. (c) 2.2.14. 奇 2.2.15. 奇
2.3 自测练习 2.3.1. OC, 上拉电阻 2.3.2. 0,1,Z 2.3.3. (b) 2.3.4. (c) 2.3.5. F = A ⋅ B , Z
1.3.8. 1.3.9. 1.3.10. 1.3.11. 1.3.12. 1.3.13.
28.375 100010.11 135.625 570.1 120.5 2659.A
1.4 自测练习 1.4.1. BCD
Binary coded decimal 二—十进制码
1.4.2. (a)
1.4.3. 1.4.4. 1.4.5.
0.904710 = 0.1110012 = 0000.10010000010001118
1.17
1310 = 000100118421BCD = 01000110XS3 = 1011Gray,
1001.01011000 XS3 = 0101.01Gray,
0.12510 =
6.2510 = 0110.001001018421BCD = 0000.0001001001018421BCD =
1.14 (a)4094, (b)1386, (c)49282
1.15 (a)23, (b)440, (c)2777
1.16 198610 = 111110000102 = 00011001100001108421BCD, 67.31110 = 1000011.010012 = 01100111.0011000100018421BCD, 1.183410 = 1.0010112 = 0001.00011000001101008421BCD ,
5F.6816
1.10 168 = 1410,1728 = 12210,61.538 = 49.671875,126.748 = 86.937510
1.11
2A16 = 4210 = 1010102 = 528, B2F16 = 286310 = 1011001011112 = 54578, D3.E16
A
B
C
F
0
0
0
0
0
0
1
1
0
1
0
1
0
1
1
0
1
0
0
1
1
0
1
0
1
1
0
0
1
1
1
1
(b)
A
B
C
D
F
0
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
0
1
1
1
0
1
0
0
0
0
1
0
1
0
0
1
1
0
1
0
1
1
1
0
1
0
0
0
0
1
0
0
1
1
1
0
1
0
1
1
0
1
1
1
1
0
0
1
1
1
0
1
0
1
1
1
0
0
1
1
1
1
0
2.10 Y = AB + AC 2.11
A
B
C
Y
0
1.4.24. 1001011
1.4.25. ASCII 1.4.26. (b)
1.4.27. (b)
1.4.28. 11011101
1.4.29. -15
1.4.30. 1.1001
1.4.31. 1.1001
习题
1.1 (a)(d)是数字量,(b)(c)是模拟量,用数字表时(e)是数字量,用模拟表时(e) 是模拟量
第一章 数制与编码
1.1 自测练习 1.1.1、模拟量 数字量 1.1.2、(b) 1.1.3、(c) 1.1.4、(a)是数字量,(b)(c)(d)是模拟量
1.2 自测练习
1.2.1. 2 1.2.2. 比特 bit
1.2.3. 10
1.2.4. 1.2.5. 1.2.6.
二进制 十进制 (a)
1.2.7. (b)
1101 8 进制 (a)
1.2.22. 1.2.23. 1.2.24.
0,1,2,3,4,5,6,7 十六进制 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
1.2.25. (b)
1.3 自测练习 1.3.1. 122 1.3.2. 675.52 1.3.3. 011111110.01 1.3.4. 52 1.3.5. 1BD.A8 1.3.6. 1110101111.1110 1.3.7. 3855
2.4 自测练习 2.4.1. TTL, CMOS 2.4.2. Transisitor Transistor Logic 2.4.3. Complementary Metal Oxide Semicoductor
2.4.4. 2.4.5. 2.4.6. 2.4.7. 2.4.8. 2.4.9. 2.4.10. 2.4.11. 2.4.12. 2.4.13. 2.4.14. 2.4.15.
1001000 1101001 1100111 1101000 0100000 1010110 1101111 1101100 1110100 1100001
1100111 1100101
1.25 0100010 1011000 0100000 0111101 0100000 0110010 0110101 0101111 1011001
0100101 补
1.23
01110000 补 = 11210, 00011111 补 = 3110, 11011001 补 = -3910, 11001000 补
= -5610 1.24 1000011 1000001 1010101 1010100 1001001 1001111 1001110 0100001 0100000
1.4.13. XS3
1.4.14. XS3
1.4.15. 1000.1011
1.4.16. 100110000011
1.4.17. 52
1.4.18. 11011
1.4.19. 010111
1.4.20. (b)
1.4.21. 1.4.22. 1.4.23.
ASCII (a) ASCII
American Standard Code for Information Interchange 美国信息交换标准码
分别为 0.2 V 时,输出是高电平,绿灯亮。 2.25 三极管不会导通, LED 灯不会点亮
3.1 自测练习答案
1. 逻辑函数 2. 逻辑表达式、真值表、逻辑电路图、卡诺图和波形图 3.
表 3-1 F = ABC 真值表
0
0
0
0
0
1
0
0
1
0
1
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
0
1
1
1
1
2.12
2.13
(a) F = (x1 + x2 )x3 + x4 (b) F = (x1 + x2 )(x3 + x4 x6 ) + x5 (x6 + x3 x4 )
2.14 F1 = A(B+C),
F2=A+BC
A
B
C
F1
F2
0
0
0
(b) 8421BCD 码,4221BCD 码,5421BCD (a)
1.4.6. 011001111001.1000
