阴影部分面积(五年级)
求阴影部分面积 五年级 含答案

小学五年级数学求阴影部分面积习题1、下图中,已知阴影部分面积是30平方厘米,AB=15厘米,求图形空白部分的总面积。
2、下图,一个长方形和一个三角形重叠在一起,已知三角形ADE的面积比长方形ABCD 的面积小4平方厘米,求CE的长。
3、如图,求直角梯形中阴影部分的面积。
(单位:厘米)4、阴影部分面积是40平方米,求空白部分面积。
(单位:米)5、求下图阴影部分的面积。
(单位:厘米)6、下图,ABCD是直角梯形,已知AE=EF=FD,AB为6厘米,BC为10厘米,阴影部分面积为6平方厘米。
求直角梯形ABCD的面积。
7、下图是由一个三角形和一个梯形组成,已知三角形的面积是1平方分米,求这个图形的面积。
(单位:分米)8、如图,平行四边形面积240平方厘米,求阴影部分面积。
9、下图ABCD是梯形,它的面积是140平方厘米,已知AB=15厘米,DC=5厘米。
求阴影部分的面积。
10、求下面阴影部分的面积(单位:厘米)11、如图,求长方形中的梯形面积。
(单位:厘米)12、求下图阴影部分的面积(单位:厘米)13、求梯形的面积。
(单位:厘米)14、如图,已知梯形ABCD的面积为37.8平方厘米,BE长7厘米,EC长4厘米,求平行四边形ABED 的面积。
15、求空白部分面积。
(单位:厘米)16、如图,已知平行四边形ABCD中,阴影部分面积为72平方厘米,求三角形BCD的面积。
17、求梯形中阴影部分的面积。
(单位:cm)18、下图,ABCD是一个等腰梯形,ADFE是边长为4厘米的正方形,CF=2厘米,求阴影部分的面积。
19、下图ABCD是梯形,它的面积是200平方厘米,已知AB=20厘米,DC=5厘米,求阴影部分的面积。
(单位:厘米)20、在平行四边形ABCD中,CE上的高是6厘米,AD=8厘米,BE=11厘米,求三角形ABC 的面积。
21、在下图中,已知直角梯形ABCD的面积是60平方厘米,DC长6厘米,AB长24厘米,求:三角形AED的面积。
五年级下数学——求阴影部分面积 沪教版

五年级下数学——求阴影部分面积 沪教版
F
A
D
B
C
解析:长方形和平行四 边形等底等高,面积相 等,同时减去三角形 BCE的面积后,余下两 个梯形面积相等,即求 阴影面积就相当于求梯 形ABEC面积
五年级下数学——求阴影部分面积 沪教版
A
பைடு நூலகம்
DF
G
E
B
C
五年级下数学——求阴影部分面积 沪教版
思维发散
1、如图:两个相同的直角三角形叠在一起, 求阴影部分面积
五年级下数学——求阴影部分面积 沪教版
15
五年级下数学——求阴影部分面积 沪教版
• 例2:已知边长分别为3和4的正方形拼在一 起连接对角线,求对角线右上方阴影部分 面积。(单位:米)
解析:阴影部分面 积是不规则图形, 不能直接求出,可 以用两个正方形面 积减去空白部分的 面积。
五年级下数学——求阴影部分面积 沪教版
五年级下数学——求阴影部分面积 沪教版
8 3
4
五年级下数学——求阴影部分面积 沪教版
思维发散
2、两个底部为8的直角三角形重合,求 右边阴影比左边阴影的面积多多少?
五年级下数学——求阴影部分面积 沪教版
6 4
8
五年级下数学——求阴影部分面积 沪教版
挑战竞赛
如图:长方形ABCD中AB=4厘米, BC=6厘米,三角形EDF的面积比三角形 ABF的面积大6平方厘米,求ED的长。
我们可以说 数学是使人智慧的学问
例1:
一个梯形ABCD的上底AD为2厘米,组成矩 形
ABCE中的△CED面积为10平方厘米,DE为5厘
米,求梯形ABCD的面积
解析:由AD,DE 可知 A
最新五年级上学期数学阴影图形面积解析大全(重磅推出)

阴影图形面积应知应会基础图形的面积:【1】平行四边形的面积=底×高字母公式:S=ah÷2【2】三角形的面积=底×高字母公式:S=ah÷2【3】梯形的面积=(上底+下底)×高÷2字母公式:s梯形=(a+b)×h÷2a=s梯形×2÷h-bb=s梯形×2÷h-ah=s梯形×2÷(a+b)二、求阴影图形的面积的方法(一)分析思路:计算时需转化成已学的基本图形,通过加、减进行计算。
(二)具体方法:1、分割法:将组合图形分成几个基本图形,通过加,求几个基本图形的和。
2、填补法:将组合图形补成一个基本图形,通过大面积减小面积,求两个基本图形的差。
阴影图形的面积直接计算:根据公式计算阴影三角形的面积【1】分析:图中的阴影三角形和平行四边形等底等高,因此三角形的面积等于平行四边形面积的一半。
解:S阴影三角形=底×高÷2=14×10÷2 =70(平方厘米)根据图中已知图形面积和所求图形面积之间的关系计算:S 三角形形=S 大平行四边形面积÷2【2】如图,空白部分的面积是13.5平方厘米,求平行四边形的面积是多少平方分米? 解:S 空白部分=S 阴影三角形=平行四边形的底×高÷2 =S 平行四边形面积÷2所以S 平行四边形面积=S 空白部分×2=13.5×2=27(平方厘米) 先求出所需数据,再根据公式计算阴影三角形的面积【3】分析: 图中的阴影三角形和平行四边形等高,因此只需计算出三角形的底,再计算出三角形的面积。
解:14-10=6(厘米) S 阴影三角形=底×高÷2 =14×10÷2 =70(平方厘米)先求出所学数据,再计算梯形面积。
【4】寻找合适的条件,求出下面涂色部分的面积。
苏教版五年级下册数学重点求阴影部分面积专项和答案 (1)

解:将两个同样的图形拼在一起成为 圆减等腰直角三角形
[π ÷4- ×5×5]÷2
=( π- )÷2=3.5625平方厘米
解:面积为4个圆减去8个叶形,叶形面积为: π -1×1= π-1
所以阴影部分的面积为:4π -8( π-1)=8平方厘米
例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。如果圆周π率取3.1416,那么花瓣图形的的面积是多少平方厘米?
分析:连接角上四个小圆的圆心构成一个正方形,各个小圆被切去 个圆,
(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)
例8.求阴影部分的面积。(单位:厘米)
解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为 圆,
所以阴影部分面积为: π( )=3.14平方厘米
例9.求阴影部分的面积。(单位:厘米)
解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,
所以面积为:1×2=2平方厘米
例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
解:设小圆半径为r,4 =36, r=3,大圆半径为R, =2 =18,
将阴影部分通过转动移在一起构成半个圆环,
所以面积为:π( - )÷2=4.5π=14.13平方厘米
例21.图中四个圆的半径都是1厘米,求阴影部分的 面积。
例31.如图是一个正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,求阴影部分的面积。
解:连PD、PC转换为两个三角形和两个弓形,
两三角形面积为:△APD面积+△QPC面积= (5×10+5×5)=37.5
小学数学五年级上册有关阴影部分的面积难题好题压轴题汇总附答案解析
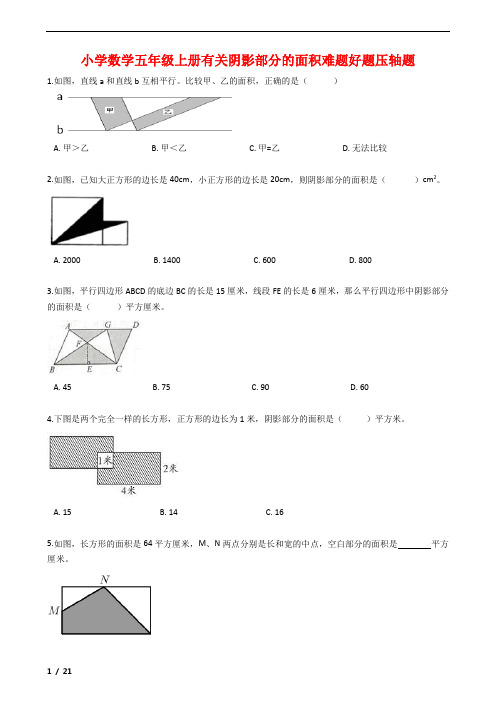
小学数学五年级上册有关阴影部分的面积难题好题压轴题1.如图,直线a和直线b互相平行。
比较甲、乙的面积,正确的是()A. 甲>乙B. 甲<乙C. 甲=乙D. 无法比较2.如图,已知大正方形的边长是40cm,小正方形的边长是20cm,则阴影部分的面积是()cm2。
A. 2000B. 1400C. 600D. 8003.如图,平行四边形ABCD的底边BC的长是15厘米,线段FE的长是6厘米,那么平行四边形中阴影部分的面积是()平方厘米。
A. 45B. 75C. 90D. 604.下图是两个完全一样的长方形,正方形的边长为1米,阴影部分的面积是()平方米。
A. 15B. 14C. 165.如图,长方形的面积是64平方厘米,M、N两点分别是长和宽的中点,空白部分的面积是平方厘米。
6.下图中每个小方格的面积是1cm2,则阴影部分的面积是 cm2。
7.一个梯形上底6厘米,下底12厘米,如果上底增加4厘米,面积就增加16平方厘米,原来梯形的面积是________平方厘米。
8.如图,三角形ABC的面积是24平方厘米,AD=DE=EC,F是BC的中点,FG=GC,阴影部分的面积是________.9.ABCD是直角梯形,AEFC是长方形,已知BC比AD长6厘米,CD=8厘米,梯形的面积是80平方厘米,阴影部分的面积是平方厘米。
10.一个直角梯形的上底长5分米,下底长8分米,两条腰分别是4分米和5分米,这个直角梯形面积是________平方分米。
11.如图,阴影部分周长的和是20厘米,大正方形的周长是________厘米,面积是________平方厘米。
12.把一个边长20m的正方形拉成平行四边形后,它的面积减少80m²,这个平行四边形的高是________m。
13.如图,四边形ABCD是一个梯形,由三个直角三角形拼成,它的面积是________cm2。
14.如图,在平行四边形中,甲的面积是36平方厘米,乙的面积是63平方厘米,则丙的面积是________平方厘米。
小学五年级阴影面积练习题

小学五年级阴影面积练习题在小学五年级的数学学习中,阴影面积是一个重要的知识点。
通过练习题的形式,可以帮助学生更好地理解和掌握阴影面积的计算方法。
本文将为小学五年级学生提供一系列阴影面积的练习题,以巩固他们的学习成果。
1. Sarah在花园的正中央建了一个方形的游泳池,边长为6米。
现在她想要用一块阴影布将游泳池遮起来。
请问这块阴影布的面积是多少平方米?解题思路:要计算阴影布的面积,需要知道游泳池的面积。
游泳池的面积可以通过边长的平方来计算。
所以游泳池的面积为6米 × 6米 = 36平方米。
阴影布的面积应该和游泳池的面积相等,所以阴影布的面积也是36平方米。
2. 请你用一个正方形的图形模型来表示一个面积为49平方米的长方形花坛。
解题思路:长方形花坛的面积为49平方米,可以用一个边长为7米的正方形来表示。
因为正方形的面积可以通过边长的平方来计算,所以这个正方形的面积为7米 × 7米 = 49平方米。
3. 小明家的后院有一个长方形的草坪,长为8米,宽为5米。
现在他想要在草坪上放上一个桌子,桌子的面积为12平方米。
请问这个桌子能否完全放在草坪上?解题思路:要判断桌子能否完全放在草坪上,需要比较桌子的面积和草坪的面积。
草坪的面积为长乘以宽,即8米 × 5米 = 40平方米。
由于桌子的面积为12平方米,小于草坪的面积,所以这个桌子能够完全放在草坪上。
4. 请你用一个长方形的图形模型来表示一个面积为30平方米的正方形花坛。
解题思路:面积为30平方米的正方形花坛,可以用一个边长为√30米的长方形来表示。
因为正方形的面积可以通过边长的平方来计算,所以这个边长为√30米的正方形的面积为(√30米) × (√30米) = 30平方米。
通过以上的练习题,希望能够帮助小学五年级的学生们更好地掌握阴影面积的计算方法。
在解题时,需要注意计算面积的公式,并且根据题目中给出的信息来进行计算。
五年级求阴影部分面积题

五年级数学求阴影部分面积习题1、下图中,已知阴影部分面积使30平方厘米,AB=15厘米,求图形空白部分的总面积。
2、?右图,一个长方形和一个三角形重叠在一起,已知三角形ADE的面积比长方形ABCD 的面积小4平方厘米,求CE的长。
3、?如图,求直角梯形中阴影部分的面积。
(单位:厘米)4、?阴影部分面积是40平方米,求空白部分面积。
(单位:米)5、求下图阴影部分的面积。
(单位:厘米)6、?右图,ABCD只直角梯形,已知AE=EF=FD,AB为6厘米,BC为10厘米,阴影部分面积为6平方厘米。
求直角梯形ABCD的面积。
7、?下图是由一个三角形和一个梯形组成,已知三角形的面积是1平方分米,求这个图形的面积。
(单位:分米)8、如图,平行四边形面积240平方厘米,求阴影部分面积。
9、下图ABCD是梯形,它的面积是140平方厘米,已知AB=15厘米,DC=5厘米。
求阴影部分的面积。
10、?求右面图形的面积(单位:厘米)11、如图,求长方形中的梯形面积。
(单位:厘米)12、求下图阴影部分的面积(单位:厘米)13、求梯形的面积。
(单位:厘米)14、如图,已知梯形ABCD的面积为37.8平方厘米,BE长7厘米,EC长4厘米,求平行四边形ABED的面积。
15、求空白部分面积。
(单位:厘米)16、如图,已知平行四边形ABCD中,阴影部分面积为72平方厘米,求三角形BCD的面积。
17、求梯形中阴影部分的面积。
(单位:cm)18、下图,ABCD是一个等腰梯形,ADFE是边长为4厘米的正方形,CF =2厘米,求阴影部分的面积。
19、下图ABCD是梯形,它的面积是200平方厘米,已知AB=20厘米,DC =5厘米,求阴影部分的面积。
(单位:厘米)20、在平行四边形ABCD中,CE上的高是6厘米,AD=8厘米,BE=11厘米,求三角形ABC 的面积。
21、在下图中,已知直角梯形ABCD的面积是60平方厘米,DC长6厘米,AB长24厘米,求:三角形AED的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
*创作编号:BG7531400019813488897SX*
创作者: 别如克*
阴影部分面积计算
一、直接和间接方法求阴影部分面积
例1:已知右面的两个正方形边长分别为6分米和4分米,求图中阴影部分的面积。
1、如图,ABDC是一个长12厘米,宽5厘米的长方形,已知DE长3厘米,求阴影部
分三角形ACE的面积。
二、等量代换法求阴影部分的面积
例2:右图是两个相同的直角三角形叠在一起,求阴影部分的面积。
(单位:厘米)
1、下图中两个完全一样的三角形重叠在一起,求阴影部分的面积。(单位:厘米)
例3:在右图中,平行四边形ABCD的边BC长10厘米,直角三角形ECB的直角边EC
长8厘
米。已知阴影部分的总面积比三角形EFG的面积大10平方厘米,求平行四边
形ABCD的面积。
1、在右图中,三角形EDF的面积比三角形ABE的面积大75平方厘米,已知正方形ABCD
的
边长为15厘米,(1)求三角形ACF的面积(2)DF的长是多少厘米?
四、平移法求面积
例4:右图是一块长方形公园绿地,绿地长24米,宽16米,中间有一条宽为2米的
道路,
求草地(阴影部分)的面积。
1、 下图的长方形是一块草坪,中间有两条宽1米的走道,求植草的面积。
五、等高求面积
例5:求下图中阴影部分的面积。
六、按一定的比求面积
把下图三角形的底边BC四等分,在下面括号里填上“>”、“<”或“=”。
甲的面积( )乙的面积。
例6:(选讲)两条对角线把梯形ABCD分割成四个三角形。已知两个三角形的面积(如
图所示),求另两个三角形的面积各是多少?(单位:平方厘米)
1.如下图,图中BO=2DO,阴影部分的面积是4平方厘米,求梯形ABCD的面积是多少
平方
厘米?
作业:
1、已知正方形甲的边长是8厘米,正方形乙的面积是36平方厘米,那么
图中阴影部分的面积是多少?
创作编号:BG7531400019813488897SX
创作者: 别如克*
2、图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积。
3、求下图长方形ABCD的面积(单位:厘米)。
4、图中两个正方形的边长分别是10厘米和6厘米,求阴影部分的面积。
5、求图中阴影部分的面积。(单位:厘米)
6、如图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积。
创作编号:BG7531400019813488897SX
创作者: 别如克*
