九年级数学 第一章检测题
北师大版九年级上册数学第一章检测试题(附答案)
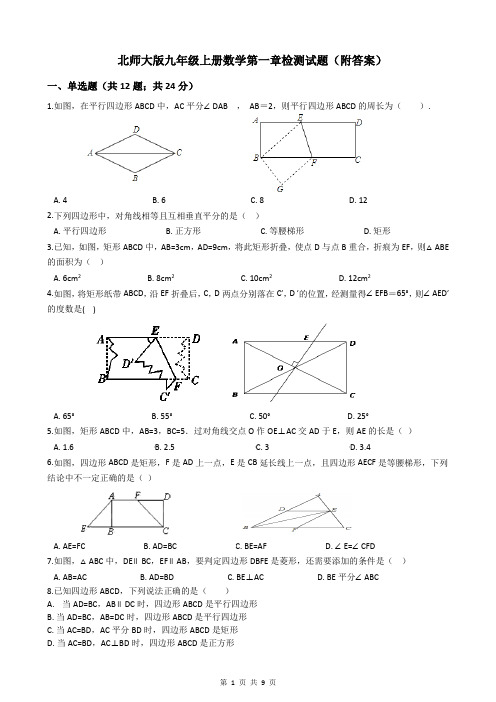
北师大版九年级上册数学第一章检测试题(附答案)一、单选题(共12题;共24分)1.如图,在平行四边形ABCD中,AC平分∠DAB ,AB=2,则平行四边形ABCD的周长为().A. 4B. 6C. 8D. 122.下列四边形中,对角线相等且互相垂直平分的是()A. 平行四边形B. 正方形C. 等腰梯形D. 矩形3.已知,如图,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE 的面积为()A. 6cm2B. 8cm2C. 10cm2D. 12cm24.如图,将矩形纸带ABCD,沿EF折叠后,C,D两点分别落在C′,D ′的位置,经测量得∠EFB=65°,则∠AED′的度数是( )A. 65°B. 55°C. 50°D. 25°5.如图,矩形ABCD中,AB=3,BC=5.过对角线交点O作OE⊥AC交AD于E,则AE的长是()A. 1.6B. 2.5C. 3D. 3.46.如图,四边形ABCD是矩形,F是AD上一点,E是CB延长线上一点,且四边形AECF是等腰梯形,下列结论中不一定正确的是()A. AE=FCB. AD=BCC. BE=AFD. ∠E=∠CFD7.如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是()A. AB=ACB. AD=BDC. BE⊥ACD. BE平分∠ABC8.已知四边形ABCD,下列说法正确的是()A.当AD=BC,AB∥DC时,四边形ABCD是平行四边形B. 当AD=BC,AB=DC时,四边形ABCD是平行四边形C. 当AC=BD,AC平分BD时,四边形ABCD是矩形D. 当AC=BD,AC⊥BD时,四边形ABCD是正方形9.已知四边形ABCD是平行四边形,下列结论中不正确的是()A. 当AB=BC时,它是菱形B. 当AC=BD时,它是正方形C. 当AC⊥BD时,它是菱形D. 当∠ABC=900时,它是矩形10.如图,正方形CEFH的边长为m,点D在射线CH上移动,以CD为边作正方形CDAB,连接AE、AH、HE,在D点移动的过程中,三角形AHE的面积()A. 无法确定B.C.D.11.如图,在△ABC中,AD平分∠BAC ,按如下步骤作图:第一步,分别以点A、D为圆心,以大于AD的长为半径在AD两侧作弧,交于两点M、N;第二步,连接MN分别交AB、AC于点E、F;第三步,连接DE、DF .若BD=6,AF=4,CD=3,则BE的长是().A. 2B. 4C. 6D. 812.在正方形ABCD中,点E为BC边的中点,点与点B关于AE对称,与AE交于点F,连接,,FC。
初三数学第一章检测试题

1 / 4初三数学第一章检测试题(满分100分,测试时间为60分钟)温馨提示:亲爱的同学们,经过你们的勤奋自学、刻苦钻研,这个暑假里应该有了丰硕的收获。
请仔细审题,细心答题,相信你一定会有出色的表现!祝你有好成绩! 一、选择题(共8题,每题3分,合计24分) 1、若等腰三角形的底角为72°,则顶角为( )A .108°B .72°C .54°D .36°2、等腰三角形的两条边长分别为3cm 和6cm ,则它的周长为( ) A .9cmB .12cmC .15cmD .12cm 或15cm3、如图,在△ABC 中,BC =8cm ,AB 的垂直平分线交AB 于点D ,交边AC 于点E ,△BCE 的周长等于18cm ,则AC 的长等于( )A .12cmB .10cmC . 8cmD . 6cm4、下列平面图形中,既是中心对称图形,又是轴对称图形的是( )A .等边三角形B .平行四边形C .圆D .等腰梯形 5、如图,在平面直角坐标系中,□ABCD 的顶点A 、B 、D 的坐标分别是 (0,0),(5,0),(2,3),则顶点C 的坐标是( )A .(3,7)B .(5,3)C .(7,3)D .(8,2) 6、已知菱形的两条对角线长分别为10、24,则它的周长等于( )A .34B .240C .52D .120 7、正方形具有而菱形不具有的性质是( )A .对角线互相平分;B .对角线相等;C .对角线互相垂直;D .对角线平分对角。
8、顺次连结等腰梯形ABCD 各边的中点,所得的四边形一定是( )A .等腰梯形B .矩形C .菱形D .平行四边形第3题图ABCDECBA第5题图2 / 4二、填空题(共10题,每题4分,合计40分)9、如图,是由边长为1m 的正方形地砖铺设的地面示意图,小明沿图中所示的折线从A →B →C 所走的路程为_______m .(结果保留根号)10、已知□ABCD 中,∠A 比∠B 小20°,那么∠C 的度数是________.11、如图,点E 、F 分别是□ABCD 对角线BD 上的两点,要使△ADE ≌△CBF ,需添加一个条件 (只需添加一个即可) 12、用两个全等的不等边三角形最多..能拼成__________个不同的平行四边形.13、写出等腰梯形的两个性质 , 。
苏教版数学九年级上,第一章 测试题

九年级第一章,测试题看一看,选一选(每小题6分,共30分)1.在△ABC中,∠A=40°,∠B=70°,则它的形状是( )A.直角三角形B等腰三角形 c.等腰直角三角形 D.等边三角形2.(2011 ·济宁)如果一个等腰三角形的两边长分别是5 cm和6 cm,那么此三角形的周长是( )A. 15cmB. 16 cmC.17 cmD. 16 cm或17 cm3.(2011.铜仁)下列关于等腰三角形的性质叙述错误的是()A.等腰三角形两底角相等B.等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合C.等腰三角形的对称轴是底边上的高D.等腰三角形是轴对称图形4.(2010.南通)在平面直角坐标系xOy中,已知点P(2,2),点Q在y轴上,△PQO是等腰三角形,则满足条件的点Q共有()A.5个 B.4个 C.3个 D.2个5..(2011,梧州)如图1-1-1,点B、C、E在同一条直线上,△ABC与△CDE都是等边三角形,则下列结论不一定成立的是()A.△ACE≅△BCDB.△BGC≅△AFCC.△DCG≅△ECFD.△ADB≅△CEA二、想一想,填一填(每小题6分,共30分)6. 若等腰三角形的顶角等于40°,则一个底角的度数为;若等腰三角形的一个底角等于40°,则它的顶角度数为.7.已知等腰△ABC的周长为20,若设腰长为x,'则x的取值范围是8.(2011.河南)如图1-1-2,在△ABC.中,AB=AC,CD平分∠ACB,∠A=36°,则∠BDC的度数为9.如果等腰三角形的周长是27 cm,一腰上的中线把三角形分成两个三角形,其周长之差是3 cm,则这个等腰三角形的底边长为。
10.如图1-1-3,在△ABC中,∠BCA=90°,BD=BC,AE=AC,则∠ECD的度数是三、试一试,答一答(每小题10分,共40分)11.如图1-1-4,AB=AC,AD=AE.求证:BD=CE.12.如图1-1-5,A、B是4×5网格中的格点,网格中的每个小正方形的边长为1,请在图中清晰标出使以A、B、C为顶点的三角形是等腰三角形的所有格点C的位置.13.已知:如图1-l-6,在△ABC中,∠BAC=90°,AB=AC,AD交BC于E,AD=AB,∠CAD-.30°,m 求∠BCD、∠DBC的度数。
北师大版九年级数学下册第一章测试题(附答案)

北师大版九年级数学下册第一章测试题(附答案)姓名:__________ 班级:__________考号:__________一、单选题(共12题;共24分)1.已知在Rt△ABC中,∠C=90°,BC=5,那么AB的长为( )A. 5sin AB. 5cos AC.D.2.在Rt△ABC中,∠C=90°,a=3,b=4,则tanB的值是()A. B. C. D.3.正方形网格中,如图放置,则的值为()A. B. C. D. 24.如图,在直角△ABC中,∠C=90°,BC=1,AC=,下列判断正确的是()A. ∠A=90°B. ∠A=45°C. cotA=D. tanA=5.在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是()A. B. 3 C. D.6.计算sin60°+cos45°的值等于()A. B. C. D.7.先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为()A. 5cosαB.C. 5sinαD.8.如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30,看这栋高楼底部C的俯角为60,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为()A. 40mB. 80mC. 120mD. 160m9.某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,那么适合该地下车库的车辆限高标志牌为()(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)A. B. C. D.10.如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端25米的B处,测得树顶A的仰角∠ABO 为,则树OA的高度为()A. 米B. 25 米C. 25 米D. 25 米11.已知△ABC中,∠C=90°,tanA=,D是AC上一点,∠CBD=∠A,则sin∠ABD=()A. B. C. D.12.如图,在直角△BAD中,延长斜边BD到点C,使DC= BD,连接AC,若tanB= ,则tan∠CAD的值()A. B. C. D.二、填空题(共8题;共16分)13.观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB 约是45m,根据以上观测数据可求观光塔的高CD是________ m.14.tan30°=________.15.如图,为测量旗杆AB的高度,在与B距离为8米的C处测得旗杆顶端A的仰角为56°,那么旗杆的高度约是________米(结果保留整数).(参考数据:sin56°≈0.829,cos56°≈0.559,tan56°≈1.483)16.计算tan1°•tan2°•tan3°•…•tan88°•tan89°=________.17.如图,在△ABC中,∠C=90°,AC=2,BC=1,则tanA的值是________.18.用科学计算器计算:8+sin56°≈________ .(精确到0.01)19.某校数学兴趣小组要测量西山植物园蒲宁之珠的高度.如图,他们在点A处测得蒲宁之珠最高点C的仰角为45°,再往蒲宁之珠方向前进至点B处测得最高点C的仰角为56°,AB=62m,根据这个兴趣小组测得的数据,则蒲宁之珠的高度CD约为 ________m.(sin56°≈0.83,tan56°≈1.49,结果保留整数)20.在△ABC中,sinA= ,AB=8,BC=6,则AC=________.三、解答题(共4题;共20分)21.如图所示,在△ABC中,AB=1,AC= ,sin B= ,求BC的长.22.如图,为了测量山顶铁塔AE的高,小明在27m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C 测得塔顶A的仰角36°52′.已知山高BE为56m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)23.“兰州中山桥“位于兰州滨河路中段白塔山下、金城关前,是黄河上第一座真正意义上的桥梁,有“天下黄河第一桥“之美誉.它像一部史诗,记载着兰州古往今来历史的变迁.桥上飞架了5座等高的弧形钢架拱桥.小芸和小刚分别在桥面上的A,B两处,准备测量其中一座弧形钢架拱梁顶部C处到桥面的距离AB=20m,小芸在A处测得∠CAB=36°,小刚在B处测得∠CBA=43°,求弧形钢架拱梁顶部C处到桥面的距离.(结果精确到0.1m)(参考数据sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin43°≈0.68,cos43°≈0.73,tan43°≈0.93)24.如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置测角仪AB,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果精确到0.1米,参考数据:≈1.414,≈1.732).四、综合题(共4题;共40分)25.重庆大坪时代天街已成为人们周末休闲娱乐的重要场所,时代天街从一楼到二楼有一自动扶梯(如图1),图2是侧面示意图.已知自动扶梯AC的坡度为i=1:2.4,AC=13m,BE是二楼楼顶,EF∥MN,B是EF上处在自动扶梯顶端C正上方的一点,且BC⊥EF,在自动扶梯底端A处测得B点仰角为42°.(sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)(1)求二楼的层高BC约为多少米;(2)为了吸引顾客,开发商想在P处放置一个高10m的《疯狂动物城》的装饰雕像,并要求雕像最高点与二楼顶层要留出2m距离好放置灯具,请问这个雕像能放得下吗?如果不能,请说明理由.26.共享单车被誉为“新四大发明”之一,如图1所示是某公司2017年向信阳市场提供一种共享自行车的实物图,车架档AC与CD的长分别为45cm,60cm,AC⊥CD,座杆CE的长为20cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2.(1)求车架档AD的长;(2)求车座点E到车架档AB的距离.(结果精确到1cm,参考数据:sin75°=0.9659,cos75°=0.2588,tan75°=3.7321)27.如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B 的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.(1)求斜坡CD的高度DE;(2)求大楼AB的高度(结果保留根号)28.如图1是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如图2所示的几何图形,若显示屏所在面的侧边AO与键盘所在面的侧边BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,当PD⊥AO时,称点P为“最佳视角点”,作PC⊥BC,垂足C在OB的延长线上,且BC=12cm.(1)当PA=45cm时,求PC的长;(2)若∠AOC=120°时,“最佳视角点”P在直线PC上的位置会发生什么变化?此时PC的长是多少?请通过计算说明.(结果精确到0.1cm,可用科学计算器,参考数据:≈1.414,≈1.732)答案一、单选题1. C2. A3.A4.D5.D6.B7. B8.D9.A 10.C 11. A 12.D二、填空题13.135 14.15.12 16.1 17.18.9.44 19.189 20.三、解答题21.解:过点A作AD⊥BC于点D,∵AB=1,sin B= ,∴AD=AB·sinB=1× =,DB= = = ,CD= = = .∴BC=CD+BD= + = .22.解:如图,过点C作CF⊥AB于点F.设塔高AE=x,由题意得,EF=BE﹣CD=56﹣27=29m,AF=AE+EF=(x+29)m,在Rt△AFC中,∠ACF=36°52′,AF=(x+29)m,则CF= ≈ = x+ ,在Rt△ABD中,∠ADB=45°,AB=x+56,则BD=AB=x+56,∵CF=BD,∴x+56= x+ ,解得:x=52,答:该铁塔的高AE为52米.23.解:过点C作CD⊥AB于D.设CD=x,在Rt△ADC中,tan36°= ,∴AD= ,在Rt△BCD中,tan∠B= ,BD= ,∴+ =20,解得x=8.179≈8.2m.答:拱梁顶部C处到桥面的距离8.2m.24.解:过点A作AH⊥CD,垂足为H,由题意可知四边形ABDH为矩形,∠CAH=30°,∴AB=DH=1.5,BD=AH=6,在Rt△ACH中,tan∠CAH= ,∴CH=AH•tan∠CAH,∴CH=AH•tan∠CAH=6tan30°=6× =2 ,∵DH=1.5,∴CD=2 +1.5,在Rt△CDE中,∵∠CED=60°,sin∠CED= ,∴CE= =4+ ≈5.7(米),答:拉线CE的长约为5.7米四、综合题25.(1)解:如图所示:延长BC交MN于H ∵BC⊥EF,EF∥MN,∴BH⊥MN,∵i=1:2.4=5:12=CH:AH,∴设CH=5k,则AH=12k在Rt△ACH中,由勾股定理AC= =13k,∵AC=13m,∴k=1,∴CH=5m,AH=12m,设BC=x,在Rt△ACH中,tan∠BAH= ,∴tan42°= ,x≈5.8 m,答:二楼层高约为5.8 m;(2)解:由题得,大厅层高为BH=BC+CH=5.8+5=10.8(m),而10+2=12m>10.8m,∴雕像放不下.26.(1)解:∵AC⊥CD,AC=45cm,CD=60cm,∴AD= (cm),即车架档AD的长是75cm(2)解:作EF⊥AB于点F,如图所示,∵AC=45cm,EC=20cm,∠EAB=75°,∴EF=AE•sin75°=(45+20)×0.9659≈63cm,即车座点E到车架档AB的距离是63cm27.(1)解:在Rt△DCE中,DC=4米,∠DCE=30°,∠DEC=90°,∴DE= DC=2米(2)解:过D作DF⊥AB,交AB于点F,∵∠BFD=90°,∠BDF=45°,∴∠BFD=45°,即△BFD为等腰直角三角形,设BF=DF=x米,∵四边形DEAF为矩形,∴AF=DE=2米,即AB=(x+2)米,在Rt△ABC中,∠ABC=30°,∴BC= = = = 米,BD= BF= x米,DC=4米,∵∠DCE=30°,∠ACB=60°,∴∠DCB=90°,在Rt△BCD中,根据勾股定理得:2x2= +16,解得:x=4+4 ,则AB=(6+4 )米.28.(1)解:当PA=45cm时,连结PO.∵D为AO的中点,PD⊥AO,∴PO=PA=45cm.∵BO=24cm,BC=12cm,∠C=90°,∴OC=OB+BC=36cm,PC= =27cm(2)解:当∠AOC=120°,过D作DE⊥OC交BO延长线于E,过D作DF⊥PC于F,则四边形DECF是矩形.在Rt△DOE中,∵∠DOE=60°,DO= AO=12,∴DE=DO•sin60°=6 ,EO= DO=6,∴FC=DE=6 ,DF=EC=EO+OB+BC=6+24+12=42.在Rt△PDF 中,∵∠PDF=30°,∴PF=DF•tan30°=42× =14 ,∴PC=PF+FC=14+6 =20 ≈34.68>27,∴点P在直线PC上的位置上升了。
数学初三第一章练习题

数学初三第一章练习题数学是一门重要的学科,也是学生们学习中常常遇到的科目之一。
在初三的数学课程中,第一章通常是关于集合的学习。
为了帮助同学们更好地掌握这一知识点,以下是一些初三数学第一章练习题,供同学们参考练习。
1. 请将下列各组数按照要求写出:a) 自然数小于10的集合;b) 偶数的集合;c) 能被3整除的自然数的集合;2. 下列命题中哪些是正确的?a) 自然数是整数的子集;b) 整数是有理数的子集;c) 正数是整数的子集;3. 将下列集合表示成列举法:a) 集合A包含在集合B中;b) 集合C与集合D相等;c) 集合E是集合F的真子集;4. 给定集合A = {4, 5, 6, 7},B = {6, 7, 8, 9},求下列集合运算的结果:a) A ∪ B;b) A ∩ B;c) A - B;d) B - A;5. 已知集合A = {1, 2, 3, 4, 5},B = {3, 4, 5, 6, 7},C = {5, 6, 7, 8, 9},求下列命题的真假:a) 3 ∈ A;b) A ⊂ B;c) B ∩ C ≠ ∅;d) A - (B ∪ C) = ∅;6. 有一个集合U,U中有10个元素,集合A包含其中的4个元素,集合B包含其中的3个元素,集合C包含其中的5个元素,问:a) A ∪ B ∪ C 中包含多少个元素?b) A ∩ B ∩ C 中包含多少个元素?c) (A ∪ B) ∩ C 中包含多少个元素?7. 用绘图的方法解下列问题:a) 在平面直角坐标系中,将集合A = {(x, y) | x + y = 5}表示出来;b) 将集合B = {(x, y) | x - y ≤ 2}表示出来;以上是一些关于初三数学第一章集合的练习题。
同学们可以根据自己的情况选择适合的时间和方式进行练习,提高自己对集合相关概念的理解和运用能力。
希望同学们通过这些练习题,能够更好地掌握初三数学第一章的知识点,为后续学习打下良好的基础。
数学九年级上册第一章检测题(BS)

数学九年级上册第一章检测题(BS)(时间:120分钟 满分:120分)分数:________一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)1.(坪山区期末)菱形、矩形、正方形都具有的性质是 ( D )A .四条边相等,四个角相等B .对角线相等C .对角线互相垂直D .对角线互相平分2.(吉安县期末)菱形的一个内角是60°,边长是5 cm ,则这个菱形的较短的对角线长是 ( B ) A.52cm B .5 cm C .5 3 cm D .10 3 cm3.如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,∠ACB =30°,则∠AOB 的大小为 ( B )A .30°B .60°C .90°D .120°4.(南昌期末)用一长一短的两根木棒,在它们的中心处固定一个小螺钉,做成一个可转动的叉形架,四个顶点用橡皮筋连成一个四边形,转动木条,当这个四边形变成菱形时,两根木棒所成角的度数是( A) A.90° B.60° C.45° D.30°5.(莲湖区期中)如图,正方形ABCD中,在BA延长线上取一点,使BE=BD,连接DE,则∠EDA的度数为 ( D) A.10° B.15°C.30° D.22.5°6.★如图,矩形ABCD中,AD=2AB,AF平分∠BAD,DF⊥AF于点F,延长BF交CD于点H.若AB=6,则CH= ( D) A.6- 2 B.12-4 3C.3 2 D.12-6 2二、填空题(本大题共6小题,每小题3分,共18分)7.(天心区期末)著名画家达芬奇不仅画艺超群,同时还是一个数学家、发明家.他曾经设计过一种圆规.如图所示,有两个互相垂直的滑槽(滑槽宽度忽略不计),一根没有弹性的木棒的两端A,B能在滑槽内自由滑动,将笔插入位于木棒中点P处的小孔中,随着木棒的滑动就可以画出一个圆来,若AB=10 cm,则画出的圆的半径为__5__cm__.8.(百色期末)已知正方形ABCD的周长是20 cm,则这个正方形的面积是__25__cm2.9.(明水县期中)如图,四边形ABCD是矩形,则只需补充条件__AB=AD__(用字母表示,只添加一个条件)就可以判定四边形ABCD是正方形.10.如图,将两条等宽的纸条重叠在一起,在四边形ABCD中,若AB=8,∠ABC=60°,则AC=__8__.11.(东平县期末)如图,过矩形ABCD的四个顶点作对角线AC,BD的平行线,分别相交于E,F,G,H四点,则四边形EFGH为__菱形__.12.★如图是一张矩形纸片ABCD,已知AB=8,AD=7,E为AB上的一点,AE=5,点P在矩形ABCD的一边上,要使△AEP是等腰三角形,则△AEP的底边长为__5或52或45__.三、(本大题共5小题,每小题6分,共30分)13.如图,在菱形ABCD中,点E,F分别为边CD,AD的中点,连接AE,CF.求证:△ADE≌△CDF.证明:∵四边形ABCD 是菱形,∴AD =DC ,又∵E ,F 为CD ,AD 的中点,∴DF =12AD ,DE =12DC , ∴DF =DE.又∵∠ADE =∠CDF ,∴△ADE ≌△CDF(SAS).14.(丹东期末)如图,AD 是△ABC 的中线,AE ∥BC ,且AE =12BC ,连接DE ,CE.(1)求证:AB =DE ;(2)当△ABC 满足什么条件时,四边形ADCE 是矩形?并说明理由.(1)证明:∵AD 是△ABC 的中线,∴BD =CD =12BC , ∵AE =12BC ,∴AE =BD , ∵AE ∥BC ,∴四边形ABDE 是平行四边形,∴AB =DE.(2)解:当△ABC 满足AB =AC 时,四边形ADCE 是矩形.理由:∵AE =12BC ,BD =CD =12BC ,∴AE =CD , ∵AE ∥BC ,∴四边形ADCE 是平行四边形,∵AB =DE ,∴当AB =AC 时,AC =DE ,∴四边形ADCE 是矩形.15.如图,在▱ABCD中,点E,F在直线AC上(点E在F点左侧),BE ∥DF.(1)求证:四边形BEDF是平行四边形;证明:连接BD,交AC于点O,∵四边形ABCD是平行四边形,∴OB=OD.由BE∥DF得∠BEO=∠DFO.又∵∠EOB=∠FOD,∴△BEO≌△DFO,∴BE=DF,又∵BE∥DF,∴四边形BEDF是平行四边形.(2)若AB⊥AC,AB=4,BC=213,当四边形BEDF为矩形时,求线段AE的长.解:∵AB⊥AC,AB=4,BC=213,∴AC=6,∴AO=3,∴在Rt△BAO中,BO=5.∵四边形BEDF是矩形,∴OE=OB=5.∴点E在OA的延长线上,∴AE=2.16.(东湖区期末)请用无刻度的直尺作图:(1)在图①中,已知点E是正方形ABCD边AB的中点,分别画出BC,CD,DA的中点F,G,H;(2)图②是正方形ABCD,E是对角线BD上任意一点(BE>DE),以AE 为边画一个菱形.解:(1)如图①,点F,G,H即为所求.(2)如图②,四边形AECF即为所画的菱形.延长AE交CD于点N,连接AC交BD于点O,连接NO并延长交AB于点M,连接CM交BD于点F,四边形AECF即为所求.17.如图,以正方形ABCD的对角线AC为一边,延长AB到E,使AE =AC,以AE为一边作菱形AEFC,若菱形的面积为92,求正方形的边长.解:设正方形的边长为x.∵AC为正方形ABCD的对角线,∴AC=2x,∴AE=2x,CB=x,∴S菱形AEFC=AE·CB=2x·x=2x2=92,解得x=±3,依题意舍去x=-3,即正方形的边长为3.四、(本大题共3小题,每小题8分,共24分)18.(河西区期中)如图,菱形花坛ABCD 的一边长AB 为20 m , ∠ABC =60°,沿着该菱形的对角线修建两条小路AC 和BD.(1)求AC 和BD 的长;(2)求菱形花坛ABCD 的面积.解:(1)∵四边形ABCD 是菱形,∴AC ⊥BD ,AO =CO ,BO =DO ,∠ABD =12∠ABC =30°, ∴AO =12AB =10 m ,BO =AB 2-AO 2=10 3 m , ∴AC =20 m ,BD =20 3 m.(2)菱形花坛ABCD 的面积=12×20×203=2003(m 2).19.已知:如图,在菱形ABCD 中,点E ,O ,F 分别为AB ,AC ,AD 的中点,连接CE ,CF ,OE ,OF.(1)求证:△BCE ≌△DCF ;(2)当AB 与BC 满足什么关系时,四边形AEOF 是正方形?请说明理由.(1)证明:∵四边形ABCD 是菱形,∴AB =BC =CD =AD ,∠B =∠D.∵点E ,F 分别为AB ,AD 的中点,∴BE =DF ,∴△BCE ≌△DCF(SAS).(2)解:当AB ⊥BC 时,四边形AEOF 是正方形.理由:由(1)得AE =OE =OF =AF ,∴四边形AEOF 是菱形.∵AB ⊥BC ,OE ∥BC ,∴OE ⊥AB ,∴∠AEO =90°,∴四边形AEOF 是正方形.20.(金水区月考)如图,在平面直角坐标系中,正方形ABOC 的两直角边分别在坐标轴的正半轴上,分别过OB ,OC 的中点D ,E 作AE ,AD 的平行线,相交于点F ,已知OB =8.(1)求证:四边形AEFD 为菱形;(2)求四边形AEFD 的面积.(1)证明:∵DF ∥AE ,EF ∥AD ,∴四边形AEFD 是平行四边形.∵四边形ABOC 是正方形,∴OB =OC =AB =AC ,∠ACE =∠ABD =90°.∵点D ,E 是OB ,OC 的中点,∴CE =BD ,在△ACE 和△ABD 中,⎩⎪⎨⎪⎧AC =AB ,∠ACE =∠ABD =90°,CE =BD ,∴△ACE ≌△ABD(SAS),∴AE =AD ,∴四边形AEFD 是菱形.(2)解:连接DE.∵S△ABD=12AB·BD=12×8×4=16,S△ODE=12OD·OE=12×4×4=8,∴S△AED=S正方形ABOC-2S△ABD-S△ODE=64-2×16-8=24,∴S菱形AEFD=2S△AED=48.五、(本大题共2小题,每小题9分,共18分)21.(大余县期末)如图,在矩形ABCD中,AB=8,BC=16,点P从点D出发向点A运动,运动到点A停止,同时,点Q从点B出发向点C 运动,运动到点C停止,点P,Q的速度都是每秒1个单位,连接PQ,AQ,CP.设点P,Q运动的时间为t s.(1)当t为何值时,四边形ABQP是矩形;解:∵在矩形ABCD中,AB=8,BC=16,∴BC=AD=16,AB=CD=8,由已知,得BQ=DP=t,AP=CQ=16-t,在矩形ABCD中,∠B=90°,AD∥BC,当BQ=AP时,四边形ABQP为矩形,∴t=16-t,解得t=8,∴当t为8时,四边形ABQP是矩形.(2)当t=6时,判断四边形AQCP的形状,并说明理由.解:四边形AQCP为菱形.理由:∵t=6,∴BQ=6,DP=6,∴CQ=16-6=10,AP=16-6=10,∴AP=CQ,AP∥CQ,∴四边形AQCP为平行四边形,在Rt△ABQ中,AQ=AB2+BQ2=82+62=10,∴AQ=CQ,∴平行四边形AQCP为菱形,即当t=6时,四边形AQCP为菱形.22.(德州期末)以四边形ABCD的边AB,AD为边分别向外侧作等边△ABF和△ADE,连接EB,FD,交点为G.(1)当四边形ABCD为正方形时(如图①),EB和FD的数量关系是__EB=FD__;(2)当四边形ABCD为矩形时(如图②),EB和FD具有怎样的数量关系?请加以证明;(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图③中求出∠EGD的度数.解:(2)EB=FD.证明:∵△AFB为等边三角形,∴AF=AB,∠FAB=60°.∵△ADE为等边三角形,∴AD=AE,∠EAD=60°,∴∠FAB+∠BAD=∠EAD+∠BAD,即∠FAD=∠BAE,∴△FAD≌△BAE,∴EB=FD.(3)不变.同(2)易证△FAD≌△BAE,∴∠AEB=∠ADF,设∠AEB=x°,则∠ADF=x°,∴∠BED=(60-x)°,∠EDF=(60+x)°,∴∠EGD=180°-∠BED-∠EDF=180°-(60-x)°-(60+x)°=60°.六、(本大题共12分)23.(吉安市期末)阅读理解:如图①,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示的形状,再展开得到图③,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB′,FD′相交于点O.(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是__正方形____;(2)当图③中的∠BCD =120°时,∠AEB ′=__80__°;(3)当图②中的四边形AECF 为菱形时,对应图③中的“完美筝形”有多少个(包含四边形ABCD).请说明理由.解:(3)当图②中的四边形AECF 为菱形时,对应图③中的“完美筝形”有5个.理由:根据题意,得BE =B ′E ,BC =B ′C ,∠B =∠CB ′E =90°, CD =CD ′,FD =FD ′,∠D =∠CD ′F =90°,∴四边形EBCB ′、四边形FDCD ′是“完美筝形”;∵四边形ABCD 是“完美筝形”,∴AB =AD ,CB =CD ,∠B =∠D =90°,∴CD ′=CB ′,∠CD ′O =∠CB ′O =90°,∵四边形AECF 为菱形,∴AE =AF ,CE =CF ,AE ∥CF ,AF ∥CE ,∴D ′E =B ′F ,∠AEB ′=∠CB ′E =90°,∠AFD ′=∠CD ′F =90°,在△OED ′和△OFB ′中,⎩⎪⎨⎪⎧∠OD ′E =∠OB ′F ,∠EOD ′=∠FOB ′,D ′E =B ′F ,∴△OED′≌△OFB′(AAS),∴OD′=OB′,OE=OF,∴四边形CD′OB′、四边形AEOF是“完美筝形”,∵包含四边形ABCD,∴对应图③中的“完美筝形”有5个.。
北师大版初三数学9年级下册 第1章(直角三角形的边角关系)章节检测(含答案)
第一章 直角三角形的边角 章节检测一、选择题(共7小题;共28分)1. 把 Rt △ABC 的三边都扩大 10 倍,关于锐角 A 的正弦值,甲同学认为扩大 10 倍,乙同学认为不变,丙同学认为缩小到原来的 110.你认为正确的应是 ( )A. 甲B. 乙C. 丙D. 都不正确2. 在 Rt △ABC 中,∠C =90∘,sin A =513,则 tan B 的值为 ( )A. 1213 B. 512 C. 1312 D. 1253. 计算 2cos30∘−tan45∘−(1−tan60∘)2 的结果是 ( )A. 23−2B. 0C. 23D. 24. 如图所示,在 Rt △ABC 中,∠BAC =90∘,AD ⊥BC 于点 D .若 BD:CD =3:2,则 tan B 的值为( )A. 32 B. 23C. 66D. 635. 如图所示,在下列网格中,小正方形的边长均为 1,点 A ,B ,O 都在格点上,则 ∠AOB 的余弦值是 ( )A. 31010B. 12C. 13D. 10106. 直角三角形纸片的两直角边长分别为 6,8,现将 △ABC 按如图所示方式折叠,使点 A 与点 B 重合,折痕为 DE ,则 tan ∠CBE 的值是 ( )A. 247B. 73C. 724D. 137. 如图所示,在四边形 ABCD 中,AB =AD =6,AB ⊥BC,AD ⊥DC,∠BAD =60∘,点 M,N 分别在边 AB,AD 上.若 AM:MB =AN:ND =1:2,则 tan ∠MCN 的值为 ( )A. 3313B. 2511C.239D. 5−2二、填空题(共5小题;共20分)8. 点 M (tan60∘,−cos60∘) 关于 x 轴的对称点 Mʹ 的坐标是 .9. 在 △ABC 中,∠A 为锐角,已知 cos (90∘−A )=32,sin (90∘−B )=32,则 △ABC —定是三角形.10. 在 △ABC 中,∠C =90∘,AB =8,cos A =34,则 BC = .11. 如图所示,在菱形 ABCD 中,DE ⊥AB 于点 E .已知 cos A =35,BE =4,则 tan ∠DBE =.12. 如图所示,已知一次函数 y =kx +b 的图象经过 A (−2,−1),B (1,3) 两点,并且交 x 轴于点 C ,交 y 轴于点 D ,则 ∠A +∠B 的正切值是 .三、解答题(共6小题;共72分)13. 如图所示,一艘渔船位于小岛 M 的北偏东 45∘ 方向、距离小岛 180 海里的 A 处,渔船从 A 处沿正南方向航行一段距离后,到达位于小岛南偏东 60∘ 方向的 B 处.(1)从A处到B处的航行过程中,渔船与小岛M之间的最小距离是多少?(结果用根号表示)(2)若渔船以20海里/时的速度从B处沿BM方向行驶,求渔船从B处到达小岛M的航行时间.(结果精确到0.1小时)(参考数据:2≈1.41,3≈1.73,6≈2.45)14. 如图所示,一艘海轮在A点时测得灯塔C在它的北偏东42∘方向上,它沿正东方向航行80海里后到达B处,此时灯塔C在它的北偏西55∘方向上.(1)求海轮在航行过程中与灯塔C的最短距离;(结果精确到0.1)(2)求海轮在B处时与灯塔C的距离.(结果保留整数)(参考数据:sin55∘≈0.819,cos55∘≈0.574,tan55∘≈1.428,tan42∘≈0.900,tan35∘≈0.700, tan48∘≈1.111,)15. 如图所示,根据图中数据完成填空,再按要求答题:sin2A1+sin2B1=.sin2A2+sin2B2=.sin2A3+sin2B3=.(2)观察上述等式,猜想:在Rt△ABC中,∠C=90∘,都有sin2A+sin2B=.(3)如图丁所示,在Rt△ABC中,∠C=90∘,∠A,∠B,∠C的对边分别是a,b,c,利用三角函数的定义和勾股定理,证明你的猜想.,求sin B的值.(4)已知∠A+∠B=90∘,且sin A=51316. 如图所示,湖中的小岛上有一座标志性建筑物,其底部为A.某人在岸边的B处测得A在B的北偏东30∘方向上;然后沿岸边直行4千米到达C处,再次测得A在C的北偏西45∘方向上(其中点A,B,C在同一平面上).求这个标志性建筑物底部A到岸边BC的最短距离.17. 一副直角三角板按如图所示方式放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90,∠E=30∘,∠A=45∘.若AC=122,求CD的长.18. 如图甲所示,有一组平行线l1∥l2∥l3∥l4,正方形ABCD的四个顶点分别在l1,l2,l3,l4上,EG过点D且垂直于l1于点E,分别交l2,l4于点F,G,EF=DG=1,DF=2.(1)AE=,正方形ABCD的边长=.(2)如图乙所示,将∠AEG绕点A顺时针旋转得到∠AEʹDʹ,旋转角为α(0∘<α<90∘),点Dʹ在直线l3上,以ADʹ为边,在EʹDʹ左侧作菱形ADʹCʹBʹ,使点Bʹ,Cʹ分别落在直线l2,l4上.①写出∠BʹADʹ与α的函数关系,并给出证明;②若α=30∘,求菱形ADʹCʹBʹ的边长.答案第一部分1. B2. D3. B4. D5. A6. C7. A【解析】∵AB=AD=6,AM:MB=AN:ND=1:2,∴AM=AN=2,BM=DN=4,连接MN,连接AC.∵AB⊥BC,AD⊥CD,∠BAD=60∘在Rt△ABC与Rt△ADC中,AB=ADAC=AC∴Rt△ABC≌Rt△ADC( HL)∴∠BAC=∠DAC=12∠BAD=30∘,MC=NC,∴BC=12AC,∴AC2=BC2+AB2,即(2BC)2=BC2+AB2,3BC2=AB2,∴BC=23,在Rt△BMC中,CM=BM2+BC2=42+(23)2=27.∵AN=AM,∠MAN=60∘,∴△MAN是等边三角形,∴MN=AM=AN=2,过M点作ME⊥CN于E,设NE=x,则CE=27−x,∴MN2−NE2=MC2−EC2,即4−x2=(27)2−(27−x)2,解得x=77,∴EC=27−77=1377,∴ME=MN2−NE2=3217,∴tan∠MCN=MEEC =3313.第二部分9. 直角10. 2711. 212. 1第三部分13. (1)过点M作MD⊥AB于点D.∵∠AME=45∘,∴∠AMD=∠MAD=45∘,∵AM=180海里,∴MD=AM⋅cos45∘=902(海里),答:渔船从A到B的航行过程中与小岛M之间的最小距离是902海里.(2)在Rt△DMB中,∵∠BMF=60∘,∴∠DMB=30∘,∵MD=902海里,∴MB=MDcos30∘=606,∴606÷20=36=3×2.45=7.35≈7.4(小时),答:渔船从B到达小岛M的航行时间约为7.4小时.14. (1)过C作AB的垂线,设垂足为D.根据题意可得:∠1=∠2=42∘,∠3=∠4=55∘,设CD的长为x海里,在Rt△ACD中,tan42∘=ADCD,则AD=x⋅tan42∘,在Rt△BCD中,tan55∘=BDCD,则BD=x⋅tan55∘,∵AB=80,∴AD+BD=80,∴x⋅tan42∘+x⋅tan55∘=80,解得x≈34.4,答:海轮在航行过程中与灯塔C的最短距离是34.4海里.(2)在Rt△BCD中,cos55∘=CDBC,∴BC=CDcos55∘≈60海里,答:海轮在B处时与灯塔C的距离约为60海里.15. (1)1;1;1(2)1(3)证明:∵sin A=ac ,sin B=bc,a2+b2=c2,∴sin2A+sin2B=a2+b2c2=c2c2=1.(4)sin B=121316. 过A作AD⊥BC于D,则AD的长度就是A到岸边BC的最短距离.在Rt△ACD中,∠ACD=45∘,设AD=x,则CD=AD=x,在Rt△ABD中,∠ABD=60∘,由tan∠ABD=ADBD ,即tan60∘=xBD,所以BD=xtan60∘=33x,又BC=4,即BD+CD=4,所以33x+x=4解得x=6−23 .答:这个标志性建筑物底部A到岸边BC的最短距离为(6−23)千米.17. 过点B作BM⊥FD于点M.在△ACB中,∠ACB=90∘,∠A=45∘,AC=122,∴BC=AC=122 .∵AB∥CF,∴BM=BC×sin45∘=122×2=12 .2CM=BM=12,在△EFD中,∠F=90∘,∠E=30∘,∴∠EDF=60∘,∴MD=BM÷tan60∘=43,∴CD=CM−MD=12−43 .18. (1)1;10【解析】由题意可得:∠1+∠3=90∘,∠1+∠2=90∘,∴∠2=∠3,在△AED和△DGC中,∠AEF=∠DGC∠3=∠2AD=CD∴△AED≌△DGC(AAS),∴AE=GD=1,∵DE=1+2=3,∴正方形ABCD的边长=12+32=10(2)①∠BʹADʹ=90∘−α.理由:过点B'作B'M垂直于l1于点M,在Rt△AE'D'和Rt△B'MA中,B'M=AE'AB′=AD',∴Rt△AE'D'≌Rt△B'MA(HL)∴∠D'AE'+∠B'AM=90∘,∠B'AD'+α=90∘,∴∠B'AD'=90∘−α②221.3过点E'作ON垂直于l1分别交l1,l3于点O,N,若 α=30∘,则 ∠E 'D 'N =60∘,AE '=1,故 E 'O =12,EʹN =53,EʹDʹ=533由勾股定理可知菱形的边长为:253+1=843=2213.。
北师大版九年级数学下册第一章测试题含答案2套
北师大版九年级数学下册第一章测试题含答案2套第一章测试卷(1)一、选择题(每题3分,共30分) 1.cos30°的值为( )A.12B.32C.22D.332.如图,已知Rt △BAC 中,∠C =90°,AC =4,tan A =12,则BC 的长是( )A .2B .8C .2 5D .4 5(第2题) (第3题)3.如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB 于D 点,已知AC =5,BC =2,那么sin∠ACD 等于( ) A.53B.23C.253D.524.若3tan(α+10°)=1,则锐角α的度数是( )A .20°B .30°C .40°D .50°5.已知cos θ=0.253 4,则锐角θ约等于( )A .14.7°B .14°7′C .75.3°D .75°3′6.如图,某课外活动小组在测量旗杆高度的活动中,已测得仰角∠CAE =33°,AB =a ,BD=b ,则下列求旗杆CD 长的式子中正确的是( ) A .CD =b sin 33°+a B .CD =b cos33°+a C .CD =b tan33°+aD .CD =btan33°+a(第6题) (第7题)7.如图,在网格中,小正方形的边长均为1,点A ,B ,C 都在格点上,则∠ABC 的正切值是( ) A .2B.255C.55D.128.在△ABC 中,∠A =30°,∠B =45°,AB =2(1+3),则BC 等于( )A .2B. 6C .2 2D .1+ 39.如图,在高楼前D 点测得楼顶的仰角为30°,向高楼前进60 m 到C 点,又测得仰角为45°,则该高楼的高度大约为( ) A .82 mB .163 mC .52 mD .30 m(第9题) (第10题)10.如图,钓鱼竿AC 长6 m ,露在水面上的鱼线BC 长3 2 m ,某钓者想看看鱼钓上的情况,把鱼竿AC 转动到AC ′的位置,此时露在水面上的鱼线B ′C ′长为3 3 m ,则鱼竿转过的角度是( ) A .60°B .45°C .15°D .90°二、填空题(每题3分,共30分)11.已知α为等腰直角三角形的一个锐角,则tan α=________. 12.若反比例函数y =kx 的图象经过点(tan30°,cos60°),则k =________.13.在△ABC 中,∠C =90°,BC =6,sin A =23,则AB =________.14.某梯子与地面所成的角α满足45°≤α≤60°时,人可以安全地爬上斜靠在墙面上的梯子的顶端,现有一个长6 m 的梯子,则使用这个梯子最高可以安全爬上__________高的墙.15.某游客在山脚处看见一个标注海拔40 m 的牌子,当他沿山坡前进50 m 时,他又看见一个标注海拔70 m 的牌子,于是他走过的山坡的坡度是__________.16.如图,△ABC 的顶点A ,C 的坐标分别是(0,23),(2,0),且∠ACB =90°,∠B =30°,则顶点B 的坐标是__________.(第16题) (第17题) (第18题) (第19题) (第20题)17.如图,一棵树的枝叶部分AB 在太阳光下的投影CD 的长是5.5 m ,此时太阳光线与地面的夹角是52°,则AB 的长约为__________ (结果精确到0.1 m .参考数据:sin 52°≈0.79,tan52°≈1.28).18.如图,秋千链子的长度OA =3 m ,静止时秋千踏板处于A 位置,此时踏板距离地面0.3m ,秋千向两边摆动,当踏板处于A ′位置时,摆角最大,此时∠AOA ′=50°,则在A ′位置,踏板与地面的距离约为________m(sin 50°≈0.766,cos50°≈0.642 8,结果精确到0.01 m).19.如图,轮船在A 处观测灯塔C 位于北偏西70°方向上,轮船从A 处以每小时20 n mile的速度沿南偏西50°方向匀速航行,1 h 后到达码头B 处,此时,观测灯塔C 位于北偏西25°方向上,则灯塔C 与码头B 的距离约是________n mile(结果精确到个位,参考数据:2≈1.4,3≈1.7,6≈2.4).20.如图,正方形ABCD 的边长为22,过点A 作AE ⊥AC ,AE =1,连接BE ,则tan E =________. 三、解答题(21题8分,26题12分,其余每题10分,共60分) 21.计算:(1)2-1-3sin 60°+(π-2 020)0+⎪⎪⎪⎪⎪⎪-12;(2)12-3+4cos60°·sin 45°-(tan60°-2)2.22.在Rt △ABC 中,∠C =90°,∠A ,∠B ,∠C 的对边分别为a ,b ,c ,2a =3b ,求∠B 的正弦、余弦和正切值.23.如图,在△ABD中,AC⊥BD于点C,BCCD=32,点E是AB的中点,tan D=2,CE=1,求sin∠ECB的值和AD的长.(第23题)24.为建设“宜居宜业宜游”山水园林城市,正在对某城市河段进行区域性景观打造.某施工单位为测得某河段的宽度,测量员先在河对岸岸边取一点A,再在河这边沿河边取两点B和C,在B处测得点A在北偏东30°方向上,在C处测得点A在西北方向上,如图,量得BC长为200 m,求该河段的宽度(结果保留根号).(第24题)25.如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为30 n mile/h,在此航行过程中,该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值)(第25题)26.如图,MN表示一段笔直的高架道路,线段AB表示高架道路旁的一排居民楼.已知点A到MN的距离为15 m,BA的延长线与MN相交于点D,且∠BDN=30°.假设汽车在高架道路上行驶时,周围39 m以内会受到噪音的影响.(1)过点A作MN的垂线,垂足为点H.如果汽车沿着从M到N的方向在MN上行驶,当汽车到达点P处时,噪音开始影响这一排居民楼,那么此时汽车与点H的距离为多少米?(2)降低噪音的一种方法是在高架道路旁安装隔音板.当汽车行驶到点Q时,它与这一排居民楼的距离QC为39 m,那么对于这一排居民楼,高架道路旁安装的隔音板至少需要多少米长?(结果精确到1 m,参考数据:3≈1.7)(第26题) 答案一、1.B 2.A 3.A 4.A 5.C 6.C 7.D 8.A 9.A10.C 点拨:∵sin ∠CAB =BC AC =326=22,∴∠CAB =45°.∵sin ∠C ′AB ′=B ′C ′AC ′=336=32,∴∠C ′AB ′=60°.∴∠CAC ′=60°-45°=15°,即鱼竿转过的角度是15°. 二、11.1 12.36 13.9 14.3 3 m 15.3∶4 16.(8,23)17.7.0 m 点拨:过点B 作BE ∥CD ,交AD 于点E .∵太阳光线与地面的夹角是52°,且太阳光线是平行的, ∴tan 52°=ABBE ,BE =CD =5.5 m.∴AB =5.5×tan 52°≈5.5×1.28=7.04≈7.0(m).18.1.37 点拨:如图,作A ′D ⊥OA 于点D ,A ′C 垂直地面于点C ,延长OA 交地面于点B .(第18题)易得四边形BCA ′D 为矩形, ∴A ′C =DB .∵∠AOA ′=50°,且OA =OA ′=3 m ,∴在Rt △OA ′D 中,OD =OA ′·cos ∠AOA ′≈3×0.642 8≈1.93(m). 又AB =0.3 m , ∴OB =OA +AB =3.3 m. ∴A ′C =DB =OB -OD ≈1.37 m. 19.2420.23 点拨:延长CA 到F 使AF =AE ,连接BF ,过B 点作BG ⊥AC ,垂足为G .根据题干条件证明△BAF ≌△BAE ,得出∠E =∠F ,然后在Rt △BGF 中,求出tan F 的值,进而求出tan E 的值.三、21.解:(1)原式=12-3×32+1+12=12-32+1+12=12;(2)原式=-(2+3)+4×12×22-(3-2)=-2-3+2-3+2=-23+ 2. 22.解:由2a =3b ,可得a b =32.设a =3k (k >0),则b =2k ,由勾股定理,得c =a 2+b 2=9k 2+4k 2=13k . ∴sin B =b c =2k 13k =21313,cos B =a c =3k 13k =31313,tan B =b a =2k 3k =23. 23.解:∵AC ⊥BD ,∴∠ACB =∠ACD =90°. ∵点E 是AB 的中点,CE =1, ∴BE =CE =1,AB =2CE =2. ∴∠B =∠ECB . ∵BC CD =32,∴设BC =3x ,则CD =2x . 在Rt △ACD 中,tan D =2, ∴ACCD =2. ∴AC =4x .在Rt △ACB 中,由勾股定理得AB =AC 2+BC 2=5x , ∴sin ∠ECB =sin B =AC AB =45.由AB =2,得x =25,∴AD =AC 2+CD 2=(4x )2+(2x )2=25x =25×25=455. 24.解:如图,过点A 作AD ⊥BC 于点D .(第24题)根据题意知∠ABC =90°-30°=60°,∠ACD =45°,∴∠CAD =45°. ∴∠ACD =∠CAD . ∴AD =CD .∴BD =BC -CD =200-AD . 在Rt △ABD 中,tan ∠ABD =ADBD ,∴AD =BD ·tan ∠ABD =(200-AD )·tan 60°=3(200-AD ). ∴AD +3AD =200 3.∴AD =20033+1=300-1003(m).答:该河段的宽度为(300-1003)m. 25.解:如图,过点A 作AP ⊥BC ,垂足为P ,设AP =x n mile.(第25题)在Rt △APC 中,∵∠APC =90°, ∠PAC =90°-60°=30°, ∴tan ∠PAC =CP AP =33. ∴CP =33x n mile.在Rt △APB 中,∵∠APB =90°, ∠PAB =45°, ∴BP =AP =x n mile.∵PC +BP =BC =30×12=15(n mile),∴33x +x =15. 解得x =15(3-3)2.∴PB =15(3-3)2 n mile. ∴航行时间为15(3-3)2÷30=3-34(h).答:该渔船从B 处开始航行3-34 h ,离观测点A 的距离最近.26.解:(1)如图,连接PA .(第26题)由已知得AP =39 m ,在Rt △APH 中,PH =AP 2-AH 2=392-152=36(m). 答:此时汽车与点H 的距离为36 m. (2)由题意,隔音板位置应从P 到Q ,在Rt △ADH 中,DH =AH tan 30°=1533=153(m);在Rt △CDQ 中,DQ =CQ sin 30°=3912=78(m).∴PQ =PH +HQ =PH +DQ -DH =36+78-153≈114-15×1.7≈89(m). 答:高架道路旁安装的隔音板至少需要89 m 长.第一章测试卷(2)一、选择题(每题3分,共30分) 1.已知cos A =32,则锐角A 的度数为( )A .30°B .45°C .50°D .60°2.在Rt △ABC 中,∠C =90°,tan B =32,BC =23,则AC 等于( )A .3B .4C .4 3D .63.在锐角三角形ABC 中,若⎝⎛⎭⎪⎫sin A -322+⎪⎪⎪⎪⎪⎪22-cos B =0,则∠C 等于( )A .60°B .45°C .75°D .105°4.如图,在由边长为1的小正方形组成的网格中,△ABC 的三个顶点均在格点上,则tan∠ABC 的值为( )A .35B .34C .105 D .1(第4题) (第5题) (第6题)5.如图,在Rt △ABC 中,CD 是斜边AB 上的中线,已知CD =5,AC =6,则tan B 的值为( )A .45B .35C .34D .436.为了测量被池塘隔开的A ,B 两点之间的距离,根据实际情况,作出如图所示的图形,其中AB ⊥BE ,EF ⊥BE ,AF 交BE 于点D ,C 在BD 上.有四位同学分别测量出以下4组数据:①BC ,∠ACB ;②CD ,∠ACB ,∠ADB ;③EF ,DE ,BD ;④DE ,DC ,BC .能根据所测数据,求出A ,B 两点之间距离的有( ) A .1组 B .2组 C .3组 D .4组7.如图,沿AE 折叠矩形纸片ABCD ,使点D 落在BC 边上的点F 处.已知AB =8,BC =10,则tan ∠EFC 的值为( )A .34B .43C .35D .458.如图所示,从热气球C 处测得地面A ,B 两点的俯角分别为30°,45°,如果此时热气球的高度CD 为100 m ,点A ,D ,B 在同一直线上,则A ,B 两点之间的距离是( ) A .200 m B .200 3 m C .220 3 m D .100(3+1)m(第8题) (第9题) (第10题) 9.如图,若△ABC和△DEF的面积分别为S1,S2,则()A.S1=12S2B.S1=72S2C.S1=85S2D.S1=S210.已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3在x轴上.若正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是()A.3+318B.3+118C.3+36D.3+16二、填空题(每题3分,共24分)11.计算:cos245°+tan 30°sin 60°=________.12.在Rt△ABC中,∠C=90°,BC=10,若△ABC的面积为5033,则∠A=_________度.13.如图,正方形ABCD的边长为4,点M在边DC上,M,N两点关于对角线AC所在的直线对称,若DM=1,则tan∠ADN=________.14.已知锐角A的正弦sin A是一元二次方程2x2-7x+3=0的根,则sin A=________.15.如图,将以A为直角顶点的等腰直角三角形ABC沿直线BC平移得到△A′B′C′,使点B′与C重合,连接A′B,则tan∠A′BC′=________.(第15题) (第16题) (第17题) (第18题)16.如图,一架梯子斜靠在墙上,若梯子底端到墙的距离AC=3 m,cos∠BAC=34,则墙高BC=________.17.如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB 的延长线上的D′处,那么tan∠BAD′=________.18.如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以10 n mile/h 的速度航行,甲沿南偏西75°方向以10 2 n mile/h的速度航行,当航行1 h后,甲在A 处发现自己的渔具掉在了乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B 处追上.则甲船追赶乙船的速度为________n mile/h. 三、解答题(19题12分,20题10分,21,22每题14分,23题16分,共66分) 19.计算:(1)3sin 60°-2cos 45°+38;(2)12-3+4cos 60°·sin 45°-(tan 60°-2)2.20.a ,b ,c 是△ABC 的三边,且满足等式b 2=c 2-a 2,5a -3c =0,求sin A +sin B 的值.21.如图,已知▱ABCD ,点E 是BC 边上的一点,将边AD 延长至点F ,使∠AFC =∠DEC.(1)求证:四边形DECF 是平行四边形.(2)若AB =13,DF =14,tan A =125,求CF 的长.22.为建设“宜居宜业宜游”山水园林城市,正在对某城市河段进行区域性景观打造.某施工单位为测得某河段的宽度,测量员先在河对岸岸边取一点A,再在河这边沿河边取两点B和C,在B处测得点A在北偏东30°方向上,在点C处测得点A在西北方向上,如图,量得BC长为200 m,求该河段的宽度(结果保留根号).23.某校教学楼后面紧邻着一个土坡,坡上面是一块平地,BC∥AD,斜坡AB长为22 m,坡角∠BAD=68°.为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.(1)求改造前坡顶与地面的距离(精确到0.1 m).(2)为了确保安全,学校计划改造时保持坡的根部A不动,坡顶B沿BC前进到F点处,问BF至少是多少?(精确到0.1 m)(参考数据:sin 68°≈0.927 2,cos 68°≈0.374 6,tan 68°≈2.475 1,sin 50°≈0.766 0,cos 50°≈0.642 8,tan 50°≈1.191 8)答案一、1.A2.A 点拨:由tan B =AC BC 知AC =BC tan B =23×32=3.3.C 点拨:由题意,得sin A -32=0,22-cos B =0.所以sin A =32,cos B =22.所以∠A =60°,∠B =45°,所以∠C =180°-∠A -∠B =180°-60°-45°=75°. 4.B 5.C6.C 点拨:对于①,可由AB =BC ·tan ∠ACB 求出AB 的长;对于②,由BC =ABtan ∠ACB,BD =AB tan ∠ADB ,BD -BC =CD ,可求出AB 的长;对于③,易知△DEF ∽△DBA ,则DEEF =BDAB ,可求出AB 的长;对于④,无法求得AB 的长,故有①②③共3组,故选C . 7.A8.D 点拨:由题意可知,∠A =30°,∠B =45°,tan A =CD AD ,tan B =CDDB ,又CD =100 m ,因此AB =AD +DB =CD tan A +CD tan B =100tan 30°+100tan 45°=1003+100=100(3+1)(m). 9.D 点拨:如图,过点A 作AM ⊥BC 于点M ,过点D 作DN ⊥EF ,交FE 的延长线于点N .在Rt △ABM 中,∵sin B =AMAB ,∴AM =3×sin 50°,∴S 1=12BC ·AM =12×7×3×sin 50°=212sin 50°.在Rt △DEN 中,∠DEN =180°-130°=50°.∵sin ∠DEN =DN DE ,∴DN =7×sin 50°,∴S 2=12EF ·DN =12×3×7×sin 50°=212sin 50°,∴S 1=S 2.故选D .10.D 点拨:依题意知:D 1E 1=12,B 2C 2=33,B 3E 4=36,B 3C 3=13,A 3C 3=23,sin ∠A 3C 3x=sin(30°+45°)=sin 75°=2+64,∴A 3到x 轴的距离3+16. 二、11.1 点拨:cos 245°+tan 30°sin 60°=⎝ ⎛⎭⎪⎫222+33×32=1.12.60 点拨:∵BC =10,∴S △ABC =BC ·AC 2=10·AC 2=5033,则AC =1033,∴tan A =BC AC =101033=3,∴∠A =60°.13.43 14.1215.13 点拨:如图,过A ′作A ′D ⊥BC ′于点D ,设A ′D =x ,则B ′D =x ,BC =2x ,BD =3x .∴tan ∠A ′BC ′=A ′D BD =x 3x =13.16.7 m 点拨:由cos ∠BAC =AC AB =34,知3AB =34,∴AB =4 m.在Rt △ABC 中,BC =AB 2-AC 2=42-32=7(m). 17.2 点拨:由题意知BD ′=BD =2 2.在Rt △ABD ′中,tan ∠BAD ′=BD ′AB =222= 2.18.(10+103) 点拨:如图,由题意可知,∠DOB =30°,∠AOD =75°,∠2=90°-60°=30°.∵∠3=∠AOD =75°,∴∠1=90°-75°=15°,故 ∠1+∠2=15°+30°=45°.如图,过点O 作OC ⊥AB 于点C ,则∠AOC =90°-∠1-∠2=90°-45°=45°.易知OA =102n mile ,∠OAB =∠AOC =45°,∴OC =AC =OA ·sin 45°=102×22=10(n mile).在Rt △OBC 中, ∠BOC =∠AOD +∠BOD -∠AOC =75°+30°-45°=60°,∴BC = OC ·tan 60°=10 3 n mile ,∴AB =AC +BC =(10+103)n mile.∵OC =10 n mile ,∠B =30°,∴OB =2OC =2×10=20(n mile),乙船从O 到B 所用时间为20÷10=2(h ).∵甲船从O 到A 所用时间为1 h ,∴甲船从A 到B 所用时间为2-1=1(h),故甲船追赶乙船的速度为(10+103)n mile/h.三、19.解:(1)原式=3×32-2×22+2=32-1+2 =52.(2)原式=-(2+3)+4×12×22-(3-2)2 =-2-3+2-(2-3) =-2.20.解:由b 2=c 2-a 2,得a 2+b 2=c 2,∴△ABC 为直角三角形,∠C =90°. ∵5a -3c =0, ∴a c =35,即sin A =35. 设a =3k ,c =5k ,则b =(5k )2-(3k )2=4k . ∴sin B =b c =45, ∴sin A +sin B =35+45=75.21.(1)证明:∵四边形ABCD 是平行四边形,∴AD ∥BC .∴∠ADE =∠DEC . 又∵∠AFC =∠DEC , ∴∠AFC =∠ADE . ∴DE ∥FC .∴四边形DECF 是平行四边形.(2)解:过点D 作DH ⊥BC 于点H ,如图所示.∵四边形ABCD 是平行四边形, ∴∠BCD =∠A ,AB =CD =13. 又∵tan A =125=tan ∠DCH =DHCH , ∴DH =12,CH =5. ∵DF =14, ∴CE =14. ∴EH =9.∴DE =92+122=15. ∴CF =DE =15.22.解:如图,过点A 作AD ⊥BC 于点D .根据题意,知∠ABC =90°-30°=60°,∠ACD =45°,∴∠CAD =45°. ∴∠ACD =∠CAD . ∴AD =CD .∴BD =BC -CD =200-AD . 在Rt △ABD 中,tan ∠ABD =ADBD ,∴AD =BD ·tan ∠ABD =(200-AD )·tan 60°=3(200-AD ). ∴AD +3AD =200 3.∴AD =20033+1=(300-1003)(m).故该河段的宽度为(300-1003)m.23.解:(1)如图,作BE⊥AD,E为垂足,则BE=AB·sin 68°=22 sin 68°≈20.4(m).即改造前坡顶与地面的距离约为20.4 m.(2)如图,作FG⊥AD,G为垂足,连接FA.则∠FAG=50°,FG=BE.∵AG=FGtan 50°≈20.41.191 8≈17.12(m),AE=AB·cos 68°=22cos 68°≈8.24(m),∴BF=GE=AG-AE≈8.9 m,即BF至少是8.9 m.。
(北师大版)初中数学九年级上册第一章综合测试01含答案解析
加油!有志者事竟成答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!第一章单元综合测试一、单选题1.已知四边形ABCD 是平行四边形,AC ,BD 相交于点O ,下列结论错误的是( ) A .OA OC =,OB OD =B .当AB CD =时,四边形ABCD 是菱形C .当90ABC ∠=︒时,四边形ABCD 是矩形D .当AC BD =且AC BD ⊥时,四边形ABCD 是正方形2.如图,四边形ABCD 是菱形,对角线AC ,BD 相交于点O ,8AC =,6BD =,点E 是CD 上一点,连接OE ,若OE CE =,则OE 的长是( )A .2B .52C .3D .4 3.如图,面积为S 的菱形ABCD 中,点O 为对角线的交点,点E 是线段BC 单位中点,过点E 作EF BD ⊥于F ,EG AC ⊥与G ,则四边形EFOG 的面积为( )A .14SB .18SC .112S D .116S 4.如图,菱形ABCD 中,对角线AC ,BD 相交于点O ,E 为AB 的中点.若菱形ABCD 的周长为32,则OE 的长为( )A .3B .4C .5D .65.如图,正方形ABCD 的面积为1,M 是AB 的中点,则图中阴影部分的面积是( )A .310B .13C .25D .496.如图,正方形ABCD 的边长8AB =,E 为平面内一动点,且4AE =,F 为CD 上一点,2CF =,连接EF ,ED ,则2EF ED +的最小值为( )A .B .C .12D .10二、填空题7.如图,在菱形ABCD 中,50B ∠=︒,点E 在CD 上,若AE AC =,则BAE ∠=________.8.如图,在矩形ABCD 中,E ,F 分别为边AB ,AD 的中点,BF 与EC ,ED 分别交于点M ,N .已知4AB =,6BC =,则MN 的长为________.9.如图,在矩形ABCD 中,9AB =,AD =,点P 是边BC 上的动点(点P 不与点B ,点C 重合),过点P 作直线PQ BD ∥,交CD 边于Q 点,再把PQC △沿着动直线PQ 对折,点C 的对应点是R 点,则CQP ∠=________.10.如图,正方形ABCD 中,点E 为对角线AC 上一点,且AE AB =,则BEA ∠的度数是________度.三、作图题11.在正方形ABCD 中,E 是CD 边上的点,过点E 作EF BD ⊥于F .(1)尺规作图:在图中求作点E ,使得EF EC =;(保留作图痕迹,不写作法) (2)在(1)的条件下,连接FC ,求BCF ∠的度数.四、综合题12.如图,ABCD 的对角线AC ,BD 相交于点O ,过点O 作EF AC ⊥,分别交AB ,DC 于点E 、F ,连接AF 、CE .(1)若32OE =,求EF 的长;(2)判断四边形AECF 的形状,并说明理由.13.如图,在ABC △中,AB AC =,点D 、E 分别是线段BC 、AD 的中点,过点A 作BC 的平行线交BE 的延长线于点F ,连接CF .(1)求证:A BDE F E △≌△;(2)求证:四边形ADCF 为矩形.14.如图,四边形ABCD 的对角线AC ,BD 交于点O ,过点D 作DE BC ⊥于E ,延长CB 到点F ,使BF CE =,连接AF ,OF .(1)求证:四边形AFED 是矩形;(2)若7AD =,2BE =,45ABF ∠=︒,试求OF 的长.15.如图,点E 是正方形ABCD 外一点,点F 是线段AE 上一点,且EBF △是等腰直角三角形,其中90EBF ∠=︒,连接CE 、CF(1)求证:ABF CBE △≌△;(2)判断CE 与EF 的位置关系,并说明理由.16.如图,菱形EFGH 的三个顶点E 、G 、H 分别在正方形ABCD 的边AB 、CD 、DA 上,连接CF .(1)求证:HEA CGF ∠∠=;(2)当AH DG =时,求证:菱形EFGH 为正方形.第一章单元综合测试答案解析一、 1.【答案】B【解析】∵四边形ABCD 是平行四边形,OA OC =∴,OB OD =,故A 正确,∵四边形ABCD 是平行四边形,AB CD =,不能推出四边形ABCD 是菱形,故B 错误,∵四边形ABCD 是平行四边形,90ABC ∠=︒, ∴四边形ABCD 是矩形,故C 正确,∵四边形ABCD 是平行四边形,AC BD =,AC BD ⊥, ∵四边形ABCD 是正方形.故D 正确.故答案为:B . 2.【答案】B【解析】∵四边形ABCD 是菱形,8AC =,6BD =,142CO AC ==∴,132OD BD ==,AC BD ⊥,5DC =∴,90EOC DOE ∠+∠=︒,90DCO ODC ∠+∠=︒,OE CE =∵,EOC ECO ∠=∠∴,DOE ODC ∠=∠∴,DE OE =∴,1522OE CD ==∴故答案为:B . 3.【答案】B【解析】∵四边形ABCD 是菱形,OA OC =∴,OB OD =,AC BD ⊥,12S AC BD =⨯, EF BD ⊥∵于F ,EG AC ⊥于G ,∴四边形EFOG 是矩形,EF OC ∥,EG OB ∥,∵点E 是线段BC 的中点,EF ∴、EG 都是OBC △的中位线,1124EF OC AC ==∴,1124EG OB BD ==,∴矩形EFOG 的面积11111=44828EF EG AC BD AC BD S ⎛⎫=⨯=⨯=⨯⨯ ⎪⎝⎭;故答案为:B . 4.【答案】B【解析】∵四边形ABCD 是菱形,AC BD ⊥∴,AB BC CD AD ===, 90AOB ∠=︒∴,又32AB BC CD AD +++=∵.8AB =∴,在Rt AOB △中,OE 是斜边上的中线,142OE AB ==∴. 故答案为:B . 5.【答案】B【解析】如图,过点E 作HF AB ⊥,AM CD ∵∥,DCE EAM ∠=∠∴,CDE EMA ∠=∠,AME CDE △∽△∴,::1:2AM DC EH EF ==∴,1FH AD ==,13EH =∴,23EF =.∴阴影部分的面积1111112343ABCD AME CDE M BC S S S S =−−−=−−−=△△△正方形. 故答案为:B . 6.【答案】B【解析】如图,在AD 上取点k ,使2AK =,连接EK ,在AEK △和ADE △中,EAK DAE ∠=∠,AEK ADE △∽△∴,12EK AE ED AD ==∴,即12EK ED =,12EF ED EF EK +=+∴,当F 、E 、K三点共线时,21EF ED FK +== ()1222()EF ED EF ED +=+=最小∴,故答案为:B 。
北师大版初中数学九下第一章综合测试试题试卷含答案
第一章综合测试一、选择题(本大题共10小题,每题3分,共30分) 1.若 的余角为°60,则tan 的值是( )A .12 B .2 C D .3 2.ABC △在正方形网格中的位置如下图所示,则cos B 的值为( )A B C .12D .2 3.在ABC Rt△中,将各边都扩大两倍,则锐角A 的正弦值( )A .扩大两倍B .缩小为原来的一半C .不变D .不能确定4.等腰三角形的底边与底边上的高的比是2:,则顶角的度数为( ) A .60°B .90°C .120°D .150°5.在ABC Rt△中,°90C A B C ,,,所对的边分别为a b c ,,,且°45A a b ,,则c 等于( )A .B .4C .D .6.如下图,一块矩形木板ABCD 斜靠在墙边(OC OB ,点A B C D O ,,,,在同一平面内),已知AB a AD b BCO x ,,,则点A 到OC 的距离等于( )A .sin sin a x b xB .cos cos a x b xC .sin cos a x b xD .cos sin a x b x7.如下图,某河坝的横断面为四边形ABCD AD BC AB CD ,∥,,坝顶宽10BC 米,坝高12米,斜坡AB 的坡度1:1.5i ,则坝底宽AD 的长度为( )A .26米B .28米C .30米D .46米8.如下图,在ABC △中,°904ACB AC BC ,,将ABC △折叠,使点A 落在BC 边上的点D 处,EF 为折痕.若3AE ,则sin BFD 的值为( )A .13B .3C .4D .359.如下图,在ABC Rt△中,°903ACB BC AC AB ,,的垂直平分线ED 交BC 的延长线于点D ,垂足为E ,连接AD ,则sin CAD 的值为( )A .14B .4C .13 D .15 10.如下图,在ABC △中,10tan 2AB AC A BE AC ,,于点E ,若点D 是线段BE 上的一个动点,则5CD BD的最小值是( )A .B .C .D .10二、填空题(本大题共6小题,每题3分,共18分)11.在ABC △中,若21sinA tan 02B,则C 的度数是________.12.如下图,将一张矩形纸片ABCD 沿DE 折叠,使顶点C 落在C 处,若36AB DE ,,则sin C DE ________.13.如图,已知ABC Rt△中,°90BAC ,斜边BC 上的高4AD ,4cos 5B,则AC ________.14.如下图,从甲楼底部A 处测得乙楼顶部C 处的仰角是30°,从甲楼顶部B 处测得乙楼底部D 处的俯角是45°,已知乙楼的高CD 是45m ,则甲楼的高AB 是________m .(结果保留根号)15.如下图,在东西方向的海岸线上有A B ,两个港口,甲货船从A 港出发,沿北偏东60°的方向以4海里/时的速度航行,同时乙货船从B 港出发,沿西北方向航行,2h 后两船在点P 处相遇,则乙货船的速度为________.16.在ABC △中,AD 是ABC △的高,若AB ,tan 2B 且2BD CD ,则BC ________. 三、解答题(本大题共6小题,共72分)17.(10分)(1)计算:°2°sin60sin 30cos45tan 60tan 45cos30;(2)已知°°075 <<,且 °sin 152 1014cos 3.14tan 3的值.18.(11分)如下图,ABC △的顶点A C ,的坐标分别是 04,, 30,,且°°9030ACB ABC ,,试求点B 的坐标.19.(12分)如下图,在ABC Rt△中,°90C D ,为BC 上一点,51AB BD ,,3tan 4B.(1)求AD 的长;(2)求sin 的值.20.(12分)如下图,山顶有一塔AB ,塔高33m .计划在塔的正下方沿直线CD 开通穿山隧道EF .从与E 点相距80m 的C 处测得A B ,的仰角分别为27°,22°,从与F 点相距50m 的D 处测得A 的仰角为45°.求隧道EF 的长度.(参考数据:°°tan220.40tan270.51 ,)21.(13分)某数学课题研究小组针对兰州市住房窗户“如何设计遮阳篷”这一课题进行了探究,过程如下: 问题提出:如下图1是某住户窗户上方安装的遮阳篷,要求设计的遮阳篷既能最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内. 方案设计:如下图2,该数学课题研究小组通过调查研究设计了垂直于墙面AC 的遮阳篷CD . 数据收集:通过查阅相关资料和实际测量:兰州市一年中,夏至这一天的正午时刻,太阳光线DA 与遮阳篷CD 的夹角最大(°77.44ADC );冬至这一天的正午时刻,太阳光线DB 与遮阳篷CD 的夹角最小(°30.56BDC ).窗户AB 的高度为2m . 问题解决:根据上述方案及数据,求遮阳篷CD 的长.(结果精确到0.1m .参考数据:°°°°sin30.560.51cos30.560.86tan30.560.59sin77.440.98 ,,,,°°cos77.440.22tan77.44 4.49 ,)22.(14分)如下图1是小红家的阳台上放置的一个晒衣架,下图2是晒衣架的侧面示意图,立杆AB CD ,相交于点O B D ,,两点位于地面.经测量:136cm 51cm 34cm AB CD OA OC OE OF ,,.现将晒衣架完全稳固张开,此时扣链EF 成一条线段,32cm EF .图1图2(1)求证:AC BD ∥;(2)求扣链EF 与立杆AB 的夹角OEF 的余弦值;(3)小红的连衣裙挂在衣架上的总长度达到122cm ,问挂在晒衣架后是否会拖落在地面?请通过计算说明理由.第一章综合测试答案解析一、 1.【答案】D【解析】若 的余角为°60,则°30,所以°tan tan 303a .故选D . 2.【答案】B【解析】如下图,连接DE ,易知DE BC ,且点D E ,都在格点上,在BED Rt△中,EB,所以cos 5BD B EB.故选B .3.【答案】C4.【答案】A【解析】因为等腰三角形的底边与底边上的高的比是2,所以底角为°60,所以顶角的度数为°60.故选A . 5.【答案】A【解析】在ABC Rt△中,°°9045C A ,,所以a b.因为a b,所以a b,所以sin 2a c AA . 6.【答案】D【解析】如下图,过点A 作AE OC 于点E ,交BC 于点M AF OB ,于点F .∵四边形ABCD 是矩形,°°9090ABC AEC AMB CME EAB BCO x ∴,∵,,∴.易知四边形AFOE 为矩形,AE FO FBA EAB x ∴∥,∴.cos sin AB a AD b FO FB BO a x b x ∵,,∴.故选D .7.【答案】D【解析】过点B 作BE AD 于点E ,过点C 作CF AD 于点F .由题意得1121.5BE i BE AE,米,所以18AE 米.因为AD BC AB CD ∥,,所以18DF AE 米,10EF BC 米,所以18101846AD AE EF DF (米).故选D . 8.【答案】A【解析】°°90445ACB AC BC A B ∵,,∴,由折叠可得3AEF DEF DE AE △≌△,,EDF A EDF B ,∴.又CDE EDF B BFD CDE BFD ∵,∴.在CDE Rt△中,11sin sin 3CE CE AC AE CDE BFD DE,∴的值为13.故选A . 9.【答案】A【解析】设 0AD x x >,因为DE 是AB 的垂直平分线,所以BD x ,所以3CD x .在ACD Rt△中,由222AC CD AD ,得 2223x x ,解得4x ,所以431CD ,所以1sin 4CD CAD AD .故选A . 10.【答案】B【解析】如下图,过点D 作DH AB 于点H ,过点C 作CM AB 于点M .°90BE AC AEB ∵,∴,tan 2BEA AE∴.设 0AE a a >,则2BE a ,根据勾股定理,得221004a a a ,∴,2BE a ∴.同理,可得CM BEsin 555DH AE DBH DH BD CD BD CD DH BD AB∵,∴,∴,又CD DH CM ∵≥,55CD BD CD BD ∴≥的最小值为.故选B .二、11.【答案】90°【解析】由题意,得°°11sin 0tan 0sin tan 306022A B A B A B,∴,,, °°°°180306090C ∴.12.【答案】2【解析】因为36CD AB DE ,,所以12CD DE,易得°30CED ,所以°60CDE ,由折叠可知C DE CDE ,所以°60C DE,所以sin 2C DE . 13.【答案】5【解析】因为°°9090CAD BAD B BAD ,,所以CAD B ,所以4cos cos 5CAD B ,即445AD AC AC ,所以5AC . 14.【答案】【解析】由题意,得°45BDA AB AD ,∴.在ADC Rt△中,°3045CAD CD ,,°tan tan303CD CAD AD∴,即453AD AB AD ,故甲楼的高AB是m . 15.【答案】【解析】过点P 作PC AB 于点C .∵甲货船从A 港出发,沿北偏东60°的方向以4海里/时的速度航行,°30428PAC AP ∴,(海里),142PC AP ∴海里.∵乙货船从B 港出发,沿西北方向航行,°°45sin 45PCPBC PB∴,∴海里.∴乙货船的速度为2 (海里/时). 16.【答案】3或1【解析】因为tan AD B BD,所以设 0AD x >,则2BD x .因为222AB AD BD,所以2222x ,解得1x 或1x (舍去),即2BD .又因为2BD CD ,所以1CD .当点D 在线段BC 上时,如下图1,则3BC BD CD ;当点D 在线段BC 的延长线上时,如下图2,则1BC BD CD .图1图2三、17.【答案】(1)2sin 60sin 30cos45tan 60tan 45cos30211211142142.(2)°°075 ∵<<,且°sin 15°°°156045 ∴,∴.114cos 3.14tan 3411323 .18.【答案】如下图,过点B 作BG x 轴于点G .435OA OC AC ∵,,∴.°°°9030tan30ACACB ABC BC∵,,∴°°9090BCG ACO ACO CAO ∵,,BCG CAO ∴,34sin cos 55BG CG BCG BCG BC BC∴,,BG CG ∴,∴点B 的坐标是 3 . 19.【答案】(1)在ABC Rt△中,3tan 4AC B BC , 设 30AC x x >,则4BC x ,2222225345AC BC AB AB x x ∵,,∴,解得1x (舍去)或1x ,34AC BC ∴,. 13BD CD ∵,∴,AD ∴.(2)如下图,过点D 作DE AB 于点E ,则°90BED . 在BDE Rt△中,3tan 4DE B BE,设 30DE y y >,则4BE y , 2222221341DE BE BD BD y y ∵,,∴,解得15y (舍去)或15y,3sin 510DE DE a AD∴.20.【答案】如下图,延长AB 交CD 于点H ,则AH CD . 在ACH Rt△中,°tan 27AHACH ACH CH,, °tan27AH CH ∴.在BCH Rt△中,°tan 22BHBCH BCH CH, °tan22BH CH ∴.33AB AH BH AB ∵,,°°tan 27tan2233CH CH ∴,300CH ∴.°tan27153AH CH ∴.在ADH Rt△中,°tan 45AHD D HD,, 153HD AH ∴.3001538050323EF CD CE FD CH HD CE FD ∴. 故隧道EF 的长度约为323m .21.【答案】在BCD Rt△中,°°9030.56tan BCBCD BDC BDC CD,,, °tan tan30.56BC CD BDC CD ∴.在ACD Rt△中,°°9077.44tan ACACD ADC ADC CD,,, °tan tan77.44AC CD ADC CD ∴.2AC BC AB AB ∵,,初中数学 九年级下册 6 / 6 °°tan77.44tan30.562CD CD ∴,4.490.592CD ∴,解得0.5CD .答:遮阳篷CD 的长约为0.5m .22.【答案】(1)OA OC AB CD OB OD ∵,,∴,°°1118018022OAC OCA AOC OBD ODB BOD ∴,, 又AOC BOD OAC OBD AC BD ∵,∴,∴∥.(2)如下图,过点O 作OM EF 于点M .34cm 32cm 16cm OE OF EF EM ∵,,∴,168cos 3417EM OEF OE ∴. (3)小红的连衣裙会拖落在地面.理由如下:如图,过点A 作AH BD 于点H .OE OF OB OD ∵,,°°1118018022OEF OFE BOD OBD ODB BOD ∴,, OEF OBD ∴,即OEM ABH , 由(2)知88cos cos 1717OEF ABH,∴,即817BH AB , 8813664cm 1717BH AB ∴,由勾股定理可得 120cm AH . 122120∵>,∴小红的连衣裙会拖落在地面.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1 页 共 5 页
九年级数学 第一章检测题
时间:120分钟 满分:120分
一、精心选一选(每小题3分,共30分)
1.(2015·玉林)计算:cos245°+sin245°=( B )
A.12 B.1 C.14 D.32
2.把△ABC三边的长度都缩小为原来的
1
3
,则锐角A的正弦值( A )
A.不变 B.缩小为原来的13 C.扩大为原来的3倍 D.不能确定
3.在Rt△ABC中,∠C=90°,若sinA=
2
3
,则cosB的值等于( C )
A.12 B.22 C.23 D.1
4.在Rt△ABC中,∠C=90°,∠B=50°,AB=10,则BC的长为( B )
A.10tan50° B.10sin40° C.10sin50° D.10cos50°
5.已知α为锐角,且sin(α-10°)=
2
2
,则α等于( B )
A.45° B.55° C.60° D.65°
6.已知锐角α满足等式3cos2α-8cosα+4=0,则cosα的值为( A )
A.23 B.2 C.2或23 D.以上都不对
7.(2015·淄博)若锐角α满足cosα<22且tanα<3,则α的范围是( B )
A.30°<α<45° B.45°<α<60° C.60°<α<90° D.30°<α<60°
8.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若BD∶AD=1∶4,则tan
∠BCD的值是( C )
A.14 B.13 C.12 D.2
错误! 错误!,第9题图) 错误!
,第10题图)
9.如图,某校数学兴趣小组用测倾器测量某大桥的桥塔高度,在距桥塔AB底部50米
的C处,测得桥塔顶部A的仰角为41.5°,已知测倾器CD的高度为1米,则桥塔AB的
高度为( C )(参考数据:sin41.5°≈0.663,cos41.5°≈0.749,tan41.5°≈0.885)
A.34米 B.38米 C.45米 D.50米
10.转化思想是中学数学中一种常用且有效的解题方法,在本章中这种思想的作用更为
突出.通过添加辅助线将非直角三角形问题转化为两个最熟悉的(锐角为30°和45°)直角
三角形来解决.试用此方法解决下面问题:如图,在△ABC中,∠B=60°,∠C=45°,
AB=6,则AC的长度是( D )
第 2 页 共 5 页
A.3 B.33 C.5 D.36
二、细心填一填(每小题3分,共24分)
11.计算:tan245°-1=__0__.
12.某坡面的坡度为1∶3,则坡角是__30°__.
13.如图,在坡屋顶的设计图中,AB=AC,屋顶的宽度l为10米,坡角α为35°,
则坡屋顶高度h为__3.5__米.(结果精确到0.1米;参考数据:sin35°≈0.57,cos35°≈0.82,
tan35°≈0.70)
,第13题图) ,第14题图)
,第15题图) ,第16题图)
14.如图,P是∠α的边OA上的一点,且点P的坐标为(1,3),则sinα=__32__.
15.如图,海中有一个小岛A,它的周围15海里内有暗礁,今有货船由西向东航行,
开始在A岛南偏西60°的B处,往东航行20海里后到达该岛南偏西30°的C处后,货船
继续向东航行,你认为货船航行途中__没有__触礁的危险.(填“有”或“没有”)
16.如图,小明在家里楼顶上的点A处,测量建在与小明家楼房同一水平线上相邻的
电梯楼的高,在点A处看电梯楼顶部点B处的仰角为60°,在点A处看这栋电梯楼底部点
C处的俯角为45°,两栋楼之间的距离为30米,则电梯楼的高BC为__82.0__米.(精确到
0.1米;参考数据:2≈1.414,3≈1.732)
17.直线y=kx-1与y轴相交所成的锐角为60°,则k=__±33__.
18.如图,两个高度相等的圆柱形水杯,甲杯装满液体,乙杯是空杯,若把甲杯中的液
体全部倒入乙杯,则图中点P与液面的距离是__6_cm__.
三、耐心做一做(共66分)
19.(8分)计算:
(1)2sin30°-tan60°+tan45°; (2)cos245°+tan60°·cos30°-3tan230°
+4sin230°.
解:(1)2-3 (2)2
20.(8分)在Rt△ABC中,∠C=90°,AC=15,∠B=60°,解这个直角三角形.
解:∠A=30°,AB=103,BC=53
第 3 页 共 5 页
21.(8分)已知锐角α使关于x的一元二次方程x2-2sinα·x+3sinα-34=0有两个
相等的实数根,求α的度数.
解:由题意得b2-4ac=(2sinα)2-4(3sinα-34)=0,即4sin2α-43sinα+3=0,
解得sinα=
3
2
.∵α为锐角,∴α=60°
22.(9分)如图,有一热气球到达离地面高度为36米的A处时,仪器显示正前方一高
楼顶部B的仰角是37°,底部C的俯角是60°.为了安全飞越高楼,气球应至少再上升多
少米?(结果精确到0.1米;参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,3
≈1.73)
解:过A作AD⊥CB,垂足为点D.在Rt△ADC中,AD=CDtan60°=363=123≈20.76.
在Rt△ADB中,BD=AD·tan37°≈20.76×0.75=15.57≈15.6(米),则气球应至少再上升15.6
米
23.(10分)为解决某地的干旱问题,在山洞C里发现了暗河(如图).经勘察,在山洞的
西面有一条南北走向的公路连接着A,B两村庄,山洞C位于A村庄南偏东30°方向,且
位于B村庄南偏东60°方向.为方便A,B两村庄的村民取水,需从山洞C处向公路AB
紧急修建一条最近的简易公路CD.现已知A,B两村庄相距6千米.
(1)求这条最近的简易公路CD的长;(精确到0.01千米)
(2)每修建1千米的简易公路需费用16000元,请求出修建该简易公路的最低费用.(精
确到个位;参考数据:2≈1.414,3≈1.732)
解:(1)过C作CD⊥AB,垂足是D.由题意知,∠A=30°,∠DBC=60°,∴∠ACB
第 4 页 共 5 页
=30°,∴BC=AB=6 km.在Rt△BCD中,CD=BC·sin60°=33≈5.20(km)
(2)5.20×16000=83200(元)
24.(11分)(2015·淄博)如图1是一把折叠椅子,图2是椅子完全打开支稳后的侧面示意
图,其中AD和BC表示两根较粗的钢管,EG表示座板平面,EG和BC相交于点F,MN
表示地面所在的直线,EG∥MN,EG距MN的高度为42 cm,AB=43 cm,CF=42 cm,∠
DBA=60°,∠DAB=80°.求两根较粗钢管AD和BC的长.(结果精确到0.1 cm;参考数
据:sin80°≈0.98,cos80°≈0.17,tan80°≈5.67,sin60°≈0.87,cos60°≈0.5,tan60°
≈1.73)
解:
如图,作FH⊥AB于H,DQ⊥AB于Q,则FH=42 cm.在Rt△BFH中,BF=
FH
sin60°
≈
420.87≈48.28,∴BC=BF+CF=48.28+42≈90.3(cm).在Rt△BDQ中,BQ=DQ
tan60°
.在
Rt△ADQ中,AQ=DQtan80°.∵BQ+AQ=AB=43,∴
DQtan60°+DQ
tan80°
=43,解得
DQ≈56.999.在Rt△ADQ中,AD=DQsin80°≈56.9990.98≈58.2(cm),则两根较粗钢管AD和BC
的长分别为58.2 cm,90.3 cm
25.(12分)如图,矩形纸片ABCD,将△AMP和△BPQ分别沿PM和PQ折叠(AP>AM),
点A和点B都与点E重合;再将△CQD沿DQ折叠,点C落在线段EQ上点F处.
(1)判断△AMP,△BPQ,△CQD和△FDM中有哪几对相似三角形?(不需说明理由)
(2)如果AM=1,sin∠DMF=
3
5
,求AB的长.
第 5 页 共 5 页
解:(1)有三对相似三角形,即△AMP∽△BPQ∽△CQD (2)设AP=x,∴由折叠知
BP=AP=EP=x,AB=DC=2x.由△AMP∽△BPQ得AMBP=APBQ,∴BQ=x2.由
△AMP∽△
CQD得
APCD=AM
CQ
,∴CQ=2,∴AD=BC=BQ+CQ=x
2
+2,MD=AD-AM=
x
2+1.∵在Rt△FDM中,sin∠DMF=35,DF=DC=2x,∴2xx2+1=35,变形得3x2
-10x+3
=0,解得x1=3,x2=
1
3
(不合题意,舍去),∴AB=2x=6
