多元统计分析课程论文
多元统计分析案例教学范文

Ⅰ.正文浙江省十一城市综合实力统计分析:基于2008年经济数据摘要:本文根据中国城市经济发展研究中心提出的城市综合经济实力和区域的概念,并利用经济学原理以及2008年各城市社会经济发展状况的截面数据,就浙江省11市的经济数据进行分析。
首先建立了评价的指标体系,其次,分别采用加权平均法、主成分分析法、因子分析法和聚类分析法对浙江省根据行政区域划分的11个市的综合经济实力进行了全面的评价和比较,并在此基础上提出了促进浙江各市经济协调发展、共同进步的相关措施。
关键词:城市经济加权平均主成分分析因子分析聚类分析Analysis of Comprehensive Economic Strength of Eleven Cities of Zhejiang Province: Based onEconomic Data in 2008Abstract:This paper focuses on the economic data analysis of 11 cities of Zhejiang Province based on the concept of comprehensive economic strength, urban areas economic by City Economic Development Center in China, principles of economics and the economic development sectional data of various cities in 2008. An index system of the evaluation is estab lished at first; then using the methods of Weighted average, Principal Component Analysis, Factor Analysis and Cluster Analysis, the comprehensive economic strength of the 11 cities divided by the regional administration in Zhejiang Province are evaluated and compared. And finally, some measure, which may potentially promote coordinated economic development and common progress are proposed.Keywords:Urban economy; Weighted average; Principal Component Analysis; Factor Analysis; Cluster Analysis正文目录一引言........................................................... I-4 二经济实力分析评价方法........................................... I-5 (一)多元统计分析的涵义...................................... I-5 (二)主成分分析法............................................ I-61 主成分分析法的原理及优点............................... I-62 主成分分析法的算法步骤....................... ..... I-7(1)原始数据的标准化...................... .... . I-7(2)求指标数据的相关矩阵............................ I-8(3)求相关矩阵R的特征根向量,确定主成分........... I-8(4)求方差贡献率,确定主成分个数................... I-8(5)对k个主成分进行综合评价........................ I-83 因子分析模型的建立及分析............................... I-94聚类分析.............................................. I-10 (1)聚类分析的概念................................. I-10(2)聚类分析的相关理论............................. I-10(3)聚类分析的主要步骤............................. I-11(4)数据的标准化................................... I-11(5)相似性测度..................................... I-11 三浙江省各地区的经济实力分析.................................... I-12 (一)加权算术平均法......................................... I-13 (二)主成分分析法........................................... I-14 (三)因子分析法............................................. I-16 (四)聚类分析............................................... I-18 四模型分析和结果讨论............................................ I-22 五结束语........................................................ I-24 六致谢.......................................................... I-25 七参考文献...................................................... I-26一、引言以区域的概念来讨论经济发展是一种很有效的方法。
多元统计分析论文
基于主成分分析的我国地区经济指标研究09统计班徐晓旺【摘要】地区经济的发展对我国现代化进程形成巨大的推动作用,而经济指标是评判地区发展水平的重要标志。
根据搜集的相应数据建立数据库,基于主成分分析、同时运用聚类分析以及判别分析的多元统计方法,对全国各地区的经济状况进行综合指标分析。
研究各省经济发展在全国的分布特征、筛选出具备可对比性的指标,进而探究造成差异的原因,同时具有针对性地提出相关建议。
【关键词】主成分分析;聚类分析;判别分析;地区经济指标一、引言随着社会的不断进步,经济发展的车轮将会继续滚动。
在整体水平提升的同时不难发现:我国各地区间发展势必存留着一定的差距,了解其具体的分布特征注定会是一个非常值得深入挖掘的信息。
结合对进出口总额、居民消费水平等9个经济指标的研究,致力于分析各地区硬件发展水平、人民生活状况的异同与经济发展的相关性。
本文将对中国31个省份地区的经济指标进行分析。
首先,应用主成分分析的方法对众多指标做降维处理并赋予各主成分以实际意义以获取综合性指标;进而,基于主成分分析结果通过聚类分析法把我国的31个地区分类;最后,根据聚类的结果建立判别函数同时运用判别分析将新疆、广东两个省份归类。
二、主成分分析搜集到的经济指标为:进出口总额、地区生产总值、固定资产投资、邮电业务量、客运量、货运量、公交车运营数、居民平均工资和居民消费水平这九项指标。
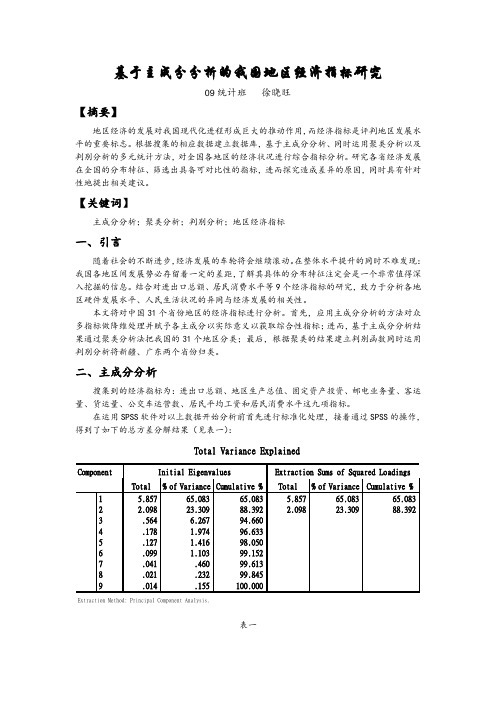
在运用SPSS软件对以上数据开始分析前首先进行标准化处理,接着通过SPSS的操作,得到了如下的总方差分解结果(见表一):表一由表一中结果可以看到保留2个主成分为宜,这2个主成分集中了原始9个变量信息的88.392%,可见效果比较好,这样原来的9个指标就可以通过这2个综合指标来反映。
此时,这2个主成分就起到了降维的作用。
通过SPSS进一步的操作还可以得到如下的主成分系数矩阵(见表二):表二由表二可以得出前2个主成分的线性组合为:Y1 = 0.852 X1 + 0.979 X2 + 0.821 X3 + 0.957 X4 + 0.885 X5 + 0.742 X6 + 0.967 X7 +0.226 X8 + 0.513 X9Y2 = 0.393 X1 - 0.113 X2 - 0.419 X3 - 0.032 X4 - 0.233 X5 - 0.483 X6 + 0.109 X7 +0.915 X8 + 0.786 X9通过对上述线性组合的观察,我们可以得出:在主成分1中进出口总额、地区生产总值、固定资产投资、邮电业务量、客运量、货运量和公交车运营数这几项指标的系数明显比主成分2的系数大,可以将Y1归类为地区经济发展中的硬件基础指标;在主成分2中平均工资和消费水平指标的系数最大,可以将Y2归类为地区经济发展中的居民生活指标。
多元统计分析论文-spss多元统计分析论文

因子分析和聚类分析在全国省会城市经济实力分析中的应用摘要:本文利用SPSS中的因子分析和聚类分析功能对全国26个省会城市经济实力进行分析。
先用因子分析,再对因子分析的结果进行聚类分析。
本文选取2012年上半年26个省会城市的9个经济指标,通过因子分析提取两个因子计算出26个省会城市的综合得分函数,再根据因子分析得出的得分函数对这些城市进行聚类分析,分类结果为:然后再对分类后的城市进行分析说明,最后针对分类的结果进而得出经济综合实力的结论。
关键词:因子分析聚类分析 SPSS 经济实力一、引言城市的发展是经济发展和社会进步的重要标志。
目前,我国正处于加快推进现代化的历史阶段。
现代城市既要有发达的经济,也要有发达的文明。
文明城市是指在全面建设小康社会、推进社会主义现代化建设新的发展阶段,物质文明、政治文明与精神文明协调发展,经济和社会事业全面进步,精神文明建设取得显著成就,市民整体素质和城市文明程度较高的城市。
文明城市,是反映一个地区现代文明程度、城市综合竞争实力的重要标志。
创建文明城市对经济社会发展所产生的现实意义和深远影响,已经远远超出了原来一般意义上的群众性精神文明建设活动。
我们要从战略高度来看待创建文明城市的重要意义,提高对创建文明城市重要性的认识。
随着改革开放的脚步,全国各地经济都有着飞速的发展,人们越来越关注各个省会城市经济实力。
经济是衡量一个地区综合实力的重要指标,而依照经济实力对城市进行分类可以看出一个地区综合实力以及发展潜力,利用经济分类,我们也可以得出该地区的发展状况,以及在哪些方面做得不够,哪些方面可以得到改进。
基于以上原因,本文运用SPSS 对全国26个省会城市,合肥, 武汉, 长沙, 郑州, 南昌, 太原, 西安, 福州, 石家庄, 沈阳, 哈尔滨, 长春, 南京, 杭州, 济南, 南宁, 成都, 贵阳, 昆明, 兰州, 西宁, 银川, 海口, 广州, 乌鲁木齐, 呼和浩特2012年上半年的9类经济指标进行因子分析,聚类分析。
研究论文:多元统计分析在企业财务危机预警中的应用

74461 企业研究论文多元统计分析在企业财务危机预警中的应用一、多元统计分析与企业财务危机预警多元统计分析在在统计学中是一种综合性的分析方法,通过多个分析方式对于同一个对象进行全方位的分析,内容包括多种应用方式。
通过多种方式的综合运用,在多个指标的共同参与之下,对于统计的规律进行揭示与挖掘,将这种多元化的分析手法应用于企业财务危机的预警中,是十分有效的,与现代企业管理的多元资金流和运作的资金链串接是有相同的运作模式的。
企业的财务危机主要是指企业在经营过程中由于无力按时偿还到期的债务而产生的危机和困难就是企业的财务危机,企业财务危机的出现有种种原因,管理不善、行业萧条、决策失误、名誉受损等等,都可能导致企业财务危机的出现,企业一般都是个体或者合营,依靠主要管理人员和决策人的共同努力发展壮大,所以对于管理人员的措施采纳和决策人的决定有严格的要求。
一般来说,判断一个企业财务危机的常用标准是企业破产和在证券交易中面临的退市现象,注意,在证券公司面临退市的现象一般指的是上市公司,中国改革开放以后,证券行业发展迅速,企业的上市已经成为一个企业发展壮大的标识,所以本文研究的企业也包括上市公司。
企业在生存发展的过程中,面临的财务危机是一项挑战,也是一项机遇,往往一个企业进行大刀阔斧的改革都是在企业财务危机之后,由于财务危机暴露了企业在发展过程中的弊端,所以企业在财务危机中能够顽强的生存下来,也就获得了成功的准备,将危机中显示出来的问题进行纠正,这样企业获得了良好的发展活力,更能在激烈的社会竞争力实现跨越式前进。
由于企业性质的不同,所以造成企业财务危机的原因也就不同,在企业财务危机预警的多元分析中,要根据企业的独特性采取相应的指标来完成分析,并且在模式模型选择过程中要根据企业财务危机的侧重点来进行选择,这样才能有针对性的提出分析的策略。
根据我们选定的财务指标,利用聚类分析法对我国企业进行科学的统计分类;再用判别分析法构造预测判别模型,对其财务危机状况进行判定预测;最后利用主成分分析法提取主成分,计算各主成分的分数和综合得分,根据主成分综合得分对样本进行排序,以发现其财务危机状况,使用Excel电子表格中软件和统计分析软件SPSS来进行数据处理和建立多变量预警模型,这就是多元分析的主要步骤。
《多元统计分析》课程实践教学创新研究

《多元统计分析》课程实践教学创新研究根据国家新一轮高校分类办学和建设应用技术型高校的需要,如何教好应用技术型高校的多元统计分析课程,一直是我们这类应用技术型高校教师在积极思考的问题,我们在教学过程中一直都在不断探索应用型教学的实现形式,总感觉到目前的教学方法存在一些问题,基于这样的要求,着力于多元统计分析的基本概念、基本方法和基本理论,充分反映应用技术型高校的指导思想,力求做到强化应用和技术创新,对《多元统计分析》课程实践教学进行创新研究。
标签:应用技术型;多元统计分析;课程实践教学doi:10.19311/ki.16723198.2017.05.0710引言多元统计分析是从经典统计学中发展起来的一个分支,是一种综合分析方法,它能够在多个对象和多个指标互相关联的情况下分析它们的统计规律,很适合自然科学和社会科学的特点。
主要内容包括多元正态分布及其抽样分布、多元正态总体的均值向量和协方差阵的假设检验、多元方差分析、直线回归与相关、多元线性回归与相关(Ⅰ)和(Ⅱ)、主成分分析与因子分析、判别分析与聚类分析、Shannon信息量及其应用。
多元统计分析是一门研究多指标随机现象统计规律的统计学科,随着计算机的普遍应用和软件的迅猛发展以及大数据时代的来临,使得自然科学和社会科学的各个领域都广泛的用到多元统计分析方法,比如在经济、金融保险、生物医学、环境数据、管理工程等相关领域。
尤其是多元分析方法在处理多维数据时,它必不可少的分析工具。
作为统计学的主要分支,多元统计分析方法正在向人类生活和生产的每一个角落渗透,其分析理论也在实际应用中逐步的完善和发展。
多元统计分析也可以对国家的宏观经济形势进行深入分析,并以直观的方式进行宏观经济建模,为经济决策提供了理论支持。
所以,作为讲授多元统计分析这门课程的老师,扮演着相当重要的角色,那就是如何引导学生学习和掌握这门课程,为学生进入理论研究部门和实际应用部门打下夯实的基础。
石油院校多元统计论文

石油院校多元统计论文1案例教学案例式教学法始创于美国哈佛商学院,其科学性、创新性已经被我国的教育工作者认同和接受,并在很多高校的教学中得到广泛应用。
案例式教学法是一种在老师引导下学生自己解决实际问题的学习方法[1]。
统计案例教学法,就是根据统计学科自身的特点、教学目的及教学要求,在教师的指导下,将统计课程中实际案例的处理过程搬入课堂,通过例题讲解渗透知识点,引导学生进行思考、分析、讨论和交流。
通过学生的独立思考或集体讨论,促进学生对教学内容的理解,进而提高学生分析问题和解决问题的能力。
该方法用于应用性特别强的多元统计分析课程,效果尤其明显。
2石油案例教学特点首先,统计案例素材来自于石油院校的各院系的真实课题。
整个解题过程涉及到大量的专业背景,完整的教学过程可以有效地将统计教学培养和专业教学培养结合起来,对于学生将来就业、提高解决实际问题的能力有很大的帮助。
其次,案例分析是进行案例教学的重要环节,它是以学生为主体对案例进行辨析并得出自己结论的一种创造性教学活动。
以石油为背景的案例教学过程,不仅可以作为多元统计分析课程的教学主体,还可以作为各专业学生实习实训的课题,同时也可以为毕业设计提供一定的参考。
最后,任何一个统计问题都需要论证和检验,这是至关重要的一步。
对于所选择的案例,结果都是客观存在的,这就促使学生思考自己所做的结论是否具有可行性。
如果学生所得到的结论比预期的结果要好,就可以适当考虑统计模型的可行性及与原始结论的差异性。
3案例教学分类依照案例性质可分为解题型、分析型。
解题型是指为了使学生正确理解统计原则和具体方法而采用的教学案例,其特点是通过实例性习题、例题进行具体的计算,简单地体现出多元统计学中的原则、定义、原理和方法。
分析型案例是指由教师提供背景和材料,并具有明确针对性地提出几个问题,引导学生自主思考,研究问题存在的状况、条件以及问题的发展演变趋势,最终提出解决问题的办法。
依照案例内容多少可分为专题型和综合型。
多元统计分析spss分析论文
用聚类分析法分析细菌性食物中毒学号:1110110047姓名:何昌业摘要:探讨我国细菌性食物中毒的发生规律,为预防细菌性食物中毒的发生提供参考。
将收集的1994—2003年766起细菌性食物中毒案件的发生情况利用SPSS软件进行聚类分析,按其中毒发生情况将全部23种细菌中毒情况分为4类。
本文选取了细菌性食物中毒的报道起数、中毒人数、死亡人数的统计量作为研究数据。
各项数据均来自于万方数据搜索。
分析结果表明:细菌性食物中毒有其规律性,根据其内在的特点,采取相应的预防措施,将有助于预防其发生.关键词:食物中毒细菌性食物中毒聚类分析引言:随着生活水平的不断提高,我们的食物也越来越丰富,但随之食物中毒的情况也越来越多.其中细菌性食物中毒比较常见,对人们生活习惯影响较大。
因此,本文对1994—2003年766起细菌性食物中毒案件的具体情况进行聚类分析。
首先对引起细菌性食物中毒的细菌进行聚类,将全部细菌分为4类,然后对中毒人数、死亡人数、中毒原因等进行分析。
通过本文的分析研究,可以清楚地了解细菌性食物中毒的分布情况,以及发生中毒的原因,最终对细菌性食物中的预防起指导作用.2 聚类分析的原理与方法2.1主要思想及原理主要思想:先将待聚类的n个样品(或者变量)各自看成一类,共有n类;然后按照实现选定的方法计算每两类之间的聚类统计量,即某种距离(或者相似系数),将关系最为密切的两类合为一类,其余不变,即得到n—1类;再按照前面的计算方法计算新类与其他类之间的距离(或相似系数),再将关系最为密切的两类并为一类,其余不变,即得到n—2类;如此下去,每次重复都减少一类,直到最后所有的样品(或者变量)都归为一类为止。
聚类分析的原理:直接比较样本中各事物之间的性质,,将性质相近的归为一类,而将性质差别比较大的分在不同类。
也就是说,同类事物之间的性质差异小,类与类之间的事物性质相差较大。
其中欧式距离在聚类分析中用得最广,它的表达式如下:其中Xik表示第i个样品的第k个指标的观测值,Xjk表示第j个样品的第k个指标的观测值,dij为第i个样品与第j个样品之间的欧氏距离。
spss多元统计分析论文
学年第一学期 吉林财经大学2012-2013学年第一学期多元统计分析多元统计分析描述统计实验报告描述统计实验报告系别:工商管理系系别:工商管理系专业:人力资源管理专业:人力资源管理学号:********** 姓名:张晓宇姓名:张晓宇城镇人均生活收入及消费支出分析一、城镇人均生活收入及消费支出分析 随着经济的发展,我国城镇居民的收入水平和消费水平的结构也发生了很大变化,居民生活水平的提高和消费的增加对于实现国民经济又好又快发展、正确处理好内需和外需的关系至关重要。
系至关重要。
二、数据来源说明1、城镇居民家庭基本情况. 数据来源于《2008中国中国统计统计年鉴》。
2、下表是要进行处理的31个省市的城镇居民消费相关的原始数据,数据来源于《2008中国统计年鉴》。
各地区城镇居民家庭平均每人生活消费支出(2007) 单位: 元地 区城镇人均生活消费支出消费支出居民人均收入食品食品 衣着衣着 家庭设备家庭设备 医疗医疗保健保健全 国2415.47 3587.04 835.48 167.34 126.07 191.51 北 京5681.09 8275.47 1836.31 451.63 303.46 575.80 天 津3261.91 6227.94 1133.62 265.16 122.41 263.24 河 北2246.29 3801.82 685.98 167.75 115.82 166.34 山 西2039.80 3180.92 659.02 227.43 98.26 142.66 内蒙古内蒙古 2378.60 3341.88 726.06 184.07 97.95 232.76 辽 宁2740.97 4090.40 866.55 242.96 112.15 267.86 吉 林2398.45 3641.13 818.37 189.90 105.11 256.28 黑龙江黑龙江 2365.23 3552.43 747.54 198.85 79.26 253.84 上 海7807.08 9138.65 2824.99 417.57 481.04 549.44 江 苏3658.19 5813.23 1283.17 222.59 199.48 232.30 浙 江5819.70 7334.81 2001.40 368.52 288.02 459.39 安 徽2050.09 2969.08 697.37 138.18 116.76 165.02 福 建3217.66 4834.75 1310.07 213.26 167.33 162.26 江 西2111.73 3459.53 777.45 130.06 105.68 159.14 山 东2867.30 4368.33 916.49 197.11 158.71 221.80 河 南1875.98 3261.03 596.73 159.46 104.75 140.55 湖 北2099.64 3419.35 686.75 144.26 134.17 172.44 湖 南2444.90 3389.62 918.18 137.66 129.51 196.54 广 东3421.56 5079.78 1498.49 151.11 148.10 197.00 广 西1917.97 2770.48 752.23 79.91 110.09 123.91 海 南1759.26 3255.53 768.24 75.15 87.85 110.92 重 庆1600.58 2873.83 577.76 113.27 117.24 159.68 四 川1816.09 3002.38 675.71 132.85 112.21 160.31 贵 州1167.92 1984.62 392.85 88.56 64.91 76.76 云 南1597.26 2250.46 530.84 93.61 83.75 138.16 西 藏1435.41 2435.02 500.57 175.18 117.00 54.37 陕 西1938.60 2260.19 612.12 138.33 94.88 195.61 甘 肃1365.33 2134.05 381.12 97.23 77.78 127.35 青 海 1657.87 2358.37 450.66 160.51 90.12 192.77 宁 夏1824.87 2760.14 523.86 159.10 104.32 187.60 新 疆 1696.40 2737.28 494.47 182.85 70.79 189.69 三、家庭总收入分析1、城镇家庭总收入单线图,城镇家庭总收入逐年增加。
多元统计分析-期末论文-不同地区不同行业薪资差异分析
我国地区行业薪资水平差异分析学院:统计学院班级:14级金融计量国际班姓名:吴亚南学号:32014120093摘要:本论文主要应用聚类分析,主成分分析,因子分析和对应分析四种多元统计方法对2015年我国31个省,市,自治区的地区薪资情况及不同的的行业对工资的影响相结合进行研究分析。
为全面的研究问题,数据选取了教育业,金融业,管理业等19个行业进行分析。
本文将首先采用聚类分析的方法将各个省市按照工资总数分类,由分类结果初步观察不同地区是否存在明显的差异;之后运用主成分分析的方法由繁至简找到两个变量代替所有变量并进行因子分析;最后根据因子分析的基础上做相应分析,观察两个因子之间的关系。
从而从不同角度分析我国各地区薪资水平存在的主要差异以及导致这些差异出现的原因,并对我国目前地区行业发展进行综合概述。
关键词:聚类分析主成分分析因子分析对应分析薪资水平一、引言在信息发达的大数据时代,我们常会遇到数量大,难分析的数据和实际问题,这时统计分析方法显得尤为重要,同时,不同地区不同行业的薪资情况差异是人们一直关心的问题,也是最根本最切合实际的问题。
因此,本文将二者联系到一起对2015年我国不同省市不同行业的薪资水平进行了分析。
本文数据来自中国统计年鉴。
二、聚类分析聚类分析概念聚类分析是研究“物以类聚”的一种方法。
聚类分析是应用最广泛的一种分类技术,它把性质相近的个体归为一类,使得同一类中的个体具有高度的同质性,不同类之间的个体具有高度的异质性。
聚类分析的职能是建立一种分类方法,它是将一批样品或变量,按照它们在性质上的相似程度进行分类。
通常我们用距离来度量样品之间的相似程度,用相似系数来度量变量之间的相似程度。
图1.1通过观察上表,我们可以看出,在整个聚类过程中,描述我国所有省、市、自治区薪资水平的31个样品都参与了聚类分析过程,没有遗漏的未参与分类的样品。
这充分说明此次聚类分析已经对全部31个样品的各个变量进行了聚类,不需要再利用判别分析再进行二度聚类。
关于多元统计的论文
关于多元统计的论文推荐文章关于体育统计学论文热度:统计学关于数据分析论文发表热度:关于统计信息化论文热度:关于统计学方面论文热度:关于统计方面论文热度:多元分析统计方法是统计学和其他学科之间形成的交叉学科,也是理论统计学发展的源泉。
下文是店铺为大家整理的关于多元统计的论文的范文,欢迎大家阅读参考!关于多元统计的论文篇1基于多元统计的汽车性能评价[摘要]本文将汽车六项主要指标作为原始数据,包括经济性(A),服务(B),设计(C),运动型汽车(D),安全性(E),易操作性(F)。
对不同型号汽车的定性变量进行分析。
利用主成分分析法提取了三个主成分,第一主成分代表汽车机动性和稳定性,在服务、设计、运动、安全这四个变量上的载荷值很大。
第二主成分反应操控性。
第三主成分体现了汽车的经济性。
通过聚类分析法将汽车品牌从非常好到非常差分为六档。
汽车性能的定量化,使得客户能更深入地了解汽车,继而有针对性地购买产品。
另一方面,为企业制定营销策略给出了建议。
[关键词]主成分分析;聚类分析;汽车性能1、引言近年来,随着我国经济的迅速发展,人民生活水平的不断提高,汽车市场也得到了快速的发展。
企业为争夺汽车销售市场,需要以客户为中心,对不同品牌汽车性能定量化,使得人们更深入的了解汽车。
本文针对汽车各项指标进行了研究,为汽车行业的营销进一步提升提供理论上的支持。
2、原始数据来源及记号汽车指标数据来自Wolfgang Hardle和Leopold Simar著的,陈诗一译的《应用多元统计分析》(第二版)附录B7。
这些数据是40个人所拥有的24种类型的汽车的平均指标数据。
这些指标从1(非常好)到6(非常差)分为6档。
变量A表示经济性,B表示服务,C表示设计,D表示运动型汽车,E是安全性,F是易操作性。
3、评价方法的选取使用SAS(9.3)软件作为统计分析工具,利用其自有的数据标准化功能,对6个指标的原始数据进行标准化处理。
采用“主成分聚类分析法”对汽车种类进行定量化的综合评价,即先做主成分分析,再取若干主成分对样品进行聚类分析,结合综合主成分得分排序对样品进行分类排名。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四川理工学院 《多元统计分析课程设计》报告 题目: 中国国有控股工业行业的经济效益评价
学 生:雷鹏程 何君 李西京 曾学成 白俊明 专 业:统计学 指导教师:柏宏斌 四川理工学院理学院
二零一 四 年十二月 中国国有控股工业行业的经济效益评价 摘要 本文主要研究了中国国有控股工业行业的经济效益,对反映行业经济效益的总资产贡献率、资产负债率、流动资产周转次数、工业成本费用利润率和产品销售率等五个经济指标进行主成分分析,提取反映行业盈利能力和市场能力的两个综合指标。然后通过因子分析法分析反映经济效益的各指标的内部结构,表明行业经济效益主要由盈利能力和市场能力两个公因子决定。根据各行业在盈利能力上的得分和市场能力上的得分将工业行业分为五类,并对各行业经济效益进行综合评价。然后用聚类分析对综合评价结果进行验证,表明综合评价较为客观合理。最后,本文给出相应的政策建议。 关键字:主成分分析、因子分析、聚类分析。
一、引言 改革开放以来,工业始终是我国经济发展的主要支柱。作为社会主义国家,我国国有及国有控股工业行业掌控着国家工业发展命脉,对国民经济、社会协调发展具有巨大推动作用。因此,考核工业行业的经济效益,对挖掘重点行业和弱势行业,提高整个国有工业企业的经济效益等具有重大的现实意义。企业或行业的经济效益由众多因素来刻画,目前反映行业经济效益主要有总资产贡献率、资产负债率、流动资产周转次数、工业成本费用利润率和产品销售率等五个经济指标1。这些众多指标虽然能从多方面对行业的经济效益进行全面考察,但也在一定程度增加了分析问题的复杂性。在损失少量信息的前提下,设计一个或少数几个综合指标,并用较少的综合指标对工业经济效益进行分析评价,能够简化问题。此外,挖掘出反映经济效益的众多指标的内在基本结构,有助于指出各行业经济效益的主要决定因素及瓶颈,也有助于对各行业经济效益进行综合评价。 二、文献综述
大量国内文献从灰色系统理论、多元统计分析方法、层次分析法、模糊综合评判
法、数据包络分析法等理论与方法,考察了中国各行业、企业或地区经济效益的研究与综合评价。华中生、梁梁等用模糊聚类方法与数据包络分析分类法考察了合肥工业行业的经济状况,将各工业行业按经济效益的状况分为高、较高、一般、较差和差等五类[1](华中生、梁梁,1995)。王树岭等人利用TOPSIS 模型,对吉林省轻工业17个主要行业的经济效益进行了综合评价与排序,确定出相应的优势行业(王树岭等,1999)。本文以2008年国有及国有控股的主要工业行业为研究对象,通过主成分分析和因子分析法,再次对各工业行业的经济效益进行分析与评价,并结合聚类分析法来验证综合评价的结果。 三、数据来源
反映经济效益的指标较多,不同文献中选取的指标不尽相同。本文采用国家统计局最新公布的五个指标:总资产贡献率、资产负债率、流动资产周转次数、工业成本费用利润率和产品销售率,分别记为1X至5X。总资产贡献率(1X)反映企业全部资产的获利能力。资产负债率(2X)既反映企业经营风险的大小,也反映企业利用债权人提供的资金从事经营活动的能力。流动资产周转次数(3X)反映投入工业企业流动资金的周转速度。成本费用利润率(4X)反映企业投入的生产成本及费用的经济效益。产品销售率(5X)反映工业产品已实现销售的程度。选取39个主要工业行业的数据整理如附录表1所示。 四、模型基本理论建立
1《国家统计年鉴2009年》用这五大指标来反映工业行业的经济效益。 4.1主成分分析的基本理论 设对某一事物的研究涉及p个指标,分别用1X,2X,…, PX表示,这p个指标构成的p维随机向量为),,(21PXXXX。设随机向量X的均值为,协方差矩阵为。 对X进行线性变换,可以形成新的综合变量,用Y表示,也就是说,新的综合向量可以由原来的变量线性表示,即满足下式: 由于可以任意地对原始变量进行上述线性变换,由不同的线性变换得到综合变量Y的统计特征也不尽相同。因此为了取得较好的效果,我们总希望XuYii的方差尽可能大且各iY之间相互独立,由于 iiiiuuXuY)var()var(,面对任意常数c,有
iiiuucXcu2)var(
因此对iu不加限制时,可以使)var(iY任意增大,问题将变得没有意义。我们将线性变换约束在下面的原则之下: (1)1iiuu(pi,,2,1)。 (2)iY与jY相互无关。(ji;pji,,2,1,) (3)1Y是1X,2X,…, PX的所有线性组合中方差最大者;2Y是与1Y不相关的
1X,2X,…, PX的所有线性组合中方差最大者;…,pY是与1Y,2Y,…,1pY不相
关的1X,2X,…, PX的所有线性组合中方差最大者。 基于以上这三条原则决定综合变量1Y,2Y,…,pY分别称为原始变量的第一,第二……第p个主成分。其中,各综合变量在总方差所占比重依次递减。在实际研究工作中,通常指挑选前几个方差较大的主成分,从而达到简化系统结构,抓住问题实质的目的。 4.2因子分析的基本理论 设有n个样品,每个样品观测p个指标,这些p个指标之间有较强的相关性。为了方便研究,并消除由观测量纲的差异及数量级不同所造成的影响,将样本的观测数据进行标准化处理,使标准化的变量均值为0,方差为1。为方便,把原始变量及标准后的变量向量均用X表示,用1F,2F,…, mF(m(1) ),,(21PXXXX是可观测随机变量,且均值向量0)(XE ,协方差矩阵
)(Xcov = ,且协方差矩阵与相关阵R相等; (2) ),,,(21MFFFF (mIF)cov(,即向量F的各分量是相互独立的; (3) ),,,(21P与F相互独立,且0)(E,的协方差矩阵是对角方阵:
)cov(=2222211pp
即的各分量之间也是相互独立的,则模型: 称为因子模型,模型的矩阵形式为: 其中A称为因子载荷矩阵,而在因子模型中,公共因子的个数少于原始变量的个数,且公共因子是不可观测的隐变量,载荷矩阵A不可逆,因而不能直接求得公共因子用原始变量表示的精确线性组合。解决该问题的一种方法是用建立回归思想求出线性组合系数的估计值,即建立如下以公共因子为因变量、原始变量为自变量的回归方程:
PjpjjjXXXF2211 j=1,2,…,m 此处因为原始变量与公共因子变量均为标准化量,因此回归方程中没有常数项。在最小二乘意义下,可以得到F估计值: 式中,A为因子载荷矩阵;R原始变量的相关阵;X为原始变量向量。这样,在得到一组样本值之后,就可以带入上面的关系式求出公共因子的估计得分,从而用少数的公共因子去描述原始变量的数据结构,用公共因子得分去描述原始变量的取值,在估计出公共因子得分后,可以利用因子得分去进行进一步分析,如样本点的聚类分析,当因子数m较少时,还可以方便地把各样本点在图上表示出来,直观地描述样本分布情况,从而便于把研究工作引向深入。 五、模型的求解与检验
5.1工业行业经济效益的综合指标确定 由主成分模型的基本原理可得,利用SPSS(19.0)软件对中国国有工业行业的经济效益指标进行主成分分析得到下表1、2:
Total Variance Explained
Component Initial Eigenvalues Extraction Sums of Squared Loadings Rotation Sums of Squared Loadings Total % of Variance Cumulative % Total % of Variance Cumulative % Total % of Variance Cumulative % 1 2.683 53.669 53.669 2.683 53.669 53.669 2.443 48.868 48.868 2 1.184 23.685 77.354 1.184 23.685 77.354 1.039 20.773 69.641 3 .630 12.593 89.948 .630 12.593 89.948 1.015 20.307 89.948 4 .376 7.527 97.475
5 .126 2.525 100.000 Extraction Method: Principal Component Analysis. 表1解释总方差表 Rotated Component Matrixa Component 1 2 3 总资产贡献率X1(%) .946 .037 -.071 资产负债率X2(%) -.847 .085 .159 流动资产周转次数X3(次/年) .050 .976 -.172 成本费用利润率X4(%) .892 .211 -.154 产品销售率X5(%) -.180 -.183 .965 表2旋转过后的主成分矩阵 由上表可得,我们选取的5个经济效益指标被提取出了3个主成分,提取的3个主成分集中了5个原始量信息的89.948%。能够很好的反映5个经济效益指标。故三个公因子表示为: 其中iZ为原始变量的相应标准化变量。第一主成分对原始变量的贡献率为48.868%,第二主成分的贡献率为20.773% ,第三个主成分对原始变量的贡献率为20.307%,其累计贡献率为89.948%,结果表明前三个个主成分提取了原始变量的绝大部分信息。由上可知,第一主成分中1Z、2Z和4Z的系数绝对值较大,第二主成分中3Z
的系数绝对值较大,第三个成分中5Z的系数绝对值较大。因此,第一主成分主要由总资产贡献率、资产负债率和工业成本费用利润率组成,第二主成分主要由流动资产周转次数和产品销售率组成。因此,第一个公因子主要由“总资产贡献率”、“资产负债率”、“成本费用利用率”组成,该三个指标主要反映一个行业的盈利能力,所以第一个综合指标可以表示为“盈利能力”,第二个公因子可得主要反映行业的运行能力,第二个综合指标可以表示为“行业运行能力”,第三个综合指标可以表示为“市场能力”。我们把5个影响行业的经济效益的自变量最终用3个综合指标进行表示,接下来我们利用这三个综合指标对每个行业进行综合评价。
