多元统计分析论文1
多元统计聚类分析论文_多元统计分析论文

多元统计聚类分析论文_多元统计分析论文多元统计分析论文篇1多元统计分析课程教学探讨摘要:多元统计分析是统计学的一个重要分支,它在自然科学、社会科学、教育卫生以及经济金融等领域具有广泛的应用。
利用多元统计分析方法分析和处理实际数据、解决实际问题是统计学专业学生必备的基本能力,因此,如何进行多元统计分析课程的教学具有相当重要的意义。
本文从教学实践出发,对多元统计分析课程的教学进行了探索和实践,提出了一些教学方法。
关键词:以人为本;案例教学;软件编程;考试改革;创新教学多元统计分析是统计学中内容极其丰富、应用极其广泛的一个重要分支。
随着计算机和统计学的发展,它在自然科学、社会科学、教育卫生以及经济金融等领域中的应用越来越广泛,它已成为进行多元数据分析与处理的非常重要的工具之一。
随着社会的发展,我们常需要处理较为复杂的多维数据以及高维或超高维数据,特别地,对于统计学专业的学生,利用多元统计分析方法分析和处理日常生活中的多维数据是他们应该具备的基本能力。
因此,如何让学生很好地掌握一些基本的多元分析方法并能在实践中加以应用是我们统计学专业的教师应该思考的重要问题。
通过多年的实践教学,我们对多元统计分析课程的教学进行了探索和实践,主要在以下几个方面进行了探索和尝试。
一、转变教育观念,树立“以人为本”的教学理念教育的对象是大学生,教育的目的是以学生的终身发展为基础的。
在教学过程中,我们教师首先应转变教育观念,处处体现以学生为本的人文关怀与教育。
关注学生的思想、学生的需要以及在当今时代下学生所面临的挑战与机遇,争取成为学生的良师益友,建立良好的师生关系;通过案例教学、启发式教学等等多种教学方法,鼓励和促使学生积极参与课堂教学,变被动学习为主动学习,使学生成为课堂的主体;正视学生之间的个体差异,不歧视差生也不偏爱优等生,实施因材施教,使每个学生都得到不同程度的提高与进步。
二、注重案例教学,培养“学以致用”的学习意识三、结合软件教学,提高学生编程和数据处理能力多元分析方法分析和处理的数据是多维数据,通常维数较多,而且观测数据也较多,计算量都比较大,通常需要计算机才能实现。
多元统计分析论文
基于主成分分析的我国地区经济指标研究09统计班徐晓旺【摘要】地区经济的发展对我国现代化进程形成巨大的推动作用,而经济指标是评判地区发展水平的重要标志。
根据搜集的相应数据建立数据库,基于主成分分析、同时运用聚类分析以及判别分析的多元统计方法,对全国各地区的经济状况进行综合指标分析。
研究各省经济发展在全国的分布特征、筛选出具备可对比性的指标,进而探究造成差异的原因,同时具有针对性地提出相关建议。
【关键词】主成分分析;聚类分析;判别分析;地区经济指标一、引言随着社会的不断进步,经济发展的车轮将会继续滚动。
在整体水平提升的同时不难发现:我国各地区间发展势必存留着一定的差距,了解其具体的分布特征注定会是一个非常值得深入挖掘的信息。
结合对进出口总额、居民消费水平等9个经济指标的研究,致力于分析各地区硬件发展水平、人民生活状况的异同与经济发展的相关性。
本文将对中国31个省份地区的经济指标进行分析。
首先,应用主成分分析的方法对众多指标做降维处理并赋予各主成分以实际意义以获取综合性指标;进而,基于主成分分析结果通过聚类分析法把我国的31个地区分类;最后,根据聚类的结果建立判别函数同时运用判别分析将新疆、广东两个省份归类。
二、主成分分析搜集到的经济指标为:进出口总额、地区生产总值、固定资产投资、邮电业务量、客运量、货运量、公交车运营数、居民平均工资和居民消费水平这九项指标。
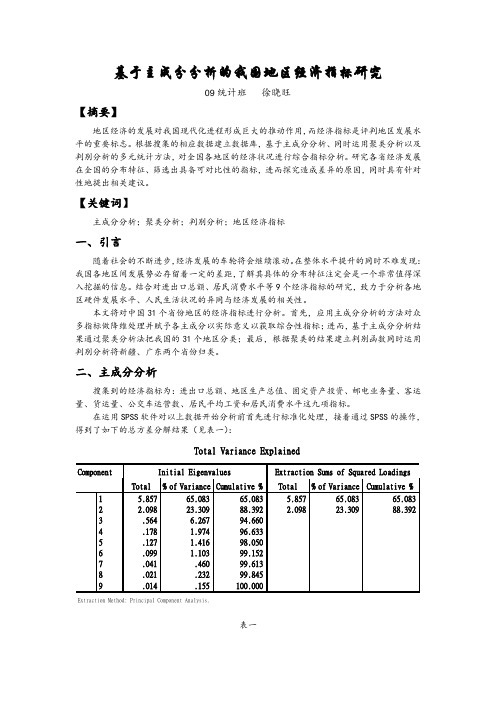
在运用SPSS软件对以上数据开始分析前首先进行标准化处理,接着通过SPSS的操作,得到了如下的总方差分解结果(见表一):表一由表一中结果可以看到保留2个主成分为宜,这2个主成分集中了原始9个变量信息的88.392%,可见效果比较好,这样原来的9个指标就可以通过这2个综合指标来反映。
此时,这2个主成分就起到了降维的作用。
通过SPSS进一步的操作还可以得到如下的主成分系数矩阵(见表二):表二由表二可以得出前2个主成分的线性组合为:Y1 = 0.852 X1 + 0.979 X2 + 0.821 X3 + 0.957 X4 + 0.885 X5 + 0.742 X6 + 0.967 X7 +0.226 X8 + 0.513 X9Y2 = 0.393 X1 - 0.113 X2 - 0.419 X3 - 0.032 X4 - 0.233 X5 - 0.483 X6 + 0.109 X7 +0.915 X8 + 0.786 X9通过对上述线性组合的观察,我们可以得出:在主成分1中进出口总额、地区生产总值、固定资产投资、邮电业务量、客运量、货运量和公交车运营数这几项指标的系数明显比主成分2的系数大,可以将Y1归类为地区经济发展中的硬件基础指标;在主成分2中平均工资和消费水平指标的系数最大,可以将Y2归类为地区经济发展中的居民生活指标。
多元统计分析课程论文

主消费因子 F1 得分前五名地区依次是上海、广东、浙江、北京、福建,其中 上海的得分为3.44500,广东的得分为2.3833,远远高于其他地区,说明上海、 广东主要消费支出远远高于其他地区, 与实际情况比较接近。 主消费因子 F1 最后 五名地区依次是新疆、河南、青海、甘肃、黑龙江,这些地区经济发展相对落后, 人均消费支出低,其主要消费支出也低,但与实际情况还存在差距,贵州城镇居 民消费应比黑龙江消费要低,黑龙江不应划为最低人均消费地区。 次消费因子 F2 得分前五名地区依次是北京、内蒙古、吉林、天津、黑龙江; 次消费因子 F2 最后五名地区依次是福建、贵州、广西、西藏、海南,衣着和医 疗器械人均消费,在实际消费过程中,人们不容易观察到,这个结论还缺乏一定 依据;综合得分 F 前五名地区依次是上海、北京、广东、浙江、天津;这五个地 区经济都发达,人均收入和消费支出都高,将这些地区分为一类比较切合实际。 综合得分 F 最后五名地区依次是新疆、云南、甘肃、贵州、青海, 这些地区 人口稀少,经济发达相当落后,人民收入和消费水平均处于全国最低水平,与人 们观察到的实际情况比较接近, 将这些地区分为一类, 其他地区则分为另外一类, 这样一来就可以将31个省、市、自治区就分为三类,第一类为因子综合得分前五 名地区,第三类为因子综合得分最后五名地区,其余地区则划分为第二类。这种 分类结果比较切合实际情况。 分类结果如下表: 类别 地区 第一类 上海、北京、广东、浙江、天津 第二类 其余地区(福建、山东、湖南等) 第三类 新疆、云南、甘肃、贵州、青海
以各因子的方差贡献率占两个因子总方差贡献率的比重作为权重进行加权汇总, 算出各地区的综合得分 F ,即 F (56.182 F1 27.662 F2 ) / 83.845 ,结果如下表:
多元统计分析课程论文

HUNAN UNIVERSITY 课程论文论文题目:有关我国居民消费因素的分析指导老师:学生名字:学生学号:专业班级:经济统计学院名称:xxx学院目录12...2.. .3. .. (3).. 310.15.18....19....20....有关我国居民消费因素的分析概述生活离不开消费,随着社会发展,生活水平提高,消费也在逐渐变化,并且随着经济发展,各个地区的发展水平的差异,消费也产生了不同的变化,此篇论文主要目的是利用多元统计的方法,借助spss软件,对我国31 个地区的居民消费情况进行分析。
了解我国31 个地区的居民消费情况与统计指标食品烟酒、衣着、居住等 8 个指标之间的一些联系。
并且通过因子得分,计算并排列出消费因素的综合得分,最后通过聚类分析,对我国31 个地区的居民消费情况做一个大致分类,进而对各个地区分类后的情况做一个分析和总结并结合文献以及资料提出一些意见和看法。
一 .引言消费在宏观经济学中,指某时期一人或一国用于消费品的总支出。
与经济活动有着密不可分的关系,消费作为社会再生产的最终阶段,是生产者生产产品的目的和导向。
如果没有了消费,生产的存在也会变得毫无意义,消费促进了生产,给生产带来了源动力。
消费者的消费需求,也推动了生产的发展。
并且消费促进了货币流通,提供了就业岗位,降低失业率,拉动了经济增长,最终有助于提高人民的生活水平。
消费是国民经济保持增长的动力,只有拉动消费需求的增长,才能促进投资,促进产业结构的调整、宏观经济的增长,满足人民的物质生活的需求,实现生活水平的提高。
故消费和生活水平有着密切的关系,从而,通过对我国居民消费水平的分析,不但可以直观了解到我国总的消费趋向,各地区不同的消费主导因素,还能客观反映我国总的生活水平也就是经济发展的大致情况。
统计年鉴中的八项指标:食品烟酒、衣着、居住、生活用及服务、交通通信、教育文化娱乐、医疗保健、其他用品及服务。
囊括了居民消费的全部项目,居民日常消费可以清楚地从数据中了解到。
多元统计分析论文范文精选3篇(全文)

多元统计分析论文范文精选3篇多元统计分析法是证券投资中非常重要的分析方法,它的理论内容包含了多个方面的理论方法,每个理论分析方法对证券投资有着不同的分析作用,应该对每个分析方法进行认真研究得出相关的结论,再应用到实际经济生活中。
1聚类分析在证券投资中的应用(1)定义:聚类分析是依据研究对象的特征对其进行分类、减少研究对象的数目,也叫分类分析和数值分析,是一种统计分析技术。
(2)在证券投资中应用聚类分析,是基于证券投资的各种基本特点而决定的。
证券投资中包含着非常多的动态的变化因素,要认真分析证券投资中各种因素的动态变化情况,找出合适的方法对这种动态情况进行把握规范处理,使投资分析更加的准确、精确。
1)弥补影响股票价格波动因素的不确定性证券市场受到非常多方面的影响,具有很大的波动性和不稳定性,这种波动性也造成了证券市场极不稳定的进展状态,这些状态的好坏对证券市场投资者和小股民有着非常重要的影响。
聚类分析的方法是建立在基础分析之上的,立足基础进展长远,并对股票的基本层面的因素进行量化分析,并认真分析掌握结果再应用于证券投资实践中,从股票的基本特征出发,从深层次挖掘股票的内在价值,并将这些价值发挥到最大的效用。
影响证券投资市场波动的因素非常多,通过聚类分析得出的数据更加的全面科学,对于投资者来说这些数据是进行理性投资必不可少的参考依据。
2)聚类分析深层次分析了与证券市场相关的行业和公司的成长性聚类分析是一种非常专业的投资分析方法,它善于利用证券投资过程中出现的各种数据来对证券所涉及的各种行业和公司进行具体的行业分析,这些数据所产生额模型是证券投资者进行证券投资必不可少的依据。
而所谓成长性是一种是一个行业和一个公司进展的变化趋势,聚类分析通过各种数据总结归纳出某个行业的进展历史和未来进展趋势,并不断的进行自我检测和自我更新。
并且,要在实际生活中更好的利用这种分析方法进行分析研究总结,就要有各种准确的数据来和不同成长阶段的不同参数,但是,猎取这种参数比较困难,需要在证券市场实际交易和对行业和公司的不断调查研究中才能得出正确的数据。
多元统计分析论文1

U浙江财经学院东方学院《多元统计分析》课程论文论文题目:2011年我国农村居民生活消费分析学生姓名徐妙学期2013年第二学期分院信息专业统计班级10统计1班学号1020430112教师彭武珍成绩2013年6月17日2011年我国农村居民生活消费分析摘要:改革开放以来,我国广大地区农村居民生活水平普遍有所提高,价值观念也发生了许多变化,但是,他们的消费水平与城镇居民相比仍然偏低。
本文综合了因子分析与聚类分析,先进行因子分析, 再用因子分析的结果进行聚类分析,本文较多运用了31个省份的因子得分,计算出单因子情况下31个省份的得分和31个省份在八项消费产生的3个因子上的综合得分, 再把该得分作为31个省份的属性, 采用离差平方和(ward)方法进行聚类, 最后将城市分为四层,对整体进行综合评价和说明。
关键词:因子分析;聚类分析;综合评价1引言当前我国农村居民的消费结构主要是偏重物质生活消费,精神生活消费的比例较低。
商品消费主要集中于食品、居住以及日常生活物质消费等方面。
而交通通讯、文教娱乐用品及服务等精神生活消费品消费比例较小。
旅游休闲、家用汽车、耐用消费品等消费在绝大多数农村地区还处于未开发状态。
因此,笔者就我国农村居民生活消费结构进行因子分析和聚类分析,以期对农村居民生活消费的问题作一研究,并以此寻求合理的解决思路。
2因子分析2.1因子分析统计思想因子分析模型是主成分分析的推广。
它也是利用降维德思想,由研究原始变量相关矩阵内部的依赖关系出发,把一些具有错综复杂关系的变量归结为少数几个综合因子的一种多变量统计分析方法。
其基本思想是根据相关性大小把原始变量分组,使得同组内的变量间相关性较高,而不同组的变量的相关性则较低。
因子分析不仅可以用来研究变量之间的相关关系,还可以用来研究样品之间的相关关系。
2.2因子的确定利用2011年各地区农村居民家庭平均每人生活消费支出资料(见附表一,摘自《中国统计年鉴(2012)》),做因子相关性分析得:表1 相关矩阵表食品衣着居住家庭设备及用品文教娱乐交通通信医疗保健其他相关食品 1.000 .760 .796 .831 .839 .923 .786 .919 衣着.760 1.000 .789 .778 .848 .883 .845 .793居住.796 .789 1.000 .888 .814 .843 .846 .846家庭设备及用品.831 .778 .888 1.000 .840 .855 .811 .825 文教娱乐.839 .848 .814 .840 1.000 .896 .883 .892交通通信.923 .883 .843 .855 .896 1.000 .874 .879医疗保健.786 .845 .846 .811 .883 .874 1.000 .862其他.919 .793 .846 .825 .892 .879 .862 1.000 Sig.(单侧)食品.000 .000 .000 .000 .000 .000 .000 衣着.000 .000 .000 .000 .000 .000 .000居住.000 .000 .000 .000 .000 .000 .000家庭设备及用品.000 .000 .000 .000 .000 .000 .000 文教娱乐.000 .000 .000 .000 .000 .000 .000交通通信.000 .000 .000 .000 .000 .000 .000医疗保健.000 .000 .000 .000 .000 .000 .000其他.000 .000 .000 .000 .000 .000 .000 由上面的结果可知,原始变量之间有较强的相关性,进行因子分析是合适的。
多元统计分析论文

河北联合大学多元统计课程论文论文题目:对中国各地区综合实力测评学院:理学院专业:统计学班级:统计1班姓名:侯雅琴学号:指导教师:高艳目录摘要、关键字、引言 (1)1 数据说明 (2)2 因子分析 (2)3 聚类分析 (7)4 判别分析 (9)5 结果分析 (12)6 参考文献 (13)附表 (14)对中国各地区综合实力测评【摘要】本文对中国各地区综合实力进行测评,以31个地区2010年的10项指标数据为样本,采用因子分析对描述各地区的实力的各项指标变量进行分析,以聚类分析和判别分析相结合对地区发展类型进行分析,再利用各指标变量间的相关性进行分析,得出相关结论以分析各地区的发展情况。
【关键词】各地区综合实力测评因子分析聚类分析判别分析引言:在这样一个信息时代,只有全面的可持续的发展才是衡量一个地区综合实力的指标,仅仅是经济发展情况不再能全面具体的体现一个地区的综合实力,经济发展水平、科技发展水平、能源储量和利用率、基础设施建设、文化发展水平等等,这些综合的因素才是体现一个地区真正的面貌,单纯的GDP指标并不能完全反映一个地区的经济发展水平,为了克服单纯GDP指标的缺陷,我们在GDP指标的基础上,综合考虑其他各方面的发展指数,本文就外商投资进出口总额、地区生产总值、地区运输路线总长度、医疗卫生室数量、创新产品项目数、创新经费、高校数目、等10个指标变量对31地区的综合实力进行测评,通过因子分析、聚类分析、等多元统计方法对各指标变量以及各地区进行统筹分析,以总结促进各地区和谐可持续发展的原因。
一、数据说明对各地区进行综合测评的各指标变量:原始数据来源:《中国统计年鉴——2010》原始数据见附录表-1二、因子分析:1.考察原有指标变量是否适合因子分析(原有变量之间是否存在一定的线性关系):借助变量的相关系数矩阵,KMO和巴特利特球度检验,进行分析。
表—2由相关矩阵可以看出外商投资进出口总额与地区生产总值、创新产品项目数、创新经费、社会服务设施数的相关系数较高(相关系数值均大于0.5),五个变量间呈现较强的线性关系,农业用地面积和林地面积高度相关,医疗卫生室数量和运输路线长度也具有较高的相关性,都可从中提取公共因子,进行因子分析。
浅谈多元统计相关论文

浅谈多元统计相关论文摘要:我国中药发展已有悠久历史,中药大多采用复方制剂,以其复方疗效显著而越来越受到重视,在其成分分析中,多元统计分析方法的运用,本质上是一种多变量协同考量的思路。
本文通过对以往多元统计分析方法在中药成分分析数据中的应用作整理总结,对今后相关研究提供理论依据。
关键词:多元统计分析中药成分分析中药物质基础的阐明和科学质量控制方法的建立是中药现代化和国际化的关键,在化学计量学中,多元统计分析方法得到了很好的应用,通过优化了化学量测过程,提高分析效果,应用统计分析方法及其他数学方法和计算机软件的应用对其数据进行整理,已较好的阐明了中药物质成分,结构与其性能之间的复杂关系。
一、应用现状1.1方法在中药成分分析中,多元统计分析方法如多元回归,多元相关分析,逐步回归分析,最大似然法,判别分析,聚类分析和主成分分析,利用电子计算机能迅速而大量地处理实验数据,还广泛采用了蒙特卡洛Monte Carlo统计模拟法,都能在某一特定方面很好的说明其成分,但尚未有统一理论支撑整个体系,也是国内着力于建立中成药数据库的缘由之一。
要进一步定性定量的确定中药成分,并很好的分析中药成分还需不断努力。
在应用中,应用最多的为多元线性回归和Logistic回归方法,其次是通径分析,因子分析和聚类分析的运用较少,比如风险模型,典型相关,MCA分析和Probit分析。
1.1.1成分提取在对中药复方有效成分的整体提取方法,指纹图谱条件优化及定量评价指标,以及基于药理活性的组方条件优化的基础上,化学模式识别方法引入中药分析体系,模式识别,指通过相关软件等用数学方法来实现模式的自动处理和判别,模式识别可大致分为用监督模式识别判别分析方法,是实现规定分类的标准和种类的数模,并且通过大批已知样本的信息处理找出规律,再预报未知样本的类型,如贝叶斯法Bayes逐步判别分析方法,人工神经网络判别法等,无监督模式识别聚类分析方法,是对一组尚无明确分类的样本,根据它们所变现的变量特征,按相似程度的大小加以归类,最终通过信息处理找出合适的分类方法并实现样本的分类,如系统聚类分析,模糊聚类分析等以及基于特征投影的降维显示方法,另外还有一类基于特征投影的降维显示方法,如主成分分析方法,基于偏最小二乘法的降维方法等,中药的化学模式识别方法可以从复杂的化学测量数据出发,进一步揭示复杂化合物之间的隐藏规律,为中药整体研究提供十分有用的信息。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
U浙江财经学院东方学院《多元统计分析》课程论文论文题目:2011年我国农村居民生活消费分析学生姓名徐妙学期2013年第二学期分院信息专业统计班级10统计1班学号1020430112教师彭武珍成绩2013年6月17日2011年我国农村居民生活消费分析摘要:改革开放以来,我国广大地区农村居民生活水平普遍有所提高,价值观念也发生了许多变化,但是,他们的消费水平与城镇居民相比仍然偏低。
本文综合了因子分析与聚类分析,先进行因子分析, 再用因子分析的结果进行聚类分析,本文较多运用了31个省份的因子得分,计算出单因子情况下31个省份的得分和31个省份在八项消费产生的3个因子上的综合得分, 再把该得分作为31个省份的属性, 采用离差平方和(ward)方法进行聚类, 最后将城市分为四层,对整体进行综合评价和说明。
关键词:因子分析;聚类分析;综合评价1引言当前我国农村居民的消费结构主要是偏重物质生活消费,精神生活消费的比例较低。
商品消费主要集中于食品、居住以及日常生活物质消费等方面。
而交通通讯、文教娱乐用品及服务等精神生活消费品消费比例较小。
旅游休闲、家用汽车、耐用消费品等消费在绝大多数农村地区还处于未开发状态。
因此,笔者就我国农村居民生活消费结构进行因子分析和聚类分析,以期对农村居民生活消费的问题作一研究,并以此寻求合理的解决思路。
2因子分析2.1因子分析统计思想因子分析模型是主成分分析的推广。
它也是利用降维德思想,由研究原始变量相关矩阵内部的依赖关系出发,把一些具有错综复杂关系的变量归结为少数几个综合因子的一种多变量统计分析方法。
其基本思想是根据相关性大小把原始变量分组,使得同组内的变量间相关性较高,而不同组的变量的相关性则较低。
因子分析不仅可以用来研究变量之间的相关关系,还可以用来研究样品之间的相关关系。
2.2因子的确定利用2011年各地区农村居民家庭平均每人生活消费支出资料(见附表一,摘自《中国统计年鉴(2012)》),做因子相关性分析得:表1 相关矩阵表食品衣着居住家庭设备及用品文教娱乐交通通信医疗保健其他相关食品 1.000 .760 .796 .831 .839 .923 .786 .919 衣着.760 1.000 .789 .778 .848 .883 .845 .793居住.796 .789 1.000 .888 .814 .843 .846 .846家庭设备及用品.831 .778 .888 1.000 .840 .855 .811 .825 文教娱乐.839 .848 .814 .840 1.000 .896 .883 .892交通通信.923 .883 .843 .855 .896 1.000 .874 .879医疗保健.786 .845 .846 .811 .883 .874 1.000 .862其他.919 .793 .846 .825 .892 .879 .862 1.000 Sig.(单侧)食品.000 .000 .000 .000 .000 .000 .000 衣着.000 .000 .000 .000 .000 .000 .000居住.000 .000 .000 .000 .000 .000 .000家庭设备及用品.000 .000 .000 .000 .000 .000 .000文教娱乐.000 .000 .000 .000 .000 .000 .000 交通通信.000 .000 .000 .000 .000 .000 .000 医疗保健.000 .000 .000 .000 .000 .000 .000 其他.000 .000 .000 .000 .000 .000 .000由上面的结果可知,原始变量之间有较强的相关性,进行因子分析是合适的。
因子相关相关矩阵反映我国农村居民消费结构的各指标之间存在较高的相关性,而变量间存在较为明显的相关关系是应用因子分析提取主因子,并以此为依据构造评价体系的基础。
因此存在可以采用因子分析进行分析的可能。
2.3因子分析过程共同度描述的是变量Xi(i=1,2,…,m)对m个因子的依赖程度,也就是用m个因子描述变量的有效性。
本文用因子分析法,选取特征值r>0.2的变量作为主因子并计算其共同度。
表2 公因子方差分析表初始提取食品 1.000 .850衣着 1.000 .810居住 1.000 .8411.000 .842家庭设备及用品文教娱乐 1.000 .890交通通信 1.000 .926医疗保健 1.000 .863其他 1.000 .891提取方法:主成份分析。
由表可以看出,主因子对每个变量指标有很强的解释力。
表3解释的方差分析表成份初始特征值提取平方和载入合计方差的% 累积% 合计方差的% 累积%1 6.914 86.420 86.420 6.914 86.420 86.4202 .301 3.769 90.1893 .274 3.425 93.6144 .182 2.275 95.8895 .133 1.667 97.5566 .100 1.250 98.8067 .071 .890 99.6968 .024 .304 100.000提取方法:主成份分析。
累计方差贡献率达到93.61%,说明主因子对变量能够起到较好的概括作用,其中第一主因子起到了尤其重要的作用,其旋转后的方差贡献率达到86.42%。
因子载荷矩阵的元素ai代表了变量Xi与因子Fi线性联系的紧密程度,而第j列的因子载荷量a1,a2,…,ai,则说明了第j个因子Fi与各变量的联系程度,在实际中,常常根据该列载荷中绝对值较大的载荷所对应的变量来说明这个因子的意义。
表4进行因子旋转分析表Component1 2 3食品.253 .763 .564衣着.857 .339 .303居住.499 .386 .735家庭设备及服务.487 .453 .710交通和通讯.573 .614 .513文教娱乐用品及服.653 .573 .388务医疗保健.848 .279 .371其他商品和服务.384 .864 .264由图可知:第一主因子在衣着、医疗保健2个指标上的系数比较大,其主要反应的是生活消费水平的提高;第二主因子在食品、交通和通讯、其他商品及服务3个指标上的系数比较大,其主要反映的是日常生活中最基本的消费情况;第三主因子在居住、家庭设备及服务、文教娱乐用品及服务等几个指标上的系数比较大,其主要反映的是生活消费水平进一步提高的情况。
3个主因子从不同的侧面反映了居民的生活质量,从整体来看,则反映了农村居民从生存型消费、数量型消费向发展型消费、质量型消费的发展方向。
第一主因子可以解释原始数据全部方差的84.131%,第二主因子可以解释原始数据全部方差的 6.933%,第三主因子可以解释原始数据全部方差的3.436%。
由此看出,我国现阶段农村居民消费的钢性支出是维护基本生活的吃、必要的的交通、通讯和商品及服务。
分析得综合因子得分:地区综合因子得分北京 2.791644浙江 1.293027黑龙江 1.226903吉林 1.087179上海0.969788辽宁0.89994内蒙古0.703707山西0.433833新疆0.414503宁夏0.355606天津0.3066陕西0.206774江苏0.201475青海0.026401河北0.002125山东-0.0682河南-0.25941重庆-0.40694西藏-0.4568安徽-0.53699福建-0.55679甘肃-0.56405湖北-0.65717江西-0.73795云南-0.75898湖南-0.77288贵州-0.85042四川-0.85338海南-1.07374广西-1.16289广东-1.202923聚类分析下面用spss软件对所取2011年的数据进项聚类分析,以便了解我国农村消费结构。
我们采用系统聚类法。
图1聚类分析结果图由此可得综合因子前10位排名:北京、天津、河北、山西、内蒙古、辽宁、吉林、黑龙江、上海、江苏。
4进一步发展我国农村消费的对策建议第一,大力发展农村经济。
努力提高农民收入。
为了加速农村经济的发展,必须夯实农村经济发展基础。
进一步加强路、水、电等基础设施的建设工作,另外,对文化娱乐设施的建设也不能忽略,要加快并保质保量的建设农村文教娱乐设施。
加强对“农家乐”等副业的扶持,积极发展乡村旅游,以此副业为龙头,带动农民步入市场,创收增收。
此外。
必须调整农业的产品结构。
开发名优特新产品,增加优质产品的比重。
第二,完善农村社会保障制度,降低农民的储蓄趋向,拉动消费。
因此,必须进一步加强农村医疗保障力度。
第三,建立和完善农村金融机构,加大资金投入。
提高农村金融供给能力。
同时,针对农村特殊的金融环境制定一套完整的法律,使农村金融活动更为合理健康的运行。
另外,建立信用风险测评机制,进一步完善农村金融事业,使之稳定快速发展。
参考文献[1] 吴栋、李乐夫、李阳子:《近年居民消费结构统计分析的研究--关于因子分析和聚类分析的应用》,清华大学经济管理学院北京;[2] 何晓群主编:《多元统计分析(第三版)》,中国人民大学出版社;[3] 《中国统计年鉴》,2012年。
附录附表1地区支出合计食品衣着居住家庭设备及用品交通通信文教娱乐医疗保健其他全国4733.35 1651.29 341.07 930.24 308.64 547.03 396.36 436.75 121.98 北京11021.2 3541.38 862.26 2346.82 714.44 1228.19 1003.67 1035.18 289.30 天津6673.27 2324.06 611.50 1346.30 352.28 781.55 542.12 571.65 143.82 河北4514.19 1396.02 333.92 1077.17 316.88 520.18 315.41 434.67 119.95 山西4355.78 1499.61 401.78 823.93 243.84 458.76 448.44 349.29 130.12 内蒙古4827.99 1479.67 394.79 788.44 243.15 728.94 525.89 534.18 132.92 辽宁5081.40 1826.52 446.12 825.00 225.38 577.71 549.96 482.85 147.86 吉林4891.64 1564.24 397.47 845.67 232.29 564.26 456.75 673.57 157.38 黑龙江5024.72 1844.29 473.78 744.21 209.46 576.31 464.71 573.59 138.36 上海10834.1 4303.50 644.52 1804.36 648.89 1308.92 916.07 908.63 299.21 江苏7709.07 2468.25 554.77 1359.19 502.82 923.89 1044.64 645.59 209.93 浙江9792.50 3554.82 717.03 1604.96 542.69 1380.56 846.10 921.31 225.03 安徽4499.35 1645.98 296.98 836.54 304.19 475.19 376.18 440.53 123.75 福建6112.99 2654.57 395.41 982.89 357.12 728.49 506.71 321.20 166.60 江西4029.49 1486.74 233.58 878.30 277.15 393.34 319.39 346.68 94.30 山东5623.58 1831.38 398.90 1126.88 411.32 753.05 482.66 508.38 111.02 河南4047.87 1323.43 362.78 811.35 327.92 427.86 278.20 399.71 116.62 湖北4382.95 1337.87 270.97 1077.19 359.36 414.36 341.87 438.20 143.14湖南4355.70 1557.91 260.34 931.91 330.16 421.67 346.62 396.54 110.55 广东6149.94 2817.84 277.31 1080.18 301.13 682.54 404.15 398.54 188.27 广西3522.59 1212.52 123.93 962.67 241.61 384.81 218.72 301.25 77.07 海南3781.63 1797.48 139.81 656.38 176.33 370.34 224.91 290.13 126.25 重庆3734.59 1360.35 308.95 536.73 348.24 401.65 334.84 375.26 68.57 四川3924.27 1424.49 281.87 713.44 300.87 431.14 276.64 413.12 82.71 贵州2670.73 880.96 186.22 619.85 192.78 304.51 183.03 246.28 57.10 云南3205.35 1147.46 209.05 644.57 208.05 393.04 241.13 309.25 52.80 西藏2235.62 880.55 331.08 326.29 185.98 348.86 40.91 65.78 56.16 陕西4254.92 1112.06 285.34 1104.74 279.86 406.68 405.56 533.44 127.24 甘肃3151.10 1060.68 246.67 570.31 198.05 366.56 292.71 339.28 76.85 青海3920.15 1103.73 346.75 1088.03 271.68 450.88 265.43 308.08 85.57 宁夏4209.55 1245.44 380.00 935.22 264.64 483.40 324.36 444.69 131.79 新疆3889.69 1138.12 368.37 976.36 194.43 530.59 229.66 376.87 75.28。
