武汉理工大学多元统计分析课程设计论文
多元统计聚类分析论文_多元统计分析论文

多元统计聚类分析论文_多元统计分析论文多元统计分析论文篇1多元统计分析课程教学探讨摘要:多元统计分析是统计学的一个重要分支,它在自然科学、社会科学、教育卫生以及经济金融等领域具有广泛的应用。
利用多元统计分析方法分析和处理实际数据、解决实际问题是统计学专业学生必备的基本能力,因此,如何进行多元统计分析课程的教学具有相当重要的意义。
本文从教学实践出发,对多元统计分析课程的教学进行了探索和实践,提出了一些教学方法。
关键词:以人为本;案例教学;软件编程;考试改革;创新教学多元统计分析是统计学中内容极其丰富、应用极其广泛的一个重要分支。
随着计算机和统计学的发展,它在自然科学、社会科学、教育卫生以及经济金融等领域中的应用越来越广泛,它已成为进行多元数据分析与处理的非常重要的工具之一。
随着社会的发展,我们常需要处理较为复杂的多维数据以及高维或超高维数据,特别地,对于统计学专业的学生,利用多元统计分析方法分析和处理日常生活中的多维数据是他们应该具备的基本能力。
因此,如何让学生很好地掌握一些基本的多元分析方法并能在实践中加以应用是我们统计学专业的教师应该思考的重要问题。
通过多年的实践教学,我们对多元统计分析课程的教学进行了探索和实践,主要在以下几个方面进行了探索和尝试。
一、转变教育观念,树立“以人为本”的教学理念教育的对象是大学生,教育的目的是以学生的终身发展为基础的。
在教学过程中,我们教师首先应转变教育观念,处处体现以学生为本的人文关怀与教育。
关注学生的思想、学生的需要以及在当今时代下学生所面临的挑战与机遇,争取成为学生的良师益友,建立良好的师生关系;通过案例教学、启发式教学等等多种教学方法,鼓励和促使学生积极参与课堂教学,变被动学习为主动学习,使学生成为课堂的主体;正视学生之间的个体差异,不歧视差生也不偏爱优等生,实施因材施教,使每个学生都得到不同程度的提高与进步。
二、注重案例教学,培养“学以致用”的学习意识三、结合软件教学,提高学生编程和数据处理能力多元分析方法分析和处理的数据是多维数据,通常维数较多,而且观测数据也较多,计算量都比较大,通常需要计算机才能实现。
多元统计分析课程毕业论文

四川理工学院《多元统计分析课程设计》报告题目: 中国国有控股工业行业的经济效益评价学生:雷鹏程何君李西京曾学成白俊明专业:统计学指导教师:柏宏斌四川理工学院理学院二零一四年十二月中国国有控股工业行业的经济效益评价摘要本文主要研究了中国国有控股工业行业的经济效益,对反映行业经济效益的总资产贡献率、资产负债率、流动资产周转次数、工业成本费用利润率和产品销售率等五个经济指标进行主成分分析,提取反映行业盈利能力和市场能力的两个综合指标。
然后通过因子分析法分析反映经济效益的各指标的内部结构,表明行业经济效益主要由盈利能力和市场能力两个公因子决定。
根据各行业在盈利能力上的得分和市场能力上的得分将工业行业分为五类,并对各行业经济效益进行综合评价。
然后用聚类分析对综合评价结果进行验证,表明综合评价较为客观合理。
最后,本文给出相应的政策建议。
关键字:主成分分析、因子分析、聚类分析。
一、引言改革开放以来,工业始终是我国经济发展的主要支柱。
作为社会主义国家,我国国有及国有控股工业行业掌控着国家工业发展命脉,对国民经济、社会协调发展具有巨大推动作用。
因此,考核工业行业的经济效益,对挖掘重点行业和弱势行业,提高整个国有工业企业的经济效益等具有重大的现实意义。
企业或行业的经济效益由众多因素来刻画,目前反映行业经济效益主要有总资产贡献率、资产负债率、流动资产周转次数、工业成本费用利润率和产品销售率等五个经济指标1。
这些众多指标虽然能从多方面对行业的经济效益进行全面考察,但也在一定程度增加了分析问题的复杂性。
在损失少量信息的前提下,设计一个或少数几个综合指标,并用较少的综合指标对工业经济效益进行分析评价,能够简化问题。
此外,挖掘出反映经济效益的众多指标的内在基本结构,有助于指出各行业经济效益的主要决定因素及瓶颈,也有助于对各行业经济效益进行综合评价。
二、文献综述大量国内文献从灰色系统理论、多元统计分析方法、层次分析法、模糊综合评判法、数据包络分析法等理论与方法,考察了中国各行业、企业或地区经济效益的研究与综合评价。
多元统计分析 课程论文.doc

HUNAN UNIVERSITY 课程论文论文题目:有关我国居民消费因素的分析指导老师:学生名字:学生学号:专业班级:经济统计学院名称: xxx学院目录概述 (1)一、引言 (2)二、数据概述系 (2)三、分析方法 (3)四、数据分析 (3)(一)相关分析 (3)(二)因子分析 (10)(三)聚类分析 (15)五、分析与建议 (18)六、心得体会 (19)参考文献 (20)有关我国居民消费因素的分析概述生活离不开消费,随着社会发展,生活水平提高,消费也在逐渐变化,并且随着经济发展,各个地区的发展水平的差异,消费也产生了不同的变化,此篇论文主要目的是利用多元统计的方法,借助spss软件,对我国31个地区的居民消费情况进行分析。
了解我国31个地区的居民消费情况与统计指标食品烟酒、衣着、居住等8个指标之间的一些联系。
并且通过因子得分,计算并排列出消费因素的综合得分,最后通过聚类分析,对我国31个地区的居民消费情况做一个大致分类,进而对各个地区分类后的情况做一个分析和总结并结合文献以及资料提出一些意见和看法。
一.引言消费在宏观经济学中,指某时期一人或一国用于消费品的总支出。
与经济活动有着密不可分的关系,消费作为社会再生产的最终阶段,是生产者生产产品的目的和导向。
如果没有了消费,生产的存在也会变得毫无意义,消费促进了生产,给生产带来了源动力。
消费者的消费需求,也推动了生产的发展。
并且消费促进了货币流通,提供了就业岗位,降低失业率,拉动了经济增长,最终有助于提高人民的生活水平。
消费是国民经济保持增长的动力,只有拉动消费需求的增长,才能促进投资,促进产业结构的调整、宏观经济的增长,满足人民的物质生活的需求,实现生活水平的提高。
故消费和生活水平有着密切的关系,从而,通过对我国居民消费水平的分析,不但可以直观了解到我国总的消费趋向,各地区不同的消费主导因素,还能客观反映我国总的生活水平也就是经济发展的大致情况。
统计年鉴中的八项指标:食品烟酒、衣着、居住、生活用及服务、交通通信、教育文化娱乐、医疗保健、其他用品及服务。
多元统计分析论文
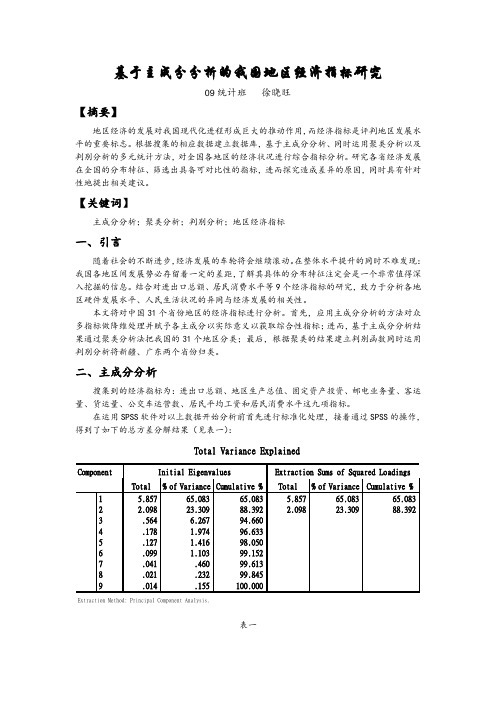
基于主成分分析的我国地区经济指标研究09统计班徐晓旺【摘要】地区经济的发展对我国现代化进程形成巨大的推动作用,而经济指标是评判地区发展水平的重要标志。
根据搜集的相应数据建立数据库,基于主成分分析、同时运用聚类分析以及判别分析的多元统计方法,对全国各地区的经济状况进行综合指标分析。
研究各省经济发展在全国的分布特征、筛选出具备可对比性的指标,进而探究造成差异的原因,同时具有针对性地提出相关建议。
【关键词】主成分分析;聚类分析;判别分析;地区经济指标一、引言随着社会的不断进步,经济发展的车轮将会继续滚动。
在整体水平提升的同时不难发现:我国各地区间发展势必存留着一定的差距,了解其具体的分布特征注定会是一个非常值得深入挖掘的信息。
结合对进出口总额、居民消费水平等9个经济指标的研究,致力于分析各地区硬件发展水平、人民生活状况的异同与经济发展的相关性。
本文将对中国31个省份地区的经济指标进行分析。
首先,应用主成分分析的方法对众多指标做降维处理并赋予各主成分以实际意义以获取综合性指标;进而,基于主成分分析结果通过聚类分析法把我国的31个地区分类;最后,根据聚类的结果建立判别函数同时运用判别分析将新疆、广东两个省份归类。
二、主成分分析搜集到的经济指标为:进出口总额、地区生产总值、固定资产投资、邮电业务量、客运量、货运量、公交车运营数、居民平均工资和居民消费水平这九项指标。
在运用SPSS软件对以上数据开始分析前首先进行标准化处理,接着通过SPSS的操作,得到了如下的总方差分解结果(见表一):表一由表一中结果可以看到保留2个主成分为宜,这2个主成分集中了原始9个变量信息的88.392%,可见效果比较好,这样原来的9个指标就可以通过这2个综合指标来反映。
此时,这2个主成分就起到了降维的作用。
通过SPSS进一步的操作还可以得到如下的主成分系数矩阵(见表二):表二由表二可以得出前2个主成分的线性组合为:Y1 = 0.852 X1 + 0.979 X2 + 0.821 X3 + 0.957 X4 + 0.885 X5 + 0.742 X6 + 0.967 X7 +0.226 X8 + 0.513 X9Y2 = 0.393 X1 - 0.113 X2 - 0.419 X3 - 0.032 X4 - 0.233 X5 - 0.483 X6 + 0.109 X7 +0.915 X8 + 0.786 X9通过对上述线性组合的观察,我们可以得出:在主成分1中进出口总额、地区生产总值、固定资产投资、邮电业务量、客运量、货运量和公交车运营数这几项指标的系数明显比主成分2的系数大,可以将Y1归类为地区经济发展中的硬件基础指标;在主成分2中平均工资和消费水平指标的系数最大,可以将Y2归类为地区经济发展中的居民生活指标。
多元统计分析实验报告_聚类分析

武汉理工大学
实验(实训)报告项目名称实验2―聚类分析
实验报告2
聚类分析(设计性实验)
实验原理:聚类分析的目的是将分类对象按一定规则分为若干类,这些类不是事先给定的,而是根据数据的特征确定的。
在同一类里的这些对象在某种意义上倾向于彼此相似,而在不同的类里的对象倾向于不相似。
系统聚类法是聚类分析中用的最多的一种,其基本思想是:开始将n个对象各自作为一类,并规定对象之间的距离和类与类之间的距离,然后将距离最近的两类合并成一个新类,
E0
N20
(1
(2
(3
(4)用最大距离法将11种语言聚为3类,并将聚类结果存储在一个SPSS数据文件中。
实验题目二:
下表给出了2010年湖北省省各地区的人均各项消费支出情况。
表-1:2010年湖北省各地区人均各项消费支出
(1((2(3
(4
实验题目一分析报告:1.实验(实训)过程(步骤、记录、数据、程序等)
2.结论(结果、分析)
实验题目二分析报告:1.实验(实训)过程(步骤、记录、数据、程序等)
2.结论(结果、分析)。
多元统计分析论文

多元统计分析论文关于各地区固定资产投资价格指数的分析摘要:本文主要通过主成分分析、聚类分析和判别分析对全国30多个省的固定资产投资指数、建筑安装工程指数、设备工器具购置指数、其他费用指数进行分析。
关键词:主成分分析、欧氏距离、系统聚类分析、判别分析Summary:This article mainly through the principal components analysis, the cluster analysis and the distinction analysis to the national more than 30 province investment in the fixed assets indices, construction and installation the project index, the equipment labor appliance purchase index, other expense index carries on the analysis.Keywords:Principal Components Analysis、Euclidean distance、Discriminant analysis一、导言:注意微量信息引起的巨变,蝴蝶效应就是微量信息在一定条件下发生作用的过程。
在我们的经济活动中,每天的信息是大量的,这就要求我们从中发现那些对经济能产生最大影响的信息,有些是微量信息,有些是次级别的信息,本文的各地区固定资产投资价格指数就是一个非常值得深入发觉的信息。
该指数可以准确地反映固定资产投资中涉及的各类投资品和取费项目价格变动趋势和变动幅度,消除按现价计算的固定资产投资指标中的价格变动因素,真实地反映固定资产投资的规模、速度、结构和效益,为国家科学地制定、检查固定资产投资计划并提高宏观调控水平,为完善国民经济核算体系提供科学的、可靠的依据。
统计学专业基础课与专业课之间的典型相关分析

统计学专业基础课与专业课之间的典型相关分析摘要本文基于统计学系0301-0302两个班的66名学生17门课程(包括专业基础课和专业课)的考试成绩,运用典型相关分析法研究了统计学系基础课和专业课的相关程度。
通过运用统计分析软件SAS运行得到变量间的相关系数以及标准化后的典型相关系数,进而求出典型相关变量。
最后结合分析结果和实际情况对教学提了一点小小的建议。
关键词:基础课;专业课;典型相关分析;典型相关系数Canonical Correlation Analysis Between The Major and BasicSubjects of The Statistics MajorAbstractWith the method of canonical correlation analysis,I study about the correlation between the major and basic subjects of the statistics major.The research is based on the examination scores of66students of classes0301and0302who are in the major of statistics,including only17 subjects,the major and basic subjects.The article then gives the standard canonical correlations between the variables from which we can know the canonical correlative variables.In the end,I give some suggestions about education,according to the output of the analysis and the matter of fact.Key word:basic subject,major,canonical correlation,canonical coefficients1引言对于统计学系的学生来说,对数学理论的理解和掌握要求比较高,而且更重要的是要做到融会贯通,举一反三,学会理论联系实际,并利用统计分析的方法来解决日常生产生活中的问题,因而专业基础课程(如数学分析和高等代数等)的学习无疑是相当重要的,因为它直接关系到后续专业课的学习效果。
多元统计分析课程论文

HUNAN UNIVERSITY 课程论文论文题目:有关我国居民消费因素的分析指导老师:学生名字:学生学号:专业班级:经济统计学院名称:xxx学院目录12...2.. .3. .. (3).. 310.15.18....19....20....有关我国居民消费因素的分析概述生活离不开消费,随着社会发展,生活水平提高,消费也在逐渐变化,并且随着经济发展,各个地区的发展水平的差异,消费也产生了不同的变化,此篇论文主要目的是利用多元统计的方法,借助spss软件,对我国31 个地区的居民消费情况进行分析。
了解我国31 个地区的居民消费情况与统计指标食品烟酒、衣着、居住等 8 个指标之间的一些联系。
并且通过因子得分,计算并排列出消费因素的综合得分,最后通过聚类分析,对我国31 个地区的居民消费情况做一个大致分类,进而对各个地区分类后的情况做一个分析和总结并结合文献以及资料提出一些意见和看法。
一 .引言消费在宏观经济学中,指某时期一人或一国用于消费品的总支出。
与经济活动有着密不可分的关系,消费作为社会再生产的最终阶段,是生产者生产产品的目的和导向。
如果没有了消费,生产的存在也会变得毫无意义,消费促进了生产,给生产带来了源动力。
消费者的消费需求,也推动了生产的发展。
并且消费促进了货币流通,提供了就业岗位,降低失业率,拉动了经济增长,最终有助于提高人民的生活水平。
消费是国民经济保持增长的动力,只有拉动消费需求的增长,才能促进投资,促进产业结构的调整、宏观经济的增长,满足人民的物质生活的需求,实现生活水平的提高。
故消费和生活水平有着密切的关系,从而,通过对我国居民消费水平的分析,不但可以直观了解到我国总的消费趋向,各地区不同的消费主导因素,还能客观反映我国总的生活水平也就是经济发展的大致情况。
统计年鉴中的八项指标:食品烟酒、衣着、居住、生活用及服务、交通通信、教育文化娱乐、医疗保健、其他用品及服务。
囊括了居民消费的全部项目,居民日常消费可以清楚地从数据中了解到。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖北省各地区经济差异的多元统计分析摘要本文通过多元统计分析的方法,对湖北省各地区主要的经济指标进行因子分析和方差分析,进而可以得出湖北省12个城市的经济发展水平的差异,由因子分析的结果可知,这12个城市的综合经济实力从大到小的排名依次为武汉、宜昌、襄樊、黄石、荆州、十堰、鄂州、荆门、随州、孝感、黄冈、咸宁。
由方差分析的结果可知,以武汉为中心,根据地理位置将这12个城市划分为四个地区:武汉以东的地区(黄石、鄂州、黄冈)、武汉以南的地区(孝感、荆州)、武汉以西的地区(宜昌、荆门、随州)、武汉以北的地区(十堰、襄樊、咸宁)这四个地区的经济发展趋于稳定。
根据分析的结果我们可以为湖北省经济的稳步发展出一份薄力。
关键词经济指标;因子分析;方差分析multivariate statistical analysis of Hubei regional economic disparitiesAbstractBy multivariate statistical analysis method Hubei region of the main economic indicators for factor analysis and analysis of variance.thus can reach12cities in Hubei Province in the level of economic development,ranging from factor analysis of the results,This12cities in the overall economic strength of the smallest order of the rankings Wuhan,Yichang,Xiangfan,Huangshi,Jingzhou,Shiyan,Ezhou,Jingmen, Suizhou,Xiaogan,Huanggang,Xianning.By analysis of variance to the results,with Wuhan at the center,according to this location12cities is divided into four areas:the area to the east of Wuhan(Huangshi,Ezhou,Huanggang),in the area south of Wuhan (Xiaogan,Jingzhou)Wuhan west of the region(Yichang,Jingmen,Suizhou),the area to the north of Wuhan(Shiyan,Xiangfan,Xianning)The four areas of economic development has become stable.According to the results of the analysis we will be able to Hubei's steady economic development of a thin edge.Key words:Economic indicators;Factor analysis;Analysis of variance1引言近几年湖北省经济得到了快速发展,但发展中还是碰到了很多问题,各个城市的经济水平还存在很大的差异,为了准确弄清楚湖北省主要的12个城市的经济差异,我们利用因子分析对各个地区的综合经济实力进行比较分析,然后再利用方差分析对各个地区的整体实力进行比较,为湖北今后的经济发展提供一些比较科学的发展方案。
2分析方法介绍2.1因子分析因子分析模型是主成分分析的推广。
它也是利用降维的思想,由研究原始变量相关矩阵内部的依赖关系出发,把一些具有错综复杂关系的变量归结为少数几个综合因子的一种多变量统计分析方法。
相对于主成分分析,因子分析更倾向于描述原始变量之间的相关关系;因此,因子分析的出发点是原始变量的相关剧增。
因子分析的思想始于1904年查尔斯·斯皮尔曼对学生考试成绩的研究。
近年来,随着电子计算机的高速发展,人们将因子分析的理论成功地应用于心理学、医院、气象、地质、经济学等各个领域,也使得因子分析的理论和方法更加丰富。
2.1.1基本思想因子分析的基本思想是根据相关性大小把原始变量分组,使得同组内的变量之间相关性较高,而不同组的变量间的相关性则较低。
每组变量代表一个基本结构,并用一个不可观测的综合变量表示,这个基本结构就称为公共因子。
对于所研究的某一具体问题,原始变量就可以分解成两部分之和的形式,一部分是少数几个不可测的所谓公共因子的线形函数,另一部分是与公共因子无关的特殊因子。
2.1.2因子分析的模型①查尔斯·斯皮尔曼提出因子分析时用到的例子①一般因子分析模型:设有n个样品,每个样品观察p个指标,这p个指标之间有较强的相关性(要求p 个指标相关性较强的理由是很明确的,只有相关性较强才能从原始变量中提取出“公共”因子)。
为了便于研究,并消除由于观测量纲的差异及数量级不同所造成的影响,将样本观测数据进行标准化处理,使标准化后的变量均值为0,方差为1。
2. 1.3因子分析的步骤①确定因子载荷:主成分法、主轴因子法、最小二乘法、极大似然法、因子α提取法等。
由于这些方法求解因子载荷的出发点不同,所得的结果也不完全相同,为此我们就本论文所用到的主成分法寻找公共因子的方法做详细介绍。
主成分寻找公共因子的方法如下:假定从相关阵出发求解主成分,没有p 个变量,则我们可以找出p 个主成分。
将所得的p 个主成分按由大到小的顺序排列,记为,则主成分与原始变量之间存在如下关系式:p Y Y Y ,,,21L (1)11111221221122221122p pp p pp p pp p Y X X X Y X X X Y X X Xγγγγγγγγγ=+++⎧⎪=+++⎪⎨⎪⎪=+++⎩L L LLLL 式中,为随机向量X 的相关矩阵的特征值所对应的特征向量的分量,因为特ij γ征向量之间彼此正交,从X 到Y 的转换关系是可逆的,很容易得出由Y 到X 的转换关系为:(2)11112121212122221122p pp p pp p pp p X Y Y Y X Y Y Y X Y Y Yγγγγγγγγγ=+++⎧⎪=+++⎪⎨⎪⎪=+++⎩L L LLLL 我们对上面每一等式只保留前m 个主成分而把后面的部分用代替,则㈡式可i ε变为:(3)1111212112121222221122m m m m p p p mp m pX Y Y Y X Y Y Y X Y Y Y γγγεγγγεγγγε=++++⎧⎪=++++⎪⎨⎪⎪=++++⎩L L LLL L 这个式子在形式上已经与因子模型相一致,且之间相互独立,为),,2,1(m i Y i L =了把转化成合适的公因子,现在要做的工作只是把主成分变为方差为1的变i Y i Y 量。
为完成此变换,必须将除以其标准差(即为特征根的平方根。
于是,i Y i λ令,则㈢式变为:ji i ij i i i a Y F γλλ==,/(4)1111122112211222221122m m m m p p p pm m pX a F a F a F X a F a F a F X a F a F a F εεε=++++⎧⎪=++++⎪⎨⎪⎪=++++⎩L L LLL L 这与因子模型完全一致,这样,就得到了载荷A 矩阵和一组初始公因子(未旋转)。
②因子旋转:因子旋转分为正交旋转与斜交旋转,正交旋转由初始载荷矩阵A左乘一正交阵而得到。
经过正交旋转而得到的新的公因子仍然保持彼此独立的性质。
而斜交旋转则放弃了因子之间彼此独立这个限制,因而可能达到更为简洁的形式,其实际意义也更容易解释。
但不论是正交旋转还是斜交旋转,都应当使新的因子载荷系数要么尽可能地接近与零,要么尽可能地远离零。
③因子得分:因子得分就是公共因子在每一个样品点上的得分。
根据因子得分我们可以知道那个城市的经济发展水平要高,那个城市的经济发展水平要底。
2.2方差分析方差分析的基本思想是根据研究目的和设计类型,将总变异中的离均差平方和SS 及其自由度分别分解成相应的若干部分,然后求各相应部分的变异;再用各部分的变异与组内(或误差)变异进行比较,得出统计量F 值;最后根据F 值的大小确定P 值,作出统计推断方差分析的检验假设H 0为各样本来自均数相等的总体,H 1为各总体均数不等或不全相等。
若不拒绝H 0时,可认为各样本均数间的差异是由于抽样误差所致,而不是由于处理因素的作用所致。
理论上,此时的组间变异与组内变异应相等,两者的比值即统计量F 为1;由于存在抽样误差,两者往往不恰好相等,但相差不会太大,统计量F 应接近于1。
若拒绝H 0,接受H 1时,可认为各样本均数间的差异,不仅是由抽样误差所致,还有处理因素的作用。
此时的组间变异远大于组内变异,两者的比值即统计量F 明显大于1。
在实际应用中,当统计量F 值远大于1且大于某界值时,拒绝H 0,接受H 1,即意味着各样本均数间的差异,不仅是由抽样误差所致,还有处理因素的作用方差分析的用途①两个或多个样本均数间的比较;②分析两个或多个因素间的交互作用;③回归方程的线性假设检验;④多元线性回归分析中偏回归系数的假设检验;⑤两样本的方差齐性检验等。
3问题分析我们给出2003年湖北省12个城市的主要经济指标,借助这些指标体系对湖北省12个城市的经济差异作出分析。
然后以武汉为中心,根据地理位置将这12个城市划分为四个地区:武汉以东的地区(黄石、鄂州、黄冈)、武汉以南的地区(孝感、荆州)、武汉以西的地区(宜昌、荆门、随州)、武汉以北的地区(十堰、襄樊、咸宁),用方差分析对这四个地区的经济进行分析比较。
4数据处理过程下表给出的是2003年湖北省12个城市的主要经济指标,为了得出它们的经济的差异,我用多元统计方法里面的因子分析和方差分析对这些数据进行处理。
表1湖北省12个城市的经济指标武汉黄石十堰宜昌襄樊鄂州116621797136610014360052332767241456712570002804368506564653097407949473524231177840836287568915902614874070224424398914137396123922682527125472013180425005134503292366133449381474692308076914523192474900152580977550216423602697305512238132997131398619375310813552742113492151786796364459664261545010232476610622821539418831570018467806336252936571116954682933784229110486932352340712542.7929.6433.2667.3373.7634.32134273309305052228599238951453595324188814749861761811816930728101252401532476795761003110852316651320011220523284297877173457796963801693310541230118875162605069208917218738116194905301723324185234992677031302044841364600399721139025127833120212623328464838续表荆门孝感荆州黄冈咸宁随州11477638554715108332734036039190011232002430071889044589200952882728627368527503429345551137461906332941892119157207205362105533394500779130842829686138384237074910264841772512857711149358722511754171183682824298138897835379794964620296227686111475959412629035421857336039991017619218001840607721352912770318652411348912588057039256658334258221214.7733.7225.0611.57 6.0620.18131552961772693199407935899125186524146910376391113466510043421555149474160231511161619401549154976254215937175395544150015242248015271828525598614700872040001100019211441952651133206001764617042026128186004470014600132002373221282320181942注:数据来源于《2004年中国统计年鉴》其中1—地区生产总值(单位:万元)2—地方财政一般预算内收入(单位:万元)3—地方财政一般预算内支出(单位:万元)4—当年合同外资金额(单位:万美元)5—环境污染治理投资额(单位:万元)6—工业总产值(单位:万元)7—建成区绿化覆盖面积(单位:公顷)8—产品销售收入(单位:万元)9—邮政业务总量(单位:万元)10—固定资产投资完成额(单位:万元)11—房地产开发投资完成额(单位:万元)12—商品房屋销售面积(单位:万平方米)13—全年新增固定资产(单位:万元)14—全年供水总量(单位:万立方米)15—年末实有铺装道路总面积(单位:万平方米)16—园林绿地面积(单位:公顷)17—工业废水排放总量(单位:万吨)18—液化石油气供气总量(单位:吨)19—高等学校学生数(单位:人)20—各类专业技术人员(单位:万人)21—医院、卫生院数(单位:个)4.1因子分析的结果由于经济指标太多,不利于我们进行问题的分析,因此我们需要对其进行降维处理。
