八年级数学上册期末检测习题讲评课件新版北师大版
八年级数学上册第六章数据的分析4数据的离散程度第1课时极差与方差作业课件(新版)北师大版

星期 品种
甲
乙
一二三四五六日 45 44 48 42 57 55 66 48 44 47 54 51 53 60
解:(1)x甲=
45+44+48+42+57+55+66 7
=51(千克),x乙=
48+44+47+54+51+53+60
7
=51(千克)
(2)s甲2=
1 7
[(45-51)2+(44-51)2+(48-51)2+(42-51)2+(57-51)2+(55-
-85)2]=160,因为70<160,所以爱国班的成绩比较稳定
解:(1)这次参加男子跳高初赛的运动员共有6÷30%=20(人),成绩为1.50 m的有
20×10%=2(人),成绩为1.70 m的有20×15%=3(人),成绩为1.60 m的有20-2-4-6
1.50×2+1.55×4+1.60×5+1.65×6+1.70×3
1 n
[(x1-x)2+(x2-x)2+…+(xn-x)2],现在的方差s2
=n1 [(3x1-2-3x+2)2+(3x2-2-3x+2)2+…+(3xn-2-3x+2)2]=n1 [9(x1-x)2+9(x2
-x)2+…+9(xn-x)2]=9s2
下列说法不正确的是( D )
A.n是样本的容量 B.xn是样本个体
C.x是样本平均数 D.s是样本方差
5.(4分)已知数据2,5,1,x,3的平均数为3,则这组数据的标准差为( B )
A.2 B. 2 C.3 D. 3
6.(4分)已知一组数据的方差是3,则这组数据的标准差是( D )
A.9 B.3 C.32
10.某排球队6名场上队员的身高(单位:cm)是:180,184,188,190,192,194. 现用一名身高为186 cm的队员换下场上身高为192 cm的队员,与换人前相比,场上 队员的身高( )A
2012-2013学年度北师大版八年级上册数学期末期末教学质量检测(二)及答案
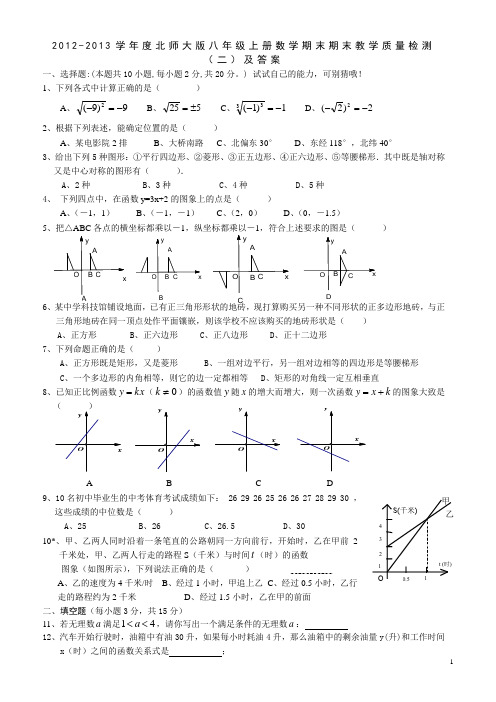
2012-2013学年度北师大版八年级上册数学期末期末教学质量检测(二)及答案一、选择题:(本题共10小题,每小题2分,共20分。
) 试试自己的能力,可别猜哦! 1、下列各式中计算正确的是( )A 、9)9(2-=- B 、525±= C 、1)1(33-=- D 、2)2(2-=-2、根据下列表述,能确定位置的是( )A 、某电影院2排B 、大桥南路C 、北偏东30°D 、东经118°,北纬40°3、给出下列5种图形:①平行四边形、②菱形、③正五边形、④正六边形、⑤等腰梯形.其中既是轴对称又是中心对称的图形有( ).A 、2种B 、3种C 、4种D 、5种 4、 下列四点中,在函数y=3x+2的图象上的点是( )A 、(-1,1)B 、(-1,-1)C 、(2,0)D 、(0,-1.5)5、把△ABC 各点的横坐标都乘以-1,纵坐标都乘以-1,符合上述要求的图是( )6、某中学科技馆铺设地面,已有正三角形形状的地砖,现打算购买另一种不同形状的正多边形地砖,与正三角形地砖在同一顶点处作平面镶嵌,则该学校不应该购买的地砖形状是( ) A 、正方形B 、正六边形C 、正八边形D 、正十二边形7、下列命题正确的是( )A 、正方形既是矩形,又是菱形B 、一组对边平行,另一组对边相等的四边形是等腰梯形C 、一个多边形的内角相等,则它的边一定都相等D 、矩形的对角线一定互相垂直8、已知正比例函数kx y =(0≠k )的函数值y 随x 的增大而增大,则一次函数k x y +=的图象大致是( )A B C D 9、10名初中毕业生的中考体育考试成绩如下: 26 29 26 25 26 26 27 28 29 30 ,这些成绩的中位数是( )A 、25B 、26C 、26.5D 、3010*、甲、乙两人同时沿着一条笔直的公路朝同一方向前行,开始时,乙在甲前2千米处,甲、乙两人行走的路程S (千米)与时间t (时)的函数 图象(如图所示),下列说法正确的是( )A 、乙的速度为4千米/时B 、经过1小时,甲追上乙C 、经过0.5小时,乙行 走的路程约为2千米D 、经过1.5小时,乙在甲的前面二、填空题(每小题3分,共15分)11、若无理数a 满足14a <<,请你写出一个满足条件的无理数a :12、汽车开始行驶时,油箱中有油30升,如果每小时耗油4升,那么油箱中的剩余油量y(升)和工作时间x (时)之间的函数关系式是 ;xyxy xy xyOOOODy xCBAO Cy xC B AOBy x C B AO A y xCB AOS(千米)12 3 4 0.51乙甲 Ot (时)13、⎩⎨⎧==1,2y x 是方程2x -ay=5的一个解,则a = ;14、已知直角三角形两边的长分别为3cm,4cm, 则以第三边为边长的正方形的面积为 。
八年级数学上册(北师大版 习题课件):第二章 实数 2.5 用计算器开方

≈1.1(秒),所以运动员跳过横杆后下落的时间为 1.1 秒
14.面积都是 50 平方米的圆和正方形的周长哪个大?大多少?(精
确到 0.1 米)
解:设圆的半径为 r m,正方形边长为 x m,因为πr2=50,r=
50 π
≈3.99,所以圆的周长为 2πr≈25.06(m),因为 x2=50,所以 x= 50≈
第二章 实数
2.5 用计算器开方
知识点 1:用科学计算器进行开方运算
1.用计算器求 8的值的按键顺序是( A )
A. 8 =
B. 8 =
C. 8
D. 8
2.用计算器求的值为(结果精确到0.001)( C ) A.12.17 B.±1.868 C.1.868 D.-1.868
3.用计算器计算,若按键顺序为 4 · 5 - 0 · 5 ÷ 2 = , 相应算式是( C )
10.用计算器求 44.86的值为(结果精确到 0.01)( C ) A.6.69 B.6.7 C.6.70 D.±6.70 11.用计算器比较 32+-11和 0.168 的大小正确的是( C ) A. 23-+11=0.168 B. 32+-11>0.168 C. 32+-11<0.168 D.以上答案都不对
12.用科学计算器探究: (1) 121×(1+2+1)=___2_2__; (2) 12 321×(1+2+3+2+1)=__3_3_3___; (3) 1 234 321×(1+2+3+4+3+2+1)=__4__4_4_4__; (4)由上面规律得到:
1 234 567 654 321×(1+2+3+4+5+6+7+6+5+4+3+2+1) =__7_7_7_7__7_7_7_.
7.07,所以正方形周长为 4x≈28.28(m),28.28-25.06=3.22≈3.2(m),
2024八年级数学上册第六章数据的分析2中位数与众数课件新版北师大版

感悟新知
知3-练
解:因为员工的总人数为 1+1+2+10+2+3+1=20(名), 所以这组数据的中位数是第 10,11 个数据的平均数,而 第 10,11 个数据分别为 5 000,5 0 0 0.
所以中位数是5
0
0
0+5 2
0
0
0
=5 000(元) .
因为数据 5 000 出现的次数最多,所以众数为 5 000 元 .
答案:D
感悟新知
知2-练
2-1. [ 中考·黑龙江 ] 已知一组数据 1,0, - 3,5, x, 2, - 3 的平均数是1,则这 组数据的众数是( C ) A. - 3
B.5 C. - 3 和 5 D.1 和 3
感悟新知
知识点 3 平均数、中位数、众数的区别和联系 知3-讲
平均数
中位数
众数
实 质
感悟新知
续表
知3-讲
区缺 别点
联 系
平均数
中位数
众数
易受极端 值的影响
不能充分利用 当各数据的重复次数大
数据所提供的 致相等时,众数 就 没
信息
有 特 别 意义了
都是用来描述数据集中趋势的统计量;都可用来反 映数据的一般水平;都可用来作为一组数据的代表
感悟新知
特别提醒
知3-讲
(1)一组数据的众数一定是这组数据中的一个数,而
(2)在(1)中的平均数、中位数和众数中,哪些统计量能反映 该公司员工月收入水平?并说明理由 .
(3)为了避免技术人员流失,该公司决定给他们每人每月加 薪 x 元至公司员工月收入的平均数,求 x 的值 .
感悟新知
北师大版八年级上册数学《平均数》数据的分析PPT课件(第1课时)

解: 因为笔试、面试、技能操作得分权重比例为2∶3∶5 所以笔试、面试、技能操作得分权重分别为0.2,0.3,0.5 小王的成绩=85 × 0.2+80 × 0.3+90 × 0.5=86 答:小王的最后成绩为86分。
平均数 第2课时
知识回顾
算术平均数 加权平均数
算术平均数
定义:一般地,对于n个数x1,x2,…,xn,我们 把 1 (x1+x2+…+xn)叫做这n个数的算术平均数;
A
85
B
95
演讲能力 95 85
演讲效果 95 95
请决出两人的名次.
选手
演讲内容 (50%)
演讲能力 (40%)
A
85
95
演讲效果 (10%)
95
B
95
是
选手B的最后得分是
85×50%+95×40%+95×10% 95×50%+85×40%+95×10%
50%+40%+10%
(1)(2)的结果不一样说明了什么?
实际问题中,一组数据的各个数据的“重要程度”未必相 同。因此,在计算这组数据的平均数时,往往给每个数据一 个“权”,如上例中的4就是创新的权、3是综合知识的权、1 是语言的权 ,而称
72 4 50 3 881 65.75 4 3 1
为A的三项测试成绩的加权平均数。
1、一组数据由2、3、4、5、6构成,其中2的权数
为0.2,3的权数为0.4,4的权数为0.1,5的权数为
0.2,则这组数据的平均数是( C)
A.3
B.3.2
C.3.6
D.3.8
2.汽车从甲地到乙地,先以60千米/时的速度行驶15分, 再以70千米/时的速度行驶25分,又以80千米/时的速度 行驶15分,那么,该车行驶这段路程的平均速度约为 ( B )(精确到1千米/时)
2024-2025学年北师大版数学八年级上册期末培优训练(含答案)

2024-2025学年北师大版数学八年级上册期末培优训练一、单选题(共10题;共30分)1.(3分)平面直角坐标系内与点关于原点对称的点的坐标是( )A .B .C .D .2.(3分)等腰三角形的底角是,则其顶角是()A .B .C .D .或 3.(3分)a−b−3+|2a−4|=0,则( )A .B .1C .2D .34.(3分)同时满足二元一次方程和的x ,y 的值为( )A .{x =3y =−6B .C .D .5.(3分)若关于x ,y 的二元一次方程组的解也是二元一次方程的解,则k 的值为( )A .2B .1C .D .6.(3分)如图,矩形内接于,分别以为直径向外作半圆.若,则阴影部分的面积是( )A.B .C .D .207.(3分)在一单位为1的方格纸上,有一列点,(其中n 为正整数)均为网格上的格点,按如图所示规律排列,点,,,,,则的坐标为( )()1,2P -()2,1-()1,2--()2,1--()1,2-70︒40︒110︒35︒110︒35︒a b +=1-9x y -=431x y +=45x y =-⎧⎨=⎩23x y =-⎧⎨=⎩45x y =⎧⎨=-⎩35x y k x y k -=⎧⎨+=⎩2310x y -=1-2-ABCD O e AB BC CD AD 、、、45AB BC ==,41π204-41π202-20π123,,,,,n A A A A 1(2,0)A 2(1,1)A -3(0,0)A 4(2,2)A 2017AA .(1008,0)B .(1010,0)C .(-1008,0)D .(-1006,0)8.(3分)若点 、 是一次函数 图象上不同的两点,记,当 时,a 的取值范围是( )A .B .C .D .9.(3分)如图,过矩形对角线的交点,作对角线的垂线,交于点,交于点,若,,则的长等于( )A .B .CD .10.(3分)1765年数学家欧拉在其著作《三角形几何学》中首次提出定理:三角形三边的垂直平分线的交点,三条中线的交点以及三条高线的交点在一条直线上,这条线也被称为欧拉线.如图,已知的三个顶点分别为,,,则的欧拉线的解析式为( )A .B .C .D .()11,x y ()22,x y 2y ax x =--+()()1212m x x y y =--0m <0a <0a >1a <-1a >-ABCD O BD AD E BC F 3AE =5BF =EF 48OAB V ()0,0O ()2,4A ()6,0B OAB V 22y x =-3xy =4y x =-+2023y x =-+二、填空题(共8题;共24分)11.(3分)已知方程组的解为由于不小心,滴上了两滴墨水,刚好遮住了两个数●和▲,则 .12.(3分)在的网格中,每个小正方形的边长为1,网格线的交点记为格点.若一圆弧过格点,则该圆弧所在圆的半径为 .13.(3分)如图,是的外角的平分线,且,则 .14.(3分)将纸片△ABC 沿DE 折叠使点A 落在A '处的位置.(1)如果A '落在四边形BCDE 的内部(如图1),∠A '与∠1+∠2之间存在怎样的数量关系?并说明理由.(2)如果A '落在四边形BCDE 的BE 边上,这时图1中的∠1变为0°角,则∠A '与∠2之间的关系是 .(3)如果A '落在四边形BCDE 的外部(如图2),这时∠A '与∠1、∠2之间又存在怎样的数量关系?并说明理由.15.(3分)一次函数的函数值随值的增大而增大,则常数的取值范围是 .16.(3分)在中,D ,E ,F 分别是上的点,,,,2210x y x y +=⎧⎨-=⎩●4x y =⎧⎨=⎩▲+=▲●46⨯,,A B C AE ABC V CAD ∠,65AB AC ABC =∠=︒DAE ∠=︒()232y a x =-+y x a ABC V ,,BC AB CA AE AF =BE BD =CF CD =,,,则 .17.(3分)将一副三角板按如图所示的位置摆放在直尺上,则的度数为 .18.(3分)观察下列图形:已知a ∥b ,在第一个图中,可得 ,则按照以上规律, 度 .三、解答题(共7题;共46分)19.(5分)如图所示,已知中,,的垂直平分线交于,交于,若,,求的长.20.(6分) 学校举行运动会,由若干名同学组成一个长方形队列.如果原队列中增加54人,就能组成一个正方形队列;如果原队列中减少74人,也能组成一个正方形队列.问原长方形队列有多少名同学?2AB AC BD DC ⋅=⋅3AB =4AC =ABC S =V 1∠12180∠+∠= 112n p p ∠+∠+∠++∠= ABC V 90C ∠=︒AB BC M AB N 6AC =2MB MC =AB21.(6分)如图,矩形内两相邻正方形的面积分别为12和2,求阴影部分的面积.22.(7分)解方程组:(1)(3分){2x−y =0x +2y =5;(2)(4分){3x +2y =54x−y =3.23.(7分)“为了安全,请勿超速”,如图所示是一条已经建成并通车的公路,且该公路的某直线路段上限速,为了检测来往车辆是否超速,交警在旁设立了观测点.若某次从观测点测得一汽车从点到达点行驶了5秒钟,已知,,.(1)(3分)求观测点到公路的距离:(2)(4)MN 60km /h MN C C A B 45CAN ∠=︒60CBN ∠=︒200m BC =C MN 1.4≈ 1.7≈24.(7分)某水果店购进苹果若干千克,销售了部分苹果后,余下的苹果进行降价销售,全部售完.销售金额y (元)与销售量x (千克)之间的函数关系的图象是如图所示的折线段.请根据图象提供的信息解答下列问题:(1)写出降价前y (元)与销售量x (千克)之间的函数表达式 ;(2)求降价后销售金额y (元)与销售量x (千克)之间的函数表达式,并写出自变量的取值范围;(3)该水果店余下的苹果每千克降价了多少元销售?25.(8分)有一块长方形木板,木工采用如图所示的方式,在木板上截出两个面积分别为18dm 2 和32dm 2的正方形木板.(1)(4分)求剩余木板的面积.(2)(4分)若木工想从剩余的木板中截出长为 1.5d m 、宽为 1 dm 的长方形木条,则最多能 截出 块.x答案解析部分1.D2.A3.B4.D5.A6.D7.B8.D9.B10.C11.41213.6514.(1)2∠=∠1+∠2,(2)2∠=∠2;(3)2∠=∠2-∠115.a >16.617.18.180(n+1)19.1220.解:设原队列有m 人,增加54人后组成a×a 的正方形队列,减少74人后组成b×b 的正方形队列.根据题意得:{a 2=m +54①b 2=m−74②1- ②:{a +b =64a−b =2,解得{a =33b =31,∴m 1=1035;{a +b =32a−b =4,解得{a =18b =14,∴m 2=270;{a +b =16a−b =8,解得{a =12b =4,∴m 3=90;综上所述,原队列有1035人或270人或90人。
2024八年级数学上册第七章平行线的证明专项突破17平行线中常用作辅助线的方法习题课件新版北师大版
∴∠ FCD +∠ D =180°.
∴∠ B +∠ BCF +∠ FCD +∠ D =180°+180°,
即∠ B +∠ BCD +∠ D =360°.
1
2
3
4
5
6
7
8
9
(3)如图②, AB ∥ EF ,根据(2)中的猜想,直接写出∠ B
+∠ C +∠ D +∠ E 的度数.
解:(3)∠ B +∠ C +∠ D +∠ E =540°.
度数;
1
2
3
4
5
6
7
8
9
解:(1)设 CE 交 AB 于点 G ,如图①.
∵ CF 平分∠ ECD ,∴∠ DCE =2∠ DCF .
∵∠ DCF =25°,∴∠ DCE =50°.
∵ AB ∥ CD ,∴∠ AGE =∠ DCE =50°.
∴∠ BGE =180°-∠ AGE =130°.
∵∠ E =20°,
80°.
1
2
3
4
5
6
7
8
9
(2)如图①,在 AB ∥ DE 的条件下,你能得出∠ B ,
∠ BCD ,∠ D 之间的数量关系吗?请说明理由.
1
2
3
4
5
6
7
8
9
解:(2)∠ B +∠ BCD +∠ D =360°.
理由如下:如图,∵ CF ∥ AB ,∴∠ B +∠ BCF =
180°.
又∵ AB ∥ DE ,∴ CF ∥ DE .
过点 E 作 EH ∥ AB ,∴∠ BEH =∠ ABE .
∵ AB ∥ CD ,∴ EH ∥ CD . ∴∠ DEH =∠ CDE .
3.2第2课时 建立平面直角坐标系-2020秋北师大版八年级数学上册习题课件(共14张PPT)
第2课时 建立平面直角坐标系 知识要点基础练
综合能力提升练
拓展探究突破练
-8-
11.如图,已知直线m⊥n,在某平面直角坐标系中,x轴∥直线m,y
轴∥直线n,点A,B的坐标分别为(-4,2),(2,-4),点A,O4,B在同一条 直线上,则坐标原点为( A )
A.O1 C.O3
B.O2 D.O4
第2课时 建立平面直角坐标系 知识要点基础练
综合能力提升练
拓展探究突破练
-4-
知识点2 平面直角坐标系内点的坐标的特征 3.在平面直角坐标系中,已知点P(2,a)在第四象限,则( A ) A.a<0 B.a≤0 C.a>0 D.a≥0 4.如图,小手盖住的点的坐标可能是( B )
A.(3,3) B.(-4,5) C.(-4,-6) D.(3,-6)
(19,0),
S 直角梯形 AOCB=12(AB+OC)×OA=12×(9+19)×10=140.
第2课时 建立平面直角坐标系 知识要点基础练
综合能力升练
拓展探究突破练
-13-
16.在平面直角坐标系中,点P的坐标为(2,6),点Q的坐标为 (2,2),M为y轴上的动点. (1)在平面直角坐标系内,画出当△PMQ的周长取最小值时点 M的位置;(保留作图痕迹) 解:(1)利用关于y轴对称点的坐标关系 得出点P1,连接P1Q交y轴于点M, 点M即为所求.图略. (2)点M的坐标为 (0,4) .
第2课时 建立平面直角坐标系 知识要点基础练
综合能力提升练
拓展探究突破练
-14-
17.如图,在Rt△OAB中,斜边OB在x轴的正半轴上,直角顶点A
在第四象限内,S△OAB=20,OA∶AB=1∶2,求A,B两点的坐标.
北师大版八年级数学上册期末复习练习题(含答案)
北师大新版八年级上册数学期末复习试卷一.选择题1.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长是()A.42B.32C.42或32D.42或372.方程x+2y=7在自然数范围内的解有()A.只有1组B.只有4组C.无数组D.以上都不对3.已知实数a满足|2009﹣a|+=a,那么a﹣20092的值是()A.2008B.2009C.2010D.20114.已知x、y为实数,,则y x的值等于()A.8B.4C.6D.165.如果一个三角形的三边长分别为1、k、4.则化简|2k﹣5|﹣的结果是()A.3k﹣11B.k+1C.1D.11﹣3k6.如图,在直角坐标系中,已知点A(﹣3,0),B(0,4),对△OAB连续作旋转变换,依次得到△1,△2,△3,△4,…,则△2019的直角顶点的坐标为()A.(8076,0)B.(8064,0)C.(8076,)D.(8064,)7.如图1,在四边形ABCD中,AB∥CD,∠ABC=90°,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是()A.6B.5C.4D.38.如图是放在地面上的一个长方体盒子,其中AB=9cm,BC=6cm,BF=5cm,点M在棱AB上,且AM=3cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为()A.10cm B.cm C.(6+)cm D.9cm9.如图,平面直角坐标系中,长方形OABC,点A,C分别在x轴,y轴的正半轴上,点B(6,3),现将△OAB 沿OB翻折至△OA′B位置,OA′交BC于点P.则点P的坐标为()A.(,3)B.(,3)C.(,3)D.()二.填空题10.已知一次函数y=kx+b(k≠0)的图象过点(2,0),且与两坐标轴围成的三角形的面积为1,则这个一次函数的解析式是.11.已知一次函数图象经过点(﹣2,0),并且与两坐标围成的封闭图形面积为6,则这个一次函数的解析式为.12.如图,在平面直角坐标系中,直线y=﹣x+3交x轴于点A,交y轴于点B,以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则直线BC的解析式为.13.对于X,Y定义一种新运算“*”:X*Y=aX+bY,其中a,b为常数,等式右边是通常的加法和乘法的运算.若成立,那么2*3=.14.若实数x、y满足,则2x+y的立方根是.15.已知A=,则A2+2A+1=.三.解答题16.设a,b,c为△ABC的三边,化简:++﹣.17.根据题意列出方程组(1)甲、乙两人在一环形场地上从点A同时同向匀速跑步,甲的速度是乙的速度的2.5倍,4min后两人首次相遇,此时乙还需要跑300m跑完第一圈.求甲、乙两人的速度及环形场地的周长.(2)将若干只鸡放入若干笼中,若每个笼中放4只.则有一鸡无笼可放;若每个笼里放5只.则有一笼无鸡可放,问有多少只鸡,多少个笼?18.像=2;;…两个含有二次根式的代数式相乘,积不含有二次根式,则称这两个代数式互为有理化因式.爱动脑筋的小明同学在进行二次根式计算时,利用有理化因式化去分母中的根号.(1);(2).勤奋好学的小明发现;可以用平方之后再开方的方式来化简一些有特点的无理数.(3)化简:.解:设x=,易知,帮x>0.由:x2=3+=2.解得x=.即=.请你解决下列问题:(1)2的有理化因式是;(2)化简:;(3)化简:.19.问题背景.在△ABC中,AB=,BC=,AC=,求这个三角形的面积,小辉同学在解答这道题时先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(△ABC的三个顶点都在正方形的顶点处),如图所示,这样不需要求△ABC的高,而借用网格就能计算它的面积.(1)请直接写出△ABC的面积;(2)我们把上述方法叫做构图法,若△ABC中,AB,BC,AC三边的长分别为,,,请你在图2的正方形网格(每个小正方形的边长为a)中画出相应的△ABC.并求其面积.20.已知平面直角坐标系中,A、B两点的坐标分别为(2,﹣3)、(4,﹣1)(1)若P(x,0)是x轴上的一个动点,当△P AB的周长最短时,求x的值;(2)若C(a,0),D(a+3,0)是x轴上的两个动点,当四边形ABDC的周长最短时,求a的值.21.已知直线(n是正整数).当n=1时,直线l1:y=﹣2x+1与x轴和y轴分别交于点A1和B1,设△A1OB1(O是平面直角坐标系的原点)的面积为s1;当n=2时,直线与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为s2,…,依此类推,直线l n与x轴和y轴分别交于点A n和B n,设△A n OB n 的面积为S n.(1)求△A1OB1的面积s1;(2)求s1+s2+s3+…+s2011的值.22.如图,已知直线AB的解析式为y=﹣x+6,点P从点A出发,沿着射线AO方向以秒1个单位长度的速度移动,同时点Q从点B出发,沿着射线BO方向以每秒2个单位度的速度移动.试问经过几秒后能使△POQ的面积为6个平方单位?23.如图,在平面直角坐标系中,长方形OABC的顶点O为坐标原点,顶点A,C分别在x轴正半轴和y轴正半轴上,顶点B的坐标为(12,8),直线y=kx+8﹣6k(k<0)交边AB于点P,交边BC于点Q.(1)当k=﹣1时,求点P,Q的坐标;(2)若直线PQ∥AC,BH是Rt△BPQ斜边PQ上的高,求BH的长;(3)若PQ平分∠OPB,求k的值.24.如图,正方形AOBC的边长为2,点O为坐标原点,边OB,OA分别在x轴,y轴上,点D是BC的中点,点P是线段AC上的一个点,如果将OA沿直线OP对折,使点A的对应点A′恰好落在PD所在直线上.(1)若点P是端点,即当点P在A点时,A′点的位置关系是,OP所在的直线是,当点P在C 点时,A′点的位置关系是,OP所在的直线表达式是.(2)若点P不是端点,用你所学的数学知识求出OP所在直线的表达式.(3)在(2)的情况下,x轴上是否存在点Q,使△DPQ的周长为最小值?若存在,请求出点Q的坐标;若不存在,请说明理由.25.在平面直角坐标系中,已知两点坐标P1(x1,y1)P2(x2,y2)我们就可以使用两点间距离公式来求出点P1与点P2间的距离.如:已知P1(﹣1,2),P2(0,3),则.通过阅读以上材料,请回答下列问题:(1)已知点P1坐标为(﹣1,3),点P2坐标为(2,1)①求P1P2=;②若点Q在x轴上,则△QP1P2的周长最小值为.(2)如图,在平面直角坐标系中,四边形OABC为长方形,点A、B的坐标分别为(4,0)(4,3),动点M、N分别从点O,点B同时出发,以每秒1个单位的速度运动,其中M点沿OA向终点A运动,N点沿BC向终点C运动,过点N作NF⊥BC交AC于F,交AO于G,连结MF.当两点运动了t秒时:①直接写出直线AC的解析式:;②F点的坐标为(,);(用含t的代数式表示)③记△MF A的面积为S,求S与t的函数关系式;(0<t<4);④当点N运动到终点C点时,在y轴上是否存在点E,使△EAN为等腰三角形?若存在,请直接写出点E的坐标,若不存在,请说明理由.参考答案一.选择题1.【解答】解:此题应分两种情况说明:(1)当△ABC为锐角三角形时,在Rt△ABD中,BD==9,在Rt△ACD中,CD==5∴BC=5+9=14∴△ABC的周长为:15+13+14=42;(2)当△ABC为钝角三角形时,在Rt△ABD中,BD=9,在Rt△ACD中,CD=5,∴BC=9﹣5=4.∴△ABC的周长为:15+13+4=32∴当△ABC为锐角三角形时,△ABC的周长为42;当△ABC为钝角三角形时,△ABC的周长为32.综上所述,△ABC的周长是42或32.故选:C.2.【解答】解:x+2y=7,x=7﹣2y,所以方程x+2y=7在自然数范围内的解有,,,,共4组,故选:B.3.【解答】解:根据题意,得a﹣2010≥0,即a≥2010;所以|2009﹣a|=a﹣2009,∵+|2009﹣a|=a,即+a﹣2009=a,∴=2009,a﹣2010=20092,∴a﹣20092=2010.故选:C.4.【解答】解:∵x﹣2≥0,即x≥2,① x﹣2≥0,即x≤2,② 由①②知,x=2;∴y=4,∴y x=42=16.故选:D.5.【解答】解:∵三角形的三边长分别为1、k、4,∴,解得,3<k<5,所以,2k﹣5>0,k﹣6<0,∴|2k﹣5|﹣=2k﹣5﹣=2k﹣5﹣[﹣(k﹣6)]=3k﹣11.故选:A.6.【解答】解:∵点A(﹣3,0)、B(0,4),∴AB==5,由图可知,每三个三角形为一个循环组依次循环,一个循环组前进的长度为:4+5+3=12,∵2019÷3=673,∴△2019的直角顶点是第673个循环组的最后一个三角形的直角顶点,∵673×12=8076,∴△2019的直角顶点的坐标为(8076,0).故选:A.7.【解答】解:∵S△ABP=AB•h,当动点P沿BC运动时,h=BP=x,∴S△ABP=AB•x,对应图象为0<x<2部分,由图象可知:点P在BC运动路程为BC=2﹣0=2;动点P沿CD运动时,h=BC,S△ABP=AB•BC为定值,对应图象2<x<5部分,由图象可知:点P在CD运动路程为CD=5﹣2=3,∴S△BCD=BC•CD=×2×3=3.所以△BCD的面积是3.故选:D.8.【解答】解:如图1,∵AB=9cm,BC=6cm,BF=5cm,∴BM=9﹣3=6,BN=5+3=8,∴MN==10;如图2,∵AB=9cm,BC=GF=6cm,BF=5cm,∴PM=9﹣3+3=9,NP=5,∴MN==,∵10<,∴蚂蚁沿长方体表面爬到米粒处的最短距离为10.故选:A.9.【解答】解:∵将△OAB沿OB翻折至△OA′B位置,OA′交BC于点P,∴∠A'OB=∠AOB,∵四边形OABC是矩形,∴BC∥OA,∴∠OBC=∠AOB,∴∠OBC=∠A'OB,∴OP=BP,∵点B的坐标为(6,3),∴AB=OC=3,OA=BC=6,设OP=BP=x,则PC=6﹣x,在Rt△OCP中,根据勾股定理得,OC2+PC2=OP2,∴32+(6﹣x)2=x2,解得:x=,∴PC=6﹣=,∴P(,3),故选:A.二.填空题10.【解答】解:∵一次函数y=kx+b(k≠0)图象过点(2,0),∴2k+b=0,b=﹣2k,∴y=kx﹣2k,令x=0,则y=﹣2k,∵函数图象与两坐标轴围成的三角形面积为1,∴×2×|﹣2k|=1,即|2k|=1,解得:k=±,则函数的解析式是y=x﹣1或y=﹣x+1.故答案为y=x﹣1或y=﹣x+1.11.【解答】解:设一次函数为y=kx+b,k≠0.则与y轴的交点为(0,b),S△=×|﹣2|×|b|=6,得|b|=6,∴b=±6,当b=6时,函数为:y=kx+6,∵函数的图象经过点(﹣2,0),得:0=﹣2k+6得到k=3,∴所求的一次函数的解析式为:y=3x+6;当b=﹣6时,函数为:y=kx﹣6,∵函数的图象经过点(﹣2,0),得:0=﹣2k﹣6,得到k=﹣3,∴所求的一次函数的解析式为:y=﹣3x﹣6.答:所求的一次函数的解析式为:y=3x+6或y=﹣3x﹣6,故答案为:y=3x+6或y=﹣3x﹣6.12.【解答】解:在直线y=﹣x+3中,令y=0,求得x=4;令x=0,求得y=3,∴点A的坐标为(4,0),点B的坐标为(0,3),∴BO=3,AO=4,∴AB==5,∵以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,∴CO=5﹣4=1,则点C的坐标为:(﹣1,0),设直线BC的解析式为y=kx+b,把B(0,3),C(﹣1,0)代入得,解得,∴直线BC的解析式为y=3x+3.故答案为y=3x+3.13.【解答】解:∵,∴a=2,∴由,得2b=,解得,b=﹣1,∵X*Y=aX+bY,∴2*3=2a+3b=2×2+3×(﹣1)=4﹣3=1;故答案是1.14.【解答】解:由题意得,、有意义,故可得x=29,y=6,从而可得2x+y=64,故可得2x+y的立方根是4.故答案为:4.15.【解答】解:A=﹣1+﹣+…+﹣=﹣1,所以A2+2A+1=(A+1)2=(﹣1+1)2=2018.故答案为2018.三.解答题16.【解答】解:根据a,b,c为△ABC的三边,得到a+b+c>0,a﹣b﹣c<0,b﹣a﹣c<0,c﹣b﹣a<0,则原式=|a+b+c|+|a﹣b﹣c|+|b﹣a﹣c|+|c﹣b﹣a|=a+b+c+b+c﹣a+a+c﹣b﹣a﹣b+c=4c.17.【解答】解:(1)设乙的速度为x米/分,则甲的速度为2.5x米/分,环形场地的周长为y米,由题意,得,即;(2)解:设笼的总数为x,鸡的总数为y只,根据题意可得:则.18.【解答】解:(1)2﹣3的有理化因式是2+3;故答案为:2+3;(2)原式=++1+2﹣=+3;(3)设x=﹣,可得<,即x<0,由题意得:x2=6﹣3+6+3﹣2=12﹣6=6,解得:x=﹣,则原式=﹣.19.【解答】解:(1)S△ABC=3×3﹣×3×1﹣×2×3﹣×1×2=;(2)如图,∵AB==a,BC==2a,AC==a,∴△ABC即为所求作三角形,则S△ABC=2a•4a﹣×a×2a﹣×2a×2a﹣×a×4a=3a2.故答案为:(1).20.解:(1)如图1先作出B关于x轴的对称点B′,连接AB′交x轴于点P,则B′点坐标为(4,1),由两点之间线段最短可知,AB′的长即为△P AB的最短周长,设过AB′两点的一次函数解析式为y=kx+b(k≠0),则,解得k=2,b=﹣7,故此一次函数的解析式为y=2x﹣7,当y=0时,2x﹣7=0,解得x=3.5.故当x=3.5时,△P AB的周长最短.(2)作点A关于x轴的对称点A′,则A′的坐标为(2,3),把A′向右平移3个单位得到点B'(5,3),连接BB′,与x轴交于点D,如图,∴CA′=CA,又∵C(a,0),D(a+3,0),∴CD=3,∴A′B′∥CD,∴四边形A′B′DC为平行四边形,∴CA′=DB′,∴CA=DB′,∴AC+BD=BB′,此时AC+BD最小,而CD与AB的长一定,∴此时四边形ABDC的周长最短.设直线BB′的解析式为y=kx+b,把B(4,﹣1)、B'(5,3)分别代入得,4k+b=﹣1,5k+b=3,解得k=4,b=﹣17,∴直线BB′的解析式为y=4x﹣17,令y=0,则4x﹣17=0,解得x=,∴D点坐标为(,0),∴a+3=,∴a=.21.【解答】解:(1)当n=1时,直线l1:y=﹣2x+1与x轴和y轴的交点是A1(,0)和B1(0,1)所以OA1=,OB1=1,∴s1=;(2)当n=2时,直线与x轴和y轴的交点是A2(,0)和B2(0,)所以OA2=,OB2=,∴s2==当n=3时,直线与x轴和y轴的交点是A3(,0)和B3(0,)所以OA3=,OB3=,∴s3==依此类推,s n=∴s1+s2+s3+…+s2011=∴s1+s2+s3+…+s2011===.22.【解答】解:∵直线AB的解析式为y=﹣x+6,令x=0,则y=6,∴B(0,6),令y=0,则0=﹣x+6,∴x=4,∴A(4,0);∴OA=4,由运动知,AP=t,BQ=2t,∴OP=|4﹣t|,OQ=|6﹣2t|,∴Q(0,6﹣2t),P(4﹣t,0);∵△POQ的面积等于6,∴×(6﹣2t)×(4﹣t)=6,∴t=1或t=6,∴经过1秒或6秒,△POQ的面积等于6.23.【解答】解:(1)当k=﹣1时,该直线表达式为y=﹣x+14,∵四边形OABC是长方形,点P,Q分别在边AB,BC上,点B(12,8),∴点P的横坐标为12,点Q的纵坐标为8,当x=12时,y=﹣1×12+14=2,当y=8时,﹣x+14=8,解得x=6,∴点P,Q的坐标分别是P(12,2),Q(6,8);(2)如图1,过点B作BH⊥PQ于H,∵长方形OABC的顶点B的坐标是(12,8),∴点A的坐标为(12,0),点C的坐标为(0,8).设直线AC表达式为y=ax+b,则解得,,∴直线AC的解析式为y=﹣x+8,∵PQ∥AC,∴k=﹣.∴直线PQ表达式为y=﹣x+12,∵当x=12时,y=4;当y=8时,8=﹣x+12,∴x=6,∴BP=4,BQ=6.在Rt△BPQ中,根据勾股定理得,PQ==2,∵S△PBQ=BQ•BP=PQ•BH,∴×4×6=××BH,∴BH=;(3)∵当x=12时,y=6k+8;当y=8时,x=6.∴点P的坐标为(12,6k+8),点Q的坐标为(6,8).∴AP=6k+8,AO=12,BQ=CQ=6,AB=OC=8.∴BP=8﹣(6k+8)=﹣6k,过点Q作QM⊥OP于点M,连接OQ,如图2,∵PQ平分∠OPB,∴∠QPB=∠QPM,又∵∠PMQ=∠B=90°,PQ=PQ,∴△BPQ≌△MPQ(AAS),∴QM=QB=6,MP=BP=﹣6k,在Rt△OCQ中,根据勾股定理得,OQ=10,在Rt△OQM中,根据勾股定理得OM=8,∴OP=OM+MP=8﹣6k,∵在Rt△OAP中,OA2+AP2=OP2,即122+(6k+8)2=(8﹣6k)2.解得,k=﹣.24.【解答】解:(1)由轴对称的性质可得,若点P是端点,即当点P在A点时,A′点的位置关系是点A,OP所在的直线是y轴;当点P在C点时,∵∠AOC=∠BOC=45°,∴A′点的位置关系是点B,OP所在的直线表达式是y=x.故答案为:A,y轴;B,y=x.(2)连接OD,∵正方形AOBC的边长为2,点D是BC的中点,∴==.由折叠的性质可知,OA′=OA=2,∠OA′D=90°.∴A′D=1.设点P(x,2),P A′=x,PC=2﹣x,CD=1.∴(x+1)2=(2﹣x)2+12.解得x=.所以P(,2),∴OP所在直线的表达式是y=3x.(3)存在.若△DPQ的周长为最小,即是要PQ+DQ为最小.∵点D关于x轴的对称点是D′(2,﹣1),∴设直线PD'的解析式为y=kx+b,,解得,∴直线PD′的函数表达式为y=﹣x+.当y=0时,x=.∴点Q(,0).25.【解答】解:(1)①P1P2==;②P1坐标关于x轴的对称点是(﹣1,﹣3),设直线P2的解析式是y=kx+b(k≠0),根据题意得:,解得:,则直线的解析式是:y=﹣x+,在解析式中令y=0,解得:x=,则Q的坐标是:(,0),则QP1+QP2=P2===6,则△QP1P2的周长最小值是:6+;故填:6+;(2)①如图,四边形ABCO是矩形,点A、B的坐标分别为(4,0)、(4,3),则C(0,3).设直线AC的解析式为:y=kx+b(k≠0),则,解得,,所以直线AC的解析式为:y=﹣x+3;故填:y=﹣x+3;②∵NF⊥BC,四边形ABCO是矩形,∴NG∥OC,BN=AG,∴=,即=,∴FG=t,∴F(4﹣t,t);③如图,S=AM•FG=(4﹣t)×t=﹣t2+t(0<t<4);④∵A(4,0),C(0,3),点N与点C重合,∴ON=3,OA=4,∴由勾股定理得到AN=5.如图,当AN=AE时,易求ON=OE=3,则E1(0,﹣3);当NE=AN时,OE=5﹣3=2,则E2(0,﹣2);当AE=NE时,设E3(0,t),则(t﹣3)2=42+t2解得,t=,∴E3(0,);综上所述,符合条件的点E的坐标分别是:E1(0,﹣3),E2(0,﹣2),E3(0,).。
北师大版八年级数学上册课件:2.6实数(1)(共18张PPT)
无理数集合
问题导学:
你能把下(列各2)数0分属别于填正入数相吗应的?集0属合于内吗负?数吗?
3
2,
4, 9
140实,,数(可703.,3以)73分实,77为数352正还7,7实可732数以,、怎(的20样307相、的,进邻个负两行数个实5逐分3,之次数类间加31呢)8,?
3
1
2, 4
,7,
,
2, 20 ,
合作探究:
请各小组研究如何在数轴上画出表示 5 的点, 并在练习本上画出。
巩固练习:
1、判断下列说法是否正确: (1)无限小数都是无理数; (2)无理数都是无限小数; (3)带根号的数都是无理数. 2、求下列各数的相反数、倒数和绝对值:
(1) 7(; 2)3 8;(3) 49
课堂小结:
谈谈你这节课的 收获吧!
2.6实数(1)
温故互查:(二人小组完成)
1.(1) 整数和分数 统称有理数; (2)有理数分为 有限小数
和 无限循环小数; (3)有理数包括 正有理数 ﹑
零﹑ 负有理数. (4)无___限__不__循__环__小___数___叫做无理数;
温故互查:(二人小组完成)
有理数的分类方法:
整数 1、有理数
3 4
3
的相反数是__4____.
0的相反数是__0___. 2) 5的绝对值是 5 , 43的绝对值是___43___.
0的绝对值是___0__.
3) 5的倒数是
1 5
,
3 4
的倒数是____34__.
0有倒数吗?
(B)在有理数中,有理数a的的相反数、绝
对值是什么?不为0的数a的倒数是什么?
a的相反数是 -a
