卫生统计学(个人整理)
卫生统计学——精选推荐
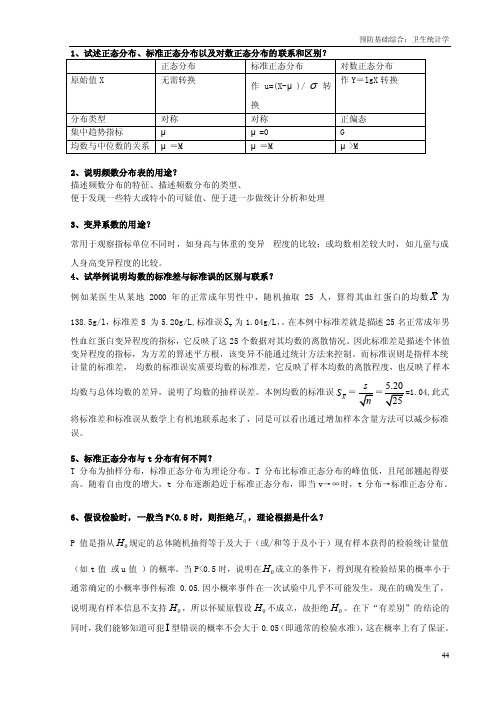
2、说明频数分布表的用途?描述频数分布的特征、描述频数分布的类型、便于发现一些特大或特小的可疑值、便于进一步做统计分析和处理3、变异系数的用途?常用于观察指标单位不同时,如身高与体重的变异程度的比较;或均数相差较大时,如儿童与成人身高变异程度的比较。
4、试举例说明均数的标准差与标准误的区别与联系?例如某医生从某地2000年的正常成年男性中,随机抽取25人,算得其血红蛋白的均数X 为138.5g/l ,标准差S 为5.20g/L,标准误x S 为1.04g/L ,。
在本例中标准差就是描述25名正常成年男性血红蛋白变异程度的指标,它反映了这25个数据对其均数的离散情况。
因此标准差是描述个体值变异程度的指标,为方差的算述平方根,该变异不能通过统计方法来控制。
而标准误则是指样本统计量的标准差, 均数的标准误实质要均数的标准差,它反映了样本均数的离散程度,也反映了样本均数与总体均数的差异,说明了均数的抽样误差。
本例均数的标准误X S 此式将标准差和标准误从数学上有机地联系起来了,同是可以看出通过增加样本含量方法可以减少标准误。
5、标准正态分布与t 分布有何不同?T 分布为抽样分布,标准正态分布为理论分布。
T 分布比标准正态分布的峰值低,且尾部翘起得要高。
随着自由度的增大,t 分布逐渐趋近于标准正态分布,即当v →∞时,t 分布→标准正态分布。
6、假设检验时,一般当P<0.5时,则拒绝0H ,理论根据是什么?P 值是指从0H 规定的总体随机抽得等于及大于(或/和等于及小于)现有样本获得的检验统计量值(如t 值 或u 值 )的概率。
当P<0.5时,说明在0H 成立的条件下,得到现有检验结果的概率小于通常确定的小概率事件标准0.05.因小概率事件在一次试验中几乎不可能发生,现在的确发生了,说明现有样本信息不支持0H ,所以怀疑原假设0H 不成立,故拒绝0H 。
在下“有差别”的结论的同时,我们能够知道可犯I 型错误的概率不会大于0.05(即通常的检验水准),这在概率上有了保证。
卫生统计学——精选推荐

卫⽣统计学第三章总体均数的区间估计和假设检验第⼀节均数的抽样误差与标准误⼀、标准误的意义及计算标准误是反映均数抽样误差⼤⼩的指标;同类性质的资料,标准误越⼩,表⽰样本均数与总体均数越接近,也就是抽样误差越⼩,说明样本均数推论总体均数的可靠性越⼤;反之,标准误越⼤,说明抽样误差越⼤,表⽰样本均数推论总体均数的可靠性越⼩。
数理统计已证明:标准误的⼤⼩与总体标准差成正⽐,⽽与样本含量的平⽅根成反⽐,即,当总体中各变量值都相等时,即σ=0,则抽取的各样本均数与总体均数必然相同,即抽样误差为零;⽽当总体中变量值间的变异度越⼤时,即σ越⼤,则抽取的各样本均数间离散度也越⼤,即抽样误差也越⼤;同时,当样本含量n越⼤时,则样本均数与总体均数越接近,抽样误差越⼩;反之,抽样误差越⼤。
因此可以适当增加样本例数来缩⼩抽样误差。
实际⼯作中总体标准差σ往往是不知道的,⽽只知道样本标准差S,所以只能⽤S代替,求得标准误的估计值,即⼆、标准误的应⽤▲表⽰抽样误差的⼤⼩,从⽽说明样本均数的可靠性。
(在医学⽂献上常⽤样本均数加减标准误的形式表⽰资料的均数及可靠程度)进⾏总体均数的区间估计进⾏均数的t检验第⼆节t分布⼀、t分布的概念如果从⼀个正态总体中,抽取样本含量为n的许多样本,分别计算其和,然后求出每⼀个t值,这样可有许多t值。
这些t值有⼤有⼩,有正有负,其频数分布是⼀种连续性分布,这就是统计上著名的t分布。
⼆、t分布曲线的特征▲特征:①t分布曲线是单峰分布,以0为中⼼,左右两侧对称,曲线的中间⽐标准正态曲线(u分布曲线)低,两侧翘得⽐标准曲线略⾼。
②当样本含量越⼩(严格地说是⾃由度v=n-1越⼩),t分布与u分布差别越⼤;当v逐渐增⼤时,t分布逐渐逼近u分布,当v=∞时,t分布就完全成为u分布。
所以t分布曲线的形状随v的变动⽽变化。
在⾃由度为v的t分布曲线下双侧尾部合计⾯积或单侧尾部⾯积为指定值α时,常把横轴上相应的t界值记为tα,v。
卫生统计学知识点汇总

● 表示符号:G
● 计算方法:直接法和加权法
(1)直接法:
适用范围:小样本资料
方法:将 n 个观察值(X1,X2,3,……Xn)直接相乘再开 n 次方。 公式:G n X1X2 Xn
用对数形式表示为: 举例:设有 5 份血清样品,滴度分别为: 1:1, 1:10, 1:100, 1:1000, 1:10000
G=lg-1 (Σf lgX/Σf ) 举例:有 95 名麻疹易感儿童,接种麻疹疫苗一个月后,血凝抑制抗体滴度见下表,试求平
均滴度(例)。 G=lg-1 (Σf lgX/Σf )=lg-195) =
即 95 名易感儿童接种疫苗一个月后,血凝抑制抗体的 平均滴度为 1:。
计算几何均数(G )注意事项:
(1)观察值不能为 0;
(2)观察值不能同时有正有负;
(3)同一组资料求得的几何均数小于算术均数。
练习:
1.有 8 份血清的抗体效价分别为:1:5, 1:10, 1:20, 1:40, 1:80, 1:160, 1:320, 1:640
G lg 1[(lg5 lg10 lg 640) / 8]
,,, , 求平均身高
178. 4 X
10
适用范围:小样本资料,n<30
169. 7
( cm )
方法:将观察值 X1、X2、X3、……、Xn 直接相加,再除以观察值的个数 n。
n
公式: X X X1 X 2 X n i1
n
n
(2)加权法:
适用范围:大样本含量的分组资料或频数表资料。
该研究方法叫抽样研究。 统计推断:样本的现象推断所研究总体的特征。即分析样本数据,获得关于总体的知识。 同质(homogeneity):指研究对象在一定范畴的各种可能影响主要观察指标的其它因素处
卫生统计学

病率、发病率、死亡率、病死率、阳性率、治愈率、有效
率、感染率等。
案例3
调查某乡甲、乙两村村民钩虫感染情况:甲村有村
民1200人,感染人数为110人;乙乡有村民1500人,感染人
数为150人。哪一个村村民的钩虫感染情况较为严重?
甲村的钩虫感染率:
110 100% 9.17% 1200 150 100% 10.00% 1500
K:比例基数,常见的有百分率、千分率、万分率等。 选择K的原则:使算得的率至少保留1—2位整数。
3.特点 (1)一般合计率或总率不等于100%,当率的分母无时间量 纲时,率的分子是分母的一部分,因而其值不会超过1。 (2)某一部分的分率改变不影响其他分率的变化。 4.应用 在医疗卫生工作和科研的分析中应用非常广泛,如患
1995年 % 49.39 16.49 9.56 12.20 12.36 病例数 2032 1143 542 767 875 5359
2000年 % 37.92 21.33 10.11 14.31 16.33
100.00
100.00
3.特点 (1)某事物内部各构成比的总和必定等于100%,即各分子 的总和等于分母。 (2)某一部分构成比的改变将影响其他构成比的变化,各
基数的影响,便于正确描述计数资料的水平及进行相互比 较。
第三章 定性资料的统计描述
第一节 常用相对数及其应用
第二节 应用相对数需注意的问题
第三节 动态数列及其应用
第四节 率的标准化
一、率(rate)
1.意义 近似地反映某一事件出现的机会大小,它说明某现
象发生的频率或强度,如发病概率、死亡概率。
2.计算公式 频率= ×K 可能发生某事件的个体数 某事件发生的个体数
(整理)《卫生统计学》第一次作业及答案

【补充选择题】A型题1.统计资料的类型可以分为A 定量资料和等级资料B 分类资料和等级资料C 正态分布资料和离散分布的资料D 定量资料和分类资料E 二项分布资料和有序分类资料2.下列符号中表示参数的为A SB uCD tE X3.统计学上所说的随机事件发生的概率P,其取值范围为A P≤1B P≥1C P≥0D1≥P≥0E1>P>04.小概率事件在统计学上的含义是A 指的是发生概率P≤0.5的随机事件B 指一次实验或者观察中绝对不发生的事件C 在一次实验或者观察中发生的可能性很小的事件,一般指P≤0.05D 以上说法均不正确E A和C正确5.描述定量资料集中趋势的指标有A 均数、几何均数、变异系数B 均数、几何均数、四分位数间距C 均数、变异系数、几何均数D 均数、四分位数间距、变异系数E 均数、几何均数、中位数6.关于频数表的说法正确的是A 都分为10个组段B 每一个组段必须组距相等C 从频数表中可以初步看出资料的频数分布类型D 不是连续型的资料没有办法编制频数表E 频数表中的每一个组段不一定是半开半闭的区间,可以任意指定7. 关于偏态分布资料说法不正确的是A正偏态资料的频数分布集中位置偏向数值大的一侧B负偏态资料的频数分布集中位置偏向数值大的一侧C 偏态分布资料频数分布左右不对称D 不宜用均数描述其集中趋势E 不宜用变异系数来描述其离散程度8. 对于一个两端都没有确切值的资料,宜用下列哪个指标来描述其集中趋势A 几何均数B 均数C 方差D 中位数E 四分位数间距9.下列关于标准差的说法中哪种是错误的A 对于同一个资料,其标准差一定小于均数B 标准差一定大于0C 同一个资料的标准差可能大于均数,也可能小于均数D 标准差可以用来描述正态分布资料的离散程度E 如果资料中观察值是有单位的,那么标准差一定有相同单位10. 下列关于标准差S和样本含量n的说法,正确的是A 同一个资料,其他条件固定不变,随着n增大,S一定减小B 同一个资料,即使其他条件固定不变,随着n增大,也不能确定S一定减小C 同一个资料,其他条件固定不变,随着n增大,S一定增大D 以上说法均正确E 以上说法均错误11. 用下列哪两个指标可以较全面地描述正态分布特征A 均数和中位数B 中位数和方差C 均数和四分位数间距D 均数和标准差E 几何均数和标准差12. 下列哪个资料适宜用几何均数来描述其集中趋势A 偏态分布的资料B 对称分布的资料C 等比级数资料D 一端不确定的资料E 正态分布资料13. 下列关于变异系数的说法,错误的是A 与标准差一样都是用来描述资料变异程度的指标,都有单位B 可以比较计量单位不同的几组资料的离散程度C 可以比较均数相差悬殊的几组资料的离散程度D 变异系数的实质是同一个资料的标准差与均数的比值E 变异系数可以用来描述正态分布资料的变异程度14. 假设将一个正态分布的资料所有的原始数据都加上一个正数,下列说法正确的是A 均数将增大,标准差不改变B 均数和标准差均增大C 均数不变,标准差增大D 不一定E 均数和标准差均没有变化15. 假设将一个正态分布的资料所有的原始数据都乘以一个大于1的常数,下列说法正确的是A 均数不发生改变B 标准差将不发生改变C 均数是否变化不一定D 变异系数不发生改变E 中位数不发生改变16. 下列关于正态分布曲线的两个参数μ和σ说法正确的是A μ和σ越接近于0时,曲线越扁平B 曲线形状只与μ有关,μ值越大,曲线越扁平C 曲线形状只与σ有关,σ值越大,曲线越扁平D 曲线形状与两者均无关,绘图者可以随意画E 以上说法均不正确17. 对于正态分布曲线的描述正确的是A 当σ不变时,随着μ增大,曲线向右移B 当σ不变时,随着μ增大,曲线向左移C 当μ不变时,随着σ增大,曲线向右移D 当μ不变时,随着σ增大,曲线将没有变化E 以上说法均不正确18. 在正态曲线下,下列关于μ-1.645σ说法正确的是A μ-1.645σ到曲线对称轴的面积为90%B μ-1.645σ到曲线对称轴的面积为10%C μ-1.645σ到曲线对称轴的面积为5%D μ-1.645σ到曲线对称轴的面积为45%E μ-1.645σ到曲线对称轴的面积为47.5%19. 在正态曲线下,小于μ-2.58σ包含的面积为A 1%B 99%C 0.5%D 0.05%E 99.5%20. 在正态曲线下,大于μ-2.58σ包含的面积为A 1%B 99%C 0.5%D 0.05%E 99.5%21. 下列关于标准正态分布的说法中错误的是A 标准正态分布曲线下总面积为1B 标准正态分布是μ=0并且σ=1的正态分布C 任何一种资料只要通过σμ-=X u 变换均能变成标准正态分布D 标准正态分布的曲线是唯一的E 因为标准正态分布是对称分布,所以u ≥-1.96与u ≤1.96所对应的曲线下面积相等22. 某年某中学体检,测得100名高一女生的平均身高X =154cm, S =6.6cm ,该校高一女生中身高在143~170cm 者所占比重为(0.00780.04752.42, 1.67u u =-=-)A 90%B 95%C 97.5%D 94.5%E 99%23. 下列关于确定正常人肺活量参考值范围说法正确的是A 只能为单侧,并且只有上限B 只能为单侧,并且只有下限C 只能为双侧,这样才能反映全面D 单双侧都可以E 以上说法均不确切24. 下列关于医学参考值范围的说法中正确的是A 医学参考值范围是根据大部分“健康人”的某项指标制定的B 医学参考值范围的制定方法不受分布资料类型的限制C 在制定医学参考值范围时,最好用95%范围,因为这个范围最能说明医学问题D 在制定医学参考值范围时,最好用95%范围,因为这样比较好计算E 以上说法均不正确25. 为了制定尿铅的正常值范围,测定了一批正常人的尿铅含量,下列哪种说法正确A 无法制定,要制定正常值范围必须测定健康人的尿铅含量B 可以制定,应为单侧上限C 可以制定,应为单侧下限D 可以制定,但是无法确定是上侧范围还是下侧范围E 可以制定双侧95%的参考值范围B型题26~30题A 中位数B 四分位数间距C 均数D 几何均数E 对数标准差的反对数26. 对于只有上限不知道下限的资料,欲描述其集中趋势宜用(A)27. 某学校测定了大学一年级新生乙肝疫苗的抗体滴度,欲描述其集中位置,宜用(D)28. 描述偏态资料的离散程度,可用(B)29. 描述近似正态分布的资料的集中趋势,最适宜用(C)30. 偏态分布的资料,如果经对数变换后服从正态分布,那么欲描述其离散程度,应选用(E)【补充选择题】A 型题1. X S 表示A 样本中实测值与总体均数之差B 样本均数与总体均数之差C 样本的抽样误差D 样本中各实测值分布的离散情况E 以上都不是2. 标准误越小,说明此次抽样所得样本均数A 离散程度越小B 可比性越好C 可靠程度越小D 系统误差越小E 抽样误差越小3. 对样本均数X 作t 变换的是A X X S μ-B XX μσ- C X μσ- D X μσ- E X X X S - 4. t 分布与正态分布的关系是A 均以0为中心,左右对称B 总体均数增大时,分布曲线的中心位置均向右移动C 曲线下两端5%面积对应的分位点均是±1.96D 随样本含量的增大,t 分布逼近标准正态分布E 样本含量无限增大时,二者分布完全一致5. 标准差与标准误的关系中,正确的是A 二者均反映抽样误差的大小B 总体标准差不变时,增大样本例数可以减小标准误C 总体标准差增大时,总体的标准误也增大D 样本例数增大时,样本的标准差和标准误都会减小E 标准差用于计算可信区间,标准误用于计算参考值范围6. 下列哪个说法是统计推断的内容A 区间估计和点估计B 参数估计与假设检验C 统计预测和统计控制D 统计描述和统计图表E 参数估计和统计预测7. 可信区间估计时可信度是指A αB βC 1α-D 1β-E 以上均不是8. σ未知且n 很小时,总体均数的95%可信区间估计的通式为A 1.96X S ±B 1.96X X S ±C 1.96X X σ±D 0.05/2,X X t S ν±E 0.05/2,X t S ν±9. 关于假设检验,下列说法正确的是A 备择假设用H 0表示B 检验水准的符号为βC P 可以事先确定D 一定要计算检验统计量E 假设检验是针对总体的特征进行10. 两样本均数比较的t 检验,差别有统计学意义时,P 越小A 说明两总体均数差别越大B 说明两样本均数差别越大C 越有理由认为两总体均数不同D 越有理由认为两样本均数不同E 犯I 型错误的可能性越大11. 方差齐性检验时,检验水准取下列哪个时,II 型错误最小A 0.20α=B 0.10α=C 0.05α=D 0.02α=E 0.01α=12. 假设检验的一般步骤中不包括哪项A 建立检验假设,确定检验水准B 对总体参数的可信区间作出估计C 选定检验方法,计算检验统计量D 确定P 值,作出统计推断结论E 直接计算P 值13. 假设检验时,应该使用单侧检验却误用了双侧检验,可导致A 增大了I 型错误B 增大了II 型错误C 减小了可信度D 增大了把握度E 统计结论更准确14. 假设检验中,P 与α的关系是A P 越大,α越大B P 越小,α越大C 二者均可事先确定D 二者均需通过计算确定E P 值的大小与α的大小无关15. 假设检验在设计时应确定的是A 总体参数B 检验统计量C 检验水准D P 值E 以上均不是16. 计量资料配对t 检验的无效假设(双侧检验)可写为A 0d μ=B 0d μ≠C 12μμ=D 12μμ≠E 0μμ=17. II 型错误是指A 拒绝了实际上成立的H 0B 不拒绝实际上成立的H 0C 拒绝实际上不成立的H 0D 不拒绝实际上不成立的H 0E 拒绝H 0时所犯的错误18. 下列关于I 型错误和II 型错误说法不正确的是A I 型错误的概率用α表示B II 型错误的概率用β表示C 样本量固定时,I 型错误的概率越大,II 型错误的概率也越大D 样本量固定时,I 型错误的概率越大,II 型错误的概率越小E 要同时减小I 型错误和II 型错误的概率,需增大样本量19. 不适用于正态分布计量资料的假设检验的统计量是A tB uC FD 'tE T20. 完全随机设计的方差分析中,成立的是A SS 组内 < SS 组间B MS 组内 < MS 组间C MS 组间 >1D SS 总=SS 组间+SS 组内E MS总=MS组间+MS组内21. 随机区组设计方差分析中,成立的是A SS总=SS组间+SS组内B SS总=SS组间+SS区组C SS总=SS组间+SS区组+SS误差D SS总=SS组间-SS组内E SS总=SS区组+SS误差22. 成组设计方差分析,若处理因素无作用,则理论上有A F=1B F<1C F>1D F=0E F<1.9623. 方差分析中,组间变异主要反映A 随机误差B 抽样误差C 测量误差D 个体差异E 处理因素的作用24. 完全随机设计的方差分析中,组内变异反映的是A 随机误差B 抽样误差C 测量误差D 个体差异E 系统误差25. 多组均数的两两比较中,若用t检验不用q检验,则A 会将有差别的总体判断为无差别的概率增大B 会将无差别的总体判断为有差别的概率增大C 结果更加合理D 结果会一致E 以上都不对26. 随机区组方差分析中,总例数为N,处理组数为k,配伍组数b,则处理组组间变异的自由度为A N-kB b-1C (b-1)(k-1)D k-1E N-127. 关于检验效能,下列说法错误的是A 两总体均数确有差别时,按α水准发现这种差别的能力B 两总体均数确有差别时,按1β-水准发现这种差别的能力C 与α有关D 与样本例数有关E 与两总体均数间的位置有关28. 为研究新旧两种仪器测量血生化指标的差异,分别用这两台仪器测量同 一批样品,则统计检验方法应用A 成组设计t 检验B 成组设计u 检验C 配对设计t 检验D 配对设计u 检验E 配对设计2χ检验29. 两样本均数比较的t 检验,t =1.20,0.05α=时统计推断结论为A 两样本均数的差别有统计学意义B 两样本均数的差别无统计学意义C 两总体均数的差别有统计学意义D 两总体均数的差别无统计学意义E 未给出自由度,无法进行统计推断30. 两大样本均数比较,推断12μμ=是否成立,可用A t 检验B u 检验C 方差分析D 以上三种均可以E 2χ检验31~35题某药物研究中心为研究减肥药的效果,将40只体重接近的雄性大白鼠随机分为4组,分别给予高剂量、中剂量、低剂量减肥药和空白对照4种处理方式,两个月后对这些大白鼠的体重进行了测定31. 上述资料所用的设计方法为A 完全随机设计B 随机区组设计C 交叉设计D 析因设计E 序贯试验32. 比较四组大白鼠的体重有无差别,宜用A 两两比较的 t 检验B 两两比较的u 检验C 方差分析D 2χ检验E 直线回归33. 比较四组大白鼠的体重有无差别,无效假设为A 12μμ=B 1234μμμμ===C 0μμ=D 12ππ=E 0d μ=34. 若规定0.05α=,方差分析得P <0.01,则A 各总体均数不同或不全相同B 各样本均数不同或不全相同C 各总体均数均不相同D 各样本均数均不相同E 四组总体均数的差别很大35. 为比较各剂量组与空白对照组间的差别,宜用A LSD 法B SNK 法C 新复极差法D 两两t 检验E 两两u 检验B 型题36~40题A μB σC X σD νE 以上均不是36. 决定t分布位置的是(E)37. 决定t分布形态的是(D)38. 决定正态分布位置的是(A)39. 决定正态分布形状的是(B)40. 反映抽样误差大小的是(C)41~45题A 样本均数与总体均数的t检验B 配对t检验C 成组t检验D 成组u检验E 以上都不是41. A地150名7岁女童与B地150名7岁女童的体重均数差别的检验,为简便计算,可选用(D)42. A地20名7岁女童与B地20名7岁女童的体重均数差别的检验用(C)43. A地15名7岁女童服用某保健品前后体重的变化的检验用(B)44. 检验B地70名7岁女童的体重是否服从正态分布用(E)45. B地20名女童的体重均数与同年人口普查得到的全国7岁女童的体重均数比较用(A)46~50题A SS总=SS组间+SS组内B SS总=SS处理+SS区组+SS误差C SS总=SS A+SS B+SS AB+SS误差D SS总=SS阶段+SS处理+SS个体+SS误差E 以上均不是46. 析因设计方差分析总变异的分解为(C)47. 完全随机设计方差分析总变异的分解为(A)48. 交叉设计方差分析总变异的分解为(D)49. 随机区组设计方差分析总变异的分解为(B)50. 重复测量方差分析总变异的分解为(E)。
卫生统计学基本知识

卫生统计学基本知识1.什么是卫生统计学卫生统计学是一门研究人群因健康状况而产生变化的科学,这些变化可以是疾病的发生率、死亡率、健康状况等。
卫生统计学的主要目的是收集、整理和分析有关人类健康的数据,以便更好地了解人类健康状况的变化趋势和特点,为卫生政策和决策提供科学依据。
2.卫生统计学的应用范围卫生统计学在不同领域有着广泛的应用,比如:(1)疾病流行病学调查,比如统计某种疾病的患病率、死亡率、传染源和易感人群等信息,以便控制和预防该疾病的发生和传播。
(2)公共卫生政策制定,比如通过对社会经济、民生状况和环境等因素进行分析,探索影响健康的各种因素,从而制定出相应的卫生政策。
(3)评估卫生计划或项目的效果,通过对卫生计划或项目实施前后的数据进行比较分析,评估卫生计划或项目的有效性,为后续的卫生计划和项目提供参考。
(4)医疗资源的管理,比如通过对医院的病床使用率、医生和护士的配备情况等进行统计分析,优化医疗资源的利用,提高医疗服务的质量和效率。
3.卫生统计学的主要指标卫生统计学中常用的指标包括:(1)患病率:指人群中某种疾病患者所占的比例。
(2)死亡率:指人群中某种疾病导致死亡的人数占总人口数的比例。
(3)出生率:指每千人中新生儿的出生数量。
(4)人口增长率:指一定时期内人口总数的增长速度。
(5)预期寿命:指生活在一定条件下的人群中,平均预期寿命。
4.卫生统计学的方法卫生统计学主要采用问卷调查、抽样调查、临床观察等方法收集数据,然后再利用各种数学统计方法对所得数据进行整理、分析和解释。
常用的数学统计方法包括频率分布、平均数、标准差、方差、偏度、峰度、t检验、方差分析、回归分析等。
同时,卫生统计学还需要使用计算机辅助分析工具和软件,如SPSS、SAS等。
5.卫生统计学的局限性卫生统计学作为一门科学,虽然能够帮助我们对健康状况进行统计分析,但在实际应用中,仍然存在一些局限性。
(1)数据质量问题:收集到的数据存在缺失、误报、漏报等情况,会影响对健康状况的判断和分析。
卫生统计学知识点汇总

1、卫生统计学是应用概率论和数理统计学的基本原理和方法,研究居民卫生状况以及卫生服务领域中数据的收集、整理和分析的一门科学,是卫生及其相关领域研究中不可缺少的分析问题和解决问题的重要工具。
2、统计工作的基本步骤:①设计;②收集资料;③整理资料;④分析资料3、分析资料是根据研究目的计算有关指标描述数据的基本特征,选择适当统计方法对资料进行分析,阐明事物的内在联系和规律的过程。
统计分析包括:①统计描述:是指选用统计指标、统计表或统计图等对资料的数量特征及其分布规律进行测定和描述②统计推断:是指选择恰当的统计方法由已知的样本信息推断总体的特征,包括参数估计和假设检验4、(1)①同质:在统计学中,若某些观察对象具有相同的特征或属性,我们就称之为同质,或具有同质性②变异:我们将同质个体的某项特征或属性的观察值或测量值之间的差异称为变异(2)①总体:根据研究目的确定的同质观察单位的全体,更确切地说,是同质的所有观察单位某种特征或属性的观察值或测量值的集合。
若总体明确了特定的时间和空间范围且包含有限个观察单位,称为有限总体。
若总体没有特定的时间和空间范围的限制,且包含的观察单位个数是无限的或几乎是不可能准确计数的,称该总体为无限总体②样本:从总体中随机抽取的具有代表性的部分观察单位的集合(3)①参数:反映总体特征的指标称为参数②统计量:根据样本观察值计算出来的指标称为统计量(4)①变量:确定总体之后,研究者需要对每个观察单位的某项特征或属性进行观察或测量,这种特征或属性称为变量。
变量的观察值或测量值称为变量值或观察值②资料:变量值的集合称为资料。
资料可分为定量资料(又称计量资料)和定性资料(又称分类资料)两类。
定性资料又可分为计数资料和等级资料(5)①抽样研究:从总体中随机抽取样本,通过样本信息推断总体特征的研究方法称为抽样研究②抽样误差:由随机抽样造成的样本统计量与总体参数之间、样本统计量之间的差异称为抽样误差产生抽样误差的根源在于个体变异,由于个体变异是普遍存在的,因此在抽样研究中抽样误差是不可避免的,但它具有一定的规律性,可以用统计学方法估计其大小(6)概率:随机事件发生可能性大小的数值度量当某事件发生的概率P≤0.05时,统计学中习惯上称该事件为小概率事件,表示在一次实验或观察中该事件发生的可能性很小,可以视为很可能不发生。
卫生统计学

400 0.5 360 P X 400 1 P X 400 1 1 2.13 0.0166 试估计该放射性物质半小时内发出的脉冲数大于 400 个的概率为 1.66%。
例 5-1 某市随机调查了 50 岁以上的中老年妇女 776 人, 其中患有骨质疏松症者 322 人, 患病率为 41.5%,试计算该样本频率的抽样误差。 答:p = 41.5% = 0.415,n = 776
答:不可以 用单样本率比较的μ检验
第十章 第十一章 1. 求得 r 值后可推论为:E A. 两变量间有相关关系 B. 两变量间无相关关系 C.|r|大时就有意义 D.n 大时就有意义 E.对 r 值作假设检验后才能推论 2. 根据样本算得两个随机变量 X 与 Y 的相关系数 r, 经 t 检验, P<0.01, 可认为 D A. X 与 Y 间密切相关 C. 总体相关系数ρ=0 E. 总体相关系数ρ >0 B. 总体相关系数ρ很大 D. 总体相关系数ρ≠0
A 两样本均数不同 B 两样本均数差异很大 C 两总体均数差异很大 D 两样本均数来自同一总体 E 两样本均数来自不同总体 3. 两样本比较时,分别取以下检验水准,下列何者所取第二类错误最小。 D A.α=0.05 B.α=0.01 C.α=0.10 D.α=0.20 4、已知某地 25 岁正常成年男性的平均收缩压为 113.0mmHg,从该地抽取 20 名 25 岁正常 成年男性,测得其平均收缩压为 119.0mmHg。113mmHg 与 119.0mmHg 不同,原因是( )B A、样本例数太少 B、抽样误差 C、总体均数不同 D、系统误差 E、个体差异太大 5、从上述第一题中的同一个地区中再随机抽取 20 名 8 岁正常男孩,测得其平均收缩压为 90.0mmHg,标准差为 9.8mmHg。90.0mmHg 与 113.0mmHg 不同,原因是 C A、样本例数太少 C、总体均数不同 第七章 B、抽样误差 D、系统误差 E、样本均数不可比
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
卫生统计学一、概述1、卫生统计学的概念(熟练掌握)统计学是研究数据的收集、整理和分析的一门科学,帮助人们分析所占有的信息,达到去伪存真、去粗取精、正确认识世界的一种重要手段。
卫生统计学是应用数统计学的原理与方法研究居民健康状况以及卫生服务领域中数据的收集、整理和分析的一门科学。
由此看出:统计学是处理资料中变异性的科学和艺术,是在收集、归类、分析和解释大量数据的过程中获取可靠结果的一门学科。
这里强调了“过程”,但在实际工作中,许多人往往是忽略了设计、收集和归类(整理),到了分析数据时才想到统计学,此时难免发生“悔之晚矣”的憾事。
作为统计学的应用者应充分认识到这一点。
卫生统计学的内容(了解):1)健康统计:医学人口统计、疾病统计和生长发育统计等;2)卫生服务统计:包括卫生资源利用、医疗卫生服务的需求、医疗保健体制改革等方面的统计学问题。
2、卫生统计学的工作步骤(熟练掌握)统计学对统计工作的全过程起指导作用,任何统计工作和统计研究的全过程都可分为以下四个步骤:1)、设计:在进行统计工作和研究工作之前必须有一个周密的设计。
设计是在广泛查阅文献、全面了解现状、充分征询意见的基础上,对将要进行的研究工作所做的全面设想。
其内容包括:明确研究目的和研究假说,确定观察对象、观察单位、样本含量和抽样方法,拟定研究方案、预期分析指标、误差控制措施、进度与费用等。
设计是整个研究工作中最关键的一环,也是指导以后工作的依据2)、收集资料:遵循统计学原理采取必要措施得到准确可靠的原始资料。
及时、准确、完整是收集统计资料的基本原则。
卫生工作中的统计资料主要来自以下三个方面:①统计报表:是由国家统一设计,有关医疗卫生机构定期逐级上报,提供居民健康状况和医疗卫生机构工作的主要数据,是制定卫生工作计划与措施、检查与总结工作的依据。
如法定传染病报表,职业病报表,医院工作报表等。
②经常性工作记录:如卫生监测记录、健康检查记录等。
③专题调查或实验。
3)、整理资料:收集来的资料在整理之前称为原始资料,原始资料通常是一堆杂乱无章的数据。
整理资料的目的就是通过科学的分组和归纳,使原始资料系统化、条理化,便于进一步计算统计指标和分析。
其过程是:首先对原始资料进行准确性审查(逻辑审查与技术审查)和完整性审查;再拟定整理表,按照“同质者合并,非同质者分开”的原则对资料进行质量分组,并在同质基础上根据数值大小进行数量分组;最后汇总归纳。
4)、分析资料:其目的是计算有关指标,反映数据的综合特征,阐明事物的内在联系和规律。
统计分析包括统计描述和统计推断。
前者是用统计指标与统计图(表)等方法对样本资料的数量特征及其分布规律进行描述;后者是指如何抽样,以及如何用样本信息推断总体特征。
进行资料分析时,需根据研究目的、设计类型和资料类型选择恰当的描述性指标和统计推断方法。
统计工作的四个步骤紧密相连、不可分割,任何一步的缺陷,都将影响整个研究结果。
3、基本概念:1)、同质与变异。
严格地讲,同质是指被研究指标的影响因素完全相同。
但在医学研究中,有些影响因素往往是难以控制的(如遗传、营养等),甚至是未知的。
所以,在统计学中常把同质理解为对研究指标影响较大的、可以控制的主要因素尽可能相同。
例如研究儿童的身高时,要求性别、年龄、民族、地区等影响身高较大的、易控制的因素要相同,而不易控制的遗传、营养等影响因素可以忽略。
同质基础上的个体差异称为变异。
如同性别、同年龄、同民族、同地区的健康儿童的身高、体重不尽相同。
事实上,客观世界充满了变异,生物医学领域更是如此。
哪里有变异,哪里就需要统计学。
若所研究的同质群体中所有个体一模一样,只需观察任一个体即可,无须进行统计研究。
2)、总体与样本任何统计研究都必须首先确定观察单位,亦称个体。
观察单位是统计研究中最基本的单位,可以是一个人、一个家庭、一个地区、一个样品、一个采样点等。
总体是根据研究目的确定的同质观察单位的全体,或者说,是同质的所有观察单位某种观察值(变量值)的集合。
例如欲研究山东省2002年7岁健康男孩的身高,那么,观察对象是山东省2002年的7岁健康男孩,观察单位是每个7岁健康男孩,变量是身高,变量值(观察值)是身高测量值,则山东省2002年全体7岁健康男孩的身高值构成一个总体。
它的同质基础是同地区、同年份、同性别、同为健康儿童。
总体又分为有限总体和无限总体。
有限总体是指在某特定的时间与空间范围内,同质研究对象的所有观察单位的某变量值的个数为有限个,如上例;无限总体是抽象的,无时间和空间的限制,观察单位数是无限的,如研究碘盐对缺碘性甲状腺病的防治效果,该总体的同质基础是缺碘性甲状腺病患者,同用碘盐防治;该总体应包括已使用和设想使用碘盐防治的所有缺碘性甲状腺病患者的防治效果,没有时间和空间范围的限制,因而观察单位数无限,该总体为无限总体。
在实际工作中,所要研究的总体无论是有限的还是无限的,通常都是采用抽样研究。
样本是按照随机化原则,从总体中抽取的有代表性的部分观察单位的变量值的集合。
如从上例的有限总体(山东省2002年7岁健康男孩)中,按照随机化原则抽取100名7岁健康男孩,他们的身高值即为样本。
从总体中抽取样本的过程为抽样,抽样方法有多种。
抽样研究的目的是用样本信息推断总体特征。
统计学好比是总体与样本间的桥梁,能帮助人们设计与实施如何从总体中科学地抽取样本,使样本中的观察单位数(亦称样本含量)恰当,信息丰富,代表性好;能帮助人们挖掘样本中的信息,推断总体的规律性。
3)、资料与变量及其分类总体确定之后,研究者应对每个观察单位的某项特征进行测量或观察,特征称为变量。
如“身高”、“体重”、“性别”、“血型”、“疗效”等。
变量的测定值或观察值称为变量值或观察值,亦称为资料。
按变量的值是定量的还是定性的,可将变量分为以下类型,变量的类型不同,其分布规律亦不同,对它们采用的统计分析方法也不同。
在处理资料之前,首先要分清变量类型。
1)数值变量:其变量值是定量的,表现为数值大小,可经测量取得数值,多有度量衡单位。
如身高(cm)、体重(kg)、血压(mmHg kPa)、脉搏(次/min)和白细胞计数(×10 9 /L)等。
这种由数值变量的测量值构成的资料称为数值变量资料,亦称为定量资料。
大多数的数值变量为连续型变量,如身高、体重、血压等;而有的数值变量的测定值只能是正整数,如脉搏、白细胞计数等,在医学统计学中把它们也视为连续型变量。
2)分类变量:其变量值是定性的,表现为互不相容的类别或属性。
分类变量可分为无序变量和有序变量两类:(1)无序分类变量是指所分类别或属性之间无程度和顺序的差别。
它又可分为①二项分类,如性别(男、女),药物反应(阴性和阳性)等;②多项分类,如血型(O、A、B、AB),职业(工、农、商、学、兵)等。
对于无序分类变量的分析,应先按类别分组,清点各组的观察单位数,编制分类变量的频数表,所得资料为无序分类资料,亦称计数资料。
(2)有序分类变量各类别之间有程度的差别。
如尿糖化验结果按-、±、+、++、+++分类;疗效按治愈、显效、好转、无效分类。
对于有序分类变量,应先按等级顺序分组,清点各组的观察单位个数,编制有序变量(各等级)的频数表,所得资料称为等级资料。
变量类型不是一成不变的,根据研究目的的需要,各类变量之间可以进行转化。
例如血红蛋白量(g/L)原属数值变量,若按血红蛋白正常与偏低分为两类时,可按二项分类资料分析;若按重度贫血、中度贫血、轻度贫血、正常、血红蛋白增高分为五个等级时,可按等级资料分析。
有时亦可将分类资料数量化,如可将病人的恶心反应以0、1、2、3表示,则可按数值变量资料(定量资料)分析。
4、随机事件与概率医学研究的现象,大多数是随机现象,对随机现象进行实验或观察称为随机试验。
随机试验的各种可能结果的集合称为随机事件,亦称偶然事件,简称事件。
例如用相同治疗方案治疗一批某病的患者,治疗转归可能为治愈、好转、无效、死亡四种结果,对于一个刚入院的患者,治疗后究竟发生哪一种结果是不确定的,可能发生的每一种结果都是一个随机事件。
对于随机事件来说,在一次随机试验中,某个随机事件可能发生也可能不发生,但在一定数量的重复试验后,该随机事件的发生情况是有规律可循的。
概率是描述随机事件发生的可能性大小的数值,常用P表示。
例如,投掷一枚均匀的硬币,随机事件A表示“正面向上”,用 n表示投掷次数;m表示随机事件A发生的次数;f表示随机事件A发生的频率(f=m/n),0≤m≤n, 0≤f≤1。
用不同的投掷次数n作随机试验,结果如下:m/n=8/10=0.8, 7/20=0.35,…… , 249/500=0.498, 501/1000=0.501, 10001/2000=0.5000,由此看出当投掷次数n 足够大时,f=m/n→0.5,称P(A)=0.5,或简写为:P=0.5。
当n足够大时,可以用f估计P。
随机事件概率的大小在0与1之间,即0<P<1,常用小数或百分数表示。
P越接近1,表示某事件发生的可能性越大;P越接近0,表示某事件发生的可能性越小。
P=1表示事件必然发生,P=0表示事件不可能发生,它们是确定性的,不是随机事件,但可以把它们看成随机事件的特例。
若随机事件A的概率P(A)≤a,习惯上,当a=0.05时,就称A为小概率事件。
其统计学意义是小概率事件在一次随机试验中不可能发生。
例如,某都市大街上疾驶的汽车撞伤行人的事件的发生概率为1/万,但大街上仍有行人,这是因为“被撞”事件是小概率事件,所以行人认为自己上街这“一次试验”中不会发生“被撞”事件。
“小概率”的标准a是人为规定的,对于可能引起严重后果的事件,如术中大出血等,可规定a=0.01,甚至更小。
误差是指测定结果与真实结果之间的差值。
对任何一个物理量进行的测量都不可能得出一个绝对准确的数值,即用测量技术所能达到的最完善的方法,测出的数值也和真实值存在差异,这种测量值和真实值的差异称为误差。
误差的分类误差分为绝对误差和相对误差。
也可以根据误差的来源分为系统误差(又称偏性)和随机误差(又称机会误差)。
1、绝对误差是测量值对真值偏离的绝对大小,因此它的单位与测量值的单位相同。
2、相对误差则是绝对误差与真值的比值,因此它是一个百分数。
一般来说,相对误差更能反映测量的可信程度。
相对误差等于测量值减去真值的差的绝对值除以真值,再乘以百分之一百。
3、系统误差是由一些固有的因素(如测量方法的缺陷)产生的,理论上总是可以通过一定的手段来消除。
如天平的两臂应是等长的,可实际上是不可能完全相等的;天平配置的相同质量的砝码应是一样的,可实际上它们不可能达到一样。
4、随机误差是由于在测定过程中一系列有关因素微小的随机波动而形成的具有相互抵偿性的误差(也称为偶然误差和不定误差)。
