土方量计算方法及算例讲解
土石方计算例题

土石方计算例题概述:土石方计算是土木工程中常见的一项技术任务,其主要目的是确定工程中所需要挖掘或填方的土体的数量。
在设计和施工过程中,土石方计算是非常重要的,因为它对工程的成本和进度都具有重要的影响。
本文将介绍土石方计算的基本原理和一个实际的例题,以帮助读者更好地理解这一技术。
一、土石方计算的基本原理土石方计算是根据工程中的设计剖面线,通过测量地面高程和土层厚度,计算出各个剖面的面积和体积。
具体操作包括:测量地面高程和土层厚度、确定截线点和测量点的位置、绘制剖面线、计算剖面面积和体积等。
根据计算结果,可以确定需要挖掘或填方的土体的数量,从而设计和安排相应的施工方案。
二、土石方计算的步骤1. 确定设计剖面线:根据工程设计图纸和要求,确定各个剖面线的位置和方向。
2. 测量地面高程:在每个剖面线上选择一定数量的测量点,使用水准仪或GPS等测量工具,测量每个点的地面高程。
3. 测量土层厚度:在每个剖面线上的截线点位置,使用尺子或测高仪测量各个土层的厚度。
4. 绘制剖面线:根据测量结果,在设计图纸上绘制出每个剖面线,并标注测量点的高程和土层厚度。
5. 计算剖面面积:根据剖面线上的测量点,计算出每个剖面的面积。
可以使用简单的图形计算方法,也可以使用现代化的测绘软件进行计算。
6. 计算剖面体积:根据剖面面积和土层厚度,计算出每个剖面的体积。
可以使用简单的数学公式,例如:体积 = 面积×厚度。
7. 汇总计算结果:将每个剖面的面积和体积进行汇总,得到整个工程所需要挖掘或填方的土体的总数量。
三、土石方计算的例题分析假设某工程需要进行土石方计算,设计师给出了以下信息:- 设计剖面线的长度为100米;- 地面高程从起点到终点递增,以10米为间隔依次为10米、20米、30米......100米;- 在每个剖面线上,有3个测量点,分别位于起点、中点和终点;- 土层由0-10米为表土层,10-20米为中土层,20-30米为底土层。
1.3 土方工程量计算

土方量 (m3)
备注
3.81
47.88
50.4
59.61
83.89
…
4、工程量签证
工程名称 ****大道绿化工程
施工部位 K0+020~K2+111
建设单位 ****住房和城乡建设局
施工单位 云南****园艺有限公司
签证原因: 我单位进场后,发现****大道绿化工程回填土方质量不能满足绿化种植要求,经与监理方、建设 方代表协调,决定将原回填土方更换为素红土。
建设单位
监理单位
施工单位
年月 日
年月 日
年月 日
三、方格网法
在建园过程中,地形改造除挖湖堆山,还有将原 来高低不平的、比较破碎的地形按设计要求整理 成为平坦的具一定坡度的场地,如:停车场、集 散广场、体育场、露天演出场等等,整理这类地 块的土方计算最适宜用方格网法。
方格网法是把平整场地的设计工作和土方量计算 工作结合在一起进行的。
当 S1=S2 时 V=S×L
断面法计算土方体积的计算精度取决于截取断面 的数量,多则精,少则粗。
断面法根据其取断面的方向不同可分垂直断 面法、水平断面法(或等高面法)及成角断面法。
1、垂直断面法
适用于带状地形单体或土方工程(如带状山体、 水体、沟、堤、路堑、路槽等)的土方量计算。
垂直断面法计算方法:
公式求中截面面积
(l-29) ② 用 S1 及 S2 各边的算术
平均值求 S0的面积。
2、水平断面法(等高面法) :
等高面法是沿等高线取断面,等高距即为二相邻 断面的高,计算方法同断面法。
水平断面法计算公式:
式中 V---土方体积(m3) S---断面面积(m2); h---等高距(m)
土方工程量计算PPT课件

H0= 4N(∑h1+2∑h2+3∑h3+4∑h4) 式中:h1——计算时使用一次的角点高程;
h2——计算时使用二次的角点高程; h3——计算时使用三次的角点高程; h4——计算时使用四次的角点高程。
第29页/共42页
H0 =41N(∑h1+2∑h2+3∑h3+4∑h4)
• ∑h1=角点之和 =(20.29+20.23+19.37+19.64+18.79+19.32)=117.75
• 2∑h2=2*(边点之和) =2*(20.54+20.89+21.00+19.50+19.39+19.35)=241.34
• 3∑h3=3*(拐点之和) =3*(19.91+20.15)=120.18
• 4∑h4=4*(中间点之和) =4*(20.21+20.50)=162.84
代入公1 式:N=8
第1页/共42页
第2页/共42页
Байду номын сангаас
一、公式法估算
即把地形近似的假定为锥体、棱台、球缺、圆台 等几何体,利用立体几何公式计算土方量
此法简单易于操作但精确度差,所以一般多用于 方案规划、设计阶段的土方量估算。
套用近似规则图形估算土方工程量
第3页/共42页
几何体积计算公式
第4页/共42页
二、断面法
断面法是以一组等距(或不等距)的互相平行的截面将拟 计算的地块、地形单体(如山、溪涧、池、岛等)和土方工程 (如堤、沟渠、路堑、路槽等)分截成“段”。分别计算这些 “段”的体积。再将各“段”体积相加,以求得该计算对象的 总土方量。此法适用于计算长条形单体的土方量。
土方量计算公式范文

土方量计算公式范文
1.简化土方量计算公式
简化土方量计算公式适用于简单形状的场地,如矩形或梯形地块。
公式如下:
土方量=底面积×均高
其中,底面积是土方区域的底部面积,均高是土方区域的平均高度。
2.斜坡土方量计算公式
斜坡土方量计算公式适用于需要考虑坡度的场地,如挖掘坡地或填筑坡地。
公式如下:
土方量=(踏面面积+坡面面积)×坡度×0.5
其中,踏面面积是挖掘或填筑区域的底部面积,坡面面积是挖掘或填筑区域的斜坡面积,坡度为斜坡的坡度,0.5是修正系数。
3.多边形土方量计算公式
多边形土方量计算公式适用于不规则形状的土方区域,如多边形或复杂曲线。
公式如下:
土方量=面积×均高
其中,面积是土方区域的面积,均高是土方区域的平均高度。
4.异形土方量计算公式
异形土方量计算公式适用于包含多个不同形状的区域,如含有多个平台或凹陷部分的场地。
公式如下:
土方量=(边坡最大面积+边坡最小面积)×坡度×0.5+圆形区域体积+长方形区域体积+…
其中,边坡最大面积是挖掘或填筑区域的最大边坡面积,边坡最小面积是挖掘或填筑区域的最小边坡面积,坡度为边坡的坡度,0.5是修正系数,圆形区域体积是圆形区域的体积,长方形区域体积是长方形区域的体积,以此类推。
在实际工程中,土方量计算还需要考虑地下水位、岩石质量、土层的厚度等因素,并通过现场勘测和测量来获取准确数据。
土方量计算公式只是计算土方量的基本方法,具体计算时还需根据具体情况和要求进行调整和修正。
土方工程量计算(含计算案例)
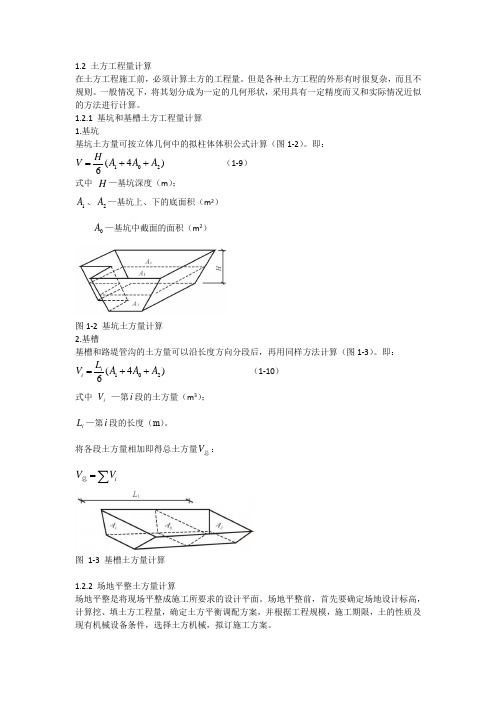
1.2 土方工程量计算在土方工程施工前,必须计算土方的工程量。
但是各种土方工程的外形有时很复杂,而且不规则。
一般情况下,将其划分成为一定的几何形状,采用具有一定精度而又和实际情况近似的方法进行计算。
1.2.1 基坑和基槽土方工程量计算 1.基坑基坑土方量可按立体几何中的拟柱体体积公式计算(图1-2)。
即:)4(6201A A A HV ++=(1-9) 式中 H —基坑深度(m ); 1A 、2A —基坑上、下的底面积(m 2)0A —基坑中截面的面积(m 2)图1-2 基坑土方量计算 2.基槽基槽和路堤管沟的土方量可以沿长度方向分段后,再用同样方法计算(图1-3)。
即:)4(6201A A A L V ii ++=(1-10) 式中 i V —第i 段的土方量(m 3);i L —第i 段的长度(m )。
将各段土方量相加即得总土方量总V :∑=i V V 总图 1-3 基槽土方量计算1.2.2 场地平整土方量计算场地平整是将现场平整成施工所要求的设计平面。
场地平整前,首先要确定场地设计标高,计算挖、填土方工程量,确定土方平衡调配方案,并根据工程规模,施工期限,土的性质及现有机械设备条件,选择土方机械,拟订施工方案。
1.场地设计标高的确定确定场地设计标高时应考虑以下因素: ①满足建筑规划和生产工艺及运输的要求; ②尽量利用地形,减少挖填方数量;③场地内的挖、填土方量力求平衡,使土方运输费用最少; ④有一定的排水坡度,满足排水要求。
场地的设计标高一般应在设计文件中规定,如果设计文件对场地设计标高无明确规定和特殊要求,可参照下述步骤和方法确定: (1)初步计算场地设计标高初步计算场地设计标高的原则是场地内挖、填方平衡,即场地内挖方总量等于填方总量。
如图1-4所示,将场地地形图划分为边长 a=10~20m 的若干个方格。
每个方格的角点标高,在地形平坦时,可根据地形图上相邻两条等高线的高程,用插入法求得;当地形起伏较大(用插入法有较大误差)或无地形图时,则可在现场用木桩打好方格网,然后用测量的方法求得。
挖基础土方计算案例

挖基础土方计算案例假设工程要新建一栋办公楼,总建筑面积为6000平方米,建筑的基础采用扩展基础形式,长度为50米,宽度为20米,深度为2米。
现在需要计算挖基础的土方量。
首先,需要根据基础的几何形状计算基础的体积。
基础的体积计算公式为:体积=长度×宽度×深度。
在这个案例中,基础的体积为50米×20米×2米=2000立方米。
接下来,需要计算挖土的量。
挖土量可以用以下公式计算:挖土量=填充体积-基础体积。
其中,填充体积可以通过挖土的面积与挖土深度的乘积来计算。
在这个案例中,挖土的面积为50米×20米=1000平方米,挖土深度为2米。
因此,填充体积为1000平方米×2米=2000立方米。
然后,需要考虑挖土的损耗率。
在实际施工中,挖土过程中会有一定的损耗,例如,挖土时有可能土方发生塌方,导致实际挖土量小于预计挖土量。
根据经验,可以设置一个挖土损耗率。
假设挖土损耗率为10%,则实际挖土量为填充体积×(1-损耗率)=2000立方米×(1-0.1)=1800立方米。
最后,需要考虑土方的运输和处理成本。
挖出的土方需要运输到指定的地点并进行处理,例如疏筛、填埋等。
这部分成本可以根据实际情况来进行预估。
通过以上的计算,可以得出在这个工程中,需要挖掘的土方量为1800立方米。
这个结果可以作为安排挖土工序和资源的依据,同时也可以帮助合理控制施工成本。
需要注意的是,不同的工程情况和要求可能会有不同的土方计算方法和参数设置。
因此,在实际工程中,需要根据具体情况进行土方计算,并且结合实际施工中的经验进行调整和修正。
土石方计算实例课件

软件二:GIS系统
总结词
操作复杂、需要专业培训的土石方计算软件
详细描述
相对于其他土石方计算软件,GIS系统的操 作较为复杂,需要用户具备一定的专业知识 和技能。同时,GIS系统的学习成本也相对
THANKS
详细描述
积距法的基本原理是将土石方量计算转化为距离和体积的乘积。首先,确定计算 区域的高程点,然后计算相邻高程点之间的距离,最后将距离与单位体积相乘, 得到土石方量。这种方法适用于地形起伏较小、高程变化不大的区域。
截面法
总结词
截面法是通过计算土石方填挖的截面积,然后乘以填挖的距离来计算土石方量的方法。
问题二:如何处理复杂地形?
详细描述
引入地形分析软件:如ArcGIS等 ,可以土石方 计算中的一大挑战,需要采取相 应措施。
采用数字高程模型(DEM):利 用DEM数据可以更准确地模拟复 杂地形,提高计算精度。
考虑地形坡度和高度变化:在计 算过程中充分考虑地形坡度和高 度变化,可以更准确地模拟土石 方移动和堆积。
总结词:提高计算精度是土石方计算中 的重要问题,可以通过多种方法解决。
考虑土壤类型和性质:不同土壤类型和 性质对土石方移动和堆积有较大影响, 应充分考虑并进行相应修正。
引入GIS技术:利用地理信息系统(GIS )技术,可以更准确地获取地形地貌数 据,提高计算精度。
详细描述
采用高精度算法:如有限元法、有限差 分法等,可以更准确地模拟土石方的分 布和移动。
软件一:AutoCAD Civil 3D
总结词
高度集成、易于使用的土石方计算软件
土石方工程预算工程量计算说课讲解

第四章 土建工程预算(yùsuàn)工程 量计算
第二页,共38页。
建筑工程造价
第三节 工程量计算(jìsuàn)规则
3.挖填土方的起点标高: 一般为设计室外地坪标高。
4.土壤类别划分(huà fēn): 普氏分类:一、二、三、四类土。 5.挖土施工方法: 明确开挖的方法 机械类型 是否排除地下水等 6.干土与湿土的划分(huà fēn): 地下常水位以上为干土,以下为湿土。
解: 外墙沟槽(ɡōu cáo)长度: L中,沟槽(ɡōu cáo)= (12+0.06×2+10.2+0.06×2)×2 =44.88m 内墙沟槽(ɡōu cáo)长度 L内,沟槽(ɡōu cáo)=(10.2-0.46×2-0.3×2) ×2 +(5.1- 0.46×2-0.3×2) +(4.8-0.46×2-0.3×2)×2 =27.5m
3. 回填土:
第四章 土建工程预算(yùsuàn)工程 量计算
第二十七页,共38页。
建筑(jiànzhù)工程造价
第三节 工程量计算(jìsuàn)规则
3. 回填(huítián)土: (1) 基础回填(huítián)土:
是指基础工程完成后,将槽、坑四周未做基础部分进 行回填(huítián)至室外设计地坪标高。 V基础回填(huítián)土=V挖土-V设计室外地坪以下基础、 垫层 (2)房心回填(huítián)土:
距,超过5m时,按人工运土项目计算,运距不再扣
减5m。
3.挖出的土如部分用于灰土垫层时,余土外运工程量
中不扣除。
4.机械挖土方机械行驶(xíngshǐ)坡道的计算,只有坑下作业
才
可计算。
5.人工挖沟槽、地坑深超过3m时,应分层开挖,底分层按深
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
土方量的计算方法及算例姓名:***班级:装备0802学号:************摘要:土方量的计算在工程测量中经常遇见,如道路设计,土地平整,矿场开采等,都需要精确地计算出其土方量。
土方量计算是这些工程设计的一个重要组成部分,直接关系到工程造价,但它的精度如何,误差有大却很难直接检核出来。
本文列述一些常见的计算方法和一些算例。
土方量的计算是建筑工程施工的一个重要步骤。
工程施工前的设计阶段必须对土石方量进行预算,它直接关系到工程的费用概算及方案选优。
在现实中的一些工程项目中,因土方量计算的精确性而产生的纠纷也是经常遇到的。
如何利用测量单位现场测出的地形数据或原有的数字地形数据快速准确的计算出土方量就成了人们日益关心的问题。
比较经常的几种计算土方量的方法有:方格网法、等高线法、断面法、DTM法、区域土方量平衡法和平均高程法等。
关键字:土方量的计算方格网法断面法 DTM法目录第一章土方外业测量方法及精度比较 (4)1.1 水准仪法 (4)1.2 经纬仪法 (4)1.3 全站仪法 (5)第二章土方量计算方法 (6)2.1 断面法 (6)2.2 方格网法 (6)2.3 DTM法(不规则三角网法) (10)第三章土方量计算算例及方法比较 (14)3.1 实例计算 (14)3.2 比较分析 (17)第四章全文总结 (20)参考文献 (21)第一章 土方外业测量方法及精度比较在土地平整中通常需要确定地面高程、施工范围和计算土方量等,以便控制施工进度。
土地平整测量外业常采用水准仪、经纬仪和全站仪的测量仪器,内业计算有方格网法、断面法、等高线法、DTM 法等方法。
采用不同的测量计算方法会有不同的结果,可见选择合适的测量计算方法有利于提高平整结果,提高精度和速度,甚至可以减少纠纷。
土方量的误差主要是在外业中产生,即主要是由高程测量中误差m h 和面积测量中误差m s 造成。
在相同观测条件下,4个方格顶点高程测量精度是相同的,则平均高程测量中误差m h 按如下计算:2m nm m hhh ==(1-1) 此外方格面积测量的中误差(m S )主要是由距离误差(m D )造成,因此按如下公式计算:D D m 2m g ⨯= (1-2) 根据误差传播定律,土方量的中误差(m v )按如下公式计算: 2h 22222h 22S 2m m h 1621m S m h m S D D V +±=+±=)()( (1-3)1.1水准仪法用5m 塔尺将现场划分成若干个边长是五米的正方形方格,用水准仪测量每个方格定点的高程,按照40m 的设计高程用方格法计算土方量。
S3级微顷水准仪毎站水准测量高差(或高程)的精度为±2.4mm 。
另外,水准仪测量的距离通常用皮尺丈量,其精度为±100mm ,因此计算出土方量中误差为±10.0m ³,相对中误差为1/25。
1.2经纬仪法用经纬仪按照地形测量(比例尺为1:500)的要求,将现场测绘成地形图,在地形图上用方格法(边长为5m )手工计算土方量。
J6经纬仪测量的视距精度约为1/500,距离中误差为±200mm ,测量单点高程的精度为±60mm ³。
经纬仪采集点位数据展绘在图纸上画上方格网,根据碎步点高程通过目估内插法确定方格顶点的高程。
方格顶点的高程精度取决于碎步点的高程,也与测量员的站尺位置、数量、环境条件有关,其主要误差包括地形点高程测量误差、地面概括误差和平面位移误差。
经纬仪测绘1:500 比例尺地形图后,对于坡度为15º的坡地,地面概括误差为±0.23m,平面位移误差为±0.17m 。
由误差传播定律得出地形图上方格顶点高程中误差为±0.29m 。
因此用土方量的中误差计算公式,可得出经纬仪测量计算土方量的中误差为±20.0m ³,相对中误差约为1/12。
1.3全站仪法用全站仪代替经纬仪测量地形,生成数字化地形图上用方格法(边长为5m)由计算机利用Cass软件计算土方量。
全站仪计算土方的精度也是由距离误差和高差误差决定的。
研究结果表明,全站仪采样位置的平面点位中误差为±0.02m。
方格顶点的高程中误差是DTM插求点的高程中误差。
一般认为影响DEM精度的主要因素有地形类别、内插方法、采样方式和粗差剔除程度等。
通过实验,方格顶点的高程中误差为0.35m左右。
因此按照土方量的中误差计算公式求得全站仪计算土方量的中误差为±4.8m³,相对中误差约为1/52。
说明全站仪法在3种仪器测量方法中计算精度最高。
以S=100m、D=5m、h=10m、S=25m2的土方面积为例,水准仪法、经纬仪法和全站仪法测量土方量的计算精度土方量测量精度比较;水准仪和经纬仪采集的数据,应用方格法通过手工计算土方量;将全站仪采集的数据传到计算机上,然后用Cass6.1软件生成数字化地形图,用方格法计算土方量。
3种仪器测量土方量的结果见表1。
表1 不同测量方法测量土方量的结果注:挖方量的真值为10442.9m³从表1可知,以挖方量为例,在面积和设计高程相同的情况下,以3种测量结果的平均值作为最或是值(真值),为10442.9m³,挖方量的拟真误差表现为:全站仪<经纬仪<水准仪。
说明全站仪测量土方的精度最高。
第二章 土方量的计算方法2.1断面法当地形复杂起伏变化较大,或地狭长、挖填深度较大且不规则的地段,宜选择横断面法进行土方量计算。
上图为一渠道的测量图形,利用横断面法进行计算土方量时,可根据渠LL ,按一定的长度L 设横断面A 1、A 2、A 3……A i 等。
断面法的表达式为 ()2/212∑∑=-=+==ni i i i n i iL A AV V (2-1)在(2-1)式中,Ai -1,A i 分别为第i 单元渠段起终断面的填(或挖)方面积;L i 为渠段长;V i 为填(或挖)方体积。
土石方量精度与间距L 的长度有关,L 越小,精度就越高。
但是这种方法计算量大, 尤其是在范围较大、精度要求高的情况下更为明显;若是为了减少计算量而加大断面间隔,就会降低计算结果的精度; 所以断面法存在着计算精度和计算速度的矛盾。
2.2方格网法对于大面积的土石方估算以及一些地形起伏较小、坡度变化平缓的场地适宜用格网法。
这种方法是将场地划分成若干个正方形格网,然后计算每个四棱柱的体积,从而将所有四棱柱的体积汇总得到总的土方量。
2.1.1方格网计算步骤及方法⑴ 划方格网 根据地形图划分方格网,尽量使其与测量或施工坐标网重合,方格一般采用20m ×20m~40m ×40m ,将相应设计标高和自然地面标高分别标注在方格点的右上角和右下角,求出各点的施工高度(挖或填),填在方格网左上角,挖方为(+),填方为(-)。
⑵ 计算零点位置 计算确定方格网中两端角点施工高度符号不同的方格边上零点位置,标于方格网上,联接零点,即得填方与挖方区的分界线。
零点的位置按下式计算图2-1 断面法计算土方量图2-2零点位置图a h h h x ⨯+=2111 ; a h h h x ⨯+=2122 (2-2)式中 x 1、x 2——角点至零点的距离 m ;h 1、h 2——相邻两角点的高程 m ,均用绝对值; a ——方格网的边长m 。
⑶ 计算土方工程量 按方格网底面图形和下表体积计算公式,计算每个方格内的挖方或填方量。
由于零线通过方格的部位不同,可将方格划分为一点填方(挖方)、二点填方(挖方)、三点填方(挖方)、四点填方(挖方)四种类型。
①一点填方或挖方(三角形)图2-3一点填方或(挖方)63213bch h bc V ==∑ 当 a c b ==时, 326h a V = (2-3)②二点填方或挖方 (梯形)图2-4二点填方或(挖方)()()31842h h c b ah a c b V ++=+=∑- (2-4 ) ()()42842h h c b ah a e d V ++=+=∑+ (2-5) ③三点填方或挖方 (五角形)图2-5三点填方或(挖方)525232122h h h bc a h bc a V ++⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=∑ (2-6)④四点填方或挖方 (正方形)图2-6四点填方或(挖方)()43212244h h h h a h a V +++==∑ (2-7)⑷ 汇总 分别将挖方区和填方区所有方格计算土方量汇总,即得该建筑场地挖方区和填方区的总土方量。
在传统的方格网计算中,土方量的计算精度不高。
现在我们引入一种新的高程内插的方法,即杨赤中滤波推估法。
2.1.2杨赤中推估杨赤中滤波与推估法就是在复合变量理论的基础上,对已知离散点数据进行二项式加权游动平均,然后在滤波的基础上,建立随即特征函数和估值协方差函数,对待估点的属性值(如高程等)进行推估。
2.1.3待估点高程值的计算首先绘方格网, 然后根据一定范围内的各高程观测值推估方格中心O 的高程值H 0。
绘制方格时要根据场地范围绘制。
由离散高程点计算待估点高程为∑==ni iiHP H 10 (2-8)其中,H 1,H 2……H i 为参加估值计算的各离散点高程观测值,P i 为各点估值系数。
而后进一步求得最优估值系数,进而得到最优的高程估值。
2.1.4挖(填)土方量区域面积的计算如果土方量计算的面积为不规则边界的多边形。
那么在面积进行计算时,先对判断方格网中心点是否在多边形内,如果在,那么就要计算该格网的面积,否则可以将该格网面积略去。
如图2-7所示,首先对格网中心点P 进行判断,可以采用垂线法,即过P (x 0,y 0)点作平行于y 轴向下的射线⎩⎨⎧<=00y y x x ①设多边形任意一边的端点为i (x i ,y i ),i+1(x i+1,y i+1),令()()()()()⎪⎩⎪⎨⎧--=-+=--=-++i i i i i i s i x x x x y y y y x x x x i 111/λλδ ②(1)当δ<0时,若y>y s ,则射线与该边有交点,否则无交点,若y=y s ,则知P 在多边形上。
(2)当δ=0时,若x=x i ,则当y>y i 时,二者有交点(x i ,y i ),当y<y i 时,不予考虑。
当y=y i 时,说明P 在多边形上。
若x=x i+1,方法同上。
(3)当δ>0时,不予考虑。
对多边形各边进行上述判断,并统计其交点个数m ,当m 为奇数时,则P 在多边形内部,否则P 不在多边形内部。
通过对图中P 1、P 2点的判断可以知道,P 1位于多边形内,P 2位于多边形外。
