涡激振动
高原风力发电风轮叶片的涡激振动与失效分析

高原风力发电风轮叶片的涡激振动与失效分析随着可再生能源的需求不断增加,风能作为其中重要的组成部分得到了广泛关注。
而高原地区由于地理环境的特殊性,其风力资源相比平原地区更为丰富。
因此,高原地区的风力发电项目越来越多。
在高原风力发电中,风轮叶片作为风转动力的接受者和转化器,其性能和可靠性直接影响风力发电系统的整体效率和运行稳定性。
然而,高原地区的特殊地理和气候条件,使得风轮叶片面临着一系列挑战,其中之一就是涡激振动和失效问题。
首先,我们需要了解涡激振动是什么以及为什么会在高原地区特别显著。
涡激振动是指当风经过叶片表面时,会形成一系列旋转的涡流,这种涡流会对叶片表面施加周期性的压力和拉力,从而引起叶片的振动。
而高原地区的气候条件,如气温低、大气稀薄等,会导致风速较高,气流较不稳定。
这些因素使得涡激振动在高原地区的风力发电系统中更加显著。
接下来,我们将进行高原风力发电风轮叶片的涡激振动分析。
在分析之前,我们需要收集相关的数据和样品以进行实验和测试。
通过检测风轮叶片在高原地区典型工况下的振动情况,我们可以获得叶片的自然频率、振型特征以及响应幅值等数据。
同时,我们还需对叶片材料进行力学性能测试,以了解叶片的强度和刚度等参数。
在实际应用中,我们可以利用计算机模拟的方法,对高原风力发电风轮叶片进行涡激振动分析。
通过建立数学模型,运用数值计算方法,我们可以得到叶片受到涡激振动的具体响应情况。
在分析时,我们需考虑叶片结构的复杂性和非线性特征,同时还需考虑高原地区的环境因素,如风速、大气条件等。
通过模拟分析,可以评估叶片的疲劳寿命、振动稳定性和失效风险等指标。
除了涡激振动对叶片的影响外,高原地区特殊的气候条件也会对叶片的可靠性造成影响。
例如,气温的变化可以导致叶片材料的热膨胀不均匀,从而引起叶片的应力集中和破裂。
而大气稀薄则会增加风力发电系统中的振动和冲击负荷,加剧叶片的疲劳破损。
针对高原地区风力发电风轮叶片的失效问题,我们可以采取一系列的措施来提高其可靠性和耐久性。
包括涡激振动

一、侧力系数和作用在柱体上的气动力
图 4-3
单自由度驰振模型
1、基于准定常理论的分析
平均阻力和平均升力在y方向上邓哈托判别式:
四、横风向效应与顺风向效应的组合
假设结构任意高度处横风向的风效应用 RL ( z) 表示,而 顺风向的风效应用 RD ( z) 表示,则 z高度处最大风效应 表达如下:
注:这里,顺风向振动应按随机振动考虑, 风速取为与横风向相同的临界风速
五、涡激随机振动
5 6 1 10 Re 3.5 10 当雷诺数Re处于超临界范围( )时,结 构物背后的湍流尾流将引起横风向的随机振动,应按随机振 动的理论进行分析。 但这里最大的区别是应采用横风向的 脉动风速谱和对应的相干函数;
三、抖振 (强迫振动)
4.2 涡激振动
一、雷诺数
定义:惯性力与粘性力之比
Re vD
6.9 104 vD
卡门涡列
二、斯超海尔数和锁定现象
前述尾流现象最显著的规律性是由斯超海尔 (Strouhal)最先提出的
锁定现象
三、 圆柱体结构的涡激共振力
1. 临界风速
2. 共振区高度
3. 横风向共振风振力 运动方程:
第四章 结构横风向风振
主要讨论工程结构中易于遇到且机 理相对清楚的横风向风振内容,包括涡 激振动(Vortex-induced vibration)、驰 振(Galloping)、颤振(Flutter)及抖振 (Buffeting)
4.1 主要横风向风振机理分析
一、涡激振动
二、驰振、颤振 (自激振动)
4.3 横风向驰振
上一节所述的涡激振动是在结构物背后由交替的旋 涡脱落产生的,可以认为是一种稳定的振动,其激发能 量在一个特殊的频率处有一个确定的值。本节所讨论的 横风向驰振对特殊截面形状的细长结构物具有典型的不 稳定性,其截面形状如矩形、D字形或—些裹冰输电线的 有效截面形状.这些结构在垂直于气流方向上会表现出 大幅度的振动,振幅可达1—10倍以上横风向截面尺寸, 其振动频率远低于相同截面的旋涡脱落频率。 驰振是—种失稳式振动,驰振一旦发生,便成为剧 烈的振动,有导致结构破坏的危险性;
涡激振动方法的

0引言结构的涡激振动(VIV )在许多工程领域具有实际意义[1]。
例如,涡激振动可以引起热交换器管的振动;涡激振动还影响上升管道将石油从海底运输到岸上的动力;涡激振动对于工程结构设计具有重要意义,例如桥梁、大烟囱,还有船舶和陆地车辆的设计;并且涡激振动还能引起海洋中的绳索结构的大幅度振动。
关于涡激振动的众多问题中的这几个事例是非常重要的。
1研究涡激振动的目的研究流体涡激振动的目的总的来说就是研究许多对于一般的流激振荡和对于特殊的涡激振动的影响因素,并且通过物理和数值试验,理论分析和物理的角度指导设计数据的获取。
研究流体涡激振动的最终目的是为了理解,预测和防止涡激振动(最好是没有阻力的情况),一部分就像研究在工业中较为关注的流体-结构耦合一样通过基础的直接数值模拟(DNS 谱方法),通过获得尽可能多的Navier-Stokes (N-S )数据点(控制参数在期望范围内),还有一部分通过采用雷诺时均Navier –Stokes 方程(RANS ),大涡模拟(LES )(用改进的亚格子尺度模型),和他们的各种结合来研究。
数值模拟方法是受到全新的测量和流体的流动显示技术的指导和启发,主要是无干扰技术:数字粒子图像测速技术(DPIV),激光多普勒测速技术(LDV),TR-PIV ,压敏涂料,智能材料和其他一些在未来几年一定会出现的手段。
这些技术与大规模的基准实验必定会增强对于采用非常大雷诺数的数值模拟实验的指导作用[2]。
2涡激振动的实验研究从根本上说,有两种方法用来研究漩涡脱落引起的振动的影响。
第一种方法,通过分析作用在安装在水中或风洞中的圆柱的强迫振动得到结果。
第二种方法,漩涡脱落与物体振动之间的相互作用是通过直接研究安装在弹性基础上的圆柱得到的,即自激振动。
这个基座使用可调弹簧与阻尼器做成的。
事实上,第二种选择是试图直接研究涡街脱落现象的方法。
从另一方面说,第一种方法就是一种分析漩涡脱落与结构体的振动之间的相互作用的间接方法。
结构风工程讲义--涡激振动
结构风工程学习资料---涡激振动当风流经细长钝体时,会产生流动分离以及周期性的旋涡脱落,从而在钝体上下表面出现正负压力的交替变化,这种压力的交替变化形成作用于钝体的涡激气动力,在一定条件下,会引起结构在横风向或扭转方向发生涡激共振。
涡振是一种带有强迫和自激双重性质的风致限幅振动,是结构中一种常见的风致振动。
涡振虽不具有很强的破坏性质,但由于其发生风速较低,长时间持续的振动将会造成结构损伤或疲劳破坏。
对于高层建筑,涡振引起的加速度会影响人的居住。
对于桥梁,涡振会影响行车的舒适性和安全性。
研究涡振主要关心三个问题:涡振风速、涡振频率和振幅。
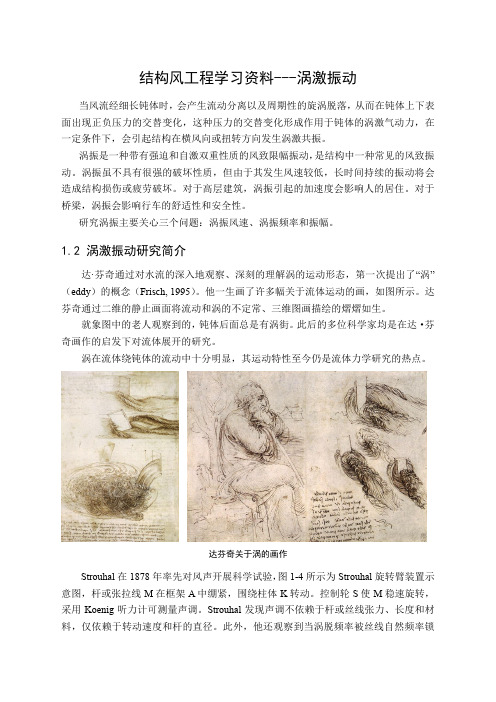
1.2 涡激振动研究简介达·芬奇通过对水流的深入地观察、深刻的理解涡的运动形态,第一次提出了“涡”(eddy)的概念(Frisch, 1995)。
他一生画了许多幅关于流体运动的画,如图所示。
达芬奇通过二维的静止画面将流动和涡的不定常、三维图画描绘的熠熠如生。
就象图中的老人观察到的,钝体后面总是有涡街。
此后的多位科学家均是在达·芬奇画作的启发下对流体展开的研究。
涡在流体绕钝体的流动中十分明显,其运动特性至今仍是流体力学研究的热点。
达芬奇关于涡的画作Strouhal在1878年率先对风声开展科学试验,图1-4所示为Strouhal旋转臂装置示意图,杆或张拉线M在框架A中绷紧,围绕柱体K转动。
控制轮S使M稳速旋转,采用Koenig听力计可测量声调。
Strouhal发现声调不依赖于杆或丝线张力、长度和材料,仅依赖于转动速度和杆的直径。
此外,他还观察到当涡脱频率被丝线自然频率锁定时丝线振动将会出现同步现象。
图1-4 Strouhal 旋转臂装置Strouhal 试验结果显示在一定条件下,气流流经固定的钝体时会脱落出交替的旋涡,其主频率f 可以由Strouhal 关系式得出:St UfD (1-1) 式中St 为Strouhal 数,D 代表物体的横风向尺寸,U 为浸没物体均匀流动的平均速度。
基于功率方程的圆柱体涡激振动研究

基于功率方程的圆柱体涡激振动研究涡激振动是一种重要的流固耦合问题,通常发生在流体经过圆柱体等物体时,因尾流和湍流的作用而产生的激励力,导致物体发生振动。
圆柱体涡激振动在许多领域中都有着广泛的应用,比如建筑工程、风力发电、航空航天等。
为了更好地研究圆柱体涡激振动问题,我们可以基于功率方程来进行研究。
首先,我们需要了解功率方程在涡激振动中的应用。
功率方程是描述振动过程中能量转换的重要方程,可以帮助我们分析涡激振动中的能量转换过程。
在圆柱体涡激振动中,流体经过圆柱体时会受到激励力的作用,使圆柱体发生振动。
这时,我们可以通过功率方程来计算激励力对圆柱体的功率输入,从而了解振动过程中的能量交换情况。
其次,我们可以通过分析功率方程中的各项来探讨涡激振动中的耗散机制。
在圆柱体涡激振动中,由于粘性阻力等因素的存在,能量会不可避免地被耗散掉。
通过功率方程,我们可以计算出振动系统中各个环节的功率损失,从而揭示出耗散机制对振动系统的影响。
另外,我们还可以通过功率方程来优化圆柱体的结构设计。
在实际工程中,圆柱体的结构参数对涡激振动有着重要的影响。
通过分析功率方程,我们可以得出不同结构参数对振动系统能量转换效率的影响,从而指导优化圆柱体的设计方案,减小振动系统的能量损耗,提高系统的性能。
总之,基于功率方程的圆柱体涡激振动研究可以帮助我们更深入地理解振动系统中的能量转换和耗散过程,为优化设计提供理论支持。
未来,在圆柱体涡激振动领域的研究中,我们可以进一步深化功率方程的应用,结合数值模拟和实验研究,探索出更多新颖的振动控制方法,为实际应用提供更好的技术支持。
风电机组塔筒吊装时怎样抑制涡激振动

第 1 页 共 2 页 风电机组塔筒吊装时怎样抑制涡激振动 在风电场,风力发电机组吊装时有一个规定,顶段塔筒吊装完后,当天必需吊装完机舱,缘由是什么呢?下面我给大家简洁分析一下。 从流体的角度来分析,任何非流线型物体,在恒定流速下,都会在物体两侧交替地产生脱离结构物表面的旋涡。这种交替发放的旋涡又会在柱体上生成顺流向及横流向周期性变化的脉动压力。假如此时柱体是弹性支撑的,或者柔性管体允许发生弹性变形,那么脉动流体力将引发柱体(管体)的周期性振动,这种规律性的柱振动反过来又会转变其尾流的旋涡发放形态。这种流体与结构物相互作用的问题被称作"涡激振动'。 假如塔筒的自振频率与漩涡的发放频率相接近,就会使塔筒发生共振破坏,因此这种涡激振动是极其有害的,需实行措施阻挡它的发生。在我们风电行业内一般有五种方法来抑制涡激振动。 一、塔筒上安装扰流条可抑制涡激振动 其原理也比较简洁,该方案主要是通过加施在塔筒上的扰流条打乱来风的轨迹,使其不能形成频率稳定的漩涡。扰流条大多由塑料泡沫制作的三角柱串联而成,三根扰流条等距缠绕在塔筒上段,底部由细绳牵引至地固定。 二、阻尼器法抑制涡激振动 从涡激振动的特点看,集中质量式摆锤方案既便利又有效:作为调谐质量块,摆锤利用反方向惯性力可显着抑制塔筒振动的响应幅值。需要说明的是,摆锤的质量和摆长取决于塔筒本身的质量 第 2 页 共 2 页
和刚度,那么不恰当的设计不仅不能达到减振效果,而且可能会恶化振动状况。 三、缆风绳抑制涡激振动 简洁说,该方案通过缆风绳施加外力,破坏塔筒两侧的气动受力状况,并限制塔筒初始晃动的位移幅度,从而无法产生刚体自由状态下的涡激从而抑制摆振,导致塔筒无法让涡激过程中晃动产生的振动能量产生累计。 四、安装机舱、发电机、叶轮抑制涡激振动 这里分两种状况,第一机舱、发电机安装后,不管风从哪个角度吹来,都会不同程度地受到机舱、发电机的影响,形成引起塔筒共振的稳定漩涡会打一些折扣。其次叶轮安装后,不管风从哪个角度吹来,都会受到风轮叶面的影响,进而快速发生的流场变化就难以形成引起塔筒共振的稳定漩涡。 五、吊装时,塔筒门关闭,可使涡激振动不至于增大 当塔筒底部门关闭时,由于空气本身的流通性和不行压缩性,会在塔筒内部起到阻尼器的效果,从而会减小塔筒的振动幅度。但当塔筒底部门打开时,塔筒内部由空气构成的阻尼器就失去了效果,因而无法减小塔筒的振动幅度,而且内部流通的气流会和外部的涡流产生叠加效应,从而放大了塔筒的振动幅度。
海洋立管的涡激振动模型预测方法

海洋立管的涡激振动模型预测方法海洋立管的涡激振动是指在海水流动下,立管表面附近形成的涡流引起立管产生振动的过程。
这种振动会对海洋工程设施的稳定性和寿命产生重要的影响。
为了预测和评估海洋立管的涡激振动,可以使用多种数值模拟方法,其中包括CFD方法、子结构方法和模型试验方法等。
1.CFD方法:计算流体力学(CFD)方法是一种基于数值求解流体力学方程的计算方法。
对于涡激振动问题,可以使用CFD方法模拟流体流动并预测立管的振动响应。
CFD方法的优点在于可以考虑复杂的流动场和立管的几何形状,可以提供详细的流场信息和振动特性。
然而,CFD方法需要大量的计算资源和较长的计算时间,并且对参数的设定和模型的准确性有一定要求。
2.子结构方法:子结构方法是将立管分解为多个小的部分,然后对每个部分进行振动分析的方法。
该方法可以减小计算的复杂性,并将问题简化为多个子问题的求解。
子结构方法可以在不同的涡流条件下对立管的振动特性进行预测,并可以考虑不同部位的结构响应差异。
然而,子结构方法忽略了整体流场和结构之间的相互作用,可能会导致结果的不准确。
3.模型试验方法:模型试验是通过建立立管的物理模型,进行涡激振动实验,并测量振动响应和流场信息。
模型试验方法可以提供直观的实验结果,并可以考虑实际中不可预测的因素。
模型试验方法的缺点是成本高昂,需要大量的实验设备和时间。
此外,模型试验结果的适用性可能受到尺寸效应和相关性的限制。
综上所述,预测海洋立管的涡激振动模型可以使用CFD方法、子结构方法和模型试验方法等。
这些方法各有优劣,研究人员可以根据具体的需求和限制选择合适的方法或将它们结合起来使用,以便更好地预测和评估海洋立管的振动特性。
第八讲 涡激振动问题

R(y1, y2) = exp⎜⎜⎝⎛−
y1 − y2 nD
⎟⎟⎠⎞
对于单位模态:n
=
⎧5.6 ⎩⎨3.3
均匀流矩形 紊流矩形
LL
∫ ∫ R(y1, y2)dy1dy2 = 2(nD)2{L/(nD)−1+exp[− L/(nD)]}
00
z(5) 运动相关力
[ ] Lz (y,t) =
1 2
ρU
2 (ωD
非线性振动试验结果准确大量工程应用kkk11202022122212214012sin211221yydmydtydyudymtcdyydydyyduyytl??????????????????????????????????e
桥梁及结构风振理论及其控制
——之第八讲
涡激振动问题
葛耀君 主讲教师:
博士.教授
z(2)
涡激力:
w(z,t) =
1 2
ρU
2
(z
)C
L
D(z
)
z(3)
准定常假定:
σw(z) =
1 2
ρU 2 (z)D(z)σ CL
z(4) 基本假定
(a) — 均匀流; (b) — D不变; (c) — 涡激力窄带谱; (d) — 涡激力简谐变化; (e) — 大尺度紊流
高斯过程谱:
z(5) 带宽参数ν
; K1 = 0
∫φi2 (z)dz
h
∫φi2 (z)dz
; K2 =
0
h
∫φi2 (z)dz
0
0
0
z(8) 涡振响应
[ ( ) ] σai / D0 = C Ksi − K1 + K2 σai / D0 2 −1/2
