高中数学人教a版高二选修4-1学业分层测评3_相似三角形的判定 含解析
高中数学人教A版选修4-1配套课件1.3 相似三角形的判定及性质

往往需先证两个三角形相似,以此作铺垫,再证另两个三角形相 似.
【变式 2】 如图所示,设 BD、CE 分别是△ABC 边 AC、AB 上的 高.求证:△ADE∽△ABC. 证明 ∵BD、CE 是△ABC 的高, ∴∠AEC=∠ADB=90° . 又∵∠A=∠A, ∴△AEC∽△ADB, AE AC ∴AD=AB. 又∵∠A=∠A,∴△ADE∽△ABC.
4.相似三角形的性质定理的内容归纳起来主要有两个方面:一
是相似三角形的对应线段(高、中线、角平分线以及周长)的比
等于相似比;二是相似三角形面积的比等于相似比的平方, 运用性质定理,拓宽思路,可以探讨得到:两个相似三角形 中的所有对应图形(所有对应线段,如等分线段,等分角线以 及外接圆与内切圆的直径、周长、面积等)与相似比都有一定 的关系.
2.相似三角形的判定定理
(1)预备定理:平行于三角形一边的直线和其他两边(或两边的 延长线)相交,所构成的三角形与原三角形相似. 如 图 ( 1 ) ( 2 ) ( 3 ) 所 示 , 在 △ ABC 中 , DE∥BC , 则 △ABC∽△ADE.
(2)判定定理1:对于任意两个三角形,如果一个三角形的两个角 与另一个三角形的两个角对应相等,那么这两个三角形相似.简
第3课时
相似三角形的判定及性质
【课标要求】
1.了解相似三角形的定义及三个判定定理的证明.
2.理解相似三角形的判定定理及相似比. 3.用相似三角形的判定定理解决问题. 【核心扫描】 1.应用相似三角形的判定定理证明相关几何问题.(重、难点)
2.相似三角形的判定.(重点)
自学导引 1.相似三角形 对应角相等,对应边成比例的两个三角形叫做相似三角 形.相似三角形对应边的比值叫做相似比(或相似系数).
2018-2019学年高中数学(人教A版)选修4-1同步讲义:第一讲 三相似三角形的判定及性质Word版含答案

三相似三角形的判定及性质[学习目标]1.理解相似三角形的定义.2.理解预备定理的本质.3.会证明判定定理1,2,3,理解这些定理的内容,能应用这些定理证明相关的几何问题.4.掌握直角三角形相似的判定定理,会应用定理证明相关的几何问题.[知识链接]1.在初中我们学习过相似三角形,想一想,相似三角形及相似比是如何定义的?提示对应角相等,对应边成比例的两个三角形叫做相似三角形.相似三角形对应边的比值叫做相似比(或相似系数).2.判断下列各命题的正确性,正确的打“√”,错误的打“×”(1)两个等边三角形相似(√)(2)两个直角三角形相似(×)(3)两个等腰直角三角形相似(√)(4)有一个角为50°的两个等腰三角形相似(×)(5)有一个角为100°的两个等腰三角形相似(√)[预习导引]1.相似三角形(1)定义:对应角相等,对应边成比例的两个三角形叫作相似三角形,相似三角形对应边的比值叫作相似比(或相似系数).(2)记法:两个三角形相似,用符号“∽”表示,例如△ABC与△A′B′C′相似,记作△ABC∽△A′B′C′.2.相似三角形的判定3.直角三角形相似的判定定理(1)如果两个直角三角形有一个锐角对应相等,那么它们相似.(2)如果两个直角三角形的两条直角边对应成比例,那么它们相似.(3)如果一个直角三角形的斜边和一条直角边与另一个三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.4.相似三角形的性质定理(1)相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.(2)相似三角形周长的比等于相似比.(3)相似三角形面积的比等于相似比的平方.5.两个相似三角形外接(内切)圆的直径比、周长比、面积比与相似比的关系相似三角形外接(内切)圆的直径比、周长比等于相似比,外接(内切)圆的面积比等于相似比的平方.6.相似三角形的性质和全等三角形的性质比较要点一 相似三角形的判定例1 如图所示,∠ABC =∠D =90°,AC =a ,BC =b ,当BD 与a ,b 之间满足怎样的关系时,△ABC 与△CDB 相似? 解 (1)∵∠ABC =∠CDB =90°, ∴当AC BC =BCBD 时,△ABC ∽△CDB . 即a b =b BD ,∴BD =b 2a 时,△ABC ∽△CDB .(2)∵∠ABC =∠BDC =90°, ∴当AC BC =ABBD 时,△ABC ∽△BDC ,即a b =a 2-b 2BD , ∴BD =ba 2-b 2a时,△ABC ∽△BDC . 综上,当BD =b 2a 或BD =b a 2-b 2a时,△ABC 与△CDB 相似. 规律方法 解决此类问题,重点应放在“对应关系”上,根据“对应关系”进行合理的讨论是解题的关键.跟踪演练1 如图所示,等腰三角形ABC 中,AB =AC ,D 为CB 延长线上一点,E 为BC 延长线上一点,满足AB 2=DB ·CE . (1)求证:△ADB ∽△EAC ;(2)若∠BAC =40°,求∠DAE 的度数.(1)证明 ∵AB =AC ,∴∠ABC =∠ACB ,∴∠ABD =∠ECA . 又∵AB 2=DB ·CE ,∴AB DB =CE AB =CEAC , ∴AB CE =DBAC ,∴△ADB ∽△EAC .(2)解 ∵AB =AC ,∠BAC =40°,∴∠ABC =70°. 又∵△ADB ∽△EAC ,∴∠D =∠EAC ,∴∠DAE =∠DAB +∠BAC +∠EAC =∠DAB +∠BAC +∠D =∠ABC +∠BAC =70°+40°=110°. 要点二 直角三角形的判定例2 如图所示,矩形ABCD 中,AB ∶BC =5∶6,点E 在BC 上,点F 在CD 上,且EC =16BC ,FC =35CD . 求证:△AFD ∽△FEC .证明 设EC =x ,则BC =AD =6x ,AB =DC =5x ,∴FC =3x ,FD =2x , ∴AD FC =6x 3x =2,FD EC =2xx =2, ∴AD FC =FDEC ,又∵∠D =∠C =90°, ∴△AFD ∽△FEC .规律方法 直角三角形相似的判定方法很多,既可根据一般三角形相似的判定方法,又有其独特的判定方法,在求证、识别的过程中可由已知条件结合图形特征,确定合适的方法.跟踪演练2 如图所示,直线EF 交AB ,AC 于点F ,E ,交BC 的延长线于点D ,AC ⊥BC ,且AB ·CD =DE ·AC .。
人教版高中数学选修4-1《1.3相似三角形的判定及性质》

讲授新课
(2)两个相似三角形的外接圆的直径比、周长 比、面积比与相似比有什么关系? (3)两个相似三角形的内切圆的直径比|、周长 比、面积比与相似比有什么关系?
课堂练习
教材19面第1、2、3、4题.
1.3相似三角形的判定及性质 第2课时
复习引入
复习引入
讲授新课
例题讲解
例1.△ABC∽△ABC,AD和AD分别是 △ABC和△ABC的角平分线,且AD:AD =5:3,下面给出四个结论: ①BC:BC=5:3; ②△ABC的周长与△ABC的周长之比为 5: 3; ③△ABC与△ABC的对应高之比为5:3; ④△ABC与△ABC的对应中线之比为5:3. 其中正确的有( ) A.1个 B.2个 C.3个 D.4个
例题讲解
例2.如图,已知两条互相垂直的道路交于 点O,甲以3米/秒的速度从A点由西向东 前进到C点,乙以5米/秒的速度从B点由 南向北前进到D点,若AO=6米, BO= 8米,问经过几秒后,由C、D、O三点 组成的三角形恰好与△AOB相似.
A
甲
O
乙 B
例题讲解
讲授新课
(1)由相似三角形的性质定理可知,相似 三角形的高、中线、内角平分线、周长、 面积等要素都与相似比有关.拓宽思路, 考虑与三角形有关但不在三角形内的其他 元素,这些元素是否与三角形的相似比有 联系呢?你想到了哪些元素?
人教新课标版数学高二A版选修4-1课前导引 第一讲第三节相似三角形的判定

高中数学-打印版精心校对 第三节 相似三角形的判定课前导引情景导入高楼大厦与建筑模型,实景与照片等都给人以相似的形象,两个三角形满足什么条件就相似呢?知识预览1.定义:对应角相等,对应边成比例的两个三角形叫做相似三角形,相似三角形对应边的比叫做相似比.2.判定方法(1)预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.(2)判定定理1:对于任意两个三角形,如果一个三角形与另一个三角形的两个角对应相等,那么这两个三角形相似.简述为两角对应相等,两三角形相似.(3)判定定理2:对任意两个三角形,如果一个三角形的两边和另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似,简述为两边对应成比例,且夹角相等,两三角形相似.(4)判定定理3:对于任意两个三角形,如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似,简述为三边对应成比例,两三角形相似.3.直角三角形相似的判定方法(1)如果两个直角三角形有一个锐角对应相等,那么它们相似.(2)如果两个直角三角形的两条直角边对应成比例,那么它们相似.(3)如果一个直角三角形的斜边和一条直角边与另一个三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.4.引理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.5.证明方法:(1)直接证法;(2)间接证法.“同一法”就是一种间接证明方法.6.相似三角形具有对称性和传递性.(1)对称性:若△A 1B 1C 1∽△A 2B 2C 2,相似比为k,那么△A 2B 2C 2∽△A 1B 1C 1,相似比为k1. (2)传递性:若△A 1B 1C 1∽△A 2B 2C 2, △A 2B 2C 2∽△A 3B 3C 3,那么△A 1B 1C 1∽△A 3B 3C 3.。
高中数学 13相似三角形的判定及性质课后习题解答 新人教A版选修41
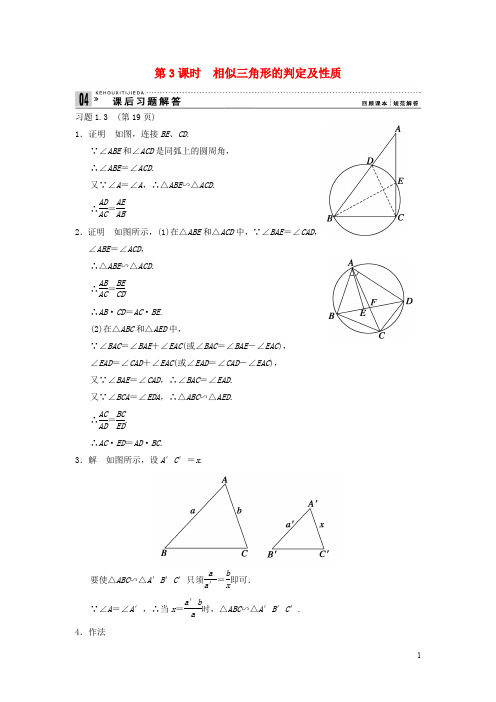
第3课时 相似三角形的判定及性质习题1.3 (第19页)1.证明 如图,连接BE 、CD .∵∠ABE 和∠ACD 是同弧上的圆周角, ∴∠ABE =∠ACD .又∵∠A =∠A ,∴△ABE ∽△ACD . ∴AD AC =AE AB.2.证明 如图所示,(1)在△ABE 和△ACD 中,∵∠BAE =∠CAD ,∠ABE =∠ACD ,∴△ABE ∽△ACD . ∴AB AC =BE CD. ∴AB ·CD =AC ·BE . (2)在△ABC 和△AED 中,∵∠BAC =∠BAE +∠EAC (或∠BAC =∠BAE -∠EAC ), ∠EAD =∠CAD +∠EAC (或∠EAD =∠CAD -∠EAC ), 又∵∠BAE =∠CAD ,∴∠BAC =∠EAD . 又∵∠BCA =∠EDA ,∴△ABC ∽△AED . ∴AC AD =BC ED. ∴AC ·ED =AD ·BC .3.解 如图所示,设A ′C ′=x .要使△ABC ∽△A ′B ′C ′只须a a ′=bx即可. ∵∠A =∠A ′,∴当x =a ′ba时,△ABC ∽△A ′B ′C ′. 4.作法(1)作线段B ′C ′,使B ′C ′=32BC ;(2)以B ′为顶点,B ′C ′为始边,作∠D ′B ′C ′=∠B ; (3)在B ′D ′上截取线段B ′A ′,使B ′A ′=32AB ;(4)连接A ′C ′,则△A ′B ′C ′为所作三角形.5.证明 ∵EF ∥AD ∥BC ,∴GE GB =EF BC ,HE HA =EF AD. ∵AD =BC ,∴GE GB =HE HA .∴AE HE =BEGE. 又∵∠AEB =∠HEG ,∴△AEB ∽△HEG . ∴∠ABE =∠HGE .∴GH ∥AB . 6.证明 ∵DE ∥AB ,∴DE AB =OD OA =OEOB.①又∵EF ∥BC ,∴EF BC =OE OB =OFOC.②∴DE AB =EF BC.由①、②知OD OA =OFOC, 而∠FOD =∠COA ,∴△FOD ∽△COA .∴DF AC =OD OA. ∴在△ABC 和△DEF 中,有DE AB =EF BC =DFAC. ∴△ABC ∽△DEF .7.证明 在△ACD 和△BCE 中,∵∠ADC =∠BEC =90°,∠ACD =∠BCE , ∴△ACD ∽△BCE .∴AD BE =AC BC,即AD ·BC =BE ·AC .8.解方案1:(1)在地面适当位置选取一点C,连接BC,测量出BC的距离;(2)在点C竖立一根垂直于地面的标尺杆;(3)在BC的延长线上取一点D,使点D、标尺杆的顶点E和树尖在一条直线上;(4)测量CD的距离.在这个方案中,由于△DCE∽△DBA,而BC、CD、CE的长可以由测量而得,所以可以求出树高AB的长.(没有考虑测量仪的脚架高)方案2:(1)在地面上选取一点C,连接BC;(2)测出∠BCA;(3)在地面上选取一点D,使∠DCB=∠BCA;(4)过D作BC的垂线,交BC于E;(5)测量DE、CE、BC的长,由这三个量可以求得AB的长.因为按方案2的实施,易知Rt△ABC∽Rt△DEC.(没有考虑测量仪的脚架高)方案3:(1)把一面镜子放在离树a米的点E;(2)一个人望着镜子后退到点D,这时恰好在镜子里望到树梢点A;(3)量得ED为b米,人的眼睛距地面的高度为c米,即可求AB的长.因为根据光学中的反射定律,知∠AEB=∠CED,所以△ABE∽△CDE.9.证明 如图所示,设△ABC ∽△A ′B ′C ′,相似比为k .(1)设AD 是△ABC 中BC 边上的中线,A ′D ′是△A ′B ′C ′中B ′C ′边上的中线. ∵△ABC ∽△A ′B ′C ′,∴AB A ′B ′=BCB ′C ′. 又∵D 、D ′分别为BC 、B ′C ′的中点, ∴AB A ′B ′=BC B ′C ′=2BD 2B ′D ′=BDB ′D ′. 又∵∠B =∠B ′,∴△ABD ∽△A ′B ′D ′. ∴AD A ′D ′=ABA ′B ′=k . 其余两组对应中线之比同理可证.(2)设AE 、A ′E ′分别是△ABC 、△A ′B ′C ′中∠A 和∠A ′的内角平分线. ∵△ABC ∽△A ′B ′C ′,∴∠BAC =∠B ′A ′C ′,∠B =∠B ′. ∴∠BAE =∠B ′A ′E ′.∴△ABE ∽△A ′B ′E ′. ∴AE A ′E ′=ABA ′B ′=k . 同理可证,其余两个对应角的内角平分线之比也等于相似比. 10.解 在△AEF 和△CDF 中,∵∠DCF =∠EAF ,∠DFC =∠EFA , ∴△AEF ∽△CDF . ∴△AEF 的周长△CDF 的周长=AE CD =13.∴S △AEF S △CDF =k 2=19.而S △AEF =6, ∴S △CDF =9S △AEF =9×6=54 (cm 2).11.解 问题1:相似三角形对应角的外角平分线之比等于相似比.证明:设△ABC ∽△A ′B ′C ′.AD 、A ′D ′分别是∠A 、∠A ′的外角平分线,分别交BC 、B ′C ′的延长线于D 、D ′.∵△ABC ∽△A ′B ′C ′,∴∠BAC =∠B ′A ′C ′. 又∵∠BAC +∠1+∠2=∠B ′A ′C ′+∠3+∠4, 而∠1=∠2,∠3=∠4,∴∠1=∠3. ∴∠BAD =B ′A ′D ′. 又∵∠B =∠B ′, ∴△ABD ∽△A ′B ′D ′. ∴AD A ′D ′=ABA ′B ′=k . 问题2:△ABC ∽△A ′B ′C ′,以△ABC 的三条边为直径,分别向△ABC 外作半圆(如图所示),同样,以△A ′B ′C ′的三条边为直径,分别向△A ′B ′C ′外作半圆.则两个三角形中三个对应半圆的面积之比等于相似比的平方.说明 将三个半圆改为三个等边三角形、正方形、正多边形等,可以得到更多的命题. 问题3:如图所示,△ABC ∽△A ′B ′C ′,相似比为k ,BD CD =B ′D ′C ′D ′.则AD A ′D ′=k .说明该题是一个开放型问题,可以由联想、类比等方法得到许多新问题.在教学中应引导、启发和鼓励学生去探究、猜想.。
2017-2018学年高中数学人教A版选修4-1学业分层测评4 相似三角形的性质 Word版含解析

学业分层测评(四)(建议用时:45分钟)[学业达标]一、选择题1.如图1-3-32,D ,E ,F 是△ABC 的三边中点,设△DEF 的面积为14,△ABC 的周长为9,则△DEF 的周长与△ABC 的面积分别是( )图1-3-32A.92,1 B .9,4 C.92,8D.94,16【解析】 ∵D ,E ,F 分别为△ABC 三边的中点, ∴EF 綊12BC ,DE 綊12AC ,DF 綊12AB. ∴△DFE ∽△ABC ,且EF BC =12,∴l △DEF l △ABC =EF BC =12.又∵l △ABC =9,∴l △DEF =92. 又∵S △DEF S △ABC =EF 2BC 2=14,S △DEF =14,∴S △ABC =1,故选A. 【答案】 A2.如图1-3-33,在▱ABCD 中,AB =10,AD =6,E 是AD 的中点,在AB 上取一点F ,使△CBF ∽△CDE ,则BF 的长是( )图1-3-33 A.5 B.8.2 C.6.4 D.1.8【解析】由△CBF∽△CDE,得BFDE=CBCD,又点E是AD的中点,AB=CD=10,AD=BC=6,∴DE=3,即BF3=610,∴BF=1.8.【答案】 D3.如图1-3-34所示,D是△ABC的AB边上一点,过D作DE∥BC交AC 于E.已知AD∶DB=1∶3,则△ADE与四边形BCED的面积比为()图1-3-34A.1∶3B.1∶9C.1∶15 D.1∶16【解析】因为DE∥BC,所以△ADE∽△ABC.又因为AD∶DB=1∶3.所以AD∶AB=1∶4,其面积比为1∶16,则所求两部分面积比为1∶15.【答案】 C4.某同学自制了一个简易的幻灯机,其工作情况如图1-3-35所示,幻灯片与屏幕平行,光源到幻灯片的距离是30 cm,幻灯片到屏幕的距离是1.5 m,幻灯片上小树的高度是10 cm,则屏幕上小树的高度是() 【导学号:07370017】图1-3-35A .50 cmB .500 cmC .60 cmD .600 cm【解析】 设屏幕上小树的高度为x cm ,则10x =3030+150,解得x =60(cm).【答案】 C5.如图1-3-36,△ABC 中,DE ∥BC ,DE 分别交AB ,AC 于D ,E ,S △ADE =2S △DCE ,则S △ADES △ABC=( )图1-3-36A.14B.12C.23D.49【解析】 ∵DE ∥BC ,∴△ADE ∽△ABC , 由S △ADE =2S △DCE ,得AD AB =23,∴S △ADE S △ABC =49.【答案】 D 二、填空题6.如图1-3-37,在△ABC 中,D 为AC 边上的中点,AE ∥BC ,ED 交AB 于G ,交BC 延长线于F ,若BG ∶GA =3∶1,BC =10,则AE 的长为________.图1-3-37【解析】 ∵AE ∥BC ,∴△BGF ∽△AGE ,∴BF AE =BG GA =31, ∵D 为AC 中点,∴AE CF =ADDC =1,∴AE =CF , ∴BC ∶AE =2∶1,∵BC =10,∴AE =5. 【答案】 57.如图1-3-38,AB 与CD 相交于点E ,过E 作BC 的平行线与AD 的延长线交于点P ,已知∠A =∠C ,PD =2DA =2,则PE =________.图1-3-38【解析】 因为PE ∥BC ,所以∠C =∠PED .又因为∠C =∠A ,所以∠A =∠PED .又∠P =∠P ,所以△PDE ∽△PEA ,则PD PE =PEP A ,即PE 2=PD ·P A =2×3=6,故PE = 6.【答案】68.(2016·湛江高三调研)如图1-3-39,在△ABC 中,已知DE ∥BC ,△ADE 的面积是a 2,梯形DBCE 的面积是8a 2,则ADAB =________.图1-3-39【解析】 ∵S △ADE =a 2,S DBCE =8a 2,∴S △ABC =S △ADE +S BDCE =a 2+8a 2=9a 2,∴⎝ ⎛⎭⎪⎫AD AB 2=S △ADE S △ABC=a29a 2=19,∴AD AB =13. 【答案】 13 三、解答题9.如图1-3-40,已知在△ABC 中,D 是BC 边的中点,且AD =AC ,DE ⊥BC ,DE 与 AB 相交于点E ,EC 与AD 相交于点F .图1-3-40(1)求证:△ABC ∽△FCD ;(2)若S △FCD =5,BC =10,求DE 的长. 【解】 (1)证明:∵DE ⊥BC ,D 是BC 的中点,∴EB =EC ,∴∠B =∠1, 又∵AD =AC , ∴∠2=∠ACB. ∴△ABC ∽△FCD .(2)过点A 作AM ⊥BC ,垂足为点M . ∵△ABC ∽△FCD ,BC =2CD , ∴S △ABCS △FCD =⎝ ⎛⎭⎪⎫BC CD 2=4. 又∵S △FCD =5,∴S △ABC =20. ∵S △ABC =12BC ·AM ,BC =10, ∴20=12×10×AM ,∴AM =4.又∵DE ∥AM ,∴DE AM =BDBM . ∵DM =12DC =14BC =52, BM =BD +DM ,BD =12BC =5,∴DE 4=55+52, ∴DE =83.10.如图1-3-41,△ABC 是一块锐角三角形余料,边BC =200 mm ,高AD =300 mm ,要把它加工成长是宽的2倍的矩形零件,使矩形较短的边在BC 上,其余两个顶点分别在AB ,AC 上,求这个矩形零件的边长.图1-3-41【解】 设矩形EFGH 为加工成的矩形零件,边FG 在BC 上,则点E ,H 分别在AB ,AC 上,△ABC 的高AD 与边EH 相交于点P ,设矩形的边EH 的长为x mm.∵EH ∥BC ,∴△AEH ∽△ABC , ∴AP AD =EH BC ,∴300-2x 300=x200, 解得x =6007 (mm),2x =1 2007(mm).答:加工成的矩形零件的边长分别为6007mm 和1 2007mm.[能力提升]1.如图1-3-42所示,已知在△ABC 中,∠C =90°,正方形DEFG 内接于△ABC ,DE ∥AC ,EF ∥BC ,AC =1,BC =2,则AF ∶FC 等于( )图1-3-42A .1∶3B .1∶4C .1∶2D .2∶3【解析】 设正方形边长为x ,则由△AFE ∽△ACB , 可得AF ∶AC =FE ∶CB ,即x 2=1-x1, 所以x =23,于是AF FC =12. 【答案】 C2.如图1-3-43,AB ∥EF ∥CD ,已知AB =20,DC =80,那么EF 的值是( )图1-3-43A .10B .12C .16D .18【解析】 ∵AB ∥EF ∥CD , ∴AE EC =AB DC =2080=14, ∴EF AB =EC AC =45, ∴EF =45AB =45×20=16. 【答案】 C3.在△ABC 中,如图1-3-44所示,BC =m ,DE ∥BC ,DE 分别交AB ,AC 于E ,D 两点,且S △ADE =S 四边形BCDE ,则DE =________. 【导学号:07370018】图1-3-44【解析】 ∵DE ∥BC , ∴△ADE ∽△ACB.又∵S △ADE +S 四边形BCDE =S △ABC ;S △ADE =S 四边形BCDE , ∴S △ADE =12S △ABC , ∴⎝ ⎛⎭⎪⎫DE BC 2=12,∴⎝ ⎛⎭⎪⎫DE m 2=12, ∴DE =22m . 【答案】 22m4.某生活小区的居民筹集资金1 600元,计划在一块上、下两底分别为10 cm 、20 cm 的梯形空地上种植花木.(1)他们在△AMD 和△BMC 地带上种植太阳花,单价为8元/m 2,当△AMD 地带种满花后(如图1-3-45阴影部分)共花了160元,请计算种满△BMC 地带所需的费用;图1-3-45(2)若其余地带要种的有玫瑰和茉莉花两种花木可供选择,单价分别为12元/m 2和10元/m 2,应选择种哪种花木可以刚好用完所筹集的资金?【解】 (1)∵四边形ABCD 是梯形,∴AD ∥BC , ∴△AMD ∽△CMB ,∴S △AMD S △CMB =⎝ ⎛⎭⎪⎫AD BC 2=14.∵种植△AMD 地带花费160元,∴S △AMD =1608=20 (m 2),∴S △CMB =80 (m 2). ∴△BMC 地带的花费为80×8=640(元).(2)设△AMD ,△BMC 的高分别为h 1,h 2,梯形ABCD 的高为h , ∵S △AMD =12×10h 1=20,∴h 1=4(m). 又∵h 1h 2=12,∴h 2=8(m).∴h =h 1+h 2=12(m).∴S 梯形ABCD =12(AD +BC )h =12×30×12 =180 (m 2),∴S △AMB +S △DMC =180-20-80=80 (m 2). ∴160+640+80×12=1 760(元), 160+640+80×10=1 600(元). ∴应种植茉莉花刚好用完所筹资金.。
高中数学第一讲三1相似三角形的判定课件新人教A版选修4-1
相似三角形的应用 [例 2] 如图,D 为△ABC 的边 AB 上一点,过 D 点作 DE∥ BC,DF∥AC,AF 交 DE 于 G,BE 交 DF 于 H,连接 GH.
求证:GH∥AB. [思路点拨] 根据此图形的特点可先证比例式GDEE=EEHB成 立,再证△EGH∽△EDB,由相似三角形的定义得∠EHG= ∠EBD 即可.
成比例且夹角相等.故选项 A、B、D 都能推出两三角形相
似.在 C 项的条件下推不出两三角形相似.
答案:C
2.如图,在四边形 ABCD 中,AEEB=FADF, BGGC=DHHC,EH,FG 相交于点 O. 求证:△OEF∽△OHG. 证明:如图,连接 BD. ∵AEEB=FADF, ∴EF∥BD. 又∵BGGC=DHHC,
1.如图,D,E 分别是 AB,AC 上的两点,CD 与 BE 相交于点
O,下列条件中不能使△ABE 和△ACD 相似的是 ( )
A.∠B=∠C
பைடு நூலகம்
B.∠ADC=∠AEB
C.BE=CD,AB=AC D.AD∶AC=AE∶AB 解析:在选项 A、B 的条件下,两三角形有两组对应角相等,
所以两三角形相似,在 D 项的条件下,两三角形有两边对应
相似三角形的判定
[例 1] 如图,已知在△ABC 中,AB=AC,∠ A=36°,BD 是角平分线,证明:△ABC∽△BCD.
[思路点拨] 已知 AB=AC,∠A=36°,所以 ∠ABC=∠C=72°,而 BD 是角平分线,因此,可 以考虑使用判定定理 1.
判定两三角形相似,可按下面顺序进行: (1)有平行截线,用预备定理; (2)有一对等角时,①找另一对等角,②找夹这个角 的两边对应成比例; (3)有两对应边成比例时,①找夹角相等,②找第三 边对应成比例,③找一对直角.
人教版数学高二A版选修4-1第一讲三相似三角形的判定及性质(第2课时)
预习导航1.相似三角形的性质定理(1)相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.(2)相似三角形周长的比等于相似比.(3)相似三角形面积的比等于相似比的平方.思考1相似三角形与全等三角形的性质有哪些不同?提示:如下表所示.2.两个相似三角形外接圆的直径比、周长比、面积比与相似比的关系相似三角形外接圆的直径比、周长比等于相似比,外接圆的面积比等于相似比的平方. 思考2 两个相似三角形的内切圆的直径比、周长比、面积比与相似比有怎样的关系?并试着证明.提示:两个相似三角形的内切圆的直径比、周长比等于相似比,面积比等于相似比的平方.下面给出这个结论的证明.已知△ABC ∽△A ′B ′C ′,⊙O 和⊙O ′分别为△ABC 和△A ′B ′C ′的内切圆,相似比为k .求证:⊙O 和⊙O ′的直径比为k ,周长比为k ,面积比为k 2. 证明:连接O 和切点D ,O ′和切点D ′, 所以OD ⊥AB ,O ′D ′⊥A ′B ′. 连接OA ,OB ,O ′A ′,O ′B ′.因为△ABC ∽△A ′B ′C ′,所以∠BAC =∠B ′A ′C ′. 又∠DAO =12∠BAC ,∠D ′A ′O ′=12∠B ′A ′C ′,所以∠DAO =∠D ′A ′O ′. 同理∠DBO =∠D ′B ′O ′.所以△AOB ∽△A ′O ′B ′,相似比为k .因为OD ,O ′D ′分别为△AOB 和△A ′O ′B ′的高, 所以OD O ′D ′=k ,即r r ′=k ,所以2r2r ′=k .因为⊙O 的周长为2π·OD ,⊙O ′的周长为2π·O ′D ′, 所以⊙O 的周长⊙O ′的周长=k .因为⊙O 的面积=π(OD )2,⊙O ′的面积=π(O ′D ′)2, 所以⊙O 的面积⊙O ′的面积=OD 2O ′D ′2=k 2.于是结论得证.。
高中数学人教A版选修4-1学业分层测评4 相似三角形的性质 Word版含解析.doc
学业分层测评(四)(建议用时:45分钟)[学业达标]一、选择题1.如图1-3-32,D,E,F是△ABC的三边中点,设△DEF的面积为14,△ABC的周长为9,则△DEF的周长与△ABC的面积分别是()图1-3-32A.92,1B.9,4C.92,8 D.94,16【解析】∵D,E,F分别为△ABC三边的中点,∴EF綊12BC,DE綊12AC,DF綊12AB.∴△DFE∽△ABC,且EFBC=12,∴l△DEFl△ABC=EFBC=12.又∵l△ABC =9,∴l△DEF=92.又∵S△DEFS△ABC=EF2BC2=14,S△DEF=14,∴S△ABC=1,故选A.【答案】 A2.如图1-3-33,在▱ABCD中,AB=10,AD=6,E是AD的中点,在AB 上取一点F,使△CBF∽△CDE,则BF的长是()图1-3-33 A.5 B.8.2 C.6.4 D.1.8【解析】由△CBF∽△CDE,得BFDE=CBCD,又点E是AD的中点,AB=CD=10,AD=BC=6,∴DE=3,即BF3=610,∴BF=1.8.【答案】 D3.如图1-3-34所示,D是△ABC的AB边上一点,过D作DE∥BC交AC 于E.已知AD∶DB=1∶3,则△ADE与四边形BCED的面积比为()图1-3-34A.1∶3B.1∶9C.1∶15 D.1∶16【解析】因为DE∥BC,所以△ADE∽△ABC.又因为AD∶DB=1∶3.所以AD∶AB=1∶4,其面积比为1∶16,则所求两部分面积比为1∶15.【答案】 C4.某同学自制了一个简易的幻灯机,其工作情况如图1-3-35所示,幻灯片与屏幕平行,光源到幻灯片的距离是30 cm,幻灯片到屏幕的距离是1.5 m,幻灯片上小树的高度是10 cm,则屏幕上小树的高度是() 【导学号:07370017】图1-3-35A.50 cm B.500 cmC.60 cm D.600 cm【解析】设屏幕上小树的高度为x cm,则10x=3030+150,解得x=60(cm).【答案】 C5.如图1-3-36,△ABC中,DE∥BC,DE分别交AB,AC于D,E,S△ADE=2S△DCE ,则S△ADES△ABC=()图1-3-36A.14 B.12C.23 D.49【解析】∵DE∥BC,∴△ADE∽△ABC,由S△ADE =2S△DCE,得ADAB=23,∴S△ADES△ABC=49.【答案】 D二、填空题6.如图1-3-37,在△ABC中,D为AC边上的中点,AE∥BC,ED交AB 于G,交BC延长线于F,若BG∶GA=3∶1,BC=10,则AE的长为________.图1-3-37【解析】∵AE∥BC,∴△BGF∽△AGE,∴BFAE=BGGA=31,∵D为AC中点,∴AECF=ADDC=1,∴AE=CF,∴BC∶AE=2∶1,∵BC=10,∴AE=5.【答案】 57.如图1-3-38,AB 与CD 相交于点E ,过E 作BC 的平行线与AD 的延长线交于点P ,已知∠A =∠C ,PD =2DA =2,则PE =________.图1-3-38【解析】 因为PE ∥BC ,所以∠C =∠PED .又因为∠C =∠A ,所以∠A =∠PED .又∠P =∠P ,所以△PDE ∽△PEA ,则PD PE =PEP A ,即PE 2=PD ·P A =2×3=6,故PE = 6.【答案】68.(2016·湛江高三调研)如图1-3-39,在△ABC 中,已知DE ∥BC ,△ADE 的面积是a 2,梯形DBCE 的面积是8a 2,则ADAB =________.图1-3-39【解析】 ∵S △ADE =a 2,S DBCE =8a 2,∴S △ABC =S △ADE +S BDCE =a 2+8a 2=9a 2,∴⎝ ⎛⎭⎪⎫AD AB 2=S △ADE S △ABC=a29a 2=19,∴AD AB =13. 【答案】 13 三、解答题9.如图1-3-40,已知在△ABC 中,D 是BC 边的中点,且AD =AC ,DE ⊥BC ,DE 与 AB 相交于点E ,EC 与AD 相交于点F .图1-3-40(1)求证:△ABC ∽△FCD ;(2)若S △FCD =5,BC=10,求DE 的长. 【解】 (1)证明:∵DE ⊥BC ,D 是BC 的中点, ∴EB =EC ,∴∠B =∠1, 又∵AD =AC , ∴∠2=∠ACB. ∴△ABC ∽△FCD .(2)过点A 作AM ⊥BC ,垂足为点M . ∵△ABC ∽△FCD ,BC =2CD , ∴S △ABC S △FCD =⎝ ⎛⎭⎪⎫BC CD 2=4. 又∵S △FCD =5,∴S △ABC =20. ∵S △ABC =12BC ·AM ,BC =10, ∴20=12×10×AM ,∴AM =4. 又∵DE ∥AM ,∴DE AM =BDBM . ∵DM =12DC =14BC =52, BM =BD +DM ,BD =12BC =5,∴DE 4=55+52, ∴DE =83.10.如图1-3-41,△ABC 是一块锐角三角形余料,边BC =200 mm ,高AD =300 mm ,要把它加工成长是宽的2倍的矩形零件,使矩形较短的边在BC 上,其余两个顶点分别在AB ,AC 上,求这个矩形零件的边长.图1-3-41【解】设矩形EFGH为加工成的矩形零件,边FG在BC上,则点E,H 分别在AB,AC上,△ABC的高AD与边EH相交于点P,设矩形的边EH的长为x mm.∵EH∥BC,∴△AEH∽△ABC,∴APAD=EHBC,∴300-2x300=x200,解得x=6007(mm),2x=1 2007(mm).答:加工成的矩形零件的边长分别为6007mm和1 2007mm.[能力提升]1.如图1-3-42所示,已知在△ABC中,∠C=90°,正方形DEFG内接于△ABC,DE∥AC,EF∥BC,AC=1,BC=2,则AF∶FC等于()图1-3-42A.1∶3B.1∶4C.1∶2 D.2∶3【解析】设正方形边长为x,则由△AFE∽△ACB,可得AF∶AC=FE∶CB,即x2=1-x1,所以x=23,于是AFFC=12.【答案】 C2.如图1-3-43,AB∥EF∥CD,已知AB=20,DC=80,那么EF的值是()图1-3-43A.10 B.12C.16 D.18【解析】 ∵AB ∥EF ∥CD , ∴AE EC =AB DC =2080=14, ∴EF AB =EC AC =45, ∴EF =45AB =45×20=16. 【答案】 C3.在△ABC 中,如图1-3-44所示,BC =m ,DE ∥BC ,DE 分别交AB ,AC 于E ,D 两点,且S △ADE =S 四边形BCDE ,则DE =________. 【导学号:07370018】图1-3-44【解析】 ∵DE ∥BC , ∴△ADE ∽△ACB.又∵S △ADE +S 四边形BCDE =S △ABC ;S △ADE =S 四边形BCDE , ∴S △ADE =12S △ABC , ∴⎝ ⎛⎭⎪⎫DE BC 2=12,∴⎝ ⎛⎭⎪⎫DE m 2=12, ∴DE =22m . 【答案】 22m4.某生活小区的居民筹集资金1 600元,计划在一块上、下两底分别为10 cm 、20 cm 的梯形空地上种植花木.(1)他们在△AMD 和△BMC 地带上种植太阳花,单价为8元/m 2,当△AMD 地带种满花后(如图1-3-45阴影部分)共花了160元,请计算种满△BMC 地带所需的费用;图1-3-45(2)若其余地带要种的有玫瑰和茉莉花两种花木可供选择,单价分别为12元/m 2和10元/m 2,应选择种哪种花木可以刚好用完所筹集的资金?【解】 (1)∵四边形ABCD 是梯形,∴AD ∥BC , ∴△AMD ∽△CMB ,∴S △AMD S △CMB =⎝ ⎛⎭⎪⎫AD BC 2=14. ∵种植△AMD 地带花费160元,∴S △AMD =1608=20 (m 2),∴S △CMB =80 (m 2). ∴△BMC 地带的花费为80×8=640(元).(2)设△AMD ,△BMC 的高分别为h 1,h 2,梯形ABCD 的高为h , ∵S △AMD =12×10h 1=20,∴h 1=4(m). 又∵h 1h 2=12,∴h 2=8(m).∴h =h 1+h 2=12(m).∴S 梯形ABCD =12(AD +BC )h =12×30×12 =180 (m 2),∴S △AMB +S △DMC =180-20-80=80 (m 2). ∴160+640+80×12=1 760(元), 160+640+80×10=1 600(元). ∴应种植茉莉花刚好用完所筹资金.。
高中数学第一讲相似三角形的判定及有关性质章末分层突破课件新人教A版选修4-1
图 1-8
利用相似三角形证明线段相等 证明两条线段相等,一般情况下,利用等角对等边或全等三角形的性质来 解决.但有些证明两条线段相等的几何题利用前面的方法得不出来,或过程比 较繁琐,此时可以借助于相似三角形的有关比例线段来解决.
射影定理 射影定理揭示了直角三角形中两直角边在斜边上的射影,斜边及两直角边 之间的比例关系,此定理常作为计算与证明的依据,在运用射影定理时,要特 别注意弄清射影与直角边的对应关系,分清比例中项,否则在做题中极易出错.
巩 固 层
·
知
识
整 合
章 末
章末分层突破
综 合
测
提
评
升
层
· 能 力 强 化
________________________________________________________________ ________________________________________________________________ ________________________________________________积线段或成比例线段
利用相似三角形的性质可以得到等积式或比例式,是解决这类问题的基本 方法.解决这类问题一般可分为三步:
(1)把等积式化为比例式,从而确定相关的两个三角形相似. (2)确定两个相关的三角形的方法是:把比例式横看或者竖看,将两条线段 中的相同字母消去一个,由余下的字母组成三角形. (3)设法找到证明这两个三角形相似的条件.
转化思想 在证明一些等积式时,往往将其转化为比例式加以证明.当证明的比例式 中的线段在同一条直线上时,常转化为用相等的线段、相等的比、相等的等积 式来代换相应的量.证明比例式成立也常利用中间比来转化证明.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1页 共8页
高中数学人教a版高二选修4-1学业分层测评3_相似三角形的判定 含
解析
学业分层测评(三)
(建议用时:45分钟)
[学业达标]
一、选择题
1.如图1-3-12,在正方形网格上有6个三角形:①△ABC,②△BCD,③△BDE,
④△BFG,⑤△FGH,⑥△EFK.其中,②~⑥中与三角形①相似的是
( )
图1-3-12
A.②③④ B.③④⑤
C.④⑤⑥ D.②③⑥
【解析】 由相似三角形判定定理知选B.
【答案】 B
2.如图1-3-13,在△ABC中,M在BC上,N在AM上,CM=CN,且AMAN=BMCN,
下列结论中正确的是( )
图1-3-13
A.△ABM∽△ACB
B.△ANC∽△AMB
C.△ANC∽△ACM
D.△CMN∽△BCA
【解析】 ∵CM=CN,∴∠CMN=∠CNM.
∵∠AMB=∠CNM+∠MCN,
第2页 共8页
∠ANC=∠CMN+∠MCN,∴∠AMB=∠ANC.
又AMAN=BMCN,
∴△ANC∽△AM B.
【答案】 B
3.如图1-3-14,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则AODO等于( )
图1-3-14
A.25 5 B.13
C.23 D.12
【解析】 ∵AF⊥DE,∴Rt△DAO∽Rt△DEA,
∴AODO=AEDA=12.
【答案】 D
4.如图1-3-15,在等边三角形ABC中,E为AB中点,点D在AC上,使得ADAC=
1
3
,则有( )
图1-3-15
A.△AED∽△BED
B.△AED∽△CBD
C.△AED∽△ABD
D.△BAD∽△BCD
第3页 共8页
【解析】 因为∠A=∠C,BCAE=CDAD=2,所以△AED∽△CBD.
【答案】 B
5.如图1-3-16所示,已知点E,F分别是△ABC中AC,AB边的中点,BE,CF相
交于点G,FG=2,则CF的长为( )
图1-3-16
A.4 B.4.5
C.5 D.6
【解析】 ∵E,F分别是△ABC中AC,AB边的中点,∴FE∥BC,由相似三角
形的预备定理,得△FEG∽△CBG,∴FGGC=EFBC=12.
又FG=2,∴GC=4,∴CF=6.
【答案】 D
二、填空题
6.如图1-3-17,BD⊥AE,∠C=90°,AB=4,BC=2,AD=3,则DE=________,
CE=________.
图1-3-17
【解析】 在Rt△ACE和Rt△ADB中,∠A为公共角,∴△ACE∽△ADB,∴
AB
AE
=ADAC,
∴AE=AB·ACAD=ABAB+BCAD=4×4+23=8,则DE=AE-AD=5,
在Rt△ACE中,CE=AE2-AC2=82-4+22=27.
【答案】 5 27
7.如图1-3-18,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,
第4页 共8页
则AE=________.
图1-3-18
【解析】 由∠B=∠D,AE⊥BC及∠ACD=90°可以推得:
Rt△ABE∽Rt△ADC,故AEAC=ABAD
∴AE=6×412=2.
【答案】 2
8.如图1-3-19,在平行四边形ABCD中,E在DC上,若DE∶EC=1∶2,则BF∶
BE=________.
图1-3-19
【解析】 ∵DE∶EC=1∶2,
∴DC∶EC=3∶2,∴AB∶EC=3∶2.
∵AB∥EC,
∴△ABF∽△CEF,
∴BFEF=ABEC=32,∴BFBE=35.
【答案】 3∶5
三、解答题
9.如图1-3-20,已知△ABC中,AB=AC,AD是中线,P是AD上一点,过C作
CF∥AB,延长BP交AC于E,交CF于点F.
求证:PB2=PE·PF.
第5页 共8页
图1-3-20
【证明】 连接PC.
∵AB=AC,
∴∠ABC=∠ACB.
∵AD是中线,∴AD垂直平分BC,
∴PB=PC,
∴∠PBD=∠PCD,
∴∠ABP=∠ACP.
又∵CF∥AB,∴∠ABP=∠F=∠ACP,
而∠CPE=∠FPC.
∴△PCE∽△PFC,
∴PEPC=PCPF,∴PC2=PE·PF,
即PB2=PE·PF.
10.如图1-3-21,某市经济开发区建有B,C,D三个食品加工厂,这三个工厂和开
发区A处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且AB=CD
=900米,AD=BC=1 700米.自来水公司已经修好一条自来水主管道AN,B,C两厂
之间的公路与自来水主管道交于E处,EC=500米.若自来水主管道到各工厂的自来
水管道由各厂负责修建,每米造价800元.
图1-3-21
(1)要使修建自来水管道的造价最低,这三个工厂的自来水管道路线应怎样设计?
并在图中画出该路线;
(2)求出各厂所修建的自来水管道的最低造价各是多少元?
【解】 (1)如图,过B,C,D分别作AN的垂线段BH,CF,DG
交AN于H,F,G,BH,CF,DG即为所求的造价最低的管道路线.
(2)在Rt△ABE中,AB=900米,
BE=1 700-500=1 200米,
第6页 共8页
∴AE=1 2002+9002=1 500(米),
由△ABE∽△CFE,得到CFAB=CEAE,
即CF900=5001 500,
可得CF=300(米).由△BHE∽△CFE,
得BHCF=BECE,
即BH300=1 200500,可得BH=720(米).
由△ABE∽△DGA,得ABDG=AEAD,
即900DG=1 5001 700,
可得DG=1020(米).
所以,B,C,D三厂所建自来水管道的最低造价分别是720×800=576 000(元),
300×800=240 000(元),1 020×800=816 000(元).
[能力提升]
1.如图1-3-22所示,要使△ACD∽△BCA,下列各式中必须成立的是( )
图1-3-22
A.ACAB=ADBC B.ADCD=ACBC
C.AC2=CD·CB D.CD2=AC·AB
【解析】 ∠C=∠C,只有ACCD=CBAC,即AC2=CD·CB时,才能使△ACD∽△BCA.
【答案】 C
2.如图1-3-23所示,∠AOD=90°,OA=OB=BC=CD,则下列结论正确的是( )
图1-3-23
第7页 共8页
A.△DAB∽△OCA
B.△OAB∽△ODA
C.△BAC∽△BDA
D.△OAC∽△ABD
【解析】 设OA=OB=BC=CD=a,
则AB=2a,BD=2a,
∴ABBD=22,BCAB=a2a=22,
∴ABBD=BCAB,且∠ABC=∠DBA,
∴△BAC∽△BDA.
【答案】 C
3.如图1-3-24所示,∠BAC=∠DCB,∠CDB=∠ABC=90°,AC=a,BC=B.
当BD=__________时,△ABC∽△CDB.
图1-3-24
【解析】 由ACBC=BCBD即可得到.
【答案】 b2a
4.如图1-3-25所示,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连
接FC(AB>AE).
图1-3-25
(1)△AEF与△ECF是否相似?若相似证明你的结论;若不相似,请说明理由;
(2)设ABBC=k,是否存在这样的k值 ,使得△AEF与△BFC相似,若存在,证明你
第8页 共8页
的结论,并求出k的值;若不存在,说明理由.
【解】 (1)相似.在矩形ABCD中,∠A=∠D=90°.
∵EF⊥EC,A,E,D共线,∴∠AEF+∠DEC=90°.
又∵∠DCE+∠DEC=90°,∴∠AEF=∠DCE,
∴△AEF∽△DCE,∴EFEC=AFDE,
∴AE=DE,∴EFEC=AFAE.
又∵∠A=∠FEC=90°,∴△AEF∽△ECF.
(2)存在.由于∠AEF=90°-∠AFE<180°-∠CFE-∠AFE=∠BFC,
∴只能是△AEF∽△BCF,∠AEF=∠BCF.
由(1)知∠AEF=∠DCE=∠ECF=∠FCB=30°.
∴ABBC=CDBC=CD2DE=32,即k=32.
反过来,在k=32时,DECD=13,∠DCE=30°,
∠AEF=∠DCE=30°,∠ECF=∠AEF=30°,
∠BCF=90°-30°-30°=30°=∠AEF.
∴△AEF∽△BCF.
