【南方新中考】(南粤专用)2016中考数学+第一部分+第五章+第1讲+图形的轴对称、平移与旋转复习课件
2016年全国中考数学真题广东省中考试题(解析版-精品文档)

2016年广东省初中毕业生学业考试数 学一、选择题(本大题10小题,每小题3分,共30分) 1、-2的绝对值是( )A 、2B 、-2C 、12D 、1-2答案:A考点:绝对值的概念,简单题。
解析:-2的绝对值是2,故选A 。
2、如图1所示,a 和b 的大小关系是( ) 图1 A 、a <b B 、a >b C 、a=b D 、b =2a 答案:A考点:数轴,会由数轴上点的位置判断相应数的大小。
解析:数轴上从左往右的点表示的数是从小往大的顺序,由图可知b >a ,选A 。
3、下列所述图形中,是中心对称图形的是( )A 、直角三角形B 、平行四边形C 、正五边形D 、正三角形 答案:B考点:中心对称图形与轴对称图形。
解析:直角三角形既不是中心对称图形也不轴对称图形,正五边形和正三角形是轴对称图形,只有平行四边是中心对称图形。
4、据广东省旅游局统计显示,2016年4月全省旅游住宿设施接待过夜旅客约27700000人,将27700000用科学计数法表示为( )A 、70.27710⨯B 、80.27710⨯C 、72.7710⨯D 、82.7710⨯ 答案:C考点:本题考查科学记数法。
解析:科学记数的表示形式为10n a ⨯形式,其中1||10a ≤<,n 为整数,27700000=72.7710⨯。
故选C 。
中点连接EF为边的正方形EFGH的周长为()AB、1 D、1答案:B考点:三角形的中位线,勾股定理。
解析:连结BD,由勾股定理,得BDE、F为中点,所以,EF=2,所以,正方形EFGH的周长为。
6、某公司的拓展部有五个员工,他们每月的工资分别是3000元,4000元,5000元,7000元和10000元,那么他们工资的中位数为()A、4000元B、5000元C、7000元D、10000元答案:B考点:考查中位数的概念。
解析:数据由小到大排列,最中间或最中间的两个数的平均数为中位数,所以,中位数为5000元。
广东省深圳市2016年中考数学真题试题(含答案)

2016年广东省深圳市中考数学试卷第一部分 选择题(本部分共12小题,每小题3分,共36分。
每小题给出4个选项,其中只有一个选项是正确的) 1.下列四个数中,最小的正数是( )A .—1 B. 0 C. 1 D. 2 2.把下列图形折成一个正方体的盒子,折好后与“中”相对的字是( )A .祝 B.你 C.顺 D.利3.下列运算正确的是( )A.8a-a=8B.(-a)4=a 4C.a 3×a 2=a 6D.(a-b )2=a 2-b 24.下列图形中,是轴对称图形的是( )5.据统计,从2005年到2015年中国累积节能1570000000吨标准煤,1570000000这个数用科学计数法表示为( )A.0.157×1010B.1.57×108C.1.57×109D.15.7×1086.如图,已知a ∥b,直角三角板的直角顶点在直线b 上,若∠1=60°,则下列结论错误的是( ) A. ∠2=60° B. ∠3=60° C. ∠4=120° D. ∠5=40° 7.数学老师将全班分成7个小组开展小组合作学习,采用随机抽签法确定一个小组进行展示活动。
则第3小组被抽到的概率是( ) D.101A.71B. 31C. 2118.下列命题正确是( )A.一组对边平行,另一组对边相等的四边形是平行四边形B.两边及一角对应相等的两个三角形全等C.16的平方根是4D.一组数据2,0,1,6,6的中位数和众数分别是2和69.施工队要铺设一段全长2000米,的管道,因在中考期间需停工两天,实际每天施工需比原来计划多50米,才能按时完成任务,求原计划每天施工多少米。
设原计划每天施工x 米,则根据题意所列方程正确的是( )A.25020002000=+-x x B.22000502000=-+x x C.25020002000=--x x D.22000502000=--xx 10.给出一种运算:对于函数n x y =,规定1-=n nx y 丿。
【南方新中考】(南粤专用)2015中考数学 第一部分 数代数 第五章 第2讲 图形的相似检测复习

第2讲 图形的相似1.(2014年某某某某)若两个相似多边形的面积之比为1∶4,则它们的周长之比为( )A .1∶4B .1∶2C .2∶1D .4∶12.(2014年某某某某)如图5210,四边形ABCD 和四边形CEFG 都是正方形,点G 在线段CD 上,连接BG ,DE ,DE 和FG 相交于点O .设AB =a ,CG =b (a >b ).下列结论:①△BCG ≌△DCE ;②BG ⊥DE ;③DG GC =GO CE;④(a -b )2·S △EFO =b 2·S △DGO .其中结论正确的个数是( )A .4个B .3个C .2个D .1个图5210 图52113.(2014某某某某)如图5211,双曲线y =k x 经过Rt △BOC 斜边上的点A ,且满足AO AB=23,与BC 交于点D, S △BOD =21,则k =________. 4.(2013年某某某某)如图5212,网格图中每个方格都是边长为1的正方形.若A ,B ,C ,D ,E ,F 都是格点,试说明△ABC ∽△DEF .图52125.(2012年某某某某)如图5213,AC 是⊙O 的直径,弦BD 交AC 于点E . (1)求证:△ADE ∽△BCE ;(2)如果AD 2=AE ·AC ,求证:CD =CB .图52136.(2012年某某某某)如图5214,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,连接BE,交AD于点P.求证:(1)D是BC的中点;(2)△BEC∽△ADC;(3)AB·CE=2DP·AD.图5214A级基础题1.下列各组线段(单位:cm)中,是成比例线段的为( )A.1,2,3,4 B.1,2,2,4 C.3,5,9,13 D.1,2,2,32.(2013年)如图5215,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20 m,EC=10 m,CD=20 m,则河的宽度AB=( )A.60 m B.40 m C.30 m D.20 m图5215 图52163.(2013年某某)如图5216,已知在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD∶DB=3∶5,那么CF∶CB=( )A.5∶8 B.3∶8 C.3∶5 D.2∶54.(2014年某某)在研究相似问题时,甲、乙同学的观点如下:对于两人的观点,下列说法正确的是( )A.两人都对 B.两人都不对C.甲对,乙不对 D.甲不对,乙对5.(2013年某某某某)如图5217,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,AD=1,BC=4,则△AOD与△BOC的面积之比等于( )A.12B.14C.18D.116图5217图52186.(2013年某某威海)如图5218,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD.下列结论错误的是( )A.∠C=2∠A B.BD平分∠ABCC.S△BCD=S△BOD D.点D为线段AC的黄金分割点7.(2014年某某某某)如图5219,小明用长为3 m的竹竿CD做测量工具,测量学校旗杆AB的高度.移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点O,此时O点与竹竿的距离OD=6 m,竹竿与旗杆的距离DB=12 m,则旗杆AB的高为________m.图5219图5220图5221 8.(2014年某某某某)如图5220,在平行四边形ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,请从图中找出一组相似的三角形________.9.(2013年某某某某)如图5221,在平面直角坐标系xOy中,点A,B的坐标分别为(3,0),(2,-3),△AB′O′是△ABO关于点A的位似图形,且O′的坐标为(-1,0),则点B′的坐标为________.10.(2012年某某株洲)如图5222,在矩形ABCD中,AB=6,BC=8,沿直线MN对折,使A,C重合,直线MN交AC于点O.(1)求证:△∽△CBA;(2)求线段OM的长度.图5222B级中等题11.如图5223,大江的同一侧有A,B两个工厂,它们都有垂直于江边的小路,AD,BE的长度分别为3 km和2 km,且两条小路之间的距离为5 km.现要在江边建一个供水站向A,B两厂送水,欲使供水管路最短,则供水站应建在距E处多远的位置?图522312.(2012年某某株洲)如图5224,在△ABC 中,∠C =90°,BC =5 m ,AC =12 m .点M 在线段CA 上,从C 向A 运动,速度为1 m/s ;同时点N 在线段AB 上,从A 向B 运动,速度为2 m/s ,运动时间为t s .(1)当t 为何值时,∠AMN =∠ANM ;(2)当t 为何值时,△AMN 的面积最大,并求出这个最大值.图5224C 级 拔尖题BA =CD ,BC =20 cm ,BC ,EF 平行于地面AD 且到地面AD 的距离分别为40 cm,8 cm ,为使板凳两腿底端A ,D 之间的距离为50 cm ,那么横梁EF 应为多长(材质及其厚度等暂忽略不计)?图5225第2讲 图形的相似【真题·南粤专练】 1.B2.B 解析:①由四边形ABCD 、CEFG 都是正方形, 可得BC =DC ,CG =CE ,∠BCG =∠DCE . ∴△BCG ≌△DCE (SAS).故①正确.②如图59,延长BG 交DE 于点H ,由①,得∠CDE =∠CBG ,∠DGH =∠BGC .∴∠BCG =∠DHG =90°.故②正确.③由GF ∥CE ,可证△DGO ∽△DCE .∴DG DC =GO CE ,而不是DG GC =GO CE.故③不正确.④△EFO ∽△DGO ,S △EFO S △DGO 等于“相似比”的平方,即S △EFO S △DGO =⎝ ⎛⎭⎪⎫EF DG 2=b 2a -b2.∴(a -b )2S △EFO =b 2S △DGO .故④正确.故选B.图59 图603.8 解析:如图60,过A 作AE ⊥x 轴于点E .∵S △OAE =S △OCD ,∴S 四边形AECB=S △BOD =21.∵AE ∥BC ,∴△OAE ∽△OBC .S △OAE S △OBC =S △OAE S △OAE +S 四边形AECB =⎝ ⎛⎭⎪⎫AO OB 2=425. ∴S △OAE k =8.4.解:∵AC =2,BC =10,AB =4,DF =2 2,EF =210,DE =8,∴AC DF =BC EF =AB DE=12. ∴△ABC ∽△DEF .5.证明: (1)∵CD =CD ,∴∠A =∠B . 又∵∠CEB =∠AED ,∴△ADE ∽△BCE .图61(2)如图61,由AD 2=AE ·AC ,得AE AD =AD AC. 又∵∠A =∠A ,∴△ADE ∽△ACD . ∴∠AED =∠ADC . 又∵AC 是⊙O 的直径,∴∠ADC =90°,即有∠AED =90°. ∴直径AC ⊥BD .∴CD =BC .∴CD =CB .6.证明:(1)∵AB 是直径,∴∠ADB =90°,即AD ⊥BC . 又∵AB =AC ,∴D 是BC 的中点. (2)在△BEC 与△ADC 中, ∵∠C =∠C ,∠CAD =∠CBE ,∴△BEC ∽△ADC .(3)∵△BEC ∽△ADC ,∴AC BC =CD CE. 又∵D 是BC 的中点, ∴2BD =2CD =BC . ∴AC 2BD =BD CE.则2BD 2=AC ·CE .① 在△BPD 与△ABD 中,有∠BDP =∠BDA . 又∵AB =AC ,AD ⊥BC ,∴∠CAD =∠BAD . 又∵∠CAD =∠CBE ,∴∠DBP =∠BAD . ∴△BPD ∽△ABD .∴BD PD =AD BD.则BD 2=PD ·AD .②∴由①,②,得AC ·CE =2BD 2=2PD ·AD . ∴AB ·CE =2DP ·AD . 【演练·巩固提升】8.△DCF ∽△EBF (或△DCF ∽△EAD ,△DCF ∽△BAP ,△EAD ∽△BAP ,△BAP ∽△EBF ,△EAD ∽△EBF ,答案不唯一).9.⎝ ⎛⎭⎪⎫53,-4 10.(1)证明:∵A 与C 关于直线MN 对称, ∴AC ⊥MN .∴∠=90°.在矩形ABCD 中,∠B =90°,∴∠=∠B . 又∵∠ACB =∠MCO ,∴△∽△CBA . (2)解:∵在Rt △CBA 中,AB =6,BC =8, ∴AC =10,∴OC =5. ∵△∽△CBA ,∴OC CB =OM AB ,OM =154.11.解:如图62,作出点B 关于江边的对称点C ,连接AC ,则BF +FA =CF +FA =CA .根据两点之间线段最短可知,当供水站在点F 处时,供水管路最短.∵△ADF ∽△CEF ,∴设EF =x ,则FD =5-x . 根据相似三角形的性质,得EF FD =CE AD ,即x 5-x =23.解得x =2. 故供水站应建在距点E 2 km 处.图6212.解:(1)由题意,得AM =12-t ,AN =2t . 若∠AMN =∠ANM ,则AM =AN .从而12-t =2t .解得t =4. ∴当t 为4 s 时,∠AMN =∠ANM . (2)如图63,过点N 作NH ⊥AC 于点H ,图63∴∠NHA =∠C =90°.∵∠A 是公共角,∴△NHA ∽△BCA .∴AN AB =NH BC ,即2t 13=NH 5.∴NH =10t 13. 从而有S △AMN =12(12-t )·10t 13=-513t 2+6013t =-513(t -6)2+18013.∴当t =6 s 时,S 有最大值为18013m 2.13.解:如图64,过点C 作CM ∥AB ,交EF ,AD 于点N ,M ,作CP ⊥AD ,交EF ,AD 于点Q ,P .图64由题意,得四边形ABCM 是平行四边形, ∴EN =AM =BC =20.∴MD=AD-AM=50-20=30(cm).由题意知,CP=40,PQ=8,∴CQ=32. ∵EF∥AD,∴△F∽△CMD.∴NFMD=CQCP,即NF30=3240.解得NF=24.∴EF=EN+NF=20+24=44(cm).答:横梁EF应为44 cm.。
专题02 探索轴对称图形(解析版)
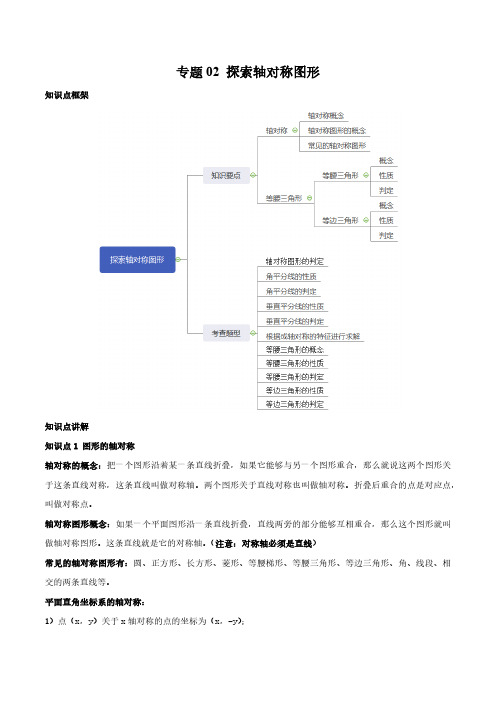
专题02 探索轴对称图形知识点框架知识点讲解知识点1 图形的轴对称轴对称的概念:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴。
两个图形关于直线对称也叫做轴对称。
折叠后重合的点是对应点,叫做对称点。
轴对称图形概念:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,那么这个图形就叫做轴对称图形。
这条直线就是它的对称轴。
(注意:对称轴必须是直线)常见的轴对称图形有:圆、正方形、长方形、菱形、等腰梯形、等腰三角形、等边三角形、角、线段、相交的两条直线等。
平面直角坐标系的轴对称:1)点(x,y)关于x轴对称的点的坐标为(x,-y);2)点(x,y)关于y轴对称的点的坐标为(-x,y);3)点(x,y)关于原点(0, 0)的对称点为(-x,-y);4)点(x,y)关于(a,b)的对称点为(2a-x,2b-y)。
知识点2垂直平分线垂直平分线的概念:经过线段的中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(或线段的中垂线)。
性质:线段的垂直平分线上的点到这条线段两个端点的距离相等;反过来,到一条线段两个端点距离相等的点在这条线段的垂直平分线上。
知识点3 线段、角的轴对称性1)线段的轴对称性:①线段是轴对称图形,对称轴有两条;一条是线段所在的直线,另一条是这条线段的垂直平分线。
②线段的垂直平分线上的点到线段两端的距离相等。
③到线段两端距离相等的点,在这条线段的垂直平分线上。
结论:线段的垂直平分线是到线段两端距离相等的点的集合2)角的轴对称性:Array①角是轴对称图形,对称轴是角平分线所在的直线。
②角平分线上的点到角的两边距离相等。
③到角的两边距离相等的点,在这个角的平分线上。
结论:角的平分线是到角的两边距离相等的点的集合知识点4 等腰三角形等腰三角形概念:有两边相等的三角形角等腰三角形。
等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角。
2016年广东省中考数学试卷(含答案解析)

绝密★启用前广东省2016年初中毕业生学业考试数 学本试卷满分120分,考试时间100分钟.第Ⅰ卷(选择题 共30分)一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.2-的相反数是( )A .2B .2-C .12D .12- 2.如图,a 与B 的大小关系是( )A .a b <B .a b >C .a b =D .2b a =3.下列所述图形中,是中心对称图形的是( )A .直角三角形B .平行四边形C .正五边形D .正三角形4.据广东省旅游局统计显示,2016年4月全省旅游住宿设施接待过夜游客约27700000人,将27700000用科学记数法表示为( ) A .70.27710⨯B .80.27710⨯ C .72.710⨯D .82.7710⨯5.如图,正方形ABCD 的面积为1,则以相邻两边中点连线EF 为边的正方形EFGH 的周长为 ( ) A .2B .22C .21+D .221+6.某公司的拓展部有五个员工,他们每月的工资分别是3000元,4000元,5000元,7000元和10000元,那么他们工资的中位数是( )A .4000元B .5000元C .7000元D .10000元 7.在平面直角坐标系中,点()2,3P --所在的象限是( )A .第一象限B .第二象限C .第三象限D .第四象限-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------________________ _____________8.如图,在平面直角坐标系中,点A 的坐标为(4,3),那么cos α的值是( )A .34 B .43 C .35D .459.已知方程238x y -+=,则整式2x y -的值 为( )A .5B .10C .12D .1510.如图,在正方形ABCD 中,点P 从点A 出发,沿着正方形的边顺时针方向运动一周,则APC △的面积y 与点P 运动的路程x 之间形成的函数关系图象大致是( )ABCD第Ⅱ卷(非选择题 共90分)二、填空题(本大题共6小题,每小题4分,共24分.把答案填写在题中的横线上) 11.9的算术平方根是 .12.分解因式:24m -= .13.不等式组122,2132x x x x --⎧⎪-⎨⎪⎩≤>的解集是 .14.如图,把一个圆锥沿母线OA 剪开,展开后得到扇形AOC ,已知圆锥的高h 为12cm ,13cm OA =,则扇形AOC 中»AC 的长是 cm (计算结果保留π).15.如图,矩形ABCD 中,对角线23AC =,E 为BC 边上一点,3BC BE =.将矩形ABCD 沿AE 所在的直线折叠,B 点恰好落在对角线AC 上的'B 处.则AB = .16.如图,点P 是四边形ABCD 外接圆O e 上任意一点,且不与四边形顶点重合.若AD 是O e 的直径,AB BC CD ==,连接PA ,PB ,PC .若PA a =,则点A 到PB 和PC 的距离之和AE AF += .三、解答题(本大题共9小题,共66分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分6分)计算:011|3|(2016sin30)()2---+--o .18.(本小题满分6分) 先化简,再求值:223626699a a a a a a +-+++-g ,其中31a =-.19.(本小题满分6分)如图,已知ABC △中,D 为AB 的中点.(1)请用尺规作图法作边AC 的中点E ,并连接DE (保留作图痕迹,不要求写作法); (2)在(1)条件下,若4DE =,求BC 的长.20.(本小题满分7分)某工程队修建一条长1200m 的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务. (1)求这个工程队原计划每天修道路多少米?(2)在这项工程中,如果要求工程队提前2天完成任务,那么实际平均每天修建道路的工效比原计划增加百分之几?21.(本小题满分7分)如图,Rt ABC △中,30B ∠=o ,90ACB ∠=o ,CD AB ⊥交AB 于点D .以CD 为较短的直角边向CDB △的同侧作Rt DEC △,满足30E ∠=o ,90DCE ∠=o ,再用同样的方法作Rt FGC △,90FCG ∠=o ,继续用同样的方法作Rt HIC △,90HCI ∠=o .若AC a =,求CI 的长.22.(本小题满分7分)某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项.为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过调查获得的数据进行整理,绘制出以下两幅不完整的统计图.请根据统计图回答问题:(1)这次活动一共调查了 名学生; (2)补全条形统计图;(3)在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于 度; (4)若该学校有1500人,请你估计该学校选择足球项目的学生人数约是 人.23.(本小题满分9分)如图,在直角坐标系中,直线1(0)y kx k =+≠与双曲线2y x=(0)x >相交于点(1,)P m . (1)求k 的值;(2)若点Q 与点P 关于直线y x =成轴对称,则点Q 的坐标是Q ( );(3)若过P ,Q 两点的抛物线与y 轴的交点为5(0,)3N ,求该抛物线的函数解析式,并求出抛物线的对称轴方程.24.(本小题满分9分)-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------如图,O e 是ABC △的外接圆,BC 是O e 的直径,30ABC ∠=o .过点B 作O e 的切线BD ,与CA 的延长线交于点D ,与半径AO 的延长线交于点E .过点A 作O e 的切线AF ,与直径BC 的延长线交于点F . (1)求证:ACF DAE △∽△; (2)若3=4AOC S △,求DE 的长; (3)连接EF ,求证:EF 是O e 的切线.25.(本小题满分9分)如图,BD 是正方形ABCD 的对角线,2BC =.边BC 在其所在的直线上平移,将通过平移得到的线段记为PQ ,连接PA ,QD ,并过点Q 作QO BD ⊥,垂足为O ,连接OA ,OP .图1图2(1)请直接写出线段BC 在平移过程中,四边形APQD 是什么四边形? (2)请判断OA ,OP 之间的数量关系和位置关系,并加以证明;(3)在平移变换过程中,设OPB y S ∆=,BP x =(02)x ≤≤,求y 与x 之间的函数关系式,并求出y 的最大值.广东省2016年初中毕业生学业考试数学答案解析第Ⅰ卷一、选择题 1.【答案】A【解析】-2的绝对值是2,故选A. 【考点】相反数 2.【答案】A【解析】数轴上从左往右的点表示的数是从小往大的顺序,由图可知b a >,选A . 【考点】数轴,会由数轴上点的位置判断相应数的大小 3.【答案】B【解析】直角三角形既不是中心对称图形也不是轴对称图形,正五边形和正三角形是轴对称图形,只有平行四边是中心对称图形.【考点】中心对称图形与轴对称图形 4.【答案】C【解析】科学记数的表示形式为10n a ⨯形式,其中1||10a ≤<,n 为整数,727 700000 2.7710⨯ =.故选C. 【考点】科学记数法 5.【答案】B【解析】连结BD ,由勾股定理,得BD =E 、F 为中点,所以,2EF =,所以,正方形EFGH的周长为【考点】三角形的中位线,勾股定理 6.【答案】B【解析】数据由小到大排列,最中间或最中间的两个数的平均数为中位数,所以,中位数为5000元. 【考点】中位数 7.【答案】C【解析】因为点P 的横坐标与纵坐标都是负数,所以,点P 在第三象限. 【考点】平面直角坐标 8.【答案】D【解析】过点A 作AB 垂直x 轴与B ,则3AB =,4OB =,由勾股定理,得5OA =,所以,4cos 5OB OA α==,选D.【考点】三角函数,勾股定理 9.【答案】A【解析】把2x y -看成一个整体,移项,得2=83=5x y --. 【考点】整体思想 10.【答案】C【解析】设正方形的边长为a ,当点P 在AB 上时,2111()222y a a a x ax =-⨯⨯-=,是一次函数,且0a >,所以,排除A 、B 、D ,选C ;当点P 在BC 、CD 、AD 上时,同理可求得是一次函数.【考点】三角形的面积,函数图象第Ⅱ卷二、填空题 11.【答案】3【解析】9的算术平方根为3,注意与平方根概念的区别. 【考点】算术平方根的概念 12.【答案】(2)(2)m m +-【解析】由平方差公式,得22242(2)(2)m m m m -=-=+- 【考点】因式分解,平方差公式 13.【答案】31x -<≤【解析】由122x x -≤-,得1x ≤,由2132x x ->,得3x >-,所以,原不等式组的解集为31x -<≤ 【考点】不等式的解法,不等式组的解法 14.【答案】10π5, 扇形的弧长=圆锥的底面圆周长=2π510π⨯= 【考点】勾股定理,圆锥的侧面展开图,弧长公式15.【解析】由折叠知,三角形ABE 与三角形'E AB 全等,所以,'AB AB =,'BE E B =,9'0A E A B BE ∠=∠=︒,又3BC BE =,有2EC BE =,所以,'2EC E B =,所以,30ACE ∠=︒,60?BAC ∠=,又由折叠知30'AE B B AE ∠=∠=︒,所以,30EAC ECA ∠=∠=︒,所以,EA EC =,又9'0A E B ∠=︒,由等腰三角形性质,知'B 为AC 中点,所以,12B AC AB A '===【考点】三角形的全等的性质,等腰三角形的判定与性质16.【答案】12a 【解析】连结OB 、OC ,因为AB BC CD ==,所以,弧AB 、弧BC 、弧CD 相等,所以,60AOC BOC COD ∠=∠=∠=︒,所以,30CPB APB ∠=∠=︒,所以,1122AE PA a ==,60APC ∠=︒,在直角三角形APF 中,可求得AF =所以,E A AF =+【考点】三角函数,圆的性质定理 三、解答题 17.【答案】4【解析】3124=-+=原式 【考点】实数运算 18.1 【解析】原式=()()()()22336333a a a a a a -+++-+g ()()6233aa a a a =+++2(a 3)(a 3)2a a +=+=当1a =时, 原式1=.【考点】分式的化简与求值 19.【答案】(1)如图DE 即为所求.(2)由三角形中位线定理,知:28BC DE == 【考点】尺规作图,三角形的中位线定理 20.【答案】100米【解析】设(1)这个工程队原计划每天修建道路x 米,得:120012004(150%)x x=++,解得100x = 经检验,100x =是原方程的解答:这个工程队原计划每天修建100米. 【考点】列方程解应用题,分式方程 21.【答案】98a【解析】由题意,知60A EDC GFC IHC ∠=∠=∠=∠=o ,因为AC a =,故sin60DC AC =︒=,同理3sin604CF DC a =︒=,sin60CH CF =︒=,9sin608CI CH a =︒=【考点】三角形的内角和,三角函数的应用 22.【答案】(1)由题意8025032%=人,总共有250名学生. (2)篮球人数25080405575---=人,作图如下(3)依题意得75360108250⨯︒=︒ (4)依题意得15000.32480⨯=(人) 【考点】条形统计图,扇形统计图,统计知识 23.【答案】(1)把P (1,m )代入2y x=,得2m =, ∴P (1,2)把(1,2)代入1y kx =+,得1k =. (2)(2,1)(3)设抛物线的解析式为2y ax bx c =++,得2421421a b c a b c a b c ++=⎧⎪++=⎨⎪++=⎩,解得23a =-,1b =,53c = ∴22533y x x =-++, ∴对称轴方程为23132x =÷=.11 / 13【考点】一次函数,反比例函数,二次函数24.【答案】(1)∵BC 为⊙O 的直径,∴90BAC ∠=︒又30ABC ∠=︒,∴60ACB ∠=︒,又OA OC =,∴△OAC 为等边三角形,即60OAC AOC ∠=∠=︒,∵AF 为⊙O 的切线,∴90OAF ∠=︒,∴30CAF AFC ∠=∠=︒,∵DE 为⊙O 的切线,∴90DBC OBE ∠=∠=︒,∴30D DEA ∠=∠=︒,∴D CAF ∠=∠,DEA AFC ∠=∠,∴ACF DAE △∽△;(2)∵△AOC 为等边三角形,∴2AOC S =△, ∴1OA =,∴2BC =,1OB =,又30D BEO ∠=∠=︒,∴BD =,BE =∴DE =(3)如图,过O 作OM ⊥EF 于M ,∵OA OB =,90OAF OBE ∠=∠=︒,BOE AOF ∠=∠,∴OAF OBE △≌△,∴OE OF =,∵120EOF ∠=︒,∴30OEM OFM ∠=∠=︒,∴30OEB OEM ∠=∠=︒,即OE 平分BEF ∠,又90OBE OME ∠=∠=︒,∴OM OB =,12 / 13 ∴EF 为⊙O 的切线.【考点】三角形的相似,三角形的全等,圆的切线的性质与判定定理,三角形的面积公式25.【答案】(1)四边形APQD 为平行四边形;(2)OA OP =,OA ⊥OP ,理由如下:∵四边形ABCD 是正方形,∴AB BC PQ ==,45ABO OBQ ∠=∠=︒,∵OQ ⊥BD ,∴45PQO ∠=︒,∴45ABO OBQ PQO ∠=∠=∠=︒,∴OB OQ =,∴AOB OPQ △≌△,∴OA OP =,AOB POQ ∠=∠∴90AOP BOQ ∠=∠=︒,∴OA ⊥OP ;(3)如图,过O 作OE ⊥BC 于E①如图1,当点P 在点B 右侧时,则2BQ x =+,22x OE +=, ∴1222x y x +=⨯⨯,即()211144y x =+-,又∵02x ≤≤,∴当2x =时,y 有最大值为2;②如图2,当点P 在B 点左侧时,则2BQ x =-,22xOE -=, ∴1222xy x -=⨯⨯,即()211144y x =--+,又∵02x ≤≤,∴当1x =时,y 有最大值为14;综上所述,∴当2x =时,y 有最大值为2;【考点】特殊四边形的判定与性质,三角形的全等,二次函数13/ 13。
2016年广东省中考数学试题(含答案)

机幣*启用前2016年广东省初中毕业生学业考试数学说明:1•全卷共4页,满分为120分,若试用时为100分钟.2-答卷前,希生务必用黑色字迹的鳖字笔或钢笔在答题卡填写自己的准考证号、姓 名、考场号、座位号.用2B 铅笔把对应该号码的标号涂然” 3+选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂 黑,如需改动,用橡皮擦干净后,再选涂苴他答案,答案不能答在试题上.4- 非选择题必须用黑色字迹钢笔或签字笔作答、答案必须写在答题卡各题目指定区 域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使 用铅笔和涂改液.不按以上要求作答的答案无效.5- 考生务必保持答题卡的整洁.考试结束时,将试卷和答题卡一并交回.一、选择题(本大题10小题,每小题3分■拄30分)在毎小题列出的四个选项中,只有一个是正确的,请把答题咔上对应题目所选的选项涂專. 1. -2的相反数是 A. 2-2C 丄22. 如题2图所示工与启的大小关系是A. a < bB. a > bC. a — bD. b = 2a3. 下列所述图形中,是中心对称图形的是 A.直角三甬形 B.平行四边形 G 正五边形4.据广东省旅游局统计显示*2016年4月全省旅游住猪设施接待过夜游客约27 700 000人,将27 700 000用科学记数法表示为 A. 0. 277 x ID 7 B. 0+277 x 10BU 2. 77 x 1075. 如题5图,正方形初CD 的面积为!,则以相邻两边中点连线EF 为 边的正方形EFCH 的周快为 扎72 B. 2血 匚血十1 II 2^/2 + 1 6-某公司的拓展部有五个员工,他们每月的工资分别是3000元’ 4000元2000元,7000元和10000元,那么他们工资的中位数是 A. 4000 元 B. 5000 元 C. 7000 元 0 10000 元 7・在平面直角坐标系中,点P ( -2,-3)所在的象限是九第煥限&第二象限C 第三象限D.第四象限D.•I I|]0 0 b题2图D.正三角形题5图数学试题第1页(共4页》8-如题8图,在平面直角坐标系中,点A 的坐标为(4,3)t 那么COSOf 的值是鱼已知方程X - 2y + 3 = 8,则整式x-2y 的值为A. 5 B* 10 C. 12二、填空题(本大题召小题,毎小题4分,共24分)请将下列各题的正确答案填写在答题卡相应 的位置上.11. 9的算术平方根是 12. 分解因式:亦-4 = _______ +X — 1 C 2 - 2x, 2x 口的解集是_*T >14,如题14图,把一个圆锥沿母线0A 剪开,展开后得到扇形AOC,已知圆锥的髙h 为12cm, 0A = I3cm t则扇形AOf 中紀 的长是 _______________ 吋(计算结果保留"15.如题15图,矩形ABCD .对角线AC 二込E 为BC 边上一点上C = 3RE.将矩形ABCD 沿 AE 所在的直线折叠上点恰好落在对角线AC 上的訓处.则— +16”如题16图,点P 是四边形ABCD 外接圆00上任意一点’且不与四边形顶点重合.若AD 是 O0的直径,AB = RC = CD,连接PAH,PG 若PA 则点*到PB 和PC 的距离之和 AE + AF = *{D. 1510如题10图,在正方形ABCD 中,点P 从点M 出发,沿着正方形的边顺时针方向运动一周,则 △APC的面积y 与点P 运动的路程弟之间形成的函数关系图象大致是题10图 AB C D题16图三、解答题(一)(本大题3小题,每小题6分,共18分) 17,计算:|-3|- (2016 + sin30°)°(2) 补全条形统计图;(3) _______________________________________________________ 在扇形统计图中,选择篮球项目的人数所在扇形的圖心角等于 _____________________________ ___ # ;(4) 若该学校有1500人,请你估计该学校选择足球项目的学生人数约是 _________ 人•数学试题第3页(共4页)先化简,再求值:心 a6 a 1+ 6a + 9琴二吕其中“冷-1.a * 919.如题19图,已知△ARC 中Q 为AB 的中点.(1) 请用尺规作图法作边AC 的中点&并连结DE (保留作图痕 迹,不要求写作法);(2) 在(1)的条件下,若DE = 4,求目的长• 四、解答题(二)(本大题3小题,每小题7分,共21分) 26某工程队修成任务+(1) 求这个工程队原计划每天修建道路多少米?(2) 在这项工程中,如果要求工程队提前2天完成任务,那么实 际平均每天修建道路的工效比原计划增加百分之几?21. 如题 21 图.Ri^ABC 中,乙B = 30% LACB = 90%C5 丄 AH 交A 召于D.以CD 为较短的直角边向ACDB 的同侧作 Rt^DEC,満足二30°,^DCE= 90S 再用同样的方法作 RthFGC, LFCG = 90\继续用同样的方法作R 仏H1C 、 LHCI = 90°.若皿二a,求C7的长.22. 某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项+为了解选择各种体育活动项目的学生人数,随机 抽取了部分学生进行调查,并将通过调査获得的数据进行整理,绘制出以下两幅不完整的 统计图+请棍据统计图回答问题:各项目人数扇形统计图五、解答题(三)(本大题3小题,每小题9分,共27分) 23. 如题23图’在直角坐标系中,直线y 二滋十1(去护0)与双2曲线—(实> 0)相交于点P (1N )・ (1) 求A 的值;(2) 若点Q 与点P 关于直线y 二X 成轴对称,则点Q 的坐标是 Q( _______ );(3) 若过P 、Q 二点的抛物线与y 轴的交点为N(0,*),求该 抛物线的函数解析式,并求出抛物线的对称轴方程■24■如题24图QO 是△ARC 的外接圆,叱是OO 的直径,^ABC = 30°.过点R 作。
【南方新中考】(南粤专用)2015中考数学+第一部分+第五章+第2讲+图形的相似复习课件
)
图 5-2-9
1 A.6
1 B.3
1 C.2
2 D.3
解析:∵O′是正方形 ABCD 的对角线 AC 的中点,AC= 3 2,∴A(0,3),O′(1.5,1.5). 2 ∵A′(1,2),∴O′A= 2 ,AA′= 2,O′A′= 2 . O′A′ 1 ∴k= =3.故选 B. O′A
答案:B
∴∠DAC =∠ECA.∴CE∥AD.
(3)∵CE∥AD,∴∠DAF =∠ECF,∠ADF =∠CEF.
AD AF ∴△AFD∽△CFE.∴ = . CE CF
1 ∵CE=2AB=3,AD=4, 4 AF AF 4 AC 7 得3=CF.∴AC=7.∴AF =4.
名师点评:(1)相似的判定方法可类比全等三角形的判定方
=36°,AB=AC,当点 P 在 AC 的垂直平分线上时,过点 P 的
△ABC 的相似线最多有______ 3 条.
图 5-2-2
4.高 6 m 的旗杆在水平地面上的影子长为 4 m,同一时刻 30 附近有一建筑物的影子长为 20 m,则该建筑物的高为______m. 5.在△ABC 中,D,E 分别是边AB 与AC 的中点,BC=4, 下列四个结论:①DE=2;②△ADE∽△ABC;③△ADE 的面 积与△ABC 的面积之比为 1∶4;④△ADE 的周长与△ABC 的
法,找对应边(角)时应遵循一定的对应原则,如长(大)对长(大),
短(小)对短(小),或找相等的角(边)帮助确定. (2)证明等积式的方法是:先把等积式化成等比式,再利用 对应线段找相似三角形,应用相似三角形的对应边成比例;若 边不全在两个三角形中,则要通过线段相等转化,达到证明线 段成比例的目的.
相似三角形的性质及综合应用
2016年广东省中考数学试卷(附答案解析)
数学试卷第2页(共14页)绝密★启用前广东省2016年初中毕业生学业考试数学本试卷满分120分,考试时间100分钟.第Ⅰ卷(选择题共30分)一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.2-的相反数是 ()A.2B.2-C.12D.12-2.如图,a与B的大小关系是 ()A.a b<B.a b>C.a b=D.2b a=3.下列所述图形中,是中心对称图形的是 ()A.直角三角形B.平行四边形C.正五边形D.正三角形4.据广东省旅游局统计显示,2016年4月全省旅游住宿设施接待过夜游客约27700000人,将27700000用科学记数法表示为 ()A.70.27710⨯B.80.27710⨯C.72.710⨯D.82.7710⨯5.如图,正方形ABCD的面积为1,则以相邻两边中点连线EF为边的正方形EFGH的周长为( )A.2B.22C.21+D.221+6.某公司的拓展部有五个员工,他们每月的工资分别是3000元,4000元,5000元,7000元和10000元,那么他们工资的中位数是 ()A.4000元B.5000元C.7000元D.10000元7.在平面直角坐标系中,点()2,3P--所在的象限是 ()A.第一象限B.第二象限C.第三象限D.第四象限8.如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是 ()A.34B.43C.35D.459.已知方程238x y-+=,则整式2x y-的值为( )A.5B.10C.12D.1510.如图,在正方形ABCD中,点P从点A出发,沿着正方形的边顺时针方向运动一周,则APC△的面积y与点P运动的路程x之间形成的函数关系图象大致是 ( )A BC D第Ⅱ卷(非选择题共90分)二、填空题(本大题共6小题,每小题4分,共24分.把答案填写在题中的横线上)11.9的算术平方根是.12.分解因式:24m-=.13.不等式组122,2132x xx x--⎧⎪-⎨⎪⎩≤>的解集是.14.如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,13cmOA=,则扇形AOC中»AC的长是cm(计算结果保留π).毕业学校_____________姓名________________考生号_____________________________________________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷第1页(共14页)数学试卷 第3页(共14页)数学试卷 第4页(共14页)15.如图,矩形ABCD 中,对角线23AC =,E 为BC 边上一点,3BC BE =.将矩形ABCD 沿AE 所在的直线折叠,B 点恰好落在对角线AC 上的'B 处.则AB = .16.如图,点P 是四边形ABCD 外接圆O e 上任意一点,且不与四边形顶点重合.若AD 是O e 的直径,AB BC CD ==,连接PA ,PB ,PC .若PA a =,则点A 到PB 和PC 的距离之和AE AF += .三、解答题(本大题共9小题,共66分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分6分)计算:011|3|(2016sin30)()2---+--o .18.(本小题满分6分) 先化简,再求值:223626699a a a a a a +-+++-g ,其中31a =-.19.(本小题满分6分)如图,已知ABC △中,D 为AB 的中点.(1)请用尺规作图法作边AC 的中点E ,并连接DE (保留作图痕迹,不要求写作法);(2)在(1)条件下,若4DE =,求BC 的长.20.(本小题满分7分)某工程队修建一条长1200m 的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务.(1)求这个工程队原计划每天修道路多少米?(2)在这项工程中,如果要求工程队提前2天完成任务,那么实际平均每天修建道路的工效比原计划增加百分之几?21.(本小题满分7分)如图,Rt ABC △中,30B ∠=o ,90ACB ∠=o ,CD AB ⊥交AB 于点D .以CD 为较短的直角边向CDB △的同侧作Rt DEC △,满足30E ∠=o ,90DCE ∠=o ,再用同样的方法作Rt FGC △,90FCG ∠=o ,继续用同样的方法作Rt HIC △,90HCI ∠=o .若AC a =,求CI 的长.22.(本小题满分7分)某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项.为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过调查获得的数据进行整理,绘制出以下两幅不完整的统计图.请根据统计图回答问题:数学试卷 第5页(共14页)数学试卷 第6页(共14页)(1)这次活动一共调查了 名学生;(2)补全条形统计图;(3)在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于 度; (4)若该学校有1500人,请你估计该学校选择足球项目的学生人数约是 人.23.(本小题满分9分)如图,在直角坐标系中,直线1(0)y kx k =+≠与双曲线2y x=(0)x >相交于点(1,)P m . (1)求k 的值;(2)若点Q 与点P 关于直线y x =成轴对称,则点Q 的坐标是Q ( ); (3)若过P ,Q 两点的抛物线与y 轴的交点为5(0,)3N ,求该抛物线的函数解析式,并求出抛物线的对称轴方程.24.(本小题满分9分)如图,O e 是ABC △的外接圆,BC 是O e 的直径,30ABC ∠=o .过点B 作O e 的切线BD ,与CA 的延长线交于点D ,与半径AO 的延长线交于点E .过点A 作O e 的切线AF ,与直径BC 的延长线交于点F . (1)求证:ACF DAE △∽△;(2)若3=AOC S △,求DE 的长; (3)连接EF ,求证:EF 是O e 的切线.25.(本小题满分9分)如图,BD 是正方形ABCD 的对角线,2BC =.边BC 在其所在的直线上平移,将通过平移得到的线段记为PQ ,连接PA ,QD ,并过点Q 作QO BD ⊥,垂足为O ,连接OA ,OP .图1图2(1)请直接写出线段BC 在平移过程中,四边形APQD 是什么四边形? (2)请判断OA ,OP 之间的数量关系和位置关系,并加以证明;(3)在平移变换过程中,设OPB y S ∆=,BP x =(02)x ≤≤,求y 与x 之间的函数关系式,并求出y 的最大值.广东省2016年初中毕业生学业考试毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第7页(共14页) 数学试卷 第8页(共14页)数学答案解析第Ⅰ卷一、选择题 1.【答案】A【解析】-2的绝对值是2,故选A. 【考点】相反数 2.【答案】A【解析】数轴上从左往右的点表示的数是从小往大的顺序,由图可知b a >,选A . 【考点】数轴,会由数轴上点的位置判断相应数的大小 3.【答案】B【解析】直角三角形既不是中心对称图形也不是轴对称图形,正五边形和正三角形是轴对称图形,只有平行四边是中心对称图形. 【考点】中心对称图形与轴对称图形 4.【答案】C【解析】科学记数的表示形式为10na ⨯形式,其中1||10a ≤<,n 为整数,727 700000 2.7710⨯ =.故选C.【考点】科学记数法 5.【答案】B【解析】连结BD,由勾股定理,得BD =E 、F为中点,所以,EF =所以,正方形EFGH的周长为 【考点】三角形的中位线,勾股定理 6.【答案】B【解析】数据由小到大排列,最中间或最中间的两个数的平均数为中位数,所以,中位数为5000元. 【考点】中位数 7.【答案】C【解析】因为点P 的横坐标与纵坐标都是负数,所以,点P 在第三象限.【考点】平面直角坐标 8.【答案】D【解析】过点A 作AB 垂直x 轴与B ,则3AB =,4OB =,由勾股定理,得5OA =,所以,4cos 5OB OA α==,选D. 【考点】三角函数,勾股定理 9.【答案】A【解析】把2x y -看成一个整体,移项,得2=83=5x y --. 【考点】整体思想 10.【答案】C【解析】设正方形的边长为a ,当点P 在AB 上时,2111()222y a a a x ax =-⨯⨯-=,是一次函数,且0a >,所以,排除A 、B 、D ,选C ;当点P 在BC 、CD 、AD 上时,同理可求得是一次函数. 【考点】三角形的面积,函数图象第Ⅱ卷二、填空题 11.【答案】3【解析】9的算术平方根为3,注意与平方根概念的区别. 【考点】算术平方根的概念 12.【答案】(2)(2)m m +-【解析】由平方差公式,得22242(2)(2)m m m m -=-=+- 【考点】因式分解,平方差公式 13.【答案】31x -<≤【解析】由122x x -≤-,得1x ≤,由2132x x ->,得3x >-,所以,原不等式组的解集为31x -<≤【考点】不等式的解法,不等式组的解法 14.【答案】10π数学试卷 第9页(共14页) 数学试卷 第10页(共14页)5=, 扇形的弧长=圆锥的底面圆周长=2π510π⨯= 【考点】勾股定理,圆锥的侧面展开图,弧长公式 15.【解析】由折叠知,三角形ABE 与三角形'E AB 全等,所以,'AB AB =,'BE E B =,9'0A E A B BE ∠=∠=︒,又3BC BE =,有2EC BE =,所以,'2EC E B =,所以,30ACE ∠=︒,60?BAC ∠=,又由折叠知30'AE B B AE ∠=∠=︒,所以,30EAC ECA ∠=∠=︒,所以,EA EC =,又9'0A E B ∠=︒,由等腰三角形性质,知'B 为AC中点,所以,12B AC AB A '=== 【考点】三角形的全等的性质,等腰三角形的判定与性质 16.【解析】连结OB 、OC ,因为AB BC CD ==,所以,弧AB 、弧BC 、弧CD 相等,所以,60AOC BOC COD ∠=∠=∠=︒,所以,30CPB APB ∠=∠=︒,所以,112AE PA a ==,60APC ∠=︒,在直角三角形APF 中,可求得AF =所以,EA AF =+【考点】三角函数,圆的性质定理 三、解答题 17.【答案】4【解析】3124=-+=原式 【考点】实数运算 18.1 【解析】原式=()()()()22336333a a a a a a -+++-+g ()()6233aa a a a =+++2(a 3)(a3)2a a +=+=当1a =时,原式1=.【考点】分式的化简与求值 19.【答案】(1)如图DE 即为所求.(2)由三角形中位线定理,知:28BC DE == 【考点】尺规作图,三角形的中位线定理 20.【答案】100米【解析】设(1)这个工程队原计划每天修建道路x 米,得: 120012004(150%)x x =++,解得100x = 经检验,100x =是原方程的解 答:这个工程队原计划每天修建100米. 【考点】列方程解应用题,分式方程 21.【答案】98a【解析】由题意,知60A EDC GFC IHC ∠=∠=∠=∠=o ,因为AC a =,故sin60DC AC =︒=,同理3sin604CF DC a =︒=,sin60CH CF =︒=,9sin608CI CH a =︒=【考点】三角形的内角和,三角函数的应用数学试卷 第11页(共14页) 数学试卷 第12页(共14页)22.【答案】(1)由题意8025032%=人,总共有250名学生. (2)篮球人数25080405575---=人,作图如下(3)依题意得75360108250⨯︒=︒(4)依题意得15000.32480⨯=(人) 【考点】条形统计图,扇形统计图,统计知识23.【答案】(1)把P (1,m )代入2y x=,得2m =,∴P (1,2)把(1,2)代入1y kx =+,得1k =. (2)(2,1)(3)设抛物线的解析式为2y ax bx c =++,得2421421a b c a b c a b c ++=⎧⎪++=⎨⎪++=⎩,解得23a =-,1b =,53c =∴22533y x x =-++, ∴对称轴方程为23132x =÷=.【考点】一次函数,反比例函数,二次函数24.【答案】(1)∵BC 为⊙O 的直径,∴90BAC ∠=︒ 又30ABC ∠=︒, ∴60ACB ∠=︒, 又OA OC =,∴△OAC 为等边三角形,即60OAC AOC ∠=∠=︒, ∵AF 为⊙O 的切线, ∴90OAF ∠=︒, ∴30CAF AFC ∠=∠=︒, ∵DE 为⊙O 的切线, ∴90DBC OBE ∠=∠=︒, ∴30D DEA ∠=∠=︒,∴D CAF ∠=∠,DEA AFC ∠=∠,∴ACF DAE △∽△;(2)∵△AOC 为等边三角形,∴2AOC S =△, ∴1OA =,∴2BC =,1OB =, 又30D BEO ∠=∠=︒,∴BD =,BE =∴DE =(3)如图,过O 作OM ⊥EF 于M ,∵OA OB =,90OAF OBE ∠=∠=︒,BOE AOF ∠=∠, ∴OAF OBE △≌△, ∴OE OF =, ∵120EOF ∠=︒,∴30OEM OFM ∠=∠=︒,∴30OEB OEM ∠=∠=︒,即OE 平分BEF ∠, 又90OBE OME ∠=∠=︒, ∴OM OB =, ∴EF 为⊙O 的切线.【考点】三角形的相似,三角形的全等,圆的切线的性质与判定定理,三角形的面积公数学试卷 第13页(共14页) 数学试卷 第14页(共14页)式25.【答案】(1)四边形APQD 为平行四边形; (2)OA OP =,OA ⊥OP ,理由如下: ∵四边形ABCD 是正方形,∴AB BC PQ ==,45ABO OBQ ∠=∠=︒, ∵OQ ⊥BD , ∴45PQO ∠=︒,∴45ABO OBQ PQO ∠=∠=∠=︒, ∴OB OQ =, ∴AOB OPQ △≌△, ∴OA OP =,AOB POQ ∠=∠ ∴90AOP BOQ ∠=∠=︒, ∴OA ⊥OP ;(3)如图,过O 作OE ⊥BC 于E ①如图1,当点P 在点B 右侧时,则2BQ x =+,22x OE +=, ∴1222x y x +=⨯⨯,即()211144y x =+-,又∵02x ≤≤,∴当2x =时,y 有最大值为2; ②如图2,当点P 在B 点左侧时,则2BQ x =-,22xOE -=, ∴1222x y x -=⨯⨯,即()211144y x =--+,又∵02x ≤≤,∴当1x =时,y 有最大值为14; 综上所述,∴当2x =时,y 有最大值为2;【考点】特殊四边形的判定与性质,三角形的全等,二次函数。
【中考易】广东省2016中考数学总复习 第五章 四边形 第25课时 正方形课件
考点四: 正方形的判定
7.(1)有一组邻边相等的矩形是正方形. (2)有一个角是直角的菱形是正方形. 温馨提示: 矩形、菱形、正方形都是平行四边形, 且是特殊的平行四边形.矩形是有一内角为直角的 平行四边形,菱形是有一组邻边相等的平行四边形; 正方形既是有一组邻边相等的矩形,又是有一内角 为直角的菱形.
.有一组邻边相等的矩形是正方形.
考点二: 正方形的性质
2.正方形对边平行;
3.正方形四边相等;
4.正方形四个角都是直角;
5.正方形对角线相等,互相垂直且互相平分,每条对
角 线平分 一组对角.
考点三: 正方形是对称图形
6.正方形既是轴对称图形也是中心对称图形,对称 轴有4条,对称中心是对角线的交点.
【南方新中考】(南粤专用)2015中考数学+第一部分+第四章+第3讲+第2课时+特殊的平行四边形复习课件
1 1 解析:∵四边形 ABCD 是菱形,∴AO=2AC,BO=2BD, AC⊥BD.∴AO∶BO=AC∶BD=1∶2.∵菱形 ABCD 的周长为 8 5,∴AB=2 5k=2 5.设 AO=k,BO=2k,则 AB= k2+2k2=
5.∴k=2.∴AO=2,BO=4.∴菱形 ABCD 的面积 S=
又∵EF⊥AD,∴平行四边形 AEDF 为菱形.
名师点评:菱形的性质可以用于证明线段相等、角相等、
直线平行、垂直等,常与三角形全等、勾股定理、方程相结合
进行相关问题的计算与证明.
矩形的性质与判定 3.(2014 年福建厦门翔安)如图 4-3-28,在 Rt△ABC 中, ∠C=90°,AC=3,BC=4,P 为 AB 边上(不与 A,B 重合)的
为半径画弧,两弧相交于点 D,连接 DE,DF.
(1)请你判断所画四边形的形状,并说明理由; (2)连接 EF,若 AE=8,∠A=60°,求线段 EF 的长.
图 4-3-25
解:(1) 四边形 AEDF 为菱形. 理由:由尺规作图的过程可知,AE=AF=ED=DF. (2)连接 EF.∵AE=AF,∠A=60°,
A.对角线相等
B.对角线互相平分
C.对角线平分一组对角
D.对角线互相垂直
2.如图 4-3-22,在矩形 ABCD 中,对角线 AC,BD 相交于
点 O.若∠AOB=60°,AB=4 cm,则 AC 的长为( B )
图 4-3-22 A.4 cm B.8 cm C.12 cm D. 4 5 cm
3.如图 4-3-23,两个完全相同的三角尺 ABC 和 DEF 在直
考点 2 特殊平行四边形之间的关系及相互转化 如图 4-3-21.
图 4-3-21
