巧借Excel在AutoCAD中设计凸轮轮廓曲线
机械设计-凸轮轮廓曲线的设计

4.对心直动尖端从动件盘形凸轮轮廓设计 -ω 对心直动尖顶推杆凸轮机构中,已知凸轮的基圆半径r0,角速
度ω和推杆的运动规律,设计该凸轮轮廓曲线。
8’ 9’
ω
7’
11’
5’ 3’
1’
12’
13’ 14’
12345678 9 11 13 15
凸轮轮廓线的设计
凸轮轮廓曲线的设计
1 凸轮轮廓曲线的设计 2 凸轮机构设计中的几个问题
一、凸轮轮廓曲线的设计
1.设计方法 (1)图解法:直观,简单;但误差大,效率低,适用于不重要
的凸轮。 (2)解析法:精确,高效,可直接用于数控加工编程,适用于
高速和高精度凸轮。
2.反转法作图的原理 假设在整个机构上加上一个与凸轮角速度大小相等、 方向相反
7’
11’
5’ 3’
1’
12’
13’ 14’
1 3 5 7 8 9 11 13 15
设计步骤:
①选比例尺μl作基圆r0。 ②反向等分各运动角。原则是:陡密缓疏。 ③确定反转后,从动件滚子中心在各等份点的位置。
④将各中心点连接成一条光滑曲线。 ⑤作各位置滚子圆的内(外)包络线(中心轨迹的等距曲线)。
ω ω
压力角许用值
αmax≤[α]
推程: 移动从动件 [α] =30°, (当载荷小时 [α]=45°); 摆动从动件 [α] = 45°。 回程: 通常取[α] ≤ 70°~80°。
最大压力角可测量或计算确定。
用角度尺测量压力角
3、凸轮基圆半径的确定
➢ 基圆半径越小,凸轮的外廓尺寸越小。 ➢ 基圆半径越小,凸轮理论廓线的最小曲率半径越小,滚子凸轮的实际轮廓容易变
AutoCAD在凸轮轮廓曲线设计中的应用

AutoCAD在凸轮轮廓曲线设计中的应用
丁守宝
【期刊名称】《《CAD/CAM与制造业信息化》》
【年(卷),期】2001(000)007
【总页数】3页(P49-51)
【作者】丁守宝
【作者单位】
【正文语种】中文
【中图分类】TP3
【相关文献】
1.AutoCADVBA技术在凸轮轮廓设计中的应用 [J], 张斌
2.CAD方法在凸轮轮廓曲线设计中的应用 [J], 周家泽
3.技术研究与应用:CAD方法在凸轮轮廓曲线设计中的应用 [J], 周家泽
4.电子计算机在机械设计中的应用一例——盘形凸轮轮廓曲线设计 [J], 龙吟
5.计算机辅助设计在凸轮轮廓曲线设计中的应用 [J], 何风梅;刘元林;麻晓红
因版权原因,仅展示原文概要,查看原文内容请购买。
用仿真生成凸轮轮廓线的步骤

用仿真生成凸轮轮廓线的步骤一、引言凸轮是机械传动中常用的一种元件,用于控制机械运动。
通过凸轮的运动,可以实现对其他机械元件的运动轨迹和速度的控制。
为了设计和制造高效可靠的凸轮,需要对凸轮的轮廓线进行仿真和优化。
本文将介绍使用仿真方法生成凸轮轮廓线的步骤。
二、建立凸轮模型需要在计算机软件中建立凸轮的三维模型。
可以使用CAD软件或者仿真软件来完成这一步骤。
在建立凸轮模型时,需要考虑凸轮的形状、轴向和径向尺寸以及凸轮上的凸起部分。
三、确定凸轮运动规律凸轮的轮廓线是根据凸轮的运动规律来确定的。
凸轮运动规律可以通过数学方法建立,也可以通过运动学仿真来确定。
在确定凸轮运动规律时,需要考虑凸轮的转动角度和运动速度。
四、进行凸轮仿真在进行凸轮仿真之前,需要确定仿真软件和仿真参数。
常用的凸轮仿真软件有ADAMS、CATIA、SolidWorks等。
在进行凸轮仿真时,需要输入凸轮模型和凸轮运动规律,并设置仿真参数,如仿真时间、时间步长等。
然后,通过仿真软件进行凸轮的运动仿真,得到凸轮的轨迹数据。
五、生成凸轮轮廓线通过凸轮仿真得到的凸轮轨迹数据,可以用来生成凸轮的轮廓线。
常用的方法有两种:一种是将凸轮轨迹数据导入CAD软件中,然后根据轨迹数据绘制凸轮轮廓线;另一种是使用数学方法,根据凸轮运动规律和凸轮轨迹数据,通过插值和拟合等方法生成凸轮轮廓线。
六、优化凸轮轮廓线生成凸轮轮廓线后,还可以对凸轮轮廓线进行优化。
通过调整凸轮轮廓线的形状和尺寸,可以改变凸轮的运动规律和运动速度,从而满足实际需求。
常用的优化方法有形状优化和参数优化。
形状优化是通过改变凸轮的形状来优化凸轮的运动规律;参数优化是通过改变凸轮的尺寸和凸起部分的位置来优化凸轮的运动速度。
七、验证凸轮轮廓线在生成和优化凸轮轮廓线之后,需要对其进行验证。
可以通过数学方法和实验方法进行验证。
数学方法是通过计算凸轮轮廓线的数学模型来验证凸轮的运动规律和运动速度;实验方法是通过实际的凸轮测试来验证凸轮的运动轨迹和速度。
摆动从动件盘形凸轮轮廓曲线的精确绘制

I l
冀 ;
^
睁
窖
黟
;p ; 錾
0
引
l 毫 8i
I | l釜
臻
,
3u 35 so 2 . 奠 ; 34
—
驴 Biblioteka i r 6 善 l 3 s 2 味 9 I 6 彳 1 5 婚。 3 i
0.s拳三3 摹球.3转 0 3嚣 = } 篁。 譬 .g06 王 蟮
21 0 1年 2月
十 堰 职 业 技 术 学 院 学 报
J u n lo hy n Te h ia n tt t o r a fS ia c n c lI s iu e
Fe ., 0l b 2 J
第 2 4卷 第 l 期
V0. N0 1 24 .1
摆 动 从 动 件 盘 形 凸 轮 轮 廓 曲线 的精 确 绘 制
鲁 春发
(十堰 职业 技术 学 院 图文信息 中心 ,湖北 十 堰 4 2 0 4 0 0)
[ 摘
要] 通过 对摆 动从 动件 凸轮 轮 廓 曲线 的 几何 分析 , 用 办公 软 件 Exe 准确 计 算 出轮 廓 运 cl
曲线上 各点 的 坐标后 用 Wo d或 C r AD精 确地 绘制 出摆动 从 动件 凸轮机 构 中凸轮 的轮 廓 曲线 。
利 — 3 用 Wod精 确 绘 制 摆 动 从 动 件 盘 形 凸轮 绘制 出尖顶 从动 件 盘 形 凸轮 轮廓 曲线 后 , 用 Au r tC o AD软 件中 的偏 移工具 进行 绘制 , 方法是 : 机构 凸轮 的 轮 廓 曲 线 ( ) 人“ 移” 1输 偏 命令 ; 用 E cl x e 中插 入 图表 的功 能 插 入 以 F列 为数 据 ( ) 出 偏 移 的 距 离 ( 滚 子 的 半 径 ); 2给 即 源 的雷达 图 , 除 不 必 要 的线 后 选 中该 图点 击 “ 清 复 () 3 选择 要偏 移的实 体 ( 即尖 顶从 动件 盘形 凸轮 制” 然后 在 Wo d中 “ , r 粘贴 ” 图 , 准 确地 得 到 了 此 即 轮 廓 曲 线 ) ; 凸轮 的轮 廓 曲线 如 图 3所示 。 ( ) 定偏移 的方位 ( 鼠标 点击尖 顶从 动件 盘 4指 用 形 凸轮轮 廓 曲线 的 内 侧 即 可) 。此 时 C AD 就 自动 绘 出了滚 子从 动件 盘形 凸轮 的轮 廓 曲线 。
基于AutoCAD凸轮轮廓曲线设计

,
[ Ke y wo r d s ]Au t o C AD, c a m p r o i f l e, c u r v e ra g p h me ho t d, a n a l y t i c me ho t d , VBA
.
0 引言
凸轮 机构是实现机械 自动 化和半 自动化 中应用较广泛 的一 种机构 。由于它பைடு நூலகம்有结构 简单、紧凑 ,易于实现 复杂运动 等特 点使其在 机械、电子、 自动控制 、计算 机等许 多行业 中被广 泛 地采用 。 凸轮机构设计的传统方法有:解析 法和 图解法两种方法。 图解法直 观、清晰,比较简单 易行,但 作图误差 大,因而其使 用范围 已受到 很大的限制 ,只适用 于速度 比较 低的凸轮机构 , 而高速和精度 要求高的凸轮机构 ,则必须用解析 法,解析法的 精度较高 ,但计算过程较为复杂 ,计算工作量大 。随着 C AD的 普及 ,C AD方法逐步为广大工程技术人员及科研人员所掌握 , 在 C AD环境下的工程 图解法极大地提高了传统 图解法的设计精 度, 以其相对来说更直观、 更形象简单和高精度而获得广泛应用 。
s t e p s a n d p r o c e d u r e s o f t h e d e s i g n o f h e a r t s ra t i g h t mo v i n g d i s k c a m p r o i f l e c u r v e . T h e n , he t e s t a b l i s h i n g o f ma t h e ma t i c a l mo d e l nd a he t
将excel数据导入CAD画图的方法

将e x c e l数据导入C A D画图的方法(总4页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除Set xlbook = "D:\cadvba\") '打开EXCEL的路径及名称,早期‘excel的扩展名是xls。
= False’隐藏工作簿Set xlsheet = ("eat") '选用EXCEL中名为“eat”的工作表中的数据i = (1, 6) 'i为线条线数m = (2, 6) '这里表示第2行第6列那个单元格里的数值n = (3, 6)T = (4, 6)For p = 0 To i - 2 Step 1k1 = (2 + p, 1)h1 = (2 + p, 2)k3 = (2 + p, 3)k2 = (3 + p, 1)h2 = (3 + p, 2)h3 = (3 + p, 3)Dim 直线 As AcadLineDim 起点(2) As DoubleDim 端点(2) As Double起点(0) = k1 + m起点(1) = h1 + n起点(2) = k3 + T端点(0) = k2 + m端点(1) = h2 + n端点(2) = h3 + TSet 直线 = 起点, 端点)NextZoomExtents '缩放至满幅Set xlapp = NothingEnd Sub3.打开vba编辑器的工具→引用,从引用对话窗找到Microsoft Excel Object Library,点击其左边的□,出现勾符号(如果没有此项,可浏览打开文件即可,文件位置一般此是C:\Progr am Files\Microsoft Office\Officexx,其扩展名可能未显示),然后确定。
4.做好这几步之后就保存编辑内容,然后点击工具栏上的▲(向右)或按F5或点击工具菜单→运行就可以画出折线了,到cad界面可见。
利用CAD画凸轮机构
精品文档
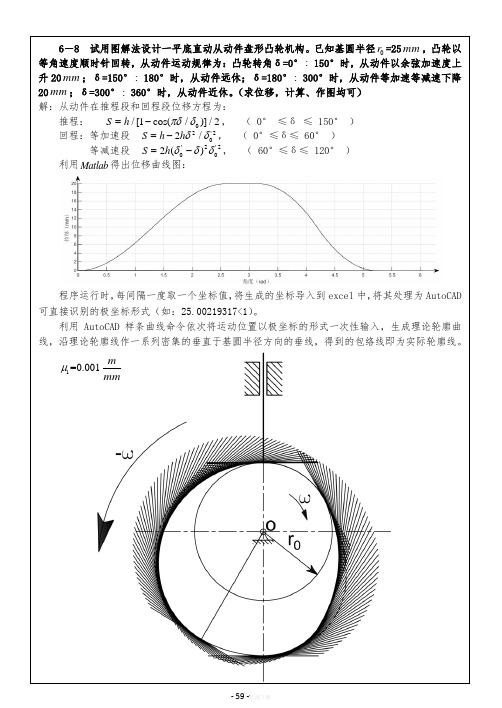
6-8 试用图解法设计一平底直动从动件盘形凸轮机构。
已知基圆半径0r =25mm ,凸轮以等角速度顺时针回转,从动件运动规律为:凸轮转角δ=0°:150°时,从动件以余弦加速度上升20mm ;δ=150°:180°时,从动件远休;δ=180°:300°时,从动件等加速等减速下降20mm ;δ=300°:360°时,从动件近休。
(求位移,计算、作图均可) 解:从动件在推程段和回程段位移方程为: 推程: 0/[1cos(/)]/2S h πδδ=-, ( 0° ≤δ ≤ 150° ) 回程:等加速段 2'202/S h h δδ=-, ( 0°≤δ≤ 60° ) 等减速段 '2'2002()S h δδδ=-, ( 60°≤δ≤ 120° ) 利用Matlab 得出位移曲线图: 程序运行时,每间隔一度取一个坐标值,将生成的坐标导入到excel 中,将其处理为AutoCAD 可直接识别的极坐标形式(如:25.00219317<1)。
利用AutoCAD 样条曲线命令依次将运动位置以极坐标的形式一次性输入,生成理论轮廓曲线,沿理论轮廓线作一系列密集的垂直于基圆半径方向的垂线,得到的包络线即为实际轮廓线。
1=0.001μm mm
精品文档
欢迎您的下载,
资料仅供参考!
致力为企业和个人提供合同协议,策划案计划书,学习资料等等
打造全网一站式需求。
凸轮轮廓曲线的设计1

第七章凸轮机构及其设计——设计凸轮的轮廓曲线(1)一、凸轮廓线设计方法的基本原理反转原理:依据此原理可以用几何作图的方法设计凸轮的轮廓曲线。
给整个凸轮机构施以-ω时,不影响各构件之间的相对运动,此时,凸轮将静止,而从动件尖顶复合运动的轨迹即凸轮的轮廓曲线。
§7-3 凸轮轮廓曲线的设计O -ωω3’1’2’331122对心直动尖顶从动件凸轮机构中,已知凸轮的基圆半径r 0,角速度ω 和从动件的运动规律,设计该凸轮轮廓曲线。
1.对心直动尖顶从动件盘形凸轮机构二、直动从动件盘形凸轮轮廓的绘制设计步骤小结:①选比例尺μl 作基圆r 0。
②反向等分各运动角。
③确定反转后,从动件尖顶在各等份点的位置。
④将各尖顶点连接成一条光滑曲线。
1’3’5’7’8’1357891113159’11’13’12’14’-ωωe A偏置直动尖顶从动件凸轮机构中,已知凸轮的基圆半径r 0,角速度ω和从动件的运动规律和偏心距e ,设计该凸轮轮廓曲线。
2.偏置直动尖顶从动件盘形凸轮1’3’5’7’8’1357891113159’11’13’12’14’-ωωO 15’14’13’12’11’10’9’设计步骤小结:①选比例尺μl 作基圆r 0;②反向等分各运动角;③确定反转后,从动件尖顶在各等份点的位置;④将各尖顶点连接成一条光滑曲线。
1514131211109k 9k 10k 11k 12k 13k 14k 15k 1k 2k 3k 5k 4k 6k 7k 8小结•反转原理•对心直动尖顶从动件盘形凸轮机构•偏置直动尖顶从动件盘形凸轮机构问题?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巧借Excel在AutoCAD中设计凸轮轮廓
曲线
摘 要:本文介绍一种借用EXCEL应用程序来计算并保存数据,并与
CAD精确绘图巧妙地结合,设计凸轮轮廓曲线的方法,该方法也可用于其它二
维或三维曲线的绘制中。论文 毕业论文关键词:凸轮 轮廓曲
线 AutoCAD 图解法1. 问题的提出本文以设计二维凸轮轮廓曲线为例,
介绍一种一般操作者就能方便做到的,借用EXCEL应用程序来计算并保存数
据,并与AutoCAD精确绘图巧妙地结合,绘制二维或三维非规则曲线的方法,
以供大家参考。2. 概述在凸轮机构中,最常用的就是平面凸轮机构,要设计
平面凸轮的轮廓曲线。设计方法通常有图解法和解析法两种。作图法简便易
行、直观,作图误差较大,精度较低,适用于低速对从动件运动规律要求不高
的一般精度凸轮设计;对于精度要求高的高速凸轮、靠模凸轮等,必须用解析
法列出凸轮的轮廓曲线方程,用计算机辅助设计精确地设计凸轮机构。我们沿
用原有的图解法思路,使用CAD作为工具,两者的联合运用,能产生意想不到
的更简单、直接、方便的处理方法。在这种基于AutoCAD的图解法基础上,利
用AutoCAD与其它文档交换信息和数据的功能,对于一些计算量较大输入点较
多的图形,与EXCEL应用程序相结合,使作图更加简便快捷。如设计下面的偏
置滚子从动件盘形凸轮轮廓曲线,已知偏距e=10㎜,基圆半径r0=40㎜,行程
h=25㎜,滚子半径rT=10㎜。凸轮以角速度ω顺时针转动,从动件的运动规
律为:运动阶段1,推程Φ=180°、凸轮转角φ(°)为0~180,运动形式:等
加速-等减速运动,运动方程方程:s=(2h/Φ2)φ2=(2*25/1802)φ
(0≤φ≤90)或s=h-2h(Φ-φ)2/Φ2=25-2*25*(180-
φ)2/1802 (90≤φ≤180)运动阶段2,远休止ΦS=30°、凸轮转角φ(°)
为180~210,运动形式:静止不动,运动方程方程: s=h=25
(180≤φ≤210)运动阶段3,回程Φ=90°、凸轮转角φ(°)为210~300,
运动形式:等加速-等减速运动,运动方程方程: s= h-(2h/Φ’2)/φ’2=25-
(2*25/180)2/(φ-210)2(180≤φ≤210)或s=2h(Φ’-
φ’)2/Φ’2=2*25*(90-(φ-210))2/902(180≤φ≤210)运动阶段4,远休
止ΦS=60°、凸轮转角φ(°)为300~360,运动形式:静止不动,运动方程
方程: s=0(300≤φ≤360)3、解题思路要使基于CAD技术的图解法充分发挥
软件精确、高效绘图的作用,就要首先改进原来的作图方法。图解法和解析法
其本质完全相同,只是求解手段、求解过程不同,这里我们不用作图法确定曲
线上点的方法,而是直接利用解析法里凸轮轮廓曲线的极坐标方程,求出凸轮
轮廓曲线上若干个点(越多曲线越准确)的极坐标值(ρ,θ),再用spline (绘
制样条曲线)命令,输入各点坐标值,作出凸轮的轮廓曲线。如果是滚子从动
件,得到理论轮廓线后,直接用offset(偏移)命令,输入滚子半径即可得到凸
轮的实际轮廓曲线。这里有两个问题需要解决。首先是计算,为了得到更为准
确的曲线,取点要尽量多,求这些点的极坐标值是一个很大的计算量,如何计
算,计算后数据保存在哪里?其次是绘制曲线时点的坐标的输入,如果一个个
输入要输二十多次,非常费时而且很容易出错。4、 解决办法4.1数据的计算
EXCEL是我们大家比较熟悉的应用程序,可以执行计算、分析信息并管理表格
等,我们就用它来进行计算和保存数据。按从动件的运动规律所给数据,由于
凸轮轮廓曲线要对应推程运动角(Φ)、远休止角(ΦS)、回程运动角(Φ’)、近
休止角(Φ’S)四个部分。根据运动规律,推程运动角(Φ)和回程运动角(Φ’)
对应的是不规则的二维曲线,远休止角(ΦS)和近休止角(Φ’S)对应的是正圆
弧,我们都用SPLINE命令绘制。为使曲线尽量准确,各段都要均分为若干份。
推程运动角(Φ)和回程运动角(Φ’)因为对应角都较大各分成8分共16个点;
远休止角(ΦS)较小分成2份共,近休止角(Φ’S)分成4份共6个点,合计共
取22个点。先把这些数据输入EXCEL表格,按从动件的运动规律所给数据计算
各点对应于基圆的位移值S、运动过程中通过各分点的导路方向与基圆半径的
夹角β及起始位置点B0对应的夹角β0,凸轮轮廓曲线上各点对应极半径ρ
和夹角θ等,最后才能合成各点的极坐标值。这个过程计算量比较大,但无论
采用何种方法设计,初始数据的取得都要经过计算,计算过程中所用公式及各
参数的含义请参阅相关资料,因篇幅有限,这里不多作说明。4.2极坐标的合
成如图2所示,经过计算得到极半径ρ和夹角θ的值后,要合并成极坐标
(ρ<θ)的形式。使用连接运算符即“与”号(&)连接F列和G列两个数字串,
两数字串中间还要用表示角度的符号“<”连接,操作方法如下:在H2单元格
内输入公式“=A2&“<”&B2”,并按下Enter键,H2中就出现了一对极坐标
值,再用鼠标拖动的方法将H2的的公式进行复制,就可以得到一组极坐标值。
这就是我们需要的凸轮轮廓曲线上各点的极坐标,将数据保存备用。如果引号
中间括起的是“,”号,就可以得到直角坐标的形式,在以直角坐标绘制曲线
时可用。以此类推开去,这样合并或连接,可得到任何你需要的数据。4.3数
据的输入,理论轮廓曲线的形成选出凸轮轮廓曲线上的点的极坐标值,即图中
H列数据,将其复制到剪贴板上,可用Excel中的复制按钮或者直接按下
Ctrl+C键来完成此工作。打开AutoCAD,在命令行处键入spline(绘制样条曲
线)命令,出现提示:"输入第一点或[对象(O)]",在此位置处点击鼠标右键,
从弹出的菜单中选择“粘贴”菜单项,这样在Excel中的极坐标值就传送到了
AutoCAD中,并自动连接成曲线,单击鼠标右键或按下Enter键,取消继续画
线状态,你需要的曲线就立刻出现在你面前,既简捷又不会出错,比一次次输
入点的坐标值不知要快上了多少倍。4.4实际轮廓曲线的形成如果是尖顶从动
件,上面的曲线即为所求凸轮的轮廓曲线。对于滚子从动件,我们得到理论轮
廓线后,直接用offset(偏移)命令,出现提示:“指定偏移距离或[通过(T)]<
通过>:”,输入滚子半径rT=10㎜,选择轮廓曲线作为偏移对象,指定内侧为
偏移方向,即可得到凸轮的实际轮廓曲线。4.5其它需要解决的问题如果需要
表示曲线及基圆上各分点等,可以依照上述方法推广,在EXCEL表格中得出各
分点的极坐标,在CAD中设置点样式用绘制点的命令一次输入各点坐标值即
可。凸轮的基圆、偏距圆等,用相应命令绘制,非常简单,不必多说。该方法
还可推广到绘制其它二维或三维曲线。如渐开线、阿基米德螺旋线、摆线等二
维曲线。三维曲线如绘制三维螺旋线也属此类问题,可以先在EXCEL表格中得
到螺旋线的柱面坐标值如图3所示,这用上面的方法也不难得到,然后再用
spline命令将在EXCEL表格中得到的各分点坐标值粘贴过来就可完成三维螺旋
线的绘制,如果需要多圈,再复制或阵列即可。上述方法方便快捷,简单易
行,不需任何编程,对.于不太熟悉CAD二次开发的用户是一种快速绘制二维或
三维曲线的好办法。参考文献:[1]陈立德 机械设计基础 (第2版) 北
京 高等教育出版社[M] 2004.7 62-72[2]张帆等 AutoCAD辅助设计专
家 北京 清华大学出版社[M] 2005.2 366-369[3]王有良、唐跃
刚 AutoCAD开发与应用[J] 山东大学学报 2005,
