高中数学同步备课 复数的四则运算
《复数的四则运算》课件

练习
1 计算 $(2+3i)+(4+5i)$ 3 计算 $(2+3i) \times (4+5i)$
2 计算 $(2+3i)-(4+5i)$ 4 计算 $\frac{2+3i}{4+5i}$
《复数的四则运算》PPT 课件
本课件将带你了解复数的四则运算,包括加法、减法、乘法和除法。通过简 洁明了的内容和丰富多样的排版,希望能够使你轻松理解和掌握这些运算。
复数概述
定义
形如 $a+bi$ 的数称为复 数,其中 $a$ 和 $b$ 是实 数,且 $i^2=-1$
实部和虚部
$a$ 为实部,$b$ 为虚部
复共轭
$a-bi$ 称为 $a+bi$ 的共 轭复数
复数的加法和减法
加法
$(a+bi)+(c+di)=(a+c)+(b+d)i$
减法
$(a+bi)-(c+di)=(a-c)+(b-d)i$
复数的乘法
乘法
$(a+bi) \times (c+di)=(ac-bd)+(ad+bc)i$
复数的除法
除法
总结
1 复数的四则运算包
括加法、减法、乘
法和除法
2ቤተ መጻሕፍቲ ባይዱ计算时需要注意
$i^2=-1$,并进行
配方法化简
3 复数的共轭复数是
重要的概念,应该
掌握
复数的四则运算(2个课时)(课件)高一数学(人教A版2019必修第二册)

i2021 i45051 (i4 )505 i i
2i 5 5
55
3.实系数一元二次方程在复数集内的解
x2 2x 1 0在复数集内的解: 析 : (2)2 4 1 (1) 8 0, 配方得(x 1)2 2 ( 2 )2
x 1 2, x 1 2.
求根公式: x 2 8 1 2
②若 b2 4ac 0, 方程系数化为1得x2 b x c 0,
aa
配方得(x
b )2 2a
b2 4ac 4a2
[(b2 4ac)] 4a2
[(b2 4ac)]i2 4a2
x b 2a
(b2 4ac) i, x
b
2a
2a
b2 4ac i b 2a
b2 4ac i 2a
(1)z 1; (2)z i; (3)z (2 i) 复数加减法→对应向量加减法
(1)记OZ1 (1,0),则z 1对应的向量是OZ OZ1 OA1.
(2)记OZ2 (0,1),则z i对应的向量是OZ OZ2 Z2Z.
(3)记OZ3 (2,1),则z (2 i)对应的向量是OZ OZ3 OA2.
y
y
A2
y
Z A1
Z
Z
Z2
Z3
Z1
x
x
x
[例6]复数z满足 | z i | 2,求复数z对应的点Z在复平面内的轨迹. 析 : 设i对应的点Z1(0,1).
| z 1|| OZ OZ1 | | Z1Z | 2
即Z与Z1(0,1)的距离为2. 点Z的轨迹是以(0,1)为圆心,以2为半径的圆.
[变1]复数z满足| z i | 1 3i,求复数z对应的点Z 在复平面内的轨迹. 析 : 即 | z i | 2. (同上)
高二数学复数的运算PPT教学课件

怎样定义复数的加、减、乘运算呢?运算律仍成立吗?
注意到 i2 1,虚数单位 i 可以和实数进行运 算且运算律仍成立,所以复数的加、减、乘运算我 们已经是自然而然地在进行着,只要把这些零散的 操作整理成法则即可了!
1.复数加、减法的运算法则: 已知两复数z1=a+bi, z2=c+di(a,b,c,d是实数) (1)加法法则:z1+z2=(a+c)+(b+d)i;
另外不难证明: z 1 z 2 z 1 z 2,z 1 z 2 z 1 z 2
我们知道,两个向量的和满足平行四边形 法则, 复数可以表示平面上的向量,那么复数 的加法与向量的加法是否具有一致性呢?
设z1=a+bi z2=c+di,则z1+z2=(a+c)+(b+d)i
如图, z1 对应向量 OZ1 , z2 对应向量 OZ2 ,根据向量
(1)2( 2
3i)2 2
01; 3 1 44
例3、 下 列 命 题 中 正 确 的 是 (1)如果 Z1 Z2是实数, Z1、 则Z2互为共轭复数 (2)纯 虚Z数 的 共 轭 复数Z。 是 (3)两 个 纯 虚 数 的 差 虚还 数是 纯 (4)两 个 虚 数 的 差 还 。是 虚 数
可得
x2x24, x23x220.
解得
x3或x2 x3或x6
所以 x3.
课外练习:
1.计算:(1+2 i )2
3 4i
2.计算(i-2)(1-2i)(3+4i) -20+15i 3.计算 (1 i)3 -2+2i 4.若 z C 且 (3 z)i 1 ,则 z -__3_-_i_ . 3
高中数学—— 复数代数形式的四则运算

3.2.1 复数代数形式的 加、减运算及其几何意义
目标导航 预习导引
课前预习导学
KEQIAN YUXI DAOXUE
课堂合作探究
KETANG HEZUO TANJIU
3.复数加减法的几何意义 设复数 z1,z2 对应的向量为������������1 , ������������2 ,则复数 z1+z2 是以������������1 , ������������2 为邻 边的平行四边形的对角线������������所对应的复数,z1-z2 是向量������2 ������1 所对应的 复数.
3.2 复数代数形式的四则运算
3.2.1
复数代数形式的加、减运算及其几何意义
3.2.1 复数代数形式的 加、减运算及其几何意义
目标导航 预习导引
课前预习导学
KEQIAN YUXI DAOXUE
课堂合作探究
KETANG HEZUO TANJIU
学习目标 重点难点
1.能记住复数的加法与减法的运算法则,并知道它们的几何意义; 2.能运用复数的加法与减法的运算法则解决相关问题. 重点:复数加法与减法的运算法则; 难点:复数加法与减法的几何意义.
问题导学 当堂检测
课前预习导学
KEQIAN YUXI DAOXUE
课堂合作探究
KETANG HEZUO TANJIU
迁移与应用 1.若复数 z 满足 z+2-3i=-1+5i,则复数 z= 答案:-3+8i 解析:由 z+2-3i=-1+5i,得 z=(-1+5i)-(2-3i)=-3+8i. 2.计算:(1)2i-[(3+2i)-(-1+3i)]; (2)a+bi+(2a-3bi)-4i(a,b∈R); (3)(10-9i)+(-8+7i)-(3+3i). 解:(1)原式=2i-[(3+1)+(2-3)i]=2i-(4-i)=-4+3i; (2)原式=(a+2a)+(b-3b)i-4i=3a+(-2b-4)i=3a-(2 b+4)i; (3)原式=(10-8-3)+(-9+7-3)i=-1-5i. .
3.2复数的四则运算

Z x2 y2
一.复数的加法与减法
1.复数加法的运算法则
(a+bi ) + (c+di) = (a+c) + (b+d)i
很明显,两个复数的和仍然是一个复数
2. 加法的运算律
1. z1 z2 z2 z1(交换律); 2. (z1 z2 ) z3 z1 (z2 z3)(结合律)
高中数学 选修2-2
3.2复数的四则运算
复数a+bi(a,b∈R)
a—实部
b—虚部
复数 a+bi
实数a (b=0) 纯虚数bi(a=0)
虚数 (b‡0) 非纯虚数a+bi(ab‡0)
两个复数相等
设z1=a+bi,z2=c+di(a、b、c、dR),
a c
则 z1=z2 b d , 即实部等于实部,虚部等于虚部
|z1-z2|表示什么? 表示复平面上两点Z1 ,Z2的距离
已知复数z对应点A,说明下列各式所表示的几何意义.
(1)|z-(1+2i)|
点A到点(1,2)的距离
(2)|z+(1+2i)|
点A到点(-1, -2)的距离
(3)|z-1|
点A到点(1,0)的距离
(4)|z+2i|
点A到点(0, -2)的距离
另外不难证明: z1 z2 z1 z2 , z1 z2 z1 z2
例题选讲
复数的乘法也可大胆运 用乘法公式来展开运算.
例4:计算 ① (1+i)2
人教版高中数学教案-复数的四则运算

複數中的幾個結論及共應用數系由實數系擴充到複數系之後,實數系中哪些公式和法則仍然成立,哪些不成立,又有哪些新的公式和法則,是同學們不易弄清的問題,以下給出幾則在複數系中仍然成立的公式和法則及幾個新的公式和法則,並簡單舉例說明其應用.一、中點公式:A 點對應的複數為1111()a b i a b +∈∈R R ,,B 點對應的複數為2222()a b i a b +∈∈R R ,,C 點為A B ,兩點的中點,則C 點對應的複數為11222a b i a b i+++,即121222a ab b i +++. 例1 四邊形ABCD 是複平面內的平行四邊形,A B C ,,三點對應的複數分別為132i i i +-+,,,求D 點對應的複數.解:由已知應用中點公式可得A C ,的中點對應的複數為322i +,所以D 點對應的複數為32[22(1)]352i i ⨯+⨯--=+.二、根與係數的關係:若實係數方程20(0)ax bx c a ++=≠的兩複根為11a b i +,22a b i +,則有1122b a b i a b i a +++=-,1122()()ca b i a b i a++=·.推論:若實係數方程20(0)ax bx c a ++=≠有兩虛數根,則這兩個虛數根共軛. 例2 方程20x ax b ++=的一個根為1i +,求實數a ,b 的值.解:已知實係數方程的一個根為1i +,由推論知方程的另一根為1i -,由根與係數的關係可知(11)2a i i =-++-=-,(1)(1)2b i i =+-=·.三、相關運算性質:①z 為實數2220z z z z z ⇔=⇔>⇔=,z 為純虛數200(0)z z z z ⇔<⇔+=≠;②對任意複數有z z =;③1212z z z z ±=±;④1212z z z z =··,特別地有22()z z =;⑤1122z z z z ⎛⎫= ⎪⎝⎭;⑥2z z z =·.例3 設1z =,且z i ≠±,求證21zz +為實數. 證明:由條件可知0z ≠,則21z z z ==·,所以11z z z -==,1212222211()11()11z z z z z z z z z z z z--⎛⎫=-=== ⎪++++⎝⎭++,所以21zz+為實數.四、兩則幾何意義:①0z z -的幾何意義為點z 到點0z 的距離;②0(0)z z r r -=>中z 所對應的點為以複數0z 所對應的點為圓心,半徑為r 的圓上的點.例4 若z C ∈,且221z i +-=,則22z i --的最小值為 .解:221z i +-=即(22)1z i --+=,z 對應的點為到點(22)-,的距離為定值1的所有的點,即以(22)-,為圓心,1為半徑的圓O 上的點.22z i --即(22)z i -+,為圓O 上的點與點(22),之間的距離減去圓O 的半徑,可得結果為3.複數與平行四邊形家族菱形、矩形、正方形等特殊的平面幾何圖形與某些複數式之間存在某種聯繫及相互轉化的途徑.在求解複數問題時,要善於考察條件中給定的或者是通過推理所得的複數形式的結構特徵,往往能獲得簡捷明快、生動活潑的解決方法.下面略舉幾例,以供參考. 一、複數式與長方形的轉化例1 複數1z ,2z 滿足120z z ≠,1212z z z z +=-,證明:21220z z <.解析:設複數1z ,2z 在複平面上對應的點為1Z ,2Z ,由1212z z z z +=-知,以1OZ ,2OZ 為鄰邊的平行四邊形為矩形,12OZ OZ ⊥∴,故可設12(0)z ki k k z =∈≠R ,,所以222212210z k k z ==-<. 例2 已知複數1z ,2z 滿足171z ,271z =,且124z z -=,求12z z 與12z z +的值.解析:設複數1z ,2z 在複平面上對應的點為1Z ,2Z ,由於222(71)(71)4+=,故2222112z z z z +=-,故以1OZ ,2OZ 為鄰邊的平行四邊形是矩形,從而12OZ OZ ⊥,則127147371z i i z ++=±=±-;12124z z z z +=-=.二、複數式與正方形的轉化例3 已知複數12z z ,滿足121z z ==,且122z z -=,求證:122z z +=. 證明:設複數12z z ,在複平面上對應的點為1Z ,2Z ,由條件知121222z z z z -==,以1OZ ,2OZ 為鄰邊的平行四邊形為正方形,而12z z +在複平面上對應的向量為正方形的一條對角線,所以122z z +=.點評:複數與向量的對應關係賦予了複數的幾何意義,複數加法幾何意義的運用是本題考查的重點.三、複數式與菱形的轉化例4 已知12z z ,∈C ,121z z ==,123z z +=,求12z z -.解析:設複數12z z ,,12z z +在複平面上對應的點為123Z Z Z ,,,由121z z ==知,以1OZ ,2OZ 為鄰邊的平行四邊形是菱形,22z a =∴,z a =∴,考慮到z a =±時,22220z a z a -=+;z ai =±時,2222z a z a -+無意義,故使2222z a z a -+(0)a >為純虛數的充要條件是z a =,且z a ≠±,z ai ≠±.複數的加減法符合平行四邊形法則,是複數與平行四邊形家族聯姻的前提.通過本文我們發現深入抓住複數加減法的幾何意義的本質,可使我們求解複數問題的思路更加廣闊,方法也更加靈活.。
高二数学复数的四则运算1

1.复数加减法的运算法则:
(1)运算法则:设复数z1=a+bi,z2=c+di, 那么:z1+z2=(a+c)+(b+d)i;
z1-z2=(a-Байду номын сангаас)+(b-d)i.
即:两个复数相加(减)就是实部与
实部,虚部与虚部分 别相加(减).
(2)复数的加法满足交换律、结合律,
即对任何z1,z2,z3∈C,有
z1z2=z2z1;
(z1z2)z3=z1(z2z3); z1(z2+z3)=z1z2+z1z3.
( 1 ) (a bi)(a bi) 例2:计算
a abi abi b i
2
2 2
a b
2
2
2
2 2 2
(2) (a bi) a 2abi b i
a 2abi b
i __ , i __ , i __ , i __
5 6 7 8
你能发现规律吗?有怎样的规律?
i
4n
1 ,
i
4 n 1
i ,
i
4n2
1
, i
4 n 3
i
【例3】求值: i i
2
i i
3
2 3 4
2006
解:原式 (i i i i ) (i i i i ) ...
(1)复数乘法的法则 复数的乘法与多项式的乘法是类似 的,但必须在所得的结果中把i2换成-1, 并且把实部合并.即:
2 (a+bi)(c+di)=ac+bci+adi+bdi
高一下学期数学人教A课件:复数的四则运算
+ ( + )( − )
+ + −
=
=
=
+ ( + )( − )
+
例4.计算: + ÷ − .
新课讲解
例3.计算:
①
+ −
=
;
② | + | =
;
③ | − + + | =
;
观察各复数与它们乘积的模,你有什么发现?
你能证明它们吗?
= + , = ( + )
新课讲解
复数的乘除运算:
结合复数乘法模的计算特征,
你觉得复数除法的模也有类似特征吗?
例5.化简 =
−+ +
+
,并计算 .
1
|1 |
=
2
|2 |
新课讲解
例6.在复数范围内解下列方程:
① + + =
② =
课堂小结
若 = + , = +
则 + =
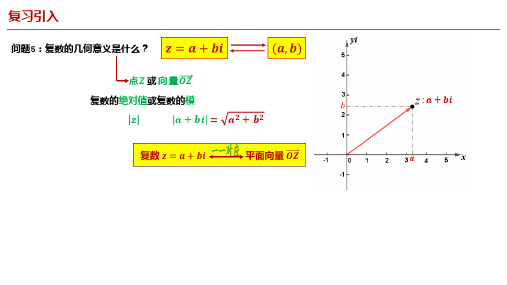
复习引入
问题5:复数的几何意义是什么?
点 或 向 量
复数的绝对值或复数的模
| + | =
: +
+
新课讲解
复数的加减运算:
问题:若 = + , = + ,你认为应该如何定义 + ?为什么?
问题:若 = + , = + ,则 − =
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1课时复数的加减与乘法运算已知复数z1=a+bi,z2=c+di(a,b,c,d∈R).问题1:多项式的加减实质是合并同类项,类比想一想复数如何加减?提示:两个复数相加(减)就是把实部与实部、虚部与虚部分别相加(减).问题2:复数的加法满足交换律和结合律吗?提示:满足.1.复数的加法、减法法则设z1=a+bi,z2=c+di(a,b,c,d∈R),则z1+z2=(a+bi)+(c+di)=(a+c)+(b+d)i,z1-z2=(a+bi)-(c+di)=(a-c)+(b-d)i.即两个复数相加(减)就是把实部与实部、虚部与虚部分别相加(减).2.复数加法的运算律(1)交换律:z1+z2=z2+z1;(2)结合律:(z1+z2)+z3=z1+(z2+z3).设z1=a+bi,z2=c+di,(a,b,c,d∈R)问题1:如何规定两复数相乘?提示:两个复数相乘,类似于两个多项式相乘,只要在所得的结果中把i2换成-1,并且把实部与虚部分别合并即可.即z1z2=(a+bi)(c+di)=ac+bci+adi+bdi2=(ac-bd)+(bc+ad)i.问题2:试验复数乘法的交换律.提示:z1z2=(a+bi)(c+di)=(ac-bd)+(bc+ad)i,z2z1=(c+di)(a+bi)=(ac-bd)+(bc+ad)i.故z1z2=z2z1.1.复数的乘法设z 1=a +bi,z 2=c +di 是任意两个复数,那么它们的积(a +bi)(c +di)=ac +bci +adi +bdi 2=(ac -bd)+(ad +bc)i(a,b,c,d ∈R).2.复数乘法的运算律 对于任意z 1、z 2、z 3∈C,有交换律 z 1·z 2=z 2·z 1 结合律 (z 1·z 2)·z 3=z 1·(z 2·z 3) 乘法对加法的分配律z 1(z 2+z 3)=z 1z 2+z 1z 3问题:复数3+4i 与3-4i,a +bi 与a -bi(a,b ∈R)有什么特点? 提示:两复数的实部相等,虚部互为相反数.1.把实部相等,虚部互为相反数的两个复数叫做互为共轭复数. 2.复数z =a +bi 的共轭复数记作z -,即z -=a -bi.3.当复数z =a +bi 的虚部b =0时,z =z -,也就是说,实数的共轭复数仍是它本身.1.复数加、减法的规定:实部与实部相加(减)、虚部与虚部相加(减).两个复数的和或差仍是一个复数.2.复数的乘法与多项式的乘法是类似的,有一点不同即必须在所得结果中把i 2换成-1,再把实部,虚部分别合并、两个复数的积仍是一个复数,可推广到任意多个复数,任意多个复数的积仍然是一个复数.[例1] 计算: (1)(3+5i)+(3-4i); (2)(-3+2i)-(4-5i);(3)(5-5i)+(-2-2i)-(3+3i).[思路点拨] 解答本题可根据复数加减运算的法则进行.[精解详析] (1)(3+5i)+(3-4i)=(3+3)+(5-4)i=6+i.(2)(-3+2i)-(4-5i)=(-3-4)+[2-(-5)]i=-7+7i.(3)(5-5i)+(-2-2i)-(3+3i)=(5-2-3)+[-5+(-2)-3]i=-10i.[一点通] 复数加减运算法则的记忆方法:(1)复数的实部与实部相加减,虚部与虚部相加减.(2)把i看作一个字母,类比多项式加减中的合并同类项.1.(3-5i)+(-4-i)-(3+4i)=________.解析:(3-5i)+(-4-i)-(3+4i)=(3-4-3)+(-5-1-4)i=-4-10i.答案:-4-10i2.若(-7i+5)-(9-8i)+(x+yi)=2,则x+y=________.解析:(-7i+5)-(9-8i)+(x+yi)=(5-9+x)+(-7+8+y)i=(x-4)+(y+1)i.∴(x-4)+(y+1)i=2,即x-4=2,y+1=0.∴x=6,y=-1.∴x+y=5.答案:53.计算:(1)(1+2i)+(3-4i)-(5+6i);(2)5i-[(3+4i)-(-1+3i)].解:(1)原式=(4-2i)-(5+6i)=-1-8i;(2)原式=5i-(4+i)=-4+4i.[例2] 计算:(1)(1-i)(1+i)+(-1+i);(2)(2-i)(-1+5i)(3-4i)+2i.[思路点拨] 应用复数的乘法法则及乘法运算律来解.[精解详析] (1)(1-i)(1+i)+(-1+i)=1-i2-1+i=1+i.(2)(2-i)(-1+5i)(3-4i)+2i =(-2+10i +i -5i 2)(3-4i)+2i =(-2+11i +5)(3-4i)+2i =(3+11i)(3-4i)+2i =(9-12i +33i -44i 2)+2i =53+21i +2i =53+23i.[一点通] (1)三个或三个以上的复数相乘,可按从左向右的顺序运算,或利用结合律运算.混合运算的顺序与实数的运算顺序一样.(2)平方差公式,完全平方公式等在复数范围内仍然成立.一些常见的结论要熟记:i 2=-1,(1±i)2=±2i.4.(浙江高考改编)已知i 是虚数单位,则(-1+i)(2-i)=________. 解析:(-1+i)(2-i)=-2+i +2i -i 2=-1+3i. 答案:-1+3i5.若(1+i)(2+i)=a +bi,其中a,b ∈R,i 为虚数单位,则a +b =________. 解析:∵(1+i)(2+i)=1+3i =a +bi,∴a =1,b =3, 故a +b =4. 答案:46.计算下列各题. (1)(1+i)2;(2)(-1+3i)(3-4i); (3)(1-i)⎝ ⎛⎭⎪⎫-12+32i (1+i).解:(1)(1+i)2=1+2i +i 2=2i.(2)(-1+3i)(3-4i)=-3+4i +9i -12i 2=9+13i. (3)法一:(1-i)⎝ ⎛⎭⎪⎫-12+32i (1+i)=⎝ ⎛⎭⎪⎫-12+32i +12i -32i 2(1+i)=⎝ ⎛⎭⎪⎫3-12+3+12i (1+i)=3-12+3+12i +3-12i +3+12i 2=-1+3i.法二:原式=(1-i)(1+i)⎝ ⎛⎭⎪⎫-12+32i=(1-i 2)⎝ ⎛⎭⎪⎫-12+32i =2⎝ ⎛⎭⎪⎫-12+32i =-1+3i.[例3] 已知z∈C ,z 为z 的共轭复数,若z·z -3iz =1+3i,求z. [思路点拨]设z =a +bi (a ,b ∈R )―→z =a -bi(a,b ∈R)―→代入等式利用复数相等的条件求解.[精解详析] 设z =a +bi(a,b ∈R), 则z =a -bi(a,b ∈R),由题意得(a +bi)(a -bi)-3i(a -bi)=1+3i, 即a 2+b 2-3b -3ai =1+3i,则有⎩⎪⎨⎪⎧a 2+b 2-3b =1,-3a =3,解得⎩⎪⎨⎪⎧a =-1,b =0或⎩⎪⎨⎪⎧a =-1,b =3, 所以z =-1或z =-1+3i. [一点通](1)实数的共轭复数是它本身,即z∈R ⇔z =z,利用此性质可以证明一个复数是实数. (2)若z ≠0且z +z =0,则z 为纯虚数,利用此性质可证明一个复数是纯虚数.7.已知复数z =1+i,z 为z 的共轭复数,则z ·z -z -1= ________.解析:∵z=1+i,∴z =1-i,∴z ·z =(1+i)(1-i)=2, ∴z ·z -z -1=2-(1+i)-1=2-1-i -1=-i. 答案:-i8.复数z 满足(1+2i)z =4+3i,则z =________. 解析:设z =a +bi,则z =a -bi.∴(1+2i)(a -bi)=4+3i,∴a -bi +2ai +2b =4+3i, 即(a +2b)+(2a -b)i =4+3i,∴⎩⎪⎨⎪⎧a +2b =4,2a -b =3,解之得a =2,b =1.∴z=2+i. 答案:2+i9.已知复数 z =1+i,求实数 a,b 使 az +2bz =(a +2z)2成立.解:∵z=1+i,∴az +2bz =(a +2b)+(a -2b)i,(a +2z)2=(a +2)2-4+4(a +2)i =(a 2+4a)+4(a+2)i.∵a,b 都是实数,∴由 az +2bz =(a +2z)2,得⎩⎪⎨⎪⎧a +2b =a 2+4a ,a -2b =4(a +2).两式相加,整理得 a 2+6a +8=0.解得 a 1=-2,a 2=-4,对应得 b 1=-1,b 2=2. ∴所求实数为 a =-2,b =-1 或 a =-4,b =2.1.复数的加减运算把复数的代数形式z =a +bi 看作关于“i ”的多项式,则复数的加法、减法运算,类似于多项式的加法、减法,只需要“合并同类项”就行,不需要记加、减法法则.2.复数的乘法运算复数的乘法可以把虚数单位i 看作字母,按多项式乘法的法则进行,注意要把i 2化为-1,进行最后结果的化简.一、 填空题1.计算(-i +3)-(-2+5i)的结果为________. 解析:(-i +3)-(-2+5i)=-i +3+2-5i =-6i +5. 答案:5-6i2.若复数z =1-2i,则z·z +z 的实部是________. 解析:∵z=1-2i, ∴z =1+2i,∴z ·z =(1-2i)(1+2i)=5, ∴z ·z +z =5+1-2i =6-2i. 答案:63.已知3+i -(4+3i)=z -(6+7i),则z =________. 解析:∵3+i -(4+3i)=z -(6+7i) ∴z =3+i -(4+3i)+(6+7i) =(3-4+6)+(1-3+7)i=5+5i. 答案:5+5i4.(北京高考)若(x +i)i =-1+2i(x∈R),则x =________. 解析:(x +i)i =-1+xi =-1+2i,由复数相等的定义知x =2. 答案:25.已知z 1=3+4i,z 2=t +i,且z 1·z 2是实数,则实数t =________. 解析:∵z 2=t +i,∴z 2=t -i, ∴z 1·z 2=(3+4i)(t -i) =3t -3i +4ti -4i 2=(3t +4)+(4t -3)i, 又∵z 1·z 2是实数, ∴4t -3=0,即t =34.答案:34二、解答题6.计算:(1)⎝ ⎛⎭⎪⎫2-12i +⎝ ⎛⎭⎪⎫12-2i ; (2)(3+2i)+(3-2)i ;(3)(6-3i)+(3+2i)-(3-4i)-(-2+i).解:(1)原式=⎝ ⎛⎭⎪⎫2+12-⎝ ⎛⎭⎪⎫12+2i =52-52i ;(3)(3+2i)+(3-2)i =3+(2+3-2)i =3+3i ; (3)(6-3i)+(3+2i)-(3-4i)-(-2+i) =[6+3-3-(-2)]+[-3+2-(-4)-1]i =8+2i. 7.计算:(1)⎝ ⎛⎭⎪⎫12+32i (4i -6)+2+i ; (2)⎝ ⎛⎭⎪⎫-12+32i ⎝ ⎛⎭⎪⎫32+12i (1+i). 解:⎝ ⎛⎭⎪⎫12+32i (4i -6)+2+i =2i +6i 2-3-9i +2+i =-7-6i.(2)⎝ ⎛⎭⎪⎫-12+32i ⎝ ⎛⎭⎪⎫32+12i (1+i) =⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫-34-34+⎝⎛⎭⎪⎫34-14i (1+i)=⎝ ⎛⎭⎪⎫-32+12i (1+i) =⎝⎛⎭⎪⎫-32-12+⎝ ⎛⎭⎪⎫12-32i =-1+32+1-32i.8.(江西高考改编)z 是z 的共轭复数.若z +z =2,(z -z)i =2(i 为虚数单位),求z. 解:法一:设z =a +bi(a,b ∈R),则z =a -bi, ∵z +z =2a =2,∴a =1. 又(z -z)i =2bi 2=-2b =2. ∴b =-1. 故z =1-i.法二:∵(z-z)i =2,∴z -z =2i =-2i.又z +z =2.∴z -z +(z +z)=-2i +2,∴2z =-2i +2, ∴z =1-i.第2课时 复数的乘方与除法运算问题1:在实数中,若a·b=c(a≠0),则b =c a .反之,若b =ca ,则a·b=c.那么在复数集中,若z 1·z 2=z 3,有z 1=z 3z 2(z 2≠0)成立吗?提示:成立.问题2:若复数z 1=a +bi,z 2=c +di(a,b,c,d ∈R,c +di ≠0),则z 1z 2如何运算?提示:通常先把(a +bi )÷(c+di)写成a +bic +di 的形式,再把分子与分母都乘分母的共轭复数c -di,化简后可得结果,即a +bi c +di =(a +bi )(c -di )(c +di )(c -di )=(ac +bd )+(bc -ad )ic 2+d 2=ac +bd c 2+d 2+bc -ad c 2+d2i(c +di ≠0).1.复数范围内正整数指数幂的运算性质 对任意复数z,z 1,z 2和m,n ∈N *,有 (z)m·(z)n=(z)m +n;(z m )n=z mn; (z 1·z 2)n=z n1·z n2.2.虚数单位i n(n∈N *)的周期性 i 4n=1,i4n +1=i,i4n +2=-1,i4n +3=-i .3.复数的除法运算及法则把满足(c +di)(x +yi)=a +bi(c +di ≠0)的复数x +yi(x,y ∈R)叫做复数a +bi 除以复数c +di 的商.且x +yi =a +bi c +di =(a +bi )(c -di )(c +di )(c -di )=ac +bd c 2+d 2+bc -adc 2+d2i .由a +bi c +di =(a +bi )(c -di )(c +di )(c -di )=(ac +bd )+(bc -ad )i c 2+d 2=ac +bd c 2+d 2+bc -ad c 2+d2i,可以看出复数除法的运算实质是将分母化为实数的过程即分母实数化.[例1] 求1+i +i 2+…+i2 016的值.[思路点拨] 利用i n的性质计算,i 4n=1,i 4n +1=i,i4n +2=-1,i4n +3=-i,还可以利用等比数列求和来解.[精解详析] 法一:1+i +i 2+…+i 2 016=1-i 2 0171-i =1-i 2 016·i 1-i =1-i 1-i=1.法二:∵i n +in +1+in +2+in +3=0(n∈N *),∴1+i +i 2+…+i2 016=1+(i +i 2+i 3+i 4)+(i 5+i 6+i 7+i 8)+…+(i 2 009+i2 010+i2 011+i2 012)+(i2 013+i2 014+i2 015+i2 016)=1.[一点通] 等差、等比数列的求和公式在复数集C 中仍适用,i 的周期性要记熟,即i n +in +1+in +2+in+3=0(n∈N *).1.若z =-1-i 2,则z 2 014+z 102=________.解析:∵z 2=⎝⎛⎭⎪⎫-1-i 22=-i,∴z2 014+z 102=(-i)1 007+(-i)51=(-i)1 004·(-i)3+(-i)48·(-i)3=i +i =2i. 答案:2i2.设z 1=i 4+i 5+i 6+…+i 12,z 2=i 4·i 5·i 6·… ·i 12,则z 1与z 2的关系为z 1________z 2(用“=”或“≠”填).解析:∵z 1=i 4(1-i 9)1-i =i 4(1-i )1-i =1,z 2=i4+5+6+…+12=i (4+12)×92=i 72=(i 4)18=1,∴z 1=z 2. 答案:=[例2] 计算:(1)i -231+23i+(5+i 2)-⎝ ⎛⎭⎪⎫1+i 22;(2)(2+2i )3(4+5i )(5-4i )(1-i ).[思路点拨] 解答较为复杂的复数相乘、除时,一个方面要利用复数乘、除的运算法则、运算律,另一方面要注意观察式子中数据的特点,利用题目中数据的特点简化运算.[精解详析] (1)原式=(1+23i )i 1+23i +(5+i 2)-⎝ ⎛⎭⎪⎫1+i 22=i +5-1-i =i +4-i =4.(2)原式=22(1+i )3(5-4i )i(5-4i )(1-i )=22(1+i )4i (1-i )(1+i )=22[(1+i )2]2i 2=2·(2i)2i =-42i.[一点通] 复数的除法就是分子,分母同乘以分母的共轭复数,从而使分母实数化,熟悉以下结论对简化运算很有帮助.b -ai =(a +bi)(-i),-b +ai =(a +bi)i.3.设复数z =2i -1+i ,则复数z 2的实部与虚部的和为________. 解析:∵z=2i -1+i =2i (-1-i )(-1+i )(-1-i )=2i (-1-i )2=-i +1, ∴z 2=(1-i)2=1-2i -1=-2i.实部为0,虚部为-2.因此,实部与虚部的和为-2.答案:-24.若复数z 满足z(2-i)=11+7i(i 为虚数单位),则z =________.解析:∵z(2-i)=11+7i,∴z =11+7i 2-i =(11+7i )(2+i )(2-i )(2+i )=15+25i 5=3+5i. 答案:3+5i5.化简:()-1+3i 3(1+i )6+-2+i 1+2i =________. 解析:原式=⎝ ⎛⎭⎪⎫-1+3i 2i 3+(-2+i )(1-2i )5=i +i =2i. 答案:2i1.复数除法的运算技巧在实际进行的复数除法运算中,每次都按乘法的逆运算进行计算将十分麻烦.我们可以用简便方法操作:先把两个复数相除写成分式形式,然后把分子与分母都乘以分母的共轭复数,使分母“实数化”,最后再化简.2.注意复数计算中常用的整体(1)i 的性质:i 4n =1,i 4n +1=i,i 4n +2=-1,i 4n +3=-i (n∈N *); (2)(1±i)2=±2i,1+i 1-i =i,1-i 1+i=-i ; (3)设ω=-12+32i,则ω3=1,ω2+ω+1=0,ω2=ω,ω3=1.一、填空题1.(新课标全国卷Ⅱ改编)设复数z 满足(1-i)z =2i,则z =________. 解析:z =2i 1-i =2i (1+i )(1-i )(1+i )=2i (1+i )2=-1+i. 答案:-1+i2.设i 是虚数单位,复数103-i的虚部为________. 解析:103-i =10(3+i )(3-i )(3+i )=3+i. 答案:13.如果z 1=-2-3i,z 2=3-2i (2+i )2,则z 1z 2=________. 解析:∵z 1=-2-3i,z 2=3-i (2+i )2, ∴z 1z 2=(-2-3i )(2+i )23-2i =-i (3-2i )(2+i )23-2i=-i(2+i)2=-(3+4i)i =4-3i.答案:4-3i4.(浙江高考)已知 i 是虚数单位,计算1-i (1+i )2 =________. 解析:1-i (1+i )2 =1-i 2i =(1-i )i -2=-1-i 2=-12-12i. 答案:-12-12i 5.i 是虚数单位,i +2i 2+3i 3+…+8i 8=________.解析:设S =i +2i 2+3i 3+…+8i 8①则iS =i 2+2i 3+…+7i 8+8i 9②①-②得(1-i)S =i +i 2+i 3+…+i 8-8i 9=i (1-i 8)1-i-8i =-8i.∴S =-8i 1-i =-8i (1+i )(1-i )(1+i )=-8i (1+i )2=4-4i.答案:4-4i二、解答题6.计算⎣⎢⎡⎦⎥⎤(1+2i )·i 100+⎝ ⎛⎭⎪⎫1-i 1+i 52-⎝ ⎛⎭⎪⎫1+i 220. 解:⎣⎢⎡⎦⎥⎤(1+2i )·i 100+⎝ ⎛⎭⎪⎫1-i 1+i 52-⎝ ⎛⎭⎪⎫1+i 220 =[](1+2i )·1+(-i )52-i 10 =(1+i)2-i 10=1+2i.7.复数z =(1+i )2+3(1-i )2+i ,若z 2+a z<0,求纯虚数a. 解:z =(1+i )2+3(1-i )2+i =2i +3-3i 2+i =3-i 2+i=1-i. ∵a 为纯虚数,∴设a =mi (m≠0),则z 2+a z =(1-i)2+mi 1-i =-2i +mi -m 2=-m 2+⎝ ⎛⎭⎪⎫m 2-2i <0, ∴⎩⎪⎨⎪⎧-m 2<0,m 2-2=0,∴m =4.∴a=4i.8.已知1+i 是实系数方程x 2+ax +b =0的一个根.(1)求a 、b 的值;(2)试判断1-i 是否是方程的根.解:(1)∵1+i 是方程x 2+ax +b =0的根,∴(1+i)2+a(1+i)+b =0,即(a +b)+(a +2)i =0,∴⎩⎪⎨⎪⎧a +b =0,a +2=0,∴⎩⎪⎨⎪⎧a =-2,b =2. ∴a 、b 的值为a =-2,b =2.(2)方程为x 2-2x +2=0,把1-i代入方程,左边=(1-i)2-2(1-i)+2=-2i-2+2i+2=0显然方程成立.∴1-i也是方程的一个根.。
