精选部编版数学八年级上 第13章-第10课 13.4最短路径问题 练习(教师版)
数学人教版八年级上册13.4课题学习 最短路径问题同步练习题

数学人教版八年级上册13.4课题学习最短路径问题同步练习题解答题有两棵树位置如图,树脚分别为A,B.地上有一只昆虫沿A?B的路径在地面上爬行.小树顶D处一只小鸟想飞下来抓住小虫后,再飞到大树的树顶C处,问小鸟飞至AB之间何处时,飞行距离最短,在图中画出该点的位置.【答案】见解析【解析】试题分析:根据两点之间线段最短,做出点D关于AB 的对称点D′,连接CD′与AB的交点即为所求的点.试题解析:如图,作D关于AB的对称点D′,连接CD′交AB 于点E,则点E就是所求的点.解答题已知,如图所示,甲、乙、丙三个人做传球游戏,游戏规则如下:甲将球传给乙,乙将球立刻传给丙,然后丙又立刻将球传给甲.若甲站在∠AOB内的P点,乙站在OA上,丙站在OB上,并且甲、乙、丙三人的传球速度相同.问乙和丙必须站在何处,才能使球从甲到乙、乙到丙、最后丙到甲这一轮所用的时间最少?【答案】见解析【解析】试题分析:分别作出点P关于OA、OB的对称点P1、P2,连接P1P2与OA、OB的交点即为乙、丙的位置.试题解析:如图所示,(1)分别作点P关于OA,OB的对称点P1,P2,(2)连接P1P2,与OA,OB分别相交于点M,N,因为乙站在OA上,丙站在OB上,所以乙必须站在OA上的M 处,丙必须站在OB上的N处才能使传球所用时间最少.解答题如图所示,P,Q为△ABC边上的两个定点,在BC上求作一点R,使△PQR的周长最小.【答案】见解析【解析】试题分析:作出点P关于BC的对称点P′,连接QP′交BC于R,那么△PQR的周长最小试题解析:(1)作点P关于BC所在直线的对称点P′,(2)连接P′Q,交BC于点R,则点R就是所求作的点(如图所示).解答题七年级(1)班同学做游戏,在活动区域边OP放了一些球(如图),则小明按怎样的路线跑,去捡哪个位置的球,才能最快拿到球跑到目的地A?【答案】见解析【解析】试题分析:作出小明关于OP的对称点A′,连接AA′,与OP交点即为满足条件的点.试题解析:如图,作小明关于活动区域边线OP的对称点A′,连接AA′交OP于点B,则小明行走的路线是小明→B→A,即在B处捡球,才能最快拿到球跑到目的地A.解答题公园内两条小河MO,NO在O处汇合,两河形成的半岛上有一处景点P(如图所示).现计划在两条小河上各建一座小桥Q和R,并在半岛上修三段小路,连通两座小桥与景点,这两座小桥应建在何处才能使修路费用最少?请说明理由.【答案】见解析【解析】试题分析:可过点P分别作关于OM,ON的对称点P′,P″,连接P′P″,与OM、ON的交点即为满足条件的建桥地点.试题解析:如图,作P关于OM的对称点P′,作P关于ON的对称点P″,连接P′P″,分别交MO,NO于Q,R,连接PQ,PR,则P′Q=PQ,PR=P″R,则Q,R就是小桥所在的位置.理由:在OM上任取一个异于Q的点Q′,在ON上任取一个异于R的点R′,连接PQ′,P′Q′,Q′R′,P″R′,PR′,则PQ′=P′Q′,PR′=P″R′,且P′Q′+Q′R′+R′P″>P′Q+QR+RP″,所以△PQR的周长最小,故Q,R就是我们所求的小桥的位置.解答题如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD,且AC=BD。
最新人教版八年级数学上册13.4 课题学习 最短路径问题习题课件

E , F 分别是 BC , DC 上的点 , 当△ AEF 的周长最小时 , ∠ E70° D.80°
7.(10分)如图,已知M,N分别是∠AOB的边OA上任意两点. (1)尺规作图:作∠AOB的平分线OC; (2)在∠AOB的平分线OC上求作一点P,使PM+PN的值最小.(保留 作图痕迹,不写画法)
解:连接DE交AC于点P,得PB=PD,则点P即为所求,作图略
5.(5分)如图,点P是∠AOB内任意一点,OP=5 cm,点M和点N分别
是射线OA和射线OB上的动点,△PMN周长的最小值是5 cm,则∠AOB
的度数是( B )
A.25 ° B.30° C.35° D.40°
6.(5分)如图,在四边形ABCD中,∠C=50°,∠B=∠D=90°,
,则AQ+PQ+BP即为所求的最短路径
3.(6分)如图,需要在高速公路旁边修建一个飞机场,使飞机场到A, B两个城市的距离之和最小,请作出机场的位置.
解:做点A关于直线的对称点A',连接A'B交直线于点P,则点P即为 飞机场所在的位置,作图略
4.(6分)如图,在正方形ABCD中,点E是AB的中点,在AC上确定一点 P,使PE+PB最短,请在图上画出点P的位置.(不写作法,保留作图痕 迹)
解:(1)作图略
(2)作点M关于OC的对称点M′,连接M′N交OC于点P
,则MN的长度即为PM+PN的最小值
【综合运用】
8.(10分)如图,牧马人从A地出发,先到草地边某一处牧马,再到河
边饮马,然后回到B处,请画出最短路径.
解:分别作点A关于草地边界的对称点A',点B关于河岸的对称点B'
,连接A'B'分别交草地边界和河岸于点Q,P,此时A'Q=AQ,B'P=BP
初中数学人教版八年级上册第十三章 轴对称13.4 课题学习 最短路径问题-章节测试习题(2)

章节测试题1.【答题】如图,在△ABC中,AB=6,BC=7,AC=4,直线m是△ABC中BC边的垂直平分线,点P是直线m上的一动点.则△APC周长的最小值为()A. 10B. 11C. 11.5D. 13【答案】A【分析】根据题意知点C关于直线m的对称点为点B,故当点P与点D重合时,AP+CP值的最小,求出AB长度即可得到结论.【解答】∵直线m垂直平分AB,∴B、C关于直线m对称,设直线m交AB于D,∴当P和D重合时,AP+CP的值最小,最小值等于AB的长,∴△APC周长的最小值是6+4=10.选A.2.【答题】如图所示,在等边△ABC中,E是AC边的中点,AD是BC边上的中线,P是AD上的动点,若AD=5,则EP+CP的最小值为()A. 2B. 4C. 5D. 7【答案】C【分析】要求EP+CP的最小值,需考虑通过作辅助线转化EP,CP的值,从而找出其最小值求解.【解答】作点E关于AD的对称点F,连接CF,∵△ABC是等边三角形,AD是BC边上的中线,∴AD⊥BC,∴AD是BC的垂直平分线,∴点E关于AD的对应点为点F,∴CF就是EP+CP的最小值.∵△ABC是等边三角形,E是AC边的中点,∴F是AB的中点,∴CF是△ABC的中线,∴CF=AD=5,即EP+CP的最小值为5,选C.3.【答题】如图,△ABC中,点D在BC边上,过D作DE⊥BC交AB于点E,P为DC上的一个动点,连接PA、PE,若PA+PE最小,则点P应该满足()A. PA=PCB. PA=PEC. ∠APE=90°D. ∠APC=∠DPE【答案】D【分析】作点E关于直线BC的对称点F,连接AF交BC于P,此时PA+PE的值最小,依据轴对称的性质即可得到∠APC=∠DPE.【解答】如图,作点E关于直线BC的对称点F,连接AF交BC于P,此时PA+PE的值最小.由对称性可知:∠EPD=∠FPD,∵∠CPA=∠FPD,∴∠APC=∠DPE,∴PA+PE最小时,点P应该满足∠APC=∠DPE,选D.4.【答题】如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P、Q分别是边OB,OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1,∠2的数量关系正确的是()A. ∠1+∠2=90°B. 2∠2-∠1=30°C. 2∠1+∠2=180°D. ∠1-∠2=90°【答案】D【分析】如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小,根据外角的性质得到∠1=∠O+∠OPM,∠OPM=∠1-∠O=∠1-30°,由轴对称的性质得到∠OPM=∠OPM′,∠OPM′=∠QPN,于是得到∠QPN=∠1+30°,由于∠3=∠O+∠2=30°+∠2,∠NQN′=∠QPN+∠2=∠1-30°+∠2,∠NQN′=2∠3,即可得到结论.【解答】如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小,∵∠1=∠O+∠OPM,∴∠OPM=∠1-∠O=∠1-30°,∵∠OPM=∠OPM′,∠OPM′=∠QPN,∴∠QPN=∠PQO+30°∵∠3=∠O+∠2=30°+∠2,∠NQN′=∠QPN+∠2=∠1-30°+∠2,∠NQN′=2∠3,∴∠1-30°+∠2=2(30°+∠2),∴∠1-∠2=90°.选D.5.【答题】如图,点E在等边△ABC的边BC上,BE=6,射线CD⊥BC于点C,点P是射线CD上一动点,点F是线段AB上一动点,当EP+PF的值最小时,BF =9,则AC为()A. 14B. 13C. 12D. 10【答案】C【分析】根据等边三角形的性质得到AC=BC,∠B=60°,作点E关于直线CD的对称点G,过G作GF⊥AB于F,交CD于P,则此时,EP+PF的值最小,根据直角三角形的性质得到BG=2BF=18,求得EG=12,于是得到结论.【解答】∵△ABC是等边三角形,∴AC=BC,∠B=60°,作点E关于直线CD的对称点G,过G作GF⊥AB于F,交CD于P,则此时,EP+PF的值最小,∵∠B=60°,∠BFG=90°,∴∠G=30°,∵BF=9,∴BG=2BF=18,∴EG=12,∵CE=CG=6,∴AC=BC=12,选C.6.【答题】如图,等腰△ABC的底边BC长为6,面积是36,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为()A. 6B. 10C. 15D. 16【答案】C【分析】根据对称性和等腰三角形的性质,连接AD交EF于点M,此时△CDM周长最小,进而可求解.【解答】如图:连接AD交EF于点M,∵等腰△ABC的底边BC长为6,点D为BC边的中点,∴AD⊥BC,BD=CD=3,∵EF是腰AC的垂直平分线,连接CM,∴AM=CM,此时△CDM的周长为:CM+DM+CD=AM+DM+CD=AD+CDCD的长为3固定,∴根据两点之间线段最短,△CDM的周长最小.∵S△ABC BC•AD,∴6•AD=36,∴AD=12,∴AD+CD=12+3=15.选C.7.【答题】如图所示,∠MON=45°,点P为∠MON内一点,点P关于OM、ON对称的对称点分别为点P1、P2,连接OP、OP1、OP2、PP1、PP2、P1P2,P1P2分别与OM、ON交于点A、B,连接AP,BP,则∠APB的度数为()A. 45°B. 90°C. 135°D. 150°【答案】B【分析】依据轴对称的性质,即可得到∠APO=∠AP1O,∠AOP=∠AOP1,∠BPO=∠BP2O,∠BOP=∠BOP2,进而得出∠OP1P2+∠OP2P1=90°,再根据∠APB=∠APO+∠BPO=∠AP1O+∠BP2O,即可得出结论.【解答】由轴对称可得,OP=OP1、AP=AP1,而AO=AO,∴△AOP≌△AOP1(SSS),∴∠APO=∠AP1O,∠AOP=∠AOP1,同理可得,∠BPO=∠BP2O,∠BOP=∠BOP2,∴∠P1OP2=2∠AOB=90°,∴∠OP1P2+∠OP2P1=90°,∴∠APB=∠APO+∠BPO=∠AP1O+∠BP2O=90°,选B.8.【答题】如图,四边形ABCD中,∠BAD=121°,∠B=∠D=90°,在BC、CD上分别找到一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为()A. 118°B. 121°C. 120°D. 90°【答案】A【分析】如图,四边形ABCD中,∠BAD=121°,∠B=∠D=90°,在BC、CD上分别找到一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为【解答】如下图,作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,∵∠DAB=121°,∴∠HAA′=59°,∴∠AA′M+∠A″=∠HAA′=59°,∵∠MA′A=∠MAA′,∠NAD=∠A″,且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×59°=118°.选A.9.【答题】如图,∠AOB=20°,M,N分別是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是()A. β-α=30°B. β-α=40°C. β+α=180°D. β+α=200°【答案】D【分析】如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小易知∠OPM=∠OPM′=∠NPQ,∠OQP =∠AQN′=∠AQN,KD∠OQN=180°-20°-∠ONQ,∠OPM=∠NPQ=20°+∠OQP,∠OQP=∠AQN=20°+∠ONQ,由此即可解决问题.【解答】如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小,易知∠OPM=∠OPM′=∠NPQ,∠OQP=∠AQN′=∠AQN,∵∠OQN=180°-20°-∠ONQ,∠OPM=∠NPQ=20°+∠OQP,∠OQP=∠AQN=20°+∠ONQ,∴α+β=180°-20°-∠ONQ+20°+20°+∠ONQ=200°.选D.10.【答题】已知:如图,∠AOB=45°,点P为∠AOB内部的点,点P关于OB,OA的对称点P1,P2的连线交OA,OB于M,N两点,连接PM,PN,若OP=2,则△PMN的周长=______.【答案】【分析】根据题意和轴对称的性质,利用勾股定理可以得到P1P2的长,从而可以得到△PMN的周长.【解答】连接OP1,OP2,由题意可得,OP1=OP,OP2=OP,∠P1OB=∠POB,∠POA=∠P2OA,∵∠AOB=45°,OP=2,∴∠P1OP2=90°,OP1=OP2=2,∴P1P2=2,∵PN=P1N,PM=P2M,∴PM+PN+MN=P2M+P1N+MN=P1P2=2,即△PMN的周长=2,故答案为:2.11.【答题】如图,等腰三角形ABC的底边BC长为2,面积是4,腰AC的垂直平分线EF分别交AC、AB边于E、F点,若点D为BC边的中点,点M为线段EF 上一动点,则△CDM周长的最小值是______.【答案】5【分析】连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据三角形的面积公式求出AD的长,再再根据EF是线段AC的垂直平分线可知,点C关于直线EF的对称点为点A,故AD的长为CM+MD的最小值,由此即可得出结论.【解答】连接AD,∵△ABC是等腰三角形,点D是BC边的中点,∴AD⊥BC,∴S△ABC BC•AD2×AD=4,解得AD=4,∵EF是线段AC的垂直平分线,∴点C关于直线EF的对称点为点A,∴AD的长为CM+MD的最小值,∴△CDM周长的最小值=(CM+MD)+CD=AD BC=42=4+1=5.故答案为:5.12.【答题】如图,等边△ABC中,作∠ABP=18°交AC于点P,Q为边BC上一点,连接PQ,当BP+PQ的值最小时,∠BPQ=______°.【答案】48【分析】过B点作PQ′⊥BC于Q′,根据角的和差关系求出∠PBQ′,再根据直角三角形的性质求出当BP+PQ的值最小时∠BPQ的度数,从而求解.【解答】过B点作PQ′⊥BC于Q′,∵△ABC是等边三角形,∴∠ABC=60°,∵∠ABP=18°,∴∠PBQ′=60°-18°=42°,∴当BP+PQ的值最小时,∠BPQ=90°-42°=48°.故答案为:48.13.【答题】如图,直线m是△ABC中BC边的垂直平分线,点P是直线m上的一动点.若AB=6,AC=4,BC=7,则△APC周长的最小值是______.【答案】10【分析】根据题意知点C关于直线m的对称点为点B,故当点P与点D重合时,AP+CP值的最小,求出AB长度即可得到结论.【解答】∵直线m垂直平分AB,∴B、C关于直线m对称,设直线m交AB于D,∴当P和D重合时,AP+CP的值最小,最小值等于AB的长,∴△APC周长的最小值是6+4=10.故答案为10.14.【答题】如图,AB⊥BC,AD⊥DC,∠BAD=100°,在BC、CD上分别找一点M、N,当△AMN的周长最小时,∠AMN+∠ANM的度数是______.【答案】160°【分析】根据要使△AMN的周长最小,即利用点的对称,使三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,即可得出∠AA′M+∠A″=∠AA″A′=80°,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″),即可得出答案.【解答】作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.∵∠DAB=100°,∴∠AA′M+∠A″=80°.由轴对称图形的性质可知:∠MA′A=∠MAA′,∠NAD=∠A″,且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×80°=160°.故答案为:160°.15.【答题】如图,在等边三角形ABC中,AD⊥BC,垂足为D,且AD=6,E是AC边上的中点,M是AD边上的动点,则EM+CM的最小值是______.【答案】6【分析】连接BE,交AD于M,则BE就是PE+PC的最小值,根据等边三角形的三线合一的性质从而证得BE=AD=6.【解答】如图所示:∵AD是BC边上的中线,∴AD等边三角形ABC的边BC上的高,∴AD是BC的垂直平分线,连接BE,交AD于M,则BE就是EM+CM的最小值,∵E是AC的中点,∴BE是等边三角形ABC的边AC上的高,∴BE=AD,∵等边三角形ABC的边BC上的高为6,∴BE=AD=6.∴EM+CM的最小值是6.故答案为:6.16.【答题】如图,在等边三角形ABC中,BC边上的高AD=6,E是高AD上的一个动点,F是边AB的中点,在点E运动的过程中,存在EB+EF的最小值,则这个最小值是______.【答案】6【分析】先连接CF,再根据EB=EC,将FE+EB转化为FE+CE,最后根据两点之间线段最短,求得CF的长,即为FE+EB的最小值.【解答】连接CF,∵等边△ABC中,AD是BC边上的中线∴AD是BC边上的高线,即AD垂直平分BC∴EB=EC,当B、F、E三点共线时,EF+EC=EF+BE=CF,∵等边△ABC中,F是AB边的中点,∴AD=CF=6,∴EF+BE的最小值为6,故答案为:617.【答题】如图,牧马人从A地出发,先到草地边MN的某处点C牧马,再到河边EF的某处点D牧马,然后回到B处,若从A到B走的是最短路径,CA与DB 的延长线交于点H,设锐角∠1=α,则∠2的的大小为______(用含α的式子表示).【答案】180°-2α【分析】作A于MN的对称点A′,B关于EF的对称点B′,连接A′B′交MN于C,交EF于D,此时AC+CD+BD的值最小.【解答】作A于MN的对称点A′,B关于EF的对称点B′,连接A′B′交MN于C,交EF于D,此时AC+CD+BD的值最小.∵∠2=180°-(∠ACD+∠BDC)∠ACD=180°-2∠NCD,∠BDC=180°-2∠NDC,∴∠2=180°-[360°-2(∠NCD+∠NDC)]=180°-[360°-2(180°-∠1)]=180°-2∠1=180°-2α,故答案为180°-2α.18.【题文】用直尺和圆规作图:(保留作图痕迹,不写作法)在直线m上求作一点P,使得PA+PB最短.【答案】见解答【分析】作点A关于直线m的对称点A′,连接BA′交直线m于点P,点P即为所求.【解答】如图,点P即为所求.19.【题文】如图,点A,B,C都在网格的格点上,每小方格是边长为1个单位长度的正方形.利用格点和直尺画图并填空:(1)画出格点△ABC关于直线MN轴对称的△A′B'C′;(2)画出△ABC中BC边上的高线AD;【答案】见解答【分析】(1)利用网格特点和对称的性质画出A、B、C的对称点A′、B′、C′即可;(2)利用网格特点和三角形高的定义画图;【解答】(1)如图,△A′B'C′为所作;(2)如图,AD为所作;20.【题文】如图所示,有两个村庄A,B在一公路CD的一侧,如果把A,B村庄的位置放在格点图中.(1)请作出A点关于CD的对称点A′;(2)若要在公路CD上修建一个菜鸟驿站P,使得驿站到两个村庄的线段距离和最小,请作出P点的位置.【答案】见解答【分析】(1)直接利用对称点的性质进而得出答案;(2)直接利用轴对称设计求最短路线的方法得出P点位置.【解答】(1)如图所示:A′点即为所求;(2)如图所示:点P即为所求.。
八年级数学上册第十三章轴对称13.4课题学习最短路径问题同步训练新版新人教版

13.4 课题学习最短路径问题[学生用书P63]1.如图13-4-6,已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,∠APB的度数是( )A.40° B.100° C.140° D.50°图13-4-62.如图13-4-7所示,四边形EFGH是一个矩形的台球桌面,有黑白两球分别位于A,B 两点,试说明怎样撞击B,才能使白球先撞击台球桌边EF,反弹后又能击中黑球A?图13-4-73.如图13-4-8,点A,B在直线m的同侧,点B′是点B关于m的对称点,AB′交m 于点P.(1)AB′与AP+BP相等吗?为什么?(2)在m上再取一点N,并连接AN与BN,比较AN+BN与AP+BP的大小,并说明理由.图13-4-84.[2015·鄂尔多斯]如图13-4-9,A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMMNNB最短的是(假定河的两岸是平行直线,桥要与河岸垂直)( D )图13-4-9A BC D5.[2015·营口改编]如图13-4-10,点P 是∠AOB 内任意一点,OP =5 cm ,点M 和点N 分别是射线OA 和射线OB 上的动点,△PMN 周长的最小值是5 cm ,求∠AOB 的度数.图13-4-106.[2016·百色]如图13-4-11,等边△ABC的边长为2,过点B的直线l⊥AB,且△ABC 与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是( A )图13-4-11A.4 B.3 2C.2 D.2+ 3参考答案【归类探究】例1略例2略【当堂测评】1.B 2.D 3.略【分层作业】1.B 2.略3.(1)AB′=AP+BP,理由略;(2)AN+BN>AP+BP,理由略.4.D 5.∠AOB=30° 6.A。
八年级数学上册 13.4课题学习最短路径问题课件2_6-10

当堂练习
1.如图,直线m同侧有A、B两点,A、A′关于直线m对称,A、B关于 直线n对称,直线m与A′B和n分别交于P、Q,下面的说法正确的是 ( A) A.P是m上到A、B距离之和最短的
点,Q是m上到A、B距离相等的点 B.Q是m上到A、B距离之和最短的
点,P是m上到A、B距离相等的点 C.P、Q都是m上到A、B距离之和最
问题解决
A
如图,平移A到A1,使AA1等于河宽,连接A1BA1 交河岸于N作桥MN,此时路径AM+MN+BN最
短.
M
M1
N
N1
B
理由:另任作桥M1N1,连接AM1,BN1,A1N1. 由平移性质可知,AM=A1N,AA1=MN=M1N1,AM1=A1N1.
AM+MN+BN转化为AA1+A1B, 而AM1+M1N1+BN1转化为AA1+A1N1+BN1.
短的点 D.P、Q都是m上到A、B距离相等
的点
” 说完,马倒下死了。大家都推得满头大汗,鞋袜尽沾污泥,而有一个聪明人,光站在一旁指挥: “向这边,向这边,我看到了,轮子差不多要上来了。既然如此,何必一定要将他人的优点充作自已的,而把自已的缺点推给别人呢。
综艺在线观看 https:///index.php/vod/type/id/3.html
“想不想听月下演唱会?”阿土笑着问。” 一天,狐狸到处找吃的,实在饿极了,他一把抓住鸭子。,它继续向前走着,忽然看见了它的好朋友小牛,小牛见小木桥上有一个洞,于是拿来工具认认真真地修补起来
AC+CD+DB=AC+CD+CE=AC+CE+MN,
在△+MN>AE+MN, 即AC+CD+DB >AM+MN+BN,
八年级数学上册第十三章轴对称13.4课题学习最短路径问题同步训练新版新人教版
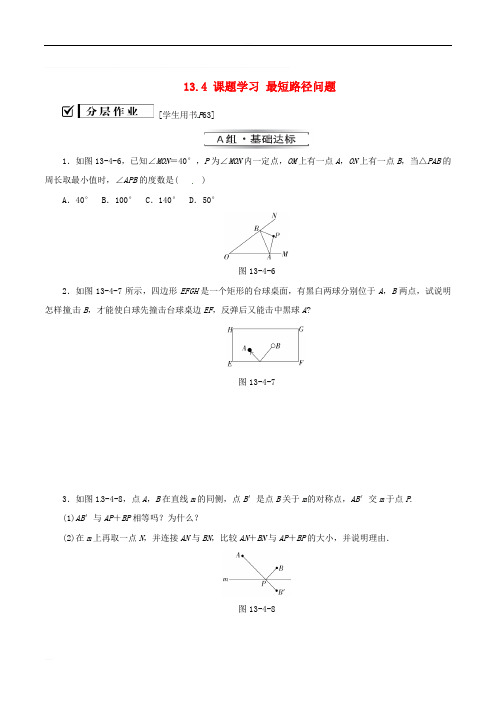
13.4 课题学习最短路径问题[学生用书P63]1.如图13-4-6,已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,∠APB的度数是( )A.40° B.100° C.140° D.50°图13-4-62.如图13-4-7所示,四边形EFGH是一个矩形的台球桌面,有黑白两球分别位于A,B两点,试说明怎样撞击B,才能使白球先撞击台球桌边EF,反弹后又能击中黑球A?图13-4-73.如图13-4-8,点A,B在直线m的同侧,点B′是点B关于m的对称点,AB′交m于点P.(1)AB′与AP+BP相等吗?为什么?(2)在m上再取一点N,并连接AN与BN,比较AN+BN与AP+BP的大小,并说明理由.图13-4-84.[2015·鄂尔多斯]如图13-4-9,A 和B 两地在一条河的两岸,现要在河上造一座桥MN ,使从A 到B 的路径AMMNNB 最短的是(假定河的两岸是平行直线,桥要与河岸垂直)( D )图13-4-9A BC D5.[2015·营口改编]如图13-4-10,点P 是∠AOB 内任意一点,OP =5 cm ,点M 和点N 分别是射线OA 和射线OB 上的动点,△PMN 周长的最小值是5 cm ,求∠AOB 的度数.图13-4-106.[2016·百色]如图13-4-11,等边△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是( A )图13-4-11A.4 B.3 2C.2 D.2+ 3参考答案【归类探究】例1略例2略【当堂测评】1.B 2.D 3.略【分层作业】1.B 2.略3.(1)AB′=AP+BP,理由略;(2)AN+BN>AP+BP,理由略.4.D 5.∠AOB=30°6.A。
人教版初中数学八年级上册精品教学课件 第13章 轴对称 13.4 课题学习 最短路径问题
互动课堂理解
利用轴对称求最短路径 【例题】 如图,在△ABC中,BC=5,S△ABC=15,AD⊥BC于点D,EF 垂直平分AB,交AB于点E,交AC于点F,在EF上确定一点P使PB+PD 最小,则这个最小值为( ). A.3 B.4 C.5 D.6 分析根据三角形的面积公式得AD=6,由EF垂直平分AB,知点A,B 关于直线EF对称,于是得到AD的长度为PB+PD的最小值,即可得出 结论.
关闭
D
答案
快乐预习感知
1
2
3
2.在直角坐标系中有A,B两点,要在y轴上找一点C,使得它到A,B两点 的距离之和最小,现有如下四种方案,其中正确的是( ).
关闭
C
答案快乐预习感知1源自233.已知点A(-2,1),B(3,2),在x轴上求一点P,使AP+BP最小,下列作法正 确的是( ). A.使点P与O(0,0)重合 B.连接AB并延长交x轴于点P,点P即为所求 C.过点A作x轴的垂线,垂足为P,点P即为所求 D.作点A关于x轴的对称点A',连接A'B,交x轴于点P,点P即为所求
13.4 课题学习 最短路径问题
快乐预习感知
1.前面我们研究过一些关于“两点的所有连线中,线段最短”“连接 直线外一点与直线上各点的所有线段中,垂线段最短”等的问题,我 们称它们为 最短路径 问题.
2.在解决最短路径问题时,我们通常利用 轴对称 、 平移 等 变化把已知问题转化为容易解决的问题,从而作出最短路径的选 择.
关闭
D
答案
谢谢聆听
互动课堂理解
解析: ∵BC=5,S△ABC=15,AD⊥BC于点D, ∴AD=6. ∵EF垂直平分AB, ∴点A,B关于直线EF对称.
人教版数学 八年级上册 13.4 课题学习 最短路径问题 课后练习题
一、单选题1. 如图所示,∠AOB=60°,点P是∠AOB内一定点,并且OP=2,点M、N分别是射线OA,OB上异于点O的动点,当△PMN的周长取最小值时,点O到线段MN 的距离为()A.1 B.2 C.4 D.1.52. 某开发商的经适房的三个居民小区A、B、C在同一条直线上,位置如图所示.其中小区B到小区A、C的距离分别是70m和150m,现在想在小区A、C之间建立一个超市,要求各小区居民到超市总路程的和最小,那么超市的位置应建在()A.小区A B.小区B C.小区C D.AC的中点3. 如图,等腰三角形的底边长为4,面积是24,腰的垂直平分线分别交边于点.若点为边上的中点,点为线段上一动点则周长的最小值为( )A.12 B.14 C.16 D.244. 如图,某公司有三个住宅区,A,B,C各区分别住有职工10人,15人,45人,且这三个区在一条大道上(A,B,C三点共线),已知AB=150m,BC=90m.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在()A.点A B.点B C.点A,B之间D.点C5. 把一条弯曲的公路改成直道,可以缩短路程.用几何知识解释其道理正确的是()A.两点确定一条直线B.垂线段最短C.两点之间线段最短D.以上结论都不对二、填空题6. 阅读下面材料:在数学课上,老师提出如下问题:如图,在一个圆锥形状的包装盒的底部A处有一只壁虎,在侧面B处有一只小昆虫,壁虎沿着什么路线爬行,才能以最短的路线接近小昆虫?请你设计一种最短的爬行路线.下面是班内三位同学提交的设计方案:根据以上信息,你认为________同学的方案最正确,理由是______________________.7. 有一长、宽、高分别是5cm,4cm,3cm的长方体木块,一只蚂蚁要从长方体的一个顶点A处沿长方体的表面爬到长方体上和A相对的顶点B处,则需要爬行的最短路径长为_____.8. 如图,在等边三角形ABC中,BC边上的中线,E是AD上的一个动点,F 是边AB上的一个动点,在点E、F运动的过程中,的最小值是______.三、解答题9. 如图所示,点为(其中为锐角)内的一点,,分别为点P关于,的对称点,连接,交于点M,交于点N,已知.连接,.(1)求的周长.(2)若一动点从点P出发,到达上一点,再从这点出发到达上一点,然后又回到点P,所经过的最短路程是多少?请说明理由.10. 如图,在长度为1个单位长度的小正方形组成的正方形网格中,△ABC的三个顶点A、B、C都在格点上.(1)在图中画出与△ABC关于直线L成轴对称的△A′B′C′;(2)求△ABC的面积.(3)在直线L上找出一点P,使得PA+PC的值最小.(在图上直接标记出点P的位置)11. 如图,一个五棱柱的盒子(有盖),有一只蚂蚁在A处发现一只虫子在D处,立刻赶去捕捉,你知道它怎样去的吗?请在图中画出它的爬行路线,如果虫子正沿着DI方向爬行,蚂蚁预想在点I处将它捕捉,应沿着什么方向?请在图中画出它的爬行路线.。
人教版八年级数学上册练习13.4 课题学习 最短路径问题 课后训练
课后训练基础巩固1.有两棵树位置如图,树脚分别为A,B.地上有一只昆虫沿A—B的路径在地面上爬行.小树顶D处一只小鸟想飞下来抓住小虫后,再飞到大树的树顶C处,问小鸟飞至AB 之间何处时,飞行距离最短,在图中画出该点的位置.2.已知,如图所示,甲、乙、丙三个人做传球游戏,游戏规则如下:甲将球传给乙,乙将球立刻传给丙,然后丙又立刻将球传给甲.若甲站在∠AOB内的P点,乙站在OA上,丙站在OB上,并且甲、乙、丙三人的传球速度相同.问乙和丙必须站在何处,才能使球从甲到乙、乙到丙、最后丙到甲这一轮所用的时间最少?3.如图所示,P,Q为△ABC边上的两个定点,在BC上求作一点R,使△PQR的周长最小.4.七年级(1)班同学做游戏,在活动区域边OP放了一些球(如图),则小明按怎样的路线跑,去捡哪个位置的球,才能最快拿到球跑到目的地A?能力提升5.公园内两条小河MO,NO在O处汇合,两河形成的半岛上有一处景点P(如图所示).现计划在两条小河上各建一座小桥Q和R,并在半岛上修三段小路,连通两座小桥与景点,这两座小桥应建在何处才能使修路费用最少?请说明理由.6.如图,牧童在A处放牛,其家在B处,A,B到河岸CD的距离分别为AC,BD,且AC=BD,若A到河岸CD的中点的距离为500 m.(1)牧童从A处把牛牵到河边饮水后再回家,试问在何处饮水,所走路程最短?在图中作出该处,并说明理由;(2)最短路程是多少?参考答案1.解:如图,作D关于AB的对称点D′,连接CD′交AB于点E,则点E就是所求的点.2.解:如图所示,(1)分别作点P关于OA,OB的对称点P1,P2;(2)连接P1P2,与OA,OB分别相交于点M,N.因为乙站在OA上,丙站在OB上,所以乙必须站在OA上的M处,丙必须站在OB上的N处才能使传球所用时间最少.3.解:(1)作点P关于BC所在直线的对称点P′;(2)连接P′Q,交BC于点R,则点R就是所求作的点(如图所示).4.解:如图,作小明关于活动区域边线OP的对称点A′,连接AA′交OP于点B,则小明行走的路线是小明→B→A,即在B处捡球,才能最快拿到球跑到目的地A.5.解:如图,作P关于OM的对称点P′,作P关于ON的对称点P″,连接P′P″,分别交MO,NO于Q,R,连接PQ,PR,则P′Q=PQ,PR=P″R,则Q,R就是小桥所在的位置.理由:在OM上任取一个异于Q的点Q′,在ON上任取一个异于R的点R′,连接PQ′,P′Q′,Q′R′,P″R′,PR′,则PQ′=P′Q′,PR′=P″R′,且P′Q′+Q′R′+R′P″>P′Q+QR+RP″,所以△PQR的周长最小,故Q,R就是我们所求的小桥的位置.6.解:(1)作法:如图作点A关于CD的对称点A′;连接A′B交CD于点M.则点M即为所求的点.证明:在CD上任取一点M′,连接AM′,A′M′,BM′,AM,因为直线CD是A,A′的对称轴,M,M′在CD上,所以AM=A′M,AM′=A′M′,所以AM+BM=A′M+BM=A′B,在△A′M′B中,因为A′M′+BM′>A′B,所以AM′+BM′=A′M′+BM′>AM+BM,即AM+BM最小.(2)由(1)可得AM=A′M,A′C=AC=BD,所以△A′CM≌△BDM,即A′M=BM,CM=DM,所以M为CD的中点,且A′B=2AM,因为AM=500m,所以A′B=AM+BM=2AM=1 000 m.即最短路程为1 000 m.。
数学人教八年级上册《13 .4课题学习 最短路径问题》习题2
《13.4课题学习最短路径问题》习题
1、如图,村庄A、B位于一条小河的两侧,若河岸a、b彼此平行,现在要建设一座与河岸垂直的桥CD,问桥址应如何选择,才能使A村到B村的路程最近?
2、如图,小河边有两个村庄A、B.要在河边建一自来水厂向A村与B村供水.
(1)若要使厂部到A、B村的距离相等,则应选择在哪建厂?
(2)若要使厂部到A、B村的水管最省料,应建在什么地方?
3、如图,两条公路OA、OB相交,在两条公路的中间有一个油库,设为点P,如在两条公路上各设置一个加油站,
(1)若要使油库分别到两个加油站距离最短,应在何处设置加油站?
(2)若要使运油车从油库出发,经过一个加油站,再到另一个加油站,最后回到油库所走的路程最短,应如何设置?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
13.4课题学习最短路径问题课时练习
一、选择题
1.如图,在直角坐标系中有线段AB,AB=50cm,A、B到x轴的距离分别为10cm和40cm,B点到y轴
的距离为30cm,现在在x轴、y轴上分别有动点P、Q,当四边形PABQ的周长最短时,则这个值为( )
A.50 B.505 C.505-50 D.505+50
2.如图,在平面直角坐标系中,点A(-2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的
距离之和最小,则点P的坐标是( )
A.(-2,0) B.(4,0) C.(2,0) D.(0,0)
3.如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若
AE=2,当EF+CF取得最小值时,则∠ECF的度数为( ).
A.15° B.22.5° C.30° D.45°
4.如图,∠AOB=30°,内有一点P且OP=6,若M、N为边OA、OB上两动点,那么△PMN的周长
最小为( ).
A.62 B. 6 C.621 D.6
5.已知两点M(3,5),N(1,-1),点P是x轴上一动点,若使PM+PN最短,则点P的坐标应为( ).
A.(21,-4) B.(32,0) C.(34,0) D.(23,0)
二、填空题
6.如图,已知AB⊥AD,CD⊥AD,垂足分别为A、D,AD=6,AB=5,CD=3,P是线段AD上的一个
动点,设AP=x,DP=y,92522yxa,则a的最小值是______.
7.已知如图所示,∠MON=40°,P为∠MON内一点,A为OM上一点,B为ON上一点,则当△PAB的
周长取最小值时,∠APB的度数为_____.
8.如图,在△ABC中,AC=BC=2,∠ACB=90°,D是BC边的中点,E是AB边上一动点,则EC+ED
的最小值是_____.
9.已知:如图所示,M(3,2),N(1,-1).点P在y轴上使PM+PN最短,则P点坐标为_________.
10.如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4,E是AB边的中点,F是AC边的中点,
则(1)EF=____;(2)若D是BC边上一动点,则△EFD的周长最小值是____.
三、解答题
11.已知:如图,在∠POQ内部有两点M、N,∠MOP=∠NOQ.
(1)画图并简要说明画法:在射线OP上取一点A,使点A到点M和点N的距离和最小;在射线OQ上
取一点B,使点B到点M和点N的距离和最小;
(2)直接写出AM+AN与BM+BN的大小关系.
12.某大型农场拟在公路L旁修建一个农产品储藏、加工厂,将该农场两个规模相同的水果生产基地A、B
的水果集中进行储藏和技术加工,以提高经济效益.请你在图中标明加工厂所在的位置C,使A、B两地到
加工厂C的运输路程之和最短.(要求:用尺规作图,保留作图痕迹,不写作法和证明)
参考答案
1.D
2.C
3.C
4.D
5.C
6.10
7.100°
8.5
9.(0,-41)
10.2;2+213
11.(1)如图所示.
画法:
①作点M关于射线OP的对称点M',
②连接M'N交OP于点A.
③作点N关于射线OQ的对称点N',
④连接N'M交OQ于点B.
(2)答:AM+AN与BM+BN的大小关系是:AM+AN=BM+BN.
12.如图
