割补法生活中的应用

合集下载

6年级与圆的面积和周长相关的问题平移旋转割补对称的应用(答案)

六年级篇
与圆的面积和周长相关的问题
解决圆相关问题常用的思想方法： ①转化思想(复杂转化为简单，不熟悉的转化为熟悉的) ②等积变形(割补、平移、旋转、翻转、对称等) ③整体局部 ④内外结合(从会求的图形或者能求的图形入手，看与要求的部分之间的”关系”) 第一部分平移、旋转、割补、对称在曲线型面积中的应用
分析与解：看到这道题，一下就会知道解决方法就是求出空白部分的面积，再通过作差来求出阴影部分面积，因为阴影部分非常不规则，无法入手．这样，平移和旋转就成了我们首选的方法．
法 1:我们只用将两个半径为 10 厘米的四分之一圆减去空白的①、②部分面积之和即可，其中①、②面积相等．易知①、②部分均是等腰直角三角形，但是①部分的直角边 AB 的长度未知．单独求①部分面积不易，于是我们将①、 ②部分平移至一起，如右下图所示，则①、②部分变为一个以 AC 为直角边的等腰直角三角形，而 AC 为四分之一圆的半径，所以有 AC 10．两个四分之一圆的面积和为 150，而①、②部分的面积和为 10 10 50 ，所以阴影部分的面积为 150 50 100 (平方厘米)．法 2:欲求图①中阴影部分的面积，可将左半图形绕 B 点逆时针方向旋转 180°，使 A 与 C 重合，从而构成如右图②的样子，此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积．所以阴影部分面积为 102 10 10 100 (平方厘米)．
8
6
(2)
分析与解：在图(1)中，阴影部分经过切割平移变成了一个底为 10，高为 5 的三角形，利用三角形面积公式可以求得 S阴影 10
1 2 10 25 ； 2
在图(2)中，阴影部分经过切割平移变成了一个长为 b，宽为 a 的长方形，利用长方形面积公式可以求得 S阴影 a b ab ． 6.如图， ABCD 是正方形，且 FA AD DE 1 ，求阴影部分的面积．(取 π 3 )

割补法技巧总结

割补法技巧总结割补法是一种常用于修复软件漏洞的技术，它通过对漏洞进行分析，找出并修复其中的问题，从而提高软件的安全性和稳定性。

本文将从割补法的基本原理、具体步骤以及常见技巧三个方面进行总结，帮助读者更好地理解和应用割补法。

一、基本原理割补法的基本原理是通过对软件漏洞的分析，找出漏洞的根本原因，并修复其中的问题。

它的核心思想是将漏洞视为一个整体，并通过分析漏洞的特点和影响来确定修复的方案。

在修复过程中，割补法通常会采用一些特定的技巧和方法，以确保修复的效果和安全性。

二、具体步骤割补法的具体步骤包括漏洞分析、修复方案设计、代码实现和测试验证等几个关键环节。

首先，需要对漏洞进行详细的分析，找出漏洞的产生原因和可能的影响范围。

然后，根据分析结果设计相应的修复方案，并对修复方案进行实施。

最后，通过测试验证修复效果，确保修复的漏洞不再存在。

三、常见技巧1. 异常处理：在代码实现中，合理处理异常情况是割补法的重要技巧之一。

通过对可能出现的异常情况进行预判，并进行相应的处理，可以有效地避免漏洞的产生。

2. 输入验证：对于用户输入的数据，割补法通常会进行验证和过滤，以防止恶意输入导致的安全问题。

常见的验证方法包括长度检查、类型检查和特殊字符过滤等。

3. 边界检查：在代码实现中，对于循环、数组和指针等结构，割补法会进行边界检查，以避免数组越界、循环溢出和空指针引用等问题。

4. 内存管理：合理的内存管理是割补法的关键技巧之一。

通过使用动态内存分配函数和垃圾回收机制，可以避免内存泄漏和内存溢出等问题。

5. 日志记录：割补法通常会加入日志记录功能，以便对软件的运行情况进行监控和分析。

通过记录关键操作和异常情况，可以及时发现和修复潜在的漏洞。

6. 加密算法：在涉及到数据安全性的场景下，割补法会采用加密算法来保护敏感数据的安全性。

常见的加密算法包括对称加密和非对称加密等。

7. 安全审计：割补法还可以通过安全审计来检查软件的安全性。

六年级数学割补法巧求面积教案

六年级数学割补法巧求面积教案教案标题：六年级数学割补法巧求面积教学目标：1. 理解割补法求面积的概念和原理；2. 掌握使用割补法求解简单图形的面积；3. 培养学生的逻辑思维和问题解决能力。

教学准备：1. 教师准备：教学课件、黑板、粉笔、割补法求面积的示意图；2. 学生准备：学生课本、练习册、纸和铅笔。

教学过程：一、导入（5分钟）1. 引入课题：通过展示一张简单图形，例如一个矩形，引导学生思考如何求解这个图形的面积。

2. 学生回答问题，并引导他们思考是否有其他方法来求解面积。

二、概念讲解（10分钟）1. 教师通过课件或黑板，简要介绍割补法求面积的概念和原理。

2. 引导学生理解割补法的思想，即将复杂的图形割分成更简单的几何图形，再求解各个几何图形的面积之和。

三、示例演练（15分钟）1. 教师通过课件或黑板，展示一个复杂图形的示例，并解释如何使用割补法求解该图形的面积。

2. 引导学生一起参与计算过程，解释每一步的思路和方法。

四、练习与巩固（20分钟）1. 学生独立或分组完成练习册上的相关练习题，巩固割补法求面积的方法。

2. 教师巡回指导学生解题过程，并及时纠正错误。

五、拓展与应用（10分钟）1. 引导学生思考如何应用割补法求解其他图形的面积，例如三角形、梯形等。

2. 学生讨论并分享自己的思路和方法。

六、总结与反思（5分钟）1. 教师对本节课的内容进行总结，并强调割补法求面积的重要性和应用范围。

2. 学生回答教师提出的问题，对本节课的学习进行反思和总结。

教学延伸：1. 学生可以在家中或课余时间继续探索割补法求面积的应用，挑战更复杂的图形。

2. 引导学生思考割补法与其他求面积方法的异同，并进行比较分析。

教学评估：1. 教师观察学生在课堂上的参与度和理解程度；2. 教师检查学生在练习册上的完成情况，并批改作业；3. 学生之间互相评价和讨论解题思路的正确性和合理性。

教学资源：1. 教学课件或黑板；2. 学生课本、练习册、纸和铅笔。

八年级数学坐标的应用(割补法求面积)(北师版)(专题)(含答案)

坐标的应用（割补法求面积）（北师版）（专题）一、单选题(共10道，每道10分)1.如图所示，点A，B在平面直角坐标系中的坐标分别是（-1，2），（3，-2），则△AOB的面积为( )A.4B.2C.6D.3答案：B解题思路：如图，设AB交x轴于点CA点坐标为（-1，2），B点坐标为（3，-2），C点坐标为（1，0）故选B试题难度：三颗星知识点：略2.如图，在平面直角坐标系中，已知点A（2，3），B（4，1），则△AOB的面积为( )A.5B.7.5C.10D.15答案：A解题思路：如图，过点A作AC⊥y轴于点C，过点B作BD⊥x轴于点D，AC与BD交于点E，∵A（2，3），B（4，1），∴OC=3，OD=4，AC=2，AE=2，BE=2，BD=1，故选A．试题难度：三颗星知识点：略3.平面直角坐标系中有A（-4，3），B（-2，-1），则△ABO的面积为( )A.3B.6C.8D.5答案：D解题思路：如图，分别过点A作AC⊥y轴于点C，过点B作BD⊥y轴于点D，过点A作AE⊥BD于点E，∵A（-4，3），B（-2，-1），∴AC=4，OC=3，OD=1，BD=2，BE=2，AE=4，故选D．试题难度：三颗星知识点：略4.平面直角坐标系中有M（-2，3），N（3，-1），则△MON的面积为( )A.5B.4.5C.4D.3.5答案：D解题思路：如图，过点M作MP⊥x轴于点P，过点N作NQ⊥MP于点Q，∵M（-2，3），N（3，-1）,∴MP=3，OP=2，PQ=1，NQ=3+2=5，MQ=4，故选D．试题难度：三颗星知识点：略5.如图，在平面直角坐标系中，四边形ABCD的面积是( )A.4B.C. D.5答案：C解题思路：如图，过点A作AE⊥x轴于点E，故选C．试题难度：三颗星知识点：略6.如图所示的直角坐标系中，四边形ABCD各顶点的坐标分别为A（-1，4），B（-4，3），C （-5，0），D（4，0）．则四边形ABCD的面积是( )A. B.20C.22D.25答案：C解题思路：如图，过点A作AE⊥x轴于点E，∵A（-1，4），B（-4，3），C（-5，0），D（4，0）∴AF=4，OF=1，BE=3，OE=4，OC=5，OD=4，∴CE=1，EF=3，FD=5，故选C.试题难度：三颗星知识点：略7.在如图所示的平面直角坐标系中，四边形ABCD各个顶点的坐标分别是A(0，0)，B(1，2)，C(3，4)，D(5，0)，则四边形ABCD的面积为( )A.16B.C.22D.11答案：D解题思路：由于四边形ABCD是不规则的四边形，所以选择割补法求面积，如图，分别过点B，C作BE⊥x轴于点E，CF⊥x轴于点F，则故选D．试题难度：三颗星知识点：略8.在如图所示的平面直角坐标系中，四边形ABCD各顶点的坐标分别为A（-1，3），B（-3，-2），C（4，-2），D（3，2），则四边形ABCD的面积是( )A. B.20C.27D.25答案：D解题思路：如图，分别过点A，D作AE⊥BC于点E，DF⊥BC于点F．∵B（-3，-2），C（4，-2），两点的纵坐标相同，∴BC∥x轴，∵AE⊥BC，DF⊥BC，∴AE∥y轴，DF∥y轴，∵A（-1，3），D（3，2），∴E（-1，-2），F（3，-2），∴BE=2，AE=5，EF=4，DF=4，CF=1，故选D．试题难度：三颗星知识点：略9.如图，在平面直角坐标系中，四边形ABCD各顶点的坐标分别为A（-1，2），B（-3，4），C（-2，9），D（7，0）．则四边形ABCD的面积是( )A.32B.33C.37D.38答案：B解题思路：如图，作如下长方形DFGH，∵A（-1，2），B（-3，4），C（-2，9），D（7，0），∴AE=2，OE=1，BF=4，OF=3，DH=9，OD=7，∴CH=9，CG=1，BG=5，EF=2，ED=8，DF=10，故选B.试题难度：三颗星知识点：略10.如图，在平面直角坐标系中，四边形ABCD各顶点的坐标分别为A（-3，4），B（-4，-2），C（2，0），D（2，3），且AB与x轴交点E的坐标为（-，0）．则四边形ABCD的面积是( )A. B.25C.27D.28答案：A解题思路：如图，过点A作AF⊥x轴于点F，过点B作BG⊥x轴于点G，∵C（2，0），D（2，3），∴CD∥y轴，即CD⊥x轴，∴四边形AFCD为直角梯形，又∵A（-3，4），B（-4，-2），E（-，0）∴AF=4，CD=3，CF=5，EF=，BG=2，CE=，故选A．试题难度：三颗星知识点：略。

【精品】五年级(上) 数学应用题及解析-类型二平面图形应用题人教新课标版(2014秋)

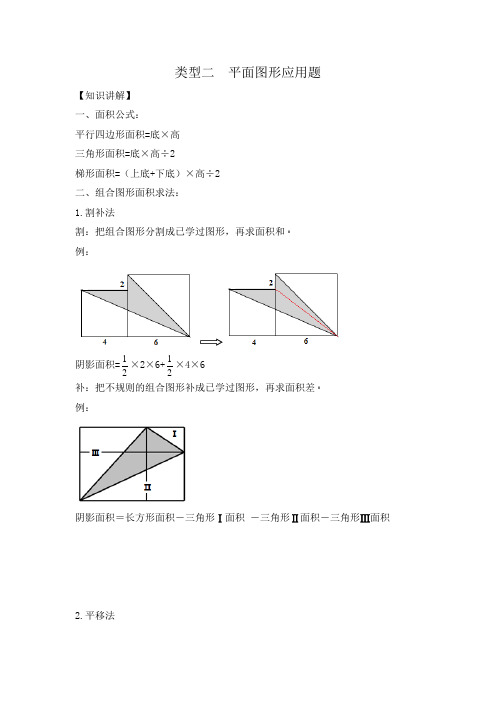
类型二平面图形应用题【知识讲解】一、面积公式：平行四边形面积=底×高三角形面积=底×高÷2梯形面积=（上底+下底）×高÷2二、组合图形面积求法：1.割补法割：把组合图形分割成已学过图形，再求面积和例：阴影面积=12×2×6+12×4×6补：把不规则的组合图形补成已学过图形，再求面积差例：阴影面积＝长方形面积－三角形Ⅰ面积－三角形Ⅱ面积－三角形Ⅲ面积2.平移法阴影面积=大长方形面积-小长方形面积【例题讲解】【例题1】计算下面图形的面积【解析】分别根据三角形的面积公式和梯形的面积公式计算出面积，然后相加即可解答【答案】解：60×（78﹣48）÷2+（60+100）×48÷2=60×30÷2+160×48÷2=900+3840=4740（平方米）答：图形的面积是4740平方米【小结】本题主要考查了三角形和梯形面积公式的应用，三角形的面积=长×宽÷2，梯形的面积=（上底+下底）×高÷2【例题2】在一长方形草地里有一条宽1米的曲折小路，如图所示，草坪的面积是________平方米【解析】如图，小路的宽为1米，如果把小路两边的草坪利用平移的性质将他们平移到一起，正好组成一个长为10﹣1=9，米宽为8﹣1=7米的长方形，由此计算得出这个长方形的面积就是草坪的面积【答案据题干分析：（10﹣1）×（8﹣1）=63（平方米），答：草坪的面积是63平方米【小结】根据平移的性质，将草坪平移到一个长方形中，利用长方形的面积公式计算即可解决问题【巩固练习】一、平行四边形1.把一个平行四边形割补成一个长方形后，面积不变，周长（）A．扩大了 B．缩小了 C．不变2.如图，把平行四边形沿高剪开，在把三角形向右平移（）cm，可以得到一个与原图形面积相等的长方形A．2 B．5 C．83. 用手拉一个活动的长方形框架，使它成为一个平行四边形，这个平行四边形的面积（）原来长方形面积A．大于 B．小于 C．等于4. 在图中，平行四边形的面积是阴影部分面积的（）A．3倍 B．4倍 C．6倍5. 平行四边形的底是0.6米，高是0.4米，与它等底等高的三角形的面积是（）A．0.12平方米 B．0.48平方米 C．0.24平方米6. 一个平行四边形，底扩大12倍，高缩小4倍，那么这个平行四边形的面积（）A．扩大12倍 B．缩小4倍 C．不变 D．扩大3倍7. 用两个完全一样的直角三角形拼成一个平行四边形，有下面两种拼法．（1）拼成的两个平行四边形的面积相等吗？（）（2）拼成的两个平行四边形的周长相等吗？（）A.相等B.不相等8. 如图：阴影部分甲与阴影部分乙比较（）A.甲＞乙B.甲＜乙C.甲=乙D.无法比较9. 如图，在矩形ABCD中，横向阴影部分是矩形，另一阴影部分是平行四边形，其中a=10，b=5，c=1，计算图中空白部分的面积，其面积是（）A.34B.35C.36D.3710. 一个平行四边形的面积是8平方分米，如果它的底和高分别扩大到原来的3倍，它的面积就变成平方分米11. 如图：已知三角形的面积是60平方米，求阴影部分梯形面积．（单位：米）12. 一个长方形木框，长10dm，宽8dm，将它拉成一个平行四边形，面积变，这个平行四边形的周长为 dm13. 有一块平行四边形的麦田，底275米，高60米，共收小麦19.8吨．这块麦田有多少公顷？平均每公顷收小麦多少吨？14. 有一块平行四边形钢板，底是8.4分米，高是3.5分米．如果每平方分米钢板重0.75千克，这块钢板重多少千克？15. 一块平行四边形的广告牌，每平方米大约要用油漆0.34千克，油漆工人带来15千克油漆，要刷完这块广告牌，这些油漆够吗？16. 你能准确地填出下表吗？底/cm 2.4 1.2高/cm 3.2 4.8平行四边形的面积/cm2 3.84 3.8417. 有一块平行四边形菜地（如图），在它的四周围一圈篱笆，请你求出篱笆的长度18. 一块平行四边形的草坪中有一条长8米、宽1米的小路，草坪的面积是多少？如果铺每平方米草坪的价格是16元，那么铺好这些草坪需要多少钱？二、三角形19. 用一张长方形纸剪同样的三角形（如图），最多能剪成（）个这样的三角形20. 图中，平行线间的三个图形，它们的面积相比（）A．平行四边形的面积大 B．三角形的面积大C．梯形的面积小 D．面积都相等21. 长、宽分别相等的两个长方形中，各有一个涂颜色的三角形（如图）．这两个三角形的面积（）A．一样大 B．不一样大 C．无法比较22. 等腰三角形一边长为4，另一边长为2，则其周长为（）A.10B.10或8C.8D.623. 已知一个等腰三角形的周长为12cm，一条边为3cm，另有一条边为（）cmA.6B.4.5C.6或4.524. 求阴影部分面积（单位：厘米）25. 你知道吗，我国古代数学名著《九章算术》中记载了一些常见图形的面积计算方法，如三角形面积的计算方法，数学家刘徽在注文中用“以盈补虚”的方法加以说明．如果三角形的底12厘米，高6厘米，用如下图的方法将三角形转化成长方形，那么转化成的长方形的长是厘米，宽是厘米，面积是平方厘米．（“广”指三角形的底，“从”指三角形的高）26. 公园里有两块空地，计划分别种玫瑰和牡丹玫瑰每棵占地1m2每棵6元牡丹每棵占地2m2每棵10元种玫瑰一共需要多少钱？牡丹园和玫瑰园一共占地多少平方米？三、梯形27. 如图，用篱笆围成一块梯形菜地，梯形一边是利用房屋墙壁，篱笆总长80米，这块梯形菜地的面积是（）A．600㎡ B．487.5㎡ C．712.5㎡ D．975㎡28. 工地上有一堆钢管，横截面是一个梯形，已知最上面一层有2根，最下面一层有12根，共堆了11层，这堆钢管共有根29. 如图，A点是长方形一边上的中点，如果长方形的面积是40平方厘米，梯形的面积是平方厘米，三角形的面积是平方厘米四、组合图形30. 求阴影部分的面积31. 某市有一块工业园，地面形状如图，根据图上所标的长度计算这块地有多少公顷？32. 如图中，大梯形面积是阴影部分面积的倍33. 如图，一面装饰墙的墙面是由两种颜色的瓷砖贴成的．黑与白两种瓷砖的面积比是34. 计算下面图形的面积35. 计算下面图形的面积36. 求图形中阴影部分的面积．（单位：dm）参考答案与解析1. 【解析】根据题意可知，把一个平行四边形割补成一个长方形后，面积不变，但是平行四边形有两条斜边变成了直边（长方形的宽），长度减少了，所以周长也会减少周长变小了【答案】解：据分析可知：把一个平行四边形割补成一个长方形后，面积不变，周长变小了故选：B2. 【解析】根据平行四边形的面积公式和长方形的面积公式来进行解答【答案】解：因移动后得到的长方形的面积和平行四边形的面积相等，平行四边形的高和长方形的高相等，所以长方形的长要和平行四边形的底相等，要是8厘米所以要把三角形向右平移8厘米可得到一个与原图形面积相等的长方形故选：C3. 【解析】把一个活动的长方形框架拉成一个平行四边形，周长没变，面积比原来长方形的面积小了【答案】解：把一个活动的长方形框架拉成一个平行四边形，周长没变，由于拉成的平行四边形的高小于原来长方形的宽，所以面积比原来长方形的面积小答：它的面积则小于原来的长方形面积故选：B4. 【解析】图阴影部分三角形和平行四边形的高相等，底等于平行四边形底的一半，所以平行四边形的面积是阴影部分面积的2×2=4倍据此解答【答案】解：设平行四边形的底是a，高是h，所以，ah÷（12ah×12）=4所以平行四边形的面积是阴影部分面积的2×2=4倍故选：B5. 【解析】根据题意，三角形的底为0.6米，高为0.4米，那么根据三角形的面积公式进行计算即可得到答案【答案】解：0.6×0.4÷2，=0.12（平方米）；答：与它等底等高的三角形的面积是0.12平方米故选：A6. 【解析】平行四边形的面积=底×高，若底扩大12倍，高缩小4倍，那么面积就扩大12÷4=3倍，据此解答【答案】解：因为平行四边形的面积=底×高，若底扩大12倍，高缩小4倍，那么面积就扩大12÷4=3倍答：这个平行四边形的面积扩大了3倍故选：D7. 【解析】用两个完全一样的直角三角形拼成一个平行四边形，用三种拼法，无论哪一种拼法面积都相等，但是不同的拼法得到的平行四边形周长不相等【答案】解：（1）拼成的两个平行四边形的面积相等．这种说法是对的（2）拼成的两个平行四边形的周长不相等．这种说法是错误的故选：（1）A；（2）B8. 【解析】根据长方形的面积等于与它同底等高的平行四边形的面积，得出阴影部分甲+空白三角形的面积=阴影部分乙+空白三角形的面积，再将等式两边同时减去空白三角形的面积，即可得出阴影部分甲与阴影部分乙的面积相等【答案】解：观察图形可知：阴影部分甲+空白三角形的面积=阴影部分乙+空白三角形的面积，所以阴影部分甲的面积=阴影部分乙的面积故选C9. 【解析】矩形ABCD的面积为a×b=10×5=50；横向阴影部分面积为c×a=1×10=10；另一阴影部分面积为c×b=1×5=5，两个阴影重复的部分是底为1高为1的平行四边形，面积为1，则空白部分的面积为矩形面积减去横向阴影部分面积减去另一阴影部分面积再加上两个阴影重复的部分面积，计算即可故选：C10. 【解析】根据平行四边形的面积公式：s=ah，再根据积的变化规律：积扩大的倍数等于因数扩大倍数的乘积．如果平行四边形的底和高都扩大3倍，那么它的面积就扩大3的平方倍，解答即可【答案】解：8×3×3=8×9=72（平分米）答：它的面积是72平方分米故答案为：7211. 【解析】首先根据三角形的面积公式：s=ah÷2，那么h=2s÷a，把数据代入公式求出三角形的高（梯形的高），再根据梯形的面积公式：s=（a+b）×h÷2，把数据代入公式解答【答案】解：60×2÷8=15（米），（8+24+24）×15÷2=56×15÷2=840÷2=420（平方米）答：阴影部分的面积是420平方米12. 【解析】把长方形木框拉成平行四边形，它的高变短了，所以它的面积就变小了，而四个边的长度没变，则其周长不变，所以长方形的木框的周长就是这个平行四边形的周长【答案】解：长方形木框拉成平行四边形，它的高变短了，所以它的面积就变小了；周长是（10+8）×2=18×2=36（分米）答：面积变小，这个平行四边形的周长为36分米故答案为：小，3613.【解析】先利用平行四边形的面积公式求出麦田的面积；总产量已知，总产量除以总面积就是单产量．【答案】解：275×60=16500（平方米）=1.65（公顷）；19.8÷1.65=12（吨）；答：这块麦田有1.65公顷，平均每公顷收小麦12吨14. 【解析】根据“平行四边形的面积=底×高”先计算出钢板的面积，进而根据“每平方分米钢板重（0.75）×钢板的面积=钢板的重量”进行解答即可【答案】解：0.75×（8.4×3.5）=0.75×29.4=22.05（千克）答：这块钢板重22.05千克15. 【解析】广告牌的底和高已知，利用平行四边形的面积公式先求出广告牌的面积，每平方米的用漆量已知，乘广告牌的面积就是总的用漆量，将得数与15千克相比，就可以知道这些油漆够不够【答案】解：（5×4）×0.34=20×0.34=6.8（千克）6.8千克＜15千克答：要刷完这块广告牌，15千克油漆足够16. 【解析】根据平行四边形的面积公式=底×高进行计算即可得到答案【答案】解：3.84÷2.4=1.6（厘米）1.2×3.2=3.84（平方厘米）3.84÷4.8=0.8（厘米）底/cm 0.8高/cm 1.6平行四边形的面积/cm2 3.8417. 【解析】首先根据平行四边形的面积公式：s=ah，求出这块菜地的面积，然后求出高24米所对应的底边长是多少米，进而求出平行四边形的周长据此列式解答【答案】解：30×18÷24=22.5（米）（30+22.5）×2=52.5×2=105（米）答：篱笆的长度是105米18. 【解析】将两边草地向中间平移，可得底为20﹣1=19米，高为8米的平行四边形草地，再根据平行四边形面积公式求解即可，用草地的面积乘单位面积的草坪的价格，就是铺这块草坪需要的总钱数【答案】解：（20﹣1）×8=19×8=152（平方米）152×16=2432（元）答：草地的面积为152平方米，铺好这些草坪需2432元钱19. 【解析】剪的两个同样的三角形可组成一个长10厘米，宽4厘米的长方形．只要求出在长50厘米的边上，能剪几个4厘米宽的长方形，就能求出最多能剪几个这样的三角形．据此解答【答案】解：50÷4=12（个）…2（厘米），12×2=24（个）答：最多能剪24个这样的三角形故选：B20. 【解析】在图中，三个图形的高相等，梯形的上底、下底、平行四边形的底、三角形的底都已知，再依据三者的面积公式即可判断它们的面积大小【答案】解：平行四边形的面积=3×h=3h，三角形的面积=12×6×h=3h，梯形面积=（2+1）×h÷2=1.5h，所以梯形的面积最小故选：C21. 【解析】阴影部分都是这个长方形面积的一半，所以它们的面积相等【答案】故选：A22. 【解析】因为在三角形中任意两边的和大于第三边，所以根据题意4+4＞2，2+2=4，判断4为等腰三角形的腰长，由此把三角形的三条边加起来就是三角形的周长【答案】解：4+4+2=10；故选：A23. 【解析】已知中等腰三角形的周长为12cm，一边长为3cm，但没有明确指明3cm是底边还是腰，因此要分两种情况，分类讨论【答案】解：因为等腰三角形的周长是12cm，一条边长是3cm，所以当3cm为底时，其它两边都为4.5cm，且3cm、4.5cm、4.5cm可以构成三角形；当3cm为腰时，其它两边为3cm和6cm，且3cm、3cm、6cm不可以构成三角形．所以另两边是4.5cm、4.5cm故选：B24. 【解析】（1）阴影的部分的面积等于平行四边形的面积减去空白三角形的面积，根据平行四边形的面积公式：s=ah，三角形的面积公式：s=ah÷2，把数据代入公式求出它们的面积差即可（2）阴影部分的面积等于梯形的面积减去空白三角形的面积，根据梯形的面积公式：s=（a+b）×h÷2，三角形的面积公式：s=ah÷2，把数据代入公式求出它们的面积差即可【答案】解：（1）12×6﹣8×6÷2=72﹣24=48（平方厘米）答：阴影部分的面积是48平方厘米（2）（8+10）×6÷2﹣8×6÷2=18×6÷2﹣48÷2=54﹣24=30（平方厘米）答：阴影部分的面积是30平方厘米25. 【解析】观察图形发现，按照图形的方法将三角形转化成长方形，那么转化成的长方形的长是三角形的底，宽是三角形高的一半，求面积是多少平方厘米用长方形的面积公式计算．所以三角形的面积就等于底乘高除以2【答案】解：6÷2=3（厘米）12×3=36（平方厘米）答：将三角形转化成长方形，那么转化成的长方形的长是12厘米，宽是3厘米，面积是36平方厘米26. 【解析】（1）先利用三角形的面积公式S=ah÷2计算出玫瑰园的面积，再除以每棵玫瑰占的面积计算出棵数，再乘上单价即可得解；（2）分别利用三角形的面积公式S=ah÷2计算出各自的面积，再相加即可得解【答案】解：60×20÷2÷1×6=600×6=3600（元）60×20÷2+30×20÷2=600+300=900（平方米）答：种玫瑰一共需要3600元钱，牡丹园和玫瑰园一共占地900平方米27. 【答案】解：（80﹣15）×15÷2=65×15÷2=975÷2=487.5平方米）答：梯形的面积是487.5平方米故选：B28. 【解析】根据梯形的面积公式等于梯形的上、下底之和乘以高除以2直接解答即可【答案】解：（2+12）×11÷2=14×11÷2=77（根）答：这堆钢管共有77根故答案为：7729. 【解析】如图所示，由“A点是长方形一边上的中点，长方形的面积是40平方厘米”可知，三角形的面积=12×长×宽×12=14×长×宽，由此可得三角形的面积是长方形面积的14，从而可以求出三角形的面积和梯形的面积【答案】解：三角形的面积=12×长×宽×12=14×长×宽=14×40=10（平方厘米），梯形的面积=40﹣10=30（平方厘米）；故答案为：30、1030. 【解析】（1）阴影部分的面积=长方形的面积﹣梯形的面积，利用长方形的面积公式S=ab和梯形的面积公式S=（a+b）h÷2即可求解；（2）阴影部分的面积=梯形的面积﹣长方形的面积，利用长方形的面积公式S=ab 和梯形的面积公式S=（a+b）h÷2即可求解【答案】解：（1）52×34﹣（52+26）×12÷2=1768﹣78×12÷2=1690﹣468=1222（平方分米）答：阴影部分的面积是1222平方分米（2）（20+40）×15÷2﹣15×8=60×15÷2﹣120=450﹣120=330（平方厘米）答：阴影部分的面积是330平方厘米31. 【解析】观察图形可知，这个工业园的面积等于上面的梯形的面积与下面的三角形的面积之和，据此根据梯形和三角形的面积公式进行计算即可解答问题【答案】解：（200+420）×200÷2+420×300÷2=62000+63000=125000（平方米）=12.5公顷答：这块地的面积是12.5公顷32. 【解析】观察图形可知，AB是这个梯形的中位线，所以可得出这条中位线的长度是（x+2x+x）÷2=2x，据此可得出阴影部分的小梯形的上底是x，下底是2x，又根据梯形的中位线的性质可得，阴影部分的小梯形的高等于大梯形的高的一半，据此设小梯形的高是h，则大梯形的高就是2h，据此根据梯形的面积=上下底之和×高÷2，分别表示出这两个梯形的面积，再相除即可解答【答案】解：根据题干分析可得：AB是大梯形的中位线，设小梯形的高是h，则大梯形的高就是2h，则小梯形的面积是：（x+2x）×h÷2=32xh，大梯形的面积是：（x+3x）×2h÷2=4xh，4xh÷32xh=83，答：大梯形的面积是小梯形的面积的83倍33. 【解析】根据图可知：两个白色的三角形的瓷砖的面积和为整个四边形面积的14，两个小正方形的面积和为整个四边形面积的14的12，即整个四边形面积的1 4×12=18；则整个白色瓷砖的面积和为整个四边形面积的（14+18）=38，则整个黑色瓷砖的面积为整个四边形面积的（1﹣38）=58，然后根据题意进行比即可【答案】解：14+14×12=38，1-38=58，则黑与白两种瓷砖的面积比：58：38=5：3；34. 【解析】解（1）8×10+（10﹣5）×（12﹣8）÷2=80+5×4÷2=90答：面积是90（2）6×4÷2=24÷2=12答：阴影部分的面积是12（3）4×4+3×3﹣（4+3）×4÷2=16+9﹣14=25﹣14=11答：阴影部分的面积是1135. 【解析】这道题乍一看觉得难，仔细观察可以找到简单的算法，做题前要仔细观察观察可以发现甲比乙少的面积正好等于大三角形的面积减长方形的面积【答案】6×（5+4）÷2-6×4=3（平方厘米）答：阴影部分的面积是3平方厘米36. 【解析】由题意可知：阴影部分的面积就等于大正方形的面积的一半加上右侧梯形的面积再减去下面空白的大三角形的面积，据此解答即可【答案】解：8×8÷2+（6+8）×6÷2﹣（8+6）×6÷2=32+42﹣42=32（平方分米）答：图形中阴影部分的面积是32平方分米。

《多边形的面积》单元的相关数学文化及其课堂运用

《多边形的面积》单元的相关数学文化及其课堂运用随着基础教育课程改革的不断深入，“数学教育应重视数学文化的教育”已经引起广大教育工作者包括小学数学教师的重视。

教材是学校教育和文化传播的主要载体，数学文化走进教材，渗入实际教学，有利于激发学生的学习兴趣，帮助学生了解数学、认识数学，使学生真正感受到文化渲染，产生文化共鸣，体会数学的文化品位，从而体察到社会文化和数学文化之间互动，感受到数学文化在人类文明和社会发展中的重要意义。

[1]《义务教育数学课程标准（2011年版）》在教材编写建议中谈到：数学文化作为教材的组成部分，应渗透在整套教材中。

[2]为此，教材可以适时地介绍有关背景知识，包括数学在自然与社会中的应用以及数学发展史的有关资料，帮助学生了解数学在人类文明发展中的作用，激发学生学习数学的兴趣，感受数学家治学的严谨，欣赏数学的优美。

青岛版教材注重数学文化的渗透，从文化的高度来建设数学课程。

一、教材中的数学文化通过对教材分析研究发现，本单元共有36项与数学文化有关的内容，其中情境窗（C1）5项，合作探究及自主练习（C2）31项。

通过分析本单元的数学文化类型，我们发现：“数学与现实生活”的内容最多，共32项，C1中5项，C2中有27项，充分体现了数学与生活的密切联系及其应用价值；与“数学与科技”有关的内容有2项，主要体现在C2中；与“数学与人文艺术”有关的内容有1项，主要体现在C2中；教材中没有明显的与“数学史”相关的内容，只是在一处自主探究中体现的“割补法”来自于我国古代数学研究成果，故将其算作1项数学史内容。

（相关数据统计如表1）。

1.数学史。

教材66页自主探究环节出示的“割补法”（如图1）源自于我国古代数学家刘徽所提出的“出入相补”（又称“以盈补虚”），故将其算作一处数学史，属于显性数学史。

2.数学与现实生活。

本单元的数学文化主要体现在“数学与现实生活”这一方面，充分体现了数学与生活的密切联系。

中考：等面积法

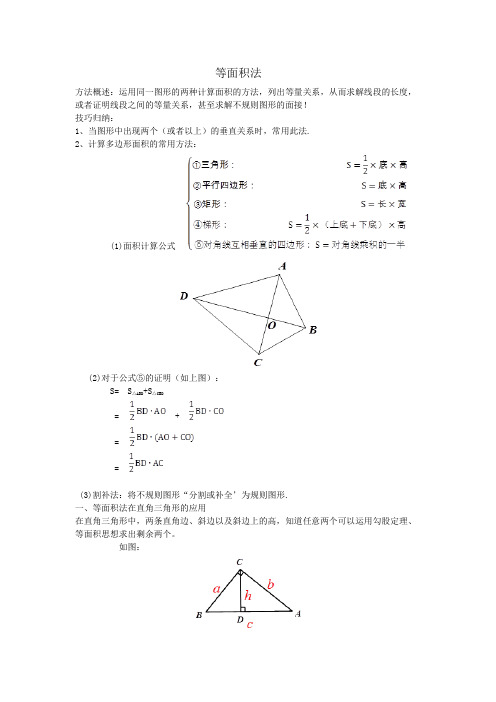
等面积法方法概述：运用同一图形的两种计算面积的方法，列出等量关系，从而求解线段的长度，或者证明线段之间的等量关系，甚至求解不规则图形的面接！技巧归纳：1、当图形中出现两个（或者以上）的垂直关系时，常用此法.2、计算多边形面积的常用方法：(1)面积计算公式(2)对于公式⑤的证明（如上图）：S= S△ABD+S△CBD= +==(3)割补法：将不规则图形“分割或补全’为规则图形.一、等面积法在直角三角形的应用在直角三角形中，两条直角边、斜边以及斜边上的高，知道任意两个可以运用勾股定理、等面积思想求出剩余两个。

如图：基本公式: ①勾股定理:②等面积法：证明②：即：,例题1：如图，在Rt ABC ,∠C=90°，当直角边AC =4，斜边AB =5时，求该直角三角形斜边AB上的高CD ?例题2：如图，在Rt ABC (BC AC ) ,∠C=90°，当斜边AB =10cm，斜边AB上的高CD =4.8cm 时，求该直角三角形直角边AC和BC的长度?巩固练习：1、如图，在Rt ABC,∠C=90°，且AC=24, BC=7，作ABC 的三个内角的角平分线交于点P，再过点P 依次作PD⊥AB于D，作PE⊥BC于E, 作PF⊥AC于F .(1)求证：PD = PE = PF ;(2)求出：PD的值.2、如图，△ABC的顶点A，B，C在边长为1的正方形网格的格点上，则BC边长的高为（）A.22二、等面积法在等腰三角形的应用在等腰三角形中，可以运用“割补法”的等面积思想，先建立有关“腰以及腰上的高”的等式，再通过等式两边约分来探索出线段之间的数量关系！例题1：如图,在△ABC 中, AB=AC, AC 边上的高BD=10cm.（1）如图1,求AB 边上高CE 的长；（2）如图2,若点P 为BC 边上任意一点, PM⊥AB 于点M, PN⊥AC 于点N,求PM+PN 的值；（3）如图3,若点P 为BC 延长线上任意一点,PM⊥AB 于M,PN⊥AC 于点N,在①PM+PN ；②PM PN 中有一个是定值,判断出来并求值.例题2：已知等边△ABC和内部一点P，设点P 到△ABC三边的AB、BC 、AC 的距离分别是h1，h2，h3，△ABC的高为h，问h1、h2、h3 与h 之间有怎样的数量关系？请说明理由。