神经网络数学建模实验报告
数学建模实验报告

湖南城市学院数学与计算科学学院《数学建模》实验报告专业:学号:姓名:指导教师:成绩:年月日目录实验一 初等模型........................................................................ 错误!未定义书签。
实验二 优化模型........................................................................ 错误!未定义书签。
实验三 微分方程模型................................................................ 错误!未定义书签。
实验四 稳定性模型.................................................................... 错误!未定义书签。
实验五 差分方程模型................................................................ 错误!未定义书签。
实验六 离散模型........................................................................ 错误!未定义书签。
实验七 数据处理........................................................................ 错误!未定义书签。
实验八 回归分析模型................................................................ 错误!未定义书签。
实验一 初等模型实验目的:掌握数学建模的基本步骤,会用初等数学知识分析和解决实际问题。
实验内容:A 、B 两题选作一题,撰写实验报告,包括问题分析、模型假设、模型构建、模型求解和结果分析与解释五个步骤。
数学建模实验报告

数学建模实验报告1.流⽔问题问题描述:⼀如下图所⽰的容器装满⽔,上底⾯半径为r=1m,⾼度为H=5m,在下地⾯有⼀⾯积为B0.001m2的⼩圆孔,现在让⽔从⼩孔流出,问⽔什么时候能流完?解题分析:这个问题我们可以采⽤计算机模拟,⼩孔处的⽔流速度为V=sqrt[2*g*h],单位时间从⼩孔流出的⽔的体积为V*B,再根据⼏何关系,求出⽔⾯的⾼度H,时间按每秒步进,记录点(H,t)并画出过⽔⾯⾼度随时间的变化图,当⽔⾯⾼度⼩于0.001m 时,可以近似认为⽔流完了。
程序代码:Methamatic程序代码:运⾏结果:(5)结果分析:计算机仿真可以很直观的表现出所求量之间的关系,从图中我们可以很⽅便的求出要求的值。
但在实际编写程序中,由于是初次接触methamatic 语⾔,对其并不是很熟悉,加上个⼈能⼒有限,所以结果可能不太精确,还请见谅。
2.库存问题问题描述某企业对于某种材料的⽉需求量为随机变量,具有如下表概率分布:每次订货费为500元,每⽉每吨保管费为50元,每⽉每吨货物缺货费为1500元,每吨材料的购价为1000元。
该企业欲采⽤周期性盘点的),(S s 策略来控制库存量,求最佳的s ,S 值。
(注:),(S s 策略指的是若发现存货量少于s 时⽴即订货,将存货补充到S ,使得经济效益最佳。
)问题分析:⽤10000个⽉进⾏模拟,随机产⽣每个⽉需求量的概率,利⽤计算机编程,将各种S 和s 的取值都遍历⼀遍,把每种S,s的组合对应的每⽉花费保存在数组cost数组⾥,并计算出平均⽉花费average,并⽤类answer来记录,最终求出对应的S和s。
程序代码:C++程序代码:#include#include#include#include#define Monthnumber 10000int Need(float x){int ned = 0;//求每个⽉的需求量if(x < 0.05)ned = 50;else if(x < 0.15)ned = 60;else if(x < 0.30)ned = 70;else if(x < 0.55)ned = 80;else if(x < 0.75)ned = 90;else if(x < 0.85)ned = 100;else if(x < 0.95)ned = 110;else ned = 120;return ned;}class A{public:int pS;int ps;float aver;};int main(){A answer;answer.aver=10000000;//int cost[Monthnumber+1]={0}; float average=0;int i;float x;int store[Monthnumber];//srand((int)time(0));for(int n=6;n<=12;n++){// int n=11;int S=10*n;for(int k=5;k{// int k=5;int s=k*10;average=0;int cost[Monthnumber+1]={0};for(i=1;i<=Monthnumber;i++){store[i-1]=S;srand(time(0));x=(float)rand()/RAND_MAX; //产⽣随机数//cout<<" "<//cout<int need=Need(x);if(need>=store[i-1]){cost[i]= 1000*S + (need - store[i-1])*1500 + 500;store[i]=S;}else if(need>=store[i-1]-s){cost[i]=1000*(need+S-store[i-1]) + 50*(store[i-1]-need) + 500; store[i]=S;}else{cost[i]=(store[i-1]-need)*50;store[i]=store[i-1]-need;}average=cost[i]+average;}average=average/Monthnumber;cout<<"n="<cout<<"花费最少时s应该为:"<cout<<"平均每⽉最少花费为:"<}运⾏结果:结果分析:⽤计算机模拟的结果和⽤数学分析的结果有⼀定的差异,由于计算机模拟时采⽤的是随机模型⽽我⽤time函数和rand函数产⽣真随机数,所以在每次的结果上会有所差异,但对于⼀般的⽣产要求亦可以满。
DEEP大数据分析实验报告
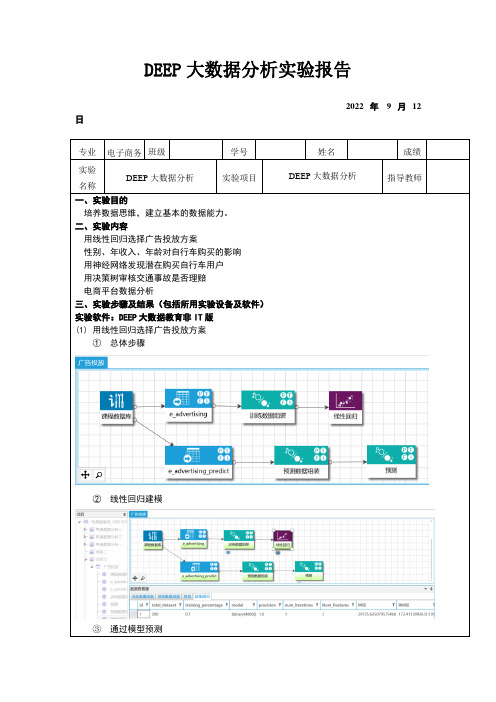
DEEP大数据分析实验报告2022 年9 月12 日专业电子商务班级学号姓名成绩实验DEEP大数据分析实验项目DEEP大数据分析指导教师名称一、实验目的培养数据思维,建立基本的数据能力。
二、实验内容用线性回归选择广告投放方案性别、年收入、年龄对自行车购买的影响用神经网络发现潜在购买自行车用户用决策树审核交通事故是否理赔电商平台数据分析三、实验步骤及结果(包括所用实验设备及软件)实验软件:DEEP大数据教育非IT版(1)用线性回归选择广告投放方案①总体步骤②线性回归建模③通过模型预测(2)性别、年收入、年龄对自行车购买的影响①性别、年收入是否影响购买可以看出,男性和女性购买自行车的数量都没要显著差异,因此可以任务性别这个因素基本上对购买自行车的行为不产生影响。
②客户年龄离散化③年龄是否影响购买从图中可以看出,各个年龄段的总人数和购买者有着明显的差异,33岁到63岁之间人群是购买自行车的主力。
(3)用神经网络发现潜在购买自行车用户在图中,predict列的1表示需要购买自行车。
这样,可以对需要购买自行车的人员进行精准营销。
(4)用决策树审核交通事故是否理赔①计算相关系数②使用决策树审核其中“col_1”是预测结果,0表示理赔,1表示不理赔。
(5)电商平台数据分析母婴电商数据分析可视化仪表盘用户行为分析四、问题讨论及实验心得大数据全链路处理工作流程一般包括六个步骤:数据源、数据汇集、数据湖、数据加工、分析挖掘、数据可视化。
数据源是指原始数据的最初来源,它存贮在企业不同业务部门之间的。
数据汇集是指根据业务目标,把这些不同部门之间原始数据进行整合,转化为容易分析的统一存储格式进行存储的过程。
数据湖是指把数据汇集结果集中存贮起来,以便后续分析挖掘。
这种方式极大的方便用户对数据进行分析和利用。
数据加工是指对数据湖中的数据进行诸如去重、处理空值、数据降维、数据标准化等数据预处理过程,其工作量一般占整个流程的大约60%。
数学模型实验报告模板

院(系) 课程名称:数学模型与数学实验日期:年 月日
班级
学号
实验室
专业
姓名
计算机号
实验
名称
多元函数的极值
成绩评定
所用
软件
Matlab
指导教师
实验
目的
1、多元函数偏导数的求法。
2、多元函数自由极值的求法
3、多元函数条件极值的求法.
4、学习掌握MATLAB软件有关的命令。
实验
内容
1、求 的极值。
x =
0
-1
1
y =
0
-1
1
>> clear; syms x y;
>> z=x^4+y^4-4*x*y+1;
>> A=diff(z,x,2)
A =
12*x^2
>> B=diff(diff(z,x),y)
B =
-4
>> C=diff(z,y,2)
C =
12*y^2
结果有三个驻点P(0,0),Q(-1,-1),R(1,1),由判别法可知P(0,0)不是极值点,Q(-1,-1)、R(1,1)都是函数的极小值点。
为最远点。
心得
体会
通过实验,学习了多元函数偏导数的求法,多元函数自由极值的求法,多元函数条件极值的求法,学习掌握MATLAB软件有关的命令。基本上达到了实验的学习目的。
1/3*3^(1/2)
u =
-1/3*3^(1/2)
1/3*3^(1/2)
通过判断得点x= 1/2*3^(1/2),y=-1/3*3^(1/2),z=-1/3*3^(1/2),u=-1/3*3^(1/2)
深度学习的实验报告(3篇)

第1篇一、实验背景随着计算机技术的飞速发展,人工智能领域取得了显著的成果。
深度学习作为人工智能的一个重要分支,在图像识别、语音识别、自然语言处理等方面取得了突破性进展。
手写数字识别作为计算机视觉领域的一个重要任务,具有广泛的应用前景。
本实验旨在利用深度学习技术实现手写数字识别,提高识别准确率。
二、实验原理1. 数据集介绍本实验采用MNIST数据集,该数据集包含60000个训练样本和10000个测试样本,每个样本为28x28像素的手写数字图像,数字范围从0到9。
2. 模型结构本实验采用卷积神经网络(CNN)进行手写数字识别,模型结构如下:(1)输入层:接收28x28像素的手写数字图像。
(2)卷积层1:使用32个3x3卷积核,步长为1,激活函数为ReLU。
(3)池化层1:使用2x2的最大池化,步长为2。
(4)卷积层2:使用64个3x3卷积核,步长为1,激活函数为ReLU。
(5)池化层2:使用2x2的最大池化,步长为2。
(6)卷积层3:使用128个3x3卷积核,步长为1,激活函数为ReLU。
(7)池化层3:使用2x2的最大池化,步长为2。
(8)全连接层:使用1024个神经元,激活函数为ReLU。
(9)输出层:使用10个神经元,表示0到9的数字,激活函数为softmax。
3. 损失函数与优化器本实验采用交叉熵损失函数(Cross Entropy Loss)作为损失函数,使用Adam优化器进行参数优化。
三、实验步骤1. 数据预处理(1)将MNIST数据集分为训练集和测试集。
(2)将图像数据归一化到[0,1]区间。
2. 模型训练(1)使用训练集对模型进行训练。
(2)使用测试集评估模型性能。
3. 模型优化(1)调整学习率、批大小等超参数。
(2)优化模型结构,提高识别准确率。
四、实验结果与分析1. 模型性能评估(1)准确率:模型在测试集上的准确率为98.5%。
(2)召回率:模型在测试集上的召回率为98.2%。
(3)F1值:模型在测试集上的F1值为98.4%。
数学建模 -实验报告1

������������⁄������������ = ������������(1 − (������ + ������)) − ������1������∗������,
(4 − 3)
������������∗⁄������������ = −������1������∗������ + ������2������
二、 问题分析
建立肿瘤细胞增长模型时,我们可以从自由增长模型开始分析,引进 Logistic 阻滞增长模型,构成肿瘤细胞增长初步框架。再者肿瘤细胞不同于普 通细胞,其生长受到人体自身免疫系统的制约。于是综合考虑正常细胞转化,癌 细胞增殖,癌细胞死亡,癌细胞被效应细胞消除等情况,建立动力学方程。并对 模型进行适当简化求解。在放射治疗方案的设计中,我们可以引入放射生物学中 广泛接受的 LQ 模型对问题进行分析,由于放疗对人体伤害相当大,因此我们采 取分次逐次放疗的方式进行治疗。我们具体分两种情形进行讨论,一是在总剂量 一定的条件下,不同的分次剂量组合对生物效应的影响;二是在产生相同生物效 应的情况下,分析最优的分次剂量组合。
易算出癌细胞转入活动期已有 300 多天,故如何在早期发现癌症是攻克癌症的关键之一 (2)手术治疗常不能割去所有癌细胞,故有时需进行放射疗法。射线强度太小无法杀
死癌细胞,太强病人身体又吃不消且会使病人免疫功能下降。一次照射不可能杀死全部癌细 胞,请设计一个可行的治疗方案(医生认为当体内癌细胞数小于 100000 个时即可凭借体内 免疫系统杀灭)。
进一步简化,根据(4-4),(4-5)式可知,效应细胞������∗和复合物������有出有进.假 设出入保持平衡,则有
������ + ������∗ = C (C 为常数)
研究生_实验报告
实验题目:基于深度学习的图像识别算法研究一、实验目的本次实验旨在研究基于深度学习的图像识别算法,通过对图像数据的处理和分析,实现对图像的自动识别和分类。
通过实验,加深对深度学习算法的理解,提高在图像处理领域的实际应用能力。
二、实验背景随着计算机视觉技术的不断发展,图像识别技术在各个领域得到了广泛应用。
深度学习作为一种新兴的机器学习技术,在图像识别领域取得了显著的成果。
本实验选取卷积神经网络(CNN)作为深度学习算法,通过搭建CNN模型,对图像进行识别和分类。
三、实验内容1. 数据集准备本次实验选用CIFAR-10数据集,该数据集包含10个类别,每个类别有6000张32×32的彩色图像,共计60000张图像。
数据集分为训练集和测试集,其中训练集包含50000张图像,测试集包含10000张图像。
2. 模型构建(1)网络结构设计本实验采用卷积神经网络(CNN)作为图像识别模型,网络结构如下:- 输入层:接收32×32的彩色图像;- 卷积层1:使用32个3×3的卷积核,步长为1,激活函数为ReLU;- 池化层1:使用2×2的最大池化;- 卷积层2:使用64个3×3的卷积核,步长为1,激活函数为ReLU;- 池化层2:使用2×2的最大池化;- 全连接层1:使用128个神经元,激活函数为ReLU;- 全连接层2:使用10个神经元,对应10个类别,激活函数为softmax。
(2)损失函数与优化器损失函数采用交叉熵损失函数(Cross-Entropy Loss),优化器选择Adam。
3. 模型训练与测试(1)训练过程使用训练集对模型进行训练,设置学习率为0.001,迭代次数为10000次。
在训练过程中,每100次迭代输出一次训练集和验证集的准确率。
(2)测试过程使用测试集对训练好的模型进行测试,计算模型在测试集上的准确率。
四、实验结果与分析1. 训练过程经过10000次迭代后,模型在训练集上的准确率达到99.75%,在验证集上的准确率达到99.68%。
股票价格预测中的神经网络模型研究
股票价格预测中的神经网络模型研究股票市场是一个复杂而又不确定的系统,股票价格受到许多因素的影响,包括政治、经济、社会和自然因素等等。
预测股票价格的变化一直是投资者、交易员和分析师们关注的焦点问题。
随着计算机技术的不断发展和人工智能技术的应用,神经网络在股票价格预测中得到了越来越广泛的应用。
一、神经网络模型的概念神经网络是一种模仿生物神经系统工作方式和结构的数学建模工具,也称为人工神经网络(Artificial Neural Network,ANN)。
神经网络模型由输入层、隐层和输出层组成,其中输入层接受外界输入数据,输出层输出预测结果,隐层是神经网络的核心部分,通过训练学习数据,提取数据中的特征关系。
神经网络模型可以模拟非线性、复杂的系统,并具有良好的适应性、泛化能力和容错性。
二、神经网络在股票价格预测中的应用股票价格受到很多因素的影响,因此需要充分利用各种与股票价格相关的信息。
神经网络模型可以处理海量、复杂的数据,并能快速、准确地预测股票价格变化。
神经网络模型在股票价格预测中的应用主要包括以下几个方面:1.技术分析技术分析主要是基于历史股票价格变化和交易量等数据,通过趋势线、指标等技术手段进行分析和预测。
神经网络模型可以对技术分析中的各种指标进行学习和建模,从而做出较为准确的预测。
2.基本面分析基本面分析主要是基于公司的财务数据和经营情况等因素进行分析和预测。
神经网络模型可以对公司的财务数据进行学习和建模,并从中提取出关键的特征信息,从而做出更为准确的预测。
3.情感分析情感分析主要是基于股票标的相关新闻、社交媒体等信息,分析市场情绪和预测股票价格的变化。
神经网络模型可以对文本信息进行分析和情感打分,从而作出预测。
三、神经网络模型在股票价格预测中的优势神经网络模型在股票价格预测中具有许多优势,主要包括以下几个方面:1.非线性建模能力股票价格受到的影响因素非常复杂,往往存在着非线性关系。
神经网络模型作为一种非线性建模工具,可以更好地处理这种复杂性,对其特征进行充分提取,从而做出更为准确的预测。
机器学习建模实验报告(3篇)
第1篇一、实验背景随着大数据时代的到来,机器学习技术在各个领域得到了广泛应用。
本实验旨在通过实际操作,掌握机器学习建模的基本流程,包括数据预处理、特征选择、模型选择、模型训练和模型评估等步骤。
通过实验,我们将深入理解不同机器学习算法的原理和应用,提高解决实际问题的能力。
二、实验目标1. 熟悉Python编程语言,掌握机器学习相关库的使用,如scikit-learn、pandas等。
2. 掌握数据预处理、特征选择、模型选择、模型训练和模型评估等机器学习建模的基本步骤。
3. 熟悉常见机器学习算法,如线性回归、逻辑回归、决策树、支持向量机、K最近邻等。
4. 能够根据实际问题选择合适的机器学习算法,并优化模型参数,提高模型性能。
三、实验环境1. 操作系统:Windows 102. 编程语言:Python3.83. 机器学习库:scikit-learn 0.24.2、pandas 1.3.4四、实验数据本实验使用鸢尾花数据集(Iris dataset),该数据集包含150个样本,每个样本有4个特征(花瓣长度、花瓣宽度、花萼长度、花萼宽度)和1个标签(类别),共有3个类别。
五、实验步骤1. 数据导入与预处理首先,使用pandas库导入鸢尾花数据集,并对数据进行初步查看。
然后,对数据进行标准化处理,将特征值缩放到[0, 1]范围内。
```pythonimport pandas as pdfrom sklearn import datasets导入鸢尾花数据集iris = datasets.load_iris()X = iris.datay = iris.target标准化处理from sklearn.preprocessing import StandardScalerscaler = StandardScaler()X = scaler.fit_transform(X)```2. 特征选择使用特征重要性方法进行特征选择,选择与标签相关性较高的特征。
人工智能实验报告
人工智能实验报告在当今科技飞速发展的时代,人工智能(AI)已经成为了最具创新性和影响力的领域之一。
为了更深入地了解人工智能的工作原理和应用潜力,我进行了一系列的实验。
本次实验的目的是探索人工智能在不同任务中的表现和能力,以及分析其优势和局限性。
实验主要集中在图像识别、自然语言处理和智能决策三个方面。
在图像识别实验中,我使用了一个预训练的卷积神经网络模型。
首先,准备了大量的图像数据集,包括各种物体、场景和人物。
然后,将这些图像输入到模型中,观察模型对图像中内容的识别和分类能力。
结果发现,模型在常见物体的识别上表现出色,例如能够准确地识别出猫、狗、汽车等。
然而,对于一些复杂的、少见的或者具有模糊特征的图像,模型的识别准确率有所下降。
这表明模型虽然具有强大的学习能力,但仍然存在一定的局限性,可能需要更多的训练数据和更复杂的模型结构来提高其泛化能力。
自然语言处理实验则侧重于文本分类和情感分析。
我采用了一种基于循环神经网络(RNN)的模型。
通过收集大量的文本数据,包括新闻、评论、小说等,对模型进行训练。
在测试阶段,输入一些新的文本,让模型判断其所属的类别(如科技、娱乐、体育等)和情感倾向(积极、消极、中性)。
实验结果显示,模型在一些常见的、结构清晰的文本上能够做出较为准确的判断,但对于一些语义模糊、多义性较强的文本,模型的判断容易出现偏差。
这提示我们自然语言的复杂性和多义性给人工智能的理解带来了巨大的挑战,需要更深入的语言模型和语义理解技术来解决。
智能决策实验主要是模拟了一个简单的博弈场景。
通过设计一个基于强化学习的智能体,让其在与环境的交互中学习最优的决策策略。
经过多次训练和迭代,智能体逐渐学会了在不同情况下做出相对合理的决策。
但在面对一些极端情况或者未曾遇到过的场景时,智能体的决策效果并不理想。
这说明智能决策系统在应对不确定性和新颖情况时,还需要进一步的改进和优化。
通过这些实验,我对人工智能有了更深刻的认识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
云南财经大学实验报告 系 (院): 统计与数学学院 专 业: 信息与计算科学 班 级: 信计09-1 学 号: 200905001465 姓 名: 课程名称: 数学建模 实验时间: 2012年6月20日 指导教师:
云南财经大学教务处制 1
实验名称 利用人工神经网络方法进行股票数据预测
实验目的
1. 学习运用matlab中的神经网络工具箱;
2. 学习利用人工神经网络进行对股票的预测;
实验内容(算法、程序、步骤和方法)流程图
股票数据预测 算法: 1. 利用matlab中的函数premnmx,对输入数据进行归一化处理,归一化处理的目的是避免BP神经网络无法收敛或者学习速度变慢甚至无效; 2. 利用函数newff,对归一化后的数据进行训练; 3. 利用函数sim,对训练好的网络对原始数据进行仿真; 4. 用仿真结果与已知数据进行对比测试,并继续对新数据进行仿真; 5. 将预测结果与已知结果绘图并进行比较; 步骤: 1. 利用函数premnmx,输入已知输入数据矩阵以及目标输出数据矩阵; 2. 对输入矩阵及目标输出矩阵进行归一化处理; 3. 利用函数newff,对归一化后的数据进行训练; 4. 利用函数sim,利用训练好的网络对原始数据进行仿真; 5. 用原始数据预测结果与已知数据进行对比测试; 6. 观察预测数据和原始数据的差异大小及吻合程度; 程序: clc % 时间序列作为输入数据 time=1:48; % 开盘价、最低价、最高价、收盘价作为输出数据 kpj1=[9.98 10.00 9.91 9.88 9.85 9.74 9.61 9.74 9.84 9.83 9.76... 9.78 9.70 9.75 9.68 9.58 9.65 9.71 9.53 9.50 9.66 9.71 9.70 9.78 ... 9.86 9.85 9.70 9.91 9.94 9.88 9.86 9.76 9.68 9.65 9.8 9.83 9.88 9.96... 9.98 9.85 9.81 9.96 10.02 10.08 10.06 10.19 10.11 10.10]; %开盘价 zgj1=[9.99 10.05 9.95 9.93 9.88 9.76 9.84 9.80 9.86 9.87... 9.77 9.85 9.75 9.78 9.68 9.77 9.80 9.76 9.65 9.68 9.74 9.79 9.85... 9.90 9.86 9.90 9.99 10.0 9.95 9.93 9.86 9.78 9.72 9.86 9.89 9.92... 9.98 10.03 9.98 10.02 9.98 10.03 10.13 10.15 10.28 10.28 10.23 10.16]; %最高价 zdj1=[9.91 9.91 9.85 9.83 9.72 9.58 9.55 9.66 9.75 9.78 9.70... 2
9.69 9.63 9.66 9.57 9.56 9.58 9.59 9.45 9.46 9.57 9.62 9.67 9.74... 9.75 9.50 9.60 9.8 9.82 9.80 9.72 9.72 9.55 9.63 9.77 9.81 9.87 9.91... 9.85 9.84 9.79 9.92 10.0 10.03 10.03 10.10 10.05 10.05]; %最低价 spj1=[9.94 9.92 9.88 9.85 9.77 9.60 9.70 9.79 9.78 9.81 9.73... 9.80 9.71 9.69 9.57 9.63 9.77 9.60 9.57 9.63 9.70 9.76 9.81 9.87... 9.76 9.81 9.98 9.99 9.89 9.92 9.73 9.74 9.65 9.83 9.86 9.88 9.89... 9.98 9.88 9.89 9.96 9.96 10.11 10.04 10.13 10.19 10.06 10.09]; %收盘价 p=time; t=[kpj1;zgj1;zdj1;spj1]; % 归一化处理 [pn,minp,maxp,tn,mint,maxt]=premnmx(p,t); dx=[-1,1]; % 网络训练 net=newff(dx,[4],{'tansig'},'traingdx'); net.trainparam.show=1000; net.trainparam.Lr=0.05; net.trainparam.epochs=100; net.trainparam.goal=1e-3; net=train(net,pn,tn); % 对原始数据进行仿真 an=sim(net,pn); a=postmnmx(an,mint,maxt); % 用仿真结果与已知数据进行对比测试 x=1:48; new1=a(1,:); new2=a(2,:); new3=a(3,:); new4=a(4,:); % 对新数据进行仿真 pnew=73:120; pnewn=tramnmx(pnew,minp,maxp); anewn=sim(net,pnewn); anew=postmnmx(anewn,mint,maxt) % 与原始目标数据进行比较 3
%目标数据 kpj2=[10.15 10.16 10.11 9.92 9.86 9.80 9.78 9.78 9.66 9.68 9.66 9.74... 9.74 9.60 9.57 9.67 9.63 9.70 9.69 9.66 9.66 9.53 9.53 9.57 9.51... 9.57 9.55 9.69 9.66 9.76 9.76 9.71 9.64 9.75 9.79 9.79 9.72 9.89... 9.97 10.01 10.10 10.02 10.06 10.17 10.10 10.3 10.21 10.27]; %开盘价 zgj2=[11.26 10.20 10.14 9.95 9.93 9.81 9.81 9.80 9.75 9.70 9.80 9.78... 9.76 9.75 9.66 9.67 9.71 9.73 9.74 9.73 9.67 9.68 9.68 9.60 9.66... 9.66 9.70 9.79 9.81 9.89 9.82 9.77 9.78 9.83 9.86 9.88 9.91 10.04... 10.08 10.15 10.21 10.07 10.28 10.25 10.35 10.33 10.3 10.31]; %最高价 zdj2=[10.11 10.09 9.88 9.89 9.79 9.76 9.68 9.69 9.62 9.63 9.65 9.71 9.39... 9.55 9.52 9.55 9.59 9.64 9.61 9.64 9.50 9.48 9.52 9.50 9.48 9.35... 9.54 9.65 9.64 9.71 9.68 9.59 9.60 9.73 9.69 9.70 9.70 9.88 9.85... 9.98 10.01 9.98 10.0 10.06 10.01 10.10 10.16 10.22]; %最低价 spj2=[10.8 10.12 9.92 9.91 9.81 9.79 9.77 9.70 9.68 9.65 9.72 9.77 9.46... 9.59 9.62 9.66 9.70 9.70 9.68 9.66 9.55 9.56 9.64 9.51 9.63 9.63... 9.68 9.70 9.75 9.83 9.71 9.68 9.77 9.79 9.74 9.75 9.80 9.96 10.03... 10.12 10.04 10.06 10.20 10.09 10.32 10.12 10.26 10.26]; %收盘价 %绘图 figure(4); subplot(2,2,1);plot(x,new1,'r-',x,kpj2,'b--+'); legend('预测开盘价','实际开盘价'); subplot(2,2,2);plot(x,new2,'r-',x,zgj2,'b--+'); legend('预测最高价','实际最高价'); subplot(2,2,3);plot(x,new3,'r-',x,zdj2,'b--+'); legend('预测最低价','实际最低价'); subplot(2,2,4);plot(x,new4,'r-',x,spj2,'b--+'); legend('预测收盘价','实际收盘价');
结论 (结果)
预测数据结果:(第1,2,3,4行分别对应预测的开盘价、最高价、最低价、收盘价数据) anew = Columns 1 through 7 10.1900 10.1900 10.1900 10.1900 10.1900 10.1900 10.1900 10.2800 10.2800 10.2800 10.2800 10.2800 10.2800 10.2800 10.1000 10.1000 10.1000 10.1000 10.1000 10.1000 10.1000
