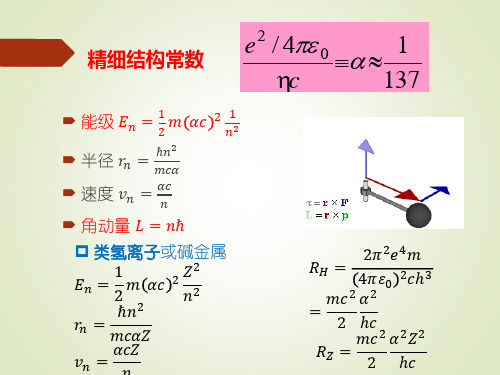
索末菲对玻尔理论的推广(2)——相对论计算
第二章 原子的玻尔—索末菲理论 (4)
principal
diffuse
fundament al
(next in alphabet after f)
g
4
18
5th shell and higher (theoretically)
原子实极化和轨道贯穿
碱金属原子的光谱可以用类似氢原子的公式表示。这些原 子的能级,当n较大时,非常近氢原子的能级,只有当 n较小 时差别较大。如果考虑到碱金属原子化学上是一价的,它们 容易电离成为带一个单位电荷的离子等情况,可以设想上节 讨论过的那些光谱也是由于单电子的活动产生的。
此式中第一项就是玻尔理论的结果,第二项起则是相对论效 应的修正。显然,对同一n不同nφ,第二项的数值是不同的。 由此可见,同一n而nφ不同的那些轨道运动具有不同的能量。 这样,原来的能级简并在考虑了相对论修正后就消除了。不 过,第二项代表的数值比第一项小得多,所以分裂的能级只 有微小的差别。这个差别被称为能级的精细结构,与它相联 系的常数α称为精细结构常数。索末菲的功绩之一就是引入了 这一十分重要的常数。
n nr n 1,2,3,; n 1,2,3,,n.
上式所表达的是索末菲推广到椭圆轨道后得到的结果,把 它们与玻尔的圆运动情况相比较,不难看出:能量的表达 式没变,但轨道的半径有了长、短半轴之分,且出现了两 个量子数n和nφ。这个结果所包含的物理意义是:轨道的 长半轴和体系的能量只决定于主量子数 n,而与nφ无关; 轨道角动量决定于角量子数nφ,形状取决于 之比。
①椭圆轨道推广 索末菲认为电子绕原子核在一个平面上作椭圆运动,是一 个二维的运动。描述椭圆运动中电子的位置,可用平面极坐 标中的坐标φ和r,与这两个坐标对应的广义动量就是角动量 L 和动量Pr。这体系的能量可表示为
物理学中的“大师之师”——阿诺尔德·索末菲

“无冕之王,大师之师”在物理学史上,最伟大的物理学家们大都获得过物理学界的最高荣誉——诺贝尔物理学奖。
然而,也有少数物理学巨匠与诺贝尔奖失之交臂,德国理论物理学家阿诺尔德•索末菲算得上其中最了不起的一位。
索末菲的了不起体现在两个方面——“无冕之王”和“大师之师”。
索末菲之所以被称为“无冕之王”,是因为他崇高的学术地位。
作为量子力学和原子物理学的创始人之一,索末菲是可以与普朗克、爱因斯坦、玻尔等人齐名的最顶尖的物理学家。
在50年的学术生涯里,索末菲为物理学做出了许多非常重要的贡献,他推广了玻尔的氢原子模型,提出了角量子数和自旋量子数的概念,提出了精细结构常数并且开创了X射线波动理论。
这些科学贡献与其他的诺贝尔物理学奖得主的成就相比,一点都不逊色。
长时间处于学术巅峰,索末菲一次又一次地得到诺贝尔奖评奖委员会的认可,在索末菲的一生中,他创纪录地总共获得了81次诺贝尔物理学奖提名(经常是一年获得不同专家的分别提名)。
可以说,索末菲距离最终得奖所差的只是一点点运气,他是物理学界名副其实的“无冕之王”。
与普朗克、爱因斯坦等人相比,索末菲对物理学还有更加突出的贡献,那就是他非常善于教学生。
除了科学研究,索末菲大部分的时间都在教书育人,以他为核心成员的慕尼黑大学理论物理研究所,出现了著名的“慕尼黑学派”。
在索末菲的发掘和提携下,“慕尼黑学派”的大批年轻学者成长为杰出的物理学家或者化学家,其中就包括海森堡、泡利、德拜等7位诺贝尔奖得主。
这让索末菲成为物理学史上培养出最多诺贝尔奖得主的导师,因此他又有“大师之师”的美誉。
下面,我们就来回顾一下这位伟大物理学家的一生。
从柯尼斯堡到慕尼黑1868年12月5日,阿诺尔德·索末菲出生于德国东普鲁士城市柯尼斯堡,如今这里已经是俄罗斯的加里宁格勒市。
1886年,中学毕业的索末菲以优异的成绩考入柯尼斯堡大学,主修的专业是数学,他幸运地得到了德国著名数学家大卫·希尔伯特的指导。
玻尔理论半径公式推导

玻尔理论半径公式推导波尔理论半径的公式推导mv^2/r是向心力。
(4πε0R^2) 这是2电荷间的作用力。
波尔能级公式推导假设一个原子核为Z个正电(电荷=Ze),质量为m的电子以v的切线速度绕原子核运行,r=Ze*e/r^2整理可得rmv^2=Ze^22.该电子的能量等於动能减去库仑力所提供的电位能E=(1/可以得到E=-Ze^2/要想办法代换掉rmvr=n(h/2pi)5.把1的式子平方后除以4的式子mr=(n^2)(h^2)/(4pi^2)(Ze^2)r=(n^2)(h^2)/量子激子半径:什么是激子波尔半径sarin上转换发光纳米粒子为什么无生物背景荧光半导体量子点(QDs)是一种有II-VI族或III-V族元素组成的、粒径小于或接近于激子波尔半径的纳米颗粒,如量子尺寸效应、比表面积效应、量子隧道效应等,从而表现出尺寸依赖的荧光性质。
量子点具有独特的光学性质和生物特性:量子点可根据尺寸大小来调节其发射波长;量子点的荧光强度和稳定性比染料要高,同时修饰后的量子点也具有一定的生物相容性,能进行生物活体标记和检测。
量子点作为一种新型的荧光探针在生物分子检测、细胞荧光成像、多色标记等研究领域中发挥了重要的作用。
在生物荧光标记也得到了快速发展。
r=(m0/mn)εr是求波尔半径公式吗这个公式的根据是牛顿第二定律...也就是电场力提供向心力...e*e/(4πε0r*r) 就是表示电场力其中 e/(4πε0r*r) 表示电场强度1/利用波尔-索末菲的量子化条件求:在均匀磁场中做圆周运动的电子轨道的可能半径不知道硒化汞的波尔半径是多少?不知道波尔半径的推导mv^2/r是向心力。
(4πε0R^2) 这是2电荷间的作用力;波尔的量子假设,怎样推导出氢原子的半径波尔理论基态氢原子能量 E1=-13.6ev动能Ek1=1/2mv^2=E1 势能 Ep1=-eφ1=2Ek1=-27.2evφ1=27.2Vφ1=Ke/波尔半径氢原子核外电子基态轨道的半径就是波尔半径是53pm(10负12次方米)。
第二章 原子的玻尔—索末菲理论 (4)
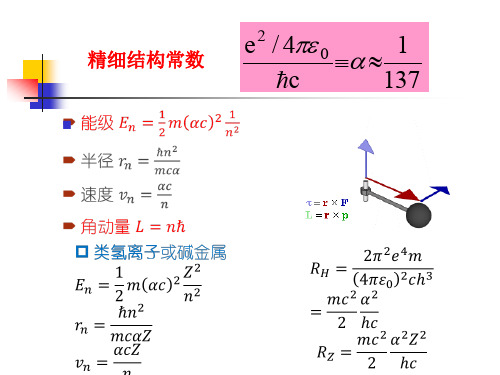
之比。
这即意味着,当n相同nφ不同时,在不同轨道中运动的体系会具有相同的 能量,这种情况称为简并(或退化)。例如对同一n,由于nφ=1,2,…, n,便有n个可能的轨道,我们说它有n个状态,但这n个状态的能量是相 同的,故这种情况就被称为n度简并(或退化)。下图所示的是氢原子能 级简并(或退化)的情况。
n 4 n
在上面的简单推导过程中,我们不难看出相对论效应是如何被考虑进去的。显 而易见,上式中第一项就是玻尔理论原来给出的,第二基则是考虑了相对论效 应后增加的修正项。虽然这一简单推导只对圆轨道才成立,但是,它已包含了 相对论修正引起的主要效果。
值得指出,在作上述展开时,认为β<< 1,至少是β<1,那么当β=αZ/n>1,
T
m
m0
c
2
m0c
2
1
1
2
1
与经典公式不同,当v << c ,即β很小时,对上式右
边第一项作级数展开,且略去高阶无穷小量,就得到了动 能的经典表述形式。
下面将用相对论对圆周轨道进行修正。让我们从能量 角度看,能量可写成动能与势能之和,即
E
T
V
m
m0
c
2
精细结构常数
e2 / 4 0 1
c
137
光谱
类氢离子,毕克林系 折合质量,里德堡常数随不同类氢离子变化
Franck-Hertz实验
广义量子化条件和索末菲理论
A. 广义量子化条件
玻尔在氢原子理论中得出,只有满足角动量量子化条件
Ln,n1,2,3,
的电子轨道运动才是实际上可能存在的,将上式改写一下,即
玻尔模型的原理和应用

玻尔模型的原理和应用1. 简介玻尔模型,又称为玻尔-索末菲模型,是位于量子力学早期阶段的一种模型。
它由丹麦物理学家尼尔斯·玻尔于1913年提出,用于解释氢原子的光谱线的产生机制。
玻尔模型成功地揭示了原子的稳定结构和能级的离散性质,并为后来量子力学的发展奠定了基础。
本文将介绍玻尔模型的原理及其在物理学和化学中的应用。
2. 玻尔模型的原理玻尔模型基于以下几个假设:1.电子只能在规定的轨道上运动,每个轨道对应一个特定的能级。
2.电子在轨道上运动时,不会辐射能量。
3.电子只有在跃迁到另一个较低能级的轨道上时,才会辐射出能量(光子),形成光谱线。
根据这些假设,玻尔推导得到了以下关于氢原子能级的公式:$$E = -\\frac{{2\\pi^2me^4Z^2}}{{h^2n^2}}$$其中,E为能级,m为电子质量,e为电子电荷,Z为原子核中质子数,h为普朗克常数,n为轨道的主量子数。
这个公式表明了能级与主量子数n的平方反比,能级越低,主量子数越小;能级越高,主量子数越大。
同时,这个公式也说明了能级的离散性质,即只有特定的能级值是允许的。
3. 玻尔模型的应用3.1 光谱线的解释玻尔模型的最初目的是解释氢原子光谱线的产生机制。
根据玻尔模型,当电子从一个较高的轨道跃迁到一个较低的轨道时,会释放出一个光子,其频率与能级差相关,从而形成光谱线。
通过对氢原子光谱线的研究,玻尔模型成功地解释了氢原子光谱线的频率和能级之间的关系。
3.2 原子结构的研究玻尔模型的成功启示了科学家们研究其他原子结构的思路。
通过将玻尔模型的原理推广到其他原子和离子系统中,科学家们能够预测和解释不同原子的能级结构和光谱线。
玻尔模型为我们理解原子的结构和性质提供了一个重要的基础。
3.3 量子力学的发展玻尔模型的提出对后来量子力学的发展产生了重要的影响。
玻尔模型的成功解释了氢原子光谱线和能级结构的实验现象,同时也暴露出了经典物理学的局限性。
原子物理参考文献

原子物理参考文献原子物理是研究原子结构、原子核性质以及原子与辐射相互作用的学科。
在这个领域中,有许多重要的参考文献可以作为学习和研究的基础。
以下是一些具有代表性的原子物理参考文献。
一、经典原子物理1. Bohr, N. (1913). "On the constitution of atoms and molecules". Philosophical Magazine. 26: 1–25.这篇文章是尼尔斯·玻尔提出的玻尔模型的基础,它为我们理解原子结构的量子理论奠定了基础。
2. Sommerfeld, A. (1916). "Zur Quantentheorie der Spektrallinien". Annalen der Physik. 51: 1–94.阿诺德·索末菲尔德在这篇文章中进一步发展了玻尔模型,并引入了椭圆轨道和细分结构的概念,为原子物理的量子理论提供了重要的突破。
二、量子力学原子物理1. Schrödinger, E. (1926). "An Undulatory Theory of the Mechanics of Atoms and Molecules". Physical Review. 28 (6): 1049–1070.薛定谔方程的提出是量子力学的重要里程碑。
这篇文章详细介绍了薛定谔方程的推导和应用,为我们理解原子结构和性质提供了新的数学工具。
2. Dirac, P. A. M. (1928). "The Quantum Theory of the Electron". Proceedings of the Royal Society of London. Series A. 117 (778): 610–624.保罗·狄拉克在这篇文章中提出了著名的狄拉克方程,描述了电子的相对论性量子力学。
玻尔的氢原子理论
玻尔的氢原子理论
为此,J.汤姆孙在1904年提出了原子结构的枣糕式模型.该模型认 为,原子可以看作一个球体,原子的正电荷和质量均匀分布在球内, 电子则一颗一颗地镶嵌其中.1909年,J.汤姆孙的学生卢瑟福为了验证 原子结构的枣糕式模型,完成了著名的α粒子散射实验.实验发现α粒 子在轰击金箔时,绝大多数α粒子都穿透金箔,方向也几乎不变,但 是大约有1/8 000的α粒子会发生大角度偏转,即被反弹回来.这样的 实验结果是枣糕式模型根本无法解释的,因为如果说金箔中的金原子 都是枣糕式的结构,那么整个金箔上各点的性质应该近乎均匀,α粒 子轰击上去,要么全部透射过去,要么全部反弹回来,而不可能是一 些穿透过去,一些反弹回来.
玻尔的氢原子理论
二、 原子结构模型
1897年,J.汤姆孙发现了电子.在此之前,原 子被认为是物质结构的最小单元,是不可分的,可 是电子的发现却表明原子中包含带负电的电子.那 么,原子中必然还有带正电的部分,这就说明原子 是可分的,是有内部结构的.执着的科学家就会继 续追问:原子的内部结构是什么样的?简洁的里德 伯光谱公式是不是氢原子内部结构的外在表现?
玻尔的氢原子理论
三、 玻尔的三点基本假设
为了解决原子结构有核模型的稳定性和氢原子光谱的分 立性问题,玻尔提出以下三个假设:
(1)定态假设.原子中的电子绕着原子核做圆周运动, 但是只能沿着一系列特定的轨道运动,而不能够任意转动, 当电子在这些轨道运动时,不向外辐射电磁波,原子系统处 于稳定状态,具有一定的能量.不同的轨道,具有不同的能 量,按照从小到大的顺序记为E1、E2、E3等.
玻尔的氢原子理论
可是这个模型却遭到很多物理学家的质疑.因为按照当时的物 理理论(包括经典力学、经典电磁理论及热力学统计物理),这 样一个模型是根本不可能的,原因有以下两个:
原子物理学第三次作业答案 (7)
第一章 量子力学前的原子物理学§1.1 原子的外部和内部特性“原子”的原始慨念:组成物质的最基本单元 (最小,不可再分离:atom -希腊文) 提出者:古希腊哲学家-德膜克利特(~B.C. 400)古代中国人: 金,木,水,火,土 (五行说); 古代云南彝族: 铜,木,水,火,土。
问题:不可再分离?原子→电子、原子核;原子核→质子,中子;质子,中子→ 基本粒子(中微子、光子、介子、超子,…); 基本粒子→夸克→弦,…说明:人们对“最基本单元”的认识是无止境的。
意义: 闪烁着人类认识世界的哲学光芒,但是,不具备科学的“实证”特征。
“实证”(有实验证据):多大?多重?内部结构特性? 1.1.1 原子的外部特性19世纪初:掌握了原子的外部特性:多大?多重? (i) 摩尔(Mol )定义(1971年国际计量会议):一个系统物质的数量,该系统中包含的基本单元数与0.012 kgC 126的原子数相同。
说明: 1,“基本单元”可以是原子、分子或带电粒子等;2,0.012 kgC 126的原子数=6.022×1023,或N A (阿伏伽德罗常数)=6.022×1023/Mol 。
(ii) 原子的相对质量(原子量,A )定义(1971年国际计量会议):1摩尔某种物质的质量[M(A)]和1摩尔C 126的质量[M(C 126)]的1/12的比值,是这种物质的原子量(A )。
(iii) 原子的绝对质量(原子质量,m A ) 已知: N A ,A按定义:A=M(A)/[M(C 126)/12], M(A)= A M(C 126)/12= A (g )则: m A =A (g )/ N A =A ×1.661×10-24(g )=A ×1.661×10-27(kg )例:C 126,A =12.0000, 一个C 126原子的重量:12×1.661×10-27(kg)=19.93×10-27(kg);H 11, A =1.0078,一个H 11原子的重量:1.0078×1.661×10-27(kg)=1.674×10-27(kg);(vi )原子的尺寸已知: N A ,A ,ρ(g/cm 3); 则: 一个摩尔的原子所占的体积:V mol =A(g)/ρ;另一方面,设r A 为原子半径,一个原子的体积(球体)=(4πr A 3/3); 一个摩尔的原子所占的体积:V mol =N A (4πr A 3/3)所以,r A = (3A/4πρ N A )1/3 ~10-8cm ~ 10-10m=1 A例:H (H 11) , A =1.0078, ρ =0.09(g/cm 3)r H ~1.6×10-8 (cm) =1.6 A 量子力学计算值: r H =a =0.53 A 1.1.2 原子的内部特性19世纪末-20世纪初:基本掌握了原子的内部特性:原子由带正电的原子核和带负电的电子组成,整体呈电中型;电子绕着原子核做圆周运动。
第二章,氢原子光谱
Back
Next
第五节:玻尔理论的推广
玻尔—索末非模型 碱金属的光谱 Back
第五节:玻尔理论的推广
玻尔—索末非模型
碱金属的光谱
Next
第五节:玻尔理论的推广
玻尔—索末非模型
碱金属的光谱
Back
Next
第五节:玻尔理论的推广
原子实是一个球形对称的 结构,它里边的原子核带 有Ze正电荷和(Z-1)e负 电荷,在原子最外层运动 的价电子好象是处在一个 单位正电荷的库仑场中, 当价电子运动到靠近原子 实时,由于价电子的电场 作用,原子实中带正电的 原子核与带负电的电子的 中心会发生微小的偏移, 于是负电的中心不再在原 子核上,形成一个电偶极 子。这就是原子实的极化。
rnn2a 0
c vnn
n1 ,2 ,3 ,K
a0 4m πee0h22 0.53Å 玻尔半径
En
1 2n2
e2 4π0a0
e2 1 精细结构常数 4π0hc 137
1 2n2
m e
2c 2
n 1 E 1 1 3 . 6 e V r 1 a 0 基态(ground state)
n 2 激发态(excited state)
质心系
核系
En
1 2n2
Z 2e2 4π0a0
1 2n2
Z
2
2c 2
rnn Z 2a0
vnZ nc n1 ,2 ,3 ,K
r1n
me rn
n2
Z
4π0h2
mee2
e4
1
RM4π4π02h3c1m e MR
R1 0 7m 1 M 1 .0 9 73 7 3 1
1 1H 1 .0 9 67 7 58 1 2D 1 .0 9 70 7 42 1 3T 1 .0 9 7 1 7 35 4 2H e 1 .0 9 72 2 27 3 7L i2 1 .0 9 72 8 80 9 4H e3 1 .0 9 73 0 70
玻尔-索末菲的椭圆轨道理论的推导
玻尔-索末菲的椭圆轨道理论的推导
索末菲椭圆轨道理论玻尔原来的理论仅考虑氢原子中电子绕核作圆轨道运动,索末菲推广考虑了椭圆轨道。
平面椭圆轨道有两个自由度,需要两个量子化条件,空间椭圆轨道则需要3个量子化条件。
索末菲采用推广了的玻尔量子化条件,得出氢原子系统的能量是量子化的,仍由主量子数n确定,与玻尔理论结果相同,而氢原子的角动量由角量子数确定,相同主量子数不同椭圆轨道上的角动量不同,且是量子化的,椭圆形状也是量子化的。
