电机的矩阵分析1
矩阵变换器-永磁同步电机矢量 控制系统的新型电流控制方法

2007年 3 月电工技术学报Vol.22 No.3 第22卷第3期TRANSACTIONS OF CHINA ELECTROTECHNICAL SOCIETY Mar. 2007矩阵变换器−永磁同步电机矢量控制系统的新型电流控制方法葛红娟周波苏国庆张绍(南京航空航天大学自动化学院南京 210016)摘要分析了基于电流滞环控制的矩阵变换器−永磁同步电机(MC-PMSM)系统的开关组合状态和存在的缺点:系统侧电流存在较大的5次和7次谐波分量。
提出了一种改进电流控制方法,该方法采用电机电流双环控制,得出三相电机电流的6个电流控制信号,并将输入三相电压分成12个相区,根据电流控制信号和相区号的不同,选择不同的输入相与输出相连接,确定出矩阵变换器开关组合状态。
在该方法中,每个输入相在整个周期内都参与调制,降低了系统输入电流的谐波分量,提高了系统输入电流的正弦度。
关键词:矩阵变换器永磁同步电机谐波分量电流双环控制矢量控制中图分类号:TM301Novel Current Modulation Approach for the Vector Control ofMC-PMSM SystemGe Hongjuan Zhou Bo Su Guoqing Zhang Shao(Nanjing University of Aeronautics and Astronautics Nanjing 210016 China)Abstract An improved current hysteresis-loop modulation approach for the vector control of matrix converter-permanent magnet synchronous motor (MC-PMSM) system is presented in this paper.With the approach, the three-phase input voltages are divided into twelve sections and three pairs of current control signals are deduced by comparing the reference values and the measured values of the output currents based on double current loops. Then, the states of the switches in the MC-PMSM system are determined according to the section number of the input voltages and one of the three pairs of current control signals, so that the modulation of every input voltage phase hold in the whole periods.Hence the 5th harmonic, the 7th harmonic, and the total harmonic distortion (THD) of the input currents, which are relative large when the based current hysteresis-loop modulation method is adopted in the system, are obviously reduced and the input currents of the system become more sinusoidal.Keywords:Matrix converter, permanent magnet synchronous motor, harmonic components, double current loop modulation, vector control1引言矩阵变换器可以实现输入电流和输出电压波形的正弦化,输入功率因数可调,没有大体积的直流环节,因此,在交流传动系统中蕴藏着良好的应用前景。
矩阵理论在李雅普洛夫稳定性分析上的应用

矩阵理论在李雅普洛夫稳定性分析上的应用矩阵理论在李雅普洛夫稳定性分析上的应用一引言一个自动控制系统要能正常的工作,必须首先是稳定的系统,即当系统受到外界干扰时,它的平衡被破坏但是在外界干扰去掉之后,它仍能够有能力自动地恢复到平衡态下继续工作,系统的这种性能称为稳定性。
例如,电压自动调节系统中保持电机电压为恒定的能力,电机自动调速系统中保持电机转速为一定的能力以及火箭飞行中保持航向为一定的能力等。
也可以说,系统的稳定性就是系统在受到外界干扰后,系统的状态变量或者输出变量的偏差量过渡过程的收敛性,用数学方法就是表示为:ε≤∆∞→|)(|lim t x n式中,)(t x ∆为系统被调量偏离其系统位置的变化量,ε为任意小的规定量。
如果系统在受到外界干扰后偏差量越来越大显然不是一个稳定的系统。
李雅普洛夫第二法也称为直接法,它的特点是通过定义李雅普洛夫函数,直接判断分析系统的稳定性。
二 李雅普洛夫意义下的稳定性定义 :对于由状态方程),(t x f x =∙描述的系统对于任意给定的实数0>ε和任意给定的初始时刻0t ,都对应存在一个实数0),(0>t εδ使得对于从任意位于平衡态e x 的球域),(δe x S 的初始状态0x 出发的状态方程的解x 都位于球域),(δe x S 内,则称系统的平衡态e x 是李雅普洛夫意义下的稳定性。
李雅普洛夫稳定性示意图 李雅普洛夫不稳定性的示意图 1) 李雅普洛夫第二法的相关定理 矩阵论相关知识:x2O x1ε δ X(0) x2O x1 1 δ ε① 范数范数在数学中定义为度量n 维空间的点之间的距离。
在工程中常用的是2-范数,就欧几里得范数,其定义式为:∑=-=-ni i i x x x x 12,2,1221)( 其中的i x ,1和i x ,2分别为向量1x 和2x 的各分量。
② 各点组成的空间成为球域,记为),(0δx S 。
即),(0δx S 包含满足δ≤-20x x 的n 维空间中的各点x③ 定义:设对称矩阵P 为二次型函数)(x V 的权矩阵,当)(x V 分别为正定,负定,非负定,非正定与不定时,则对称阵P 相应的为正定,负定,非负定,非正定与不定。
机械手末端姿态矩阵1

述 探索机器人:
水下、太空、空间、危险环境
服务机器人:
清洁、护理、救援、娱乐、保安
其它机器人:医疗、福利、林业·、渔业、建筑等
四、机器人技术的进展
第
工业机器人技术在机械本体、控制系统、传感
一
系统、可靠性和网络功能方面取得了突破性进
节 展:
机器人操作机已实现了优化设计(包括材料、构型和
意为“苦力”、 “劳役”,是一种人造劳动者。
概 述
英语Robot由此衍生而来。 该剧中,卡佩克提出了机器人的安全、感
知和自我繁殖问题。科学技术的进步很可能引
发人类不希望出现的问题。虽然科幻世界只是
一种想象,但人类社会将可能面临这种现实。
机器人三原则与机器人学
第 Isaac Asimov 在《I’m Robot》中提出了 一 “机器人三原则” : 节 A robot must not harm a human being or, through
第
三
机器人动力学研究的是机器人手臂的关节
节 力矩和在关节力矩作用下的动态响应之间得关
系问题。
机
首先要建立机器人的动力学方程。
器
建立动力学方程的方法有两种:牛顿——
人 欧拉方程法和拉格朗日方程法。
动
力
学
第 一、建立动力学方程的步骤
二 节 计算任一连杆上任一质点得速度;
计算各连杆的动能和机械臂的总动能;
人 正向运动学问题(用于机构设计)
运 已知各关节变量,求取机械手末端位姿;
动 逆向运动学问题(用于运动控制) 学 已知机械手末端位姿,求取各关节变量;
第
一、基本概念
二 节
转动关节
第三章电力系统潮流分析与计算(电力网络方程和网络矩阵)

(5)
3
4
6
§2 如何建立网络方程? 一、电力网络的数学抽象
发电机
串联元件
负荷 并联元件
网络: 网络元件 联结
网络元件特性约束(考虑无源线性元件):
U&b = ZbIb &
元件特性约束与元件联结关系无关
7
网络拓扑约束
把元件抽象成支路,研究支路之间的联结关系。
Kirchhoft定律
KCL ik = 0
回路电压列向量
E1 = Z1I1
回路阻抗矩阵
回路电流列向量
独立方程个数l=b-n,l:回路数,b:支路数,n:
节点数(树支数)
回路方程:由Zl反映El和 Il 间关系
Zl ≠ Zn
14
五、两种网络方程的比较
节点方程
方程个数 状态变量
n(少)
Un(直接)
选向问题
无
适应网络变化
易
回路方程
b-n(多)
3、如何形成节点导纳矩阵?(重要!计算机对矩阵兴趣) 4、节点导纳矩阵有何物理意义和性质? 5、如何形成节点阻抗矩阵?(重要!计算机对矩阵兴趣) 6、节点阻抗矩阵有何物理意义和性质?
2
§1 如何从原始接线到计算模型? 变电站 (计算机拓扑(Topology)分析)原始模型
电网
厂站(Station)拓扑分析
I1=U1y10 (U1 U2 )y12 (U1 U3)y13 I2 =U2y30 (U2 U1)y12 (U2 U3 )y23 I3 =U3y30 (U3 U1)y13 (U3 U2 )y32 y12
U1
y y 13
U3 23
I1
y10 I3
y30 I 2
一 bcg矩阵分析

发展: 发展:继续大量投资,目的是扩大战略事业单位的市 场份额。主要针对有发展前途的问题业务和明星业务。 维持:投资维持现状,目标是保持业务单位现有的市 维持: 场份额,主要针对强大稳定的现有金牛业务。 收获: 收获:实质上是一种榨取,目标是在短期内尽可能地 得到最大限度的现金收入,主要针对处境不佳的现有 金牛业务及没有发展前途的问题业务和瘦狗业务。 放弃: 放弃:目标在于出售和清理某些业务,将资源转移到 更有利的领域。这种目标适用于无利可图的瘦狗和问 题业务。
五.综合案例分析 综合案例分析
BCG矩阵分析法 矩阵分析法
案例三
Y公司曾是一家生产系列电风扇的大企业,80年代末期, 该公司生产的系列电风扇所占市场份额名列前茅。公司 领导层决定扩大生产规模。扩建厂房、购进机械设备、 再装备三倍于现规模的电风扇生产流水线。由于当时电 风扇生产厂家剧增,特别是沿海一带乡镇企业生产的电 风扇大举进攻内地市场,电风扇市场迅速饱和,结果未 等到公司新生产流水线全部正式投产运作时,公司产品 囤积剧增,大量产品找不到销路。结果既没有及时地培 育明星业务,又导致一头好端端的“金牛”过早胀死。
五.综合案例分析 综合案例分析
BCG矩阵分析法 矩阵分析法
荣事达人并不满足于此,1994年3 月又与日本三洋电机 株式会社、三洋贸易株式会社、丰田通商株式会社、长 城贸易株式会社组建合资公司——合肥三洋洗衣机有限 公司,生产具有国际一流水准人工智能模糊控制全自动 洗衣机,在国内市场独占鳌头。1995年8月荣事达管理者 又从“金牛”身上取资与港台企业合资兴建“荣事达橡 塑制品有限公司”、“荣事达日用电器有限公司”等, 不断开发“问号”业务,培育“明星”业务,不仅实现 了公司资产保值增值,而且使组织机体始终处于良性循 环之中。1997年末荣事达集团产值、销售收入、利润分 别比上年增长31%、13%和18.8%,集团资产增长到26.2 亿元,比上年增长21.69%。
电机设计及有限元分析
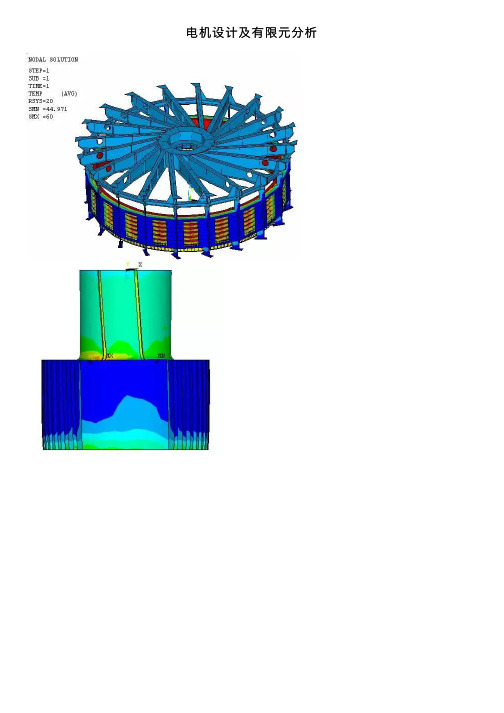
电机设计及有限元分析详细介绍:随着电⽓化和产品智能化⽔平的提⾼,电机、变压器以及⾼低压电器在各种装备和⽣活中的应⽤越来越多,电机和电器朝着容量⼤型化、体积⼩型化以及智能化的⽅向发展。
现今的电机电器设计⾯临着更复杂的技术挑战,只有充分运⽤现代⼯程仿真技术才能应对这些挑战。
典型应⽤领域1)电磁仿真。
电磁仿真在电机电器设计中扮演⾮常重要的⾓⾊,电磁仿真可以预测电磁转换的效率、各个部件的损耗和发热量、电磁⼒/⼒矩等参数,是进⼀步进⾏热仿真和结构仿真的基础;2)电场仿真。
随着电器设备容量和⼯作电压的提⾼,电场仿真的必要性性更加迫切,电场仿真能够预测设备的绝缘性、放电和击穿的可能性等性能指标;3)热仿真。
过热会使电机的可靠性降低,甚⾄于烧毁,因此热分析与热设计在电机电器设计中⾮常重要,热分析可以优化冷却⽅案,改善冷却效果。
4)结构强度、疲劳仿真。
利⽤结构分析软件研究电机电器在机械载荷和热载荷作⽤下的强度、刚度、振动和疲劳寿命,可提⾼设备的可靠性。
5)噪声分析。
模拟结构振动噪声和电磁噪声。
电磁仿真稳态磁场分析: 激励不随时间变化,如永磁体的磁场、稳恒电流产⽣的磁场等谐性磁场分析: 激励按正余弦规律变化,如感应式电机瞬态磁场分析: 激励随时间⽆规律变化混合励磁车⽤发电机三维电磁场有限元⽹格发电机永磁励磁的磁密分布转⼦磁感应强度⽮量右视图定⼦磁感应强度⽮量值定⼦磁场强度标量值定⼦磁场强度⽮量值转⼦磁场强度⽮量通过温度场计算,得到电机整机或部件的温度分布、热量的获取和损失、热梯度、热流密度等.稳态温度场分析:热源不随时间变化瞬态温度场分析:热源随时间变化定⼦铁⼼与机座温度分布上机架和定⼦温度分布电机流场分析电机结构分析部件刚强度计算接触应⼒计算固有频率计算动态响应计算临界转速计算⾼速发电机转⼦轴应⼒计算发电机转⼦轴应⼒计算定⼦和上机架联合计算序号⼯况载荷1起吊运输⼯况⾃重额定扭矩,正常运⾏⼯况2正常运⾏⼯况磁拉⼒,⾃重,温升半数磁极短路磁拉⼒3半数磁极短路⾃重,温升4地震⼯况地震加速度正常运⾏⼯况结构综合应⼒正常运⾏⼯况结构径向变形半数磁极短路⼯况结构综合应⼒半数磁极短路⼯况结构径向变形下机架有限元模型图结构应⼒分布云图载荷:⽔推⼒、机组转动、部分总重量定⼦铜环引线结构强度计算循环对称模型定⼦铜环引线结构整体应⼒分布短路⼯况,铜环引线发热定⼦铜环引线⽀架应⼒分布定⼦铜环引线结构变形分布主轴法兰强度分析发电机最⼤容量时主轴法兰应⼒强度发电机半数磁极短路⼯况时主轴法兰应⼒强度联轴器应⼒和紧量计算汽轮发电机转⼦齿头和槽楔应⼒计算计算模型应⼒分布发电机端部振动模态分析俄制500MW汽轮发电机定⼦端部振动模态分析电磁⼲扰⼒下的定⼦振动定⼦铁⼼的各个部位响应值曲线临界转速计算传递矩阵法计算有限元法计算⽂章来源:伺服与运动控制。
电力系统分析第四章(1)
M ab Lbb M cb M fb M Db M gb M Qb
M ac M bc Lcc M fc M Dc M gc M Qc
M af M bf M cf Lff M Df M gf M Qf
M aD M bD M cD M fD LDD M gD M QD
M ag M bg M cg M fg M Dg Lgg M Qg
Rf
d
y D
g α
c
Q
a
ω
D
o
ffLeabharlann Dxcb
q
g Q
D
b
z
ia
2)定子三相绕组磁轴的正方向与其正向电流所产 生磁通的方向(按右手法则)相反;转子各绕组 磁轴的正方向,与其正向电流所产生磁通的方向 (按右手法则)相同。 3)定子和转子各绕组磁链的正方向与其磁轴的正 方向相同, 各绕组由磁链变化所产生的感应电动势服从楞次 定律。
M ba = ψ ba (−ia )
= −λmσ ws2 + λad ws2 cos α cos(α − 2π 3) + λaq ws2 sin α sin(α − 2π 3) = −[m0 + m2 cos 2(α + π 6)]
对于隐极同步机有λad= λaq ,所以其定子绕组的 互感系数为常数。
目前广泛使用的同步电机数学模型是在理想同步电机假设条件下建立起来的, 1) 线性磁路假设 线性磁路假设:忽略同步电机的磁路饱和效应,认为电机铁芯的导磁系 数为常数。 2) 转子对称假设 转子对称假设:同步电机转子对自身的纵向d轴和横向q轴结构对称。 3) 定子对称假设 定子对称假设:同步电机定子a、b、c三相绕组结构对称,它们的磁轴在 空间位置上依次相差2π/3(rad)电角度。 4) 气隙磁动势正弦分布假定 气隙磁动势正弦分布假定:同步电机定子电流产生的磁动势在其气隙中 按正弦分布。反之,同步电机空载,转子恒速旋转时,转子绕组的磁动势 在定子绕组感应产生的空载电动势是时间的正弦函数。 5) 定子及转子光滑表面假设 定子及转子光滑表面假设:该假设相当于认为定子及转子的槽和通风沟 不影响定子及转子绕组的电感。 符合上述条件的电机称作理想同步电机。
波士顿矩阵分析海尔公司专题培训课件
100%
提高市场占有率
90%
长期计划进行改进和扶持
80%
2011空调市场增长率
采取智囊团或项目组织等形式 70%
60%
增长率
50% 90%
40%
30%
20%
41%
31%
10%
0% 志高
海尔
奥克斯
品牌
瘦狗产品
撤退战略 海尔手机
热水器
综
产品
增长率
占有率
合 产
冰箱
80%
31.1%
品
空调
31%
2%
占 有
洗衣机
16.9%41.3%Fra bibliotek率电脑
28.9%
2.8%
增 长
热水器
10%
9%
率
手机
16%
1.9%
Hold不住就歇歇吧 = . =
波士顿矩阵的缺陷
Thank you for watching
波士顿矩 阵分析海 尔公司
波士顿矩阵
波士顿矩阵 分析海尔公司
海尔产品
波士顿矩阵是由波士顿咨询公司创 始人布鲁斯·亨德森于1970年首创的一种 用来分析和规划企业产品组合的方法。
高销售增长率 高市场占有率
低销售增长率 高市场占有率
明星类
幼童类
金牛类 瘦狗类
高销售增长率 低市场占有率
低销售增长率 低市场占有率
波士顿矩阵
波士顿矩阵 分析海尔公司
海尔产品
厨电厨 房
热水器
冰箱冷柜
电机海脑及手数尔公司彩 产品空调洗衣机
码
电
综
产品
增长率
占有率
合 产
等效电路阻抗模型、阻抗比矩阵获取及稳定性分析方法与制作流程
图片简介:本技术介绍了等效电路阻抗模型、阻抗比矩阵获取及稳定性分析方法,属于电机技术领域。
本技术建立了发电单元的dq等效电路阻抗模型,解决了电励磁凸极式发电机外特性难以表示问题。
将锁相环传递矩阵和直流母线电压控制环融入双馈异步电机等效阻抗矩阵的计算过程中,通过直流母线电压PI控制来表示电源侧变换器电流参考值,能够反映直流母线电压PI控制参数对系统整体稳定性的影响;通过将定子电压扰动与锁相环输出角度扰动间的传递函数融入双馈异步电机等效阻抗矩阵的计算过程中,锁相环PI控制参数对整体稳定性的影响也得到体现。
考虑系统自身的阻抗以及各控制环的控制效果引入的等效阻抗,是用于分析系统输入输出小信号稳定性的有效手段。
技术要求1.一种发电单元等效电路阻抗模型,所述发电单元包括:原动机、调速模块、励磁控制模块和同步发电机;原动机与同步发电机连接,用于带动同步发电机转动;调速模块,用于对原动机发出功率指令以控制原动机的运行,从而控制同步发电机的转速;励磁控制模块,用于产生励磁电压信号;同步发电机用于根据励磁控制模块产生的励磁电压信号,在发电机定子侧产生三相交流电压,同时也作为反馈信号输入励磁控制模块,其特征在于,同步发电机被等效为dq坐标系下的等效电路,其中,d轴与转子磁链方向相同,q轴由d轴向逆时针方向旋转90°获得;同步发电机d轴定子侧阻抗被等效为定子电阻Rgs与定子漏感抗sLgls之和,且耦合项(-ωgψgsq)被等效为电压源,与Rgs和sLgls串联;同步发电机d轴转子侧阻抗被等效为转子阻尼电阻Rkd与转子阻尼漏感抗sLlkd之和及转子励磁电阻Rf与转子励磁漏感抗sLlf之和的并联阻抗;同步发电机d轴互感抗sLgmd与同步发电机d轴转子侧阻抗并联后,再与同步发电机d轴定子侧阻抗串联,从而构成同步发电机d轴等效电路阻抗模型;同步发电机q轴定子侧阻抗被等效为定子电阻Rgs与定子漏感抗sLgls之和,且耦合项ωgψgsd被等效为电压源,与Rgs和sLgls串联;同步发电机d轴转子侧阻抗被等效为转子阻尼电阻Rkq与转子阻尼漏感抗sLlkq之和;同步发电机q轴互感抗sLgmq与同步发电机q轴转子侧阻抗并联后,再与同步发电机q轴定子侧阻抗串联,从而构成同步发电机q轴等效电路阻抗模型,其中,s表示s域算子,Lgls表示定子漏磁电感,Llkd表示转子阻尼漏电感,Llkq表示转子阻尼漏电感,Llf表示转子励磁漏电感,Lgmd表示转子励磁漏互感,Lgmq表示转子阻尼漏互感,ωg表示同步发电机角速度,ψgsd、ψgsq分别为同步发电机d、q轴定子磁链。
6.5 异步电动机的动态数学模型和坐标变换
6.5 异步电动机的动态数学模型和坐标变换本节提要异步电动机动态数学模型的性质三相异步电动机的多变量非线性数学模型坐标变换和变换矩阵三相异步电动机在两相坐标系上的数学模型三相异步电动机在两相坐标系上的状态方程一、异步电动机动态数学模型的性质2. 交流电机数学模型的性质(1)异步电机变压变频调速时需要进行电压(或电流)和频率的协调控制,有电压(电流)和频率两种独立的输入变量。
在输出变量中,除转速外,磁通也得算一个独立的输出变量。
因为电机只有一个三相输入电源,磁通的建立和转速的变化是同时进行的,为了获得良好的动态性能,也希望对磁通施加某种控制,使它在动态过程中尽量保持恒定,才能产生较大的动态转矩。
多变量、强耦合的模型结构由于这些原因,异步电机是一个多变量(多输入多输出)系统,而电压(电流)、频率、磁通、转速之间又互相都有影响,所以是强耦合的多变量系统,可以先用图来定性地表示。
图6-43 异步电机的多变量、强耦合模型结构模型的非线性(2)在异步电机中,电流乘磁通产生转矩,转速乘磁通得到感应电动势,由于它们都是同时变化的,在数学模型中就含有两个变量的乘积项。
这样一来,即使不考虑磁饱和等因素,数学模型也是非线性的。
模型的高阶性(3)三相异步电机定子有三个绕组,转子也可等效为三个绕组,每个绕组产生磁通时都有自己的电磁惯性,再算上运动系统的机电惯性,和转速与转角的积分关系,即使不考虑变频装置的滞后因素,也是一个八阶系统。
总起来说,异步电机的动态数学模型是一个高阶、非线性、强耦合的多变量系统。
二、三相异步电动机的多变量非线性数学模型假设条件:(1)忽略空间谐波,设三相绕组对称,在空间互差120°电角度,所产生的磁动势沿气隙周围按正弦规律分布;(2)忽略磁路饱和,各绕组的自感和互感都是恒定的;(3)忽略铁心损耗;(4)不考虑频率变化和温度变化对绕组电阻的影响。
1. 电压方程三相定子绕组的电压平衡方程为:电压方程(续)与此相应,三相转子绕组折算到定子侧后的电压方程为:电压方程的矩阵形式将电压方程写成矩阵形式,并以微分算子 p 代替微分符号 d /dt或写成(6-67b)2. 磁链方程每个绕组的磁链是它本身的自感磁链和其它绕组对它的互感磁链之和,因此,六个绕组的磁链可表达为:或写成(6-68b)电感矩阵式中,L 是6×6电感矩阵,其中对角线元素 LAA, LBB, LCC,Laa,Lbb,Lcc 是各有关绕组的自感,其余各项则是绕组间的互感。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电机理论的发展
电机的发展 -直流机、两相交流机、三相交流机 -电机种类繁多,原理各不相同 克朗电机统一理论 -寻找电机的共性 -提出原型电机 -利用矩阵变换
电机统一理论的特点和要求
核心-线性变换 适用于具有常系数微分方程或经过变换后具有常 系数微分方程的装置 电机的假定条件 -交流电机的定转子至少一方是隐极,且该隐极 方的绕组对称 -忽略空间谐波 -忽略磁路饱和 -角速度为常数
一、矩阵代数和常用矩阵类型
矩阵代数特点: -矩阵形式简明,同类变量和参数能用一 个简单的符号表示 -能提供求解的常规方法 -通过线性变换和矩阵分块能使求解问题 得到简化
1-1 矩阵的运算
1矩阵的加法和减法 -只能在阶数相同的情况下进行,即矩阵列数 和行数均相同
M aa M ba M ab N aa ± N M bb ba N ab M aa ± N aa = M ± N N bb ba ba M ab ± N ab M bb ± N bb
1-1 矩阵的运算
3矩阵的微分和积分
dM aa dM dt = dt dM ba dt dM ab dt dM bb dt
pM aa pM ba
pM ab = pM bb
M aa p M ba
M ab M bb
1-1 矩阵的运算
2-2 基本旋转电机的矩阵方程
异步电机的矩阵方程
u = Zi = Ri + pΨ = Ri + p(Li )
矩阵的转置 矩阵的共轭 矩阵的求逆
1-2 联立方程组的矩阵求解
1联立方程组的矩阵表示
y1 = a11 x1 + a12 x2 y2 = a21 x1 + a22 x2
y1 a11 y = a 2 21 a12 x1 a22 x2
Y = AX
基本整流子电机的矩阵方程
q
iq
uq
Ω
d
iD
D
id
ud
uD
2-2 基本旋转电机的矩阵方程
基本整流子电机的电压回路方程 -端电压 -电阻压降 -自感电势 -互感电势 -旋转电势(速度电势)
2-2 基本旋转电机的矩阵方程
旋转电枢式凸极同步电机 d、q双轴同步电机
u = Zi = Ri + Lpi + GΩi
1-2 联立方程组的矩阵求解
2应用矩阵代数解联立方程组 -已知A -已知A、X求Y -已知A、Y求X 已知A 需要求A 需要求A的逆阵 -常规方法 -分块矩阵法 -线性变换法
1-3 电机分析中常用矩阵的类型
方阵 对称矩阵 斜对称矩阵 厄米特矩阵 对角线矩阵 标量矩阵 么矩阵(单位矩阵) 么矩阵(单位矩阵) 零矩阵 奇异矩阵 正交矩阵 单式矩阵
本教材中的一些规定
两极电机,即电角度和机械角度相等 假设转子为隐极,多相对称或整流子绕组 电枢的旋转正方向规定为逆时针方向 电动机惯例
矩阵分析的优点
求解计算方面 控制理论方面
主要学习内容
矩阵代数 旋转电机的共同问题 电机统一理论 电机中常用变换 直流电机矩阵分析 异步电机矩阵分析 同步电机矩阵分析
ห้องสมุดไป่ตู้ 二、旋转电机的共同问题
传动系统动态的功率平衡 电机中磁场的储能 电机的电磁转矩 基本旋转电机的矩阵方程
2-1 机电系统的功率平衡
传动系统基本型式
2-1 机电系统的功率平衡
系统能量流动图
Pe1
dWm dt
dWkin1 dt
dWkin2 dt
Pmech 2
pe1
p mech1
p mech 2
2-2 基本旋转电机的矩阵方程
M ±N
1-1 矩阵的运算
2矩阵的乘法 标量与矩阵相乘 矩阵与矩阵相乘 -被乘矩阵的行数必须等于乘矩阵的列数 -不满足交换律
M aa M ab N aa N ab P = M ×N = N M ba M bb ba N bb M aa N aa + M ab N ba M aa N ab + M ab N bb = M ba N aa + M bb N ba M ba N ba + M bb N bb
