实验五 树的存储与遍历操作
树的遍历题目

树的遍历题目
摘要:
1.树的遍历概念
2.树的遍历方法
3.树的遍历应用
正文:
树的遍历题目是计算机科学中常见的算法问题,它涉及到对树这种数据结
构的操作和处理。树是一种非线性的数据结构,它由若干个节点组成,每个节
点又可以包含若干个子节点。树的遍历,就是对树中的每个节点进行访问,通
常需要按照某种特定的顺序进行。
树的遍历方法主要有三种:前序遍历、中序遍历和后序遍历。前序遍历是
指先访问根节点,然后依次遍历左子树和右子树;中序遍历是指先遍历左子
树,然后访问根节点,最后遍历右子树;后序遍历是指先遍历左子树,然后遍
历右子树,最后访问根节点。
树的遍历在实际应用中有很多用处,比如在搜索无向树中的某个节点时,
需要使用树的遍历方法来查找;在实现二叉树的删除操作时,也需要使用树的
遍历方法来找到待删除的节点。此外,树的遍历也是许多算法问题的基础,比
如二叉树的遍历可以作为二叉查找树、二叉堆等高级数据结构的基础。
23树和森林的存储和遍历

森林的先序遍历
A F H I K K JJ
森林对应的二叉链表
A B C D E E K G F
B
C
D D
E E
G
H I
J
先序遍历序列为: ABCDE FG HIKJ
课堂练习
B E F A C D G H I J K
森林的中序遍历
森林不空,则 中序遍历森林中第一棵树的子树森林; 访问森林中第一棵树的根结点; 中序遍历森林中(除第一棵树之外)其余树构成的森林。
A B E B F C D G
A E C F G
D
}利用二者的先序遍历结果相同
构造树
和二叉树类似,不同的定义相应有不同的算法。 假设以二元组(F,C)的形式自上而下、自左而右依 次输入树的各边,建立树的孩子-兄弟链表。
构造树
对左侧所示树的输入序列应为: A B C D
(‘#’, ‘A’) (‘A’, ‘B’) (‘A’, (‘A’, ‘C’) ‘C’) (‘A’, (‘A’, ‘D’) ‘D’) (‘C’, (‘C’, ‘E’) ‘E’) (‘C’, ‘F’) (‘E’, ‘G’) (‘ ‘,’#’) A B C
A
B E F
C
D
G
求根到所有叶子结点的路径
A B E C D G 左图的输出结果为:
F
H I J K
A A A A A A
B B C D D D
E F
G H I G H J G H K
求根到所有叶子结点的路径
对树先根遍历(深度优先) ,设立一个栈
1、T为空,则栈中存放的是从根到T的父结点的路径 2、将T压栈,栈中存放的是从根到T的路径 3、递归访问T的子树
树的遍历题目

树的遍历题目
摘要:
1.树的遍历概念
2.树的遍历方法
3.树的遍历应用实例
正文:
树的遍历是指访问树中每个节点的顺序,通常分为深度优先遍历和广度优先遍历两种方式。
深度优先遍历又分为先序遍历、中序遍历和后序遍历。
下面我们详细介绍一下这两种遍历方法。
一、深度优先遍历
深度优先遍历是指从树的某个节点开始,沿着树的层次一层一层地访问,直到访问完整棵树。
深度优先遍历有以下三种方式:
1.先序遍历:先访问根节点,然后依次遍历左子树和右子树。
2.中序遍历:先遍历左子树,然后访问根节点,最后遍历右子树。
3.后序遍历:先遍历左子树,然后遍历右子树,最后访问根节点。
二、广度优先遍历
广度优先遍历是指从树的某个节点开始,沿着树的宽度一层一层地访问,直到访问完整棵树。
在广度优先遍历过程中,同一层的节点会被先访问。
树的遍历在实际应用中有很多用处,例如在搜索某个节点是否存在、判断树是否平衡、求树的深度等。
下面举一个应用实例:
例题:给定一个二叉树,判断其是否为满二叉树。
解:可以通过深度优先遍历,统计树的节点数量。
如果节点数量为n,且
最后一层节点数量为n/2(向上取整),则该二叉树为满二叉树。
二叉树存储与遍历实验报告

二叉树的存储与遍历实验题目:二叉树的存储与递归遍历。
实验目的:掌握二叉树的定义、存储及遍历的算法及上机的基本操作。
实验内容与步骤:(1)树结构的基本操作,即操作者使用先序遍历的原理创建一个由多个节点组成的二叉树结构,并使用递归算法按先序、中序、后序对二叉树进行遍历。
(2)程序及部分注释如下:#include <stdio.h>#include <malloc.h>#include <stdlib.h>#define OK 1#define ERROR 0#define OVERFLOW -1#define MAX(a,b) (a>b?a:b)typedef char TElemType;typedef int Status;//二叉树的二叉链表存储结构typedef struct BiTNode{TElemType data;struct BiTNode *lchild,*rchild;}BiTNode,*BiTree;//先序遍历生成二叉树Status CreatBiTree(BiTree &T){TElemType ch,temp;printf("输入一个元素: ");scanf("%c",&ch);temp=getchar(); //结束回车if(ch==' ') T=NULL; //输入空格表示结点为空树else{if(!(T=(BiTree)malloc(sizeof(BiTNode))))exit(OVERFLOW);T->data=ch; //生成根结点CreatBiTree(T->lchild); //构造左子树CreatBiTree(T->rchild); //构造右子树}return OK;}//打印元素Status PrintElem(TElemType e){printf("%c ",e);return OK;}//先序遍历二叉树Status PreOrderTraverse(BiTree T,Status (* Visit)(TElemType e)) {if(T){ //二叉树不为空时if(Visit(T->data)) //访问根结点if(PreOrderTraverse(T->lchild,Visit)) //先序遍历左子树if(PreOrderTraverse(T->rchild,Visit)) return OK; //先序遍历右子树return ERROR;}else return OK;}//中序遍历二叉树Status InOrderTraverse(BiTree T,Status (* Visit)(TElemType e)) {if(T){if(InOrderTraverse(T->lchild,Visit))if(Visit(T->data))if(InOrderTraverse(T->rchild,Visit)) return OK;else return ERROR;}return OK;}//后序遍历二叉树Status PostOrderTraverse(BiTree T,Status (* Visit)(TElemType e)){ if(T){if(PostOrderTraverse(T->lchild,Visit))if(PostOrderTraverse(T->rchild,Visit))if(Visit(T->data)) return OK;else return ERROR;}return OK;}void main(){BiTree T;Status (* Visit)(TElemType);Visit=PrintElem;CreatBiTree(T);printf("\n先序遍历:");PreOrderTraverse(T,Visit);printf("\n中序遍历:");InOrderTraverse(T,Visit);printf("\n后序遍历:");PostOrderTraverse(T,Visit);printf("\n程序结束.\n");}分析与体会:(1)本程序采用的是递归的算法实现了二叉树的三种遍历,相对于非递归的算法较为简单。
如何在C++中实现树的遍历和节点查找

如何在C++中实现树的遍历和节点查找树是一种常见的数据结构,用于存储具有层次关系的数据。
在编程中,我们经常需要对树进行遍历和节点查找操作。
本文将介绍如何在C++中实现树的遍历和节点查找。
首先,我们需要定义树的节点结构。
节点通常由两部分组成:一个存储数据的值和指向子节点的指针。
在C++中,我们可以使用如下结构体来定义树的节点:```cppstruct Node {int val; //节点的值Node* left; //左子节点指针Node* right; //右子节点指针Node(int value) {val = value;left = nullptr;right = nullptr;}};```接下来,我们可以使用递归的方式来遍历树。
树的遍历有三种常见的方式:前序遍历、中序遍历和后序遍历。
下面分别介绍每种遍历方式的实现。
1.前序遍历:首先访问根节点,然后分别递归遍历左子树和右子树。
```cppvoid preorderTraversal(Node* root) {if(root != nullptr) {//访问根节点cout << root->val << " ";//递归遍历左子树preorderTraversal(root->left);//递归遍历右子树preorderTraversal(root->right);}}```2.中序遍历:先递归遍历左子树,然后访问根节点,最后递归遍历右子树。
```cppvoid inorderTraversal(Node* root) {if(root != nullptr) {//递归遍历左子树inorderTraversal(root->left);//访问根节点cout << root->val << " ";//递归遍历右子树inorderTraversal(root->right);}}```3.后序遍历:先递归遍历左子树,然后递归遍历右子树,最后访问根节点。
实验五 图的遍历及其应用实现
实验五图的遍历及其应用实现一、实验目的1.熟悉图常用的存储结构。
2.掌握在图的邻接矩阵和邻接表两种结构上实现图的两种遍历方法实现。
3.会用图的遍历解决简单的实际问题。
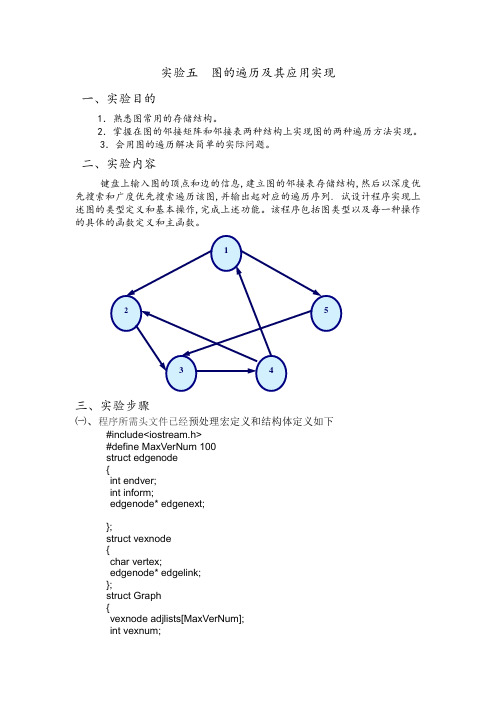
二、实验内容键盘上输入图的顶点和边的信息,建立图的邻接表存储结构,然后以深度优先搜索和广度优先搜索遍历该图,并输出起对应的遍历序列. 试设计程序实现上述图的类型定义和基本操作,完成上述功能。
该程序包括图类型以及每一种操作的具体的函数定义和主函数。
12534三、实验步骤㈠、程序所需头文件已经预处理宏定义和结构体定义如下#include<iostream.h>#define MaxVerNum 100struct edgenode{int endver;int inform;edgenode* edgenext;};struct vexnode{char vertex;edgenode* edgelink;};struct Graph{vexnode adjlists[MaxVerNum];int vexnum;int arcnum;};1、队列的定义及相关函数的实现struct QueueNode{int nData;QueueNode* next;};struct QueueList{QueueNode* front;QueueNode* rear;};void EnQueue(QueueList* Q,int e){QueueNode *q=new QueueNode;q->nData=e;q->next=NULL;if(Q==NULL)return;if(Q->rear==NULL)Q->front=Q->rear=q;else{Q->rear->next=q;Q->rear=Q->rear->next;}}void DeQueue(QueueList* Q,int* e){if (Q==NULL)return;if (Q->front==Q->rear){*e=Q->front->nData;Q->front=Q->rear=NULL;}else{*e=Q->front->nData;Q->front=Q->front->next;}}2、创建无向图void CreatAdjList(Graph* G){int i,j,k;edgenode* p1;edgenode* p2;cout<<"请输入顶点数和边数:"<<endl;cin>>G->vexnum>>G->arcnum;cout<<"开始输入顶点表:"<<endl;for (i=0;i<G->vexnum;i++){cin>>G->adjlists[i].vertex;G->adjlists[i].edgelink=NULL;}cout<<"开始输入边表信息:"<<endl;for (k=0;k<G->arcnum;k++){cout<<"请输入边<Vi,Vj>对应的顶点:";cin>>i>>j;p1=new edgenode;p1->endver=j;p1->edgenext=G->adjlists[i].edgelink;G->adjlists[i].edgelink=p1;p2=new edgenode;p2->endver=i;p2->edgenext=G->adjlists[j].edgelink;G->adjlists[j].edgelink=p2;//因为是无向图,所以有两次建立边表的过程}}3、深度优先遍历void DFS(Graph *G,int i,int visit[]){cout<<G->adjlists[i].vertex<<" ";visit[i]=1;edgenode *p=new edgenode;p=G->adjlists[i].edgelink;if(G->adjlists[i].edgelink&&!visit[p->endver]){DFS(G,p->endver,visit);}}void DFStraversal(Graph *G,char c)//深度优先遍历{cout<<"该图的深度优先遍历结果为:"<<endl;int visit[MaxVerNum];for(int i=0;i<G->vexnum;i++){visit[i]=0;//全部初始化为0,即未访问状态}int m;for (i=0;i<G->vexnum;i++){if (G->adjlists[i].vertex==c)//根据字符查找序号{m=i;DFS(G,i,visit);break;}}//继续访问未被访问的结点for(i=0;i<G->vexnum;i++){if(visit[i]==0)DFS(G,i,visit);}cout<<endl;}4、广度优先遍历void BFS(Graph* G,int v,int visit[]){QueueList *Q=new QueueList;Q->front=Q->rear=NULL;EnQueue(Q,v);while(Q->rear!=NULL){int e=0;DeQueue(Q,&e);cout<<G->adjlists[e].vertex<<" ";visit[e]=1;edgenode* p=new edgenode;p=G->adjlists[e].edgelink;if(p){int m=p->endver;if(m==0){EnQueue(Q,m);while(visit[m]==0){p=p->edgenext;if(p==NULL)break;m=p->endver;EnQueue(Q,m);}}}}}void BFStraversal(Graph *G,char c){cout<<"该图的广度优先遍历结果为:"<<endl;int visited[MaxVerNum];for (int i=0;i<G->vexnum;i++){visited[i]=0;}int m;for (i=0;i<G->vexnum;i++){if (G->adjlists[i].vertex==c){m=i;BFS(G,i,visited);break;}}//继续访问未被访问的结点for(i=0;i<G->vexnum;i++){if(visited[i]==0)BFS(G,i,visited);}cout<<endl;}㈡程序调试及运行结果分析㈢实验总结通过做这次实验,发现自己在数据结构这门课中还有很多不足有很多知识还没掌握,所以在写程序的时候出现了很多的错误,及还有很多的知识不以灵活运用。
二叉树的建立和遍历的实验报告
竭诚为您提供优质文档/双击可除二叉树的建立和遍历的实验报告篇一:二叉树遍历实验报告数据结构实验报告报告题目:二叉树的基本操作学生班级:学生姓名:学号:一.实验目的1、基本要求:深刻理解二叉树性质和各种存储结构的特点及适用范围;掌握用指针类型描述、访问和处理二叉树的运算;熟练掌握二叉树的遍历算法;。
2、较高要求:在遍历算法的基础上设计二叉树更复杂操作算法;认识哈夫曼树、哈夫曼编码的作用和意义;掌握树与森林的存储与便利。
二.实验学时:课内实验学时:3学时课外实验学时:6学时三.实验题目1.以二叉链表为存储结构,实现二叉树的创建、遍历(实验类型:验证型)1)问题描述:在主程序中设计一个简单的菜单,分别调用相应的函数功能:1…建立树2…前序遍历树3…中序遍历树4…后序遍历树5…求二叉树的高度6…求二叉树的叶子节点7…非递归中序遍历树0…结束2)实验要求:在程序中定义下述函数,并实现要求的函数功能:createbinTree(binTreestructnode*lchild,*rchild;}binTnode;元素类型:intcreatebinTree(binTreevoidpreorder(binTreevoidInorder(binTreevoidpostorder(binTreevoidInordern(binTreeintleaf(bi nTreeintpostTreeDepth(binTree2、编写算法实现二叉树的非递归中序遍历和求二叉树高度。
1)问题描述:实现二叉树的非递归中序遍历和求二叉树高度2)实验要求:以二叉链表作为存储结构3)实现过程:1、实现非递归中序遍历代码:voidcbiTree::Inordern(binTreeinttop=0;p=T;do{while(p!=nuLL){stack[top]=p;;top=top+1;p=p->lchild;};if(top>0){top=top-1;p=stack[top];printf("%3c",p->data);p=p->rchild;}}while(p!=nuLL||top!=0);}2、求二叉树高度:intcbiTree::postTreeDepth(binTreeif(T!=nuLL){l=postTreeDepth(T->lchild);r=postTreeDepth(T->rchil d);max=l>r?l:r;return(max+1);}elsereturn(0);}实验步骤:1)新建一个基于consoleApplication的工程,工程名称biTreeTest;2)新建一个类cbiTree二叉树类。
树的四种遍历方式
树的四种遍历方式
树是一种非常重要的数据结构,在计算机科学中被广泛应用。
树的遍历是指按照某种规则依次访问树中的所有节点。
树的遍历方式有四种,分别是前序遍历、中序遍历、后序遍历和层次遍历。
前序遍历是指先访问根节点,再依次访问左子树和右子树。
中序遍历是指先访问左子树,再访问根节点,最后访问右子树。
后序遍历是指先访问左子树,再访问右子树,最后访问根节点。
而层次遍历则是按照树的层次逐层遍历,从左到右访问每个节点。
不同的遍历方式有不同的特点和应用场景。
前序遍历可以用来复制一颗树,中序遍历可以用来对树进行排序,后序遍历可以用来释放一颗树的内存,而层次遍历可以用来查找树的层数和节点个数等信息。
在实际应用中,遍历方式的选择取决于具体的需求和情况。
熟练掌握四种遍历方式,可以帮助我们更好地理解和应用树这种数据结构。
- 1 -。
树的四种遍历方式
树的四种遍历方式树是一种非常常见的数据结构,它由节点和边组成,每个节点可以有多个子节点,但只有一个父节点。
树的四种遍历方式分别是前序遍历、中序遍历、后序遍历和层次遍历。
前序遍历是指从根节点开始,先访问根节点,然后按照从左到右的顺序依次访问每个子节点。
这种遍历方式可以用递归或者栈来实现。
递归实现的代码如下:```void preorderTraversal(TreeNode* root) {if (root == nullptr) {return;}cout << root->val << " ";preorderTraversal(root->left);preorderTraversal(root->right);}```中序遍历是指从根节点开始,先访问左子树,然后访问根节点,最后访问右子树。
同样可以用递归或者栈来实现。
递归实现的代码如下:void inorderTraversal(TreeNode* root) {if (root == nullptr) {return;}inorderTraversal(root->left);cout << root->val << " ";inorderTraversal(root->right);}```后序遍历是指从根节点开始,先访问左子树,然后访问右子树,最后访问根节点。
同样可以用递归或者栈来实现。
递归实现的代码如下:```void postorderTraversal(TreeNode* root) {if (root == nullptr) {return;}postorderTraversal(root->left);postorderTraversal(root->right);cout << root->val << " ";```层次遍历是指从根节点开始,按照从上到下、从左到右的顺序依次访问每个节点。
树的遍历算法
树的遍历算法
树的遍历算法是指按照一定的顺序遍历树中的所有节点。
树的遍历算
法分为三种:前序遍历、中序遍历和后序遍历。
前序遍历是指先访问根节点,然后按照从左到右的顺序依次访问左子
树和右子树。
具体实现方式为:先访问根节点,然后递归地访问左子树,最后递归地访问右子树。
中序遍历是指先访问左子树,然后访问根节点,最后访问右子树。
具
体实现方式为:先递归地访问左子树,然后访问根节点,最后递归地
访问右子树。
后序遍历是指先访问左子树,然后访问右子树,最后访问根节点。
具
体实现方式为:先递归地访问左子树,然后递归地访问右子树,最后
访问根节点。
以上三种遍历方式都可以用递归算法实现,也可以用非递归算法实现。
非递归算法实现方式为使用栈来模拟递归过程。
在实际应用中,树的遍历算法经常被用来搜索树中的某个节点,或者
对树中的节点进行排序。
例如,在二叉搜索树中,中序遍历可以得到
一个有序的节点序列。
总之,树的遍历算法是树结构中最基本的算法之一,掌握好树的遍历算法对于理解和应用树结构具有重要的意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验五 树的存储与遍历操作
一、实验内容:
1、写出一个算法建立一棵二叉树并且完成对这棵二叉树的先序遍历、中
序遍历和后序遍历。
2、利用树的遍历求二叉树的结点数
3、利用树的遍历求二叉树的叶子数
二、实验目的:
通过这个实验,学生学会对树的定义,对树的存储方法,遍历的基本操
作有一个清楚的认识。并且能够用程序模拟树的遍历过程。
三、实验提示:
3.1 建立一棵二叉树并且完成对这棵二叉树的先序遍历、中序遍历和后序遍历
二叉链表的结点结构如下图所示。
二叉链表的结点用C++中的结构类型描述为:
template < class T >
struct BiNode
{
T data;
BiNode < T > *lchild, *rchild;
};
设计实验用二叉链表类BiTree,类中包含遍历操作。
template < class T >
class BiTree
{
public:
BiTree(BiNode < T > *root); //有参构造函数,初始化一棵二叉树,
其前序序列由键盘输入
~BiTree( ); //析构函数,释放二叉链表中各结点的存储
空间
void PreOrder(BiNode < T > *root); //前序遍历二叉树
void InOrder(BiNode < T > *root); //中序遍历二叉树
void PostOrder(BiNode < T > *root); //后序遍历二叉树
private:
BiNode < T > *root; //指向根结点的头指针
void Creat(BiNode < T > *root); //有参构造函数调用
void Release(BiNode < T > *root); //析构函数调用
};
计构造函数,建立一棵二叉树的二叉链表存储。
将二叉树中每个结点的空指针引出一个虚结点,其值为一特定值如
“#”,以标识其为空,把这样处理后的二叉树称为原二叉树的扩展二叉
树。扩展二叉树的一个遍历序列就能唯一确定一棵二叉树。假设扩展二
叉树的前序遍历序列由键盘输入,root为指向根结点的指针,二叉链表
的建立过程是:首先输入根结点,若输入的是一个“#”字符,则表明该
二叉树为空树,即root=NULL;否则输入的字符应该赋给root->data,,
之后依次递归建立它的左子树和右子树。建立二叉链表的递归算法如下:
前序遍历的递归算法如下:
中序和后序遍历的算法请仿照前序遍历的递归算法自行设计。
3.2利用树的遍历求二叉树的节点数(叶子数)
求二叉树中结点的个数,即求二叉树的所有结点中左、右子树均为不为
空的结点个数之和;求二叉树中叶子结点的个数,即求二叉树的所有结
点中左、右子树均为空的结点个数之和。这2个要求可在一段程序中完
成,下面以叶子节点为例,说明:
因此可以将此问题转化为遍历问题,在遍历中“访问一个结点”时判断
该结点是不是叶子,若是则将计数器累加。算法如下:
