2015研究生数学建模MATLAB程序(完整版)
matlab数学建模程序代码

matlab数学建模程序代码【实用版】目录1.MATLAB 数学建模概述2.MATLAB 数学建模程序代码的基本结构3.常用的 MATLAB 数学建模函数和命令4.MATLAB 数学建模程序代码的编写流程5.MATLAB 数学建模程序代码的示例正文一、MATLAB 数学建模概述MATLAB(Matrix Laboratory)是一款强大的数学软件,广泛应用于数学建模、数据分析、可视化等领域。
通过 MATLAB,用户可以方便地进行数学计算、编写程序以及绘制图表等。
在数学建模领域,MATLAB 为研究人员和工程师提供了丰富的工具箱和函数,使得数学模型的构建、求解和分析变得更加简单高效。
二、MATLAB 数学建模程序代码的基本结构MATLAB 数学建模程序代码通常分为以下几个部分:1.导入 MATLAB 库:在建模过程中,可能需要使用 MATLAB 提供的某些库或工具箱,需要在代码开头进行导入。
2.定义变量和参数:在建模过程中,需要定义一些变量和参数,用于表示模型中的各个要素。
3.建立数学模型:根据实际问题,编写相应的数学表达式或方程,构建数学模型。
4.求解模型:通过调用 MATLAB 内置函数或使用自定义函数,对数学模型进行求解。
5.分析结果:对求解结果进行分析,提取所需的信息,例如计算均值、方差等统计量。
6.可视化结果:使用 MATLAB 绘制图表,将结果以直观的形式展示出来。
三、常用的 MATLAB 数学建模函数和命令MATLAB 提供了丰富的数学建模函数和命令,例如:1.线性规划:使用`linprog`函数求解线性规划问题。
2.非线性规划:使用`fmincon`或`fsolve`函数求解非线性规划问题。
3.优化问题:使用`optimize`函数求解优化问题。
4.数据处理:使用`mean`、`std`等函数对数据进行统计分析。
5.图表绘制:使用`plot`、`scatter`等函数绘制各种图表。
MATLAB数学建模教程

MATLAB选修课讲义第一讲:矩阵运算第二讲:函数作图第三讲:符号演算第四讲:简单编程第五讲:数值计算第六讲:综合实例1第一讲:矩阵运算1.基本操作启动退出终止(Alt+. 或Ctrl +C)翻页召回命令分隔符,禁显符;续行符…注释符%设置显示格式format 常用:short,short g,long 清除变量clear关闭图形close清除图形clf演示Demo帮助help2.基本常数2pi I j inf eps NaN exp(1)3.算术运算+ - * /, \, ^ sqrt .*./.^4.内部函数(一般都有数组运算功能)sin(x) tan(x) asin(x) atan(x)abs(x) round(x) floor(x) ceil(x)log(x) log10(x) length(v) size(A) sign(x) [y, p]=sort(x)5.矩阵运算(要熟练掌握)(1)矩阵生成:手工输入:[1 2 3; 4 5 6]输入数组: linspace(a, b, n)命令输入:zeros(m,n) ones(m,n) eye(n)3magic(n) rand(m, n)diag(A) diag ( [a11 a22 . . . a nn] ) (2)矩阵操作赋值A(i, j) =2 A(2, :)=[1 2 3]删除A( [2,3], :)=[ ] 添加A(6,8)=5定位find(A>0) 定位赋值A(A<0)= -1由旧得新B=A([2,3,1], :) B=A([1,3],[2,1])定位矩阵B=(A>1) B=(A==1)下三角阵tril(A) 上三角阵triu(A)左右翻转fliplr(A) 上下翻转flipud(A)重排矩阵reshape(A, m, n)(3)矩阵运算:转置A’和A+B 差A-B 积A*B4左除A\b(=A-1 b)右除b/A(=b A-1 )幂A^k点乘A.*B 点除A./B 点幂A.^2行列式det(A) 数量积dot(a,b) 向量积cross(a,b)行最简形rref(A) 逆矩阵inv(A) 迹trace(A)矩阵秩rank(A) 特征值eig(A) 基础解系null(A,’r’) 方程组特解x=A\b注意:2+A,sin(A)练习一:矩阵操作1、用尽可能简单的方法生成下列矩阵:56102000100012101/21/31/1112040022002311/31/41/12,,,0330600054082210010191/111/121/200750⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎢⎥-⎣⎦2、设有分块矩阵⎪⎪⎭⎫⎝⎛=⨯⨯⨯2232233S OR E A ,⎪⎪⎭⎫⎝⎛⋅=⨯⨯⨯23222233E O J R E B ,其中23,E E 是单位矩阵,32⨯O 是零矩阵,23⨯R 是随机矩阵,⎪⎪⎭⎫ ⎝⎛=⨯011022S ,J是2阶全1矩阵,验证B A=2。
数学建模常用MATLAB程序代码

V1到V11的最短路径及其长度:P53>> a(2,3)=6;a(2,5)=1;a(3,4)=7;a(3,5)=5;a(3,6)=1;a(3,7)=2;a(4,7)=9;a(5,6)=3;a(5,8)=2;a(5,9)=9;a(6,7)=4;a(6,9)=6;a(7,9)=3;a(7,10)=1;a(8,9)=7;a(8,11)=9;a(9,10)=1;a(9,11)=2;a(10,11)=4;a=a';[i,j,v]=find(a);b=sparse(i,j,v,11,11);[x,y,z]=graphshortestpath(b,1,11,'Directed',false)x =13y =1 2 5 6 3 7 10 9 11z =0 1 6 1 2 5 3 5 10 7 9灰色预测GM(1,1)模型程序代码:P375x0=[71.1 72.4 72.4 72.1 71.4 72 71.6]';n=length(x0);lamda=x0(1:n-1)./x0(2:n);range=minmax(lamda');x1=cumsum(x0)B=[-0.5*(x1(1:n-1)+x1(2:n)),ones(n-1,1)]Y=x0(2:n);u=B\Yx=dsolve('Dx+a*x=b','x(0)=x0')x=subs(x,{'a','b','x0'},{u(1),u(2),x0(1)})yuce1=subs(x,'t',[0:n-1])y=vpa(x,n-1)yuce=[x0(1),diff(yuce1)]epsilon=x0'-yucedelta=abs(epsilon./x0')rho=1-(1-0.5*u(1))/(1+0.5*u(1))*lamda'x1 =71.1143.5215.9288359.4431.4503B =-107.3 1-179.7 1-251.95 1-323.7 1-395.4 1-467.2 1u =0.002343872.657x =(b - exp(-a*t)*(b - a*x0))/ax =41884064296049311744/1351100916648171 - (41788001020875628544*exp(-(1351100916648171*t)/576460752303423488))/135110091664 8171yuce1 =71.1 143.51 215.74 287.81 359.71 431.44 503y =31000.0 - 30928.9*exp(-0.00234379*t)yuce =71.1 72.406 72.236 72.067 71.898 71.73 71.562epsilon =0 -0.0057414 0.16376 0.032871 -0.49842 0.2699 0.037824delta =0 7.9302e-05 0.0022619 0.00045592 0.0069806 0.0037486 0.00052827rho =0.020255 0.002341 -0.0018101 -0.0074399 0.010655 -0.0032325用Krusksl算法求最小生成树的Matlab程序代码:P47-48a(1,2)=50;a(1,3)=60;a(2,4)=65;a(2,5)=40;a(3,4)=52;a(3,7)=45;a(4,5)=50;a(4,6)=30;a(4,7)=42;a(5,6)=70;>> [i,j,b]=find(a);>> data=[i';j';b'];index=data(1:2,:);>> loop=length(a)-1;>> result=[];>> while length(result)<looptemp=min(data(3,:));flag=find(data(3,:)==temp);flag=flag(1);v1=index(1,flag);v2=index(2,flag);if v1~=v2result=[result,data(:,flag)];endindex(find(index==v2))=v1;data(:,flag)=[];index(:,flag)=[];end>> resultresult =6 57 7 2 54 2 4 3 1 430 40 42 45 50 50求得最小生成树的边集为{v6v4, v5v2, v7v4, v7v3, v2v1, v5v4}。
数学建模Matlab数据拟合详解
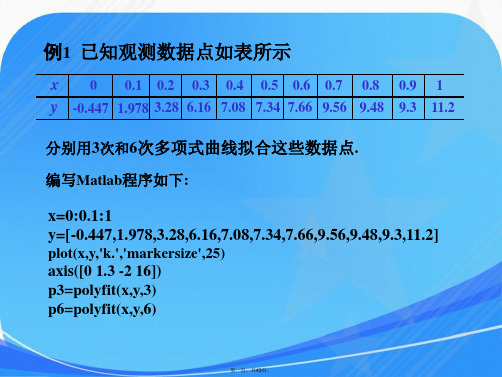
第十八页,共43页。
插值问题
已知 n+1个节点 (xj,yj)(j0,1, n,其中 x j
数学建模比赛前准备的Matlab和lingo代码

Matlab和lingo代码Matlab 0基础知识 .............................................................. 错误!未定义书签。
Polyval (2)Polyfit (3)interrep1 (3)回归分析 (4)牛顿迭代法求解非线性方程组 (5)建模课上的代码 (11)lingo求解部分 (20)目标规划 (24)第10章数据的统计描述和分析 (29)!7个工人,7个工作的分配问题; (30)案例分析 (31)差分方程 (34)!三阶段面试模型; (36)装配线平衡模型 (38)露天矿生产的车辆安排(CMCM2003B) (40)Matlab基础知识相关系数矩阵的方式,通过Matlab 软件进行相关性分析,得到主成分种类与重要指标的线性组合:4321375.0395.0398.0375.01x x x x z +++= (10)prod 连乘积for k=1:100p(k)=1-prod(365-k+1:365)/365^k;endfplot('f(x)',[xmin,xmax,ymin,ymax]) syms xint(f(x), x,a,b)Polyval 计算对多项式p(x)=1+2*x+3*x^2,计算在x=5,7,9的值。
>> p = [3 2 1];>> x=[5,7,9];>> polyval(p,[5 7 9])%结果为ans =86 162 262Polyfit 拟合曲线x=[1,2,4,7,9,12,13,15,17]';F=[1.5,3.9,6.6,11.7,15.6,18.8,19.6,20.6,21.1]';plot(x,F,'.')%从图像上我们发现:前5个数据应与直线拟合,后5个数据应与二次曲线拟合。
于是键入 : a=polyfit(x(1:5),F(1:5),1); a=polyfit(x(5:9),F(5:9),2)生日概率模型for n=1:100p(n)=1-prod(365-n+1:365)/365^n;endplot(p)c5=polyfit(n,p,5)c5 =-0.0000 0.0000 -0.0001 0.0023 -0.0046 -0.0020该多项式即为:0020.00046.00023.00001.00023456524334251--+-+=+++++x x x x x c x c x c x c x c x c 在Matlab 环境下继续键入下列指令:>> p5=polyval(c5,n); ////////用多项式近似计算100个概率值>> plot(n,p,n,p5,'.') ////////画出拟合多项式的图象与概率曲线作比较interrep1x0=[0,3,5,7,9,11,12,13,14,15]';y0=[0,1.2,1.7,2.0,2.1,2.0,1.8,1.2,1.0,1.6]'plot(x0,y0) %完成第一步工作x=0:0.1:15;y=interp1(x0,y0,’x'); %用分段线性插值完成第二步工作plot(x,y)y=spline(x0,y0,’x');←plot(x,y) %用三次样条插值完成第二步工作指数模型t=1790:10:1980;x(t)=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 150.7 179.3 204.0 226.5 ];y=log(x(t));a=polyfit(t,y,1)r=a(1),x0=exp(a(2))x1=x0.*exp(r.*t);plot(t,x(t),'r',t,x1,'b')%%%%%%阻滞增长模型(或 Logistic 模型)%%%%%%%%%%建立函数文件curvefit_fun2.mfunction f=curvefit_fun2 (a,t)f=a(1)./(1+(a(1)/3.9-1)*exp(-a(2)*(t-1790)));在命令文件main.m中调用函数文件curvefit_fun2.m% 定义向量(数组)x=1790:10:1990;y=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76 ...92 106.5 123.2 131.7 150.7 179.3 204 226.5 251.4];plot(x,y,'*',x,y); % 画点,并且画一直线把各点连起来hold on;a0=[0.001,1]; % 初值% 最重要的函数,第1个参数是函数名(一个同名的m文件定义),第2个参数是初值,第3、4个参数是已知数据点a=lsqcurvefit('curvefit_fun2',a0,x,y);disp(['a=' num2str(a)]); % 显示结果% 画图检验结果xi=1790:5:2020;yi=curvefit_fun2(a,xi);plot(xi,yi,'r');% 预测2010年的数据x1=2010;y1=curvefit_fun2(a,x1)hold off回归分析←设回归模型为 y=β0+β1x,←在MATLAB命令窗口中键入下列命令进行回归分析(px_reg11.m)x=0.1:0.01:0.18;x=[x,0.2,0.21,0.23]';y=[42,41.5,45,45.5,45,47.5,49,55,50,55,55.5,60.5]';X=[ones(12,1),x]; %一元回归[b,bint,r,rint,stats]=regress(y,X,0.05);b,bint,stats,rcoplot(r,rint)←得结果和图←b =← 27.0269← 140.6194←bint =← 22.3226 31.7313← 111.7842 169.4546←stats =← 0.9219 118.0670 0.0000 3.1095←结果含义为←β0=27.0269 β1=140.6194←β0的置信区间是 [22.3226,31.7313]←β1的置信区间是 [111.7842,169.4546]←R2=0.9219 F=118.0670, p<10-4.←R是衡量y与x的相关程度的指标,称为相关系数。
2015年全国研究生数学建模竞赛资料

参赛密码第十二届“中关村青联杯”全国研究生数学建模竞赛学校西安工程大学参赛队号10709012队员姓名1.卞京红2.张茜3.张永强参赛密码第十二届“中关村青联杯”全国研究生数学建模竞赛题目:旅游路线规划问题摘要随着我国国民经济的快速发展,人们生活水平得到很大提升,越来越多的人积极参与有益于身心健康的旅游活动,其已逐步成为全球经济发展的重要动力之一。
本文针对旅游路线的规划问题,进行了多方面研究,设计了可行有效的旅游方案。
针对问题一,首先依据TSP优化理论,建立了数学模型,其次利用DIJKSTRA算法求得任意两省会之间的最短距离,运用LINGO编写程序进行模型求解,运用MATLAB编写程序。
在旅游费用不限的情况下,设计出了畅游全国5A级景区的较佳旅游路线,并得出最短旅游年限约为13年。
针对问题二,采用聚类分析的方法按省会城市的离散程度进行分类,借助MATLAB软件对数据进行处理,同时,假定以西安为中心,综合考虑飞机,高铁和自驾租车等交通方式,依据题中所给的各种费用和时间限定信息,设计出了每一天具体的出行方式、出发地、费用、路途时间、游览景区和每个景区的游览时间。
最终算出总费用为4.7193e+006元。
针对问题三,在第二问的基础上,以北京市为中心,以自驾为主,费用最低为目标,进行旅游线路设计,规划出了更适合十年旅游计划的自驾游爱好者的旅游路线;根据旅游景区的现状及旅游者的兴趣,提供了相应的建议,以便于旅游者更好的游玩,同时也方便相关部门为游客提供更好的服务。
针对问题四,根据5A级旅游景区的评定信息,结合周边的4A级景区,利用遗传算法,根据其离散程度对全国进行分区,共分为7个区域,分别为华北地区,东北地区,华东地区,华中地区,华南地区,西北地区,西南地区。
依据分区结果,更合理的安排旅游者的十年旅游计划。
关键字:旅游线路,MATLAB,DIJKSTRA算法,聚类分析,最优线路问题一、问题重述1、背景随着科技的进步和社会的发展,旅游已成为人们的一种生活方式,是提高人们生活质量的重要活动。
数据建模常规方法的Matlab实现(实例)
MATLAB(liti21)
3)运算结果为: f =0.0043 0.0051 0.0056 0.0059
0.0062 0.0062 0.0063 0.0063 x = 0.0063 -0.0034 0.2542
0.0061 0.0063
4)结论:a=0.0063, b=-0.0034, k=0.2542
的。
1. lsqcurvefit
已知数据点: xdata=(xdata1,xdata2,…,xdatan),
ydata=(ydata1,ydata2,…,ydatan) lsqcurvefit用以求含参量x(向量)的向量值函数
F(x,xdata)=(F(x,xdata1),…,F(x,xdatan))T 中的参变量x(向量),使得
6 0.28 15
-0.02
解:(1)画出散点图: x=[0;0.4;1.2;2;2.8;3.6;4.4;5.2;6;7.2;8;9.2;10.4;11.6;12.4;13.6; 14.4;15]; y=[1;0.85;0.29;-0.27;-0.53;-0.4;-0.12;0.17;0.28;0.15;-0.03;0.15;-0.071;0.059;0.08;0.032;-0.015;-0.02]; plot(x,y,'r*')
matlab数学建模pdf
matlab数学建模pdfMATLAB是一种高级编程语言和交互式环境,主要用于数值计算、数据分析和可视化。
它在数学建模方面具有广泛的应用,因为它提供了一个方便的编程环境,支持矩阵和数组操作、函数和方程求解、数据分析和可视化等功能。
以下是一些使用MATLAB进行数学建模的示例:1.线性回归模型:MATLAB提供了一个名为`fitlm`的函数,用于拟合线性回归模型。
以下是一个简单的示例:```matlab%创建自变量和因变量数据x=[1,2,3,4,5];y=[2.2,2.8,3.6,4.5,5.1];%拟合线性回归模型lm=fitlm(x,y);%显示模型摘要summary(lm)```2.非线性最小二乘法拟合:MATLAB提供了一个名为`fitnlm`的函数,用于拟合非线性最小二乘法模型。
以下是一个简单的示例:```matlab%创建自变量和因变量数据x=[1,2,3,4,5];y=[1.2,2.5,3.7,4.6,5.3];%定义非线性模型函数modelfun=@(params,xdata) params(1)*exp(-params(2)*xdata)+params(3); %拟合非线性最小二乘法模型startPoint=[1,1,1];%初始参数值options=optimset('Display','off');%不显示优化过程信息lm=fitnlm(x,y,modelfun,startPoint,options); %显示模型摘要summary(lm)```3.微分方程求解:MATLAB提供了一个名为`ode45`的函数,用于求解常微分方程。
以下是一个简单的示例:```matlab%定义微分方程dy/dx=f(x,y)f=@(x,y)-0.5*y;%初始条件和时间跨度y0=1;tspan=[0,10];%使用ode45进行求解[t,y]=ode45(f,tspan,y0);%可视化结果plot(t,y(:,1))%y是解的矩阵,(:,1)表示取第一列数据作为纵坐标进行绘图xlabel('Time(s)')ylabel('Solution')```。
2015MATLAB-09A-梯子问题ppt
绘图效果(最短)
x=atan((b / a) ^ (1 / 3)); x_max=x/(2 * 3.1415926) * 360; fprintf('梯子最短要:%4.2f米,你的梯子够长。成%4.2f度时!', c_min,x_max); %%------------------------------------------绘图 figure1 = figure('PaperPosition',[0 0 30 30],'PaperSize',[30 30]); %% Create axes axes1 = axes('PlotBoxAspectRatio',[30 30 1],'Parent',figure1); axis(axes1,[0 30 0 30]); box(axes1,'on'); hold(axes1,'all'); grid on; %%------------------------------------------矩形 rectangle('Position',[0, 0, 5, 30],'FaceColor',[0.1686 0.5059 0.3373]) rectangle('Position',[5, 0, a, b],'FaceColor',[0.3686 0.0001 0.0001]) %%------------------------------------------线,角度最大时的梯子效果(紧贴着玻璃房顶角) %%x轴要多加5,楼房厚度 line([5 5+a+b/tan(x)],[b+a*tan(x) 0], 'Color',[1 0 0]);
数学建模算法的matlab代码
数学建模算法的matlab代码句柄图形(图形窗口)二,hamiton回路算法提供一种求解最优哈密尔顿的算法---三边交换调整法,要求在运行jiaohuan3(三交换法)之前,给定邻接矩阵C和节点个数N,结果路径存放于R 中。
bianquan.m文件给出了一个参数实例,可在命令窗口中输入bianquan,得到邻接矩阵C和节点个数N以及一个任意给出的路径R,,回车后再输入jiaohuan3,得到了最优解。
由于没有经过大量的实验,又是近似算法,对于网络比较复杂的情况,可以尝试多运行几次jiaohuan3,看是否能到进一步的优化结果。
%%%%%%bianquan.m%%%%%%%N=13;for i=1:Nfor j=1:NC(i,j)=inf;endendfor i=1:NC(i,i)=0;endC(1,2)=6.0;C(1,13)=12.9;C(2,3)=5.9;C(2,4)=10.3;C(3,4)=12.2;C(3,5)=17.6;C(4,13)=8.8;C(4,7)=7.4;C(4,5)=11.5;C(5,2)=17.6;C(5,6)=8.2;C(6,9)=14.9;C(6,7)=20.3;C(7,9)=19.0;C(7,8)=7.3;C(8,9)=8.1;C(8,13)=9.2;C(9,10)=10.3;C(10,11)=7.7;C(11,12)=7.2;C(12,13)=7.9;for i=1:Nfor j=1:Nif C(i,j) < infC(j,i)=C(i,j);endendendfor i=1:NC(i,i)=0;endR=[4 7 6 5 3 2 1 13 12 11 10 9 8]; %%%%%%%%jiaohuan3.m%%%%%%%%%% n=0; for I=1:(N-2)for J=(I+1):(N-1)for K=(J+1):Nn=n+1;Z(n,:)=[I J K];endendendR=1:Nfor m=1:(N*(N-1)*(N-2)/6)I=Z(m,1);J=Z(m,2);K=Z(m,3);r=R;if J-I~=1&K-J~=1&K-I~=N-1for q=1:(J-I)r(I+q)=R(J+1-q);endfor q=1:(K-J)r(J+q)=R(K+1-q);endendif J-I==1&K-J==1r(K)=R(J);r(J)=R(K);endif J-I==1&K-J~=1&K-I~=N-1 for q=1:(K-J)r(I+q)=R(I+1+q);endr(K)=R(J);endif K-J==1&J-I~=1&K~=N for q=1:(J-I)r(I+1+q)=R(I+q);endr(I+1)=R(K);endif I==1&J==2&K==Nfor q=1:(N-2)r(1+q)=R(2+q);endr(N)=R(2);endif I==1&J==(N-1)&K==N for q=1:(N-2)r(q)=R(1+q);endr(N-1)=R(1);endif J-I~=1&K-I==N-1for q=1:(J-1)r(q)=R(1+q);endr(J)=R(1);endif J==(N-1)&K==N&J-I~=1r(J+1)=R(N);for q=1:(N-J-1)r(J+1+q)=R(J+q);endendif cost_sum(r,C,N)<cost_sum(r,c,n)< p="">R=rendendfprintf('总长为%f\n',cost_sum(R,C,N))%%%%%%cost_sum.m%%%%%%%%functiony=cost_sum(x,C,N)y=0;for i=1:(N-1) y=y+C(x(i),x(i+1));endy=y+C(x(N),x(1));三,灰色预测代码clearclcX=[136 143 165 152 165 181 204 272 319 491 571 605 665 640 628];x1(1)=X(1);X1=[];for i=1:1:14x1(i+1)=x1(i)+X(i+1);X1=[X1,x1(i)];endX1=[X1,X1(14)+X(15)]for k=3:1:15p(k)=X(k)/X1(k-1);p1(k)=X1(k)/X1(k-1);endp,p1clear kZ=[];for k=2:1:15z(k)=0.5*X1(k)+0.5*X1(k-1);Z=[Z,z(k)];endZB=[-Z',ones(14,1)]Y=[];clear ifor i=2:1:15Y=[Y;X(i)];endYA=inv(B'*B)*B'*Yclear ky1=[];for k=1:1:15y(k)=(X(1)-A(2)/A(1))*exp(-A(1)*(k-1))+A(2)/A(1); y1=[y1;y(k)];endy1clear kX2=[];for k=2:1:15x2(k)=y1(k)-y1(k-1);X2=[X2;x2(k)];endX2=[y1(1);X2]e=X'-X2m=abs(e)./X's=e'*en=sum(m)/13clear ksyms ky=(X(1)-A(2)/A(1))*exp(-A(1)*(k-1))+A(2)/A(1)Y1=[];for j=16:1:21y11=subs(y,k,j)-subs(y,k,j-1);Y1=[Y1;y11];endY1%程序中的变量定义:alpha是包含α、μ值的矩阵;%ago是预测后累加值矩阵;var是预测值矩阵;%error是残差矩阵; c是后验差比值function basicgrey(x,m) %定义函数basicgray(x)if nargin==1 %m 为想预测数据的个数,默认为1 m=1;endclc; %清屏,以使计算结果独立显示if length(x(:,1))==1 %对输入矩阵进行判断,如不是一维列矩阵,进行转置变换x=x';endn=length(x); %取输入数据的样本量x1(:,1)=cumsum(x); %计算累加值,并将值赋与矩阵be for i=2:n %对原始数列平行移位Y(i-1,:)=x(i,:);endfor i=2:n %计算数据矩阵B的第一列数据z(i,1)=0.5*x1(i-1,:)+0.5*x1(i,:);endB=ones(n-1,2); %构造数据矩阵BB(:,1)=-z(2:n,1);alpha=inv(B'*B)*B'*Y; %计算参数α、μ矩阵for i=1:n+m %计算数据估计值的累加数列,如改n+1为n+m可预测后m个值ago(i,:)=(x1(1,:)-alpha(2,:)/alpha(1,:))*exp(-alpha(1,:)*(i-1))+alpha(2,:)/alpha(1,:);endvar(1,:)=ago(1,:);for i=1:n+m-1 %可预测后m个值var(i+1,:)=ago(i+1,:)-ago(i,:); %估计值的累加数列的还原,并计算出下m个预测值end[P,c,error]=lcheck(x,var); %进行后验差检验[rela]=relations([x';var(1:n)']); %关联度检验ago %显示输出预测值的累加数列alpha %显示输出参数α、μ数列var %显示输出预测值error %显示输出误差P %显示计算小残差概率 c %显示后验差的比值crela %显示关联度judge(P,c,rela) %评价函数显示这个模型是否合格function judge(P,c,rela)%评价指标并显示比较结果if rela>0.6'根据经验关联度检验结果为满意(关联度只是参考主要看后验差的结果)' else'根据经验关联度检验结果为不满意(关联度只是参考主要看后验差的结果)' endif P>0.95&c<0.5'后验差结果显示这个模型评价为“优”'else if P>0.8&c<0.5'后验差结果显示这个模型评价为“合格”'else if P>0.7&c<0.65'后验差结果显示这个模型评价为“勉强合格”'else'后验差结果显示这个模型评价为“不合格”'endendendfunction [P,c,error]=lcheck(x,var)%进行后验差检验n=length(x);for i=1:nerror(i,:)=abs(var(i,:)-x(i,:)); %计算绝对残差endc=std(abs(error))/std(x); %调用统计工具箱的标准差函数计算后验差的比值cs0=0.6745*std(x);ek=abs(error-mean(error));pk=0;for i=1:nif ek(i,:)<s0< p="">pk=pk+1;endendP=pk/n; %计算小残差概率%附带的质料里有一部分讲了关联度function [rela]=relations(x)%以x(1,:)的参考序列求关联度[m,n]=size(x);for i=1:mfor j=n:-1:2x(i,j)=x(i,j)/x(i,1);endendfor i=2:mx(i,:)=abs(x(i,:)-x(1,:)); %求序列差endc=x(2:m,:);Max=max(max(c)); %求两极差Min=min(min(c));p=0.5; %p称为分辨率,0<p< p="">for i=1:m-1for j=1:nr(i,j)=(Min+p*Max)/(c(i,j)+p*Max); %计算关联系数endendfor i=1:m-1rela(i)=sum(r(i,:))/n; %求关联度end四,非线性拟合function f=example1(c,tdata)f=c(1)*(exp(-c(2)*tdata)-exp(-c(3)*tdata));function f=zhengtai(c,x)f=(1./(sqrt(2.*3.14).*c(1))).*exp(-(x-c(1)).^2./(2.*c(2)^2));x=1:1:12;y=[01310128212]';c0=[2 8];for i=1:1000c=lsqcurvefit(@zhengtai,c0,x,y);c0=c;endy1=(1./(sqrt(2.*3.14).*c(1))).*exp(-(x-c(1)).^2./(2.*c(2)^2));plot(x,y,'r-',x,y1);legend('实验数据','拟合曲线')x=[0.25 0.5 0.75 1 1.5 2 2.5 3 3.5 4 4.5 5 6 7 8 9 10 11 12 13 14 15 16]';y=[30 68 75 82 82 77 68 68 58 51 50 41 38 35 28 25 18 15 12 10 7 7 4]';f=@(c,x)c(1)*(exp(-c(2)*x)-exp(-c(3)*x));c0=[114 0.1 2]';for i=1:50opt=optimset('TolFun',1e-3);[c R]=nlinfit(x,y,f,c0,opt)c0=c;hold onplot(x,c(1)*(exp(-c(2)*x)-exp(-c(3)*x)),'g')endt=[0.25 0.5 0.75 1 1.5 2 2.5 3 3.5 4 4.5 5 6 7 8 9 10 11 12 1314 15 16];y=[30 68 75 82 82 77 68 68 58 51 50 41 38 35 28 25 1815 12 10 7 7 4];c0=[1 1 1];for i=1:50 c=lsqcurvefit(@example1,c0,t,y);c0=c;endy1=c(1)*(exp(-c(2)*t)-exp(-c(3)*t));plot(t,y,'+',t,y1);legend('实验数据','拟合曲线')五,插值拟合相关知识在生产和科学实验中,自变量与因变量间的函数关系有时不能写出解析表达式,而只能得到函数在若干点的函数值或导数值,或者表达式过于复杂而需要较大的计算量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
代码一: % 解密过程及破译密文统计 clear clc fid1=fopen('mingwen1.txt','r'); str1=fgets(fid1); fclose(fid1); fid2=fopen('jiemihou1.txt','r'); str2=fgets(fid2); fclose(fid2); % 删去单词之间的间隔和标点符号 ad=find(str2==',');str2(ad)='';ad=find(str2=='.');str2(ad)='';ad=find(str2==';');str2(ad)=''; ad=find(str2=='''');str2(ad)='';ad=find(str2=='?');str2(ad)='';ad=find(str2==':');str2(ad)=''; ad=find(str2=='"');str2(ad)='';ad=find(str2=='-');str2(ad)='';ad=find(str2=='/');str2(ad)=''; ad=find(str2==' ');str2(ad)=''; for i=0:25; ad=find(str1=='A'+i);str1(ad)='a'+i; end for i=0:25; ad=find(str2=='A'+i);str2(ad)='a'+i; end n1(1,26)=0; n2(1,26)=0; n1(1)=sum(str1=='a');n2(1)=sum(str2=='a'); n1(2)=sum(str1=='b');n2(2)=sum(str2=='b'); n1(3)=sum(str1=='c');n2(3)=sum(str2=='c'); n1(4)=sum(str1=='d');n2(4)=sum(str2=='d'); n1(5)=sum(str1=='e');n2(5)=sum(str2=='e'); n1(6)=sum(str1=='f');n2(6)=sum(str2=='f'); n1(7)=sum(str1=='g');n2(7)=sum(str2=='g'); n1(8)=sum(str1=='h');n2(8)=sum(str2=='h'); n1(9)=sum(str1=='i');n2(9)=sum(str2=='i'); n1(10)=sum(str1=='j');n2(10)=sum(str2=='j'); n1(11)=sum(str1=='k');n2(11)=sum(str2=='k'); n1(12)=sum(str1=='l');n2(12)=sum(str2=='l'); n1(13)=sum(str1=='m');n2(13)=sum(str2=='m'); n1(14)=sum(str1=='n');n2(14)=sum(str2=='n'); n1(15)=sum(str1=='o');n2(15)=sum(str2=='o'); n1(16)=sum(str1=='p');n2(16)=sum(str2=='p'); n1(17)=sum(str1=='q');n2(17)=sum(str2=='q'); n1(18)=sum(str1=='r');n2(18)=sum(str2=='r'); n1(19)=sum(str1=='s');n2(19)=sum(str2=='s'); n1(20)=sum(str1=='t');n2(20)=sum(str2=='r'); n1(21)=sum(str1=='u');n2(21)=sum(str2=='u'); n1(22)=sum(str1=='v');n2(22)=sum(str2=='v'); n1(23)=sum(str1=='w');n2(23)=sum(str2=='w'); n1(24)=sum(str1=='x');n2(24)=sum(str2=='x'); n1(25)=sum(str1=='y');n2(25)=sum(str2=='y'); n1(26)=sum(str1=='z');n2(26)=sum(str2=='z'); [N1,IX1]=sort(n1,'descend') [N2,IX2]=sort(n2,'descend') % 频率对应 idx=find(str2=='v');str2(idx)='E'; idx=find(str2=='g');str2(idx)='T'; idx=find(str2=='l');str2(idx)='A'; idx=find(str2=='m');str2(idx)='N'; idx=find(str2=='z');str2(idx)='I'; idx=find(str2=='h');str2(idx)='S'; idx=find(str2=='r');str2(idx)='O'; idx=find(str2=='t');str2(idx)='R'; idx=find(str2=='i');str2(idx)='D'; idx=find(str2=='s');str2(idx)='L'; idx=find(str2=='o');str2(idx)='H'; idx=find(str2=='w');str2(idx)='F'; idx=find(str2=='x');str2(idx)='U'; idx=find(str2=='f');str2(idx)='C'; idx=find(str2=='u');str2(idx)='G'; idx=find(str2=='k');str2(idx)='P'; idx=find(str2=='d');str2(idx)='Y'; idx=find(str2=='n');str2(idx)='M'; idx=find(str2=='y');str2(idx)='B'; idx=find(str2=='e');str2(idx)='K'; idx=find(str2=='b');str2(idx)='W'; idx=find(str2=='p');str2(idx)='V'; idx=find(str2=='q');str2(idx)='Q'; idx=find(str2=='a');str2(idx)='J'; idx=find(str2=='c');str2(idx)='X'; idx=find(str2=='j');str2(idx)='Z'; %%%%%%%% for i=0:25; ad=find(str2=='A'+i);str2(ad)='a'+i; end n3(1,26)=0; for i=0:25; n3=sum(str2=='a'+i); end %破译得到的明文及频率 disp(str2) [N3,IX3]=sort(n3,'descend') N3/(sum(N3))
代码二: % 基于频率分析,寻找最佳修改位置 % p1-----传输过程中每个字符出现丢失的概率 % p2-----传输过程中每个字符出现篡改的概率 % p3-----传输过程中每个字符出现被添加的概率 % derta-----各字母间频率差异 % derta_n-----各字母需要改变的数目 l2=size(str2); syms p1 p2 p3 p1=0.1;p2=0.1;p3=0.1; A=n1./sum(n1); B=n3./sum(n3); derta=A-B; derta_n=round(sum(n3).*derta.*p1+sum(n3).*derta.*p2);
% l(i)-----某一字符左侧可能连接的字符 % r(i)-----某一字符右侧可能连接的字符 % count_l-----统计某一字符左侧可能连接的字符总数 % count_r-----统计某一字符右侧可能连接的字符总数 % max_l-----某一字符左侧出现最多的字符 % max_r-----某一字符右侧出现最多的字符 % ad-----字符所在位置
length_str2=length(str2); for i=1:26 if derta_n(i)<0 z=zeros(length_str2,1); n0=find(str2=='a'+i-1); n1=sum(str2=='a'+i-1); ll=zeros(n1,1); rr=zeros(n1,1); for j=1:n1 for t=1:n1 l1(j)=str2(n0(t)-1); r1(j)=str2(n0(t)+1); end end l1_i=l1(:); r1_i=r1(:); for m1=1:26; n1(m1)=sum(str1=='a'+m1); end [r,c]=max(n1) for ii=1:size(str2) ad=find(str2=='a'+c-1) end for k1=1:derta_n(i) str2(ad(k1))=([c 'a'+i]); end
elseif derta_n(i)>0 z=zeros(length_str2,1); n0=find(str2=='a'+i-1); n1=sum(str2=='a'+i-1); ll=zeros(n1,1); rr=zeros(n1,1); for j=1:n1 l2(j)=str2(n0(j)-1); r2(j)=str2(n0(j)+1); end l2_i=l2(:); r2_i=r2(:); for m1=1:26; n1(m1)=sum(str1=='a'+m1); end [r,c]=min(n1) for k1=1:derta_n(i) ad(k1)=find(str2=='a'+c-1); str2(ad(k1))=([ ]); end end end end disp(str2) for m1=1:26; n1(m1)=sum(str2=='a'+m1-1); end [N3,IX3]=sort(n3,'descend') N3/(sum(N3))
