河南省2019年中考数学专题复习专题七类比探究题训练
河南省2019年中考数学总复习核心母题一全等在几何探究题中的应用深度练习word格式
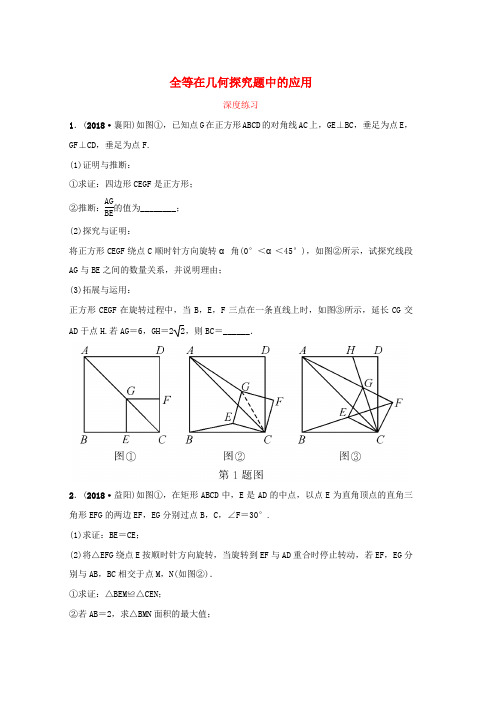
全等在几何探究题中的应用深度练习1.(2018·襄阳)如图①,已知点G 在正方形ABCD 的对角线AC 上,GE ⊥BC ,垂足为点E ,GF ⊥CD ,垂足为点F. (1)证明与推断:①求证:四边形CEGF 是正方形; ②推断:AGBE 的值为________;(2)探究与证明:将正方形CEGF 绕点C 顺时针方向旋转α角(0°<α<45°),如图②所示,试探究线段AG 与BE 之间的数量关系,并说明理由; (3)拓展与运用:正方形CEGF 在旋转过程中,当B ,E ,F 三点在一条直线上时,如图③所示,延长CG 交AD 于点H.若AG =6,GH =22,则BC =______.2.(2018·益阳)如图①,在矩形ABCD 中,E 是AD 的中点,以点E 为直角顶点的直角三角形EFG 的两边EF ,EG 分别过点B ,C ,∠F =30°. (1)求证:BE =CE ;(2)将△EFG 绕点E 按顺时针方向旋转,当旋转到EF 与AD 重合时停止转动,若EF ,EG 分别与AB ,BC 相交于点M ,N(如图②). ①求证:△BEM ≌△CEN ;②若AB =2,求△BMN 面积的最大值;③当旋转停止时,点B恰好在FG上(如图③),求sin∠EBG的值.参考答案1.(1)证明: ①∵四边形ABCD 是正方形,∴∠BCD =90°,∠BCA =45°. ∵GE ⊥BC ,GF ⊥CD ,∴∠CEG =∠CFG =∠ECF =90°.∴四边形CEGF 是矩形,∠CGE =∠ECG =45°. ∴EG =EC.∴四边形CEGF 是正方形. ②AGBE= 2. (2)解:如解图①,连接CG ,由旋转性质可知∠BCE =∠ACG =α. 在Rt △CEG 和Rt △CBA 中,CE CG =cos 45°=22,CB CA =cos 45°=22.∴CG CE =CA CB = 2.∴△ACG ∽△BCE.∴AG BE =CACB = 2. ∴线段AG 与BE 之间的数量关系为AG =2BE. (3)解:如解图②,连接DF ,由(2)知△BCE ∽△ACG , ∴∠BEC =∠AGC. ∵四边形CEGF 是正方形,∴∠CEF =∠CFE =∠CGF = 45°,CG ⊥EF. ∵∠BEC =180°-∠CEF =135°,∴∠AGC =135°. ∴∠AGC +∠CGF =135°+45°=180°. ∴A ,G ,F 三点在一条直线上. 又∠BCD =∠ECF =90°, ∴∠BCE =∠DCF. 而BC =DC ,EC =FC ,第1题解图②∴△BEC ≌△DFC(SAS).∴BE =DF ,∠BEC =∠DFC.∵AGBE=2,AG =6,∴BE =DF =3 2.∵∠BEC =135°,∠CFE =45°,∴∠BFD =∠DFC -∠CFE =135°-45°=90°.又CH ⊥BF ,∴CH ∥DF.∴△AGH ∽△AFD.∴GH FD =AG AF =AHAD.∴2232=66+GF =AHAD.∴GF =3,AH AD =23.设AH =2x ,则AD =3x ,DH =x.又由正方形ABCD 和正方形CEGF ,知AD =CD =3x ,GC =2GF =32, ∴在Rt △CDH 中,由DH 2+CD 2=CH 2,得x 2+(3x)2=(22+32)2,解得x 1=5,x 2=-5(不合题意,舍去).∴AD =35,即BC =3 5.故答案为3 5.2.解:(1)∵矩形ABCD ,∴AB =DC ,∠A =∠D =90°,∵AE =DE ,∴△ABE ≌△DCE ,∴BE =CE ;(2)①∵∠AEB +∠ABE =90°,∠AEB +∠CED =90°,第2题解图∴∠ABE =∠CED , ∵∠CED =∠ECB , ∴∠ABE =∠ECB ,∵∠BEC =∠MEN =90°,∴∠BEM =∠CEN ,由(1)得BE =CE ,∴△BEM ≌△CEN ;②由(1)得△ABE ≌△DCE ,∴∠BEA =∠CED ,∵∠ABE =∠CED ,∴∠BEA =∠ABE ,∴AB =AE =DE =2,设BM =x ,由①得△BEM ≌△CEN ,∴BM =CN =x ,∴BN =4-x ,∴△BMN 面积=12x(4-x)=-12(x -2)2+2,又0≤x ≤2,∴当x =2时,△BMN 面积最大,最大值为2.③如解图,过点E 作EH ⊥FG 于点H.在Rt △ABF 中,∠F =30°,AB =2,∴FA =23,∴FE =FA +AE =23+2,∴EH =3+1,在Rt △BEH 中,∵BE =22,∴sin ∠EBG =EH BE =3+122=6+24.。
【数学】2019年河南省中考真题(解析版)

2019年河南省中考数学试卷一、选择题(每小题3分,共30分)下列各小题均有四个答案,其中只有一个是正确的。
1.﹣的绝对值是()A.﹣B.C.2D.﹣2【答案】B【解析】|﹣|=,故选:B.2.成人每天维生素D的摄入量约为0.0000046克.数据“0.0000046”用科学记数法表示为()A.46×10﹣7B.4.6×10﹣7C.4.6×10﹣6D.0.46×10﹣5【答案】C【解析】0.0000046=4.6×10﹣6.故选:C.3.如图,AB∥CD,∠B=75°,∠E=27°,则∠D的度数为()A.45°B.48°C.50°D.58°【答案】B【解析】∵AB∥CD,∴∠B=∠1,∵∠1=∠D+∠E,∴∠D=∠B﹣∠E=75°﹣27°=48°,故选:B.4.下列计算正确的是()A.2a+3a=6a B.(﹣3a)2=6a2C.(x﹣y)2=x2﹣y2D.3﹣=2【答案】D【解析】2a+3a=5a,A错误;(﹣3a)2=9a2,B错误;(x﹣y)2=x2﹣2xy+y2,C错误;=2,D正确;故选:D.5.如图①是由大小相同的小正方体搭成的几何体,将上层的小正方体平移后得到图②.关于平移前后几何体的三视图,下列说法正确的是()A.主视图相同B.左视图相同C.俯视图相同D.三种视图都不相同【答案】A【解析】图①的三视图为:图②的三视图为:故选:A.6.一元二次方程(x+1)(x﹣1)=2x+3的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.只有一个实数根D.没有实数根【答案】A【解析】原方程可化为:x2﹣2x﹣4=0,∴a=1,b=﹣2,c=﹣4,∴△=(﹣2)2﹣4×1×(﹣4)=20>0,∴方程由两个不相等的实数根.故选:A.7.某超市销售A,B,C,D四种矿泉水,它们的单价依次是5元、3元、2元、1元.某天的销售情况如图所示,则这天销售的矿泉水的平均单价是()A.1.95元B.2.15元C.2.25元D.2.75元【答案】C【解析】这天销售的矿泉水的平均单价是5×10%+3×15%+2×55%+1×20%=2.25(元),故选:C.8.已知抛物线y=﹣x2+bx+4经过(﹣2,n)和(4,n)两点,则n的值为()A.﹣2B.﹣4C.2D.4【答案】D【解析】抛物线y=﹣x2+bx+4经过(﹣2,n)和(4,n)两点,可知函数的对称轴x=1,∴=1,∴b=2;∴y=﹣x2+2x+4,将点(﹣2,n)代入函数解析式,可得n=4;故选:D.9.如图,在四边形ABCD中,AD∥BC,∠D=90°,AD=4,BC=3.分别以点A,C为圆心,大于AC长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O.若点O是AC的中点,则CD的长为()A.2B.4C.3D.【答案】A【解析】如图,连接FC,则AF=FC.∵AD∥BC,∴∠F AO=∠BCO.在△FOA与△BOC中,,∴△FOA≌△BOC(ASA),∴AF=BC=3,∴FC=AF=3,FD=AD﹣AF=4﹣3=1.在△FDC中,∵∠D=90°,∴CD2+DF2=FC2,∴CD2+12=32,∴CD=2.故选:A.10.如图,在△OAB中,顶点O(0,0),A(﹣3,4),B(3,4),将△OAB与正方形ABCD 组成的图形绕点O顺时针旋转,每次旋转90°,则第70次旋转结束时,点D的坐标为()A.(10,3)B.(﹣3,10)C.(10,﹣3)D.(3,﹣10)【答案】D【解析】∵A(﹣3,4),B(3,4),∴AB=3+3=6,∵四边形ABCD为正方形,∴AD=AB=6,∴D(﹣3,10),∵70=4×17+2,∴每4次一个循环,第70次旋转结束时,相当于△OAB与正方形ABCD组成的图形绕点O 顺时针旋转2次,每次旋转90°,∴点D的坐标为(3,﹣10).故选:D.二、填空题(每小题3分,共15分。
2019年河南省中考数学试卷(含答案与解析)

数学试卷 第1页(共36页) 数学试卷 第2页(共36页)绝密★启用前河南省2019年普通高中招生考试数 学本试卷满分120分,考试时间100分钟.第Ⅰ卷(选择题 共30分)一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.12-的绝对值是( )A .12-B .12C .2D .2-2.成人每天维生素D 的摄入量约为0.000 004 6克.数据“0.000 004 6”用科学记数法表示为( ) A .74610-⨯B .74.610-⨯C .64.610-⨯D .50.4610-⨯ 3.如图,AB CD ∥,75B ∠=,27E ∠=,则D ∠的度数为( ) A .45 B .48 C .50 D .584.下列计算正确的是( ) A .236a a a +=B .22(3)6a a -=C .222()x y x y -=-D.=5.如图1是由大小相同的小正方体搭成的几何体,将上层的小正方体平移后得到图2.关于平移前后几何体的三视图,下列说法正确的是( ) A .主视图相同 B .左视图相同C .俯视图相同D .三种视图都不相同6.一元二次方程()12()13x x x +-=+的根的情况是( )A .有两个不相等的实数根B .有两个相等的实数根C .只有一个实数根D .没有实数根7.某超市销售A ,B ,C ,D 四种矿泉水,它们的单价依次是5元、3元、2元、1元.某天的销售情况如图所示,则这天销售的矿泉水的平均单价是( ) A .1.95元 B .2.15元 C .2.25元 D .2.75元8.已知抛物线24y x bx =-++经过()2,n -和(4,)n 两点,则n 的值为( ) A .2-B .4-C .2D .49.如图,在四边形ABCD 中,AD BC ∥,90D ∠=,4AD =,3BC =.分别以点A ,C 为圆心,大于12AC 长为半径作弧,两弧交于点E ,作射线BE 交AD 于点F ,交AC 于点O .若点O 是AC 的中点,则CD 的长为( ) A.B .4 C .3图1图2毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共36页) 数学试卷 第4页(共36页)D10.如图,在OAB △中,顶点()0,0O ,4()3,A -,()3,4B .将OAB △与正方形ABCD 组成的图形绕点O 顺时针旋转,每次旋转90,则第70次旋转结束时,点D 的坐标为( )A .(10,3)B .()3,10-C .(10,)3-D .(3,)10-第Ⅱ卷(非选择题 共90分)二、填空题(本大题共5小题,每小题3分,共15分.把答案填写在题中的横线上)11.12-= .12.不等式组1,274xx ⎧-⎪⎨⎪-+⎩≤>的解集是 .13.现有两个不透明的袋子,一个装有2个红球、1个白球,另一个装有1个黄球、2个红球,这些球除颜色外完全相同.从两个袋子中各随机摸出1个球,摸出的两个球颜色相同的概率是 .14.如图,在扇形AOB 中,120AOB ∠=,半径OC 交弦AB 于点D ,且OC OA ⊥.若OA =,则阴影部分的面积为 .15.如图,在矩形ABCD 中,1AB =,BC a =,点E 在边BC 上,且35BE α=.连接AE ,将ABE △沿AE 折叠,若点B 的对应点B '落在矩形ABCD 的边上,则a 的值为 .三、解答题(本大题共8小题,共75分.解答应写出文字说明、证明过程或演算步骤) 16.(本小题满分8分)先化简,再求值:2212(1)244x x xx x x +--÷--+,其中x17.(本小题满分9分)如图,在ABC △中,BA BC =,90ABC ∠=.以AB 为直径的半圆O 交AC 于点D ,点E 是BD 上不与点B ,D 重合的任意一点,连接AE 交BD 于点F ,连接BE 并延长交AC于点G .(1)求证:ADF BDG ≅△△; (2)填空:①若4AB =,且点E 是BD 的中点,则DF 的长为 ;②取AE 的中点H ,当EAB ∠的度数为 时,四边形OBEH 为菱形.18.(本小题满分9分)某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下: a .七年级成绩频数分布直方图:数学试卷 第5页(共36页) 数学试卷 第6页(共36页)b .七年级成绩在7080x ≤<这一组的是:70 72 74 75 76 76 77 77 77 78 79 c .根据以上信息,回答下列问题:(1)在这次测试中,七年级在80分以上(含80分)的有 人; (2)表中m 的值为 ;(3)在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;(4)该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数.19.(本小题满分9分)数学兴趣小组到黄河风景名胜区测量炎帝塑像(塑像中高者)的高度.如图所示,炎帝塑像DE 在高55 m 的小山EC 上,在A 处测得塑像底部E 的仰角为34,再沿AC 方向前进21 m 到达B 处,测得塑像顶部D 的仰角为60,求炎帝塑像DE 的高度.(精确到1 m .参考数据:sin340.56≈,cos340.83=,tan340.67≈ 1.73)20.(本小题满分9分)学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A 奖品和2个B 奖品共需120元;购买5个A 奖品和4个B 奖品共需210元. (1)求A ,B 两种奖品的单价;(2)学校准备购买A ,B 两种奖品共30个,且A 奖品的数量不少于B 奖品数量的13.请设计出最省钱的购买方案,并说明理由.21.(本小题满分10分)模具厂计划生产面积为4,周长为m 的矩形模具.对于m 的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下: (1)建立函数模型设矩形相邻两边的长分别为x ,y .由矩形的面积为4,得4xy =,即4y x=;由周长为m ,得2()x y m +=,即2my x =-+.满足要求的(),x y 应是两个函数图象在第________象限内交点的坐标; (2)画出函数图象 函数4(0)y x x =>的图象如图所示,而函数2my x =-+的图象可由直线y x =-平移得到.请在同一直角坐标系中直接画出直线y x =-;-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________数学试卷 第7页(共36页) 数学试卷 第8页(共36页)(3)平移直线y x =-,观察函数图象 ①当直线平移到与函数4(0)y x x=>的图象有唯一交点(2,2)时,周长m 的值为 ;②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长m 的取值范围. (4)得出结论若能生产出面积为4的矩形模具,则周长m 的取值范围为 .22.(本小题满分10分)在ABC △中,CA CB =,ACB α∠=.点P 是平面内不与点A ,C 重合的任意一点,连接AP ,将线段AP 绕点P 逆时针旋转α得到线段DP ,连接AD ,BD ,CP . (1)观察猜想 如图1,当60α=时,BDCP的值是 ,直线BD 与直线CP 相交所成的较小角的度数是 ; (2)类比探究如图2,当90α=时,请写出BDCP的值及直线BD 与直线CP 相交所成的小角的度数,并就图2的情形说明理由; (3)解决问题当90α=时,若点E ,F 分别是CA ,CB 的中点,点P 在直线EF 上,请直接写出点C ,P ,D 在同一直线上时ADCP的值.图1图2备用图23.(本小题满分11分) 如图,抛物线212y ax x c =++交x 轴于A ,B 两点,交y 轴于点C .直线122y x =--经过点A ,C . (1)求抛物线的解析式;(2)点P 是抛物线上一动点,过点P 作x 轴的垂线,交直线AC 于点M ,设点P 的横坐标为m .①当PCM △是直角三角形时,求点P 的坐标;②作点B 关于点C 的对称点B ',则平面内存在直线l ,使点M ,B ,B '到该直线的距离都相等.当点P 在y 轴右侧的抛物线上,且与点B 不重合时,请直接写出直线l :y kx b =+的解析式.(k ,b 可用含m 的式子表示)数学试卷 第9页(共36页) 数学试卷 第10页(共36页)备用图数学试卷 第11页(共36页) 数学试卷 第12页(共36页)河南省2019年普通高中招生考试数学答案解析第Ⅰ卷一、选择题 1.【答案】B 【解析】解:11||22-=,故选:B . 【提示】根据一个负数的绝对值是它的相反数进行解答即可. 【考点】绝对值的概念. 2.【答案】C【解析】解:60.0000046 4.610-=⨯. 【提示】本题用科学记数法的知识即可解答. 【考点】科学记数法. 3.【答案】B【解析】解:∵AB CD ∥,∴1B ∠=∠, ∵1D E ∠=∠+∠,∴752748D B E ∠=∠-∠=-=, 故选:B .【提示】根据平行线的性质解答即可. 【考点】平行线的性质,三角形外角的性质. 4.【答案】D【解析】解:235a a a +=,A 错误;22(3)9a a -=,B 错误;222(2)x y xxy y -=-+,C错误;=D 正确;故选:D .【提示】根据合并同类项法则,完全平方公式,幂的乘方与积的乘方的运算法则进行运算即可.【考点】整式的运算. 5.【答案】C【解析】解:观察几何体,确定三视图,此几何体将上层的小正方体平移后俯视图相同,故选C .【提示】根据三视图解答即可. 【考点】几何体的三视图. 6.【答案】A【解析】解:原方程可化为:2240x x --=, ∴1a =,2b =-,4c =-, ∴2241()(4)200∆=--⨯⨯-=>, ∴方程由两个不相等的实数根. 故选:A .【提示】先化成一般式后,再求根的判别式.【考点】一元二次方程根的情况. 7.【答案】C【解析】解:这天销售的矿泉水的平均单价是510%315%255%120% 2.25⨯+⨯+⨯+⨯=(元), 故选:C .【提示】根据加权平均数的定义列式计算可得. 【考点】加权平均数的计算. 8.【答案】B【解析】解:抛物线24y x bx =-++经过()2,n -和(4,)n 两点, 可知函数的对称轴1x =, ∴12b=, ∴2b =;数学试卷 第13页(共36页) 数学试卷 第14页(共36页)∴224y x x =-++,将点()2,n -代入函数解析式,可得4n =; 故选:B .【提示】根据()2,n -和(4,)n 可以确定函数的对称轴1x =,再由对称轴的2bx =即可求解.【考点】二次函数点的坐标特征,二元一次方程组的解法. 9.【答案】A【解析】解:如图,连接FC ,则AF FC =. ∵AD BC ∥, ∴FAO BCO ∠=∠. 在FOA △与BOC △中,FAO BCOOA OCAOF COB ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴()ASA FOA BOC ≅△△, ∴3AF BC ==,∴3FC AF ==,431FD AD AF =-=-=. 在FDC △中,∵90D ∠=, ∴222CD DF FC +=, ∴21232CD +=,∴CD = 故选:A .【提示】连接FC ,根据基本作图,可得OE 垂直平分AC ,由垂直平分线的性质得出AF FC =.再根据ASA 证明FOA BOC ≅△△,那么3AF BC ==,等量代换得到3FC AF ==,利用线段的和差关系求出1FD AD AF =-=.然后在直角FDC △中利用勾股定理求出CD 的长.【考点】尺规作图,平行线的性质,勾股定理,角平分线的性质,全等三角形的判定与性质. 10.【答案】D【解析】解:∵4()3,A -,()3,4B , ∴336AB =+=, ∵四边形ABCD 为正方形, ∴6AD AB ==, ∴0()3,1D -, ∵704172=⨯+,∴每4次一个循环,第70次旋转结束时,相当于OAB △与正方形ABCD 组成的图形绕点O 顺时针旋转2次,每次旋转90, ∴点D 的坐标为(3,)10-. 故选:D .【提示】先求出6AB =,再利用正方形的性质确定0()3,1D -,由于704172=⨯+,所以第70次旋转结束时,相当于OAB △与正方形ABCD 组成的图形绕点O 顺时针旋转2次,每次旋转90,此时旋转前后的点D 关于原点对称,于是利用关于原点对称的点的坐标特征可出旋转后的点D 的坐标. 【考点】图形的旋转,点的坐标的确定.第Ⅱ卷二、填空题 11.【答案】3221-数学试卷 第15页(共36页) 数学试卷 第16页(共36页)122=- 32=. 故答案为:32.【提示】本题涉及二次根式化简、负整数指数幂两个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果. 【考点】实数的相关运算. 12.【答案】2x -≤【解析】解:解不等式12x -…,得:2x -≤, 解不等式74x -+>,得:3x <, 则不等式组的解集为2x -≤, 故答案为:2x -≤.【提示】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集. 【考点】解不等式组. 13.【答案】49由表知,共有9种等可能结果,其中摸出的两个球颜色相同的有4种结果, 所以摸出的两个球颜色相同的概率为49, 故答案为:49. 【提示】列表得出所有等可能结果,从中找到两个球颜色相同的结果数,利用概率公式计算可得. 【考点】概率的计算. 14.π【解析】解:作OE AB ⊥于点F ,∵在扇形AOB中,120AOB ∠=,半径OC 交弦AB 于点D ,且OC OA⊥.OA=2,∴90AOD ∠=,90BOC ∠=,OA OB =, ∴30OAB OBA ∠=∠=,∴tan30232OD OA ===,4AD =,226AB AF ==⨯=,OF∴2BD =, ∴阴影部分的面积是:πAOD BDOOBC S S S +--=△△扇形,π.【提示】根据题意,作出合适的辅助线,然后根据图形可知阴影部分的面积是AOD △的面积与扇形OBC 的面积之和再减去BDO △的面积,本题得以解决. 【考点】不规则图形面积的计算. 15.【答案】53【解析】解:分两种情况: ①当点B '落在AD 边上时,如图1.数学试卷 第17页(共36页) 数学试卷 第18页(共36页)图1∵四边形ABCD 是矩形, ∴90BAD B ∠=∠=,∵将ABE △沿AE 折叠,点B 的对应点B '落在AD 边上, ∴1452BAE B AE BAD ∠=∠'=∠=, ∴AB BE =, ∴315a =,∴53a =;②当点B '落在CD 边上时,如图2.图2∵四边形ABCD 是矩形,∴90BAD B C D ∠=∠=∠=∠=,AD BC a ==. ∵将ABE △沿AE 折叠,点B 的对应点B '落在CD 边上, ∴90B AB E ∠=∠'=,1AB AB ='=,35EB EB a ='=,∴DB '==355EC BC BE a a =-=-=. 在ADB '△与B CE '△中,9090B AD EBC AB DD C '''⎧∠=∠=-∠⎨∠=∠=⎩, ∴ADB B CE ''△△,∴DB AB CE B E ''=',即12355a a =,解得1a =,20a =(舍去). 综上,所求a 的值为53.故答案为53.【提示】分两种情况:①点B '落在AD 边上,根据矩形与折叠的性质易得AB BE =,即可求出a 的值;②点B '落在CD 边上,证明ADB B CE ''△△,根据相似三角形对应边成比例即可求出a 的值. 【考点】图形的折叠,勾股定理. 三、解答题16.【答案】解:原式212(2)()22(2)x x x x x x x +--=-÷--- 322x x x -=-3x=, 当x =,=【解析】解:原式212(2)()22(2)x x x x x x x +--=-÷--- 322x x x -=-3x=, 当x=,=【提示】先根据分式的混合运算顺序和运算法则化简原式,再将x 的值代入计算可得. 【考点】分式的化简求值.17.【答案】解:(1)证明:如图1,∵BA BC =,90ABC ∠=,数学试卷 第19页(共36页) 数学试卷 第20页(共36页)图1∴45BAC ∠= ∵AB 是O 的直径, ∴90ADB AEB ∠=∠=,∴90DAF BGD DBG BGD ∠+∠=∠+∠= ∴DAF DBG ∠=∠ ∵90ABD BAC ∠+∠= ∴45ABD BAC ∠=∠= ∴AD BD =∴()ASA ADF BDG ≅△△; (2)①4-②30【解析】解:(1)证明:如图1,∵BA BC =,90ABC ∠=,图1∴45BAC ∠= ∵AB 是O 的直径, ∴90ADB AEB ∠=∠=,∴90DAF BGD DBG BGD ∠+∠=∠+∠= ∴DAF DBG ∠=∠ ∵90ABD BAC ∠+∠= ∴45ABD BAC ∠=∠=∴AD BD =∴()ASA ADF BDG ≅△△;(2)①如图2,过F 作FH AB ⊥于H ,∵点E 是BD 的中点,图2∴BAE DAE ∠=∠ ∵FD AD ⊥,FH AB ⊥ ∴FH FD =∵2sin sin45FH ABD BF =∠==,∴FD BF =,即BF ∵4AB =,∴4cos4522BD ==即BF FD+=,1)FD =∴4FD ==-故答案为4-②连接OE,EH ,∵点H 是AE 的中点,∴OH AE ⊥, ∵90AEB ∠= ∴BE AE ⊥ ∴BE OH ∥∵四边形OBEH 为菱形,∴12BE OH OB AB ===∴1sin 2BE EAB AB ∠==∴30EAB ∠=. 故答案为:30.【提示】(1)利用直径所对的圆周角是直角,可得90ADB AEB ∠=∠=,再应用同角的余角相等可得DAF DBG ∠=∠,易得AD BD =,ADF BDG △≌△得证;(2)作FH AB ⊥,应用等弧所对的圆周角相等得BAE DAE ∠=∠,再应用角平分线性质可得结论;由菱形的性质可得BE OB =,结合三角函数特殊值可得30EAB ∠=. 【考点】圆的相关性质,全等三角形的判定和性质,菱形的判定和性质,圆周角定理. 18.【答案】(1)23 (2)77.5(3)甲学生在该年级的排名更靠前.∵七年级学生甲的成绩大于中位数78分,其名次在该班25名之前, 八年级学生乙的成绩小于中位数78分,其名次在该班25名之后, ∴甲学生在该年级的排名更靠前.(4)估计七年级成绩超过平均数76.9分的人数为515840022450++⨯=(人). 【解析】解:(1)在这次测试中,七年级在80分以上(含80分)的有15823+=人,故答案为:23;(2)七年级50人成绩的中位数是第25、26个数据的平均数,而第25、26个数据分别为78、79, ∴777877.52m +==, 故答案为:77.5;(3)甲学生在该年级的排名更靠前.∵七年级学生甲的成绩大于中位数78分,其名次在该班25名之前, 八年级学生乙的成绩小于中位数78分,其名次在该班25名之后, ∴甲学生在该年级的排名更靠前.(4)估计七年级成绩超过平均数76.9分的人数为515840022450++⨯=(人). 【提示】(1)根据条形图及成绩在7080x ≤<这一组的数据可得; (2)根据中位数的定义求解可得;(3)将各自成绩与该年级的中位数比较可得答案;(4)用总人数乘以样本中七年级成绩超过平均数76.9分的人数所占比例可得. 【考点】统计知识的实际应用.19.【答案】解:∵90ACE ∠=,34CAE ∠=,55m CE =,∴tan CECAE AC ∠=, ∴5582.1m tan340.67CE AC ==≈,∵21m AB =,∴61.1m BC AC AB =-=, 在Rt BCD △中,tan60CDBC=,∴ 1.7361.1105.7m CD =≈⨯≈, ∴105.75551m DE CD EC =-=-≈, 答:炎帝塑像DE 的高度约为51 m .【解析】解:∵90ACE ∠=,34CAE ∠=,55m CE =,∴tan CECAE AC ∠=, ∴5582.1m tan340.67CE AC ==≈,∵21m AB =,∴61.1m BC AC AB =-=, 在Rt BCD △中,tan60CDBC==,∴ 1.7361.1105.7m CD ≈⨯≈, ∴105.75551m DE CD EC =-=-≈, 答:炎帝塑像DE 的高度约为51 m . 【提示】由三角函数求出82.1m tan34CEAC =≈,得出61.1mBC AC AB =-=,在Rt BCD △中,由三角函数得出105.7m CD =≈,即可得出答案.【考点】解直角三角形的实际应用.20.【答案】解:(1)设A 的单价为x 元,B 的单价为y 元,根据题意,得3212054210x y x y +=⎧⎨+=⎩,∴3015x y =⎧⎨=⎩,∴A 的单价30元,B 的单价15元;(2)设购买A 奖品z 个,则购买B 奖品为30-z ()个,购买奖品的花费为W 元, 由题意可知,13)3(0z z -≥, ∴152z ≥, 30153045(51)0W z z z =+-=+,当8z =时,W 有最小值为570元,即购买A 奖品8个,购买B 奖品22个,花费最少. 【解析】解:(1)设A 的单价为x 元,B 的单价为y 元,根据题意,得3212054210x y x y +=⎧⎨+=⎩,∴3015x y =⎧⎨=⎩,∴A 的单价30元,B 的单价15元;(2)设购买A 奖品z 个,则购买B 奖品为30-z ()个,购买奖品的花费为W 元, 由题意可知,13)3(0z z -≥, ∴152z ≥, 30153045(51)0W z z z =+-=+,当8z =时,W 有最小值为570元,即购买A 奖品8个,购买B 奖品22个,花费最少.【提示】(1)设A 的单价为x 元,B 的单价为y 元,根据题意列出方程组3212054210x y x y +=⎧⎨+=⎩,即可求解;(2)设购买A 奖品z 个,则购买B 奖品为(30)z -个,购买奖品的花费为W 元,根据题意得到由题意可知,13)3(0z z -≥,30153045(51)0W z z z =+-=+,根据一次函数的性质,即可求解.【考点】二元一次方程组,不等式及一次函数解决实际问题. 21.【答案】(1)一 (2)图象如下所示:(3)①8②在直线平移过程中,交点个数有:0个、1个、2个三种情况, 联立4y x =和2my x =-+并整理得:21402x mx -+=,214404m ∆=-⨯≥时,两个函数有交点,解得:8m ≥; (4)8m ≥【解析】解:(1),x y 都是边长,因此,都是正数, 故点(),x y 在第一象限, 答案为:一; (2)图象如下所示:(3)①把点(2,2)代入2my x =-+得: 222m=-+,解得:8m =;②在直线平移过程中,交点个数有:0个、1个、2个三种情况,联立4y x =和2my x =-+并整理得:21402x mx -+=,214404m ∆=-⨯≥时,两个函数有交点,解得:8m ≥;(4)由(3)得:8m ≥.【提示】(1),x y 都是边长,因此,都是正数,即可求解; (2)直接画出图象即可; (3)①把点()2,2代入2my x =-+即可求解;②在直线平移过程中,交点个数有:0个、1个、2个三种情况,联立4y x=和 = 2m y x -+并整理得:21402x mx -+=,即可求解;(4)由(3)可得.【考点】反比例函数与一次函数图象的应用. 22.【答案】160(2)如图2中,设BD 交AC 于点O ,BD 交PC 于点E .图2∵45PAD CAB ∠=∠=, ∴PAC DAB ∠=∠,∵AB ADAC AP= ∴DAB PAC △△, ∴PCA DBA ∠=∠,BD ABPC AC== ∵EOC AOB ∠=∠, ∴45CEO OABB ∠=∠=,∴直线BD 与直线CP 相交所成的小角的度数为45.(3)如图3-1中,当点D 在线段PC 上时,延长AD 交BC 的延长线于H .图3-1∵CE EA =,CF FB =, ∴EF AB ∥,∴45EFC ABC ∠=∠=, ∵45PAO ∠=, ∴PAO OFH ∠=∠, ∵POA FOH ∠=∠, ∴H APO ∠=∠,∵90APC ∠=,EA EC =, ∴PE EA EC ==,∴EPA EAP BAH ∠=∠=∠, ∴H BAH ∠=∠, ∴BH BA =,∵45ADP BDC ∠=∠=, ∴90ADB ∠=, ∴BD AH ⊥,∴22.5DBA DBC ∠=∠=, ∵90ADB ACB ∠=∠=, ∴A ,D ,C ,B 四点共圆,22.5DAC DBC ∠=∠=,22.5DCA ABD ∠=∠=,∴22.5DAC DCA ∠=∠=,∴DA DC =,设AD a =,则DC AD a ==,PD ,∴2ADCP==如图3-2中,当点P 在线段CD 上时,同法可证:DA DC =,设AD a =,则CD AD a ==,=2PD ,图3-2∴PC a =-,∴2AD PC ==【解析】解:(1)如图1中,延长CP 交BD 的延长线于E ,设AB 交EC 于点O .图1∵60PAD CAB ∠=∠=, ∴CAP BAD ∠=∠, ∵CA BA =,PA DA =, ∴()SAS CAP BAD ≅△△, ∴PC BD =,ACP ABD ∠=∠, ∵AOC BOE ∠=∠,∴60BEO CAO ∠=∠=, ∴1BDPC=,线BD 与直线CP 相交所成的较小角的度数是60, 故答案为1,60.(2)如图2中,设BD 交AC 于点O ,BD 交PC 于点E .图2∵45PAD CAB ∠=∠=, ∴PAC DAB ∠=∠,∵AB ADAC AP== ∴DAB PAC △△, ∴PCA DBA ∠=∠,BD ABPC AC== ∵EOC AOB ∠=∠, ∴45CEO OABB ∠=∠=,∴直线BD 与直线CP 相交所成的小角的度数为45.(3)如图3-1中,当点D 在线段PC 上时,延长AD 交BC 的延长线于H .图3-1∵CE EA =,CF FB =, ∴EF AB ∥,∴45EFC ABC ∠=∠=, ∵45PAO ∠=, ∴PAO OFH ∠=∠, ∵POA FOH ∠=∠, ∴H APO ∠=∠,∵90APC ∠=,EA EC =, ∴PE EA EC ==,∴EPA EAP BAH ∠=∠=∠,∴H BAH ∠=∠, ∴BH BA =,∵45ADP BDC ∠=∠=, ∴90ADB ∠=, ∴BD AH ⊥,∴22.5DBA DBC ∠=∠=, ∵90ADB ACB ∠=∠=, ∴A ,D ,C ,B 四点共圆,22.5DAC DBC ∠=∠=,22.5DCA ABD ∠=∠=,∴22.5DAC DCA ∠=∠=,∴DA DC =,设AD a =,则DC AD a ==,PD ,∴2ADCP=如图3-2中,当点P 在线段CD 上时,同法可证:DA DC =,设AD a =,则CD AD a ==,PD ,图3-2∴2PC a =-,∴2AD PC == 【提示】(1)如图1中,延长CP 交BD 的延长线于E ,设AB 交EC 于点O .证明()SAS CAP BAD △≌△,即可解决问题.(2)如图2中,设BD 交AC 于点O ,BD 交PC 于点E .证明△DAB ∽△PAC ,即可解决问题. (3)分两种情形:①如图3-1中,当点D 在线段PC 上时,延长AD 交BC 的延长线于H .证明AD=DC 即可解决问题.②如图3-2中,当点P 在线段CD 上时,同法可证:DA DC =解决问题. 【考点】图形变换,规律探究.23.【答案】解:(1)当0x =时,1222y x =--=-, ∴点C 的坐标为(0,)2-;当0y =时,1202x --=,解得:4x =-,∴点A 的坐标为()4,0-.将0()4,A -,2(0,)C -代入212y ax x c =++,得:16202a c c -+=⎧⎨=-⎩,解得:142a c ⎧=⎪⎨⎪=-⎩, ∴抛物线的解析式为211242y x x =+-.(2)①∵PM x ⊥轴, ∴90PMC ∠≠,∴分两种情况考虑,如图1所示.图1(i )当90MPC ∠=时,PC x ∥轴, ∴点P 的纵坐标为2-. 当2y =-时,2112242x x +-=-, 解得:12x =-,20x =, ∴点P 的坐标为(2,2)--;(ii )当90PCM ∠=时,设PC 与x 轴交于点D .∵90OAC OCA ∠+∠=,90OCA OCD ∠+∠=, ∴OAC OCD ∠=∠. 又∵90AOC COD ∠=∠=, ∴AOCCOD △△,∴OD OC OC OA =,即224OD =, ∴1OD =,∴点D 的坐标为(1,0).设直线PC 的解析式为()0y kx b k =+≠, 将2(0,)C -,()1,0D 代入y kx b =+,得:20b k b =-⎧⎨+=⎩,解得:22k b =⎧⎨=-⎩,∴直线PC 的解析式为22y x =-.联立直线PC 和抛物线的解析式成方程组,得:22211242y x y x x =-⎧⎪⎨=+-⎪⎩, 解得:1102x y =⎧⎨=-⎩,22610x y =⎧⎨=⎩,点P 的坐标为(6,10).综上所述:当PCM △是直角三角形时,点P 的坐标为(2,2)--或(6,10). ②当0y =时,2112042x x +-=, 解得:14x =-,22x =, ∴点B 的坐标为(2,0).∵点P 的横坐标为0()0m m m ≠>且,∴点P 的坐标为211(,2)42m m m +-,∴直线PB 的解析式为11(4)(4)42y m x m =+-+(可利用待定系数求出).∵点B ,B '关于点C 对称,点B ,B ',P 到直线l 的距离都相等, ∴直线l 过点C ,且直线l PB ∥直线, ∴直线l 的解析式为1(4)24y m x =+-.【解析】解:(1)当0x =时,1222y x =--=-, ∴点C 的坐标为(0,)2-;当0y =时,1202x --=,解得:4x =-,∴点A 的坐标为()4,0-.将0()4,A -,2(0,)C -代入212y ax x c =++,得: 16202a c c -+=⎧⎨=-⎩,解得:142a c ⎧=⎪⎨⎪=-⎩, ∴抛物线的解析式为211242y x x =+-.(2)①∵PM x ⊥轴, ∴90PMC ∠≠,∴分两种情况考虑,如图1所示.图1(i )当90MPC ∠=时,PC x ∥轴, ∴点P 的纵坐标为2-. 当2y =-时,2112242x x +-=-, 解得:12x =-,20x =, ∴点P 的坐标为(2,2)--;(ii )当90PCM ∠=时,设PC 与x 轴交于点D . ∵90OAC OCA ∠+∠=,90OCA OCD ∠+∠=, ∴OAC OCD ∠=∠. 又∵90AOC COD ∠=∠=, ∴AOCCOD △△,∴OD OC OC OA =,即224OD =,∴1OD =,∴点D 的坐标为(1,0).设直线PC 的解析式为()0y kx b k =+≠, 将2(0,)C -,()1,0D 代入y kx b =+,得:20b k b =-⎧⎨+=⎩,解得:22k b =⎧⎨=-⎩, ∴直线PC 的解析式为22y x =-.联立直线PC 和抛物线的解析式成方程组,得:22211242y x y x x =-⎧⎪⎨=+-⎪⎩, 解得:1102x y =⎧⎨=-⎩,22610x y =⎧⎨=⎩,点P 的坐标为(6,10).综上所述:当PCM △是直角三角形时,点P 的坐标为(2,2)--或(6,10). ②当0y =时,2112042x x +-=, 解得:14x =-,22x =, ∴点B 的坐标为(2,0).∵点P 的横坐标为0()0m m m ≠>且,∴点P 的坐标为211(,2)42m m m +-,∴直线PB 的解析式为11(4)(4)42y m x m =+-+(可利用待定系数求出).∵点B ,B '关于点C 对称,点B ,B ',P 到直线l 的距离都相等, ∴直线l 过点C ,且直线l PB ∥直线, ∴直线l 的解析式为1(4)24y m x =+-.【提示】(1)利用一次函数图象上点的坐标特征可求出点A ,C 的坐标,根据点A ,C 的坐标,利用待定系数法可求出二次函数解析式;(2)①由PM x ⊥轴可得出90PMC ∠≠,分90MPC ∠=及90PCM ∠=两种情况考虑:(i )当90MPC ∠=时,PC x ∥轴,利用二次函数图象上点的坐标特征可求出点P 的坐标;(ii )当90PCM ∠=时,设PC 与x 轴交于点D ,易证AOCCOD △△,利用相似三角形的性质可求出点D 的坐标,根据点C ,D 的坐标,利用待定系数法可求出直线PC 的解析式,联立直线PC 和抛物线的解析式成方程组,通过解方程组可求出点P 的坐标.综上,此问得解;②利用二次函数图象上点的坐标特征可得出点B ,P 的坐标,根据点P ,B 的坐标,利用待定系数法可求出直线PB 的解析式,结合题意可知:直线l 过点C ,且直线l PB ∥直线,再结合点C 的坐标即可求出直线l 的解析式.【考点】二次函数的图象和性质,直角三角形的性质,相似三角形的判定和性质,中位线定理,一次函数的性质,分类讨论思想.。
2019中考数学专题复习之归纳类比思想专项训练题二(附答案详解)

2019中考数学专题复习之归纳类比思想专项训练题二(附答案详解)1.阅读材料:求的值.解:设,①将①得:,② 由②-①得:,即.即请你仿照此法计算:(其中为正整数). 2.阅读下列材料:一般地,n 个相同的因数a 相乘n a ?a a ⋯个记为a n .如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log 28(即log 28=3).一般地,若a n =b (a >0且a≠1,b >0),则n 叫做以a 为底b 的对数,记为log a b (即log a b=n ).如34=81,则4叫做以3为底81的对数,记为log 381(即log 381=4).(1)计算:log 28=______; (2)计算: ()2331log 9log 813+; (3)log 55、log 525、log 5125之间满足怎样的关系式,请说明理由。
3.七年级教材在图形与几何部分给出了五条基本事实,在《证明》一章中我们从两条基本事实出发,把前面得到的平行线相关性质进行了严格的证明,体会了数学的公里化思想.请完成下列证明活动:活动1.利用基本事实证明:“两直线平行,同位角相等”.(在括号内填上相应的基本事实)已知:如图,直线AB 、CD 被直线EF 所截, AB CD .求证: 12∠=∠.证明:假设12∠≠∠,则可以过点O 作2EOG ∠=∠. ∵2EOG ∠=∠,∴OG CD ( ).∴过O 点存在两条直线AB 、OG 两条直线与CD 平行,这与基本事实( )矛盾. ∴假设不成立. ∴12∠=∠.活动2.利用刚刚证明的“两直线平行,同位角相等”证明“两直线平行,同旁内角互补”.(要求画图,写出已知、求证并写出证明过程) 已知: . 求证: . 证明:4.计算并观察、探究下列式子 ①_____②______③④⑤…由以上规律 (1)填空:=_______________.(2)求:的值.5.定义:可以表示为两个互质整数的商的形式的数称为有理数,整数可以看作分母为1的有理数;反之为无理数.如不能表示为两个互质的整数的商,所以几个号无理数.可以这样证明:设,a与b是互质的两个整数,且b≠0,则2=,所以a²=2b².因为b是整数且不为0,所以a是不为0的偶数.设a=2n(n是整数),所以b²=2n²,所以b也是偶数,与a与b是互质的整数矛盾,所以是无理数.仔细阅读上文,然后请证明:是无理数。
2019-2020年九年级中考数学动态几何、类比探究专项训练

2019-2020年九年级中考数学动态几何、类比探究专项训练三、解答题22. (10分)如图所示,现有一张边长为4的正方形纸片ABCD ,点P 为正方形AD 边上的一点(不与点A ,点D 重合),将正方形纸片折叠,使点B 落在P 处,点C 落在G 处,PG 交DC 于H ,折痕为EF ,连接BP ,BH .(1)求证:∠APB =∠BPH .(2)当点P 在边AD 上移动时,△PDH 的周长是否发生变化?并证明你的结论.(3)设AP 为x ,四边形EFGP 的面积为S ,求出S 与x 的函数关系式,试问S 是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.(备用图)A EBPDH GF CCFGH DPBEA备用图中考数学动态几何、类比探究专项训练(二)三、解答题22. (10分)数学课上,魏老师出示图1和下面框中条件:(1)①当点C 与点F 重合时,如图2所示,可得的值为______; ②在平移过程中,的值为__________(用含x 的代数式表示).(2)将图2中的三角板ABC 绕点C 逆时针旋转,原题中的其他条件保持不变.当点A 落在线段DF 上时,如图3所示,请计算的值.(3)将图1中的三角板ABC 绕点C 逆时针旋转度,,原题中的其他条件保持不变,如图4所示,请计算的值(用含x 的代数式表示).图3 图4中考数学动态几何、类比探究专项训练(三)三、解答题22. (10分)已知:线段OA ⊥OB ,点C 为OB 中点,D 为线段OA 上一点.连接AC ,BD 交于点P .(1)如图1,当OA =OB ,且D 为OA 中点时,求的值; (2)如图2,当OA =OB ,且时,求tan ∠BPC 的值;(3)如图3,当AD :OA :OB =1:n :时,直接写出tan ∠BPC 的值.lM AB FCEDlMABF (C )ED图3图2图1PD BC OA O DC PBA O D C P BA中考数学动态几何、类比探究专项训练四)三、解答题22.(10分)如图,在矩形ABCD中,点M是AD的中点,AD=,CD=,直角∠PME绕点M进行旋转,其两边分别和BC,CD交于点P和点E,连接PE交MC于点Q.(1)判断线段MP,ME的数量关系,并进行证明;(2)当动点P,E分别在线段BC和CD上运动时,设PC=x,MQ=y,求y与x的函数关系式;(3)在(2)中,当y取最小值时,判断PE与BM的位置关系,并说明理由.PQE M DCBA中考数学动态几何、类比探究专项训练(五)三、解答题22.(10分)如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).(1)当α=60°时,求CE的长.(2)当60°<α<90°时,①是否存在正整数k,使得∠EFD=k∠AEF?若存在,求出k的值;若不存在,请说明理由.②连接CF,当CE2CF2取最大值时,求tan∠DCF的值.F DCB EA中考数学动态几何、类比探究专项训练(六)三、解答题22. (10分)点A ,B 分别是两条平行线m ,n 上任意一点,在直线n 上找一点C ,使BC =kAB ,连接AC ,在线段AC 上任取一点E ,作∠BEF =∠ABC ,EF 交直线m 于点F .(1)如图1,当∠ABC =90°,k =1时,判断线段EF 和EB 之间的数量关系,并证明.(2)如图2,当∠ABC =90°,k ≠1时,(1)中结论还成立吗?若成立,请证明;若不成立,请重新判断线段EF 和EB 之间的数量 关系.(3)如图3,当0°<∠ABC <90°,k =1时,探究EF 和EB 之间的数量关系,并证明.mnAF CB Emn A F E CBB CEF Anm图1 图2 图3中考数学动态几何、类比探究专项训练(七)三、解答题22. (10分)如图1,在等腰Rt △ABC 和等腰Rt △CDE (CD >BC )中,点C ,B ,D 在同一直线上,点M是AE 的中点.(1)探究线段MD ,MB 的位置及数量关系,并证明.(2)将图1中的△CDE 绕点C 顺时针旋转45°,使△CDE 的斜边CE 恰好与△ABC 的边BC 垂直,如图2,原问题中的其他条件不变,则(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明.(3)若将图2中的△ABC 绕点C 逆时针旋转大于0°且小于45°的角,如图3,原问题中的其他条件不变,则(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明. 图1 图2 图3EMD C BAE MDCBAABCDME中考数学动态几何、类比探究专项训练(八)三、解答题22. (10分)如图1,四边形ABCD 是正方形,点E 是边BC 的中点.∠AEF =90°,且EF 交正方形外角∠DCG 的平分线CF 于点F . (1)求证:AE =EF .(2)如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上除B ,C 外的任意一点”,其他条件不变,那么结论“AE =EF ”仍然成立吗?如果成立,写出证明过程;如果不成立,请说明 理由.(3)如图3,点E 是BC 延长线上除C 点外的任意一点,其他条件不变,结论“AE =EF ”仍然成立吗?如果成立,写出证明过程;如果不成立,请说明理由.图 1 图 2 图 3中考数学动态几何、类比探究专项训练(九)三、解答题22. (10分)问题背景(1)如图1,△ABC 中,DE ∥BC ,分别交AB ,AC 于D ,E 两点,过点E 作EF ∥AB ,交BC 于点F .请按图示数据填空:四边形DBFE 的面积S =_________,△EFC 的面积S 1=_________,△ADE 的面积S 2=__________. 探究发现(2)在(1)中,若BF =a ,FC =b ,DE 与BC 间的距离为h .请证明S 2=4S 1S 2. 拓展迁移GAB C DFE E FDC BAG E FDC B A G(3)如图2,□DEFG 的四个顶点在△ABC 的三边上,若△ADG ,△DBE ,△GFC 的面积分别为2,5,3,试利用(2)中的结论求△ABC 的面积.中考数学动态几何、类比探究专项训练(十)三、解答题22. (10分)如图,在△ABC 中,AB =AC =10厘米,BC =12厘米,D 是BC 的中点,点P 从B 出发,以a厘米/秒(a >0)的速度沿BA 匀速向点A 运动,点Q 同时以1厘米/秒的速度从D 出发,沿DB 匀速向点B 运动,其中一个动点到达端点时,另一个动点也随之停止运动,设它们运动的时间为t 秒. (1)若a =2,△BPQ ∽△BDA ,求t 的值;(2)设点M 在AC 上,四边形PQCM 为平行四边形. ①若a =,求PQ 的长;②是否存在实数a ,使得点P 在∠ACB 的平分线上?若存在,请求出a 的值;若不存在,请说明理由.图2图1CE DGBAFS 1S 2SF E DCBA 362P Q D CB A中考数学动态几何、类比探究专项训练(十一)三、解答题22. (10分)如图,在Rt △ABC 中,∠C =90°,AB =25cm ,AC =20cm .点P 从点A 出发,沿AB 的方向匀速运动,速度为5cm/s ;同时点M 从点C 出发,沿CA 的方向匀速运动,速度为4cm/s .过点M 作MN ∥AB ,交BC 于点N .设运动的时间为t 秒(0<t <5). (1)用含t 的代数式表示线段MN 的长.(2)连接PN ,是否存在某一时刻t ,使得四边形AMNP 为菱形?若存在,求出此时t 的值;若不存在,请说明理由.(3)连接PM ,PN ,是否存在某一时刻t ,使得点P 在线段MN 的垂直平分线上?若存在,求出此时t 的值;若不存在,请说明理由.(备用图)BCACBA(备用图)AC BPNM中考数学动态几何、类比探究专项训练(十二)三、解答题22.(10分)如图,在梯形A B C D中,A D∥B C,A D=3,D C=5,A B=,∠B=45°.动点M从B点出发,沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动.设运动的时间为t秒.(1)求BC的长;(2)当MN∥AB时,求t的值;(3)试探究:t为何值时,△MNC为等腰三角形.中考数学动态几何、类比探究专项训练(一)参考答案22.(1)证明略;NM DCBA(2)△PDH的周长不发生变化,证明略;(3),当x=2时,S存在最小值,最小值为6.中考数学动态几何、类比探究专项训练(二)参考答案22.(1)①1;②;(2);(3).中考数学动态几何、类比探究专项训练(三)参考答案22.(1)=2;(2)tan∠BPC;(3)tan∠BPC.中考数学动态几何、类比探究专项训练(四)参考答案22.(1)MP=ME,证明略;(2);(3)当y取最小值时,PE∥BM,理由略.中考数学动态几何、类比探究专项训练(五)参考答案22.(1)CE=.(2)①存在,k=3;②tan∠DCF.中考数学动态几何、类比探究专项训练(六)参考答案22.(1)EF=EB,证明略;(2)不成立,此时EB=kEF;(3)EF=EB,证明略.中考数学动态几何、类比探究专项训练(七)参考答案22.(1)MD⊥MB,MD=MB,证明略;(2)不发生变化,证明略;(3)不发生变化,证明略.中考数学动态几何、类比探究专项训练(八)参考答案22.(1)证明略;(2)结论仍成立,证明略;(3)结论仍成立,证明略.中考数学动态几何、类比探究专项训练(九)参考答案22.(1)6,9,1;(2)证明略;(3)18.中考数学动态几何、类比探究专项训练(十)参考答案22.(1);(2)①PQ厘米;②不存在,理由略.中考数学动态几何、类比探究专项训练(十一)参考答案22.(1)MN=;(2)存在,;(3)存在,.可编辑修改中考数学动态几何、类比探究专项训练(十二)参考答案22.(1)BC=;(2);(3)..希望能帮到您,欢迎下载。
2020河南中考数学复习专题专题类比探究题

专题七 类比探究题专题类型突破类型一 图形旋转引起的探究 (2019·河南)在△ABC 中,CA =CB ,∠ACB=α.点P 是平面内不与点A ,C 重合的任意一点.连接AP ,将线段AP 绕点P 逆时针旋转α得到线段DP ,连接AD ,BD ,CP.(1)观察猜想如图1,当α=60°时,BD CP的值是________,直线BD 与直线CP 相交所成的较小角的度数是________.(2)类比探究如图2,当α=90°时,请写出BD CP的值及直线BD 与直线CP 相交所成的较小角的度数,并就图2的情形说明理由.(3)解决问题当α=90°时,若点E ,F 分别是CA ,CB 的中点,点P 在直线EF 上,请直接写出点C ,P ,D 在同一直线上时AD CP的值.【分析】(1)延长CP 交BD 的延长线于E ,设AB 交EC 于点O.证明△CAP≌△BAD,即可解决问题.(2)设BD 交AC 于点O ,BD 交PC 于点E.证明△DAB∽△PAC,即可解决问题.(3)分两种情况:当点D在线段PC上时,延长AD交BC的延长线于H.证明AD=DC即可解决问题;当点P在线段CD上时,同法可证DA=DC,解决问题.【自主解答】1.(2018·河南)(1)问题发现如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:①ACBD的值为________;②∠AMB的度数为________;(2)类比探究如图2,在△OAB 和△OCD 中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC 交BD 的延长线于点M.请判断AC BD的值及∠AMB 的度数,并说明理由; (3)拓展延伸在(2)的条件下,将△OCD 绕点O 在平面内旋转,AC ,BD 所在直线交于点M ,若OD =1,OB =7,请直接写出当点C 与点M 重合时AC 的长.2.(2017·河南)如图1,在Rt△ABC 中,∠A=90°,AB =AC ,点D ,E 分别在边AB ,AC 上,AD =AE ,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想图1中,线段PM 与PN 的数量关系是________,位置关系是________;(2)探究证明把△ADE 绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断△PMN 的形状,并说明理由;(3)拓展延伸把△ADE 绕A 在平面内自由旋转,若AD =4,AB =10,请直接写出△PMN 面积的最大值.图1 图23.(2015·河南)如图1,在Rt△ABC 中,∠B=90°,BC =2AB =8,点D ,E 分别是边BC ,AC 的中点,连接DE.将△EDC 绕点C 按顺时针方向旋转,记旋转角为α.(1)问题发现①当α=0°时,AE BD=________;②当α=180°时,AE BD=________; (2)拓展探究试判断:当0°≤α<360°时,AE BD的大小有无变化?请仅就图2的情形给出证明. (3)解决问题当△EDC 旋转至A ,D ,E 三点共线时,直接写出线段BD 的长.类型二 动点引起的探究(2016·河南)(1)发现如图1,点A 为线段BC 外一动点,且BC =a ,AB =b.填空:当点A 位于________时,线段AC 的长取得最大值,且最大值为________(用含a ,b 的式子表示);(2)应用点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.①请找出图中与BE相等的线段,并说明理由;②直接写出线段BE长的最大值;(3)拓展如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM 长的最大值及此时点P的坐标.【分析】(1)根据点A位于CB的延长线上时,线段AC的长取得最大值,即可得到结论;(2)①根据等边三角形的性质得到AD=AB,AC=AE,∠BAD=∠CAE=60°,推出△CAD≌△EAB,根据全等三角形的性质得到CD=BE;②由于线段BE的最大值=线段CD的最大值,根据(1)中的结论即可得到结果.(3)将△APM 绕着点P 顺时针旋转90°得到△PBN,连接AN ,得到△APN 是等腰直角三角形,根据全等三角形的性质得到PN =PA =2,BN =AM ,根据当N 在线段BA 的延长线时,线段BN 取得最大值,即可得到最大值为22+3;过P 作PE⊥x 轴于E ,根据等腰直角三角形的性质即可得到点P 的坐标.【自主解答】4.(2019·河南模拟)(1)问题发现如图1,在Rt△ABC 中,∠BAC=90°,ABAC =1,点P 是边BC 上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接CD.填空:①PB CD=________; ②∠ACD 的度数为________;(2)拓展探究如图2,在Rt△ABC 中,∠BAC=90°,AB AC=k.点P 是边BC 上一动点(不与点B 重合),∠PAD=90°,∠APD=∠B,连接CD ,请判断∠ACD 与∠B 的数量关系以及PB 与CD 之间的数量关系,并说明理由;(3)解决问题如图3,在△ABC 中,∠B=45°,AB =42,BC =12,P 是边BC 上一动点(不与点B 重合),∠PAD=∠BAC,∠APD=∠B,连接CD.若PA =5,请直接写出所有CD 的长.类型三 图形形状变化引起的探究(2019·信阳一模)(1)观察猜想如图1,点B,A,C在同一条直线上,DB⊥BC,EC⊥BC,且∠DAE=90°,AD=AE,则BC,BD,CE之间的数量关系为________;(2)问题解决如图2,在Rt△ABC中,∠ABC=90°,CB=4,AB=2,以AC为直角边向外作等腰Rt△DAC,连接BD,求BD的长;(3)拓展延伸如图3,在四边形ABCD中,∠ABC=∠ADC=90°,CB=4,AB=2,DC=DA,请直接写出BD的长.【分析】(1)通过证明△ADB≌△EAC,可得结论:BC=AB+AC=BD+CE;(2)过D作DE⊥AB,交BA的延长线于E,同理证明△ABC≌△DEA,可得DE=AB =2,AE=BC=4,最后利用勾股定理求BD的长;(3)同理证明三角形全等,设AF=x,DF=y,根据全等三角形对应边相等列方程组可得结论.【自主解答】5.(2014·河南)(1)问题发现如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE. 填空:①∠AEB的度数为________;②线段AD,BE之间的数量关系为________;(2)拓展探究如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由;(3)解决问题如图3,在正方形ABCD中,CD=2,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.参考答案类型一【例1】(1)1 60°(2)BDCP 的值为2,直线BD 与直线CP 相交所成的较小角的度数为45°.理由如下: 如图,设BD 交AC 于点O ,BD 交PC 于点E.∵∠PAD=∠CAB=45°, ∴∠PAC=∠DAB. ∵AB AC =ADAP =2, ∴△DAB∽△PAC,∴∠PCA=∠DBA,BD PC =ABAC= 2.∵∠EOC=∠AOB,∴∠CEO=∠OAB=45°,∴直线BD 与直线CP 相交所成的较小角的度数为45°. (3)ADCP的值为2+2或2- 2. 如图,当点D 在线段PC 上时,延长AD 交BC 的延长线于H.∵CE=EA ,CF =FB ,∴EF∥AB, ∴∠EFC=∠ABC=45°.∵∠PAO=45°,∴∠PAO=∠OFH.∵∠POA=∠FOH,∴∠H=∠APO.∵∠APC=90°,EA=EC,∴PE=EA=EC,∴∠EPA=∠EAP=∠BAH,∴∠H=∠BAH,∴BH=BA.∵∠ADP=∠BDC=45°,∴∠ADB=90°,∴BD⊥AH,∴∠DBA=∠DBC=22.5°.∵∠ADB=∠ACB=90°,∴A,D,C,B四点共圆,∠DAC=∠DBC=22.5°,∠DCA=∠ABD=22.5°,∴∠DAC=∠DCA=22.5°,∴DA=DC.设AD=a,则DC=AD=a,PD=2 2a,∴ADCP=aa+22a=2- 2.如图,当点P在线段CD上时,同法可证DA=DC.设AD=a,则CD=AD=a,PD =22a,∴PC=a-22a,∴AD PC =a a -22a=2+ 2. 综上所述,点C ,P ,D 在同一直线上时,ADCP 的值为2-2或2+ 2.跟踪训练 1.解:(1)①1提示:∵∠AOB=∠COD=40°, ∴∠COA =∠DOB.∵OC=OD ,OA =OB ,∴△COA≌△DOB(SAS), ∴AC=BD ,∴ACBD =1.②40°提示:∵△COA≌△DOB, ∴∠CAO=∠DBO.∵∠AOB=40°,∴∠OAB+∠ABO=140°.在△AMB 中,∠AMB=180°-(∠CAO+∠OAB+∠ABD)=180°-(∠DBO+∠OAB +∠ABD)=180°-140°=40°. (2)ACBD =3,∠AMB=90°.理由如下: 在Rt△OCD 中,∠DCO=30°,∠DOC=90°, ∴OD OC =tan 30°=33. 同理得OB OA =tan 30°=33.∵∠AOB=∠COD=90°,∴∠AOC=∠BOD,∴△AOC∽△BOD, ∴AC BD =OCOD=3,∠CAO=∠DBO, ∴∠AMB=180°-∠CAO-∠OAB -MBA =180°-(∠DAB+∠MBA+∠OBD)=180°-90°=90°. (3)23或3 3.提示:①点C 与点M 重合时,如图,同理得△AOC∽△BOD, ∴∠AMB=90°,ACBD = 3.设BD =x ,则AC =3x. 在Rt△COD 中, ∵∠OCD=30°,OD =1, ∴CD=2,∴BC=x -2.在Rt△AOB 中,∠OAB=30°,OB =7. ∴AB=2OB =27.在Rt△AMB 中,由勾股定理得AC 2+BC 2=AB 2, 即(3x)2+(x -2)2=(27)2, 解得x 1=3,x 2=-2(舍去), ∴AC=3 3.②点C 与点M 重合时,如图,同理得∠AMB=90°,ACBD= 3.设BD =x ,则AC =3x ,在Rt△AMB 中,由勾股定理得AC 2+BC 2=AB 2, 即(3x)2+(x +2)2=(27)2. 解得x 1=-3,解得x 2=2(舍去), ∴AC=2 3.综上所述,AC 的长为33或2 3. 2.解:(1)PM =PN PM⊥PN 提示:∵点P ,N 是BC ,CD 的中点, ∴PN∥BD,PN =12BD.∵点P ,M 是CD ,DE 的中点, ∴PM∥CE,PM =12CE.∵AB=AC ,AD =AE ,∴BD=CE ,∴PM=PN. ∵PN∥BD,∴∠DPN=∠ADC, ∵PM∥CE,∴∠DPM=∠DCA.∵∠BAC=90°,∴∠ADC+∠ACD=90°, ∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°, ∴PM⊥PN.(2)△PMN 为等腰直角三角形.理由如下: 由旋转知,∠BAD=∠CAE.∵AB=AC ,AD =AE ,∴△ABD≌△ACE(SAS),∴∠AB D =∠ACE,BD =CE.同(1)的方法,利用三角形的中位线定理得 PN =12BD ,PM =12CE ,∴PM=PN ,∴△PMN 是等腰三角形. 同(1)的方法得PM∥CE, ∴∠DPM=∠DCE. 同(1)的方法得PN∥BD, ∴∠PNC=∠DBC.∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB +∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC. ∵∠BAC=90°,∴∠ACB+∠ABC=90°,∴∠MPN=90°, ∴△PMN 是等腰直角三角形. (3)492.提示:同(2)的方法得△PMN 是等腰直角三角形, ∴当MN 最大时,△PMN 的面积最大, ∴DE∥BC 且DE 在顶点A 上面, ∴MN 最大=AM +AN. 如图,连接AM ,AN.在△ADE 中,AD =AE =4,∠DAE=90°, ∴AM=2 2.在Rt△ABC 中,AB =AC =10,AN =52, ∴MN 最大=22+52=72,∴S △PMN 最大=12PM 2=12×12MN 2=14×(72)2=492.3.解:(1)①52提示:当α=0°时, ∵在Rt△ABC 中,∠B=90°,∴AC=AB 2+BC 2=(8÷2)2+82=4 5. ∵点D ,E 分别是边BC ,AC 的中点, ∴AE=45÷2=25,BD =8÷2=4, ∴AE BD =254=52. ②25提示:如图,当α=180°时,则可得AB∥DE.∵AC AE =BC BD, ∴AE BD =AC BC =458=52. (2)当0°≤α≤360°时,AEBD的大小没有变化.∵∠ECD=∠ACB,∴∠ECA=∠DCB. 又∵EC DC =AC BC =52,∴△ECA∽△DCB, ∴AE BD =EC DC =52. (3)BD 的长为45或125 5提示:a.如图,∵AC=45,CD =4,CD⊥AD ,∴AD=AC 2-CD 2=(45)2-42=80-16=8. ∵AD=BC ,AB =DC ,∠B=90°, ∴四边形ABCD 是矩形, ∴BD=AC =4 5.b .如图,连接BD ,过点D 作AC 的垂线交AC 于点Q ,过点B 作AC 的垂线交AC 于点P.∵AC=45,CD =4,CD⊥AD,∴AD=AC 2-CD 2=(45)2-42=80-16=8. ∵点D ,E 分别是边BC ,AC 的中点, ∴DE=12AB =12×(8÷2)=12×4=2,∴AE=AD -DE =8-2=6, 由(2)得AE BD =52,∴BD=652=1255.综上所述,BD 的长为45或1255.类型二【例2】(1)CB 的延长线 a +b (2)①CD=BE.理由:∵△ABD 与△A CE 是等边三角形, ∴AD=AB ,AC =AE ,∠BAD=∠CAE=60°, ∴∠BAD+∠BAC=∠CAE+∠BAC, 即∠CAD=∠EAB. 在△CAD 和△EAB 中, ⎩⎪⎨⎪⎧AD =AB ,∠CAD=∠EAB,AC =AE , ∴△CAD≌△EAB, ∴CD=BE. ②4提示:∵线段BE 长的最大值等于线段CD 的最大值, 由(1)知,当线段CD 取得最大值时,点D 在CB 的延长线上, ∴线段BE 的最大值为BD +BC =AB +BC =4.(3)线段AM的最大值为22+3,点P的坐标为(2-22,2).提示:如图,将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,则△APN 是等腰直角三角形,∴PN=PA=2,BN=AM.∵点A的坐标为(2,0),点B的坐标为(5,0),∴OA=2,OB=5,∴AB=3,∴线段AM的最大值等于线段BN的最大值,∴当点N在线段BA的延长线时,线段BN取得最大值,即最大值为AB+AN.∵AN=2AP=22,∴线段AM的最大值为22+3.如图,过点P作PE⊥x轴于点E.∵△APN是等腰直角三角形,∴PE=AE=2,∴OE=BO-AB-AE=5-3-2=2-2,∴P(2-2,2).跟踪训练4.解:(1)①1②45°(2)∠ACD=∠B,PB CD=k. 理由如下:∵∠BAC=∠PAD=90°,∠B=∠APD,∴△ABC∽△APD,∴AB AC =AP AD=k. ∵∠BAP+∠PAC=∠PAC+∠CAD=90°,∴∠BAP=∠CAD,∴△ABP∽△CAD,∴∠ACD=∠B,PB CD =AB AC=k. (3)102或7102. 类型三【例3】(1)BC =BD +CE提示:∵∠B=90°,∠DAE=90°,∴∠D+∠DAB=∠DAB+∠EAC=90°,∴∠D=∠EAC.∵∠B=∠C=90°,AD =AE ,∴△ADB≌△EAC,∴BD=AC ,EC =AB ,∴BC=AB +AC =BD +CE.(2)如图,过D 作DE⊥AB,交BA 的延长线于E.由(1)同理得△ABC≌△DEA,∴DE=AB =2,AE =BC =4.在Rt△BDE 中,BE =6,∴由勾股定理得BD =62+22=210.(3)如图,过点D 作DE⊥BC 于E ,作DF⊥AB,交BA 的延长线于F.同理得△CED≌△AFD,∴CE=AF ,ED =DF.设AF =x ,DF =y ,则⎩⎪⎨⎪⎧x +y =4,2+x =y ,解得⎩⎪⎨⎪⎧x =1,y =3,∴BF=2+1=3,DF =3,由勾股定理得BD =32+32=3 2.跟踪训练5.解:(1)①60°提示:∵△ACB 和△DCE 均为等边三角形,∴CA=CB ,CD =CE ,∠ACB=∠DCE=60°,∴∠ACD=∠BCE.在△ACD 和△BCE 中,⎩⎪⎨⎪⎧AC =BC ,∠ACD=∠BCE,CD =CE ,∴△ACD≌△BCE,∴∠ADC=∠BEC.∵△DCE 为等边三角形,∴∠CDE=∠CED=60°.∵点A ,D ,E 在同一直线上,∴∠ADC=120°,∴∠BEC=120°,∴∠AEB =∠BEC-∠CED=60°.②AD=BE(2)∠AEB=90°,AE =BE +2CM.理由如下:∵△ACB 和△DCE 均为等腰直角三角形,∴CA=CB ,CD =CE ,∠ACB=∠DCE=90°,∴∠ACD=∠BCE.在△ACD 和△BCE 中,⎩⎪⎨⎪⎧CA =CB ,∠ACD=∠BCE,CD =CE ,∴△ACD≌△BCE,∴AD=BE ,∠ADC=∠BEC.∵△DCE 为等腰直角三角形,∴∠CDE=∠CED=45°.∵点A ,D ,E 在同一直线上,∴∠ADC=135°,∴∠BEC=135°,∴∠AEB=∠BEC-∠CED=90°.∵CD=CE,CM⊥DE,∴DM=ME.∵∠DCE=90°,∴DM=ME=CM,∴AE=AD+DE=BE+2CM.(3)点A到BP的距离为3-12或3+12.提示:∵PD=1,∴点P在以点D为圆心,1为半径的圆上.∵∠BPD=90°,∴点P在以BD为直径的圆上,∴点P是这两圆的交点.(i)当点P在如图所示位置时,连接PD,PB,PA,作AH⊥BP,垂足为H,过点A 作AE⊥AP,交BP于点E.∵四边形ABCD是正方形,∴∠ADB=45°,AB=AD=DC=BC=2,∠BAD=90°,∴BD=2.∵DP=1,∴BP= 3.∵∠BPD=∠BAD=90°,∴点A,P,D,B在以BD为直径的圆上,∴∠APB=∠ADB=45°,∴△PAE是等腰直角三角形.又∵△BAD是等腰直角三角形,点B,E,P共线,AH⊥BP,∴由(2)中的结论可得BP=2AH+PD,∴3=2AH+1,∴AH=3-1 2.(ii)当点P在如图所示位置时,连接PD,PB,PA,作AH⊥BP,垂足为H,过点A作AE⊥AP,交PB的延长线于点E.同理可得BP=2AH-PD,∴3=2AH-1,∴AH=3+1 2.综上所述,点A到BP的距离为3-12或3+12.(注:文档可能无法思考全面,请浏览后下载,供参考。
2019年河南省中考真题数学试题(附答案解析)
三、解答题(本大题共8小题,满分75分,解答应写出文字说明、证明过程或演算步骤)
16.先化简,再求值:
,其中
.
17.如图,在△ABC中,BA=BC,∠ABC=90°,以AB为直径的半圆O交AC于点D,点E是 BD
上不与点B,D重合的任意一点,连接AE交BD于点F,连接BE并延长交AC于点C.
⑴求证:△ADF ≌ △BDG ;
∴EO⊥AC,∴EB是AC的垂直平分线,∴AB=BC=3.
在Rt△ABM中,∠AMB=90°,AM=AD-MD=1,
∴BM= AB2 AM 2 32 12 2 2 ,
∴CD= 2 2.故选A.
10.【答案】D
【解析】由A、B两点的坐标可知线段AB的长度和它与x轴的关系,由正方形的性质可知AD=AB, 延长DA交x轴于点M,则DA⊥x轴,Rt△DMO中,MO=3,DM=10,将△OAB和正方形ABCD绕点O每 次顺时针旋转90°,Rt△DMO也同步绕点O每次顺时针旋转90°,点D的落点坐标可由Rt△DMO的旋 转得到。仔细观察图形得到点D坐标的变化规律,每旋转四次完成一个循环,从而可得到第70次旋 转后的坐标。
(A) 46×10-7 (B) 4.6×10-7 (C)4.6×10-6 (D)0.46×10-5
3.如图,AB∥CD,∠B=75°,∠E=27°,则∠D的度数为
(A)45° (B)48° (C)50° (D)58°
4.下列计算正确的是(
)
A. 2a 3a 6a
B. (3a)2 6a2
C. (x y)2 x2 y2
b.七年级成绩在70≤x<80这一组的是: 70 72 74 75 76 76 77 77 77 78 79 c.七、八年级成绩的平均数、中位数如下:
2019年河南省中考真题数学试题(解析版)
⑴求证:△ADF ≌ △BDG ;
⑵填空:
①若AB = 4,且点E是 BD 的中点,则DF的长为
;
②取 AE 的中点H,当∠EAB的度数为
时,四边形OBEH为菱形.
【解析】⑴首先根据在△ABC中,BA=BC,∠ABC=90°,判定△ABC是等腰直角三角形,得 到∠CAB=45°,再根据直径所对的圆周角是直角,得到 △ABD是等腰直角三角形,从而
DA = DB,又因为∠CAE与∠DBG对着同一条弧 DE,得到∠CAE=∠DBG,根据ASA可以判 定△ADF ≌ △BDG.
3.如图,AB∥CD,∠B=75°,∠E=27°,则∠D的度数为
(A)45° (B)48° 【答案】B
(C)50° (D)58°
【解析】如图,设CD和BE的交点为F,
∵AB∥CD,∠B=75°,∴∠B=∠CFE=75°,∵∠CFE=∠D+∠E, ∠E=27°,
∴∠D=∠CFE-∠E=75°-27°=48°.故选B.
影部分的面积为
.
【答案】 3 +π 【解析】本题考查了与圆有关的计算,(圆内半径相等),等腰三角形的性质(等边对等角), 解直角三角形,特殊角三角函数,扇形的面积,不规则图形的转化. 解法1:
1
∵在扇形AOB中,∠AOB=120°,∴OA=OB,所以∠BAO=∠ABO= (180°-120°)÷2=30°,
【答案】C
【解析】本题考查了科学记数法,解题的关键是正确确定a的值以及n的值.
0.0000046是绝对值小于1的数,这类数用科学计数法表示的方法是写成a×10-n(1≤ a <10,n>
0 )的形式,关键是确定-n,确定了n的值,-n的值就确定了.确定方法是:n 的值等于原数 中左起第一个非零数前零的个数(含整数位数上的零).故0.0000046中左起第一个非零数为4, 其左边六个零,即0.0000046=4.6×10-6.答案选C.
河南省中考数学专题复习专题类比探究题训练
专题七 类比探究题类型一 线段数量关系问题(2018·河南)(1)问题发现如图①,在△OAB 和△OCD 中,OA =OB ,OC =OD ,∠AOB=∠COD=40°,连接AC ,BD 交于点M.填空: ①ACBD的值为________; ②∠AMB 的度数为________; (2)类比探究如图②,在△OAB 和△OCD 中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC 交BD 的延长线于点M.请判断ACBD 的值及∠AMB 的度数,并说明理由;(3)拓展延伸在(2)的条件下,将△OCD 绕点O 在平面内旋转,AC ,BD 所在直线交于点M ,若OD =1,OB =7,请直接写出当点C 与点M 重合时AC 的长.【分析】 (1)①证明△COA≌△DOB(SAS),得AC =BD ,比值为1;②由△COA≌△DOB,得∠CAO=∠DBO,根据三角形的内角和定理,得∠AMB=180°-(∠DBO+∠OAB+∠ABD)=180°-140°=40°;(2)根据两边的比相等且夹角相等可得△AOC∽△BOD,则AC BD =OCOD =3,由全等三角形的性质得∠AMB 的度数;(3)正确画出图形,当点C 与点M 重合时,有两种情况:如解图①和②,同理可得△AOC∽△BOD,则∠AMB =90°,ACBD =3,可得AC 的长.【自主解答】解:(1)问题发现①1【解法提示】∵∠AOB=∠COD=40°, ∴∠COA=∠DOB. ∵OC=OD ,OA =OB , ∴△COA≌△DOB(SAS), ∴AC=BD , ∴ACBD=1. ②40°【解法提示】∵△COA≌△DOB, ∴∠CAO=∠DBO. ∵∠AOB=40°, ∴∠OAB+∠ABO=140°,在△AMB 中,∠AMB=180°-(∠CAO+∠OAB+∠ABD)=180°-(∠DBO+∠OAB+∠ABD)=180°-140°=40°. (2)类比探究ACBD=3,∠AMB=90°,理由如下: 在Rt△OCD 中,∠DCO=30°,∠DOC=90°, ∴OD OC =tan 30°=33, 同理,得OB OA =tan 30°=33,∵∠AOB=∠COD=90°, ∴∠AOC=BOD , ∴△AOC∽△BOD, ∴AC BD =OCOD=3,∠CAO=∠DBO. ∴∠AMB=180°-∠CAO-∠OAB-MBA =180°-(∠DAB+∠MBA+∠OBD)=180°-90°=90°. (3)拓展延伸①点C 与点M 重合时,如解图①, 同理得△AOC∽△BOD, ∴∠AMB=90°,ACBD =3,设BD =x ,则AC =3x , 在Rt△COD 中,∵∠OCD=30°,OD =1, ∴CD=2, ∴BC=x -2.在Rt△AOB 中,∠OAB=30°,OB =7. ∴AB=2OB =27,在Rt△AMB 中,由勾股定理,得AC 2+BC 2=AB 2, 即( 3 x)2+(x -2)2=(27)2, 解得x 1=3,x 2=-2(舍去), ∴AC=33;②点C 与点M 重合时,如解图②,同理得:∠AMB=90°,ACBD =3,设BD =x ,则AC =3x ,在Rt△AMB 中,由勾股定理,得AC 2+BC 2=AB 2, 即(3x)2+(x +2)2=(27)2解得x 1=-3,解得x 2=2(舍去). ∴AC=2 3.综上所述,AC 的长为33或2 3.图①图② 例1题解图1.(2016·河南) (1)发现如图①,点A 为线段BC 外一动点,且BC =a ,AB =b.填空:当点A 位于________________时,线段AC 的长取得最大值,且最大值为__________(用含a ,b 的式子表示). (2)应用点A 为线段BC 外一动点,且BC =3,AB =1,如图②所示,分别以AB ,AC 为边,作等边三角形ABD 和等边三角形ACE ,连接CD ,BE.①请找出图中与BE 相等的线段,并说明理由; ②直接写出线段BE 长的最大值. (3)拓展如图③,在平面直角坐标系中,点A 的坐标为(2,0),点B 的坐标为(5,0),点P 为线段AB 外一动点,且PA =2,PM =PB ,∠BPM=90°,请直接写出线段AM 长的最大值及此时点P 的坐标.2.(2015·河南)如图①,在Rt△ABC 中,∠B=90°,BC =2AB =8,点D ,E 分别是边BC ,AC 的中点,连接DE.将△EDC 绕点C 按顺时针方向旋转,记旋转角为α. (1)问题发现①当α=0°时,AE BD =2;②当α=180°时,AE BD =2;(2)拓展探究试判断:当0°≤α<360°时,AEBD 的大小有无变化?请仅就图②的情形给出证明.(3)解决问题当△EDC 旋转至A ,D ,E 三点共线时,直接写出线段BD 的长.3.(2014·河南) (1)问题发现如图①,△ACB 和△DCE 均为等边三角形,点A ,D ,E 在同一直线上,连接BE. 填空:①∠AEB 的度数为__________;②线段AD ,BE 之间的数量关系为______________. (2)拓展探究如图②,△ACB 和△DCE 均为等腰直角三角形,∠ACB=∠DCE=90°,点A ,D ,E 在同一直线上,CM 为△DCE 中DE 边上的高,连接BE ,请判断∠AEB 的度数及线段CM ,AE ,BE 之间的数量关系,并说明理由. (3)解决问题如图③,在正方形ABCD 中,CD =2,若点P 满足PD =1,且∠BPD=90°,请直接写出点A 到BP 的距离.4.(2018·南阳二模)在△ABC中,∠ACB是锐角,点D在射线BC上运动,连接AD,将线段AD绕点A逆时针旋转90°,得到AE,连接EC.(1)操作发现若AB=AC,∠BAC=90°,当D在线段BC上时(不与点B重合),如图①所示,请你直接写出线段CE和BD 的位置关系和数量关系是______________,______________;(2)猜想论证在(1)的条件下,当D在线段BC的延长线上时,如图②所示,请你判断(1)中结论是否成立,并证明你的判断.(3)拓展延伸如图③,若AB≠AC,∠BAC≠90°,点D在线段BC上运动,试探究:当锐角∠ACB等于________度时,线段CE和BD之间的位置关系仍成立(点C,E重合除外)?此时若作DF⊥AD交线段CE于点F,且当AC=32时,请直接写出线段CF的长的最大值是____.5.已知,如图①,△ABC,△AED是两个全等的等腰直角三角形(其顶点B,E重合),∠BAC=∠AED=90°,O为BC的中点,F为AD的中点,连接OF.(1)问题发现①如图①,OFEC=_______;②将△AED 绕点A 逆时针旋转45°,如图②,OFEC =_______;(2)类比延伸将图①中△AED 绕点A 逆时针旋转到如图③所示的位置,请计算出OFEC 的值,并说明理由.(3)拓展探究将图①中△AED 绕点A 逆时针旋转,旋转角为α,0°≤α≤90°,AD =2,△AED 在旋转过程中,存在△ACD 为直角三角形,请直接写出线段CD 的长.类型二 图形面积关系问题(2017·河南)如图①,在Rt△ABC 中,∠A=90°,AB =AC ,点D ,E 分别在边AB ,AC 上,AD =AE ,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点. (1)观察猜想图①中,线段PM 与PN 的数量关系是________,位置关系是________; (2)探究证明把△AD E 绕点A 逆时针方向旋转到图②的位置,连接MN ,BD ,CE ,判断△PMN 的形状,并说明理由; (3)拓展延伸把△ADE 绕A 在平面内自由旋转,若AD =4,AB =10,请直接写出△PMN 面积的最大值.图①图② 例2题图【分析】 (1)利用三角形的中位线定理得出PM =12CE ,PN =12BD ,进而判断出BD =CE ,即可得出结论,再利用三角形的中位线定理得出PM∥CE,继而得出∠DPM=∠DCA,最后用互余即可得出结论;(2)先判断出△ABD≌△ACE,得出BD =CE ,同(1)的方法得出PM =12BD ,PN =12BD ,即可得出PM =PN ,同(1)的方法即可得出结论;(3)先判断出MN 最大时,△PMN 的面积最大,进而求出AN ,AM ,即可得出MN 最大=AM +AN ,最后用面积公式即可得出结论. 【自主解答】解:(1)∵点P ,N 是BC ,CD 的中点, ∴PN∥BD,PN =12BD.∵点P ,M 是CD ,DE 的中点, ∴PM∥CE,PM =12CE.∵AB=AC ,AD =AE , ∴BD =CE , ∴PM=PN. ∵PN∥BD, ∴∠DPN=∠ADC, ∵PM∥CE, ∴∠DPM=∠DCA. ∵∠BAC=90°, ∴∠ADC+∠ACD=90°,∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°,(2)由旋转知,∠BAD=∠CAE, ∵AB=AC ,AD =AE , ∴△ABD≌△ACE(SAS), ∴∠ABD=∠ACE,BD =CE.同(1)的方法,利用三角形的中位线定理,得PN =12BD ,PM =12CE ,∴PM=PN ,∴△PMN 是等腰三角形, 同(1)的方法得,PM∥CE, ∴∠DPM=∠DCE, 同(1)的方法得,PN∥BD, ∴∠PNC=∠DBC.∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD +∠DBC=∠ACB+∠ABC. ∵∠BAC=90°, ∴∠ACB+∠ABC=90°, ∴∠MPN=90°,∴△PMN 是等腰直角三角形,例2题解图(3)如解图,同(2)的方法得,△PMN 是等腰直角三角形, ∴当MN 最大时,△PMN 的面积最大, ∴DE∥BC 且DE 在顶点A 上面, ∴MN 最大=AM +AN , 连接AM ,AN ,在△ADE 中,AD =AE =4,∠DAE=90°,在Rt△ABC 中,AB =AC =10,AN =52, ∴MN 最大=22+52=72,∴S △PMN 最大=12PM 2=12×12MN 2=14×(72)2=492.1.(2013·河南)如图①,将两个完全相同的三角形纸片ABC 和DEC 重合放置,其中∠C=90°,∠B=∠E =30°. (1)操作发现如图②,固定△ABC,使△DEC 绕点C 旋转,当点D 恰好落在AB 边上时,填空: ①线段DE 与AC 的位置关系是______________;②设△BDC 的面积为S 1,△AEC 的面积为S 2,则S 1与S 2的数量关系是______________. (2)猜想论证当△DEC 绕点C 旋转到如图③所示的位置时,小明猜想(1)中S 1与S 2的数量关系仍然成立,并尝试分别作出了△BDC 和△AEC 中BC ,CE 边上的高,请你证明小明的猜想. (3)拓展探究已知∠ABC=60°,点D 是角平分线上一点,BD =CD =4,DE∥AB 交BC 于点E(如图④).若在射线BA 上存在点F ,使S △DCF =S △BDE ,请直接写出相应的BF 的长.2.已知Rt△ABC 中,BC =AC ,∠C=90°,D 为AB 边的中点,∠EDF=90°,将∠EDF 绕点D 旋转,它的两边分别交AC ,CB(或它们的延长线)于E ,F.当∠EDF 绕点D 旋转到DE⊥AC 于E 时,如图①所示,试证明S △DEF +S △CEF =12S △ABC .(1)当∠EDF 绕点D 旋转到DE 和AC 不垂直时,如图②所示,上述结论是否成立?若成立,请说明理由;若不成立,试说明理由.(2)直接写出图③中,S△DEF,S△CEF与S△ABC之间的数量关系.3.(2018·郑州模拟)如图①所示,将两个正方形ABCD和正方形CGFE如图所示放置,连接DE,BG. (1)图中∠DCE+∠BCG=__________°;设△DCE的面积为S1,△BCG的面积为S2,则S1与S2的数量关系为______________;猜想论证:(2)如图②所示,将矩形ABCD绕点C按顺时针方向旋转后得到矩形FECG,连接DE,BG,设△DCE的面积为S1,△BCG的面积为S2,猜想S1和S2的数量关系,并加以证明;(3)如图③所示,在△ABC中,AB=AC=10 cm,∠B=30°,把△ABC沿AC翻折得到△AEC,过点A作AD 平行CE交BC于点D,在线段CE上存在点P,使△ABP的面积等于△ACD的面积,请写出CP的长.4.(2018·驻马店一模)如图①,△ABC与△CDE都是等腰直角三角形,直角边AC,CD在同一条直线上,点M,N分别是斜边AB,DE的中点,点P为AD的中点,连接AE,BD,PM,PN,MN.(1)观察猜想图①中,PM与PN的数量关系是______________,位置关系是______________;(2)探究证明将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP,BD分别交于点G,H,判断△PMN的形状,并说明理由;(3)拓展延伸把△CDE绕点C任意旋转,若AC=4,CD=2,请直接写出△PMN面积的最大值.参考答案类型一 针对训练1.解:(1)∵点A 为线段BC 外一动点,且BC =a ,AB =b ,∴当点A 位于CB 的延长线上时,线段AC 的长取得最大值,且最大值为BC +AB =a +b. (2)①CD=BE ,理由:∵△ABD 与△ACE 是等边三角形, ∴AD=AB ,AC =AE ,∠BAD=∠CAE=60°, ∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB. 在△CAD 和△EAB 中,⎩⎪⎨⎪⎧AD =AB ∠CAD=∠EAB AC =AE ,∴△CAD≌△EAB,∴CD=BE.②∵线段BE 长的最大值等于线段CD 的最大值,由(1)知,当线段CD 的长取得最大值时,点D 在CB 的延长线上, ∴线段BE 长的最大值为BD +BC =AB +BC =4;(3)∵将△APM 绕着点P 顺时针旋转90°得到△PBN,连接AN ,如解图①, 则△APN 是等腰直角三角形, ∴PN=PA =2,BN =AM.∵点A 的坐标为(2,0),点B 的坐标为(5,0), ∴OA=2,OB =5,∴AB=3,∴线段AM长的最大值等于线段BN长的最大值,∴当点N在线段BA的延长线时,线段BN取得最大值,最大值为AB+AN.∵AN=2AP=22,∴线段AM的长最大值为22+3.如解图②,过点P作PE⊥x轴于点E.∵△APN是等腰直角三角形,∴PE=AE=2,∴OE=BO-AB-AE=5-3-2=2-2,∴P(2-2,2).图①图②第1题解图2.解:(1)①当α=0°时,∵在Rt△ABC中,∠B=90°,∴AC=AB2+BC2=(8÷2)2+82=4 5.∵点D、E分别是边BC、AC的中点,∴AE=45÷2=25,BD=8÷2=4,∴AEBD=254=52.②如解图①,当α=180°时,得可得AB∥DE,∵ACAE=BCBD,∴AEBD=ACBC=458=52.(2)当0°≤α≤360°时,AEBD的大小没有变化.∵∠ECD=∠ACB, ∴∠ECA=∠DCB. 又∵EC DC =AC BC =52,∴△ECA∽△DCB, ∴AE BD =EC DC =52.图①图②图③ 第2题解图(3)①如解图②,∵AC=45,CD =4,CD⊥AD,∴AD=AC 2-CD 2=(45)2-42=80-16=8. ∵AD=BC ,AB =DC ,∠B=90°, ∴四边形ABCD 是矩形, ∴BD=AC =4 5.③如解图③,连接BD ,过点D 作AC 的垂线交AC 于点Q ,过点B 作AC 的垂线交AC 于点P , ∵AC=45,CD =4,CD⊥AD,∴A D =AC 2-CD 2=(45)2-42=80-16=8, ∵点D 、E 分别是边BC 、AC 的中点, ∴DE=12AB =12×(8÷2)=12×4=2,∴AE=AD -DE =8-2=6, 由(2),可得AE BD =52,∴BD=652=1255.综上所述,BD 的长为45或1255. 3.解:(1)∵△ACB 和△DCE 均为等边三角形, ∴CA=CB ,CD =CE ,∠ACB=∠DCE=60°, ∴∠ACD=∠BCE. 在△ACD 和△BCE 中, ⎩⎪⎨⎪⎧AC =BC ∠ACD=∠BCE CD =CE, ∴△ACD≌△BCE(SAS),∴∠ADC=∠BEC. ∵△DCE 为等边三角形,∴∠CDE=∠CED=60°. ∵点A ,D ,E 在同一直线上,∴∠ADC=120°, ∴∠BEC=120°,∴∠AEB=∠BEC-∠CED=60°. ②∵△ACD≌△BCE,∴AD=BE. (2)∠AEB=90°,AE =BE +2CM. 理由如下:∵△ACB 和△DCE 均为等腰直角三角形, ∴CA=CB ,CD =CE ,∠ACB=∠DCE=90°. ∴∠ACD=∠BCE. 在△ACD 和△BCE 中, ⎩⎪⎨⎪⎧CA =CB ∠ACD=∠BCE CD =CE, ∴△ACD≌△BCE(SAS), ∴AD=BE ,∠ADC=∠BEC.∵△DCE 为等腰直角三角形,∴∠CD E =∠CED=45°. ∵点A ,D ,E 在同一直线上, ∴∠ADC=135°,∴∠BEC=135°, ∴∠AEB=∠BEC-∠CED=90°. ∵CD=CE ,CM⊥DE,∴DM=ME. ∵∠DCE=90°,∴DM=ME =CM , ∴AE=AD +DE =BE +2CM.(3)∵PD=1,∴点P 在以点D 为圆心,1为半径的圆上.∵∠BPD=90°,∴点P在以BD为直径的圆上,∴点P是这两圆的交点.①当点P在如解图①所示位置时,连接PD,PB,PA,作AH⊥BP,垂足为H,过点A作AE⊥AP,交BP于点E.∵四边形ABCD是正方形,∴∠ADB=45°,AB=AD=DC=BC=2,∠BAD=90°,∴BD=2.∵DP=1,∴BP= 3.∵∠BPD=∠BAD=90°,∴点A、P、D、B在以BD为直径的圆上,∴∠APB=∠ADB=45°.∴△PAE是等腰直角三角形.又∵△BAD是等腰直角三角形,点B,E,P共线,AH⊥BP,∴由(2)中的结论可得:BP=2AH+PD,∴3=2AH+1,∴AH=3-1 2;②当点P在如解图②所示位置时,连接PD、PB、PA、作AH⊥BP,垂足为H,过点A作AE⊥AP,交PB的延长线于点E,同理可得:BP=2AH-PD,∴3=2AH-1,∴AH=3+1 2.综上所述,点A到BP的距离为3-12或3+12.图①图② 第3题解图4.解:(1)①∵AB=AC ,∠BAC=90°, 线段AD 绕点A 逆时针旋转90°得到AE , ∴AD=AE ,∠BAD=∠CAE, ∴△BAD≌△CAE, ∴CE=BD ,∠ACE =∠B, ∴∠BCE=∠BCA+∠ACE=90°,∴线段CE ,BD 之间的位置关系和数量关系为CE =BD ,CE⊥BD; (2)(1)中的结论仍然成立.证明如下: 如解图①,∵线段AD 绕点A 逆时针旋转90°得到AE , ∴AE=AD ,∠DAE=90°. ∵AB=AC ,∠BAC=90°, ∴∠CAE=∠BAD, ∴△ACE≌△ABD, ∴CE=BD ,∠ACE=∠B, ∴∠BCE=90°,∴线段CE ,BD 之间的位置关系和数量关系为CE =BD ,CE⊥BD; (3)45°;34.过A 作AM⊥BC 于M ,过点E 作EN⊥MA 交MA 的延长线于N ,如解图②. ∵线段AD 绕点A 逆时针旋转90°得到AE , ∴∠DAE=90°,AD =AE ,∴∠NAE=∠ADM,易证得Rt△AMD≌Rt△ENA, ∴NE=AM.∵CE⊥BD,即CE⊥MC,∴∠MCE=90°, ∴四边形MCEN 为矩形, ∴NE=MC ,∴AM=MC , ∴∠ACB=45°. ∵四边形MCEN 为矩形, ∴Rt△AMD∽Rt△DCF, ∴MD CF =AMDC,设DC =x , ∵在Rt△AMC 中,∠ACB=45°,AC =32,∴AM=CM =3,MD =3-x ,∴3-x CF =3x ,∴CF=-13x 2+x =-13(x -32)2+34,∴当x =32时,CF 有最大值,最大值为34.故答案为45°,34;图①图② 第4题解图5.解:(1)①∵△A BC ,△AED 是两个全等的等腰直角三角形, ∴AD=BC.∵O 为BC 的中点,F 为AD 的中点, ∴AF=OC.∵∠BAC=∠AED=90°,AB =AC ,AE =DE , ∴∠DAE=∠CBA=45°, ∴AD∥BC,∴四边形AFOC 是平行四边形, ∴OF=AC =22EC ,∴OF EC =22; 故答案:22; ②∵AO=22AC ,∠BAO=∠CAO=45°,∠DAE=45°, ∴∠DAE=∠CAO. ∵AE=AC , ∴AF=AO , ∴AF AE =AO AC,∴△AFO∽△AEC, ∴OF EC =AO AC =22; 故答案:22. (2)OF =22EC. 理由:在等腰直角△ADE 中,F 为AD 的中点, ∴AF=12AD =22AE.在等腰直角△ABC 中,O 为BC 的中点, 如解图①,连接AO , ∴AO=22AC ,∠BAO=∠CAO=45°. ∴∠DAE=45°,∴∠DAE=∠CAO,即∠DAO=∠CAE. ∵AE=AC , ∴AF=AO , ∴AF AE =AO AC, ∴△AFO∽△AEC, ∴OF EC =AO AC =22; (3)∵△ABC 和△AED 是两个全等的等腰直角三角形, ∴AD=BC =2, ∴ED=AE =AB =AC =1,当△ACD 为直角三角形时,分两种情况:图①图②图③ 第5题解图①当AD 与AB 重合时,如解图②,连接CD. 当△ACD 为直角三角形时,AD⊥AC, 即将△ADE 绕点A 逆时针旋转45°. ∵AD=2,AC =1,∴由勾股定理可得CD =(2)2+12=3; ②当AE 与AC 重合时,如解图③, 当△ACD 为直角三角形时,AC⊥CD,即将△ADE 绕点A 逆时针旋转90°,此时CD =AC =1. 综上所述,CD 的长为3或1. 类型二 针对训练1.解:(1)①△DEC 绕点C 旋转到点D 恰好落在AB 边上, ∴AC=CD.∵∠BAC=90°-∠B=90°-30°=60°. ∴△ACD 是等边三角形, ∴∠ACD=60°,又∵∠CDE=∠BAC=60°, ∴∠ACD=∠CDE, ∴DE∥AC;②∵∠B=30°,∠C=90°, ∴CD=AC =12AB ,∴BD=AD =AC ,根据等边三角形的性质,△ACD 的边AC ,AD 上的高相等,∴△BDC 的面积和△AEC 的面积相等(等底等高的三角形的面积相等),即S 1=S 2; (2)∵△DEC 是由△ABC 绕点C 旋转得到, ∴BC=CE ,AC =CD ,∠DCE=∠ACB=90°, ∵∠ACN+∠ACE=180°, ∴∠ACN=∠DCM.在△ACN 和△DCM 中,⎩⎪⎨⎪⎧∠ACN=∠DCM,∠N=∠CMD=90°,AC =CD∴△ACN≌△DCM(AAS), ∴AN=DM ,∴△BDC 的面积和△AEC 的面积相等(等底等高的三角形的面积相等),即S 1=S 2;第1题解图(3)如解图,过点D 作DF 1∥BE 交BA 于点F 1,易求得四边形BEDF 1是菱形,∴BE=DF 1,且BE ,DF 1边上的高相等,此时S△DCF 1=S △BDE ; 过点D 作DF 2⊥BD.∵∠ABC=60°,F 1D∥BE 交BA 于点F 2, ∴∠F 2F 1D =∠ABC=60°.∵BF 1=DF 1,∠F 1BD =12∠ABC=30°,∠F 2DB =90°,∴∠F 1DF 2=∠ABC=60° ∴△DF 1F 2是等边三角形, ∴DF 1=DF 2.∵BD=CD ,∠ABC=60°,点D 是角平分线上一点, ∴DBC=∠DCB=12×60°=30°,∴∠CDF 1=180°-∠BCD=180°-30°=150°, ∠CDF 2=360°-150°-60°=150°, ∴∠CDF 1=∠CDF 2. 在△CDF 1和△CDF 2中, ⎩⎪⎨⎪⎧DF 1=DF 2∠CDF 1=∠CDF 2CD =CD, ∴△CDF 1≌△CDF 2(SAS),∴点F 2也是所求的点. ∵∠ABC=60°,点D 是角平分线上一点,DE∥AB, ∴∠DBC=∠BDE=∠ABD=12×60°=30°.又∵BD=4,∴BE=12×4÷cos 30°=2÷32=433,∴BF 1=433,BF 2=BF 1+F 1F 2=433+433=833.故BF 的长为433或833.2.解:当∠EDF 绕D 点旋转到DE⊥AC 时,四边形CEDF 是正方形;设△ABC 的边长AC =BC =a ,则正方形CEDF 的边长为12a ,∴S △ABC =12a 2,S 正方形CEDF =(12a)2=14a 2,即S △DEF +S △CEF =12S △ABC ;(1)上述结论成立;理由如下: 连接CD ,如解图①所示.∵AC=BC ,∠ACB=90°,D 为AB 中点,∴∠B=45°,∠DCE=12∠ACB=45°,CD⊥AB,CD =12AB =BD ,∴∠DCE=∠B,∠CDB=90° ∵∠EDF=90°, ∴∠1=∠2, 在△CDE 和△BDF 中, ⎩⎪⎨⎪⎧∠1=∠2CD =BD∠DCE=∠B, ∴△CDE≌△BDF(ASA),∴S △DEF +S △CEF =S △ADE +S △BDF =12S △ABC ;图①图② 第2题解图(2)S △DEF -S △CEF =12S △ABC ;理由如下:连接CD ,如解图②所示,同(1)得:△DEC≌△DFB,∠DCE=∠DBF =135°, ∴S △DEF =S 五边形DBFEC , S △CFE +S △DBC , =S △CFE +12S △ABC ,∴S △DEF -S △CFE =12S △ABC .∴S △DEF 、S △CEF 、S △ABC 的关系是S △DEF -S △CEF =12S △ABC .3.解:(1)如解图①中,∵四边形ABCD 、EFGC 都是正方形, ∴∠BCD=∠ECG=90°.∵∠BCG+∠BCD+∠DCE+∠ECG=360°, ∴∠BCG+∠ECD=180°.图①图②图③ 第3题解图如解图①,过点E 作EM⊥DC 于点M ,过点G 作GN⊥BN 交BN 的延长线于点N , ∴∠EMC=∠N=90°.∵四边形ABCD 和四边形ECGF 均为正方形, ∴∠BCD=∠DCN=∠ECG=90°,CB =CD ,CE =CG ,∴∠1=90°-∠2,∠3=90°-∠2, ∴∠1=∠3. 在△CME 和△CNG 中, ⎩⎪⎨⎪⎧∠EMC=∠GNC ∠1=∠3EC =CG, ∴△CME≌△CNG(ASA), ∴EM=GN.又∵S 1=12CD·EM,S 2=12CB·GN,∴S 1=S 2;故答案为180°,S 1=S 2; (2)猜想:S 1=S 2,证明:如解图②,过点E 作EM⊥DC 于点M ,过点B 作BN⊥GC 交GC 的延长线于点N , ∴∠EMC=∠N=90°.∵矩形CGFE 由矩形ABCD 旋转得到的, ∴CE=CB ,CG =CD ,∵∠ECG=∠ECN=∠BCD=90°,∴∠1=90°-∠2,∠3=90°-∠2,∴∠1=∠3. 在△CME 和△CNB 中, ⎩⎪⎨⎪⎧∠EMC=∠BNC ∠1=∠3EC =CB, ∴△CME≌△CNB(AAS). ∴EM=BN.又∵S 1=12CD·EM,S 2=12CG ·BN ,∴S 1=S 2;(3)如解图③,作DM⊥AC 于M ,延长BA ,交EC 于N , ∵AB=AC =10 cm ,∠B=30°, ∴∠ACB=∠ABC=30°, ∴∠BAC=120°,根据翻折的性质,得∠ACE=∠ACB=30°, ∵AD∥CE,∴∠DAC=∠ACE=30°, ∴∠BAD=90°,DM =12AD ,∴BN⊥EC.∵AD=tan∠ABD·AB,AB =10 cm , ∴AD=tan 30°×10=103 3 (cm),∴DM=12×1033=533(cm).∵S △ABP =12AB·PN,S △ADC =12AC·DM,S △ABP =S △ADC ,AB =AC ,∴PN=DM =533.在Rt△ANC 中,∠ACN=30°,AC =10 (cm), ∴NC=cos∠ACN·AC=cos 30°×10=53(cm). ∵在EC 上到N 的距离等于533的点有两个,∴P′C=103 3 cm ,P ″C =203 3 cm.∴CP 的长为103 3 cm 或203 3 cm.4.解:(1)PM =PN ,PM⊥PN,理由如下: 如解图①,延长AE 交BD 于O , ∵△ACB 和△ECD 是等腰直角三角形, ∴AC=BC ,EC =CD ,∠ACB=∠ECD=90°. 在△ACE 和△BCD 中, ⎩⎪⎨⎪⎧AC =BC ,∠ACE=∠BCD=90°,CE =CD ,∴△ACE≌△BCD(SAS), ∴AE=BD ,∠EAC=∠CBD,∵∠EAC+∠AEC=90°,∠AEC=∠BEO, ∴∠CBD+∠BEO=90°, ∴∠BOE =90°,即AE⊥BD,∵点M 、N 分别是斜边AB 、DE 的中点,点P 为AD 的中点, ∴PM=12BD ,PN =12AE ,∴PM=PN.∵PM∥BD,PN∥AE,AE⊥BD,∴∠NPD=∠EAC,∠MPA=∠BDC,∠EAC+∠BDC=90°, ∴∠MPA+∠NPC=90°,∴∠MPN=90°, 即PM⊥PN.图①图② 第4题解图(2)△PMN 为等腰直角三角形,理由如下: 如解图②,设AE 交BC 于点O. ∵△ACB 和△ECD 是等腰直角三角形, ∴AC=BC ,EC =CD ,∠AC B =∠ECD=90°, ∴∠ACB+∠BCE=∠ECD+∠BCE, ∴∠ACE=∠BCD, ∴△ACE≌△BCD, ∴AE=BD ,∠CAE =∠CBD. 又∵∠AOC=∠BOE,∠CAE=∠CBD, ∴∠BHO=∠ACO=90°.∵点P ,M ,N 分别为AD ,AB ,DE 的中点, ∴PM=12BD ,PM∥BD,PN =12AE ,PN∥AE,∴PM=PN ,∴∠MGE+∠BHA=180°, ∴∠MGE=90°, ∴∠MPN=90°,∴PM⊥PN,即△PMN 为等腰直角三角形.(3)由(2)可知△PMN 是等腰直角三角形,PM =12BD ,∴当BD 的值最大时,PM 的值最大,△PMN 的面积最大, ∴当B ,C ,D 共线时,BD 的最大值为BC +CD =6, ∴PM=PN =3,。
河南省中考数学专题复习专题类比探究题训练
从此刻开始,不留余力地努力吧,最差的结果,也可是是大器晚成专题七类比研究题种类一线段数目关系问题( 2018·河南 )(1) 问题发现如图①,在△ OAB 和△ OCD中, OA= OB, OC= OD,∠ AOB=∠ COD=40°,连结AC, BD交于点 M.填空:AC①的值为 ________;BD②∠ AMB的度数为 ________;(2) 类比研究如图②,在△ OAB 和△ OCD中,∠ AOB=∠ COD=90°,∠ OAB=∠ OCD=30°,连结AC交 BD的延长线于点ACM.请判断的值及∠ AMB的度数,并说明原因;BD(3)拓展延长在 (2) 的条件下,将△ OCD 绕点 O在平面内旋转, AC, BD所在直线交于点 M,若 OD=1, OB= 7,请直接写出当点 C 与点 M重合时 AC的长.【剖析】 (1) ①证明△ COA≌△ DOB(SAS),得 AC= BD,比值为1;②由△ COA≌△ DOB,得∠ CAO=∠ DBO,依据三角形的内角和定理,得∠AMB=180°- ( ∠DBO+∠ OAB+∠ABD)=180°- 140°= 40°;(2) 依据两边的比相等且夹角相等可得△ AOC∽△ BOD,则AC OC3,由全等三角形的性质得∠ AMB 的度==BD OD数;(3)正确画出图形,当点 C与点 M重合时,有两种状况:如解图①和②,同理可得△ AOC∽△ BOD,则∠ AMBAC=90°,= 3,可得 AC的长.解: (1) 问题发现①1【解法提示】∵∠ AOB=∠ COD=40°,∴∠ COA=∠ DOB.∵OC= OD,OA= OB,∴△ COA≌△ DOB(SAS),∴AC= BD,AC∴= 1.BD②40°【解法提示】∵△ COA≌△ DOB,∴∠ CAO=∠ DBO.∵∠ AOB=40°,∴∠ OAB+∠ ABO=140°,在△ AMB 中,∠ AMB=180°- ( ∠CAO+∠ OAB+∠ ABD)=180°- ( ∠DBO+∠ OAB+∠ ABD)=180°- 140°=40°.(2)类比研究AC=3,∠ AMB=90°,原因以下:BD在 Rt△OCD中,∠ DCO=30°,∠ DOC=90°,OD 3 ∴=tan 30 °=3 ,OC同理,得OB 3 =tan 30 °=,OA 3∵∠ AOB=∠ COD=90°,∴∠ AOC= BOD,∴△ AOC∽△ BOD,AC OC∴==3,∠ CAO=∠ DBO.BD OD∴∠ AMB=180°-∠ CAO-∠ OAB-M BA=180°- ( ∠DAB+∠ MBA+∠ OBD)=180°- 90°= 90°.(3)拓展延长①点 C 与点 M重合时,如解图①,同理得△ AOC∽△ BOD,AC∴∠ AMB=90°,=3,BD设 BD= x,则 AC= 3x,∵∠ OCD=30°, OD= 1,∴CD= 2,∴BC= x- 2.在 Rt△AOB中,∠ OAB=30°, OB= 7. ∴AB= 2OB= 2 7,在 Rt△AMB中,由勾股定理,得2 2 2,AC+ BC=AB即 ( 3 x) 2+ (x - 2) 2=(2 7) 2,解得 x1= 3,x2=- 2( 舍去 ) ,∴AC= 3 3;②点 C 与点 M重合时,如解图②,同理得:∠AMB=90°,AC3,=BD设 BD= x,则 AC= 3x,在 Rt△AMB中,由勾股定理,得2 2 2,AC+ BC=AB即 ( 3x) 2+(x + 2) 2= (2 7) 2解得 x1=- 3,解得 x2=2( 舍去 ) .∴AC= 2 3.综上所述, AC的长为 3 3 或 2 3.图①图②例 1题解图1.( 2016·河南 )(1) 发现如图①,点 A 为线段 BC外一动点,且BC= a,AB= b.填空:当点 A 位于 ________________ 时,线段AC的长获得最大值,且最大值为__________( 用含 a, b 的式子表示 ) .点 A 为线段 BC外一动点,且 BC= 3, AB= 1,如图②所示,分别以 AB, AC为边,作等边三角形 ABD和等边三角形 ACE,连结 CD, BE.①请找出图中与BE相等的线段,并说明原因;②直接写出线段BE长的最大值.(3)拓展如图③,在平面直角坐标系中,点 A 的坐标为 (2 , 0) ,点 B 的坐标为 (5 , 0) ,点 P 为线段 AB 外一动点,且 PA= 2,PM= PB,∠ BPM=90°,请直接写出线段 AM长的最大值及此时点 P 的坐标.2.( 2015·河南 ) 如图①,在Rt△ABC中,∠ B=90°, BC= 2AB= 8,点 D, E 分别是边BC, AC的中点,连接 DE.将△ EDC绕点 C 按顺时针方向旋转,记旋转角为α.(1)问题发现AE 5①当α= 0°时,BD= __ 2 __;AE 5②当α= 180°时,=____;BD 2AE试判断:当0°≤α <360°时,的大小有无变化?请仅就图②的情况给出证明.BD(3)解决问题当△ EDC旋转至 A, D, E 三点共线时,直接写出线段BD的长.3.( 2014·河南 )(1)问题发现如图①,△ ACB 和△ DCE均为等边三角形,点A, D, E 在同向来线上,连结BE.填空:①∠ AEB 的度数为 __________;②线段 AD, BE之间的数目关系为______________.(2)拓展研究如图②,△ ACB 和△ DCE 均为等腰直角三角形,∠ACB=∠ DCE=90°,点A, D, E 在同向来线上,CM 为△DCE中 DE边上的高,连结BE,请判断∠ AEB 的度数及线段CM, AE, BE之间的数目关系,并说明原因.(3)解决问题如图③,在正方形ABCD中, CD=2,若点 P 知足 PD= 1,且∠ BPD=90°,请直接写出点A到 BP的距离.4.( 2018·南阳二模 ) 在△ ABC中,∠ ACB是锐角,点 D 在射线 BC上运动,连结 AD,将线段 AD绕点 A 逆时针旋转 90°,获得 AE,连结 EC.(1) 操作发现若 AB= AC,∠ BAC=90°,当D在线段BC上时 ( 不与点 B 重合 ) ,如图①所示,请你直接写出线段CE和 BD 的地点关系和数目关系是______________, ______________;(2) 猜想论证在 (1) 的条件下,当 D 在线段BC的延长线上时,如图②所示,请你判断(1) 中结论能否建立,并证明你的判断.(3)拓展延长如图③,若AB≠AC,∠ BAC≠90°,点D在线段 BC上运动,尝试究:当锐角∠ACB 等于 ________度时,线段 CE和 BD之间的地点关系仍建立 ( 点 C,E 重合除外 ) ?此时若作 DF⊥AD 交线段 CE于点 F,且当 AC=3 2时,请直接写出线段 CF 的长的最大值是 ____.5.已知,如图①,△ ABC,△ AED是两个全等的等腰直角三角形( 其极点B, E 重合 ) ,∠ BAC=∠ AED=90°, O为 BC的中点, F 为 AD的中点,连结OF.OF①如图①,= _______;ECOF②将△ AED绕点 A 逆时针旋转45°,如图②,=_______;EC(2)类比延长OF将图①中△ AED绕点 A 逆时针旋转到如图③所示的地点,请计算出的值,并说明原因.EC(3) 拓展研究将图①中△ AED 绕点 A 逆时针旋转,旋转角为α,0°≤α≤ 90°,AD=2,△ AED 在旋转过程中,存在△ACD为直角三角形,请直接写出线段CD的长.种类二图形面积关系问题( 2017·河南 ) 如图①,在 Rt△ABC中,∠ A=90°, AB= AC,点 D, E 分别在边 AB,AC上, AD=AE,连结 DC,点 M, P,N 分别为 DE, DC, BC的中点.(1)察看猜想图①中,线段PM与 PN的数目关系是________,地点关系是 ________;(2)研究证明把△ ADE 绕点 A 逆时针方向旋转到图②的地点,连结MN, BD, CE,判断△ PMN的形状,并说明原因;(3)拓展延长把△ ADE绕 A 在平面内自由旋转,若AD= 4, AB=10,请直接写出△ PMN 面积的最大值.图①图②例2题图1 1【剖析】(1)利用三角形的中位线定理得出PM=2CE, PN=2BD,从而判断出BD= CE,即可得出结论,再利用三角形的中位线定理得出PM∥CE,既而得出∠ DPM=∠ DCA,最后用互余即可得出结论;1 1(2) 先判断出△ ABD≌△ ACE,得出 BD= CE,同 (1) 的方法得出 PM=2BD, PN=2BD,即可得出PM= PN,同(1)的方法即可得出结论;(3) 先判断出MN最大时,△ PMN 的面积最大,从而求出AN,AM,即可得出MN最大= AM+ AN,最后用面积公式即可得出结论.【自主解答】解: (1) ∵点 P, N是 BC, CD的中点,1∴PN∥BD, PN= BD.2∵点 P, M是 CD, DE的中点,1∴PM∥CE, PM=2CE.∵AB= AC,AD= AE,∴BD= CE,∴P M= PN.∵PN∥BD,∴∠ DPN=∠ ADC,∵PM∥CE,∴∠ DPM=∠ DCA.∵∠ BAC=90°,∴∠ ADC+∠ ACD=90°,(2)由旋转知,∠ BAD=∠ CAE,∵AB= AC,AD= AE,∴△ABD≌△ ACE(SAS),∴∠ABD=∠ ACE, BD= CE.1同 (1) 的方法,利用三角形的中位线定理,得PN=2BD,1PM=2CE,∴PM= PN,∴△ PMN是等腰三角形,同 (1) 的方法得, PM∥CE,∴∠ DPM=∠ DCE,同 (1) 的方法得, PN∥BD,∴∠ PNC=∠ DBC.∵∠ DPN=∠ DCB+∠ PNC=∠ DCB+∠ DBC,∴∠ MPN=∠ DPM+∠ DPN=∠ DCE+∠ DCB+∠ DBC=∠ BCE+∠ DBC=∠ ACB+∠ ACE+∠ DBC =∠ ACB+∠ ABD +∠ DBC=∠ ACB+∠ ABC.∵∠ BAC=90°,∴∠ ACB+∠ ABC=90°,∴∠ MPN=90°,∴△ PMN是等腰直角三角形,例 2题解图(3)如解图,同 (2) 的方法得,△ PMN 是等腰直角三角形,∴当 MN最大时,△ PMN的面积最大,∴DE∥BC 且 DE在极点 A 上边,∴MN最大= AM+ AN,连结 AM, AN,在△ ADE中, AD= AE= 4,∠ DAE=90°,在 Rt △ABC 中, AB =AC = 10, AN = 5 2,∴MN =22+5 2=7 2,最大121 12 1 2 49 ∴S △PMN 最大 =2PM = 2×2MN = 4×(7 2) = 2 .1.( 2013· 河南 ) 如图①,将两个完整同样的三角形纸片ABC 和 DEC 重合搁置,此中∠ C =90°,∠ B =∠E= 30°.(1) 操作发现如图②,固定△ ABC ,使△ DEC 绕点 C 旋转,当点 D 恰巧落在 AB 边上时,填空:①线段 DE 与 AC 的地点关系是 ______________;②设△ BDC 的面积为 S 1,△ AEC 的面积为 S 2,则 S 1 与 S 2 的数目关系是 ______________ .(2) 猜想论证当△ DEC 绕点 C 旋转到如图③所示的地点时,小明猜想(1) 中 S 1 与 S 2 的数目关系仍旧建立,并试试分别作出了△ BDC 和△ AEC 中 BC , CE 边上的高,请你证明小明的猜想.(3) 拓展研究已知∠ ABC =60°,点 D 是角均分线上一点, BD = CD = 4,DE ∥AB 交 BC 于点 E( 如图④ ) .若在射线 BA 上存在点 F ,使 S △DCF = S △BDE ,请直接写出相应的 BF 的长.2.已知 Rt△ABC中, BC=AC,∠ C=90°, D 为 AB边的中点,∠ EDF=90°,将∠ EDF 绕点 D 旋转,它的两边分别交 AC, CB(或它们的延长线 ) 于 E, F. 当∠ EDF 绕点 D旋转到 DE⊥AC于 E 时,如图①所示,试证明1S△DEF+ S△CEF=2S△ABC.不建立,试说明原因.(2)直接写出图③中, S△DEF, S△CEF与 S△ABC之间的数目关系.3.( 2018·郑州模拟 ) 如图①所示,将两个正方形ABCD和正方形 CGFE以下图搁置,连结DE, BG.(1)图中∠ DCE+∠ BCG=__________°;设△ DCE 的面积为 S1,△ BCG的面积为 S2,则 S1与 S2的数目关系为______________ ;猜想论证:(2) 如图②所示,将矩形ABCD绕点 C按顺时针方向旋转后获得矩形FECG,连结 DE, BG,设△ DCE的面积为S1,△ BCG的面积为S2,猜想 S1和 S2的数目关系,并加以证明;(3) 如图③所示,在△ ABC 中, AB=AC= 10 cm,∠ B=30°,把△ ABC 沿 AC 翻折获得△ AEC,过点 A 作 AD 平行 CE交 BC于点 D,在线段CE上存在点P,使△ ABP 的面积等于△ ACD 的面积,请写出CP的长.4.( 2018·驻马店一模 ) 如图①,△ ABC 与△ CDE都是等腰直角三角形,直角边AC, CD在同一条直线上,点 M, N 分别是斜边 AB, DE的中点,点 P 为 AD的中点,连结 AE,BD, PM,PN, MN.(1) 察看猜想图①中, PM与 PN的数目关系是 ______________ ,地点关系是 ______________;(2)研究证明将图①中的△ CDE 绕着点 C 顺时针旋转α(0°<α<90°),获得图②,AE与 MP,BD 分别交于点G, H,判断△ PMN的形状,并说明原因;(3)拓展延长把△ CDE绕点 C随意旋转,若AC= 4, CD= 2,请直接写出△ PMN 面积的最大值.参照答案种类一针对训练1.解: (1) ∵点 A 为线段 BC外一动点,且BC=a, AB=b,∴当点 A 位于 CB的延长线上时,线段AC的长获得最大值,且最大值为BC+AB= a+b.(2) ①CD= BE,原因:∵△ ABD 与△ ACE是等边三角形,∴AD= AB,AC= AE,∠ BAD=∠ CAE=60°,∴∠ BAD+∠ BAC=∠ CAE+∠ BAC,即∠ CAD=∠ EAB.AD= AB在△ CAD和△ EAB中,∠CAD=∠ EAB,AC= AE∴△ CAD≌△ EAB,∴ CD= BE.②∵线段 BE长的最大值等于线段CD的最大值,由 (1) 知,当线段 CD的长获得最大值时,点D 在 CB的延长线上,∴线段 BE长的最大值为BD+BC= AB+BC= 4;(3)∵将△ APM绕着点 P 顺时针旋转 90°获得△ PBN,连结 AN,如解图①,则△ APN是等腰直角三角形,∴PN= PA=2, BN= AM.∵点 A 的坐标为 (2 ,0) ,点 B 的坐标为 (5 , 0) ,∴OA= 2, OB= 5,∴ AB= 3,∴线段 AM 长的最大值等于线段 BN 长的最大值,∴当点 N 在线段 BA 的延长线时,线段 BN 获得最大值,最大值为 AB + AN.∵AN = 2AP = 2 2,∴线段 AM 的长最大值为 2 2+ 3.如解图②,过点 P 作 PE ⊥x 轴于点 E.∵△ APN 是等腰直角三角形,∴PE = AE = 2,∴OE = BO -AB - AE =5- 3-2= 2- 2,∴P(2- 2, 2) .图①图②第 1题解图2.解: (1) ①当 α= 0°时,∵在 Rt △ABC 中,∠ B =90°,2 2 2 2∴AC = AB + BC = (8÷2) + 8 =4 5.∵点 D 、 E 分别是边 BC 、 AC 的中点,∴AE = 4 5÷2= 2 5, BD =8÷2= 4,AE 2 5 5 ∴ =4 = . BD 2②如解图①,当 α= 180°时,得可得 AB ∥DE ,∵ AC BC = ,AE BD∴ AE AC 4 5 5= = 8 = 2 .BD BCAE∵∠ ECD=∠ ACB,∴∠ ECA=∠ DCB.EC AC 5又∵==,DCBC 2∴△ ECA∽△ DCB,AE EC 5∴==.BD DC 2图①图②图③第 2题解图(3)①如解图②,∵AC= 45, CD= 4,CD⊥AD,2 2 2 2∴AD= AC- CD=( 4 5)- 4 = 80- 16= 8.∵AD= BC,AB= DC,∠ B=90°,∴四边形 ABCD是矩形,∴BD= AC=4 5.③如解图③,连结BD,过点 D 作 AC的垂线交 AC于点 Q,过点 B 作 AC的垂线交 AC于点 P,∵AC= 4 5, CD= 4,CD⊥AD,2 2 2 2∴A D= AC- CD=( 4 5)- 4 = 80- 16= 8,∵点 D、 E 分别是边 BC、 AC的中点,1 1 1∴DE=2AB=2×(8 ÷2) =2×4= 2,∴AE= AD-DE= 8- 2= 6,由 (2) ,可得AE=5,从此刻开始,不留余力地努力吧,最差的结果,也可是是大器晚成∴BD=6 12 5=.5 52综上所述, BD的长为 412 5 5 或.53.解: (1) ∵△ ACB 和△ DCE均为等边三角形,∴CA= CB,CD= CE,∠ ACB=∠ DCE=60°,∴∠ ACD=∠ BCE.在△ ACD和△ BCE中,AC= BC∠ACD=∠ BCE,CD= CE∴△ ACD≌△ BCE(SAS),∴∠ ADC=∠ BEC.∵△ DCE为等边三角形,∴∠ CDE=∠ CED=60°.∵点 A, D, E 在同向来线上,∴∠ ADC=120°,∴∠ BEC=120°,∴∠ AEB=∠ BEC-∠ CED=60°.②∵△ ACD≌△ BCE,∴ AD=BE.(2) ∠AEB=90°, AE= BE+ 2CM.原因以下:∵△ ACB和△ DCE均为等腰直角三角形,∴CA= CB,CD= CE,∠ ACB=∠ DCE=90°.∴∠ ACD=∠ BCE.在△ ACD和△ BCE中,CA= CB∠ACD=∠ BCE,CD= CE∴△ ACD≌△ BCE(SAS),∴AD= BE,∠ ADC=∠ BEC.∵△ DCE为等腰直角三角形,∴∠CD E=∠ CED=45°.∵点 A, D, E 在同向来线上,∴∠ ADC=135°,∴∠ BEC=135°,∴∠ AEB=∠ BEC-∠ CED=90°.∵CD= CE,CM⊥DE,∴ DM= ME.∵∠ DCE=90°,∴ DM= ME=CM,∴AE= AD+DE= BE+2CM.从此刻开始,不留余力地努力吧,最差的结果,也可是是大器晚成(3)∵PD= 1,∴点 P 在以点 D 为圆心, 1 为半径的圆上.∵∠ BPD=90°,∴点 P 在以 BD为直径的圆上,∴点 P 是这两圆的交点.①当点 P 在如解图①所示地点时,连结 PD, PB, PA,作 AH⊥BP,垂足为H,过点 A 作 AE⊥AP,交 BP于点 E.∵四边形ABCD是正方形,∴∠ ADB=45°, AB= AD= DC= BC=2,∠ BAD=90°,∴BD=2. ∵DP= 1,∴ BP=3.∵∠ BPD=∠ BAD=90°,∴点 A、 P、 D、 B 在以 BD为直径的圆上,∴∠ APB=∠ ADB=45°.∴△ PAE 是等腰直角三角形.又∵△ BAD是等腰直角三角形,点B, E, P 共线, AH⊥BP,∴由 (2) 中的结论可得:BP=2AH+ PD,∴3= 2AH+ 1,∴AH=3- 1;2②当点 P 在如解图②所示地点时,连结 PD、 PB、 PA、作 AH⊥BP,垂足为H,过点 A 作 AE⊥AP,交 PB的延长线于点E,同理可得: BP= 2AH- PD,∴3= 2AH- 1,3+ 1∴AH=.2综上所述,点 A 到 BP的距离为3-13+1.2或2图①从此刻开始,不留余力地努力吧,最差的结果,也可是是大器晚成图②第 3题解图4.解: (1) ①∵ AB= AC,∠ BAC=90°,线段 AD绕点 A 逆时针旋转90°获得 AE,∴AD= AE,∠ BAD=∠ CAE,∴△ BAD≌△ CAE,∴CE= BD,∠ ACE=∠ B,∴∠ BCE=∠ BCA+∠ ACE=90°,∴线段 CE, BD之间的地点关系和数目关系为CE= BD,CE⊥BD;(2)(1)中的结论仍旧建立.证明以下:如解图①,∵线段 AD绕点 A 逆时针旋转90°获得 AE,∴AE= AD,∠ DAE=90°.∵AB= AC,∠ BAC=90°,∴∠ CAE=∠ BAD,∴△ ACE≌△ ABD,∴CE= BD,∠ ACE=∠ B,∴∠ BCE=90°,∴线段 CE, BD之间的地点关系和数目关系为CE= BD,CE⊥BD;3(3)45 °;4.过 A 作 AM⊥BC 于 M,过点 E 作 EN⊥MA交 MA的延长线于N,如解图②.∵线段 AD绕点 A 逆时针旋转90°获得 AE,∴∠ DAE=90°, AD= AE,∴∠ NAE=∠ ADM,易证得Rt△AMD≌Rt△ENA,∴NE= AM.∵CE⊥BD,即CE⊥MC,∴∠ MCE=90°,∴四边形MCEN为矩形,∴NE= MC,∴ AM= MC,∴∠ ACB=45°.∵四边形MCEN为矩形,从此刻开始,不留余力地努力吧,最差的结果,也可是是大器晚成∴R t△AMD∽Rt△DCF,MD AM∴=,设 DC= x,CF DC∵在 Rt△AMC中,∠ ACB=45°, AC= 3 2,3- x 3∴AM= CM=3, MD= 3- x,∴CF =x,∴CF=-1 2+ x=-1 32 33x (x - ) +,3 2 43 3∴当 x=2时, CF有最大值,最大值为4.3故答案为45°,4;图①图②第 4题解图5.解: (1) ①∵△A BC,△ AED是两个全等的等腰直角三角形,∴AD= BC.∵O为 BC的中点, F 为 AD的中点,∴A F= OC.∵∠ BAC=∠ AED=90°,AB= AC, AE=DE,∴∠ DAE=∠ CBA=45°,∴AD∥BC,∴四边形AFOC是平行四边形,∴OF= AC=2 OF 2 EC,∴=;2 EC 22故答案: 2 ;2②∵ AO=AC,∠ BAO=∠ CAO=45°,∠ DAE=45°,2从此刻开始,不留余力地努力吧,最差的结果,也可是是大器晚成∵AE= AC,∴A F= AO,AF AO∴=,AE AC∴△ AFO∽△ AEC,OF AO 2;∴ ==EC AC 22故答案: 2.(2)OF =2EC. 2原因:在等腰直角△ ADE 中, F 为 AD的中点,1 2∴A F=2AD=2 AE.在等腰直角△ ABC 中, O为 BC的中点,如解图①,连结AO,2∴AO=2 AC,∠ BAO=∠ CAO=45°.∴∠ DAE=45°,∴∠ DAE=∠ CAO,即∠ DAO=∠ CAE.∵AE= AC,∴A F= AO,AF AO∴=,AE AC∴△ AFO∽△ AEC,OF AO 2∴ ==;EC AC 2(3)∵△ ABC 和△ AED是两个全等的等腰直角三角形,∴AD= BC=2,∴ED= AE=AB= AC=1,当△ ACD为直角三角形时,分两种状况:图①从此刻开始,不留余力地努力吧,最差的结果,也可是是大器晚成图②图③第 5题解图①当 AD与 AB 重合时,如解图②,连结CD.当△ ACD为直角三角形时, AD⊥AC,马上△ ADE绕点 A 逆时针旋转45°.∵AD=2, AC= 1,2 2∴由勾股定理可得CD=(2)+1=3;②当 AE 与 AC重合时,如解图③,当△ ACD为直角三角形时, AC⊥CD,马上△ ADE绕点 A 逆时针旋转90°,此时CD= AC= 1.综上所述, CD的长为3或 1.种类二针对训练1.解: (1) ①△ DEC 绕点 C 旋转到点 D 恰巧落在AB边上,∴AC= CD.∵∠ BAC=90°-∠ B=90°- 30°= 60°.∴△ ACD是等边三角形,∴∠ ACD=60°,又∵∠ CDE=∠ BAC=60°,∴∠ ACD=∠ CDE,∴DE∥AC;②∵∠ B=30°,∠ C=90°,1∴CD= AC=2AB,∴BD= AD=AC,依据等边三角形的性质,△ACD的边 AC,AD上的高相等,∴△ BDC的面积和△ AEC 的面积相等 ( 等底等高的三角形的面积相等) ,即 S1= S2;(2)∵△ DEC是由△ ABC绕点 C 旋转获得,∴BC= CE,AC= CD,∠ DCE=∠ ACB=90°,∵∠ ACN+∠ ACE=180°,∴∠ ACN=∠ DCM.∠ACN=∠ DCM,在△ ACN和△ DCM中,∠N=∠ CMD=90°,AC=CD∴△ ACN≌△ DCM(AAS),∴AN= DM,∴△ BDC的面积和△ AEC 的面积相等 ( 等底等高的三角形的面积相等) ,即 S1= S2;第 1题解图(3)如解图,过点 D作 DF1∥BE交 BA于点 F1,易求得四边形 BEDF1是菱形,∴ BE= DF1,且 BE,DF1边上的高相等,此时 S△DCF1= S△BDE;过点 D 作 DF2⊥BD.∵∠ ABC=60°, F1D∥BE 交 BA于点 F2,∴∠F2F1D=∠ABC=60°.1∵B F1= DF1,∠F1BD=2∠ABC=30°,∠F2DB=90°,∴∠F1DF2=∠ABC=60°∴△ DF1F2是等边三角形,∴D F1= DF2.∵BD= CD,∠ ABC=60°,点 D 是角均分线上一点,1∴DBC=∠ DCB=2×60°= 30°,∴∠ CDF1=180°-∠ BCD=180°- 30°= 150°,∠CDF2=360°- 150°- 60°= 150°,∴∠ CDF1=∠ CDF2.在△ CDF1和△ CDF2中,DF1= DF2∠CDF1=∠ CDF2,CD= CD∴△ CDF1≌△ CDF2(SAS) ,∴点 F2也是所求的点.1∴∠ DBC=∠ BDE=∠ ABD=2×60°=30°.又∵ BD= 4,1 3 4 3,∴BE=×4÷cos 30 °= 2÷=32 24 3 4 3 4 3 8 3∴BF =3,BF=BF+FF=3+3=3.1 2 1 1 24 3 8 3故BF的长为3或3 .2.解:当∠ EDF 绕 D 点旋转到DE⊥AC 时,四边形CEDF是正方形;设△ABC的边长 AC= BC= a,则正方形1CEDF的边长为a,2△ABC 1 2 正方形 CEDF 1212 △DEF△CEF1△ABC∴S=2a , S = ( 2a) =4a ,即 S +S =2S ;(1)上述结论建立;原因以下:连结 CD,如解图①所示.∵AC= BC,∠ ACB=90°, D为 AB 中点,∴∠ B=45°,∠ DCE=1∠ACB=45°, CD⊥AB, CD=1AB= BD,2 2 ∴∠ DCE=∠ B,∠ CDB=90°∵∠ EDF=90°,∴∠ 1=∠ 2,在△ CDE和△ BDF中,∠1=∠2CD= BD,∠DCE=∠B∴△ CDE≌△ BDF(ASA),1∴S△DEF+S△CEF=S△ADE+S△BDF=2S△ABC;图①从此刻开始,不留余力地努力吧,最差的结果,也可是是大器晚成图②第 2题解图1(2)S △DEF- S△CEF=2S△ABC;原因以下:连结 CD,如解图②所示,同 (1) 得:△ DEC≌△ DFB,∠ DCE=∠ DBF=135°,∴S△DEF=S五边形 DBFEC,S△CFE+ S△DBC,1=S△CFE+2S△ABC,1∴S△DEF-S△CFE=2S△ABC.∴S、S 、S 的关系是 S - S = 12S .△DEF △CEF △ABC △DEF △CEF △ABC3.解: (1) 如解图①中,∵四边形ABCD、 EFGC都是正方形,∴∠ BCD=∠ ECG=90°.∵∠ BCG+∠ BCD+∠ DCE+∠ ECG=360°,∴∠ BCG+∠ ECD=180°.图①图②图③第 3题解图如解图①,过点 E 作 EM⊥DC于点 M,过点 G作 GN⊥BN 交 BN的延长线于点N,∴∠ EMC=∠ N=90°.∵四边形ABCD和四边形ECGF均为正方形,∴∠ BCD=∠ DCN=∠ ECG=90°,CB= CD, CE=CG,∴∠ 1=90°-∠ 2,∠ 3=90°-∠ 2,∴∠ 1=∠ 3.在△ CME和△ CNG中,∠EMC=∠ GNC∠1=∠3,EC= CG∴△ CME≌△ CNG(ASA),∴EM= GN.又∵S1=1CD·EM,S2=1CB·GN,2 2∴S1=S2;故答案为180°, S1= S2;(2)猜想: S1= S2,证明:如解图②,过点 E 作 EM⊥DC于点 M,过点 B 作 BN⊥GC交 GC的延长线于点N,∴∠ EMC=∠ N=90°.∵矩形 CGFE由矩形 ABCD旋转获得的,∴CE= CB,CG= CD,∵∠ ECG=∠ ECN=∠ BCD=90°,∴∠ 1=90°-∠ 2,∠ 3=90°-∠ 2,∴∠ 1=∠ 3.在△ CME和△ CNB中,∠EMC=∠ BNC∠1=∠3,EC= CB∴△ CME≌△ CNB(AAS).∴EM= BN.1 1又∵S1=CD·EM, S2= CG· BN,2 2∴S1=S2;(3)如解图③,作 DM⊥AC于 M,延长 BA,交 EC于 N,∵AB= AC=10 cm ,∠ B=30°,∴∠ ACB=∠ ABC=30°,∴∠ BAC=120°,依据翻折的性质,得∠ ACE=∠ ACB=30°,∵AD∥CE,∴∠ DAC =∠ ACE =30°,1∴∠ BAD =90°, DM = 2AD ,∴BN ⊥EC.∵AD =tan ∠ABD ·AB , AB = 10 cm ,10∴AD =tan 30 °× 10= 3 3 (cm) ,1 10 5 3(cm) .∴DM = × 3 3=2 31=1 =S ,AB =AC ,∵S =2AB ·PN , S 2AC ·DM , S △ABP△ADC △ABP △ADC 5∴PN = DM = 3 3.在 Rt △ANC 中,∠ ACN =30°, AC = 10 (cm) ,∴NC =cos ∠ACN ·AC =cos 30 °× 10=5 3(cm) .5∵在 EC 上到 N 的距离等于 3 3的点有两个,10 ″ 20∴P ′C = 3 3 cm ,P C = 3 3 cm.1020 ∴CP 的长为 3 3 cm 或 3 3 cm.4.解: (1)PM = PN ,PM ⊥PN ,原因以下:如解图①,延长 AE 交 BD 于 O ,∵△ ACB 和△ ECD 是等腰直角三角形,∴AC = BC ,EC = CD ,∠ ACB =∠ ECD =90°.在△ ACE 和△ BCD 中,AC = BC ,∠ACE =∠ BCD =90°,CE = CD ,∴△ ACE ≌△ BCD(SAS),∴AE = BD ,∠ EAC =∠ CBD ,∵∠ EAC +∠ AEC =90°,∠ AEC =∠ BEO ,∴∠ CBD +∠ BEO = 90°,∴∠ BOE =90°,即 AE ⊥BD ,∵点 M 、 N 分别是斜边 AB 、 DE 的中点,点 P 为 AD 的中点,11 ∴PM = 2BD ,PN = 2AE ,∵PM∥BD,PN∥AE,AE⊥BD,∴∠ NPD=∠ EAC,∠ MPA=∠ BDC,∠ EAC+∠ BDC=90°,∴∠ MPA+∠ NPC=90°,∴∠ MPN=90°,即 PM⊥PN.图①图②第 4题解图(2)△PMN为等腰直角三角形,原因以下:如解图②,设 AE交 BC于点 O.∵△ ACB和△ ECD是等腰直角三角形,∴AC= BC,EC= CD,∠ ACB=∠ ECD=90°,∴∠ ACB+∠ BCE=∠ ECD+∠ BCE,∴∠ ACE=∠ BCD,∴△ ACE≌△ BCD,∴AE= BD,∠ CAE=∠ CBD.又∵∠ AOC=∠ BOE,∠ CAE=∠ CBD,∴∠ BHO=∠ ACO=90°.∵点 P, M, N 分别为 AD, AB, DE的中点,1 1∴PM=BD,PM∥BD, PN= AE,PN∥AE,2 2∴PM= PN,∴∠ MGE+∠ BHA=180°,∴∠ MGE=90°,∴∠ MPN=90°,∴PM⊥PN,即△ PMN 为等腰直角三角形.1(3) 由 (2) 可知△ PMN是等腰直角三角形,PM=2BD,∴当 BD的值最大时, PM的值最大,△ PMN 的面积最大,∴当 B, C, D 共线时, BD的最大值为BC+ CD=6,∴PM= PN=3,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题七 类比探究题 类型一 线段数量关系问题 (2018·河南)(1)问题发现 如图①,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空: ①ACBD的值为________; ②∠AMB的度数为________; (2)类比探究 如图②,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断ACBD的值及∠AMB的度数,并说明理由; (3)拓展延伸 在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=7,请直接写出当点C与点M重合时AC的长.
【分析】 (1)①证明△COA≌△DOB(SAS),得AC=BD,比值为1; ②由△COA≌△DOB,得∠CAO=∠DBO,根据三角形的内角和定理,得∠AMB=180°-(∠DBO+∠OAB+∠ABD)=180°-140°=40°; (2)根据两边的比相等且夹角相等可得△AOC∽△BOD,则ACBD=OCOD=3,由全等三角形的性质得∠AMB的度数; (3)正确画出图形,当点C与点M重合时,有两种情况:如解图①和②,同理可得△AOC∽△BOD,则∠AMB=90°,ACBD=3,可得AC的长. 【自主解答】 解:(1)问题发现 ①1【解法提示】∵∠AOB=∠COD=40°, ∴∠COA=∠DOB. ∵OC=OD,OA=OB, ∴△COA≌△DOB(SAS), ∴AC=BD, ∴ACBD=1. ②40°【解法提示】∵△COA≌△DOB, ∴∠CAO=∠DBO. ∵∠AOB=40°, ∴∠OAB+∠ABO=140°, 在△AMB中,∠AMB=180°-(∠CAO+∠OAB+∠ABD)=180°-(∠DBO+∠OAB+∠ABD)=180°-140°=40°. (2)类比探究 ACBD=3,∠AMB=90°,理由如下:
在Rt△OCD中,∠DCO=30°,∠DOC=90°, ∴ODOC=tan 30°=33, 同理,得OBOA=tan 30°=33, ∵∠AOB=∠COD=90°, ∴∠AOC=BOD, ∴△AOC∽△BOD, ∴ACBD=OCOD=3,∠CAO=∠DBO. ∴∠AMB=180°-∠CAO-∠OAB-MBA=180°-(∠DAB+∠MBA+∠OBD)=180°-90°=90°. (3)拓展延伸 ①点C与点M重合时,如解图①, 同理得△AOC∽△BOD, ∴∠AMB=90°,ACBD=3, 设BD=x,则AC=3x, 在Rt△COD中, ∵∠OCD=30°,OD=1, ∴CD=2, ∴BC=x-2. 在Rt△AOB中,∠OAB=30°,OB=7. ∴AB=2OB=27, 在Rt△AMB中,由勾股定理,得AC2+BC2=AB2, 即(3 x)2+(x-2)2=(27)2, 解得x1=3,x2=-2(舍去), ∴AC=33; ②点C与点M重合时,如解图②,同理得:∠AMB=90°,ACBD=3, 设BD=x,则AC=3x, 在Rt△AMB中,由勾股定理,得AC2+BC2=AB2, 即(3x)2+(x+2)2=(27)2 解得x1=-3,解得x2=2(舍去). ∴AC=23. 综上所述,AC的长为33或23.
图① 图② 例1题解图
1.(2016·河南) (1)发现 如图①,点A为线段BC外一动点,且BC=a,AB=b. 填空:当点A位于________________时,线段AC的长取得最大值,且最大值为__________(用含a,b的式子表示). (2)应用 点A为线段BC外一动点,且BC=3,AB=1,如图②所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE. ①请找出图中与BE相等的线段,并说明理由; ②直接写出线段BE长的最大值. (3)拓展 如图③,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.
2.(2015·河南)如图①,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE.将△EDC绕点C按顺时针方向旋转,记旋转角为α. (1)问题发现
①当α=0°时,AEBD=__52__; ②当α=180°时,AEBD=__52__; (2)拓展探究 试判断:当0°≤α<360°时,AEBD的大小有无变化?请仅就图②的情形给出证明. (3)解决问题 当△EDC旋转至A,D,E三点共线时,直接写出线段BD的长.
3.(2014·河南) (1)问题发现 如图①,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE. 填空: ①∠AEB的度数为__________; ②线段AD,BE之间的数量关系为______________. (2)拓展探究 如图②,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由. (3)解决问题 如图③,在正方形ABCD中,CD=2,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离. 4.(2018·南阳二模)在△ABC中,∠ACB是锐角,点D在射线BC上运动,连接AD,将线段AD绕点A逆时针旋转90°,得到AE,连接EC. (1)操作发现 若AB=AC,∠BAC=90°,当D在线段BC上时(不与点B重合),如图①所示,请你直接写出线段CE和BD的位置关系和数量关系是______________,______________; (2)猜想论证 在(1)的条件下,当D在线段BC的延长线上时,如图②所示,请你判断(1)中结论是否成立,并证明你的判断. (3)拓展延伸 如图③,若AB≠AC,∠BAC≠90°,点D在线段BC上运动,试探究:当锐角∠ACB等于________度时,线段CE和BD之间的位置关系仍成立(点C,E重合除外)?此时若作DF⊥AD交线段CE于点F,且当AC=32时,请直接写出线段CF的长的最大值是____.
5.已知,如图①,△ABC,△AED是两个全等的等腰直角三角形(其顶点B,E重合),∠BAC=∠AED=90°,O为BC的中点,F为AD的中点,连接OF. (1)问题发现 ①如图①,OFEC=_______; ②将△AED绕点A逆时针旋转45°,如图②,OFEC=_______; (2)类比延伸 将图①中△AED绕点A逆时针旋转到如图③所示的位置,请计算出OFEC的值,并说明理由. (3)拓展探究 将图①中△AED绕点A逆时针旋转,旋转角为α,0°≤α≤90°,AD=2,△AED在旋转过程中,存在△ACD为直角三角形,请直接写出线段CD的长.
类型二 图形面积关系问题 (2017·河南)如图①,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点. (1)观察猜想 图①中,线段PM与PN的数量关系是________,位置关系是________; (2)探究证明 把△ADE绕点A逆时针方向旋转到图②的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由; (3)拓展延伸 把△ADE绕A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值. 图① 图② 例2题图 【分析】 (1)利用三角形的中位线定理得出PM=12CE,PN=12BD,进而判断出BD=CE,即可得出结论,再利用三角形的中位线定理得出PM∥CE,继而得出∠DPM=∠DCA,最后用互余即可得出结论; (2)先判断出△ABD≌△ACE,得出BD=CE,同(1)的方法得出PM=12BD,PN=12BD,即可得出PM=PN,同(1)的方法即可得出结论; (3)先判断出MN最大时,△PMN的面积最大,进而求出AN,AM,即可得出MN最大=AM+AN,最后用面积公式即可得出结论. 【自主解答】 解:(1)∵点P,N是BC,CD的中点, ∴PN∥BD,PN=12BD. ∵点P,M是CD,DE的中点, ∴PM∥CE,PM=12CE. ∵AB=AC,AD=AE, ∴BD=CE, ∴PM=PN. ∵PN∥BD, ∴∠DPN=∠ADC, ∵PM∥CE, ∴∠DPM=∠DCA. ∵∠BAC=90°, ∴∠ADC+∠ACD=90°, ∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°, ∴PM⊥PN, (2)由旋转知,∠BAD=∠CAE, ∵AB=AC,AD=AE, ∴△ABD≌△ACE(SAS), ∴∠ABD=∠ACE,BD=CE. 同(1)的方法,利用三角形的中位线定理,得PN=12BD, PM=12CE, ∴PM=PN, ∴△PMN是等腰三角形, 同(1)的方法得,PM∥CE, ∴∠DPM=∠DCE, 同(1)的方法得,PN∥BD, ∴∠PNC=∠DBC. ∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC, ∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC. ∵∠BAC=90°, ∴∠ACB+∠ABC=90°, ∴∠MPN=90°, ∴△PMN是等腰直角三角形,
例2题解图 (3)如解图,同(2)的方法得,△PMN是等腰直角三角形, ∴当MN最大时,△PMN的面积最大, ∴DE∥BC且DE在顶点A上面, ∴MN最大=AM+AN, 连接AM,AN, 在△ADE中,AD=AE=4,∠DAE=90°,
