有理数的除法3
有理数乘法与除法(3)

胜利中学教案设计学科:七年级数学教学内容:有理数乘法与除法(3) 教师姓名:金桂玉教学目标:会将有理数的除法转化成乘法;会进行有理数的乘除混合运算;会求有理数的倒数.教学重难点:正确进行有理数除法的运算,正确求一个有理数的倒数;如何进行有理数除法的运算,求一个负数的倒数.课前准备:课时安排:一课时教学过程个人研修一情景导入复习引入:1,倒数的概念;2,说出下列各数对应的倒数:1,-43,-(-4.5),|-23|3,现实生活中,一周内的每天某时的气温之和可能是正数,可能是0,也可能是负数,如黄州市区某一周上午8时的气温记录如下:周日周一周二周三周四周五周六-30c -30c -20c -3°c 0°c -2°c -1°c问:这周每天上午8时的平均气温是多少?二自主学习探索新知:上面的问题该怎么求解呢?请大家讨论并列式计算.1,解:[(-3)+(-3)+(-2)+(-3)+0+(-2)+(-1)]÷7,即:(-14)÷7=?(除法是乘法的逆运算)什么乘以7等于-14?因为(-2)×7=-14,所以: (-14)÷7=-2又因为:(-14)×71=-2所以:(-14)÷7=(-14)×71师生一起用实例来验证这一发现;之后一起总结这种规律.2,有理数除法法则:除以一个不等于0的数等于乘以这个数的倒数;0除以任何一个不等于0的数都等于0由此可见:“除以一个数,等于乘以这个数的倒数”,在引进负数以后同样成立.三教师导学问题1,计算:(1)36÷(-9) (2)(48)÷(-6 (3)0÷(-8) (4)(-21)÷(-32) (5)0.25÷(-0.5) (6)(-2476)÷(-6) (7)(-32)÷4×(-8) (8)17×(-6)÷5思考:我们该怎么来计算?因为乘法与除法的关系,我们可以仿照乘法来计算.试试看:算后小结:能整除时,将商的符号确定后,直接将绝对值相除;不能整除时,将除数变为它的倒数,再用乘法;有乘除混合运算时,先将除法转化为乘法,再进行乘法运算,注意运算顺序.课堂练习:计算:(1)48÷[(-6)-4] (2)(-81)÷49×94÷(-16) (3)52÷(-252)-281×(-143)-0.75 四合作探究 问题3,化简下列分数: 721-,122-,317-- 练习: 1,下列说法中,不正确的是 ( ) A.一个数与它的倒数之积为1; B.一个数与它的相反数之商为-1; C.两数商为-1,则这两个数互为相反数; D.两数积为1,则这两个数互为倒数; 2,下列说法中错误的是 ( ) A.互为倒数的两个数同号; B.零没有倒数; C.零没有相反数; D.零除以任意非零数商为03,如果两个有理数在数轴上对应的点分别在原点的两侧,则这两个数相 除所得的商是( )A.一定是负数;B.一定是正数;C.等于0;D.以上都不是;4,1.4的倒数是 ; 若a,b 互为倒数,则2ab= ; 5,若一个数和它的倒数相等,则这个数是 ;若一个数和它的相反数相等,则这个数是 .五交流反馈 1,计算: (1)(-27)÷9;(2)(-45)÷[(-13)÷(-25)]; (3)(-0.91)÷(-0.13);(4)0÷(-351719)(5)(-23)÷(-3)×13; (6)1.25÷(-0.5)÷(-212);(7)(-81)÷(+314)×(-49)÷(-1113); (8)-0.125÷83 (9)(13-56+79)÷(-118); (10)-32324÷(-112). 2,列式计算:(1)一个数的413倍是-13,则此数为多少?(2)-15的相反数与-5的绝对值的商的相反数是多少?课堂小结:有理数的乘法法则及运算律;有理数的除法法则;与小学四则运算不同,有理数的加,减,乘,除首先要确定和,差,积,商的符号,然后在确定和,差,积,商的绝对值.六巩固提升补充题: 1,若0____0,0b a b a ,则><,若0____0,0b a b a ,则>>. 2,若0____0,0b a b a ,则<=,若0____0,0b a b a ,则<>.3,mn=0,则一定有( ).A.n=0且m ≠0;B.m=0或n=0;C.m=0且n ≠0;D.m=n=04,果两个有理数的和除以它们的积,所得商是0,那么这两个有理数 ( ).A.互为相反数,但不等于0B.互为倒数;C.有一个等0;D.都等于0 5,数的相反数与这个数的倒数的和为0,则这个数的绝对值为 ( ).A.2B.1C.0.5D.06,ab ≠0,则a a +bb 的值不可能是 ( ).A.0 B.1 C.2 D.-27,a a +b b +c c =1,求(abc abc )2003÷(ab bc ×bc ac ×acab )的值.8,计算:(721+343-271-187)÷(1521+743-473-387). 9,a,b,c,d 表示4个有理数,其中每三个数之和是-1,-3,2,17,求a,b,c,d.10,2001减去它的21,再减去剩余数的31,再减去剩余数的41,…,依此类推,一直减去剩余数的20011,求最后剩余的数.教学反思。
2022秋七年级数学上册第1章有理数1.4有理数的乘除法第3课时有理数的除法习题课件新人教版

1.4 有理数的乘除法 第3课时 有理数的除法
提示:点击 进入习题
1 倒数;1b;≠0
6C
7D
答案显示
2 见习题 3 C 4 C 5 A 8 除法 9 不变 10 C
11 D
12 见习题 13 B
14 A
15 见习题
16 见习题 17 见习题 18 见习题 19 见习题 20 见习题
【点拨】A.3+(-2)=1,故A不符合题意; B.3-(-2)=3+2=5,故B不符合题意; C.3×(-2)=-6,故C符合题意; D.(-3)÷(-2)=1.5,故D不符合题意.
【答案】C
*7.(2019·广东)有理数 a,b 在数轴上的对应点的位置如图所示, 下列式子成立的是( )
A.a>b C.a+b>0
A.-ba=-ab=-ab
B.--ba=- -ab=ab
C.--ab=ab
D.若 a>b,ab<0,则 a<0
12.有理数的除法可以转换为乘法,所以有理数的乘除混合 运算可以统一成乘法运算,其步骤为:
(1)__将__所__有__除__数__转__化__为__其__倒__数__,__将__除__法__转__化__为__乘__法________; (2)__运__用__乘__法__法__则__计__算__,__能__简__算__的__运__用__运__算__律__简__化__运__算____.
3.(教材 P34 例 5 变式)(2020·山西)计算(-6)÷-13的结果是( C )
A.-18
B.2
C.18
D.-2
4.下列把除法转换为乘法的过程中,正确的是( C ) A.13÷(-4)=-13×4 B.(-3)÷(-6)=3×-16 C.1÷(-4)=1×-14 D.(-3)÷4=3×14
14有理数乘除法(3)

学,明确内容和要
预习 交流
2、怎么样,在有理数运算律中,乘法 的交换律,结合律以及分配律还成立 吗?
求,进行方法指导。
3、归纳、总结
3、生生互动,质疑
答疑。通过再次预习
和讨论交流,学生基
本掌握所布置三个
的要求和目标。
1、用两种方法计算
1、教师布置学生先
(-+---) X12
2 6 2
自己独立元成例题,
6、
753
36
964
18
(说明:本节课预习作业题应在前一节导学案中体过程
思考与调整
活动内容
师生行为
(一)学生围绕教材内容和预习作业 题自学3~5分钟。
1、教师课前检查了
解学生完成预习作
要求:1、以小组为单位,仔细观察上
业情况。
面的式子与结果,把你的发现相互交
2、教帅布置学生自
1、教师布置检测题,
巡回查看学生答题
情况,当堂批阅,统 计差错及目标达成 率。
启东市七年级数学集体备课导学案
第一章(课)第4节有理数的乘除法 (3)
二备:
龚蕾(百杏中学)
学习
目标
1熟练有理数的乘法运算并能用乘法运算律简化运算.
2、让学生通过观察、思考、探究、讨论,主动地进行学习.
3、培养学生语言表达能力以及与他人沟通、交往能力,使其逐渐热爱数学这
学习
重点
正确运用运算律,使运算简化
学习
运用运算律,使运算简化
难点
教具
小黑板、实物投影、PPT等。
学具
1、
看书p32-33页并完成以下练习
(-85)X(-25)X(—4);
2、(—-)X15X(—1丄);
第3讲 有理数的乘除及乘方 -提高班
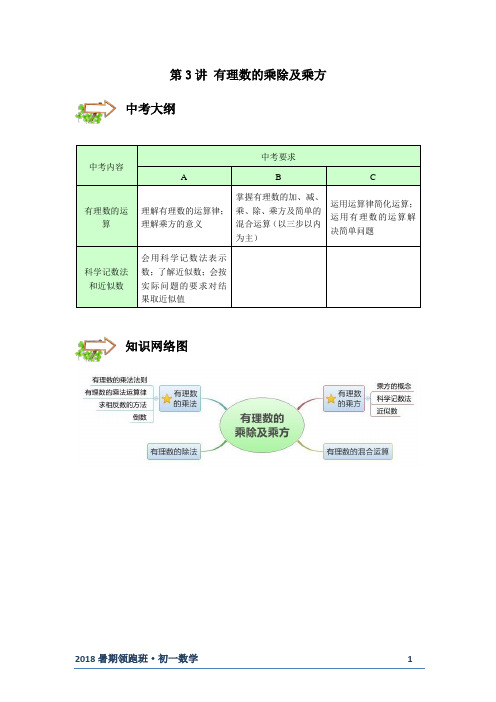
第3讲有理数的乘除及乘方中考内容中考要求A B C有理数的运算理解有理数的运算律;理解乘方的意义掌握有理数的加、减、乘、除、乘方及简单的混合运算(以三步以内为主)运用运算律简化运算;运用有理数的运算解决简单问题科学记数法和近似数会用科学记数法表示数;了解近似数;会按实际问题的要求对结果取近似值中考大纲知识网络图3.1有理数的乘法一. 有理数的乘法1. 有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘.任何数同0相乘,都得0.2. 有理数乘法的运算步骤:先确定积的符号,再确定积的绝对值.3. 有理数乘法的应用:要得到一个数的相反数,只要将它乘1-.4. 多个有理数相乘:(1)几个不是0的数相乘,负因数的个数是偶数时,积为正数;负因数的个数是奇数时,积为负数,即“奇负偶正”.(2)几个数相乘,如果其中有因数为0,那么积等于0. 5. 有理数乘法运算律:(1)乘法交换律:一般地,有理数乘法中,两个数相乘,交换因数的位置,积相等.ab ba =(2)乘法结合律:一般地,有理数乘法中,三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等.()()ab c a bc =(3)分配律:一般地,有理数乘法中,一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.()a b c ab ac +=+二. 倒数1. 倒数的概念:乘积是1的两个数互为倒数. (1)倒数是成对出现的,单独一个数不能称为倒数.(2)互为倒数的两个数的乘积一定是1,即a ,b 互为倒数,则1a b ⨯=;反之亦然. (3)0没有倒数.2. 求一个非零有理数的倒数,把它的分子和分母颠倒位置即可. (1)非零整数可以看作分母为1的分数; (2)带分数一定要先化成假分数之后再求倒数.知识概述【例】(2017秋•顺义区期末)四个互不相等的整数的积为4,那么这四个数的和是( ) A .0 B .6C .﹣2D .2【练习】(2017秋•蓬溪县期末)如果a +b <0,并且ab >0,那么( ) A .a <0,b <0 B .a >0,b >0 C .a <0,b >0 D .a >0,b <0【例】(2016秋•芝罘区期末)已知abc >0,a >c ,ac <0,下列结论正确的是( ) A .a <0,b <0,c >0 B .a >0,b >0,c <0 C .a >0,b <0,c <0 D .a <0,b >0,c >0【例】(2017秋•滨海新区期末)对于有理数a 、b ,如果ab <0,a +b <0.则下列各式成立的是( )A .a <0,b <0B .a >0,b <0且|b |<aC .a <0,b >0且|a |<bD .a >0,b <0且|b |>a3.2有理数的除法一.有理数的除法1. 有理数除法法则:(1)除以一个不等于0的数,等于乘这个数的倒数.小试牛刀再接再厉总述思考:多个不是的数相乘,先做哪一步,再做哪一步?知识概述1a b a b÷=⋅,(0b ≠)(2)法则的另一说法:两数相除,同号得正,异号得负,并把绝对值相除.0除以任何一个不等于0的数,都得0.2. 有理数除法的运算步骤:先将除法换成乘法,然后确定积的符号,最后求出结果.3. 分数:分数可以理解为分子除以分母.二.有理数的乘除混合运算先将除法换成乘法,然后确定积的符号,最后求出结果. 注意:乘除混合运算要“从左到右”运算.【例】(2017秋•临沂月考)若x=(﹣1.125)×÷(﹣)×,则x 的倒数是( ) A .1 B .﹣1 C .±1 D .2【练习】(2017秋•郯城县月考)÷(﹣10)×(﹣)÷(﹣)【例】(2017秋•昌平区期末)计算:(﹣3)×6÷(﹣2)×.【练习】(2017秋•安图县期末)÷(﹣1)×.【例】(2017秋•怀柔区期末)计算:3×(﹣)÷(﹣1).5.(2017秋•城关区校级期中)计算: (1)﹣5÷(﹣1);(2)(﹣)÷(﹣)÷(﹣1).小试牛刀再接再厉3.3有理数的乘方一. 有理数的乘方1. 乘方的概念:求n 个相同因数的积的运算叫做乘方,乘方的结果叫做幂.(1)一般地,n 个相同的因数a 相乘,即n a a a a⋅⋅⋅⋅⋅⋅⋅个,记作,读作“a 的n 次方”;(2)在中,a 叫做底数,n 叫做指数;(3)当看作a 的n 次方的结果时,读作a 的n 次幂. 注意:()224-=,其底数为()2-,()()()22224-=-⨯-=;224-=-,其底数为2,()()222121224-=-⨯=-⨯⨯=-;239=749⎛⎫⎪⎝⎭,其底数为37,2333977749⎛⎫=⨯= ⎪⎝⎭; 239=77,其底数为3,23339777⨯==; 221391224⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,带分数的乘方运算,一定要先化成假分数后再运算.2. 一个数可以看作这个数本身的一次方,例如,5就是15,指数1通常省略不写.3. 幂的正负规律:(1)负数的奇次幂是负数,负数的偶次幂是正数,即“奇负偶正”; (2)正数的任何次幂都是正数; (3)0的任何正整数次幂都是0. 二. 科学记数法n a n a n a 总述思考:加减乘除混合运算的运算顺序是什么?知识概述1. 科学记数法:把一个大于10的数表示成10n a ⨯的形式(其中110a ≤<,n 是正整数).2. 用科学记数法表示一个n 位整数,其中10的指数是1n -,10的指数比整数的位数少1. 3. 万410=,亿810= 三.近似数1. 准确数:表示实际数量的数.2. 近似数:在一定程度上反映被考察量的大小,能说明实际问题的意义,与准确数非常地接近.3. 精确度:表示近似数与准确数的接近程度. 4. 精确度的类型: (1)纯数字类按四舍五入法对圆周率π取近似数时 3π≈(精确到个位)3.1π≈(精确到十分位,或叫精确到0.1)3.14π≈(精确到百分位,或叫精确到0.01) 3.142π≈(精确到千分位,或叫精确到0.001)(2)带单位类近似数2.6万(精确到千位) (3)科学记数法类近似数43.5110⨯(精确到百位)【例】(2018•金牛区校级模拟)下列各数|﹣2|,﹣(﹣2)2,﹣(﹣2),(﹣2)3中,负数的个数有()A .1个B .2个C .3个D .4个【练习】(2018•河北二模)下列各对数中,数值相等的是( ) A .+32与+22 B .﹣23与(﹣2)3 C .﹣32与(﹣3)2 D .3×22与(3×2)2小试牛刀再接再厉【练习】(2018•绵阳)四川省公布了2017年经济数据GDP排行榜,绵阳市排名全省第二,GDP总量为2075亿元,将2075亿用科学记数法表示为()A.0.2075×1012B.2.075×1011C.20.75×1010D.2.075×1012【例】(2018•绍兴)绿水青山就是金山银山,为了创造良好的生态生活环境,浙江省2017年清理河湖库塘淤泥约116 000 000方,数字116 000 000用科学记数法可以表示为()A.1.16×109B.1.16×108C.1.16×107D.0.116×109【例】(2016秋•吴中区期末)阅读下列各式:(a•b)2=a2b2,(a•b)3=a3b3,(a•b)4=a4b4…回答下列三个问题:(1)验证:(2×)100=____,2100×()100=_____;(2)通过上述验证,归纳得出:(a•b)n=_____;(abc)n=______.(3)请应用上述性质计算:(﹣0.125)2017×22016×42015.总述总结:“奇负偶正”你了解全了吗?3.4有理数的混合运算知识概述一.有理数混合运算顺序:1.先乘方,再乘除,最后加减;2. 同级运算,从左到右进行;3. 如有括号,先做括号内的运算,按小括号、中括号、大括号的顺序依次进行. 二. 进行有理数混合运算时的易错点:1. 乘方概念错误,如326=等.2. 底数错误,如2(2)4-=-,224-=等.3. 运算顺序发生错误,如1232123÷⨯=÷=等.4. 分配律运算错误,如112(2)22241522-⨯-=-⨯-⨯=--=-等.【例】(2017秋•招远市期末)形如的式子叫做二阶行列式,其运算法则用公式表示为=xn ﹣ym ,依此法则计算的结果为( )A .17B .﹣17C .1D .﹣1【练习】(2017秋•费县期末)现定义一种新运算“*”,规定a*b=ab +a ﹣b ,如1*3=1×3+1﹣3,则(﹣2*3)*5等于( ) A .71 B .47 C .﹣47 D .﹣71【例】(2017秋•揭西县期末)计算:(﹣2)2÷×(﹣2)﹣=______.【练习】(2017秋•河口区期末)计算8﹣23÷的值为_____.【例】(2017秋•泸县期末)计算:﹣14﹣×[2﹣(﹣3)2].小试牛刀再接再厉【例】(2018•杭州二模)计算:﹣23+6÷3×圆圆同学的计算过程如下:原式=﹣6+6÷2=0÷2=0请你判断圆圆的计算过程是否正确,若不正确,请你写出正确的计算过程.【练习】(2018•邵阳县模拟)计算:﹣14+16÷(﹣2)3×|﹣3﹣1|.【巩固】(2017秋•贵阳期末)计算:(1)1﹣43×(﹣)(2)7×2.6+7×1.5﹣4.1×8.。
有理数的除法

2 (1) 5 5 2
(2)-1
(3) 1
1 7
(4)0.25
(5)16
-1
7 8
4
1 16
教学目标: 1、理解有理数除法的意义;熟练掌握有理数 除法法则;会进行有理数的除法运算. 2、体验将有理数除法运算转化为有理数乘法 运算的数学转化思想. 3、通过有理数的除法运算,培养学生的运算 能力. 教学重点: 熟练有理数的除法运算. 教学难点: 理解有理数的除法法则及商的符号的确定.
二:新知探究,合作提高 阅读教科书第34页. 注意:乘法与除法互为逆运算,小 学已经学过.本节内容在我们已有有理 数乘法知识的基础上,通过同学们经历 从具体情境中抽象出法则的过程,发现 其中的规律,掌握必要的运算技能,让 我们在有理数运算的学习中继续发展 数感,在符号法则的学习中增强符号感.
想一想:怎样计算8÷(-4)呢? 8÷(-4)= 于是 -2
1 8×( )= -2 4
1 8÷(-4)= 8×( ) 4
换其他数的 除法进行类似讨 因为(-2)×(-4)=8 论,是否仍有除 以a(a ≠0)可以转 所以8÷(-4)=-2 1 化为乘 . a
思考:0可以做除数吗?
议一议:两数相除有哪些情形? 各举一例.
• 1:同号两数相除 • (1)两正数相除 • (2)两负数相除
有理数的除法法则
除以一个不等于0的数,等于乘这个数的倒数.
● ● ● ● ●
除数变为倒数作因数
也可以表示成: 1 a ÷ b = a · b
除号变乘号
(b≠0)
有理数除法法则的另一种说法: 两数相除,同号得 正 ,异号得 负 ,并把绝对 值相 除 .0除以记忆
有理数的减法法则 有理数的除法法则
(人教版)有理数的乘除法 优秀课件3

要得到一个数
的相反数,只要
将它乘 -1.
知1-讲
总 结
先定符号,同号得正,异号得负,再算 绝对值;任何数与0相乘都得0.
知1-讲
例3 如图,数轴上A、B两点所表示的两个数 的( D ) A.和为正数 C.积为正数 B.和为负数 D.积为负数
导引:由图可知A点表示的数是负数,B点表示的数为 正数,并且这两个数的绝对值相等.
知2-练
1
1 0 没有 若数a≠0,则a的倒数是________ ,________ a
1或-1 . 倒数;倒数等于它本身的数是________ 2 若a与b互为相反数,c与d互为倒数,则5(a+b) -6cd=________ -6 .
知2-练
海南)-2 015的倒数是( A ) 3 (中考·
颠倒位置即可(整数看成分母为1的分数); (2)求带分数的倒数时,要先将其化成假分数; (3)求小数的倒数时,要先将其化成分数.
• • • • • • • • • • • • • • • • • • • • • • • • • • • • •
25、你不能拼爹的时候,你就只能去拼命! 26、如果人生的旅程上没有障碍,人还有什么可做的呢。 27、我们无法选择自己的出身,可是我们的未来是自己去改变的。励志名言:比别人多一点执着,你就会创造奇迹 28、伟人之所以伟大,是因为他与别人共处逆境时,别人失去了信心,他却下决心实现自己的目标。 29、人生就像一道漫长的阶梯,任何人也无法逆向而行,只能在急促而繁忙的进程中,偶尔转过头来,回望自己留下的蹒跚脚印。 30、时间,带不走真正的朋友;岁月,留不住虚幻的拥有。时光转换,体会到缘分善变;平淡无语,感受了人情冷暖。有心的人,不管你在与不在,都会惦念;无心的情,无论你好与不好,只是漠然。走过一段路,总能有一次领悟;经历一些事,才能看清一些人。 31、我们无法选择自己的出身,可是我们的未来是自己去改变的。 32、命好不如习惯好。养成好习惯,一辈子受用不尽。 33、比别人多一点执着,你就会创造奇迹。 1、想要体面生活,又觉得打拼辛苦;想要健康身体,又无法坚持运动。人最失败的,莫过于对自己不负责任,连答应自己的事都办不到,又何必抱怨这个世界都和你作对?人生的道理很简单,你想要什么,就去付出足够的努力。 2、时间是最公平的,活一天就拥有24小时,差别只是珍惜。你若不相信努力和时光,时光一定第一个辜负你。有梦想就立刻行动,因为现在过的每一天,都是余生中最年轻的一天。 3、无论正在经历什么,都请不要轻言放弃,因为从来没有一种坚持会被辜负。谁的人生不是荆棘前行,生活从来不会一蹴而就,也不会永远安稳,只要努力,就能做独一无二平凡可贵的自己。 4、努力本就是年轻人应有的状态,是件充实且美好的事,可一旦有了表演的成分,就会显得廉价,努力,不该是为了朋友圈多获得几个赞,不该是每次长篇赘述后的自我感动,它是一件平凡而自然而然的事,最佳的努力不过是:但行好事,莫问前程。愿努力,成就更好的你! 5、付出努力却没能实现的梦想,爱了很久却没能在一起的人,活得用力却平淡寂寞的青春,遗憾是每一次小的挫折,它磨去最初柔软的心智、让我们懂得累积时间的力量;那些孤独沉寂的时光,让我们学会守候内心的平和与坚定。那些脆弱的不完美,都会在努力和坚持下,改变模样。 6、人生中总会有一段艰难的路,需要自己独自走完,没人帮助,没人陪伴,不必畏惧,昂头走过去就是了,经历所有的挫折与磨难,你会发现,自己远比想象中要强大得多。多走弯路,才会找到捷径,经历也是人生,修炼一颗强大的内心,做更好的自己! 7、“一定要成功”这种内在的推动力是我们生命中最神奇最有趣的东西。一个人要做成大事,绝不能缺少这种力量,因为这种力量能够驱动人不停地提高自己的能力。一个人只有先在心里肯定自己,相信自己,才能成就自己! 8、人生的旅途中,最清晰的脚印,往往印在最泥泞的路上,所以,别畏惧暂时的困顿,即使无人鼓掌,也要全情投入,优雅坚持。真正改变命运的,并不是等来的机遇,而是我们的态度。 9、这世上没有所谓的天才,也没有不劳而获的回报,你所看到的每个光鲜人物,其背后都付出了令人震惊的努力。请相信,你的潜力还远远没有爆发出来,不要给自己的人生设限,你自以为的极限,只是别人的起点。写给渴望突破瓶颈、实现快速跨越的你。 10、生活中,有人给予帮助,那是幸运,没人给予帮助,那是命运。我们要学会在幸运青睐自己的时候学会感恩,在命运磨练自己的时候学会坚韧。这既是对自己的尊重,也是对自己的负责。 1、这世上,没有谁活得比谁容易,只是有人在呼天抢地,有人在默默努力。 2、当热诚变成习惯,恐惧和忧虑即无处容身。缺乏热诚的人也没有明确的目标。热诚使想象的轮子转动。一个人缺乏热诚就象汽车没有汽油。善于安排玩乐和工作,两者保持热诚,就是最快乐的人。热诚使平凡的话题变得生动。 3、起点低怕什么,大不了加倍努力。人生就像一场马拉松比赛,拼的不是起点,而是坚持的耐力和成长的速度。只要努力不止,进步也会不止。 4、如果你不相信努力和时光,那么时光第一个就会辜负你。不要去否定你的过去,也不要用你的过去牵扯你的未来。不是因为有希望才去努力,而是努力了,才能看到希望。 5、人生每天都要笑,生活的下一秒发生什么,我们谁也不知道。所以,放下心里的纠结,放下脑中的烦恼,放下生活的不愉快,活在当下。人生喜怒哀乐,百般形态,不如在心里全部淡然处之,轻轻一笑,让心更自在,生命更恒久。积极者相信只有推动自己才能推动世界,只要推动自己就能推动世界。 6、人性本善,纯如清溪流水凝露莹烁。欲望与情绪如风沙袭扰,把原本如天空旷蔚蓝的心蒙蔽。但我知道,每个人的心灵深处,不管乌云密布还是阴淤苍茫,但依然有一道彩虹,亮丽于心中某处。 7、每个人的心里,都藏着一个了不起的自己,只要你不颓废,不消极,一直悄悄酝酿着乐观,培养着豁达,坚持着善良,只要在路上,就没有到达不了的远方! 8、不要活在别人眼中,更不要活在别人嘴中。世界不会因为你的抱怨不满而为你改变,你能做到的只有改变你自己! 9、欲戴王冠,必承其重。哪有什么好命天赐,不都是一路披荆斩棘才换来的。 10、放手如拔牙。牙被拔掉的那一刻,你会觉得解脱。但舌头总会不由自主地往那个空空的牙洞里舔,一天数次。不痛了不代表你能完全无视,留下的那个空缺永远都在,偶尔甚至会异常挂念。适应是需要时间的,但牙总是要拔,因为太痛,所以终归还是要放手,随它去。
有理数的除法
有理数的除法【新知讲解】姓名1、倒数的意义:乘积为1的两个数互为倒数。
即如果1ab=,那么,a b互为倒数。
反之,如果,a b 互为倒数,那么1ab=注意:(1)0没有倒数。
(2)遇到求一个带分数的倒数时,先将带分数化为假分数,再求其倒数。
(3)倒数和相反数是数学中的两个重要概念,要注意区分。
(4)倒数是对于两个数的关系而言,单独的一个数不能说叫倒数。
如:3不能叫倒数。
2、除法的法则法则1:除以一个数等于乘以这个数的倒数。
即:1(0)a b a bb÷=⨯≠注意:法则1应用“倒数”的概念,除法就可以转化为乘法。
因为0没有倒数,所以除数不能为0。
法则2:两数相除,同号得正,异号得负,并把绝对值相除,0除以任何一个不等于0的数,都得0。
方法:有理数除法运算步骤:第一步是确定商的符号;第二步是求出商的绝对值。
【典例解析】例1、写出下列各数的倒数:31 4,3, 1.5,4,,222---.变式训练:1、写出下列各数的倒数:3531,2,,,1,1, 421015 ----.例2、计算:(1)(6)(18)-÷-;(2)81(9)÷-;(3)0(8)÷-.例3、计算:(1)( 6.6)0.13-÷;(2)32()()55-÷-;(3)21(1)3-÷-.★刘老点津★带分数参加除法运算时,先化成假分数便于约分。
分数做除数时,一般先把除数写倒数再相乘。
变式训练:计算:(1)65(13)÷-;(2)1(0.8)(5)3-÷-;(3)2()0.63-÷;(4)20(3)9÷-.例4、计算:(1)311(10)(1)43-÷-÷-;(2)53052.6(3)764÷÷-÷.★刘老点津★把除法转化为乘法。
例5、计算:(1)111(4)(10)(3)(2)232-÷-⨯-÷-;(2)5721()()129336--÷-.★刘老点津★把除法转化为乘法,合理利用运算律。
有理数的运算
一、 有理数的加法知识点1:有理数加法法则1) 同号两数相加,和的符号与加数相同,和的绝对值等于两加数绝对值之和。
2) 异号两数相加,和的符号与绝对值大的加数相同,和的绝对值等于较大的绝对值减去较小的绝对值。
3) 任意数与零相加,和等于原数。
注:从2)可知,互为相反数的两数之和为0,即0)(=-+a a 。
上述法则可用数学符号表示如下:知识点2:有理数加法的运算律 1) 交换律 2) 结合律方法与技能:考虑有理数运算结果时,既要考虑它的符号,又要考虑它的绝对值。
运算过程的第一步是确定和的符号,第二步是确定和的绝对值。
选择运用运算律进行合理计算,是简化运算过程的关键。
例1、 计算:(1)()()7-5-+ (2)()4.33.7-+ (3)⎪⎭⎫ ⎝⎛+43-54 (4)⎪⎭⎫⎝⎛+65-0例2、 计算:(1)()5.176213-76-++⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛ (2)()125.461-652-815-++⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛二、 有理数的减法知识点1:有理数减法法则减去一个数等于加上这个数的相反数,用符号表示为:()b a b a -+=-知识点2:在做有理数减法时,第一步将运算符号“—”改写为加号“+”、将减数改写成它的相反数,第二步按有理数加法法则运算。
例1、 计算:(1)()8.5--2.14 (2)325313--⎪⎭⎫ ⎝⎛ (3)⎪⎭⎫⎝⎛--530例2、 先列出算式在求解:(1) 什么数加上8-所得的和是8- (2) 6.0-减去什么数所得的差是4.0-(3) 414-加上什么数所得的和是313三、 有理数的乘法知识点1:有理数乘法法则1) 两数相乘,同号得正,异号得负,积的绝对值是两数绝对值之积。
2) 任意数与零相乘,都得0. 注:此法则用数学语言表达如下:知识点2:有理数乘法的运算律 1) 交换律 2) 结合律3) 乘法对加法的分配律 方法与技能:1) 有理数乘法运算过程的第一步是确定积的符号,第二步是确定积的绝对值。
有理数及其运算知识点总结
有理数及其运算知识点总结
1. 有理数是可以表达为两个整数的比值的数,包括正整数、负整数、零以及可以用分数表示的数。
2. 有理数的加法和减法运算:
- 相同符号的有理数相加减,绝对值相加减,结果带相同符号。
- 不同符号的有理数相加减,绝对值相减,结果带绝对值大的符号。
3. 有理数的乘法和除法运算:
- 相同符号的有理数相乘、相除,结果为正数。
- 不同符号的有理数相乘、相除,结果为负数。
4. 有理数的乘法:
- 非零有理数相乘,绝对值相乘,符号由乘法规则决定。
- 0乘以任何数等于0。
5. 有理数的除法:
- 非零有理数相除,绝对值相除,符号由除法规则决定。
- 0不能作为除数。
6. 有理数的乘方:
- 正数的乘方:底数不变,指数相乘。
- 零的非负整数次幂为0,零的负整数次幂没有定义。
- 1的任何整数次幂仍为1。
- 负数的偶次幂为正数,奇次幂为负数。
7. 有理数的相反数是指与其绝对值相等,但符号相反的数。
8. 有理数的倒数是指其倒数等于它的分子和分母互换位置后的比值。
9. 有理数的绝对值是指其去掉符号的值。
10. 有理数的大小比较:
- 两个有理数绝对值相等,但符号相反时,负数较大。
- 两个正数比较大小,绝对值大的数较大。
- 两个负数比较大小,绝对值小的数较大。
这些是有理数及其运算的基本知识点总结,能够帮助理解有理数的概念和规则。
3.2有理数的乘法与除法
§3.2有理数的的乘法导学案第一课时解留初一数学备课组于春杰【课前预习】看书学习:经历探索有理数乘法法则的过程,发展观察、归纳、猜想、验证能力;学会进行有理数的乘法运算,掌握确定多个不等于零的有理数相乘的积的符号方法以及有一个数为零积是零的情况:【课内探究】一.学习目标:1.探索有理数乘法法则及运算律.2.会进行有理数的乘法运算,能用乘法运算律简化运算.二、学习重点、难点:重点:乘法的运算律和符号法则难点:灵活运用乘法的运算律和符号法则三、学习过程:(一)、自主学习:自学课本P53至55页问题1水库的水位每小时上升3厘米,2小时上升了多少厘米?问题2水库的水位平均每小时上升-3厘米,2小时上升多少厘米?(二)合作探究:引导学生比较①,②得出:综合上面各种情况,引导学生自己归纳出有理数乘法的法则:两数相乘,同号得正,异号得负,并把绝对值相乘;任何数同0相乘,都得0.继而教师强调指出:“同号得正”中正数乘以正数得正数就是小学学习的乘法,有理数中特别注意“负负得正”和“异号得负”.用有理数乘法法则与小学学习的乘法相比,由于介入了负数,使乘法较小学当然复杂多了,但并不难,关键仍然是乘法的符号法则:“同号得正,异号得负”,符号一旦确定,就归结为小学的乘法了.因此,在进行有理数乘法时更需时时强调:先定符号后定值.1.自学课本例1完成下列题目(1).(-3)×(-5) (2).(-2)×(+8.2)(3).(-41)×32 (4).(-24)×813你能总结出进行有理数数乘法运算的基本步骤吗?(生总结)(第一步是确定积的符号。
第二步是求绝对值的积)师生共同归纳得出有理数乘法法则:2.计算(1).(-17)×1 (2).(+321)×1(3).64×(-1) (4).(-21)×(-1)你能从中总结出什么结论吗?3.请仔细阅读课本53页―――57页的知识,完成下面内容..(三)、尝试应用:(自学例题完成下列题目)1、计算(1)、(-43)×(-5)×(+34)×(+2)(2)、(-85)×143×(-516)×(-67)(3)、(21-92+65)×(-36)2、计算(1)、(-8)×5×(-0.25)(2)、(-43)×(-23)×(-2)(3)、(-73)×61×(-158)×(-21)(4)、(-73)×(-0.125)×(-231)×(-8)思考:从上面几个不等于零的有理数的乘法运算中,你发现乘积的符号与因数的符号的个数之间存在着什么规律吗?如果有一个因数为零呢?(四)、能力提升:1、若a × b > 0, 并且 a>0, 则b ___ 0若a × b < 0, 并且a>0, 则b ___ 02、一个有理数和它的相反数之积( )A .必为正数 B.必为负数 C.一定不大于零 D.一定不等于-1(五)、课堂小结:1.有理数乘法法计算的法则是什么?2.谈谈本节课,你有哪些收获?教学反思:有理数的乘法一节的内容不仅包括有理数的乘法法则,也包括乘法的运算律和有理数乘法的符号法则。
