小学 “鸡兔同笼” 讲解方法(13种),总有一种适合你!
鸡兔同笼类问题中的各种解法分析小总结

鸡兔同笼类问题中的各种解法分析小总结————————————————————————————————作者:————————————————————————————————日期:鸡兔同笼类问题中的各种解法分析小汇总1.典型鸡兔同笼问题详解例1鸡兔同笼是我国古代的著名趣题。
大约在1500年前,《孙子算经》中就记载着“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”翻译成通俗易懂的内容如下:鸡兔共有35个头,94只脚,问鸡兔各有多少只?经梳理,对于这一类问题,总共有以下几种理解方法。
(1)站队法让所有的鸡和兔子都列队站好,鸡和兔子都听哨子指挥。
那么,吹一声哨子让所有动物抬起一只脚,笼中站立的脚:94-35=59(只)那么再吹一声哨子,然后再抬起一只脚,这时候鸡两只脚都抬起来就一屁股坐地上了,只剩下用两只脚站立的兔子,站立脚:59-35=24(只)兔:24÷2=12(只);鸡:35-12=23(只)(2)松绑法由于兔子的脚比鸡的脚多出了2个,因此把兔子的两只前脚用绳子捆起来,看作是一只脚,两只后脚也用绳子捆起来,看作是一只脚。
那么,兔子就成了2只脚。
则捆绑后鸡脚和兔脚的总数:35×2=70(只)比题中所说的94只要少:94-70=24(只)。
现在,我们松开一只兔子脚上的绳子,总的脚数就会增加2只,不断地一个一个地松开绳子,总的脚数则不断地增加2,2,2,2……,一直继续下去,直至增加24,因此兔子数:24÷2=12(只)从而鸡数:35-12=23(只)(3)假设替换法实际上替代法的做题步骤跟上述松绑法相似,只不过是换种方式进行理解。
假设笼子里全是鸡,则应有脚70只。
而实际上多出的部分就是兔子替换了鸡所形成。
每一只兔子替代鸡,则增加每只兔脚减去每只鸡脚的数量。
兔子数=(实际脚数-每只鸡脚数*鸡兔总数)/(每只兔脚数-每只鸡脚数)与前相似,假设笼子里全是兔,则应有脚120只。
“鸡兔同笼”问题的几种解法
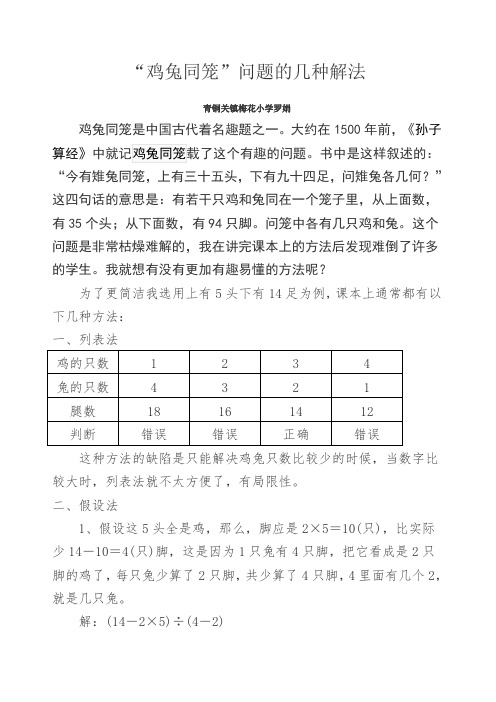
“鸡兔同笼”问题的几种解法青铜关镇梅花小学罗娟鸡兔同笼是中国古代着名趣题之一。
大约在1500年前,《孙子“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡和兔同在一个笼子里,从上面数,有35个头;从下面数,有94只脚。
问笼中各有几只鸡和兔。
这个问题是非常枯燥难解的,我在讲完课本上的方法后发现难倒了许多的学生。
我就想有没有更加有趣易懂的方法呢?为了更简洁我选用上有5头下有14足为例,课本上通常都有以下几种方法:这种方法的缺陷是只能解决鸡兔只数比较少的时候,当数字比较大时,列表法就不太方便了,有局限性。
二、假设法1、假设这5头全是鸡,那么,脚应是2×5=10(只),比实际少14-10=4(只)脚,这是因为1只兔有4只脚,把它看成是2只脚的鸡了,每只兔少算了2只脚,共少算了4只脚,4里面有几个2,就是几只兔。
解:(14-2×5)÷(4-2)=4÷2=2(只)------兔5-2=3(只)答:鸡有3只,兔有2只。
2、也可以假设5只全是兔,解答如下:解:(4×5-14)÷(4-2)=6÷2=3(只)------鸡5-3=2(只)答:鸡有3只,兔有2只。
这种方法也有缺陷,就是算着算着不知道算完后是鸡还是兔。
三、方程法解:设鸡为x只,则兔为(5-x)只。
2x+4(5-x)=142x+20-4x=14对于这个方程小学生还是比较难解的,所以在设的时候要注意设脚多的动物的脚为X。
解:设兔为x只,则鸡为(5-x)只。
4x+2(5-x)=144x+10-2x=142x=4x=25-2=3(只)答:鸡有3只,兔有2只。
这种解法对于方程学的不好的学生有一定的难度。
综合上述几种方法的教学我发现一部分同学们似懂非懂,于是就总结了许多公式,这时大部分学生们更加蒙圈了,根本不能很好的理解。
此时就引发了我的思考,难道就没有学生理解起来更加容易的方法?于是我就用一下几种方法来给学生们讲解:第一种:猜测法1、排列猜测法1鸡4兔是18条腿,不对。
(完整版)第13讲-鸡兔同笼问题与假设法

第14讲鸡兔同笼问题与假设法知识结构 :一、鸡兔同笼这个问题,是我国古代著名趣题之一.大约在1500年前,《孙子算经》中就记载了这个有趣的问题.书中是这样叙述的:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?这四句话的意思是:有若干只鸡兔同在一个笼子里,从上面数,有个头知道《孙子算经》中是如何解答这个问题的吗?二、解鸡兔同笼的基本步骤解答思路是这样的:假如砍去每只鸡、每只兔一半的脚,则每只鸡就变成了“独脚鸡”,每只兔就变成了“双;从下面数,有只脚.求笼中各有几只鸡和兔?你会解答这个问题吗?你想脚兔”.这样,鸡和兔的脚的总数就由只变成了只;如果笼子里有一只兔子,则脚的总数就比头的总数多.因此,脚的总只数与总头数的差,就是兔子的只数,即(只).显然,鸡的只数就是(只)了.这一思路新颖而奇特,其“砍足法”也令古今中外数学家赞叹不已.除此之外,“鸡兔同笼”问题的经典思路“假设法”.假设法顺口溜:鸡兔同笼很奥妙,用假设法能做到,假设里面全是鸡,算出共有几只脚,和脚总数做比较,做差除二兔找到.解鸡兔同笼问题的基本关系式是:(1)如果假设全是兔,那么则有:鸡数=(每只兔子脚数×鸡兔总数-实际脚数)÷(每只兔子脚数-每只鸡的脚数)兔数=鸡兔总数-鸡数(2)如果假设全是鸡,那么就有:兔数=(实际脚数-每只鸡脚数×鸡兔总数)÷(每只兔子脚数-每只鸡的脚数)鸡数=鸡兔总数-兔数当头数一样时,脚的关系:兔子是鸡的2倍当脚数一样时,头的关系:鸡是兔子的2倍在学习的过程中,注重假设法的运用,渗透假设法的重要性,在以后的专题中,如工程,行程,方程等专题中也都会接触到假设法。
例1 小梅数她家的鸡与兔,数头有16个,数脚有44只。
问:小梅家的鸡与兔各有多少只?分析:假设16只都是鸡,那么就应该有2×16=32(只)脚,但实际上有44只脚,比假设的情况多了44-32=12(只)脚,出现这种情况的原因是把兔当作鸡了。
鸡兔同笼问题练习及讲解

鸡兔同笼问题练习及讲解鸡兔同笼问题是中国古代著名的数学趣题之一,也是小学数学中常见的一类应用题。
它不仅能锻炼我们的逻辑思维能力,还能帮助我们更好地理解数学中的方程和算术方法。
下面我们就来一起深入探讨一下鸡兔同笼问题,并通过一些练习题来巩固我们的知识。
一、鸡兔同笼问题的基本概念鸡兔同笼问题通常是这样描述的:在一个笼子里,有若干只鸡和兔,从上面数有若干个头,从下面数有若干只脚,求鸡和兔各有多少只。
为了方便解决这类问题,我们先假设笼子里都是鸡,那么脚的总数就会比实际的少,少的部分就是因为把兔当成鸡来算,每只兔少算了 2 只脚;反之,如果先假设笼子里都是兔,那么脚的总数就会比实际的多,多的部分就是因为把鸡当成兔来算,每只鸡多算了 2 只脚。
二、解决鸡兔同笼问题的方法1、假设法假设全是鸡,那么兔的只数=(总脚数鸡脚数×总只数)÷(兔脚数鸡脚数);鸡的只数=总只数兔的只数。
假设全是兔,那么鸡的只数=(兔脚数×总只数总脚数)÷(兔脚数鸡脚数);兔的只数=总只数鸡的只数。
2、方程法设鸡的数量为 x,兔的数量为 y。
根据头的总数和脚的总数可以列出两个方程,然后联立求解。
三、练习题例 1:一个笼子里有鸡和兔共 35 只,它们的脚一共有 94 只,请问鸡和兔各有多少只?解法一(假设法):假设全是鸡,那么脚的总数为:35×2 = 70(只)比实际的脚少:94 70 = 24(只)每只兔比每只鸡多的脚数:4 2 = 2(只)兔的只数:24÷2 = 12(只)鸡的只数:35 12 = 23(只)解法二(方程法):设鸡有 x 只,兔有 y 只。
x + y = 35 (头的总数)2x + 4y = 94 (脚的总数)由第一个方程得:x = 35 y将其代入第二个方程:2×(35 y) + 4y = 942y = 24y = 12x = 35 12 = 23例 2:笼子里鸡兔共有 100 个头,248 只脚,鸡兔各有多少只?假设法:假设都是鸡,脚的总数:100×2 = 200(只)脚少的数量:248 200 = 48(只)兔的数量:48÷(4 2) = 24(只)鸡的数量:100 24 = 76(只)方程法:设鸡有 x 只,兔有 y 只。
鸡兔同笼解题方法(范文9篇)

鸡兔同笼解题方法(范文9篇)以下是网友分享的关于鸡兔同笼解题方法的资料9篇,希望对您有所帮助,就爱阅读感谢您的支持。
鸡兔同笼解题方法(1)一.笼子里有若干只鸡和兔,从上面数,有8个头,从下面数,有26只脚。
鸡和兔各有几只?解题方法:1.猜测,列表法2.假设法3.解方程法1.列表法2.假设法假设笼子里全是鸡,则共有2×8=16(只)脚,比实际少了26-16=10(只)脚,因为我们把兔子都看成了鸡,每只兔子少算了2只脚,共少了10只脚,说明兔子应该有10÷2=5(只)同理:假设笼子里的全是兔子,则一共有4×8=32(只)脚,比实际多了32-26=6(只)脚。
把鸡的脚当兔子的脚计算时,每只兔子比鸡多算了2只脚,所以鸡有6÷2=3(只)3.解方程法兔的脚数+鸡的脚数=鸡兔总脚数=26(只)设鸡有x只,那么兔就有8-x只,就有方程:2x+4(8-x)=26;解出x是鸡的只数,再求兔的只数。
鸡兔同笼解题方法(2)鸡兔同笼的解题方法【鸡兔问题公式】(1)已知总头数和总脚数,求鸡、兔各多少:(总脚数-每只鸡的脚数×总头数)÷(每只兔的脚数-每只鸡的脚数)=兔数;总头数-兔数=鸡数.或者是(每只兔脚数×总头数-总脚数)÷(每只兔脚数-每只鸡脚数)=鸡数;总头数-鸡数=兔数.例如,“有鸡、兔共36只,它们共有脚100只,鸡、兔各是多少只?”解一(100-2×36)÷(4-2)=14(只)………兔;36-14=22(只)……………………………鸡.解二(4×36-100)÷(4-2)=22(只)………鸡;36-22=14(只)…………………………兔.(答略)(2)已知总头数和鸡兔脚数的差数,当鸡的总脚数比兔的总脚数多时,可用公式(每只鸡脚数×总头数-脚数之差)÷(每只鸡的脚数+每只兔的脚数)=兔数;总头数-兔数=鸡数或(每只兔脚数×总头数+鸡兔脚数之差)÷(每只鸡的脚数+每只免的脚数)=鸡数;总头数-鸡数=兔数.(例略)(3)已知总数与鸡兔脚数的差数,当兔的总脚数比鸡的总脚数多时,可用公式. (每只鸡的脚数×总头数+鸡兔脚数之差)÷(每只鸡的脚数+每只兔的脚数)=兔数;总头数-兔数=鸡数.或(每只兔的脚数×总头数-鸡兔脚数之差)÷(每只鸡的脚数+每只兔的脚数)=鸡数;总头数-鸡数=兔数.(例略)(4)得失问题(鸡兔问题的推广题)的解法,可以用下面的公式:(1只合格品得分数×产品总数-实得总分数)÷(每只合格品得分数+每只不合格品扣分数)=不合格品数.或者是总产品数-(每只不合格品扣分数×总产品数+实得总分数)÷(每只合格品得分数+每只不合格品扣分数)=不合格品数. 例如,“灯泡厂生产灯泡的工人,按得分的多少给工资.每生产一个合格品记4分,每生产一个不合格品不仅不记分,还要扣除15分.某工人生产了1000只灯泡,共得3525分,问其中有多少个灯泡不合格?”解一(4×1000-3525)÷(4+15)=475÷19=25(个)解二1000-(15×1000+3525)÷(4+15)=1000-18525÷19=1000-975=25(个)(答略)(“得失问题”也称“运玻璃器皿问题”,运到完好无损者每只给运费××元,破损者不仅不给运费,还需要赔成本××元…….它的解法显然可套用上述公式.)(5)鸡兔互换问题(已知总脚数及鸡兔互换后总脚数,求鸡兔各多少的问题),可用下面的公式:〔(两次总脚数之和)÷(每只鸡兔脚数和)+(两次总脚数之差)÷(每只鸡兔脚数之差)〕÷2=鸡数;〔(两次总脚数之和)÷(每只鸡兔脚数之和)-(两次总脚数之差)÷(每只鸡兔脚数之差)〕÷2=兔数.例如,“有一些鸡和兔,共有脚44只,若将鸡数与兔数互换,则共有脚52只.鸡兔各是多少只?”解〔(52+44)÷(4+2)+(52-44)÷(4-2)〕÷2=20÷2=10(只)……………………………鸡〔(52+44)÷(4+2)-(52-44)÷(4-2)〕÷2=12÷2=6(只)…………………………兔(答略)鸡兔同笼解题方法(3)四年级下册鸡兔同笼数学问题解决方案:1、假设法:假设全部都是兔,(每只兔的脚数x头数-原来的总脚数)÷(每只兔的脚数-每只鸡的脚数)=鸡的只数;头数-鸡的只数=兔的只数假设全部都是鸡,(原来的总脚数-每只鸡的脚数x头数)÷(每只兔的脚数-每只鸡的脚数)=兔的只数;头数-兔的只数=鸡的只数例如:鸡兔同笼,头共有20个,脚共有50只,鸡,兔分别有多少只?(4x20-50)÷(4-2)=15(只)……鸡;20-15=5(只)……兔(50-2x20)÷(4-2)=5(只)……兔;20-5=15(只)……鸡2、列方程解:设兔有x只,鸡有20-x只。
小学五年级数学《鸡兔同笼》经典公开课教案(精选10篇)

小学五年级数学《鸡兔同笼》经典公开课教案小学五年级数学《鸡兔同笼》经典公开课教案(精选10篇)作为一名辛苦耕耘的教育工作者,有必要进行细致的教案准备工作,教案有助于学生理解并掌握系统的知识。
那么什么样的教案才是好的呢?下面是小编为大家整理的小学五年级数学《鸡兔同笼》经典公开课教案,希望能够帮助到大家。
小学五年级数学《鸡兔同笼》经典公开课教案篇1【学习目标】1、尝试用不同的方法解决“鸡兔同笼”问题,并体会代数方法的一般性。
2、解决“鸡兔同笼”问题可用猜测、列表、假设或方程解等方法。
3、体会到数学问题在日常生活中的应用。
【学习重难点】1、重点是尝试用不同的方法解决“鸡兔同笼”问题。
2、难点是在解决问题的过程中培养逻辑推理能力。
【学习过程】一、故事引入在我国古代流传着很多有趣的数学问题,“鸡兔同笼”就是其中之一。
这个问题早在1500多年前人们就已经开始探讨了。
阅读书本P112鸡兔同笼的故事,能用你自己的话表述一下题目的意思吗?二、探索新知1、阅读P113例1,根据书本提示,会用列表法求出鸡、兔各几只吗?(完成课本表格。
)2、假设笼子里都是鸡或者都是兔,脚数会发生什么变化呢?能列式解决吗?(会用假设法解决“鸡兔同笼”问题)3、自己动笔,尝试用方程的方法解决鸡兔只数的问题?(有困难的可参考书本P114)4、用假设或者解方程的方法解决P112“鸡兔同笼”问题(1)方程解:(2)算术解:解:设鸡有x只,那么兔就有(35-x)只。
解:假设都是鸡。
根据鸡兔共有94只脚来列方程式2×35=70(只)2x+(35-x)×4=9494-70=24(只)2x=4624÷(4-2)=12(只)x=2335-12=23(只)35-23=12(只)答:鸡有23只,兔有12只。
答:鸡有23只,兔有12只。
5、以上三种解法,哪一种更方便?☆友情小提示:要解决“鸡兔同笼”问题,可以采用假设法或方程解都可以。
数学老师熬夜整理!小学数学鸡兔同笼问题详细解法!

数学老师熬夜整理!小学数学鸡兔同笼问题详细解法!例题:鸡兔共有头10个,腿30个,求鸡和兔的数量?一般人教版的小学数学书中,鸡兔同笼问题是在四年级下半册的广角问题中。
很多孩子,初步接触这个题目的时候一脸懵逼,然后是二脸懵逼,之后便是无休止的抓头发中。
而我们的家长,在看了题目之后,通常会大喊一声“这么简单你都不会!“,然后挥洒汗水,讲解道”假设鸡的数量为X,兔的数量即为10-X,用方程,那么我们可以得出........“”爸爸(妈妈)什么叫方程?X又是什么意思?“孩子睁大无辜的双眼,一脸好奇地问道。
然后极为家长和孩子四目相对,徒呼奈何。
因此,在和家长的交流沟通时。
我们一直会和家长聊,课后自己教孩子时一定要注意不要超纲知识点,最好能看一下教材解法再去教导孩子。
不要超纲,这点很重要。
解法接下来,为大家整理了几种鸡兔同笼问题的解法,之后自己如果遇到这样的问题,可以生动形象地讲解给孩子听:第一种:列举法这个是比较笨,也是在数字比较小比较实用的方法。
如果孩子实在理解不了,也是可以用这样的方法的。
鸡兔共有头10个,腿30个,求鸡和兔的数量?如果鸡有1只,那么兔就是9只,腿就是38只;如果鸡有2只,那么兔就是8只,腿就是36只。
如图,我们即可以得出当鸡为5只,兔为5只的时候,腿的数量为30只。
不过这种方法比较适合的就是数值比较小的时候,否则过于繁琐。
第二种,假设法假设法有2种。
1.假设全部是兔子我们把所有的鸡都假设成兔子,那么显而易见的就是动物都是4条腿,包括那些鸡。
如果全部是兔子,那么腿的数量就为4*10=40只。
可是我们得出实际上是30只脚啊?这是为什么呢?因为我们假设鸡也是兔子,因此鸡的脚由2只变成了4只。
那么一只鸡增加了几只脚呢?增加了2只脚。
每一只鸡增加了2只脚,一共增加了10只脚。
因此,鸡的数量就是10÷2=5只,兔子数量是10-5=52.假设全部是鸡我们假设全部是鸡,那么兔子也变成了鸡,由4只脚变成2只脚,实际减少了10只脚。
小学鸡兔同笼经典讲解与例题

小学鸡兔同笼经典讲解与例题含义】这是古典的算术问题。
已知笼子里鸡、兔共有多少只和多少只脚,求鸡、兔各有多少只的问题,叫做第一鸡兔同笼问题。
已知鸡兔的总数和鸡脚与兔脚的差,求鸡、兔各是多少的问题叫做第二鸡兔同笼问题。
【数量关系】第一鸡兔同笼问题:假设全都是鸡,则有兔数=(实际脚数-2×鸡兔总数)÷(4-2)假设全都是兔,则有鸡数=(4×鸡兔总数-实际脚数)÷(4-2)第二鸡兔同笼问题:假设全都是鸡,则有兔数=(2×鸡兔总数-鸡与兔脚之差)÷(4+2)假设全都是兔,则有鸡数=(4×鸡兔总数+鸡与兔脚之差)÷(4+2)【解题思路和方法】解答此类题目一般都用假设法,可以先假设都是鸡,也可以假设都是兔。
如果先假设都是鸡,然后以兔换鸡;如果先假设都是兔,然后以鸡换兔。
这类问题也叫置换问题。
通过先假设,再置换,使问题得到解决。
例1长毛兔子芦花鸡,鸡兔圈在一笼里。
数数头有三十五,脚数共有九十四。
请你仔细算一算,多少兔子多少鸡?解假设35只全为兔,则鸡数=(4×35-94)÷(4-2)=23(只)兔数=35-23=12(只)也可以先假设35只全为鸡,则兔数=(94-2×35)÷(4-2)=12(只)鸡数=35-12=23(只)答:有鸡23只,有兔12只。
例22亩菠菜要施肥1千克,5亩白菜要施肥3千克,两种菜共16亩,施肥9千克,求白菜有多少亩?解此题实际上是改头换面的“鸡兔同笼”问题。
“每亩菠菜施肥(1÷2)千克”与“每只鸡有两个脚”相对应,“每亩白菜施肥(3÷5)千克”与“每只兔有4只脚”相对应,“16亩”与“鸡兔总数”相对应,“9千克”与“鸡兔总脚数”相对应。
假设16亩全都是菠菜,则有白菜亩数=(9-1÷2×16)÷(3÷5-1÷2)=10(亩)答:白菜地有10亩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学“鸡兔同笼”讲解方法(13种),总有一种适合你!
题目:现有一笼子,里面有鸡和兔子若干只,数一数,共有头14个,腿38条,球鸡和兔子各有多少只?(请用尽量多的方法解答)
『方法一:人见人爱的列表法』
如果二年级小朋友做这道题,可以用列表法!直观、易理解,还不容易出错~好啦,我们来看一下!
根据上面的表格,我们可以看出,鸡为9只,兔子为5只。
我们在列表的时候不要按顺序列,否则做题的速度会很慢,比如说列完鸡为0只,兔子为14只,发现腿的数量56条,和实际38条相差较大,那么下一个你可
以跳过鸡的数量为2只这种情况,直接列鸡的数量为3只,这样做速度会快一些哦!
『方法二:最快乐的画图法』
画图可以让数学变得形象化,而且经常画图还有助于创造力的培养!假设14只全部是鸡,先把鸡给画好。
14×2=28条,差38-28=10条,而每一只鸡补2条腿就变成兔子,需要把5只鸡每只补2条腿,所以有5只兔子,14-5=9只鸡。
『方法三:最酷的金鸡独立法』
分析:让每只鸡都一只脚站立着,每只兔都用两只后脚站立着,那么地上的总脚数只是原来的一半,即19只脚。
鸡的脚数与头数相同,而兔的脚数是兔的头数的2倍,因此从19里减去头数14,剩下来的就是兔的头数19-14=5只,鸡有14-5=9只。
『方法四:最逗的吹哨法』
分析:假设鸡和兔接受过特种部队训练,吹一声哨,它们抬起一只脚,还有38-14=24只腿在站着,再吹一声哨,它们又抬起一只脚,这时鸡都一屁股坐地上了,兔子还有两只脚立着。
这时还有24-14=10只腿在站着,而这10只腿全部是兔子的,所以兔子有10÷2=5只,鸡有14-5=9只。
(惊现跑男中包贝尔的抬脚法有木有!)
『方法五:最常用的假设法』
分析:假设全部是鸡,则有14×2=28条腿,比实际少38-28=10只,一只鸡变成一只兔子腿增加2条,10÷2=5只,所以需要5只鸡变成兔子,即兔子为5只,鸡为14-5=9只。
『方法六:最常用的假设法』
分析:假设全部是兔子,则有14×4=56条腿,比实际多56-38=18只,一只兔子变成一只鸡腿减少2条,18÷2=9只,所以需要9只兔子变成鸡,即鸡为9只,兔子为14-9=5只。
『方法七:最牛的特异功能法』
分析:鸡有2条腿,比兔子少2条腿,这不公平,但是鸡有2只翅膀,兔子却没有。
假设鸡有特级功能,把两只翅膀变成2条腿,那么鸡也有4条腿,此时腿的总数是14×4=56条,但实际上只有38条,为什么呢?因为我们把鸡的翅膀当作腿来算,所以鸡的翅膀有56-38=18只,鸡有18÷2=9只,兔就是14-9=5只。
『方法八:最牛的特异功能法2』
分析:假设每只鸡兔都具有“特异功能”,鸡飞起来,兔立起来,这时立在地上的脚全是兔的,它的脚数就是38-14×2=10条,因此兔的只数有10÷2=5只,进而知道鸡有14-5=9只。
鸡兔具有“特异功能”,这个方法想得太棒了!
『方法九:最牛的特异功能法3』
假设孙悟空变成兔子,说“变”,每只兔子又长出一个头来,然后对妖精说“将它劈开”,变成“一头两脚”的两只“半兔”,半兔与鸡都是两只脚,因而共有28÷2=19只鸡兔,19-14=5只,这就是兔子的数目,当然鸡就有14-5=9只。
呵呵,小朋友把兔“劈开”成“半兔”,想得奇吧!
『方法十:最古老的砍足法』
分析:假如把每只砍掉1只脚、每只兔砍掉2只脚,则每只鸡就变成了“独角鸡”,每只兔就变成了“双脚兔”。
这样,鸡和兔的脚的总数就由38只变成了19只;如果笼子里有一只兔子,则脚的总数就比头的总数多1。
因此,脚的总数19与总头数14的差,就是兔子的只数,即19-14=5(只)。
所以,鸡的只数就是14-5=9(只)了。
呵呵,这个方法是古人想出来的,但有点残忍!
『方法十一:史上最坑的耍兔法』
分析:假如刘老师喊口令:“兔子,耍酷!”此时兔子们都把两只前脚高高抬起,两只后脚着地,呈酷酷的姿态,此时鸡兔都是两只脚着地。
在地上脚的总数是14×2=28只,而原来有38只脚,多出38-28=10只。
为什么
会多呢?因为兔子们把它们的2只前脚抬了起来,所以兔的只数是10÷2=5只,鸡则是14-5=9只。
『方法十二:最万能的方程法』
分析:设鸡的数量为x只,则兔子有(14-x)只,有2x+4(14-x)=38,解出x=9,所以有鸡9只,兔子14-9=5只。
『方法十三:最万能的方程法』
分析:设兔子的数量为x只,则鸡有(14-x)只,有4x+2(14-x)=38.解得x=5,所以兔子有5只,鸡有14-5=9只。
鸡兔同笼的13种方法就给大家讲完了,最后我们来总结一下!
十三种方法
1.列表法
2.画图法
3.金鸡独立法
4.吹哨法
5.假设法
6.假设法
7.特异功能法
8.特异功能法
9.特异功能法
10.砍足法
11.耍兔法
12.方程法
13.方程法。
