5.3.3一阶电路的动态响应 - 一阶电路的动态响应2——【江苏大学电路原理 精】
一阶动态电路的分析

X (t) = X (∞)(1− e τ ), t ≥ 0
X(∞)——稳态值; τ 稳态值; τ——时间常数 X(∞) 稳态值 时间常数 3.非状态量 非状态量: t)和 (t)。 3.非状态量:iC(t)和 uL(t)。 求解方法:先求状态量,再求非状态量。 求解方法:先求状态量,再求非状态量。
−
输入为零) 一、RC 电路的零输入响应 (输入为零)
所示电路, 图(a)所示电路,开关原来在 端,电容电压已 所示电路 开关原来在1端 经达到U 时开关由1端转换到 经达到 0,在t=0时开关由 端转换到 端,如图 时开关由 端转换到2端 如图(b) 求: uC(t);iC(t), t ≥ 0
1. 定性分析
0.368U0
0
t uc(t)
τ
0 U0
2τ 3τ 4τ
τ
0.368U0 2τ
t (s)
3τ 0.050U0 4τ 0.018U0 5τ 0.007U0 ∞ 0
0.135U0
当t=0时,uC(0)=U0,当t=τ时,uC(τ)=0.368U0 时 由于波形衰减很快,实际上只要经过4~5τ的时间 由于波形衰减很快,实际上只要经过 ~ 就可以认为放电过程基本结束。 就可以认为放电过程基本结束。
= RI Se τ ,
− t
t ≥0
三、结论: 1. uC(t)和iL(t) 的零状态响应是从零按指数 t)和 规律上升到它的稳态i t)和 规律上升到它的稳态 L(∞);iC(t)和uL(t) 是按指数规律衰减到零。 是按指数规律衰减到零。 2.状态量 状态量: 初始状态为零对应的变量 初始状态为零对应的变量) 2.状态量:(初始状态为零对应的变量)
在开关闭合瞬间,电容电压不能跃变, 解:在开关闭合瞬间,电容电压不能跃变,得到 将连接电容两端的单口网络等效于一个电阻, 将连接电容两端的单口网络等效于一个电阻,为
一阶电路的零输入响应零状态响应全响应.

零状态响应
全响应
t t uC U 0e RC U (1 e RC ) (t 0) t U (U 0 U )e RC (t 0)
稳态分量
稳态值
初始值
暂态分量
结论: 全响应 = 稳态响应 +暂态响应
第四章 动态电路的时域分析
例1:电路如图,开关S闭合前电路已处于稳态。 t=0时S闭合,试求:t >0时电容电压uC和电流iC、 1 2 i1和i2 2 。 C + 1 解:用三要素法求解 Su+ 6V 3 C 求初始值 uC (0 ) - 5μ F t=0 由t=0-时电路
+
uR -
U e A R
R t L
t0
第四章 动态电路的时域分析
U i L (1 e ) R t R t di L uL L Ue Ue dt R t uR i L R U (1 e L ) uL、 uR变化曲线 2. i L、
R t L
第四章 动态电路的时域分析
(3) 求τ
R3 R4 3 6 R R2 2 4 R3 R4 3 6
RC 4 0.5 2 s
第四章 动态电路的时域分析
(4) 求uC和i。
uC 2 (6 2)e
t 2
2 4e V
t 2
t 2
t 2
第四章 动态电路的时域分析
3.3 一阶电路的零输入响应、 零状态响应和全响应
3.3.1 一阶电路的零输入响应: 一、一阶RC电路的零输入响应
实质:RC电路的放电过程。
第四章 动态电路的时域分析
定性分析:
一阶电路瞬态响应

25
一阶电路的瞬态响应
一阶线性电路的概念
一阶电路的瞬态响应分析 一阶电路的三要素分析法
电工电子学(Ⅰ)
26
一阶线性电路的概念(1)
iL t=0t=0+ 4A 4A iC 0 -6A iR 2A 2A uC 12V 12V uL 0 0
21
电工电子学(Ⅰ)
例4电路如图4所示。求在开关s闭合瞬 间(t=0+)各元件中的电流及其两端电压? 当电路到达稳态时又各等于多少?设在t=0时,电路中的储能元件均未储能。
R1
S (t 0)
例2:如图所示电路,计算开关K闭合后各元 件的电压和各支路电流的初始值。开关闭合前 电容电压为零值。
i R1 i1
解 : 因为 uC(0–)=0, 根 据
t=0 E
iC
R2
uR2
换路定律, uC(0+)=0, 作 出t=0+电路如图所示:
应用克希荷夫定律 列出电路方程如下:
电工电子学(Ⅰ) E
uR1
8
iL 2 (0) 0
L2
iR1
t= 0t= 0+ 0
iR2
0
iL1
iL2
iC1
0
iC2
0
uR2
0
uL1
0
uL2
0
uC1
uC2
0 0
0 0
0 0
0 0
24
1A -1A
1A 1A
2V -8V 8V
8V
电工电子学(Ⅰ)
电路中除元件uC、iL以外的 电容电流、电感电压以及电阻支路 电流、电压,t=0+时刻初始值是可 以突变也可以不突变的,这些电 流、电压的初始值,不能用换路定 则直接求解。
一阶电路的全响应与三要素
§5.4 一阶电路的全响应与三要素在上两节中分别研究了一阶电路的零输入响应和零状态响应,电路要么只有外激励源的作用,要么只存在非零的初始状态,分析过程相对简单。
本节将讨论既有非零初始状态,又有外激励源共同作用的一阶电路的响应,称为一阶电路的全响应。
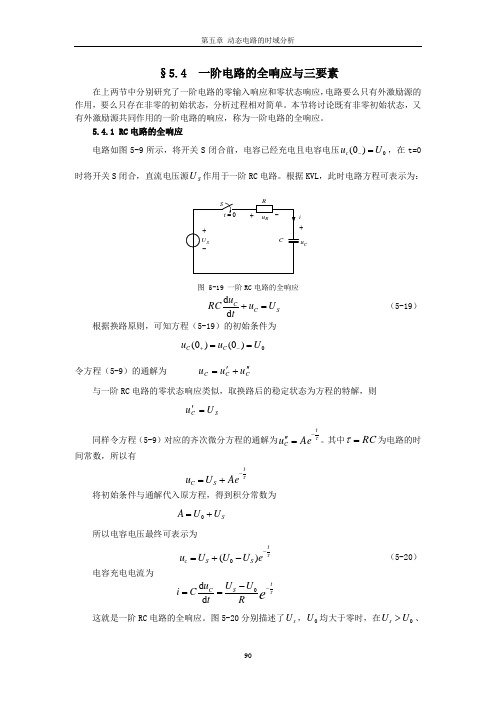
5.4.1 RC 电路的全响应电路如图5-9所示,将开关S 闭合前,电容已经充电且电容电压0)0(U u c =-,在t=0时将开关S 闭合,直流电压源S U 作用于一阶RC 电路。
根据KVL ,此时电路方程可表示为:C u图 5-19 一阶RC 电路的全响应S C CU u tu RC=+d d (5-19) 根据换路原则,可知方程(5-19)的初始条件为 0)0()0(U u u C C ==-+令方程(5-9)的通解为 C CC u u u ''+'= 与一阶RC 电路的零状态响应类似,取换路后的稳定状态为方程的特解,则S CU u =' 同样令方程(5-9)对应的齐次微分方程的通解为τtCAe u -=''。
其中RC =τ为电路的时间常数,所以有τtS C AeU u -+=将初始条件与通解代入原方程,得到积分常数为 S U U A +=0所以电容电压最终可表示为τtS S c e U U U u --+=)(0 (5-20)电容充电电流为etS C R U U t u C i τ--==0d d这就是一阶RC 电路的全响应。
图5-20分别描述了s U ,0U 均大于零时,在0U U s >、0=s U 、0U U s <三种情况下c u 与i 的波形。
(a) (b)图5-20C u ,i 的波形图将式(5-20)重新调整后,得)1(0ττtS tC e U eU u ---+=从上式可以看出,右端第一项正是电路的零输入响应,第二项则是电路的零状态响应。
显然,RC 电路的全响应是零输入响应与零状态响应的叠加,即 全响应 = 零输入响应 + 零状态响应研究表明,线性电路的叠加定理不仅适用于RC 电路,在RC 电路的分析过程中同样适用,同时,对于n 阶电路也可应用叠加定理进行分析。
一阶电路

C
t = 0+时刻
1 t uC (0 ) i ( )d C 0 0 1 0 uC (0 ) uC (0 ) i ( )d C 0
1 C
1 i( )d C
t 0
i ( )d
当i()为有限值时
uC (0+) = uC (0-) q (0+) = q (0-)
例
电阻电路
i (t=0)
i U S / R2
+
i
R1 R2 0
i U S ( R1 R2 )
us
-
t
过渡期为零
电容电路
(t = 0) Us
K
K未动作前,电路处于稳定状态
i
R
+
i = 0 , uC = 0
C K接通电源后很长时间,电容充电 完毕,电路达到新的稳定状态
uC
–
(t →) R + Us
例3
求 iC(0+) , uL(0+) L i
L
解
iC +
由0-电路得:
+u – IS
LLeabharlann RK(t=0)C
uC
–
IS
R
0-电路
0+电路 I S +u –
L
iL(0+) = iL(0-) = IS
iC + R IS –
uC(0+) = uC(0-) = RIS
由0+电路得:
R
RI S iC (0 ) I s 0 R
100 K
100
200V
200 i L (0 ) i L (0 ) 1A 200 100 uC (0 ) uC (0 ) 100V
一阶电路的全响应和三要素方法 ppt课件

故又有 :
全响应=零状态响应+零输入响应
2020/12/12
2
精品资料
你怎么称呼老师?
如果老师最后没有总结一节课的重点的难点,你 是否会认为老师的教学方法需要改进? 你所经历的课堂,是讲座式还是讨论式? 教师的教鞭
“不怕太阳晒,也不怕那风雨狂,只怕先生骂我 笨,没有学问无颜见爹娘 ……” “太阳当空照,花儿对我笑,小鸟说早早早……”
(暂态响应)
(稳态响应)
2020/12/12
13
5.一阶电路的三要素法
一阶电路的响应f(t),由初始值f(0+)、稳态值f(∞)和时间常数τ三 要素所确定,利用三要素公式可以简便地求解一阶电路在直流电 源作用下的电路响应。全响应表达式为:
f(t)f( ) [f( 0 ) f( )e] t
计算响应变量的初始值f(0+)和稳态值f(∞),分别用t=0+时的电路 和t=∞时的电路解出。作t=0+时的电路,将uC(0+)和iL(0+)分别视为电 压源和电流源。作t=∞时的电路,电容相当于开路、电感相当于短 路。时间常数τ中的电阻R,是动态元件两端电路的戴维南等效电路 电阻。
全响应=稳态分量+暂态分量
2020/12/12
1
下图给出了U>U0时,uC随时间变化的曲线。
uC 稳态分量
U
uCU[U0U]e-t
U0
全响应
上式的全响应还可以写成:
0 U0-U
暂态分量
t
uCUs(1et)U0et
t
上式中 Us(1 e ) 是电容初始值电压为零时的零状态
响应,
t
U 0e
是电容初始值电压为U0时的零输入响应。
一阶电路的全响应
一阶电路的全响应一阶电路的全响应一.全响应全响应一阶电路在外加激励和动态元件的初始状态共同作用时产生的响应,称为一阶电路的全响应(complete response)。
图5. 5-1 (a)所示的一阶RC电路,直流电压源Us是外加激励•时开关S处于断开状态.电容的初始电压叫2°时开关闭合.现讨论f上°时电路响应的变化规律。
2 °4时,响应的初始值为叫(―)二%时,响应的稳态值为叫(8)=°$1(8)= 0川亞丿川宦理计算全响应:开关闭合后,电容电压叫⑦的全响应•等于初始状态U0取独作用时产生的零输入响应叫购和电I W ' I'JU'r Hj时产生的零状态响应叫11⑦的代如II,如图5・5・1 (b) . (c)所示。
图5. 5-1 (b)中,零输入响应为= = (ao)图5. 5-1 (c)中.零状态响应为du''(f)dt(CO)1、、厂(°+)1(8)时川初始值大于稳态值.2、屮®J'%00)时川初始值小于稳态值. 则全响应由初始值开始按抬数规律逐渐増加到稳态值,这是电路对动8、当® Jr (8)时.电路换路后无过渡过程,直接进入稳态.动态根据叠加定理•图5. 5-1 (a)电路的全响应为◎(f) = Q(f) + 冬"(f)=弘五4■兀Q 一<码t i=,十(九一匚)「冠=十血Oh) - (C 0皿=1/(0 +y® =-譽尸+牛二=1(8)+哄4)-「(8护用‘①表示全响应,农示响应的初始值,心校示稳态值。
—阶电路全响应非零初始状态的一阶动态电路,包括RC电路和RL电路,在外加激励的作用下,电路中任何一条支路上的全响应为啲=r(0 十)E T+ F(CD)(1 - g『)全响应的变化规律则全响应由初始值开始按抬数规律逐渐衰减到稳态值,这是动态元件C或L对电路放电。
第章一阶动态电路分析共106页文档
T
uo
T1
E
t (a)
uC1 2E /3
E/3
t
0
t1 t2
t3
(b)
5)试验电容C1对输出信号周期的影响
将电容器C1由10 μF替换为20μF,再次测试步骤3)与4) 中测试到的波形,并记录周期T与脉冲宽度T1。在这一步骤 中我们可以发现,波形的形状基本没有改变,但波形的周期 与脉冲宽度却变大了。
电流流过电感时,在电感元件中储存有磁场能,Em
1 2
LiL2
。
当换路时,电感中储存的磁场能不能跃变,反映在电路中是
电感元件的电流iL不能跃变。
电容两端电压不能突变,流过电感的电流不能突变,是
分析过渡过程的重要定则。
2. RC电路产生过渡过程的起因
上述电路中产生暂态的起因,是电路中的开关动作。实际 上, 只要电路条件发生突然变更,诸如开关动作、电路故障、 电路参数变化及改变电源等,都会引起电路发生过渡过程。 因此我们把产生过渡过程的起因称为换路, 把出现暂态过程的 瞬间称为初始瞬间,此刻电路的状态就是初始状态,例如电 容电压的初始状态为uC(0),电感电流的初始状态为iL(0), 从电路方程来看,这就是初始条件。
从上述实验中可见:在RC放电过程中, 电容电压从某一电 压值, 即某一稳态值开始逐渐衰减,最后变为零, 达到另一 稳态值。 两个稳态值中间的变化过程就是电路的过渡过程,当 改变电容电压的初始值、电容值及电阻值时,电容的放电情况 会发生改变。在分析RC放电过程时,我们要从理论上解决上面 实验中反映的如下问题:
电路课件-一阶电路的全响应
uC (0 ) 4 2 8V
由於開關轉換時,電容電流有界,電容
電壓不能躍變,故
uC (0 ) uC (0 ) 8V
畫0+圖如右2A
4
2 i(0+)
+
+
8V 4
-
10V
-
i(0 ) 10 uC (0 ) 10 8 1A
-
iC (t)
US R1
1
e R1C
t
A
0 t R1C
1t
uC (t) US (1 e R1C ) 0 t R1C
uC (R1C ) US (1 e1)
t=R1C 時 , 第 二 次換路, 由換路 定則得:
R2
R1
iC(R1C +)
+ US(1-e-1)
-
uC (R1C ) uC (R1C ) US (1 e1)
2A
4
2 i(t)
+
+
uC 4 10V
-
-
Ro 4 // 4 // 2 1
時間常數為 τ RoC 1 0.1 0.1s
4,將初始值、終值及時間常數代 入三要素公式,得到回應運算式:
uC(t) 7 (8 7)e10t 7 1e10tV (t 0)
i(t) 1.5 (1 1.5)e10t 1.5 0.5e10t A (t 0)
(t 0)
全响应 瞬态响应 稳态响应
上式可改寫為
t
t
uC (t) U0e US (1 e ) (t 0)
全响应=零输入响应+零状态响应
也就是說電路的完全回應等於零輸入 回應與零狀態回應之和。這是線性動 態電路的一個基本性質,是回應可以 疊加的一種體現。
一阶电路的全响应.
t RC
US
t
uC (t) (U0 US )e US 全响应 固有响应 强制响应
(t 0)
全响应 瞬态响应 稳态响应
上式可改写为
t
t
uC (t) U0e US (1 e ) (t 0)
全响应=零输入响应+零状态响应
也就是说电路的完全响应等于零输入 响应与零状态响应之和。这是线性动 态电路的一个基本性质,是响应可以 叠加的一种体现。
r(t)
w(t)
(t 0)
r(0 )
r(0+)表示电容电压的初始值uC(0+)或电 感电流的初始值iL(0+); =RC 或 =GL=L/R;w(t)表示电压源的电压uS或
电流源的电流is。其通解为
t
r(t ) rh (t ) rp (t ) Ae rp (t )
r(t)
r()
[r(0
)
r()]e
t
,
t
0
r(0+) ——响应的初始值 三要素:
r() ——响应的终值,
——时间常数=RC, =L/R
r(t) 三要素公式的 r(t)
r() r(0+)
响应波形曲线
r(0+)
r()>r(0+)
r()
r()<r(0+)
t
t
可见,直流激励下一阶电路中任一响应
r
()
[rzs
(0
)
1
r()]e
t
如求全响应iC (t)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i(t)
=
-
U0
-
e
t
R
3、RL电路的零输入响应
R1
Ri
求电感电压uL(t)和电流i(t)
解: uL(t- ) = 0
+
US
u S(t=0)
L
L
–
i(0- ) =
US R1 + R
I0
i(0+ )
=
i(0- )
=
US R1 +
R
=
I0
电路方程:
L di + Ri = 0 dt
t 0+
一阶微分方程的通解:
uR = Ri
i = C duC dt
+ U0
-
S(t = 0)
R i (t)
2
+ uR -
1
C
+ uC(t)
-
uC (0-) = U0 i (0-) = 0
t≥0+ uR + uC = 0
uR = Ri
i = C duC dt
一阶齐次微分方程,其通解为:
RC
duC dt
+
uC
=
0
uC (0+ ) = U0
uC = Ae pt
特征根p:
特征方程:
RCp+1=0
p=- 1 RC
uC
=
Ae pt
=
- 1t
Ae RC
(t≥0+)
系数A由初始状态确定:uC (0+) =U0
将初始值代入:
- 1t
uC = Ae RC
A=uC(0+)=U0
uC = Ae pt
-1t
= U0e RC (t 0+ )
U0 uC
i(t ) = Ae pt
特征方程: Lp+R=0
特征根 p =
-Rt
i(t ) = Ae L
-R L
R1 US
R S(t=0)
i
+
u LL–来自i(0+)=
i(0- )
=
US R1 +
R
=
I0
uL(t- ) = 0
一阶微分方程的通解:
i(t) =
Ae pt
=
-Rt
Ae L
由初始值i(0+)= I0确定积分常数A
=
2
故电路的时间常数为:
= L = 2 s = 1s
Req 2
-t
y(t ) = y(0+ )e τ
得零输入响应为:
iL(0+ ) = 3A
i1(0+ ) = -1A i2 (0+ ) = -2A
-t
iL (t ) = iL (0+ )e τ
= 3e-t A
-t
i1 (t ) = i1 (0+ )e τ
电路的 能量来源
外施激励(即独立电源)
储能元件(C、L)储存
iL(0+)
uC(0+)
激励输入为零,仅由动态元件的初始储能(uC或 iL)引起的电路响应
动态元件的初始储能(uC或iL)为零,仅激励输入 由引起的电路响应
由激励输入、动态元件的初始储能(uC或iL)共 同引起的电路响应
——输入 ——状态
零输入响应 零状态响应
2、RC电路的零状态响应
+ US
-
S(t = 0)
R iC(t)
2
+ uR -
1
C
+ uC(t)
-
t<0时,开关S在位置1,处于稳态 ,即:uC (0-)=0(状态为0)
t = 0时,开关S打向位置2,引入 激励(输入) US, 列方程:
t
i(t) = C
duC dt
=
- U0 R
-1t
e RC (t
0+ )
0 0 i(t)
若令:τ =RC
t
(τ称为一阶RC电路的时间常数)。
-U0/R
则RC一阶电路的零输入响应可写为:
+ U0
-
S(t = 0)
R i (t)
2
+ uR -
1
C
+ uC(t)
-
-t
uC (t ) = U0e (t≥0+)
(2)同一电路中所有响应具有相同的时间常数τ 。 (3)一阶电路的零输入响应和初始值(状态)成正比,称为零输入线性。
例1. 如图a)所示电路,已知Us=6V, Rs=2, R1=6, R2=1, R3=2 , L=2H,t<0时电路已经处于稳态,t=0时开关打开。求t>0+时的 i i i L(t) 、 1(t) 和 2(t) 。
=
R2 + R3 R1 + R2 + R3
3A
=
-1A
L
R3 i2 (0+ ) = -i1(0+ ) - iL (0+ ) = -2A
3A
换路后,从L看进去的戴维南等效电阻
图b)
为:
Req
=
R1
//( R2
+
R3 ) =
R1( R2 + R3 ) R1 + R2 + R3
=
6(1 + 2) 6+1+ 2
i(0+ ) = Ae p0+ = A =I0
i(t) =
Ae pt
=
-Rt
I0e L
t 0+
R1 US
R S(t=0)
i
+
u L
L
–
i I0
0
t
-Rt
-t
i(t) = I0e L = I0e L/R (t 0+ )
uL
uL (t )
=
L
di dt
=
-t
-RI0e L/R
(t 0+)
-RI0
Rs
+ us -
i1 R1
R2 i2
iL
L
R3
图a)
解: t<0时电路已经处于稳态,L可以看作短路,则有:
iL(0- ) =
US RS
=
6 A = 3A 2
由换路定律得
iL(0+ ) = iL(0- ) = 3A
画出0+时刻的等效电路,如图b),可解得:
i1(0+ ) R1
R2 i2 (0+ )
i1(0+ )
= -e-t A
-t
i2 (t ) = i2 (0+ )e τ
= -2e-t A
注意:其他支路电流还可以这样求取:
若已经求得电感电流:
R2 i2 (t)
-t
iL (t ) = iL (0+ )e τ
= 3e-t A
i1 (t )
R1
L
iL (t)
换路后电路为:
R3
由替代定理,可得:
i1 (t ) R1
全响应
一、一阶电路的零输入响应
1、零输入响应:动态电路没有外施电源激励,仅由动态 元件的初始储能(电容电压值uC或电感电流 值iL )引起的电路响应。
2、RC电路零输入响应
图示电路,求 uC(t)和 i(t)。
解: 由图可知,
uC (0+) = uC (0-) = U0
t≥0+ uR + uC = 0
t
令τ = L/R , 称为一阶RL电路时间常数
[
]
=
[
L R
]
=
亨 [欧
]
=
[
韦 安欧
]
=
[
伏 安
秒 欧
]
=
[秒]
4、一阶电路零输入响应解的一般公式
一阶电路的零输入响应是由储能元件的初始值(状
态)引起的响应,它们都是由初始值衰减为零的指数衰
减函数。
-t
y(t ) = y(0+ )e τ
(1) τ体现了一阶电路的固有特性,衰减快慢取决于时间常数τ。RC电路τ = ReqC , RL电路τ = L/Req。 (Req为换路后从C或L两端看进去的戴维南等效电阻)
R2 i2 (t)
L
R3
iL (t)
i1(t )
=
-
R + R R1 + R2 + R3
i(t )
=
-e-t A
i2 (t )
=
-
R1
+
R R2
+
R3
i(t)
=
-2e-t A
二、一阶电路的零状态响应
1、零状态响应:电路在储能元件零初始条件下(电容电压 值uC和电感电流值iL为零),而由外施激励引 起的电路响应。
